Line Active Hybrid Lipids Determine Domain Size in Phase Separation of Saturated and Unsaturated Lipids

Abstract

A simple model of the line activity of a hybrid lipid (e.g., POPC) with one fully saturated chain and one partially unsaturated chain demonstrates that these lipids preferentially pack at curved interfaces between phase-separated saturated and unsaturated domains. We predict that the domain sizes typically range from tens to hundreds of nm, depending on molecular interactions and parameters such as molecular volume and area per headgroup in the bulk fluid phase. The role of cholesterol is taken into account by an effective change in the headgroup areas and the domain sizes are predicted to increase with cholesterol concentration.

Main Text

The lipid-raft hypothesis suggests that nanoscopic compositional inhomogeneities play an important role in a range of cellular function (1). Studies of lipid mixtures in vitro probe the thermodynamics and chemistry behind phase separation in model systems of saturated lipids such as DPPC, unsaturated lipids such as DOPC, and cholesterol. However, the domains in these studies typically coarsen with time and do not show the same nanoscopic finite sizes associated with lipid rafts in vivo (2). To be useful, these small domains must persist on biologically relevant timescales (3). This motivates consideration of an equilibrium state with finite domains in cells (but not in the simple, three-component model systems), which may include additional line-active components such as proteins (1,4) or another lipid species (5) that could stabilize finite-size domains. In a previous phenomenological thermodynamic model, we suggested that a lipid with one fully saturated hydrocarbon chain and one partially unsaturated chain, termed a hybrid lipid (5), could be line active at saturated/unsaturated interfaces. For strong interaction strengths, it may eliminate the line tension (note that small but nonzero line tensions (∼0.1 pN) may also allow small domains to become kinetically trapped (6)) between liquid-ordered and disordered domains so that finite-sized domains are thermodynamically stable. However, this treatment did not predict the domain size, nor did it relate the line activity to the molecular features of the hybrid lipid. Here we consider a molecular model of such line-active lipids and predict the equilibrium domain size as a function of the molecular geometry and cholesterol concentration.

We use packing arguments to predict the expected size of a domain stabilized by a line of hybrid lipid that saturates the interface in a one-dimensional analog of surfactants at an oil/water interface (7–9). The hybrid lipid chains are treated as incompressible, and must conserve their individual molecular volumes while minimizing the energetic costs of chain length mismatch with the surrounding bulk phases as well as the mismatch between the two different chains of the hybrid lipid themselves. The result is an effective spontaneous curvature for a hybrid lipid that depends on the asymmetry in molecular volumes (which depends on chain lengths and number of cis double bonds in the unsaturated chains) and the asymmetry in the area per headgroup of the two lipid chain types (which can be regulated by the cholesterol concentration). For a typical hybrid lipid, such as POPC, the predicted domain has positive curvature (with the saturated lipid on the inside) with a domain size of 20–200 nm, depending on the mismatch interactions and the cholesterol concentration. However, a wide variety of structures can be obtained by altering the chain properties, including domains with negative curvature (unsaturated domains in a bulk-saturated phase).

Our model focuses on the case of strong interactions (relative to k_BT), in which the phase separation of the saturated (s) and unsaturated (u) lipids is fairly complete and the interface thickness is monomolecular. In this regime (see the Supporting Material and (5)), hybrid lipid (h) saturates the interface between bulk (s) and (u) phases in a lipid mixture of saturated/unsaturated/cholesterol with a small concentration of hybrid. For simplicity, the (s) lipid has two fully saturated chains that are identical to the saturated chain of the hybrid and the (u) lipid has two partially unsaturated chains identical to the unsaturated chain of the hybrid. Generally, one expects a chain mismatch (10) free energy between the saturated chain of (h) and its (s) neighbors (see Fig. 1) and the unsaturated chain of (h) and its (u) neighbors. This energy arises due the height mismatch at the headgroups, which results in increased hydrophobic exposure of the chains within the bilayer (11). In addition, the two chains of (h) may also mismatch with a resulting free energy cost due to the tilt of the hybrid head. Fig. 1 a shows an example of hydrophobic mismatch between the hybrid chains and the bulk phases as well as between the individual hybrid chains. The mismatch free energy is the portion of the total free energy that dictates the response of the interface to bending (see the Supporting Material). The free energy associated with bending is simply due to the volumetric constraints of the hybrid lipids packing at the interface,

$$f_{\mathrm{i}}=k_{\mathrm{s}}{\left(L_{\mathrm{s}}-L_{\mathrm{s}}^0\right)}^2+k_{\mathrm{u}}{\left(L_{\mathrm{u}}-L_{\mathrm{u}}^0\right)}^2+\gamma {\left(L_{\mathrm{u}}-L_{\mathrm{s}}\right)}^2,$$ (1)

where L_s(u) is the length of the saturated (unsaturated) chain of the hybrid and $L_{\mathrm{s}\left(\mathrm{u}\right)}^0$ is the length of the equilibrium saturated (unsaturated) chain in the bulk (half of the hydrophobic width of the bilayer). The parameters k_s, k_u, and γ are the free energetic costs of mismatch between the equilibrium (s) and (u) phases and the hybrid at the interface and the mismatch between the two chains of the hybrid, respectively. We will set k_s = k_u = k; however, this can easily be generalized. In calculating the equilibrium domain size, only the ratio of γ and k enters and for many hybrid lipids, the variation in domain size is small over the entire range of γ/k. The effect of cholesterol in the bilayer will be considered below.

Figure 1.

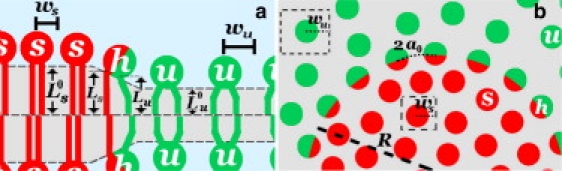
(a) Schematic showing the lipid thickness mismatch (exaggerated for demonstrative purposes) for the case where the bilayer thickness is different in the saturated (s) and unsaturated (u) domains. The hybrid (h) at the interface is mismatched (10) with the chains of the (s) domain on the left and the (u) domains on the right; in addition, the two chains of the hybrid are length-mismatched. (b) Similar schematic looking down on the bilayer. In this case, the domain curvature, H, is positive and the finite-sized domain contains the (s) phase.

The equilibrium domain size is determined by a competition of the mismatch free energies and the packing constraints that must conserve the volume per lipid chain (assumed to be incompressible). The length of the hybrid chains at the interface with curvature H = 1/R are L_s and L_u, respectively (see Fig. 1 a). These are determined from the conservation condition applied to a curved interface,

$$V_{\text{s}}=L_{\text{s}}{a}_0{w}_{\text{s}}\left(1-\frac{w_{\text{s}}H}{2}\right);V_{\text{u}}=L_{\text{u}}{a}_0{w}_{\text{u}}\left(1+\frac{w_{\text{u}}H}{2}\right),$$ (2)

where V_s(u) is the molecular volume of the saturated (unsaturated) chain, w_s(u) is the length that characterizes molecular spacing of the saturated (unsaturated) lipid heads, and a₀ is the headgroup spacing of the hybrids along the interface (which we will assume is the average of the spacing in the two bulk phases, a₀ = (w_s + w_u)/2). The curvature, H, is defined as positive when the domain includes the saturated phase and negative when the domain includes the unsaturated phase. The chain length in the equilibrium bulk phases (consisting of (u) or (s)), L_s(u), is simply the molecular volume divided by the headgroup area in the bulk phase, ${\mathit{L}}_{\text{s}\left(\text{u}\right)}^0\mathit{=}{\mathit{V}}_{\text{s}\left(\text{u}\right)}/{\mathit{w}}_{\text{s}\left(\text{u}\right)}^2$.

We now calculate the spontaneous curvature, H = H₀, of the hybrid at the (s)/(u) interface that minimizes the free energy of Eq. 1. The molecular quantities can be rewritten in terms of the average and difference in the molecular volumes, V_T = (V_u + V_s)/2 and V_d = V_u – V_s, as well as in the length per headgroup, w_T = (w_u + w_s)/2 = a₀ and w_d = w_u – w_s. Expanding the spontaneous curvature to linear order in the differences V_d and w_d gives

$$H_0=\frac{1}{w_{\text{T}}}\left(\frac{\left(1-2\mathit{\beta }\right)w_{\text{d}}}{\left(1+2\mathit{\beta }\right)w_{\text{T}}}+\frac{2\mathit{\beta }{V}_{\text{d}}}{\left(1+2\mathit{\beta }\right)V_{\text{T}}}\right),$$ (3)

where β = γ/k. When H₀ > 0, domains are those typically associated with lipid rafts of (s) surrounded by a continuum of (u). However, when the packing and interaction parameters are such that H₀ < 0, the domains will be composed of the liquid-disordered (u) phase rich in unsaturated lipids.

Using experimentally measured parameters such as the area per headgroup of the (s) and (u) phases as well as the molecular volume of each type of lipid, we can provide some estimates of the expected curvature of domains stabilized by a curved line of hybrid lipids at a (s)/(u) interface. We take molecular volumes of V_u = 985 ų and V_s = 896 ų for the unsaturated and saturated lipid chains (representative of DOPC and DPPC). The area per headgroup for these lipids in the bulk phases are A_u = 72 Ų and A_s = 64 Ų for DOPC and DPPC (12). The linear dimension of one chain is

$$w_{\text{s}\left(\text{u}\right)}=\sqrt{\left(A_{\text{s}\left(\text{u}\right)}/2\right)}\text{.}$$

Note that these values are for pure DOPC and DPPC bilayers, respectively. Fig. 2 a shows the expected domain size for this hybrid mixture for a large range of the parameter β = γ/k. The limit that β → 0 corresponds to negligible interactions between the two chains of the hybrid lipid; the (s) and (u) branches of the hybrid each minimize their free energy by matching the chain length of the bulk (s) and (u) phases, respectively. In this case, Eq. 3 is simply H₀(β = 0) = w_d/w²_T; the spontaneous curvature is dictated entirely by the difference in the area per headgroup of the (s) and (u) branches of the hybrid. For instance, in the case of POPC where the unsaturated chain has a larger area per headgroup (A_u > A_s), the area per headgroup of the (s) chain is larger on the hybrid than that of the (s) lipids in the bulk (a₀ > w_s) and the opposite is true for the (u) chain (a₀ < w_u). To maintain their optimal bulk chain lengths $\left({\mathit{L}}_{\text{s}\left(\text{u}\right)}^0\right)$ while conserving volume, the interface curves toward the component with a smaller area per headgroup. For POPC, this sets a lower limit for the domain size of POPC at 10 nm. The upper limit for the domain size of POPC corresponds to β → ∞, where H₀(β = ∞) = (V_d/V_T – w_d/w_T)/w_T, which is ∼16 nm for POPC. In this limit of k = 0, the curvature is dictated by the two branches of the hybrid minimizing the difference in their lengths while maintaining volume conservation. In the case of SOPC in DSPC/DOPC mixtures (dashed line in Fig. 2 a inset), when β is small, the situation is the same as for POPC; the area per headgroup for DSPC is approximately the same as for DPPC (14). Once again, the hybrid chains attempt to match their lengths to that of the (s) and (u) bulk phases and the curvature is positive. However, when β becomes large, the two chains of the hybrid prefer to be the same length. Therefore, the (s) chain, whose volume (504 ų per chain) is larger than that of the (u) chain, has a larger cross-sectional area—causing the interface to bend away from the (s) phase. This predicts the finite-sized domain of unsaturated lipid (H < 0) for large enough β. The point at which this crossover happens is β^c = (1/2)(1 – (w_T/w_d)(V_d/V_T))⁻¹. Hybrids where (w_TV_d/w_dV_T) > 1 do not have such a crossover, and the sign of the curvature is independent of β.

Figure 2.

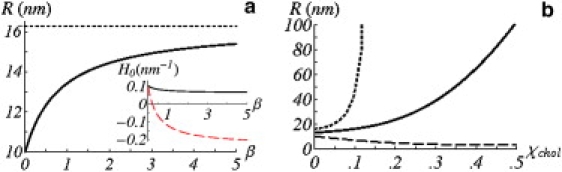
(a) Domain radius in nanometers versus β for a lipid mixture of DOPC (u) and DPPC (s) with POPC hybrid stabilizing the interface between the (s)-rich and (u)-rich phases. The black dotted line is the limit for β → ∞. (Inset) The spontaneous curvature (H = 1/R) for DOPC/DPPC mixtures with POPC as the hybrid (black solid) and DSPC/DOPC mixtures with SOPC as the hybrid (red dashed). (b) Predicted domain radius in nanometers for the same system as in panel a, but where the DPPC rich (s) phase is condensed by cholesterol whose mole fraction is denoted by χ_chol. Data for the condensing effect are taken from Edholm and Nagle (13). The parameter β = 1 for the thick solid line, whereas the dashed (β = 0) and dotted (β = ∞) lines show the other two extremes for β.

The values for the area per headgroup are also sensitive to the cholesterol concentration. We model the condensing effect of cholesterol by modifying values of the area per headgroup of the various bulk phase lipids. Because cholesterol alters the bulk-phase headgroup spacing, it changes the spontaneous curvature. We examine, again, the case of POPC as a hybrid for a system of DOPC/DPPC/chol. Although the condensing effect has been studied for DOPC/chol (15) and DPPC/chol (13) binary systems, we do not know how the cholesterol partitions within the DOPC/DPPC/chol system. To get a simple upper bound for this effect, we assume that the cholesterol partitions completely in the saturated phase. In vitro studies do show that cholesterol has a strong preference for the liquid-ordered phase (16,17). Therefore, we assume that only w_s is modified as cholesterol is added. However, this method is also generalizable to complex functions of cholesterol distribution between phases. The predicted domain radius versus mole fraction of cholesterol in the saturated phase, χ_chol, is calculated in Fig. 2 b using data for the condensing effect of cholesterol on w_s (13). When β = 1, the spontaneous curvature is given by H₀ = (2V_d/3V_T – w_d/3w_T)/w_T; the effect of the cholesterol is to decrease the average size per headgroup, w_T, while increasing the difference between the two lipids, w_d, but leaving the volumes V_s, V_u unchanged. Larger values of β simply make the domain size increase more strongly as a function of χ_chol; however, when β < ½, the domain size actually shrinks as the saturated phase condenses. In the extreme case that β = 0, the domain size shrinks to ∼3 nm when χ_chol = 0.5. These two limits of β are shown in Fig. 2 b.