Interpreting Membrane Scattering Experiments at the Mesoscale: The Contribution of Dissipation within the Bilayer

Abstract

Neutron spin-echo spectroscopy provides a means to study membrane undulation dynamics over length scales roughly spanning 10–100 nanometers. Modern interpretation of these measurements relies on the theoretical predictions of Zilman and Granek; however, it is necessary to introduce an anomalously large solvent viscosity within this theory to obtain quantitative agreement with experiment. An extended theoretical treatment is presented that includes the effects of internal dissipation within the bilayer. Within the length and time regimes appropriate to neutron spin-echo experiments, the results of Zilman and Granek are largely recovered, except that the bilayer curvature modulus κ appearing in their theory must be replaced with an effective dynamic curvature modulus $\tilde{\kappa }=\kappa +2d^2{k}_{\text{m}}$, where d is a distance comparable to the monolayer thickness (the height of the neutral surface from bilayer midplane) and $k_{\mathrm{m}}$ is the monolayer compressibility modulus. Direct comparison between theory and experiment becomes possible without any rescaling of physical parameters.

Neutron spin-echo spectroscopy (NSE) is one of few techniques well suited to the study of membrane dynamics at the mesoscale, both in terms of spatial and time resolution. An inelastic scattering technique, NSE directly measures the dynamic structure factor S(k, t) for condensed phase samples, which is both easily related to detailed real-space dynamics and provides a convenient observable for comparison to theory. Given the unique ability of NSE to directly probe membranes over an especially pertinent biophysical regime, it is critical to resolve all discrepancies between theory and NSE measurements.

Zilman and Granek (1,2) have derived theoretical expressions for S(k, t), commonly used to interpret NSE experiments on single-component fluid-phase lipid bilayers (3–12). The membrane is treated as a thin structureless Helfrich (13) sheet that resists bending and is surrounded by a viscous fluid. It is assumed that the experimental sample is prepared such that there exist nearly flat and independent L × L patches of the membrane exceeding NSE length scales (∼100 nm). The shape of a given patch is described by the height from a reference x, y plane and may be written as a Fourier series with period L,

$$h\left(\mathbf{r}\right)=h\left(x,y\right)=L^{-1}{\Sigma }_{\mathbf{q}}{e}^{i\mathbf{q}·\mathbf{r}}{h}_q.$$

The dynamics of such a membrane are well known within the context of linear response (14–16) and are conveniently summarized in terms of the autocorrelation functions for the independent Fourier modes

$$\langle h_q\left(t\right)h_{-q}\left(0\right)\rangle =\frac{k_{\text{B}}T}{\kappa q^4}\text{Exp}\left(\frac{-\kappa q^3}{4\eta }t\right),$$ (1)

where k_B is the Boltzmann constant, T is temperature, κ is the bilayer curvature modulus, and η is the viscosity of the solvent. All dissipation within this model results from viscous losses in the surrounding solvent. Equation 1 can be shown to imply (1,2)

$$S\left(k\mathrm{,}\mathit{t}\right)/S\left(k,0\right)\simeq \text{Exp}{\left(-{\Gamma }_k\mathit{t}\right)}^{2/3},$$ (2)

with relaxation rates provided by

$${\Gamma }_k=0.025\left\{\begin{array}{c}1\\ {\mathrm{\gamma }}_k\end{array}\right\}{\left(\frac{k_{\text{B}}T}{\mathit{\kappa }}\right)}^{1/2}\frac{k_{\text{B}}T}{\mathit{\eta }}\left\{\begin{array}{c}{k}_z^3\\ k^3\end{array}\right\}.$$ (3)

The two results correspond to different experimental conditions. The top result applies to oriented lamellar phases (stacking in the z direction) whereas the bottom result involves an additional orientational average and applies to samples with isotropic symmetry: vesicle phases, sponge phases, and powder lamellar phases. The factor γ_k originates from the orientational averaging; for κ/k_BT ≫ 1, γ_k approaches unity. (When κ ≈ k_BT, the orientational average must be carried out numerically (5).) The ZG theory has been verified in dynamic light scattering experiments (17,18). The scaling in Eq. 3 has also been observed using the NSE technique (3–12). However, various groups (6–11) have found it necessary to assume a solvent viscosity over three times the expected value to fit their NSE data to Eqs. 2 and 3. Below, we argue that this discrepancy between theory and experiment at short wavelengths is resolved by considering dissipative mechanisms within the bilayer itself.

Evans and Yeung (19) and Seifert and Langer (20) have considered the dynamics of a bilayer subject to bulk solvent viscosity, monolayer surface viscosity, and intermonolayer friction. The SL model fits nicely into the ZG framework introduced above and has recently been verified via detailed simulations (21); we present our results in terms of this formalism. The primary insight of the SL theory is that a proper mesoscopic bilayer model must include not only fluctuations in bilayer shape as discussed above, but also fluctuations in local monolayer surface densities (equivalently the areas/lipid). Short wavelength membrane undulations are strongly affected by the monolayer densities. It is important to mention that the possible implications of dissipation within the bilayer (6) and specifically the SL theory (20,22) have previously been discussed in the context of NSE experiments. However, these works predate ZG, and did not arrive at expressions for the dynamic structure factor for comparison to experiment.

Bilayer dynamics within the SL model remain overdamped and are analyzed within the context of linear response theory; however, the formerly independent h_q modes of Eq. 1 couple to out-of-phase lipid density modes between the two monolayers (the in-phase modes are decoupled from undulations). The behavior of Eq. 1 thus becomes a biexponential decay when density fluctuations, surface viscosity, and intermonolayer friction are included (20):

$$\langle h_q\left(t\right)h_{-q}\left(0\right)\rangle =\frac{k_{\text{B}}T}{\kappa q^4}\left(A_1\left(q\right)e^{-{\gamma }_{\mathrm{1}}\left(q\right)t}+A_2\left(q\right)e^{-{\gamma }_{\mathrm{2}}\left(q\right)t}\right).$$ (4)

The relaxation rates γ_1,2 (q) are the eigenvalues of the matrix ΨE, where $\mathbf{\Psi }=\text{diag}\left[1/4\mathit{\eta }q,q^2/2\left(2b+2\mathit{\eta }q+{\mathit{\eta }}_{\text{s}}{q}^2\right)\right],$ and

$$\mathbf{E}=\left(\begin{array}{cc}\tilde{\kappa }{\mathit{q}}^{\mathit{4}}& -2k_{\text{m}}{q}^{2}d\\ -2k_{\text{m}}{q}^{2}d& 2k_{\text{m}}\end{array}\right).$$ (5)

The amplitudes A_i (q) are given by ${\mathit{A}}_{\mathit{i}}\left(q\right)\mathit{=\kappa }{q}^{\mathrm{4}}{\left(\mathbf{UK}{\mathbf{U}}^{-1}{\mathbf{E}}^{-1}\right)}_{1,1},$ where K = diag[δ_1i, δ_2i], U is the matrix that diagonalizes ΨE, and δ_ij is the Kronecker delta. The physical constants appearing in these expressions not found in the ZG treatment include the monolayer surface viscosity η_s, monolayer compressibility modulus k_m, intermonolayer friction coefficient b, height of the monolayer neutral surface above bilayer midplane d, and the renormalized bilayer curvature modulus $\tilde{\kappa }=\kappa +2d^2{k}_{\text{m}}$. We emphasize that Eq. 1 and 4 both reduce to k_BT/κq⁴ at t = 0 so that S(k, 0) is unchanged within the SL model. Further, for $q\ll 2\eta k_{\text{m}}/b\tilde{\kappa }$, Eq. 4 reduces to Eq. 1 at all times. The influence of the density modes is felt only over sufficiently small wavelengths. This explains why dynamic light scattering measurements (17,18), which only probe long-wavelength fluctuations, are fully consistent with Eq. 2.

A fully general analytical extension of the ZG theory based upon SL does not appear possible; however, such an extension is not necessary to understand NSE experiments for lipid-bilayer systems. For typical lipids and accounting for current limitations in the NSE technique, Eq. 4 is exceedingly well approximated by the expression (see Fig. 1 for a concrete justification based on dimyristoylphosphatidylcholine, i.e., DMPC, bilayers)

$$\langle h_q\left(t\right)h_{-q}\left(0\right)\rangle =\frac{k_{\text{B}}T}{\tilde{\kappa }{q}^4}\left(\frac{\mathrm{2}{\mathit{d}}^{\mathrm{2}}{k}_{\text{m}}}{\kappa }+\text{Exp}\left[-\frac{\tilde{\kappa }{q}^3}{4\eta }t\right]\right).$$ (6)

With the exception of the additive constant and the replacement $\kappa \to \tilde{\kappa }$, this expression is identical to Eq. 1 used in ZG. The dynamic ratio measured in experiment, S(k, t)/S(k, 0), is determined by the time-dependent portion of this expression, and hence is altered from ZG simply by replacing κ with $\tilde{\kappa }$ in Eq. 3. The additive constant, when combined with the second term at t = 0, insures that S(k, 0) remains unchanged from the ZG result, as discussed above.

Figure 1.

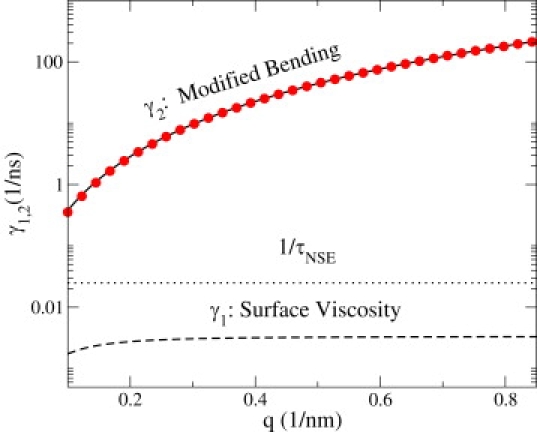
Behavior of the two relaxation modes for a DMPC bilayer (see Eq. 4) over typical NSE wavenumbers. Within this length regime, the decay rate of the modified bending mode (solid) has reached its asymptotic short wavelength behavior ${\mathit{\gamma }}_2\left(\mathit{q}\right)=\tilde{\mathit{\kappa }}{\mathit{q}}^3/\mathbf{4}\mathit{\eta }$ (red circles). Dominated by η_s, the mode associated with γ₁ relaxes more slowly than typical NSE timescales (τ_NSE ≈ 40 ns (8)) and remains effectively constant during the course of measurements. The amplitudes of these modes are nearly constant over NSE length scales, varying from the values specified in Eq. 6 by <1% over the accessible wavenumber range. The physical parameters for DMPC include: k_m = 117 mN/m (24), κ = 5.6 × 10⁻²⁰ J (24), b = 10⁷ N·s/m³ (25), η_s = 2.5 × 10⁻⁹ N·s/m (26), and ${\mathbf{\eta }}_{{\text{D}}_2\text{O}}=5.5\times {10}^{-4}$ Pa·s (8). Here we estimate d = h_pp/2, where h_pp = 3.52 nm is the peak-to-peak headgroup thickness (24).

The purpose of this letter is to emphasize that the ZG expressions (Eqs. 2 and 3) for the dynamic structure factor of membranes must be properly interpreted when applied to NSE measurements (or any scattering experiments over comparable time and length regimes). In particular, one needs to replace κ with $\tilde{\kappa }$ for NSE measurements. The physical basis of this substitution is that lateral lipid motion is completely suppressed over NSE timescales by viscous drag within the monolayers and frictional drag between the two leaflets. Bending the bilayer over these timescales is more energetically costly than an infinitely slow (thermodynamic) bending deformation that is accompanied by lateral flow and relaxation in the monolayers. The NSE structure factor does retain a dependence on κ within S(k, 0); however, the readily observable time dependence reflects the larger dynamic curvature modulus $\tilde{\kappa }$.

DMPC bilayers are well characterized (see Fig. 1) and have been studied by NSE (8). The physical parameters detailed in Fig. 1 suggest that $\tilde{\kappa }\approx \left(4-14\right)\kappa$ for DMPC membranes. (The range on $\tilde{\kappa }$ reflects ambiguity in the height of the neutral surface; this distance is not known experimentally, but is commonly assumed to lie between half and the full monolayer thickness.) The ad hoc rescaling of η by a factor of three in Yi et al. (8) (although retaining the bare bending rigidity) corresponds to a measured value of $\tilde{\kappa }=9\kappa$ in the context of this work. This value falls right in the middle of expected $\tilde{\kappa }$ values, demonstrating that our theory is fully consistent with experiment. Alternatively, the experiments of Yi et al. (8) combined with known elastic properties for DMPC lead to a measured value of d = 1.4 nm.

This work generalizes ZG only through the introduction of dissipation within the bilayer and suggests a simple analytical result only in the limiting regime that this drag jams all lateral lipid flow over NSE timescales. More generally, the theories of ZG and SL could be combined numerically with techniques similar to those reviewed in Brown (16). Both ZG and the extension described here rely on the independent, purely undulatory, motion of the probed bilayers. In a closely stacked lamellar phase, one expects additional effects due to the confinement of fluid between the bilayers (27) as well as direct bilayer-bilayer interactions. These effects have been qualitatively observed with NSE spectroscopy (12,28); however, the interlayer spacings commonly used in NSE experiments (6–9) are chosen to avoid these interactions. Recently (10), NSE measurements have been extended down to wavelengths comparable to bilayer thickness, indicating the presence of thickness fluctuations and microscopic protrusions (29,30). Modeling the effects of these additional phenomena will be grounds for future work.