Abstract
A previously established multiscale population genetics model posits that fitness can be inferred from the physical properties of proteins under the physiological assumption that a loss of stability by any protein confers the lethal phenotype to an organism. Here, we develop this model further by positing that replication rate (fitness) of a bacterial or viral strain directly depends on the copy number of folded proteins, which determine its replication rate. Using this model, and both numerical and analytical approaches, we studied the adaptation process of bacteria and viruses at varied environmental temperatures. We found that a broad distribution of protein stabilities observed in the model and in experiment is the key determinant of thermal response for viruses and bacteria. Our results explain most of the earlier experimental observations: the striking asymmetry of thermal response curves; the absence of evolutionary tradeoff, which was expected but not found in experiments; correlation between denaturation temperature for several protein families and the optimal growth temperature of their carrier organisms; and proximity of bacterial or viral optimal growth temperatures to their evolutionary temperatures. Our theory quantitatively and with high accuracy described thermal response curves for 35 bacterial species using, for each species, only two adjustable parameters—the number of rate-determining genes and the energy barrier for metabolic reactions.
Introduction
Temperature is one of the most important physical parameters in evolution. It defines fundamental properties of a species and plays an important role in many complex physiological mechanisms. Many laboratory experiments have been carried out to study fitness response to stress caused by elevated environmental temperature (1–9). Experiments showed that thermal niches for Escherichia coli and other bacteria are asymmetrical between the high temperature end and the low temperature end (3,5). This means that although bacteria that have adapted to higher environmental temperatures can easily survive at lower temperatures without sacrificing too much fitness, fitness in general declines much more sharply when temperature is raised to above optimal (3,5). Multiple competition assays have also shown that when bacteria adapt to a higher temperature, they outcompete wild-type bacteria of the same strain even when they are competing at the original wild-type environmental temperature (3,8,9), at variance with the common expectation of an evolutionary tradeoff. In addition to laboratory studies, prokaryotes that were isolated from high- and low-temperature natural environments exhibit such asymmetries as well. Many prokaryotes that were isolated from high-temperature environments are obligate thermophiles, whereas those isolated from low-temperature environments are not obligate psychrophiles and generally grow optimally at higher temperatures (10). Despite the abundance of experimental data, a quantitative and comprehensive explanation of various thermal adaptation patterns in prokaryotes has been elusive. Although previous approaches (11,12) have brought considerable insight regarding the relationship between the environmental temperature, genome size, and organism fitness, these models often use a relatively large number of adjustable parameters and sometimes fail to explain the fundamental connection between the asymmetric thermal adaptation behavior of an organism and the physical properties of their proteins. Therefore, based on our previous molecular evolutionary model (13) that all essential genes have to satisfy the minimal stability requirement for an organism's survival, we now present a model that can explain the adaptation of prokaryotes in a broad range of thermal environments. Our model explains the physical reason for the existence of the thermal niche asymmetry and lack of evolutionary tradeoff. It also provides a quantitative relationship between the number of proteins controlling the replication process in an organism (Γ), the enthalpy of activation (), and the fitness response to elevated or decreased environmental temperatures.
Model
Our previously developed evolutionary model (13) provided an insight into the distribution of stabilities of all essential genes in a genome. This model is based on recent experiments that showed that knockout of any essential gene confers a lethal phenotype to an organism (14,15). Therefore, the model assumes a fundamental minimalistic bare-bones genotype-phenotype relationship: in order for an organism to be viable, all of its essential genes must encode (at least minimally) stable proteins. This evolutionary model also assumes that protein stability is essentially a physiologically neutral trait, as long as protein possesses sufficient stability to stay in the folded state (16). Based on this model, along with other sufficient experimental evidence about protein stability distribution (17,18), we were able to provide a quantitative description of the distribution of stabilities of all essential proteins within a certain genome.
In our model, we assume that the replication rate of an organism depends on the functionality of each protein involved in its replication process. Replication rate does not necessarily depend on all genes. Instead, a smaller subset of genes in the organism may determine the replication rate, and the number of such rate-determining genes (RDGs) may vary among species and strains (19). However, an organism is only able to replicate efficiently when all protein products of these RDGs are able to function properly (20). (Below, we call protein products of RDGs rate-determining proteins (RDPs)). We note that the subset of rate determining genes may be smaller than the subset of essential proteins. The difference between the two is that essential genes (i.e., the ones whose knockout causes lethal phenotype) may not affect the growth rate directly. In contrast, the supply of functional RDPs may affect critically the ability of a cell to replicate. An example of such proteins could be ribosomal proteins, tRNA synthetases, DNA polymerases, etc. Essential but not necessarily RDPs may be enzymes involved in metabolism of certain nutrients, proteins responsible for motility under certain conditions, etc. Loss of stability of a single RDP would dramatically reduce the organismal replication rate.
RDPs, like any other protein, are active only when folded (natively unfolded proteins were not found in viruses and bacteria). If one of the RDPs loses its stability, its copy number in the folded (i.e., functional) form decreases, and as a result, the organism replication rate drops. Assuming that expression levels of all RDPs are independent of temperature, we posit that for an organism with Γ RDGs, and the fraction of the folded state for each RDP in the organism, the replication rate should be
| (1) |
This simple form of the dependence of growth rate on protein stability is motivated by the view that for cells to function and replicate, their major metabolic and biosynthetic pathways should be operational. Since many of these pathways involve various proteins in a sequential manner, the loss of copy number of any of them could result in a bottleneck effect on the total replication rate. The form of Eq. Eq. 1 is similar in spirit (but not in detail) to the weak-link hypothesis on which the recent successful model of early evolution was based (21). We can further specify by taking into consideration that folding of many protein domains is thermodynamically two-state, with only folded and unfolded states being stable or metastable. are the free energies of the folded and unfolded forms, respectively, of protein i, and is the free-energy difference between them. To avoid confusion, we note that each state—folded and unfolded—is viewed here as an ensemble of conformations corresponding to the free-energy minimum with respect to a relevant order parameter describing the degree of folding of a protein (22,23). Thus, ΔGi represents the stability of protein i. Therefore, for two-state proteins, the fraction of proteins that remain in their native state can be represented as
| (2) |
It is clear from Eq. 2 that a lower value of the free energy of protein folding translates into a higher ratio of folded to unfolded proteins in the organism. Folding free energies of proteins depend on the protein sequence, i.e., on the genotype of the organism and environmental conditions (temperature, pH, etc.) (24).
Therefore, the population growth rate, b, can be expressed as a product of the Arrhenius factor corresponding to the metabolic free-energy barrier, (12), and the folded fraction of properly functioning RDPs:
| (3) |
Because a protein's folding free energy is a function of temperature, it will change when temperature is perturbed.
The temperature dependence of protein stability is given by a classical expression (24–26):
| (4) |
where and these terms represent differences of enthalpy and entropy between folded and unfolded forms of a protein at a certain reference temperature (TR). is the difference in heat capacity between folded and unfolded proteins, which can be assumed to be temperature-independent with high accuracy (27). The last term in Eq. 4 describes changes in a protein's enthalpy and entropy with temperature. We will assume that , close to the conditions of most thermal response and adaptation experiments.
In what follows, we consider thermal response in a relatively narrow temperature range—from a drop of 15°C below to an increase of 5°C above = 37°C (2). Our concern is how protein stability changes with temperature upon temperature change from . Denoting , we get
| (5) |
| (6) |
We note that under all experimental conditions, , and that the square-bracketed term in Eq. 6 cancels in first order in and we obtain, with high accuracy, the linear dependence of protein free-energy change on temperature in the range of temperatures relevant to thermal response and adaptation experiments, i.e.,
| (7) |
where we used a typical value of for a typical protein domain at 37°C (24,26–28).
We have divided the following discussion into three parts. First, we present results from the numerical analysis of the thermal adaptation process, and we discuss thermal adaptation behavior for bacteria and viruses with semiconservative and conservative replication, respectively. In the second section, we develop a semianalytical model of thermal adaptation and discuss in quantitative terms the relationship between various parameters that are relevant for thermal adaptation and thermal response curves. In addition, we estimate an optimal growth temperature associated with each species. In the last section, we compare experimental results with model predictions. We find that our model can provide a good explanation for thermal adaptation of bacteria, using only two independent parameters for each bacterial species.
In the simulation, we first prepare initial species with 1000 identical organisms having the same genotype . Stabilities of Γ RDPs in each organism constituting the initial population take random values drawn from the analytical distribution derived in our previous work (13).
We prepared the system such that an organism initially has a probability of 0.1 of duplicating at each time step. Therefore, we define 10 time steps as an initial generation time in our simulation. This is nonetheless an approximate time, since, due to the diverse nature of the population, some organisms may evolve to replicate much faster than others.
At each time step, an organism can replicate with a probability determined by the genotype-dependent replication rate, as given by Eq. 4. An organism is eliminated as soon as a lethal mutation occurs that confers a folding-free-energy value greater than zero on any of its proteins. Upon replication, mutations may happen in a descendant organism. A mutation in our model represents the change in stability of a mutated protein in the daughter organism compared with the parent organism (see details in the Supporting Material). Here, we assume that a mutated protein folds into the same structure as the wild-type protein, as indeed has been observed in many protein engineering experiments (29). We also impose an upper limit of population size of N = 10,000 organisms by culling excess organisms at random. We ran many series of independent simulations to eliminate the effect of genetic drift due to a relatively small population size in simulations. During the numerical simulation, we let organisms evolve in a stable environment for around 20,000 generations, and studied population dynamics and evolution of protein stabilities in a range of parameters. Parameter bo establishes the correspondence between real time and time step in the simulation.
Results
Simulation of thermal adaptation
We studied evolution and adaptation for both conservative and semiconservative replication processes. In semiconservatively replicating species (DNA-based organisms that do not have a methylation mechanism to distinguish between parent and newly synthesized strands), mutations can occur in both descendant copies. Conservative replication, on the other hand, occurs in single-strand RNA viruses, and in bacteria that have methylation mechanisms to discriminate between parent and daughter strands. For conservative replication, one copy (or strand) retains the same genome sequence as previous generations, whereas the daughter copy (or strand) may acquire mutations. Bacteria species usually have a much lower mutation rate than RNA virus species (30–32), which leads to a considerable difference in their thermal responses, as well as their thermal adaptation dynamics, as will be shown below.
For semiconservative replicating species, we chose a model bacterium with a metabolic free-energy barrier of = 20 kcal/mol and Γ = 50 RDGs. For conservatively duplicated species, as RNA viruses usually have small genome sizes, we took Γ = 20 and the same free-energy barrier, = 20 kcal/mol. These values give thermal response predictions that agree well with experimental observations of thermal adaptation of mesophiles. Meanwhile, we chose the bacterium species to have a realistic mutation rate of 0.003 mutations/genome/replication (30), whereas RNA viruses have a much higher mutation rate of 1.5 mutations/genome/replication, as found in some strains of polioviruses (32).
After evolving in a steady thermal environment for 20,000 generations, the distribution of protein stabilities within a population reaches equilibrium. First, we varied the environmental temperature to observe the instantaneous fitness response To that end, we took the equilibrium species that evolved at 37°C, and then varied temperature by δT in the range from −15°C to 5°C, and with a step increment of 0.1°C, to determine the ratio of the new birth rate compared to the original birth rate.
When temperature decreased, fitness of both semiconservatively and conservatively duplicated species slowly declined, whereas a temperature increase caused a sharper drop of fitness, especially for viral species (Fig. 1, solid red line). When temperature increases above the evolutionary temperature at which the species have been cultivated, the fraction of folded form for some proteins—the least stable ones—significantly decreases, thereby decreasing the genome replication rate very rapidly. This is especially pronounced for viral strains, which have a larger proportion of less stable proteins due to their elevated mutation rate (see Fig.1 B) (33).
Figure 1.
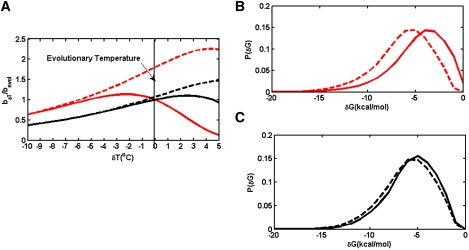
Thermal response of fitness and protein stability distributions for a model bacterium species (black lines) and a model RNA virus species (red lines (gray in print)) (see text for details). Solid lines correspond to wild-type species equilibrated at an evolutionary temperature, 37°C, and dashed lines correspond to strains evolved at 42°C. (A) Fitness response to temperature variation. (B and C) Protein stability distributions for the wild-type RNA virus (B) and bacterium (C) and the corresponding strains cultured at 42°C.
In addition to instantaneous thermal response, we also studied long-time thermal adaptation of bacteria and viruses after they had adapted to a new environment for a period of time. In our simulation, we took the wild-type bacterium strain and the RNA virus strain that were initially evolved at 37°C, increased the temperature of the environment to 42°C, and let the organisms evolve for a certain amount of time at this elevated temperature. Here, we use 10,000 generations, the same as the experimental timescale for bacterial evolution (7). (For RNA viruses, because of their high mutation rates, we set the adaptation time at 1000 generations.) We then measured relative (to the wild-type species) fitness as a function of the temperature change. After evolving the model bacteria at 42°C, we observed that the species had an elevated fitness level, even at its original temperature of 37°C (Fig. 1 A). We also compared the stability distribution of proteins of the adapted strain with that of the wild-type strain that was equilibrated at the initial evolutionary temperature of 37°C (Fig. 1, B and C).
We can see from Fig. 1 A that even after 10,000 generations at increased environmental temperature, the fitness improvement of bacteria after evolving in a 42°C environment is still relatively modest, especially when compared with that of the RNA virus. Apparently, adaptation occurs faster in RNA viruses than in DNA-based organisms. After evolving at 42°C for 1000 generations for the RNA virus and 10,000 generations for the bacterium, protein stability distribution is shifted toward more stable values for the RNA virus than for the bacterium (Fig. 1, B and C).
To better understand the distribution of protein stabilities within each strain, we studied denaturation temperatures of all proteins for each strain. As noted in the Model section, as temperature increases, some of the proteins in the organism will become unstable and get denatured. Here, we define the lethal denaturation temperature (LDT) for an organism as the temperature above the evolutionary temperature at which the least stable protein in this organism becomes denatured, i.e., its free energy is . A plot of the distribution of the organismal LDTs over all organisms in a population for each strain can be seen in Fig. 2. It is clear from Fig. 2 that highly mutating RNA virus populations form quasispecies, since the distribution of their LDTs over all organisms in the populations is broad and does not feature a pronounced peak. On the other hand, for the bacteria species, the distribution of LDTs is closer to a δ-function, and because these species have more stable proteins, they tend to have higher LDTs as well. From Fig. 2, as well as from Table 1, we can see clearly that organisms from strains cultured at higher temperatures have higher LDTs, and the magnitude of increase for RNA virus is greater than that for the bacterium, because of higher mutation rate in RNA virus and, thus, more rapid and complete adaptation. Nonetheless, we note that the distribution of LDT reflects the effect of temperature only approximately. In reality, some proteins can function at temperatures higher than this theoretical denaturation temperature, albeit with dramatically reduced functional copy numbers.
Figure 2.
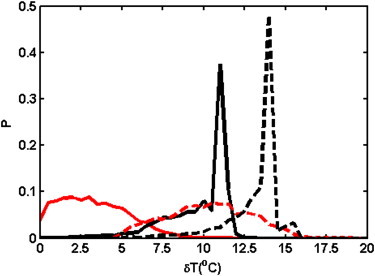
Distribution of the LDT for wild-type (solid lines) and high-temperature-evolved (dashed lines) bacteria (black lines) and viruses (red lines (gray in print)).
Table 1.
Protein denaturation temperatures for all four strains
| Minimum denaturation (°C) | Mean denaturation (°C) | |
|---|---|---|
| Bacterium wild-type | 9.7 | 27.6 |
| RNA virus wild-type | 3.3 | 17.6 |
| Bacterium cultured | 14.1 | 28.0 |
| RNA virus cultured | 10.3 | 24.7 |
Minimum denaturation(°C) is the mean (over all organisms in the population) LDT in each strain; mean denaturation (°C) is the average denaturation temperature for each protein in the population. All temperatures are measured as deviations from the original evolutionary temperature of 37°C.
Further, we study the mean denaturation temperature (MDT) for each strain, which is defined as the denaturation temperature (measured as the deviation from the original evolutionary temperature of 37°C) averaged over all proteins in all organisms in a species. The results for all strains are listed in Table 1. From this analysis, we can see that although the LDT for bacteria cultured at the elevated temperature has improved significantly (Fig. 2 and Table 1), the MDT for the cultured bacteria strain is not significantly different from that of the wild-type strain. This observation follows from the nature of the processes of mutation and selection, which occur during thermal adaptation. On the one hand, selection pressure introduced by increasing the environmental temperature would eliminate organisms that contain very unstable proteins, so that the LDT of the bacteria strain is significantly enhanced. On the other hand, the low mutation rate of the bacteria strain, as well as limited evolutionary time, gives the cultured strain only a limited opportunity to adapt to the new environment. In Fig. 1 C, it can be seen that the distribution of stabilities of all proteins in the population for thermally adapted bacteria is not significantly different from that for the wild-type bacteria. Thus at low mutation rates the adaptation process is essentially “improvement of the least fit”, while stabilities of more stable proteins, which stay folded even at elevated temperature are affected to a much lesser degree.
Semianalytical model of thermal adaptation
To get a better understanding of how various mechanisms described in our model influence the fitness of strains at different temperatures, we now apply mean-field approximation, and calculate the dependence of fitness response curves on the number of RDGs, Γ, as well as the metabolic-reaction free-energy barrier, .
According to Zeldovich et al. (13), the probability distribution of folding free energies of proteins within an organism, , denoted as , can be approximately expressed as
| (8) |
Here, is the normalization constant for the probability distribution. D, h, and L are parameters obtained from the distribution of energetic effects of the protein point mutations. D is the variance of change for a point mutation, and h is the mean of the value for a point mutation. L = is the total range of viable free energies of protein folding and (13). At room temperature, , and the value of L = is ∼20 kcal/mol. Although the distribution of stabilities given by the analytical expression (Eq. 8) is slightly different from the more accurate distributions obtained from simulations (Fig. 2) (33), it can be used as a reasonable first approximation, as qualitatively (and semiquantitatively) it captures most essential features of the experimentally observed distribution of protein stabilities (13).
From Eq. 3, the replication rate can also be presented as
| (9) |
Because the organism replication rate, b, is a function of its genotype , from Eq. 8, we also know an approximate probability distribution for the stabilities of the organism's RDPs. Given this information, it is convenient to take the mean-field approximation for the organismal birth rate and consider the ensemble average over all organisms in a species. In this way, we can calculate the average value of the organismal replication rate for a given species, and the summation over all RDGs can be approximated by integrating over the entire distribution range. Therefore, the logarithmic population growth rate can be expressed as
| (10) |
The probability distribution , after an instantaneous temperature increase, can be expressed as
| (11) |
Using Eqs. 8–11, we can expand to the second order in δT in the form
| (12) |
Here, C1–C4 are various constants (see the Supporting Material for their derivation). (See the Supporting Material for the derivation and analysis).
Analysis of Eqs. 10–12 (see the Supporting Material) shows that species-dependent thermal adaptation behavior is largely determined in our model by the species metabolic-reaction free-energy barrier and the number of its RDGs, Γ.
When which satisfies the relation , a temperature perturbation, , changes the growth rate only in the second order in , making species with RDGs the most robust to temperature fluctuations.
When is in the range 10–20 kcal/mol, and the growth temperature is ∼25°C, can be 10–20 for mesophiles. We also note that the analytical form of the protein stability distribution is shifted toward the lower-stability end than the experimental database result (whereas the numerical simulation results of P(ΔG) shown in Fig. 1 and in Chen and Shaknovich (33) are in better agreement with the experimental distribution at the lower-stability end). Therefore, substituting in Eq. 10 with experimental protein stability distributions will give higher values, up to 40–60. For organisms where Γ > ΓC, increasing temperature by a small amount, δT, will decrease the birth rate. On the other hand, if Γ < ΓC, raising the temperature by a small enough δT might modestly increase fitness (Fig. 3).
Figure 3.
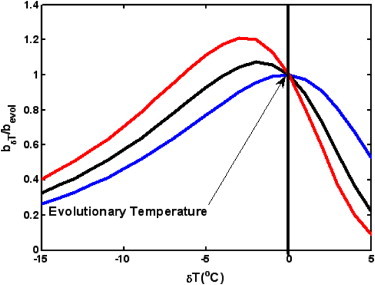
Thermal response curves for various RDG numbers: Γ = 30 (red line (light gray in print); Γ = 20 (black line); and Γ = 10 (blue line (dark gray in print)). The growth rates are measured as the ratio to the species replication rate at their original evolutionary temperature ().
From the analytical expansion form of the thermal response of the organism, we can also see that there exists some optimal growth temperature (OGT), , at which the growth rate of a specie will reach its maximum value. From the analytical expressions of , we can write that
| (13) |
In the range of realistic values, where ranges from 10 to 20 kcal/mol, Γ ranges from 10 to 50, and for T ∼ 300 K, , which brings the OGT within three Celsius of the evolutionary temperature for mesophilic organisms.
We plotted the fitness change versus temperature for bacteria having different RDG numbers (Fig. 3), using the results of semianalytical calculations. We note that at a constant metabolic free-energy barrier and environmental temperature, increasing the number of RDGs leads to a lower OGT. Analogously, increasing Γ results in a more drastic decrease of the growth rate with temperature, making it more difficult for an organism to adapt to an elevated temperature. According to Eq. 10, fitness declines more slowly with increasing temperature when is greater. This can also be seen in Fig. S1 of the Supporting Material, although the effect is relatively weak.
Comparison with experiment
Several experiments were carried out to study thermal response and adaptation behavior of bacteria and viruses (1,2,12). Ratkowski et al. (12) systematically studied 35 sets of data for thermal adaptation of different bacteria strains. Here, we analyzed thermal response curves for these 35 mesophilic strains using our model. Assuming that the metabolic-reaction free-energy barrier, , and the number of RDGs, Γ, are the only independent parameters for each strain, we fit 35 datasets of bacterial thermal response with theoretical formulae derived in the preceding section. Since we have limited information about the evolutionary temperature for each bacterial strain, we used the OGT as a proxy for evolutionary temperature, motivated by observations and our results showing that the two are not too different for mesophiles. We evaluate growth rate as a function of temperature for each bacterial strain from Eq. 10 using for P(ΔG) the distribution of experimentally measured stabilities of proteins derived in Zeldovich et al. (13) from ProTherm database (18). Equation 10 contains two parameters—the number of RDGs, Γ, and the metabolic free-energy barrier, —which we adjust for each strain and checking a posteriori that the values of these parameters are biologically reasonable.
We used the nonlinear regression method to find values of and Γ associated with each strain, and for 35 independent bacterial strains, the number of RDGs ranged from 10 to 50, which is ∼10%–30% of the number of all essential genes in a bacteria, thus representing a reasonable order-of-magnitude estimate for the number of RDGs in a species. This number is also consistent with a recent estimate by Forster and Church (34) of a minimal gene set, albeit somewhat smaller. The metabolic-reaction free-energy barrier ranges from 10 to 20 kcal/mol, and this also agrees with previous estimates. Here, we were able to obtain a relatively good fit for almost all of the datasets, and several examples comparing the experimental data with our theoretical predictions are shown in Fig. 4 (see the Supporting Material for fits for the remaining 32 strains.).
Figure 4.
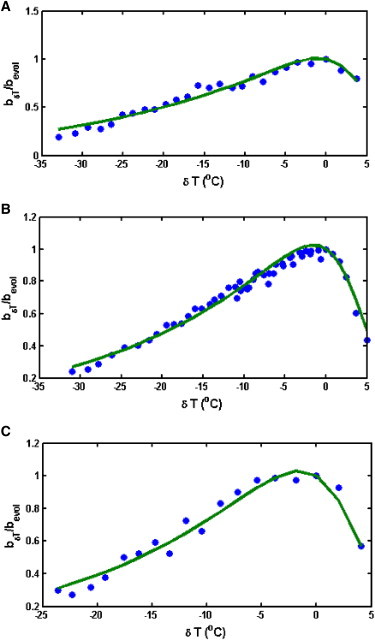
Comparison between experimental thermal response curves and predictions from the semianalytical model. Here, we show results for 3 of 35 species studied by Ratkowsky and co-authors (12). (A) Listeria monocytogenes, H# = 7.64 kcal/mol, Γ = 23. (B) Pseudomonas fluorescens (H# = 8.05 kcal/mol, Γ =34), and (C) E. coli (H# = 14.1 kcal/mol, Γ = 41).
From Fig. 4, we can see that by varying just two parameters, we can achieve a correlation of 89–99% between the experimental data and the analytical model prediction.
Discussion
Thermal adaptation in viruses and bacteria has been studied extensively in the past, and a number of qualitative features of thermal response and adaptation have been found to be common to most studied species and strains. In particular, the following observations have been made. 1), The OGT of an organism is very close to its evolutionary temperature (3–5,8). 2), There is a pronounced asymmetry of thermal response curves in viruses and bacteria, whereby their growth rate declines slowly with decreasing temperature and more rapidly upon temperature increase (4,7). 3), There is a lack of evolutionary tradeoff, so that bacteria and viruses cultivated at a higher temperature appear to be more fit than bacteria cultivated at the original evolutionary temperature in a broad temperature range, including the original evolutionary temperature (3,4,6). 4), A correlation exists between the OGT of an organism and the denaturation temperature of its proteins.
Our model, although quite minimalistic, explains all these findings, providing a unified picture of physical mechanisms of thermal adaptation. The key premise of the theory is that to function, proteins must be stable, and that one of the key determinants of the rate of growth (i.e., fitness) of an organism is the amount of folded functional RDPs available in the cell. The protein stability factor affects replication rate through modulation of the fraction of correctly folded proteins, as suggested by Eq. 1 Although Eq. 1 is empirical, it is biologically justified in the sense that it assigns equal importance to the stability of each RDP, whereas an alternative form in which replication rate is proportional to the total copy number of folded RDPs would overweight the importance of highly expressed proteins and ignore the role of less expressed RDPs (e.g., some transcription factors and DNA polymerases). Nevertheless, the dependence of replication rate on the copy number of folded RDPs given by Eq. 2 is just a first approximation, and other forms (which, e.g., put emphasis on the toxic effect of misfolded proteins in the cells (35)) are possible and will be explored in future work.
We believe that the key novel aspect of our model is that it explicitly takes into account (and derives) a broad distribution of protein stabilities in the genome of a bacterial or viral species, in contrast to earlier studies in which it was assumed that stability of a single protein determines the growth rate of bacteria (or that all proteins in an organism have the same stability) (12). Although the study of Ratkowsky and co-authors (12) was successful in fitting thermal response curves for many bacterial strains, such fitting was achieved at the expense of a large number of fitting parameters (five) for each species to describe the thermodynamics of the single RDP. A broad distribution of protein stabilities within a species is a key factor determining a prokaryotic thermal response.
The analytical approximation and simulations show that deviation of the OGT from evolutionary temperature is small, in agreement with experimental observations. Travisano and Lenski (5) systematically studied the thermal response curves of E. coli after it had evolved in a steady 37°C environment for 20,000 generations. This evolved strain shows a direct and clear trend of fitness decrease as temperature deviates from the original 37°C. That is, the OGT appeared to be <1°C different from its evolutionary temperature for this well-evolved E. coli strain. On the other hand, the ancestor strains, whose protein stability distributions may not be fully equilibrated within the population, show some small fluctuation of growth rate when the environmental temperature increases by <2°C from its evolutionary temperature, but eventually fitness declines sharply upon further increase in temperature. Our theory provides the physical rationale for this observation. Indeed, broad equilibrium distribution of stabilities of RDPs (see Fig. 1, B and C) implies that there exist weakest links, i.e., least stable proteins for which even a slight increase of temperature results in a significant decrease of equilibrium population of their folded form. It is the drop in the copy number of these folded RDPs that brings about an immediate loss of fitness upon an increase of temperature above the evolutionary temperature.
Thermal adaptation experiments showed that E. coli has a free-energy barrier for the metabolic reaction rate of ∼ = 14.3 kcal/mol (12). Our theory also gives the best-fit value of ∼14 kcal/mol for many strains (Table S1), whereas the best-fit number of RDGs in E. coli is 41. This number is ∼15% of its essential gene number, and thus may be a reasonable estimate. Then, according to the analysis of Eq. 13, the OGT of well-evolved E. coli should be within 2°C of its evolutionary temperature, which agrees well with experimental observations.
The fact that the OGT is especially close to evolutionary temperature for the equilibrated species, points to an interesting evolutionary observation. Indeed, one can argue that thermodynamic vulnerability of least stable proteins to an increase of temperature may create an evolutionary pressure to make them more stable. However, we do not observe that in this model, and experiments show that the OGT is indeed very close to evolutionary temperature. The reason there is no apparent pressure to stabilize least stable proteins is that as a bacteria evolves in a highly controlled environment (constant T), its fitness is optimized in this particular environment, without concern about adaptation in a different environment that the bacterial strain has not encountered during long evolutionary equilibration. On the other hand, evolutionary optimization of the distribution of protein stabilities beyond an optimal distribution in a given environment does not improve fitness in this fixed environment. Thus, our model shows how long-time equilibration evolves a specialist bacteria, which may be poorly adapted to challenge beyond the conditions it was exposed to. The reason is not that specialization is an advantageous trait, but that it is the easiest evolutionary solution in a given environment, and long-time equilibration helps to find this solution.
In the numerical study of thermal adaptation, we provided a quantitative insight into how viruses and bacteria respond to temperature changes. Our simulation results agree with those from previous experiments on the asymmetry of thermal response for different bacteria and viruses (1–5,7–9,12,36). The reason for such asymmetry is that different factors affect fitness at lower and higher temperatures, and partial unfolding of least stable proteins is the key factor in the decrease of fitness at high temperatures. The OGT for the subset of least stable proteins is not far from their denaturation temperature, whereas the fraction of folded proteins is most sensitive to temperature near the midfolding transition for two-state proteins. For that reason, fitness drops steeply when temperature increases above the OGT.
Our results show no evolutionary tradeoff in thermal adaptation, in agreement with many experimental studies. Several authors (1,3,4,6,8,9) have shown that bacteria and viruses that have adapted to elevated environmental temperatures acquire fitness superior to that of strains that have been growing at the original temperature for an extended period of time, even when they are competing in the same original thermal environment. It was thought that evolutionary tradeoff in thermal adaptation, whereby bacteria cultivated at higher temperatures should have lower fitness at the normal temperature than bacteria cultivated at the normal temperature (4,7), would determine thermal response in bacteria, but this is at variance with actual observations. The intuition behind the tradeoff expectations lies in the widely held belief that to function, proteins must be not too stable to allow for function-related flexibility (37). Several arguments are usually presented in support of this view. First, it is argued, the stability of real proteins is not too high; hence, there must be some tradeoff between stability and functionality (37). Second, often cited are experimental observations that some stability-increasing mutations in active sites of several enzymes may be detrimental to function (38,39). Apparently, the first argument is circular, as pointed out by Wilke and co-authors (16). The flaw in the second (experimental) argument is that it fails to recognize that in many experiments, which support the stability-function tradeoff, mutations are introduced in active sites only (38,39), making it difficult to disentangle the effect of replacement of catalytic residues from the effect of mutation on protein stability. In reality, mutations that stabilize proteins do not in most cases compromise their catalytic activity (40,41). Furthermore, Arnold and co-authors showed that for a large number of random mutations in a mesophilic enzyme esterase, stability and catalytic activity are not inversely correlated (40). Our model reproduces the distribution of protein stabilities and most of the phenomenology of thermal adaptation without assuming any functional penalty for protein stabilization, which suggests that the stability-function tradeoff may not be real, and that it is certainly not a determining factor in thermal adaptation.
Although it does not assume a particular stability-function relationship, our model is not neutral with respect to protein stability either, in contrast to some earlier studies (16). In addition to assuming that unfolding of an essential protein leads to a lethal phenotype (13), we also posit here that the stability of RDPs affects fitness through modulating the copy number of folded (and therefore functional) proteins as given by Eqs. 1 and 2. On the other hand, our model does not assume any effect of stability on catalytic rate or other functional measure of the folded protein.
It has been found that in prokaryotes, the denaturation temperature for certain protein families is correlated to their OGT (42–44). Our model provides further insight into the relation between protein stability and the OGT. Long-term adaptation upon a moderate increase of temperature (up to 5°C in our simulations and in many experiments) changes the distribution of protein stabilities in a strain,, by mostly affecting least stable proteins while leaving more stable proteins, whose denaturation temperature is considerably above the new evolutionary temperature, relatively unchanged. Fig. 2 and Table 1 show that adaptation affects mostly relatively unstable proteins in bacteria. It is noteworthy that a few cases in which a correlation between stability and the OGT was documented concerned proteins that are relatively unstable in mesophilic species (42–44). Although this coincidence is suggestive, more systematic studies are needed to confirm or falsify this prediction from our model.
The numerical study shows how fitness of bacteria and viruses exhibit different thermal responses, even for the same number of RDGs and the same metabolic-reaction free-energy barrier. Initially, bacterial proteins are more stable than those of RNA viruses (Fig. 1, B and C) due to the difference in their mutation rates. However, after evolving at elevated environmental temperature (42°C) for 10,000 generations, fitness of the RNA virus is greatly improved in a broad temperature range, including the original evolutionary temperature of 37°C, as the maximum growth rate can reach up to 1.8 times the wild-type growth rate at the original temperature, 37°C. A bacterium cultured at 42°C for the same 10,000 generations makes limited improvement compared to the RNA virus; the adapted bacterium's maximum growth rate is around 1.2 times the natural growth rate. This is in agreement with experimental results, which showed that some viruses can adapt to different environments within a short amount of time (4,6), whereas after several years of evolution, the relative fitness of different E. coli. strains shows only a limited change, from 0.8 to 1.2, depending on the specific growth conditions and initial strains (1). For a bacterium with a life cycle of around 4 h, as in Lenski's previous experiments (they estimated around generations of E. coli/day) (7), 10,000 generations is roughly five years. For E. coli growing in more optimal conditions, the life cycle can be around 1 h (45), and 5000 generations would be around 200 days. Therefore, host organism responses such as fever are effective methods to combat most bacterial infections. Viruses, whose generation time may be as short as a couple of hours, can adapt to a novel thermal environment on timescales from several days to a few months. Thus, according to our model, fever might not always be the most effective mechanism to fight certain viral infections, although it still may be an effective response to many of them. This agrees with common knowledge that fever response is more often caused by bacterial infection, since during the time course of a fever, which is around a few days, bacteria can hardly adjust to the new thermal environment, and are therefore likely to get eliminated.
Supporting Material
References
- 1.Bennett A.F., Lenski R.E. An experimental test of evolutionary trade-offs during temperature adaptation. Proc. Natl. Acad. Sci. USA. 2007;104(Suppl 1):8649–8654. doi: 10.1073/pnas.0702117104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bronikowski A.M., Bennett A.F., Lenski R.E. Evolutionary adaptation to temperature. VIII. Effects of temperature on growth rate in natural isolates of Escherichia coli and Salmonella enterica from different thermal environments. Evolution. 2001;55:33–40. doi: 10.1554/0014-3820(2001)055[0033:EATTVE]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 3.Cullum A.J., Bennett A.F., Lenski R.E. Evolutionary adaptation to temperature. IX. Preadaptation to novel stressful environments of Escherichia coli adapted to high temperature. Evolution. 2001;55:2194–2202. doi: 10.1111/j.0014-3820.2001.tb00735.x. [DOI] [PubMed] [Google Scholar]
- 4.Knies J.L., Izem R., Burch C.L. The genetic basis of thermal reaction norm evolution in lab and natural phage populations. PLoS Biol. 2006;4:e201. doi: 10.1371/journal.pbio.0040201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Travisano M., Lenski R.E. Long-term experimental evolution in Escherichia coli. IV. Targets of selection and the specificity of adaptation. Genetics. 1996;143:15–26. doi: 10.1093/genetics/143.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Holder K.K., Bull J.J. Profiles of adaptation in two similar viruses. Genetics. 2001;159:1393–1404. doi: 10.1093/genetics/159.4.1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cooper V.S., Bennett A.F., Lenski R.E. Evolution of thermal dependence of growth rate of Escherichia coli populations during 20,000 generations in a constant environment. Evolution. 2001;55:889–896. doi: 10.1554/0014-3820(2001)055[0889:eotdog]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 8.Leroi A.M., Bennett A.F., Lenski R.E. Temperature acclimation and competitive fitness: an experimental test of the beneficial acclimation assumption. Proc. Natl. Acad. Sci. USA. 1994;91:1917–1921. doi: 10.1073/pnas.91.5.1917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bennett A.F., Lenski R.E. Phenotypic and evolutionary adaptation of a model bacterial system to stressful thermal environments. EXS. 1997;83:135–154. doi: 10.1007/978-3-0348-8882-0_8. [DOI] [PubMed] [Google Scholar]
- 10.Knoll A.H., Bauld J. The evolution of ecological tolerance in prokaryotes. Trans. R. Soc. Edinb. Earth Sci. 1989;80:209–223. doi: 10.1017/s0263593300028650. [DOI] [PubMed] [Google Scholar]
- 11.Xia X. Body temperature, rate of biosynthesis, and evolution of genome size. Mol. Biol. Evol. 1995;12:834–842. doi: 10.1093/oxfordjournals.molbev.a040260. [DOI] [PubMed] [Google Scholar]
- 12.Ratkowsky D.A., Olley J., Ross T. Unifying temperature effects on the growth rate of bacteria and the stability of globular proteins. J. Theor. Biol. 2005;233:351–362. doi: 10.1016/j.jtbi.2004.10.016. [DOI] [PubMed] [Google Scholar]
- 13.Zeldovich K.B., Chen P., Shakhnovich E.I. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proc. Natl. Acad. Sci. USA. 2007;104:16152–16157. doi: 10.1073/pnas.0705366104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Herring C.D., Blattner F.R. Conditional lethal amber mutations in essential Escherichia coli genes. J. Bacteriol. 2004;186:2673–2681. doi: 10.1128/JB.186.9.2673-2681.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fraser A.G., Kamath R.S., Ahringer J. Functional genomic analysis of C. elegans chromosome I by systematic RNA interference. Nature. 2000;408:325–330. doi: 10.1038/35042517. [DOI] [PubMed] [Google Scholar]
- 16.Bloom J.D., Raval A., Wilke C.O. Thermodynamics of neutral protein evolution. Genetics. 2007;175:255–266. doi: 10.1534/genetics.106.061754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sánchez I.E., Tejero J., Serrano L. Point mutations in protein globular domains: contributions from function, stability and misfolding. J. Mol. Biol. 2006;363:422–432. doi: 10.1016/j.jmb.2006.08.020. [DOI] [PubMed] [Google Scholar]
- 18.Kumar M.D., Bava K.A., Sarai A. ProTherm and ProNIT: thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res. 2006;34(Database issue):D204–D206. doi: 10.1093/nar/gkj103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nishikawa T., Gulbahce N., Motter A.E. Spontaneous reaction silencing in metabolic optimization. PLOS Comput. Biol. 2008;4:e1000236. doi: 10.1371/journal.pcbi.1000236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Couñago R., Chen S., Shamoo Y. In vivo molecular evolution reveals biophysical origins of organismal fitness. Mol. Cell. 2006;22:441–449. doi: 10.1016/j.molcel.2006.04.012. [DOI] [PubMed] [Google Scholar]
- 21.Zeldovich K.B., Chen P., Shakhnovich E.I. A first-principles model of early evolution: emergence of gene families, species, and preferred protein folds. PLOS Comput. Biol. 2007;3:e139. doi: 10.1371/journal.pcbi.0030139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shakhnovich E.I. Protein folding thermodynamics and dynamics: where physics, chemistry, and biology meet. Chem. Rev. 2006;106:1559–1588. doi: 10.1021/cr040425u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sali A., Shakhnovich E., Karplus M. How does a protein fold? Nature. 1994;369:248–251. doi: 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
- 24.Privalov P.L. Stability of proteins: small globular proteins. Adv. Protein Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
- 25.Makhatadze G.I., Privalov P.L. Heat capacity of proteins. I. Partial molar heat capacity of individual amino acid residues in aqueous solution: hydration effect. J. Mol. Biol. 1990;213:375–384. doi: 10.1016/S0022-2836(05)80197-4. [DOI] [PubMed] [Google Scholar]
- 26.Robertson A.D., Murphy K.P. Protein structure and the energetics of protein stability. Chem. Rev. 1997;97:1251–1268. doi: 10.1021/cr960383c. [DOI] [PubMed] [Google Scholar]
- 27.Privalov P.L., Gill S.J. Stability of protein structure and hydrophobic interaction. Adv. Protein Chem. 1988;39:191–234. doi: 10.1016/s0065-3233(08)60377-0. [DOI] [PubMed] [Google Scholar]
- 28.Makhatadze G.I., Privalov P.L. Energetics of protein structure. Adv. Protein Chem. 1995;47:307–425. doi: 10.1016/s0065-3233(08)60548-3. [DOI] [PubMed] [Google Scholar]
- 29.Fersht A.R., Bycroft M., Serrano L. Pathway and stability of protein folding. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1991;332:171–176. doi: 10.1098/rstb.1991.0046. [DOI] [PubMed] [Google Scholar]
- 30.Drake J.W., Charlesworth B., Crow J.F. Rates of spontaneous mutation. Genetics. 1998;148:1667–1686. doi: 10.1093/genetics/148.4.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sniegowski P.D., Gerrish P.J., Lenski R.E. Evolution of high mutation rates in experimental populations of E. coli. Nature. 1997;387:703–705. doi: 10.1038/42701. [DOI] [PubMed] [Google Scholar]
- 32.Drake J.W. Rates of spontaneous mutation among RNA viruses. Proc. Natl. Acad. Sci. USA. 1993;90:4171–4175. doi: 10.1073/pnas.90.9.4171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen P., Shakhnovich E.I. Lethal mutagenesis in viruses and bacteria. Genetics. 2009;183:639–650. doi: 10.1534/genetics.109.106492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Forster A.C., Church G.M. Towards synthesis of a minimal cell. Mol. Syst. Biol. 2006;2:45. doi: 10.1038/msb4100090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Drummond D.A., Wilke C.O. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell. 2008;134:341–352. doi: 10.1016/j.cell.2008.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Elena S.F., Wilke C.O., Lenski R.E. Effects of population size and mutation rate on the evolution of mutational robustness. Evolution. 2007;61:666–674. doi: 10.1111/j.1558-5646.2007.00064.x. [DOI] [PubMed] [Google Scholar]
- 37.DePristo M.A., Weinreich D.M., Hartl D.L. Missense meanderings in sequence space: a biophysical view of protein evolution. Nat. Rev. Genet. 2005;6:678–687. doi: 10.1038/nrg1672. [DOI] [PubMed] [Google Scholar]
- 38.Shoichet B.K., Baase W.A., Matthews B.W. A relationship between protein stability and protein function. Proc. Natl. Acad. Sci. USA. 1995;92:452–456. doi: 10.1073/pnas.92.2.452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Beadle B.M., Shoichet B.K. Structural bases of stability-function tradeoffs in enzymes. J. Mol. Biol. 2002;321:285–296. doi: 10.1016/s0022-2836(02)00599-5. [DOI] [PubMed] [Google Scholar]
- 40.Giver L., Gershenson A., Arnold F.H. Directed evolution of a thermostable esterase. Proc. Natl. Acad. Sci. USA. 1998;95:12809–12813. doi: 10.1073/pnas.95.22.12809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bloom J.D., Labthavikul S.T., Arnold F.H. Protein stability promotes evolvability. Proc. Natl. Acad. Sci. USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Topping T.B., Gloss L.M. Stability and folding mechanism of mesophilic, thermophilic and hyperthermophilic archael histones: the importance of folding intermediates. J. Mol. Biol. 2004;342:247–260. doi: 10.1016/j.jmb.2004.07.045. [DOI] [PubMed] [Google Scholar]
- 43.Li W.T., Grayling R.A., Reeve J.N. Thermodynamic stability of archaeal histones. Biochemistry. 1998;37:10563–10572. doi: 10.1021/bi973006i. [DOI] [PubMed] [Google Scholar]
- 44.Perl D., Welker C., Schmid F.X. Conservation of rapid two-state folding in mesophilic, thermophilic and hyperthermophilic cold shock proteins. Nat. Struct. Biol. 1998;5:229–235. doi: 10.1038/nsb0398-229. [DOI] [PubMed] [Google Scholar]
- 45.Woldringh C.L. Morphological analysis of nuclear separation and cell division during the life cycle of Escherichia coli. J. Bacteriol. 1976;125:248–257. doi: 10.1128/jb.125.1.248-257.1976. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


