Thrombin Flux and Wall Shear Rate Regulate Fibrin Fiber Deposition State during Polymerization under Flow

Abstract

Thrombin is released as a soluble enzyme from the surface of platelets and tissue-factor-bearing cells to trigger fibrin polymerization during thrombosis under flow conditions. Although isotropic fibrin polymerization under static conditions involves protofibril extension and lateral aggregation leading to a gel, factors regulating fiber growth are poorly quantified under hemodynamic flow due to the difficulty of setting thrombin fluxes. A membrane microfluidic device allowed combined control of both thrombin wall flux (10⁻¹³ to 10⁻¹¹ nmol/μm² s) and the wall shear rate (10–100 s⁻¹) of a flowing fibrinogen solution. At a thrombin flux of 10⁻¹² nmol/μm² s, both fibrin deposition and fiber thickness decreased as the wall shear rate increased from 10 to 100 s⁻¹. Direct measurement and transport-reaction simulations at 12 different thrombin flux-wall shear rate conditions demonstrated that two dimensionless numbers, the Peclet number (Pe) and the Damkohler number (Da), defined a state diagram to predict fibrin morphology. For Da < 10, we only observed thin films at all Pe. For 10 < Da < 900, we observed either mat fibers or gels, depending on the Pe. For Da > 900 and Pe < 100, we observed three-dimensional gels. These results indicate that increases in wall shear rate quench first lateral aggregation and then protofibril extension.

Introduction

The conversion of fibrinogen to fibrin by the enzyme thrombin is a central event in the growth and stability of a blood clot. Fibrinogen is a large (330-kDa) rodlike protein found at high concentrations (9 μM) in plasma. Thrombin, a serine protease formed on deposited platelets at the site of a vascular injury, cleaves fibrinopeptides A and B from the fibrinogen molecule to yield fibrin monomers. The absence of fibrinopeptides leaves “holes” in which complementary “knobs” fit such that fibrin monomers assemble in a half-staggered configuration to form protofibrils. Protofibrils aggregate laterally to form fibrin fibers, which then aggregate and cross-link with each other to form a fibrin gel. The kinetic competition between protofibril extension and lateral aggregation can be regulated by salt and thrombin levels, resulting in fine or coarse gels (1,2). These mechanisms of fibrin gel formation are based on extensive studies in purified protein systems under isotropic, no-flow conditions (3–5). However, considerably less is known about how these mechanisms are affected by the shear flows in which blood clots must form in vivo.

Fibrin deposition decreases with increasing wall shear rate over the range 50–2500 s⁻¹ in whole-blood perfusions over rabbit subendothelium (6) and tissue-factor (TF)-rich extracellular matrices (7). This inverse relationship between wall shear rate and fibrin deposition is congruent with the clinical observation that venous blood clots are fibrin-rich, whereas arterial blood clots are platelet-rich. In addition to shear rate, fibrin deposition depends on the rate of thrombin generation. For instance, collagen-adherent platelets, in the absence of wall-derived TF, can induce fibrin deposition at venous shear stresses, but fibrin deposition is severely depressed at arterial shear stresses (8). Immobilized TF, in contrast, leads to thrombin generation sufficient to yield fibrin even at arterial shear stresses (9). However, even on immobilized TF, there is a shear-dependent effect on coagulation due to the dilution of thrombin and fibrin monomers by the flow field (10). The critical levels of TF needed to trigger fibrin formation at venous and arterial levels have been measured (11); however, a limitation of these flow assays is that the amount of thrombin generated is unknown and likely highly variable among individuals.

In lieu of experimental measurements of thrombin flux, theoretical studies provide insight into the interplay between flow, platelet function, and coagulation. Thrombin generation under flow is predicted to be sensitive to shear rate (12,13). In one model, thrombin flux increases almost linearly with increasing wall shear rate based on an increase in the flux of prothrombin to the prothrombinase complex at the site of an injury (12). A second model predicts that thrombin flux moderately decreases with increasing wall shear rate owing to the role platelets play in blocking the TF/VIIa complex (13). Neither of these models includes fibrin production. Recently, a simplified model of coagulation in a shear flow was used to predict the extent of fibrin gel formation as a function of wall shear rate (14). This model predicts that at venous shear rates (<300 s⁻¹), thrombin concentration dictates gel growth. However, at high shear rates, the model predicts that gel growth is limited by the rate of removal of fibrin monomers and oligomers by the flow field.

To date, there are no reports of fibrin deposition under flow in a purified system at a defined thrombin wall flux. The objective of this study is to determine under what conditions fibrin can form under flow, and how those conditions affect fibrin assembly and structure. We used a previously developed membrane-based microfluidic technique (15) to introduce thrombin at a defined flux into a flowing solution of fibrinogen. These experiments provide a link between blood flow assays and theoretical models of thrombin generation. Results demonstrate that fibrin deposition and morphology in a shear flow are dictated by the interplay between thrombin flux and wall shear rate. Scaling arguments and computational models of the relevant conservation equations suggest that fibrin deposition can be characterized by two dimensionless parameters, the Peclet number (Pe) and the Damkohler number (Da). We propose a state diagram for fibrin morphology based on these results and discuss physiological relevance to bleeding and thrombotic disorders.

Materials and Methods

Materials

Human fibrinogen (plasminogen, von Willebrand factor, and fibronectin-depleted; Enzyme Research Laboratories, South Bend, IN) was received at 38 μM (12.62 mg/mL) in 20 mM sodium citrate-HCl and diluted to 9 μM in Tris-buffered saline (TBS; 150 mM NaCl and 50 mM Tris-HCl, pH 7.4). Aliquots of 1 mL were stored at −80°C, defrosted at 37°C, and used within 2 h. Approximately 1 mL of the stock fibrinogen (9 μM) was fluorescently labeled with an Alexa 647 fluorophore (A20173, Invitrogen, Carlsbad, CA) using a protein labeling kit according to the manufacturer's instructions. Human α-thrombin was received at 3.44 mg/mL in 50 mM sodium citrate/0.2 M NaCl/0.1% PEG-8000 at pH 6.5 (Enzyme Research Laboratories) and was diluted to concentrations of 1000, 100 and 10 nM in TBS that included 1 mg/mL bovine serum albumin to block thrombin adsorption to tubing and polydimethylsiloxane (PDMS). Aliquots of 100 μL were stored at −80°C, defrosted at 4°C, and used within 2 h. Alexa-488-labeled 1-μm-sulfate-modified polystyrene beads (F8852, Invitrogen) were used for flow visualization. Fluorescein isothiocyanate (FITC), inorganic salts, and gluteraldehyde were purchased from Sigma-Aldrich (St. Louis, MO). Microfluidic channels were fabricated in PDMS (Sylgard 184, Dow Corning, Midland, MI).

Assembly and operation of membrane-microfluidic device

The membrane-microfluidic device consists of a surface-modified polycarbonate membrane reversibly bonded between two PDMS channels oriented perpendicular to each other (Fig. 1, and Fig. S1 in the Supporting Material). The fabrication and assembly of the device was previously described (15) and has been modified for this study. The geometry of the channel consisted of two different cross-sectional areas; the middle fibrin deposition zone (50 μm × 250 μm) was bracketed on each side by a fluidic resistor (15 μm × 100 μm) (Fig. S1). To incorporate the membrane into the device without leakage, we used a reversible bonding technique where the membrane was placed on a partially cured piece of PDMS (16). A detailed description of the fabrication and assembly can be found in the Supporting Material.

Figure 1.

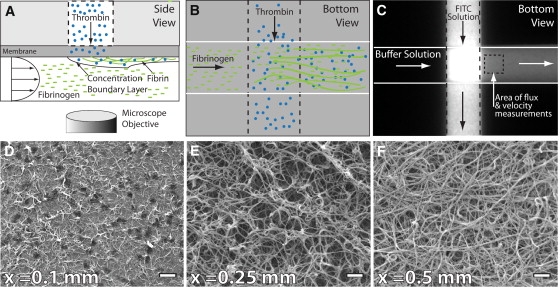
Membrane microfluidic device, operation, and data analysis. The device consists of two microfluidic channels oriented perpendicular to each other and separated by a polycarbonate membrane. Fibrinogen is perfused through the lower channel at a desired wall shear rate. Thrombin is introduced into the flowing fibrinogen at a controlled flux. (A and B) The schematic depicts the side and bottom views of the device. (C) FITC is used as a tracer molecule to measure flux through the membrane before introduction of fibrinogen and thrombin. (D–F) After the experiment, deposited fibrin is fixed and imaged by electron microscopy. The progression of the polymerization is observed as a function of distance from the channel intersection. Scale bar, 1 μm.

Solutions of fibrinogen and thrombin in 1 mL syringes were connected to the device with small-bore Tygon tubing (inner diameter 0.01 in, outer diameter 0.03 in, Small Parts, Miramar, FL). Varying the height of these fibrinogen and thrombin reservoirs controlled the wall shear rate and thrombin flux through the membrane. The hydrostatic head of the fibrinogen reservoir determined the wall shear rate within the bottom channel. The difference in hydrostatic head between the thrombin and fibrinogen reservoirs determined the transmembrane pressure and, thus, the thrombin flux through the membrane (Fig. 1). The thrombin reservoir was always positioned higher than the fibrinogen reservoir so that the pressure gradient across the membrane forced fluid from the upper channel (thrombin) into the lower channel (fibrinogen). Wall shear rate was calculated by measuring the velocity of tracer particles in the lower channel using a manual particle-tracking macro (17) in ImageJ software (18). Thrombin flux was calculated indirectly based on the flux of a FITC solution through the membrane for a given operating condition. See the Supporting Material for a detailed description of these measurements.

Before each fibrin deposition experiment, the lower channel was initially filled with TBS and the upper channel with 100 μM FITC in TBS. The reservoir containing the FITC solution was oriented 0.5–1.5 in above the TBS reservoir and adjusted appropriately to achieve a desired flux. After the measurement of the FITC flux, a thrombin solution (10, 100, or 1000 nM) was introduced into the upper channel to replace the FITC solution. After flowing through a thrombin solution for 5 min, the fibrinogen solution (9 μM) was introduced into the lower channel. The fibrinogen solution contained a molar ratio of 100:1 fibrinogen/fibrinogen-AlexaFluor 647, 20 mM CaCl₂, and 1000×-diluted polystyrene beads. The duration of the fibrin deposition experiment was 5 min. Fibrin deposition was measured every 10 s by epifluorescence using a 20× objective in the area immediately downstream from where the two channels intersect.

Scanning electron microscopy of deposited fibrin

Immediately after a flow experiment, the vacuum was released, the top PDMS piece was removed, and the membrane was peeled from the bottom piece of PDMS. The membrane was rinsed twice in TBS-BSA solution for 5 min, fixed in 2.5% gluteraldehyde for 30 min, rinsed in TBS twice for 5 min, and then rinsed in triplicate in sodium cacodylate buffer (0.2 M. pH 7.4) for 5 min. Samples were then rinsed in graded ethanol solutions (50%, 70%, 80%, 90%, 100%, and 100%) for 5 min, and dehydrated once in 50% and twice in 100% hexamethyldisilazane for 5 min each. A thin film (∼10 nm) of gold was sputtered on samples that were imaged by scanning electron microscopy (SEM; JOEL 7000 field emission SEM, Hitachi, Tokyo, Japan). SEM images were taken with an accelerating voltage of 5 kV and a 6-mm working distance. The diameter of fibrin fibers was measured manually using ImageJ software (18). In each image, 10–20 fibers were measured 10 times each. Fiber diameters were reported as averages and standard deviations. Differences between experimental conditions were determined by a Student t-test (p < 0.01). Brightness and contrast were adjusted on SEM images to optimize viewing. No other image manipulation was performed.

Theory

In the purified system used in this study, which contained only fibrinogen and thrombin, the amount of fibrinogen converted to fibrin monomers under flow was a function of the thrombin flux and wall shear rate. The thrombin flux determined the concentration of thrombin in the boundary layer and the wall shear rate determined the thickness of the boundary layer. This problem is a version of the extended Graetz problem with a Neumann boundary condition (constant wall flux) in a finite region of a confined shear flow. The nondimensionalized thrombin (c_t), fibrinogen (c_f), and fibrin monomer (c_m) conservation equations are

$$\frac{\partial c_t^{\ast }}{\partial x^{\ast }}=\frac{1}{1-y^{\ast 2}}\left[\frac{1}{P{e}^2}\frac{{\partial }^2{c}_t^{\ast }}{\partial x^{\ast 2}}+\frac{{\partial }^2{c}_t^{\ast }}{\partial y^{\ast 2}}\right],$$ (1)

$$\frac{\partial c_f^{\ast }}{\partial x^{\ast }}=\frac{1}{1-y^{\ast 2}}[\frac{1}{P{e}^2}\frac{{\partial }^2{c}_f^{\ast }}{\partial x^{\ast 2}}+\frac{{\partial }^2{c}_f^{\ast }}{\partial y^{\ast 2}}-D{a}_f{c}_f^{\ast }],$$ (2)

$$\frac{\partial c_m^{\ast }}{\partial x^{\ast }}=\frac{1}{1-y^{\ast 2}}[\frac{1}{P{e}^2}\frac{{\partial }^2{c}_m^{\ast }}{\partial x^{\ast 2}}+\frac{{\partial }^2{c}_m^{\ast }}{\partial y^{\ast 2}}+D{a}_f{c}_f^{\ast }-D{a}_m{c}_{fm}^{\ast }],$$ (3)

where Pe is the Peclet number and is defined as Pe = v_maxH/D_i (where D_i is either the thrombin, fibrinogen, or fibrin monomer diffusion coefficient in water, H is the half-height of the channel), Da_f and Da_m are the fibrinogen and monomer Damkohler numbers (defined as Da_f = k_tH²/D_f and Da_m = k_pc_f,oH²/D_m). Da is a ratio of the reaction rate to the diffusion rate. Pe represents the ratio of convective transport to diffusive transport. Equations 1–3 are coupled by the reaction rate, k_t, since the Michaelis-Menten kinetics is dependent on enzyme (thrombin) concentration. Details of the scaling analysis and boundary conditions can be found in the Supporting Material. Equations 1–3 were solved simultaneously using commercial finite-element software (COMSOL Multiphysics 3.4, COMSOL, Natick, MA) in Poiseuille flow for the physical properties shown in Table S1 and the geometry shown in Fig. S2. See the Supporting Material for details of numerical method and comparison to analytical solutions for ideal cases.

Results

We performed experimental and computational studies on the role of wall shear rate and thrombin flux on fibrin deposition and morphology. Table 1 summarizes the parameter space we explored in these studies. Experimental studies were conducted in a membrane microfluidic device (Fig. 1 and Fig. S1) that allowed independent manipulation of the wall shear rate of a fibrinogen solution and the thrombin flux into that solution. Fibrin deposition and morphology were measured by SEM and compared to simulations of combined transport and reaction governing spatial dynamics of fibrinogen, fibrin monomer, and thrombin.

Table 1.

Experimental conditions and corresponding simulation results of dimensionless parameters (Pe and Da_f,max) for the calculated boundary layer thickness and measured fibrin morphology

Wall shear rate (s−1)	Thrombin flux (nmol/μm2 s)	Pe	Daf,max∗	Boundary layer thickness δ (μm)	Measured morphology
10	10−13	19	12	>50	Film
10	10−12	19	165	>50	Gel
10	10−11	19	1647	>50	Gel
25	10−13	47	7	31	Film
25	10−12	47	118	31	Mat
25	10−11	47	1200	31	Gel
50	10−13	94	5	23	Film
50	10−12	94	85	23	Mat
50	10−11	94	951	23	Gel
100	10−13	190	4	18	Film
100	10−12	190	54	18	Mat
100	10−11	190	755	18	Mat

Fibrin morphology was measured by SEM.

^∗Da_f,max was the maximum local fibrinogen Damkohler number from the simulations and was located at y = 0 and x = 250 μm. Boundary layer thickness was defined as the height at which thrombin concentration was 1% of the wall concentration, at x = 250 μm.

Wall shear rate and flux measurements

The imposed hydrostatic head was set to provide 1), convection-dominated transport through the membrane; and 2), minimal perturbation of the flow field in the lower channel. The first requirement had to be satisfied to ensure that there was no diffusion of fibrinogen into the thrombin channel or into the pores. If this requirement went unsatisfied, fibrin would form in the pores and block the flow of thrombin into the fibrinogen channel. The second requirement had to be satisfied so that the flowing fibrinogen solution would not be displaced by the thrombin solution in the lower channel. We found that a difference hydrostatic head of 0.5–1.5 inches H₂0 (125–375 Pa) between the thrombin reservoir and the fibrinogen reservoir satisfied these requirements. This results in a pore Peclet number range (Pe_pore = v_yr_membrane/D_t) of 3–9, indicating that within a pore, convective transport was the dominant transport mechanism. In addition, when a dense suspension of beads was perfused through the lower channel at wall shear rates of 10–100 s⁻¹, these transmembrane pressures showed no evidence of perturbing the velocity profile. At higher transmembrane pressure (>2 in H₂O), the transmembrane flow displaced the oncoming fibrinogen solution off the membrane by >10 μm. The linear relationship between the wall shear rate (s⁻¹) in the lower channel and the hydrostatic head (inches H₂O) of the fibrinogen reservoir was $\overline{{\gamma }_{\text{w}}}$ = 2.79 ΔP_Fbg (R² = 0.98).

To estimate the flux of thrombin, we measured the flux of a fluorescent tracer (FITC) from the thrombin (upper) channel into the fibrinogen (lower) channel. During the measurement, a 100-μM solution of FITC was perfused through the thrombin channel and TBS was perfused through the lower channel. The concentration of FITC (c_FITC (μM)) in the lower channel immediately downstream (Fig. 1 C) from the intersection of the two channels was calculated from the fluorescence intensity (I) using a standard curve (c_FITC = 0.04 I − 11, R² = 0.97). There was good agreement between the theoretical (Eq. S32) and measured flux at wall shear rates of 10, 25, 50, and 100 s⁻¹ (Fig. S3).

Real-time fibrin deposition

Fibrin deposition during a flow experiment was measured by epifluorescence microscopy in the region 250 μm downstream from the introduction of thrombin (Fig. 1 C). We were able to qualitatively monitor in real time the growth of larger fibers (>100 nm) and fiber aggregates. In most experimental conditions, we observed a steady increase in fluorescence intensity across the channel with time, but could not resolve individual fibers. There was no decrease in flow rate in the lower channel in these experiments, as determined by the velocity of tracer beads. In these cases, SEM revealed either a thin film of fibrin or a dense mat of small fibrin fibers. At higher thrombin fluxes, there were observable fibers and fiber aggregates in the channel (Fig. S1). These larger fibers and fiber aggregates formed within the first minute of the experiment and often grew at a rate that ultimately occluded the channel before the end of the 5-min experiment. A channel was considered occluded when polystyrene tracer beads stopped flowing. However, if we stopped the experiment after 1 min, we observed a gradient of fiber sizes as a function of the downstream distance (Fig. 1, D–F). One interpretation of this data is that the axial distance represents the reaction coordinate of fibrin polymerization. At early times (Fig. 1 D), monomers have only had time to form protofibrils. However, as we move further downstream, protofibrils have had time to laterally aggregate into fibers (Figs. 1, E and F). Congruent with these observations, simulations predict that fibrin monomer concentration was initially high (∼3 μM) and then decreased as they formed dimers (Fig. S4). It is not clear whether fibers form in the bulk solution or grow on the surface, or both.

Effect of wall shear rate on mass transfer and fibrin morphology

Simulations of thrombin introduced at a defined wall flux into a flowing fibrinogen solution identified reaction-limited and mass-transfer-limited regimes over the wall shear rates of 10 s⁻¹ to 100 s⁻¹ (Fig. 2). At the lowest wall shear rate (10 s⁻¹), thrombin penetrated across the entire height of the channel within the first 250 μm downstream from its introduction into the flowing fibrinogen solution. No concentration boundary layer formed at this moderate Peclet number (Pe = 19), giving rise to a reaction-limited regime (Table 1). In the reaction-limited regime, and at a thrombin flux of 10⁻¹² nmol/μm² s, the simulation predicted that all of the fibrinogen was converted into fibrin monomers within 500 μm downstream. In the experiment, at the same conditions, we observed well-developed fibrin fibers (diameter 84 ± 22 nm) on the surface of the membrane (Fig. 3 A). In the reaction-limited regime at this thrombin flux, fibrin monomers can form protofibrils and these protofibrils can laterally aggregate into larger fibers.

Figure 2.

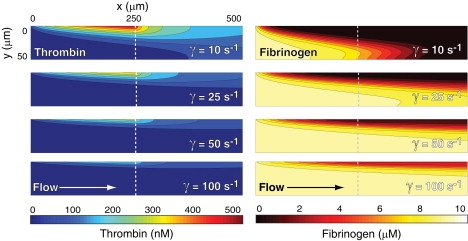
Thrombin and fibrinogen concentration profiles from simulations at wall shear rates of 10, 25, 50, and 100 s⁻¹ and a thrombin flux of 10⁻¹² nmol/μm² s. Thrombin is introduced at a constant flux from the top of the channel from the origin (x = 0 μm) to the dotted line (x = 250 μm). Direction of flow is from left to right.

Figure 3.

Fibrin morphology as a function of wall shear rate. Electron micrographs of fibrin formed after 5 min at a thrombin flux of 10⁻¹² nmol/μm² s and wall shear rates of 10 s⁻¹ (A), 25 s⁻¹ (B), 50 s⁻¹ (C), and 100 s⁻¹ (D). Dark disklike objects in D are the membrane pores. Scale bar, 1 μm.

As the wall shear rate increases, simulations predicted the formation of a concentration boundary layer and the subsequent transition to a mass-transfer-limited regime for fibrin formation (Fig. 2). At wall shear rates of >25 s⁻¹, the Peclet number was large enough for convection to dominate diffusive transport except within a thin concentration boundary layer near the wall. The thickness of the concentration boundary layer scaled as the Pe^−1/3 (Table 1), in agreement with boundary layer theory (20). Based on the simulations, we expected that as the boundary layer thickness decreased, fibrin deposition would decrease, because less fibrinogen would be converted into fibrin monomer (Fig. S4). Experiments at these wall shear rates confirmed this expectation. We observed a dramatic change in fibrin morphology between wall shear rates of 10 s⁻¹ and 25 s⁻¹ (Fig. 3, A and B). At 25 s⁻¹, the fibrin deposited on the membrane took the form of a dense mat of thin fibers interconnected by a thin film. These fibers were much smaller than the mature fibers we observed at 10 s⁻¹ and were randomly oriented on the surface. At 50 s⁻¹, a similar morphology was observed, except that the fibers were sparser and tended to align with the direction of flow.

At 100 s⁻¹, we observed no discernable fibers, only a thin film of fibrin on the membrane surface (Fig. 3 D). A weblike morphology over the 400-nm pores was consistently observed downstream of thrombin introduction. There was no evidence of these morphologies upstream of the thrombin, suggesting that this morphology was a result of fibrin monomer assembly and not just fibrinogen adsorption. We were not able to resolve this webbing over the pores by epifluorescence during the experiment. It is possible that a contiguous film formed during the experiment and the webbing is an artifact of the sample preparation for SEM. However, similar fibrin thin film morphologies have been observed in solution in static experiments between microfabricated ridges spaced 25 μm apart (21).

Fibrin deposition and morphology as a function of thrombin flux

Simulations predicted that the concentration of thrombin within the concentration boundary layer was directly proportional to the thrombin flux. However, the thickness and shape of the concentration boundary layer were solely dependent on wall shear rate. Results from simulations at thrombin fluxes at 10⁻¹³ and 10⁻¹¹ nmol/μm² were identical except for the magnitude of the thrombin concentration, as expected by the linearity of Eq. 3. For example, at 10⁻¹³ nmol/μm² s, the maximum thrombin concentration was 45 nM compared to 450 nM for 10⁻¹² nmol/μm² s.

At a constant wall shear rate of 25 s⁻¹, we observed dramatic changes in fibrin deposition and morphology over the thrombin flux range of 10⁻¹³–10⁻¹¹ nmol/μm² (Fig. 4). At the lowest thrombin flux (Fig. 4 A), we observed a thin film morphology similar to that observed at 100 s⁻¹ and 10⁻¹² nmol/μm² (Fig. 3 D). Increasing the thrombin flux one order of magnitude yielded a few layers of fully developed, cross-linked fibers (Fig. 4 B). At the highest thrombin flux, we observed a dense fibrin gel that occluded the channel within 2–3 min (Fig. 4 C).

Figure 4.

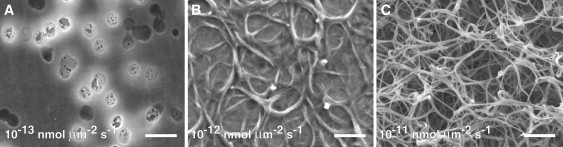
Fibrin morphology as a function of thrombin flux. Electron micrographs of fibrin formed at a wall shear rate of 50 s⁻¹ and thrombin flux of 10⁻¹³ (A), 10⁻¹² (B), and 10⁻¹¹ (C) nmol/μm² s. Dark disklike objects in A are the membrane pores. Scale bar, 1 μm.

At the lowest thrombin flux (10⁻¹³ nmol/μm² s), we did not observe fiber formation at any of the wall shear rates, only fibrin thin films. Simulations predict that the maximum thrombin concentration at this flux was between 25 and 45 nM, depending on wall shear rate (Fig. 2). The maximum fibrinogen Damkohler number at this flux ranges from 4 to 12 (Table 1) over the wall shear rate range of 100 s⁻¹ to 10 s⁻¹, indicating that fibrin monomer production was only moderately faster than diffusion out of the boundary layer. Fibrin monomer concentration was predicted to be relatively low (<1 μM) at this thrombin flux compared to the other two fluxes (Fig. S4). These simulation results suggest that either protofibrils did not reach a minimum length (∼10 monomers) or lateral aggregation did not occur before protofibrils were carried downstream at this low thrombin flux. To determine whether the absence of fibers was due to incomplete conversion of fibrinogen to monomer or not reaching a critical concentration of protofibrils, we performed a set of experiments at high thrombin flux (10⁻¹¹ nmol/μm² s) and low fibrinogen concentrations (300 nM). At this thrombin flux, the thrombin concentration within the boundary layer was as high as 4.5 μM according to simulation results, and all fibrinogen was converted to fibrin monomer within the boundary layer. Even at these high thrombin concentrations, we observed no fibrin fibers under flow, only thin films. Collectively, these experiments and simulations suggest that below a threshold concentration of monomer, fiber growth is not supported, and fibrin monomers and oligomers can assemble into a thin film on a surface.

At the medium thrombin flux (10⁻¹² nmol/μm² s), the fibrin morphology was shear-rate-dependent, as described in the previous section.

At the highest thrombin flux (10⁻¹¹ nmol/μm² s), an occlusive fibrin gel was observed at all wall shear rates except 100 s⁻¹, where we observed only a dense mat of surface fibers. There was not a statistically significant difference in fiber diameter (∼75 ± 25 nm) at wall shear rates of 10, 25, and 50 s⁻¹. Simulations at this high thrombin flux predicted that almost all fibrinogen at the wall is converted to fibrin monomer at 100 s⁻¹ and that all of that monomer was converted to dimer within 250 μm downstream of thrombin introduction. Since we observed surface fibers at 100 s⁻¹ fibers, albeit small ones compared to lower shear rates, we conclude that the limitation to gel growth was transport of reactants (monomers, oligomers, and protofibrils) out of the boundary layer rather than the kinetics of fiber growth.

Fibrin morphology state diagram

Experimental results demonstrate that fibrin morphology is a function of both thrombin flux and wall shear rate. Scaling arguments of the thrombin, fibrinogen, and fibrin monomer conservation equations suggest that fibrin morphology is a function of two dimensionless parameters; the Peclet (Pe) and Damkohler (Da) numbers. The Peclet number describes the ratio of convective to diffusive transport. At low Pe, products and reactants can diffuse across the height of the channel, and fibrin polymerization is only limited by thrombin concentration, and consequently reaction-limited. At high Pe, fibrin polymerization is mass-transfer-limited due to transport of reactants out of a thin concentration boundary layer near the wall. For fibers to form, the rate of linear polymerization and lateral aggregation must be faster than diffusion out of the boundary layer. The Damkohler number describes the ratio of these kinetic mechanisms to diffusion out of the boundary layer. The Damkohler number for fibrinogen (Da_f) is coupled to the local thrombin concentration and ranges over two orders of magnitude in experimental conditions of the study (Table 1). The Damkohler number for fibrin monomer (Da_m) is 243, suggesting that monomers, if at a sufficiently high concentration (>1 μM), will react to form a dimer before diffusing out of the boundary layer (Fig. S4). However, protofibrils must reach some critical length (∼10 monomers) before they can laterally aggregrate. Consequently, the rate of protofibril formation to diffusion may be closer to unity, although a decrease in the diffusion coefficient would be concomitant with each linear polymerization reaction.

Fig. 5 illustrates a state diagram for fibrin morphology based on the scaling of the thrombin and fibrinogen conservation equations and experimental observations. We have divided the state diagram by the three qualitative morphologies we observed; thin films, two-dimensional fiber mats, and three-dimensional gels. Under some experimental conditions the morphology was clear, but in others there were qualities of two morphologies (i.e., thin films and fibers). Therefore, the boundaries between states are unlikely to be sharp transitions. For Da_f < 10, we only observed thin films at all Pe. For 10 < Da_f < 100, we observed either mats of surface fibers or gels, depending on the Pe. For Da_f > 900 and Pe < 100, we observed three-dimensional gels. As Pe→0, we approach no-flow conditions (static gelation) and would expect gels to exist at all Damkohler numbers.

Figure 5.

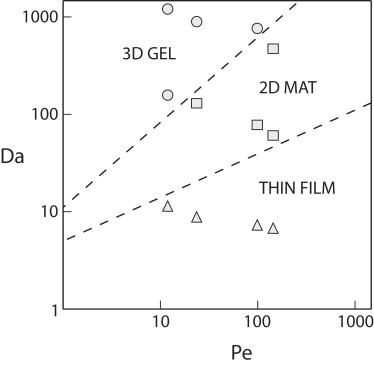
Fibrin state diagram. Fibrin morphology can be described in terms of the Peclet number and the Damkohler number as calculated from simulations. Symbols represent observations from electron miscroscopy; circles = three-dimensional gels, squares = two-dimensional mat, and triangles = thin films. Dashed lines represent the experimentally observed transitions between different morphologies.

Discussion

Fibrin provides a scaffold onto which blood clots grow and stabilize. Although the kinetics of fibrin fiber and gel assembly has been extensively studied in static systems, there is less known about the role of hemodynamics in the fibrin assembly process.

Although there are no direct measurements of the thrombin flux from a clot formed in vivo, there are several estimates based on the enzyme kinetics of the prothrombinase complex and in vitro thrombin generation measurements. Folie and McIntire performed simulations of platelet agonist distribution from model thrombi in a shear flow (12). In their study, thrombin flux was allowed to vary with wall shear rate based on the conversion of prothrombin to thrombin at the surface of thrombi according to the kinetics of the prothrombinase complex. At 100 s⁻¹, they report a thrombin flux of ∼10⁻¹¹ nmol/μm² s, which results in a maximum thrombin concentration of ∼1 μM. Since the prothrombinase reaction is fast (k_cat = 30 s⁻¹), the rate of thrombin production is only limited by the prothrombin flux to the thrombi in their simulations (22). Therefore, they report a roughly linear relationship between thrombin flux and wall shear rate.

Kuharsky and Fogelson presented a more extensive model of thrombin production under flow that includes the entire extrinsic coagulation pathway and the role of platelet accumulation in coagulation (13). In contrast to Folie and McIntire, they predict a moderate decrease in thrombin flux with increasing wall shear rate. For example, the steady-state thrombin concentration within the concentration boundary layer was reported as 70 nM at 100 s⁻¹ and 18 nM at 1500 s⁻¹ for surface TF concentration >15 fmol/cm². These thrombin concentrations correspond to a thrombin flux ∼10⁻¹² nmol/μm² s. These contrasting results are likely attributed to the fact that the Kuharsky model allows platelets to inhibit the activity of surface-bound TF/VIIa. This phenomenon of platelets inhibiting access to TF has since been supported by experimental studies, albeit under static conditions (23). The Kuharsky model also predicts that severe hemophilia A and B (<1% normal factor levels) would result in maximum thrombin concentrations of 1–10 nM, corresponding to a thrombin flux of ∼10⁻¹³ nmol/μm² s. Collectively, these models suggest that the range of thrombin fluxes (10⁻¹³–10⁻¹¹ nmol/μm² s) used in this study provided a good estimate of what is physiologically feasible. These fluxes correspond to thrombin concentrations that range from 10 to 1000 nM, which is also the typical range measured in thrombin-generation assays (24).

Our results in a shear flow showed that formation of fibrin fibers at moderate wall shear rates (100 s⁻¹) required a high thrombin flux (∼10⁻¹¹ nmol/μm² s). This flux is close to the maximum theoretical flux (1.4 × 10⁻¹¹ nmol/μm² s) by the prothrombinase complex based on 2700 binding sites per thrombin-activated platelet and a rate of moles of thrombin produced per mole of Xa of 30 s⁻¹ (25). Yet, even at arterial shear rates there is evidence of fibrin formation in the presence of TF (9,11,26). One explanation that reconciles these two observations is that fibrin polymerization is protected from flow during thrombus growth in some areas. One example is the recirculation flows that form downstream from a stenosis. Studies in flow chambers demonstrate enhanced platelet and fibrin accumulation in these areas (27,28). A second example is the space between platelets within a clot, which can be described as a Darcy-type flow through a porous media. Intravital microscopy of clots formed with the laser injury model show that fibrin accumulation is enhanced near the vessel wall and within a growing thrombus (29).

Experiments at low thrombin flux (10⁻¹³ nmol/μm² s) or low fibrinogen concentration (300 nM) led to the formation of fibrin thin films with no discernable fibers. It seems that at low monomer concentrations, the assembly to thin films is favored over fiber formation. One possible mechanism for the assembly of fibrin thin films is the conversion of fibrinogen to fibrin monomers by fibrin(ogen)-bound thrombin. Riedel and colleagues provide evidence for this mechanism of fibrin thin film growth on surfaces using different thrombin inhibitors (30). In the presence of antithrombin III and heparin, cleavage of fibrinopeptides by thrombin is inhibited in solution. However, thrombin adsorbed to fibrin(ogen) still has catalytic activity that is not blocked by antithrombin III/heparin. O'Brien and colleagues propose another mechanism in which fibrin thin films serve as a precursor to fiber formation (21). In these experiments, fibrin thin films self-assemble in gaps (25–40 μm) between microfabricated features before condensing into fibrous web. However, it is unknown whether these thin films can form in vivo on a more complex surface like the subendothelial matrix and in the presence of endogenous thrombin inhibitors like thrombomodulin.

The mechanism of fibrin fiber assembly in static studies suggests that gel morphology and fiber size are related to the relative rates of protofibril extension and lateral aggregation (5,31). Under flow, these two mechanisms must also compete with dilution of monomers and oligomers by the velocity field. Our results suggest that for a given thrombin flux, flow first quenches lateral aggregation and then protofibril extension. This proposed mechanism is based on the transitions we observed from a three-dimensional gel with mature fibers to a two-dimensional dense mat of very thin fibers, and finally to a thin film with no discernable fibers. The quenching of lateral aggregation could be due to diminished interaction between adjacent αC domains on protofibrils, which has been shown to lead to thinner fibers in certain dysfibrinogenemias (32).

It is important to recognize the differences between the purified solutions used in this study and the more complex composition of plasma when extrapolating results to physiology and pathology in the body. Thrombin inhibitors like antithrombin III in the plasma and thrombomodulin on the surface of endothelial cells are known to limit the growth of a fibrin clot. In addition, calcium concentration is known to influence lateral aggregation. In this study, we used a higher concentration of calcium (20 mM) than found in the plasma (2 mM), which may have favored more lateral aggregation. Other molecules that have been shown to affect fibrin assembly include thrombospondin, platelet factor 4, and polyphosphate (33–35). Future studies are needed to determine the role of other plasma proteins, especially thrombin inhibitors, and platelets in fibrin formation under flow. Furthermore, the rheology of a whole blood will likely influence the assembly and deposition of fibrin. Anand and colleagues developed a model of clot formation that includes the non-Newtonian constitutive relationships of whole blood and the fibrin clot (36). Although that model is much more complex than the simple two-component model of this study, similar trends are observed in terms of a threshold concentration of fibrin monomer needed for fibrin gel formation.

The proposed fibrin state flow diagram has physiological relevance to bleeding and thrombotic disorders. Individuals with hemophilia have an impaired ability to generate thrombin due to deficiencies in coagulation factors. Consequently, they form smaller, less stable clots that lead to prolonged bleeding. Clinically, hemophilia often presents itself in joint and intramuscular bleeds, which are low-shear-stress environments similar to those investigated in this study. We did not observe fibrin fibers at the thrombin fluxes we might expect in hemophilia blood. For some thrombotic disorders, such as deep-vein thrombosis, one of the primary risk factors is decreased blood flow caused by compression of veins or trauma. This decrease in blood flow could cause a transition from a mass-transfer-limited to a reaction-limited regime, resulting in an occlusive fibrin clot.