Alternans Resonance and Propagation Block during Supernormal Conduction in Cardiac Tissue with Decreased [K⁺]_o

Abstract

Cardiac restitution is an important factor in arrhythmogenesis. Steep positive action potential duration and conduction velocity (CV) restitution slopes promote alternans and reentrant arrhythmias. We examined the consequences of supernormal conduction (characterized by a negative CV restitution slope) on patterns of conduction and alternans in strands of Luo-Rudy model cells and in cultured cardiac cell strands. Interbeat intervals (IBIs) were analyzed as a function of distance during S1S2 protocols and during pacing at alternating cycle lengths. Supernormal conduction was induced by decreasing [K⁺]_o. In control [K⁺]_o simulations, S1S2 intervals converged toward basic cycle length with a length constant determined by both CV and the CV restitution slope. During alternant pacing, the amplitude of IBI alternans converged with a shorter length constant, determined also by the action potential duration restitution slope. In contrast, during supernormal conduction, S1S2 intervals and the amplitude of alternans diverged. This amplification (resonance) led to phase-locked or more complex alternans patterns, and then to distal conduction block. The convergence/divergence of IBIs was verified in the cultured strands, in which naturally occurring tissue heterogeneities resulted in prominent discontinuities of the spatial IBI profiles. We conclude that supernormal conduction potentiates alternans and spatial analysis of IBIs represents a powerful method to locate tissue heterogeneities.

Introduction

In cardiac tissue, conduction velocity (CV) and action potential duration (APD) depend on the previous diastolic interval (DI). This dependence, called restitution, is a key factor in arrhythmogenesis. Steep APD restitution slopes promote alternans, lead to wavebreak, and determine the transition between tachycardia and fibrillation (1–4). In classical restitution theory, alternans occurs when the slope of the APD restitution curve is >1 (1,5). Past studies demonstrate that not only APD restitution but also CV restitution determines the stability of conduction and arrhythmogenesis (5–7). The conjunction of both APD and CV restitution also governs the dynamics of head-tail AP interactions during reentry (8), the occurrence of conduction block during rapid pacing (9–12), and the generation of spatially discordant alternans (13–15).

Due to the intricate nonlinear behavior of the AP, this conjunct effect of APD and CV restitution is still not fully elucidated. Previous studies addressed the normal situation in which excitability (and thus CV) decreases when the DI is shortened. However, cardiac excitability and CV can exhibit a supernormal behavior. For example, in animal models, supernormal conduction was observed in the canine His-Purkinje system (16) and in guinea pig papillary muscles (17). In human subjects, supernormal conduction was reported in the atria (18), the His-Purkinje system (19), and the ventricles (20). Experimental (21) and modeling studies (22) indicate that supernormal excitability is potentiated by a decrease of the extracellular potassium concentration ([K⁺]_o). However, the consequences of supernormality on the generation of alternans and arrhythmias have not been explored in detail.

Under the influence of CV restitution, APD alternans can lead to alternation of interbeat intervals (IBIs), i.e., the time intervals between consecutive wavefronts. Thus, a situation can arise in which the AP propagates through a region that generates alternans and then enters a region that would normally not exhibit alternans if paced at a constant cycle length. It is therefore of interest to investigate how IBI alternans is transmitted through cardiac tissue, as wavefronts elicited after shorter intervals are in general more prone to conduction block at sites of structural or functional current-to-load mismatch (23).

In previous work (24), we used spectral analysis to evaluate how IBIs are modulated as a function of distance during pacing at intervals varying randomly. We observed that normal CV restitution attenuates IBI variations, whereas supernormal conduction amplifies them. These effects were maximal for the frequency of alternans, i.e., once every two beats. On this basis, our hypothesis in this study is that supernormal conduction strongly amplifies alternans (a phenomenon that we term “alternans resonance”), even if the APD restitution slope is <1, which could lead to conduction block even in homogeneous tissue. We addressed this hypothesis in simulations with the Luo-Rudy I (LR-I) model (22) and experiments, by pacing cardiac tissue at an alternating cycle length (mimicking a region that generates alternans), and by comparing the modulation of IBIs to that occurring during a conventional S1S2 protocol.

Although the simulation results were consistent with our predictions, the interpretation of our experimental results also required consideration of spatial heterogeneities that occur naturally in biological preparations. Our data suggest that the spatiotemporal analysis of IBIs during S1S2 protocols and during alternant pacing may represent a powerful approach for the detection of heterogeneities in cardiac tissue. Finally, to investigate the mechanisms of supernormal conduction, we used a simplified version of the LR-I model to isolate the contributions of the recovery kinetics of the sodium current (I_Na) and the time-course of final repolarization.

Methods

Computer simulations of conduction

Conduction in cardiac fibers (length: 1 or 10 cm) was simulated using the LR-I model (22). As done previously (7,8,24), the maximum sodium current conductance and the slow inward current conductance were reduced to 8 and 0.04 mS/cm², respectively. Tissue conductivity (lumped intracellular, extracellular, and junctional: 3.333 mS/cm) normalized by the surface/volume ratio (3636 cm⁻¹) was 0.9167 μS, giving a control CV in the range of 40 cm/s. The fiber was discretized with a spatial step size of 0.01 cm and model variables were integrated using a modified Euler method with a time-step of 0.005 ms.

The fiber was paced at one end at a given basic cycle length (BCL) until steady state was established, followed either by an S1S2 protocol or by an alternant protocol that consisted of alternating cycle lengths BCL + Δt and BCL – Δt.

Control simulations were run with [K⁺]_o = 5.4 mmol/L (normal), and supernormal conduction was induced by decreasing [K⁺]_o to 2.0 mmol/L. Activation was defined as membrane potential crossing the −35 mV level during the AP upstroke and repolarization time (determining APD and DI) was defined at −60 mV (∼60% repolarization for both [K⁺]_o).

Experiments in patterned strands of cardiac cells

Patterned strands of neonatal rat ventricular myocytes were grown on microelectrode arrays as described previously (24,25). The animals were handled in accordance with the ethical principles and guidelines of the Swiss Academy of Medical Sciences. The proliferation of fibroblasts was minimized by bromodeoxyuridine (100 μmol/L). The growth pattern was designed to represent a single convolved strand passing over 12 to 48 consecutive recording electrodes at equidistant intervals. This permitted the construction of long strands (up to 12 cm) and the mapping of conduction along their entire length.

Experiments were performed at 36°C on 3–5-days-old cultures using a custom setup described in former publications (24,25). Only structurally intact strands were used (inspection by phase contrast microscopy). All experiments were conducted in Hanks' balanced salts solution. To potentiate supernormal conduction, [K⁺] in the Hanks' balanced salts solution (5.8 mmol/L) was reduced to 2.0 mmol/L.

The strands were paced using S1S2 and alternant protocols, as in the simulations. Extracellular unipolar electrograms were sampled at 10 kHz after amplification (× 1000), and activation times were defined at the occurrence of the minimum of their first derivative (25). As done before (25), overall CV was determined by linear regression of activation time/distance, and local CV was calculated as the ratio of interelectrode distance/conduction time.

Analysis and theoretical predictions

Restitution curves

Simulations in 1-cm-long strands were used to construct S1S2 APD and DI restitution curves (at different BCLs). APD and DI were determined in the central cell of the strand. CV was determined between 0.25 and 0.75 cm. The slopes of the APD and CV S1S2 restitution curves (α and γ, respectively) were determined at the steady-state operation point at each BCL tested.

In the experiments, APD/DI could not be identified from the extracellular electrograms. Therefore, S1S2 CV restitution curves were established as a function of the interbeat interval, after steady-state pacing at a given BCL. As detailed in our previous study (24), these curves correspond to shifted versions of CV versus DI curves, with the same shape and slope.

Interbeat interval variation with distance in a homogeneous cable: theoretical predictions

Because of CV restitution, the interval between the passages of two successive wavefronts at a given position (interbeat interval, IBI) can vary with distance (IBI(x)). Of particular interest is the deviation ΔIBI(x) = IBI(x)-BCL. During steady-state pacing at BCL and stable 1:1 conduction, ΔIBI(x) is always 0. However, for the S1S2 protocol and the alternant protocol, ΔIBI(x) converges back to 0 or diverges away from 0, depending on the characteristics of CV and APD restitution.

In the presence of normal CV restitution (slope γ > 0), impulses elicited at x = 0 during an S1S2 protocol at a coupling interval (CI) shorter than BCL (the steady-state value) propagate more slowly. Consequently, with increasing x, the CI lengthens and CV increases back toward steady-state CV. This is illustrated by the rising arrow in Fig. 1 A based on a hypothetical CV restitution curve, in which the steady-state point is represented as an open circle. Conversely, impulses elicited at a CI longer than the steady-state value propagate faster, and when x increases, the CI shortens and CV decreases back toward steady-state CV (other arrow). A positive CV restitution slope thus stabilizes CV and conduction.

Figure 1.

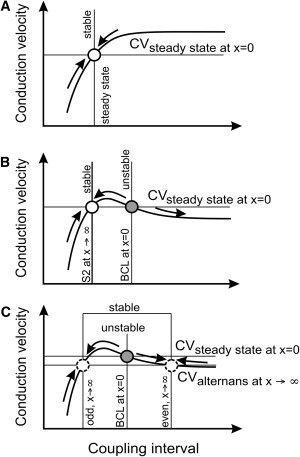
Theoretical considerations on the stability of conduction and on the deviation of the interbeat interval from BCL as a function of distance, for (A) normal conduction during an S1S2 protocol, (B) supernormal conduction during an S1S2 protocol, and (C) supernormal conduction during an alternant pacing protocol. See text for details.

In contrast, for supernormal CV restitution (slope γ < 0 at long CIs), the opposite effect occurs, resulting in a positive feedback that destabilizes CV and conduction as illustrated in Fig. 1 B. For supernormal conduction, we expect therefore that the S1S2 interval will initially diverge with x. In the presence of a biphasic supernormal CV restitution function, premature impulses may, in fact, approach a stable point situated leftward on the CV restitution curve (open circle in Fig. 1 B), for which γ > 0.

As detailed in the Supporting Material, the behavior of IBI(x) for small deviations from BCL can be derived analytically by using a linearized CV restitution function. For the S1S2 protocol, the deviation of the S1S2 interval from BCL exhibits an exponential decay or growth with x, according to the sign of γ, with a length constant Λ_S1S2,

$$\Delta \mathrm{S}1\mathrm{S}2\left(x\right)=\Delta \mathrm{S}1\mathrm{S}2\left(\text{0}\right)\text{exp}\left(-x/{\Lambda }_{\mathrm{S}1\mathrm{S}2}\right),$$ (1)

with

$${\Lambda }_{\mathrm{S}1\mathrm{S}2}=c^{\ast 2}/\gamma ,$$ (2)

where c^∗ is the steady-state CV at BCL.

Another situation of interest is when the tissue is paced at an alternating IBI, a protocol that simulates CL alternans. For normal CV restitution, the situation is similar to that in Fig. 1 A: with distance, the amplitude of alternans will decrease toward 0. For supernormal CV restitution, the unstable nature of supernormal conduction will irremediably lead to an amplification of CL alternans (alternans resonance). The initial divergence is again exponential, but the behavior at a large distance is more complex and depends on the exact shape of the restitution curve. If we assume that no wavefront is blocked, one of the possible scenarios is that the dynamics converge to a stable pattern of CL alternans if the CV restitution function is biphasic. In this case, when x → ∞, CV_odd must equal CV_even, and CL_odd + CL_even must equal 2BCL. This situation is represented by the open dashed circles in Fig. 1 C.

As shown in the Supporting Material, it is also possible to derive an analytical approximation of IBI(x) in the situation of alternant pacing (for small x in the presence of supernormal conduction) by linearizing the CV and APD restitution functions. Under the assumption of first-order APD restitution (APD depends only on the previous DI), the exponential dependence of the amplitude of CL alternans, A_alt, is now determined by a length constant Λ_alt,

$$A_{\text{alt}}\left(x\right)=A_{\text{alt}}\left(0\right)\exp \left(-x/{\Lambda }_{\text{alt}}\right),$$ (3)

with

$${\Lambda }_{\text{alt}}=c^{\ast 2}\left(1-\alpha \right)/2\gamma ={\Lambda }_{\mathrm{S}1\mathrm{S}2}\left(1-\alpha \right)/2,$$ (4)

where α is the slope of the APD restitution function.

When |α| < 1, Λ_alt is therefore always shorter than Λ_S1S2. In the absence of APD restitution (α = 0), Λ_alt = Λ_S1S2/2. This predicts that ΔIBI(x) converges/diverges faster during alternant pacing than during an S1S2 protocol.

Results

Characteristics and ionic mechanisms of supernormal conduction

To investigate the characteristics and mechanisms of supernormal conduction, simulations were conducted in cardiac fibers using the LR-I model. S1S2 APD and CV restitution curves were established at different BCLs and their slopes (α and γ, respectively) were determined at the steady-state points. Example S1S2 APD and CV restitution curves are shown in Fig. 2. In normal [K⁺]_o (Fig. 2 A), for BCL = 500 ms, α was relatively low and γ was close to 0. At shorter BCLs, these slopes increased and at BCL = 100 ms, the operating point was located in the steep region of the CV restitution curve. The APD restitution curves were slightly different for the different BCLs investigated, reflecting some degree of memory of the previous pacing history in the LR-I model. However, for CV restitution, the differences were negligibly small and the curves obtained at different BCLs overlapped. CV restitution was a monotonic increasing function of DI. In decreased [K⁺]_o (Fig. 2 B), APD was prolonged but the general aspect of the APD restitution curves was similar to that in normal [K⁺]_o. However, CV restitution curves were biphasic and exhibited a negative slope, except at very short DIs. At BCL = 500 ms, γ was close to 0, but at BCL = 320 ms, the steady-state point was located in the steep negative region of the CV restitution curve.

Figure 2.

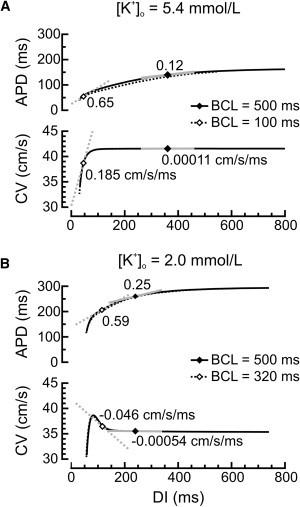
S1S2 APD and CV restitution curves in the LR-I model fiber in (A) normal and (B) decreased [K⁺]_o, for different BCLs as indicated. The markers on the curves indicate the steady-state points, for which BCL = APD + DI. The tangents illustrate the slopes of the restitution curves at these operating points (α and γ, respectively, values indicated).

As a general principle, CV depends on the difference between membrane potential (V_m) when the AP is initiated and the excitation threshold. However, CV is also determined by the availability of I_Na at the onset of the AP, i.e., by the fraction of channels that have recovered from inactivation (in the LR-I model, availability is given by the product of the gating variables h and j). To explore how the time course of V_m during the final phase of repolarization and the availability of I_Na interact to generate supernormal conduction, we used a minimal model consisting only of the Na⁺ current from the LR-I model and a linear time-independent K⁺ current I_{K, lin} defined as

$$I_{\mathrm{K},\text{lin}}=g_{\mathrm{K},\text{lin}}\left(V_{\mathrm{m}}-V_{\text{rest}}\right)\text{.}$$ (5)

In this minimal model, repolarization follows a controllable exponential time-course toward the resting membrane potential (V_rest) with a time constant τ determined by g_{K, lin}. As shown in Fig. 3, S1S2 CV restitution curves were established for two levels of V_rest corresponding to normal and decreased [K⁺]_o and two different values of τ. For V_rest corresponding to normal [K⁺]_o (Fig. 3 A), recovery from inactivation outlasted repolarization and CV was essentially dictated by I_Na availability. Therefore, CV restitution exhibited a positive slope for both values of τ. The effect of accelerated I_Na recovery was then examined by disabling the slow inactivation gate j of I_Na by setting j = 1. In this situation, I_Na recovery was complete (or almost) at a time point where V_m was still a few mV above V_rest. Consequently, beyond that point, CV was determined by the difference between V_m and the excitation threshold and conduction became supernormal. At shorter DIs, however, CV was again dictated by I_Na availability and the restitution slope was positive. The supernormal phase was more prominent in the case of slow repolarization because full I_Na recovery occurred when V_m was further from V_rest. For V_rest corresponding to decreased [K⁺]_o (Fig. 3 B), repolarization to a more negative potential itself accelerated I_Na recovery. With the nominal I_Na formulation, this led to supernormal conduction in the presence of slow repolarization, but not fast repolarization. When the j gate was disabled, supernormal conduction was exacerbated or induced.

Figure 3.

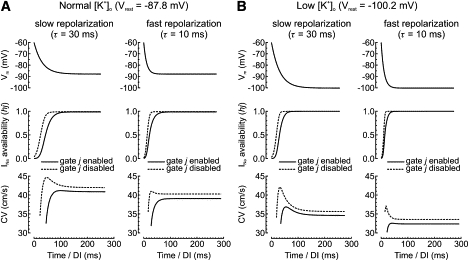
Time-course of final repolarization (top), I_Na availability (middle), and S1S2 CV restitution curves (bottom) in the minimal LR-I model, for (A) V_rest corresponding to [K⁺]_o = 5.4 mmol/L and (B) V_rest corresponding to [K⁺]_o = 2.0 mmol/L. Simulation results are shown for two repolarization time constants (30 and 10 ms). Solid lines correspond to the nominal I_Na formulation and dashed lines were obtained by disabling the j gate of I_Na, simulating accelerated recovery from inactivation. Time is measured from repolarization to −60 mV, defining the beginning of the DI.

Thus, supernormal conduction is generated by a more negative V_rest, a slow time course of final repolarization, and an accelerated recovery of I_Na—three factors that occur upon a decrease of [K⁺]_o. Our simulations indicate that supernormal conduction does not depend on time-dependent properties of plateau and repolarizing currents and that other inward currents are not necessary for supernormal conduction to occur.

Spatial behavior of the S1S2 interval and of the amplitude of IBI alternans in the LR-I model

Simulations of conduction in 10-cm-long fibers were conducted with the full LR-I model to examine the behavior of the S1S2 interval and the amplitude of IBI alternans as a function of distance. Fig. 4 A illustrates the deviation of the S1S2 interval from BCL (ΔS1S2) as a function of distance during S1S2 protocols. The BCLs and [K⁺]_o are the same as in Fig. 2. For normal [K⁺]_o, ΔS1S2 always converged toward 0. For low [K⁺]_o, ΔS1S2 either diverged away from 0 or converged to a stable value different from 0, as predicted theoretically (arrows in Fig. 1 B). The dashed curves are exponentials representing the behavior of ΔS1S2(x) predicted according to Eq. 2, with a length constant Λ_S1S2 calculated from the corresponding values of c^∗ and γ in Fig. 2. For small ΔS1S2, the simulation results were in close agreement with the theoretical prediction. However, for larger ΔS1S2, a discrepancy resulted for both [K⁺]_o because of the nonlinear characteristics of the CV restitution curves.

Figure 4.

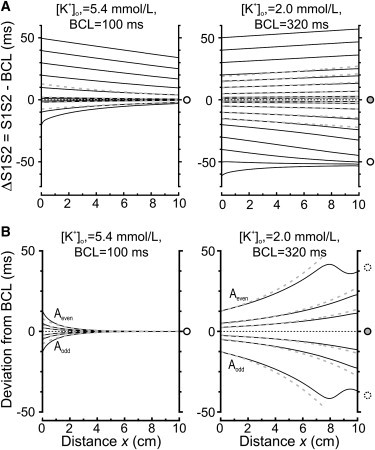
Behavior of IBI(x) in the LR-I model fiber during (A) the S1S2 protocol and (B) the alternant pacing protocol, in normal [K⁺]_o (left panels) and decreased [K⁺]_o (right panels). The BCLs are the same as those for which restitution curves are presented in Fig. 2. Similar to Fig. 1, open circles (on the right side of the plots) indicate a stable point, shaded circles an unstable point, and dotted circles approximate the stable alternating state. The dotted shaded lines represent exponential functions with length constants calculated according to Eqs. 2 and 4 with Λ_S1S2 = 8.1 cm for normal [K⁺]_o and −28.9 cm for low [K⁺]_o (in A), and Λ_alt = 1.4 cm for normal [K⁺]_o and −5.9 cm for low [K⁺]_o (in B), respectively.

A similar approach was used to examine the variation of the amplitude of IBI alternans with distance during alternant pacing protocols. In Fig. 4 B, the deviation of the IBI from mean cycle length is plotted for odd and even intervals (A_odd, A_even) as a function of distance x in the fiber (A_alt = A_even – A_odd), after all temporal transients following the onset of alternant pacing had dissipated and the alternans pattern had stabilized in the spatial domain. For normal [K⁺]_o (left), A_alt converged to 0. In contrast, for low [K⁺]_o (right), A_alt diverged away from 0. Thus, the magnitude of cycle length alternans was amplified with distance (alternans resonance). When A_alt was large enough, A_odd and A_even evolved toward two stable values as expected (arrows in Fig. 1 C). Interestingly, the stable pattern was characterized by a spatial oscillation of A_even and A_odd in the distal portion of the fiber (x > 7 cm). The dashed curves represent the behavior of A_alt predicted according to Eq. 2 (exponential functions with a length constant Λ_alt calculated using c^∗, γ, and α obtained in Fig. 2). For small A_alt, the simulation results were in close agreement with the prediction using linearized APD and CV restitution. For larger A_alt, a discrepancy then resulted from the manifest nonlinear characteristics of the CV restitution function.

Because the fiber is homogeneous, the curves in Fig. 4 are only determined by the initial condition at x = 0, i.e., by the S1S2 interval or by A_alt in the pacing protocol itself. Changing these pacing parameters is therefore equivalent to shifting the spatial reference frame. Indeed, in each individual panel of Fig. 4, the curves can be superimposed by appropriate translations along the x axis (not shown).

In decreased [K⁺]_o, at a mean BCL ≥ 320 ms, alternant pacing always resulted in a stable spatiotemporal pattern of A_even and A_odd once the transient fluctuations had dissipated. However, complex conduction patterns exhibiting persistent variations and conduction block emerged when alternant pacing was conducted at shorter mean BCLs, as shown in the Supporting Material.

Spatial behavior of the S1S2 interval and the amplitude of IBI alternans in cultured cardiomyocyte strands

Experiments were conducted in cardiomyocyte strands to test the prediction that ΔS1S2(x) and A_alt(x) converge during normal conduction, diverge during supernormal conduction, and that this convergence (respectively, divergence) is spatially more prominent during alternant pacing compared to the S1S2 protocol. In the experiment illustrated in Fig. 5, A and B, the preparation was paced at a BCL selected to be short enough to potentiate the effects of restitution on conduction patterns and long enough to guarantee 1:1 stimulation capture during the experiment (100 and 125 ms in control and decreased [K⁺]_o, respectively). Fig. 5 A illustrates ΔS1S2(x) during S1S2 protocols and Fig. 5 B shows A_even(x) and A_odd(x) during alternant pacing. ΔS1S2(x) and A_alt(x) converged to 0 in control [K⁺]_o, and diverged in low [K⁺]_o. Note the inflection of the curves in low [K⁺]_o as ΔS1S2(x), A_even(x), and A_odd(x) approached their respective equilibrium values, in agreement with our simulations.

Figure 5.

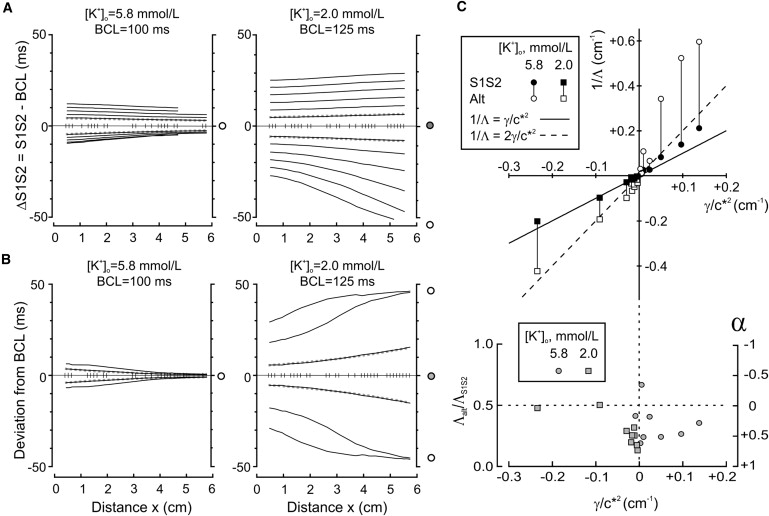
Behavior of ΔIBI(x), Λ_S1S2, and Λ_alt in cultured cardiomyocyte strands. (A) ΔIBI(x) in one preparation during the S1S2 protocol, in normal [K⁺]_o (left) and decreased [K⁺]_o (right). Same format as in Fig. 4A. The vertical markers correspond to the positions of operational electrodes. The dotted shaded curves are exponential fits to the data. (B) A_even(x) and A_odd(x) from the same preparation during alternant pacing. Same format as in panel A and Fig. 4 B. (C) (Top) Summary of Λ_S1S2 and Λ_alt values (represented as their reciprocals 1/Λ) as a function of γ/c^∗2 (according to Eqs. 2 and 4) for all preparations (n = 9). Vertical lines connect data points corresponding to the same preparation in the same [K⁺]_o. The oblique solid line corresponds to Λ_S1S2 = c^∗2/γ (Eq. 2) and the dashed line to Λ_S1S2 = c^∗2/2γ (Eq. 4 with α = 0). (Bottom) Corresponding ratios Λ_alt/Λ_S1S2, and values of α according to Eq. 4.

Estimates of Λ_S1S2 and Λ_alt were obtained by fitting an exponential function through the first and the last available data points (at x₁ and x₂) according to

$${\Lambda }_{\mathrm{S}1\mathrm{S}2}=\left(x_2-x_1\right)/\ln \left(\Delta \mathrm{S}1\mathrm{S}2\left(x_2\right)/\Delta \mathrm{S}1\mathrm{S}2\left(x_1\right)\right)$$

and

$${\Lambda }_{\text{alt}}=\left(x_2-x_1\right)/\ln \left(A_{\text{alt}}\left(x_2\right)/A_{\text{alt}}\left(x_1\right)\right),$$ (6)

respectively. To minimize the influence of restitution nonlinearities, these estimates were determined for the smallest ΔS1S2 and A_alt used in the pacing protocols (5–10 ms). As shown in Fig. 5, A and B, there was an excellent correspondence between the data and the exponential fits in this case. Λ_S1S2 and Λ_alt were both positive in normal [K⁺]_o (12.1 and 2.9 cm, respectively) and both negative in low [K⁺]_o (−15.5 and −5.2 cm, respectively). Moreover, in both high and low [K⁺]_o, Λ_alt was <1/2 of Λ_S1S2, highlighting the involvement of APD restitution during alternant pacing according to Eq. 4.

As shown in Fig. 5 C, the same analysis was conducted for all preparations (n = 9) and the parameters Λ_S1S2 and Λ_alt were compared to c^∗2/γ according to Eqs. 2 and 4 (c^∗ and γ were determined over the entire length of the preparations from S1S2 CV restitution curves). Because large values of γ (strong contribution of CV restitution) are linked to short Λ_S1S2 and Λ_alt, reciprocal values were used in the top panel of Fig. 5 C (plot of 1/Λ_S1S2 and 1/Λ_alt versus γ/c^∗2). Parameters 1/Λ_S1S2 and γ/c^∗2 were correlated (r = 0.975, slope: 1.1), supporting the validity of Eq. 2. Conduction was normal in eight out of nine cases in control [K⁺]_o and supernormal in all nine preparations in [K⁺]_o = 2 mmol/L. The ratio Λ_alt/Λ_S1S2 (Fig. 5 C, bottom), related to the APD restitution slope α by Eq. 4, was highly variable among all experiments (0.32 ± 0.14, corresponding to α = 0.37 ± 0.28), presumably because of the differences in APD restitution between individual preparations. For this reason, the correlation between 1/Λ_alt and γ/c^∗2 was not as good as that of 1/Λ_S1S2 and γ/c^∗2. However, in the majority of cases, the ratio Λ_alt/Λ_S1S2 was between 0 and 0.5, indicating that 0 < α < 1.

Analysis of interbeat intervals facilitates the identification of heterogeneities in cultured strands of cardiomyocytes

Fig. 5, A and B, illustrates the behavior of an ideally homogeneous strand, with results that are in full agreement with our theoretical predictions. However, the other eight preparations exhibited localized heterogeneities of conduction characteristics that influenced the spatial profile of ΔS1S2 and A_alt, as shown in Fig. 6. Fig. 6 A represents the stable activation profile of one of these preparations in normal [K⁺]_o. Although conduction appears uniform at first (linear regression: c^∗ = 28.7 cm/s, r = 0.9997), a slight inflection is nevertheless visible near x = 5 cm, which indicates that conduction was locally depressed. Fig. 6 B shows S1S2 CV restitution curves for the entire strand as well as the locally depressed segment, in both normal and decreased [K⁺]_o. In normal [K⁺]_o, conduction was ∼1/3 slower in the depressed segment compared to the entire strand (18 vs. 28.7 cm/s). In addition, the restitution curve was steeper for this segment (γ = 0.143 vs. 0.0196 cm/s/ms). Based on Eq. 2, the corresponding values of Λ_S1S2 were 2.4 and 42 cm, respectively. Thus, in conjunction, the reduction of CV and the increase of γ decreased Λ_S1S2 by >10-fold in the depressed segment. In this preparation, the other heterogeneities in the conduction parameters c^∗ and γ did not result in local values of Λ_S1S2 sufficiently different from the global Λ_S1S2 to result in manifestly visible discontinuities in Fig. 6 C. In low [K⁺]_o, conduction became supernormal, with a global c^∗ of 30.2 cm/s and a negative γ of −0.0034 cm/s/ms, although it remained locally normal in the segment near x = 5 cm (c^∗ = 27.0 cm/s and γ = 0.016). The corresponding values of Λ_S1S2 were −268 and 47 cm.

Figure 6.

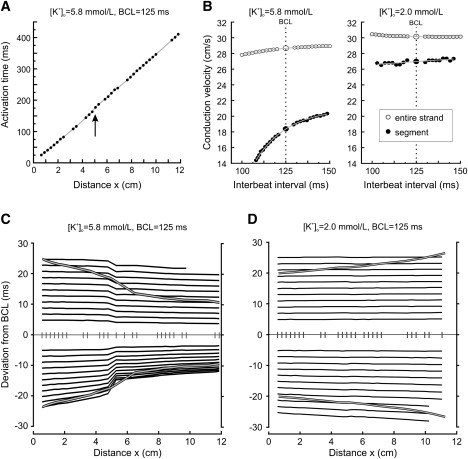
Analysis of conduction, CV restitution, and interbeat intervals in a heterogeneous cardiomyocyte strand. (A) Steady-state activation profile during pacing at BCL = 125 ms in normal [K⁺]_o. Data points correspond to operational electrodes. The arrow denotes a segment in which conduction was depressed (between x = 4.8 and 5.06 cm). (B) S1S2 CV restitution curves established globally for the entire strand and for the depressed segment, in normal [K⁺]_o (left) and decreased [K⁺]_o (right). The curves represent exponential fits to the data. (C) Deviation of the interbeat interval from BCL as a function of distance during S1S2 protocols (ΔS1S2(x), solid) and during the alternant pacing protocol (A_even(x) and A_odd(x), bold shaded traces) in normal [K⁺]_o. The vertical markers correspond to the positions of operational electrodes. (D) Same as panel C, but in decreased [K⁺]_o.

Fig. 6 C represents ΔS1S2(x) for different S1S2 protocols in this same preparation as well as A_even(x) and A_odd(x) during alternant pacing (150/100 ms), in normal [K⁺]_o. All curves converged toward 0, and A_even(x) and A_odd(x) converged with a shorter spatial scale as evidenced by the crossover of the corresponding curves. Furthermore, both ΔS1S2(x) and A_alt(x) curves exhibited a marked localized bend near x = 5 cm, consistent with the substantially lower Λ_S1S2 in this region. The aspect of the S1S2 curves was compatible with the values of Λ_S1S2 calculated above. Finally, the asymmetric pattern of the ΔS1S2(x) curves, with a more prominent convergence for ΔS1S2 < 0, was consistent with the nonlinear aspect of the CV restitution curves. When [K⁺]_o was decreased (Fig. 6 D), ΔS1S2(x), A_even(x) and A_odd(x) all diverged as a consequence of supernormal conduction, and the divergence of A_alt(x) was more pronounced compared to that of ΔS1S2(x). As expected, this divergence was less marked than the convergence in normal [K⁺]_o, consistent with the large Λ_S1S2 (in absolute value).

Similar results were observed in seven other preparations. These preparations exhibited functional heterogeneities that were hardly apparent in a representation of the steady-state activation pattern at BCL, but were enhanced by the analysis of ΔS1S2(x) and A_alt(x).

Discussion

Restitution and spatiotemporal stability in homogeneous cardiac tissue

Starting from theoretical CV restitution curves, we examined how the spatiotemporal stability of an alternating pattern of IBIs depends on CV and APD restitution and compared this behavior to that induced by an S1S2 protocol. In the spatial domain, linear restitution theory predicts an exponential decay of A_alt when γ > 0 and an exponential growth when γ < 0, with a length constant Λ_alt. During an S1S2 protocol, the decay/growth of ΔS1S2 is also exponential, but with a length constant Λ_S1S2 that is >Λ_alt for any value of the APD restitution slope in the interval [−1, 1]. In contrast to Λ_S1S2, Λ_alt depends on both APD and CV restitution characteristics because of the interaction of each beat with the previous beats, whereas, in the case of a single premature/postmature beat, all the previous beats are at BCL and therefore APD restitution does not appear in the derivation of ΔS1S2(x) (see the Supporting Material). In the absence of APD restitution, Λ_alt is expected to be half of Λ_S1S2.

Classically, alternans is generated by APD restitution slopes α > 1. However, even in tissue that is stable according to the criterion α < 1, our study shows that via the mechanism of alternans resonance, already existing IBI alternans can be strongly amplified through the unstable nature of supernormal CV restitution.

The exponential behavior in the spatial domain is based on linear restitution theory. In the case of larger deviations from BCL, nonlinearities in the CV restitution curves will start playing a role. In the case of supernormal conduction, the CV restitution curve is typically biphasic and the slope changes sign when DI decreases below a certain value. In this situation, we hypothesized that a stable point with an IBI shorter than BCL will appear for premature pulses. In the case of alternans, two stable points would appear around BCL, resulting in a stabilization of alternans amplitude. These theoretical considerations in the presence of bi- or multiphasic CV restitution are in line with the earlier work of Miller and Rinzel (26), who observed interspike interval locking in the presence of supernormal conduction in the Hodgkin-Huxley model of nerve propagation. To our knowledge, however, such emergent phenomena have never been investigated in cardiac tissue using simulations or experiments. In cardiac tissue, the precise asymptotic behavior is more difficult to predict due to the interaction of consecutive beats via APD restitution.

For small deviations from BCL, the simulations with the LR-I model confirmed the exponential behavior and the predicted length constants for both the S1S2 interval and IBI alternans amplitude. For larger deviations, the nonlinearities in the CV restitution curves then became dominant. In the S1S2 protocol, the equilibrium at IBI < BCL was observed for premature beats. In the case of IBI alternans, two scenarios were observed, depending on mean cycle length. In the first, alternans amplitude asymptotically converged with distance to slow oscillations around a stable value. In the second, alternans resonance resulted in distal block of the AP elicited after the short interval.

In a study on spatially discordant alternans, Fox et al. (27) observed that 2:1 distal block occurs during rapid pacing when the amplitude of APD alternans becomes large enough at distal sites to preclude activation after long APs. This mechanism also caused 2:1 distal block during alternant pacing in the LR-I model with decreased [K⁺]_o (see the Supporting Material). We note, however, that during alternant pacing, alternans was always concordant when α was <1. Alternans amplitude always decayed monotonically for normal conduction and increased monotonically for supernormal conduction. No node (typical of discordant alternans) was observed in the presence of supernormal conduction. When the fiber in [K⁺]_o = 2 mmol/L was paced at shorter BCL for which α ≥ 1, 2:1 conduction block occurred immediately very close to the stimulation site and discordant alternans was not generated.

As shown by Qu et al. (9,10,14) and by further investigators (11,12), conduction can also be blocked when the wavefront is unable to propagate more slowly than the preceding repolarization tail. This same mechanism also caused distal block during alternant pacing in the LR-I model with decreased [K⁺]_o (see the Supporting Material). However, we did not observe distal block in our experiments, presumably because the length constant Λ_alt was considerably longer in the cultured strands compared to the LR-I model, preventing a resonance of alternans with a sufficient gain.

Tissue heterogeneity and the spatiotemporal analysis of interbeat intervals

Our experiments confirmed that γ determines the behavior of ΔS1S2(x) and that the sign of γ determines the behavior of A_alt, i.e., attenuation or resonance of alternans. Moreover, our experiments confirmed that |Λ_alt| < |Λ_S1S2|. The experiments also showed that heterogeneities play an important role in the local spatiotemporal behavior of IBIs. The majority of our preparations were heterogeneous, illustrating the difficulty to construct long (>10 cm) but homogeneous cardiac cell strands in culture. Because we did not observe any structural alterations in our strands that would explain the observed heterogeneities, we can only conjecture about possible causes. A nonhomogeneous expression of Na⁺ channels and/or connexins would represent a straightforward explanation, as both I_Na and gap junctional coupling directly determine CV (23). However, a heterogeneous expression of other ion channels may also represent a possible mechanism. Furthermore, heterogeneities can arise from the presence of fibroblasts (28). Although the proliferation of fibroblasts was minimized by bromodeoxyuridine, we cannot exclude that clusters of residual fibroblasts may have formed during seeding or incubation.

Intact cardiac tissue is intrinsically heterogeneous as well, and recent work has pinpointed the probable involvement of structural heterogeneities and cardiac fibrosis in reentrant arrhythmogenesis in parallel to the heterogeneous expression of connexins (29). The spatiotemporal analysis of IBIs as presented in Fig. 6 illustrates how new approaches can be developed in the future to identify and locate heterogeneities of cardiac tissue by using the restitution framework. Based on our results, the representation and the analysis of the difference between S1 and S2 isochronal maps (also called isodeviation maps (13), corresponding to S1S2(x)) and between consecutive maps during alternant pacing may represent a powerful method to enhance and reveal the effects of heterogeneities and thus, enable researchers to gain further insights into arrhythmogenic mechanisms.

Clinical implications

Hypokalemia is a common electrolyte abnormality that can create a predisposition to ventricular tachyarrhythmias (30). It is considered severe when serum [K⁺] falls below 2.5 mmol/L. Therefore, the observations and mechanisms that we describe in this study may also be relevant in vivo in the context of severe hypokalemia.

Our analysis, using the minimal LR-I model, helped us to explain the generation of supernormal conduction based on the interactions among resting membrane potential, the time-course of final repolarization, and the kinetics of the recovery of I_Na from inactivation. In human subjects, certain mutations of the SCN5A gene (coding for the α-subunit of the cardiac Na⁺ channel) have been reported to accelerate I_Na recovery, such as the I1768V mutation (31). We therefore hypothesize that such mutations could potentiate supernormal conduction even at moderate levels of hypokalemia, which may further contribute to the generation of alternans and ventricular tachyarrhythmias in carrier patients.

Conclusions

Only few studies have investigated the contribution of supernormal conduction to arrhythmogenesis using the restitution framework. We show that in the presence of supernormal conduction, spatiotemporal interactions between consecutive APs can lead to alternans resonance. This positions supernormal conduction among arrhythmogenic mechanisms. Although our study focused on the effects of decreased [K⁺]_o, we believe that our findings are also relevant for supernormal conduction of any other origin, because our theoretical analysis shows that a negative CV restitution slope is a sufficient condition for the generation of alternans resonance.

As more and more detailed computer models of rodent cardiomyocytes have become available (e.g., (32,33)), it is evident that the use of the LR-I model represents a limitation of our study. However, the simplicity of this model can also be regarded as an advantage: in Fig. 3, it was possible, by using a minimized LR-I model, to untangle the factors that determine supernormal conduction. The interactions between I_Na and the final phase of repolarization we described are likely to pertain to any type of model.

Despite other limitations (conduction in only one dimension, impossibility of measuring APD with the microelectrode arrays), the framework we presented here can be developed further. It can be applied to any elaborate model of the cardiac AP in two or three dimensions and used in a variety of experimental settings, opening the way for new approaches to investigate the spatiotemporal dynamics of conduction and the consequences of cardiac tissue heterogeneities.