Collision-Based Spiral Acceleration in Cardiac Media: Roles of Wavefront Curvature and Excitable Gap

Abstract

We have previously shown in experimental cardiac cell monolayers that rapid point pacing can convert basic functional reentry (single spiral) into a stable multiwave spiral that activates the tissue at an accelerated rate. Here, our goal is to further elucidate the biophysical mechanisms of this rate acceleration without the potential confounding effects of microscopic tissue heterogeneities inherent to experimental preparations. We use computer simulations to show that, similar to experimental observations, single spirals can be converted by point stimuli into stable multiwave spirals. In multiwave spirals, individual waves collide, yielding regions with negative wavefront curvature. When a sufficient excitable gap is present and the negative-curvature regions are close to spiral tips, an electrotonic spread of excitatory currents from these regions propels each colliding spiral to rotate faster than the single spiral, causing an overall rate acceleration. As observed experimentally, the degree of rate acceleration increases with the number of colliding spiral waves. Conversely, if collision sites are far from spiral tips, excitatory currents have no effect on spiral rotation and multiple spirals rotate independently, without rate acceleration. Understanding the mechanisms of spiral rate acceleration may yield new strategies for preventing the transition from monomorphic tachycardia to polymorphic tachycardia and fibrillation.

Introduction

Spiral waves of electrical activity in the heart may overtake the rate of the natural cardiac pacemaker and give rise to a variety of cardiac arrhythmias. For example, periodic rapid activation of the ventricles by a single spiral or multiple synchronized spirals has been shown to underlie monomorphic ventricular tachycardia (VT) (1). In a similar way, a single drifting spiral, or the continuous formation and annihilation of multiple spirals, can activate different regions of the ventricle at different rates and underlie polymorphic VT and ventricular fibrillation (VF) (2). The transition from relatively slow and stable monomorphic VT into accelerated, life-threatening polymorphic VT or VF (3) is believed to be triggered by a focal electrical activity originating from early or delayed afterdepolarizations (4–6), external pacing (7–9), or sympathetic nerve discharges at the vicinity of an infarct site (10).

To date, the phenomenon of VT acceleration has been addressed in only a handful of experimental and computational studies. For example, point pacing during anatomical reentry in a ring of rabbit epicardium was shown to yield the formation of two stable, corotating waves (double-wave reentry) that activated the surrounding tissue at an accelerated rate (11,12). In a similar way, point stimuli during single spiral activity (functional reentry) in slices of sheep epicardium yielded stable rate acceleration via the formation of two counterrotating spirals (figure-of-eight reentry) (13). In computational studies, a dense, random distribution of excited and recovered regions in a large, weakly excitable medium was shown to spontaneously evolve into multiwave spirals that stably activated the medium at a rate faster than that of a single spiral (14). However, the weak excitability, method of induction of multiwave spirals, and large medium size in these studies are generally not directly applicable to cardiac tissue.

In our previous experimental studies, we optically mapped transmembrane potentials in uniformly anisotropic neonatal rat cardiac cell cultures (monolayers), which, similar to native ventricles, had dimensions comparable to the wavelength of a single propagating pulse (15,16). We demonstrated that rapid point pacing in this system could convert a single spiral into a stable multiwave spiral that activated the monolayer at an accelerated rate. Functional predictors of stable rate acceleration included a broad conduction velocity restitution curve and the presence of a relatively large excitable gap during single spiral activity. Furthermore, the degree of rate acceleration increased with the number of rotating spiral waves. It remained unclear, however, whether the stable rate acceleration could be sustained solely by dynamic interactions of multiple spiral waves, or whether the presence of microscopic structural and functional heterogeneities (characteristic of cardiac tissue) was required to support the anchoring and stability of the resulting multiwave spirals.

To further elucidate the mechanisms of rate acceleration in multiwave spirals, we conducted a series of computer simulations of homogeneous isotropic tissue, with tissue size and restitution properties comparable to those of experimental cardiac monolayers. In particular, parameters of the membrane model were varied to create tissue domains that supported stable single spirals with different excitable gaps. We found that appropriately timed and positioned point stimuli in these domains could convert a single spiral into multiple spirals, stably entrained to rotate faster than the original spiral. The resulting rate acceleration in the tissue depended on the size of the spiral excitable gap, the geometry of the colliding spiral wavefronts, and the proximity of the collision sites to the spiral tips. These studies represent a step toward understanding the dynamic factors that dictate the transition from a slower, stable VT to a faster VT or VF.

Materials & Methods

For detailed methods, including simulation parameters and data analysis algorithms, see the Supporting Material.

Simulations

Computational models

One-dimensional (1D) cables and two-dimensional (2D) sheets of homogeneous cardiac tissue were simulated using the three-variable Fenton-Karma (FK) or four-variable Fenton models (17,18). The choice of FK model parameters and tissue size was motivated by our previous experimental studies in neonatal rat ventricular cardiomyocyte monolayers (15,16). The FK parameters were varied until a default parameter set (DPS; Table S1 in the Supporting Material) was obtained to yield action potential duration (APD) and conduction velocity (CV) restitution properties similar to those measured experimentally.

APD and CV restitution

Our previous experimental studies (16) indicated that a particular restitution shape associated with a relatively large excitable gap during single spiral activity was necessary for the induction of stable wave multiplication and rate acceleration. To create a broad range of restitution shapes and resulting excitable gaps during single spiral activity, we varied three FK parameters from their DPS values, namely the percentage of the slow outward current amplitude (%I_so) relative to the default value, the recovery time constant of the fast inward current (τ_v1), and the conductance of the fast inward current (G_fi) (Table S1, shaded entries). The cycle length (CL), diastolic interval (DI), and APD were measured as shown in Fig. S1 A. Parameters derived from 1D restitution are denoted by subscript r, effectively describing plane-wave activity.

Single and multiwave spirals

A single spiral was initiated in a 2D tissue domain using a cross-field S1-S2 protocol (Fig. S1 C). To initiate a multiwave spiral, a properly timed S3 point stimulus was delivered in the wake of a single spiral wave, yielding a), termination of all activity, b), no change in the number of spiral waves in the tissue, or c), stable spiral multiplication (Fig. S2). If a stable multiwave spiral was formed, an S4 point stimulus was applied to introduce additional stable spirals in the medium. Similar to our previous experimental studies (15), multiwave spirals were classified according to the number and chirality of stably rotating spiral waves. For example, a 2/1 multiwave spiral would have two stable spirals of one chirality and one of the opposite chirality.

Spiral data analysis

2D maps and rate acceleration

For all spiral activities, the same temporal quantities (CL, DI, APD), denoted with a subscript s, were calculated at each point in the 2D tissue. Time-averaged spatial maps of CL_s, DI_s, and APD_s were created by averaging the obtained values over a minimum of 2 s (∼12 cycles) of stable spiral activity. The average temporal excitable gap (TEG) of the single spiral (Fig. S1 B) was defined as $\text{TEG}={\text{DI}}_{\text{sp}}-{\text{DI}}_{\mathrm{r}}^{\min }$, where DI_sp is DI_s averaged at the tissue periphery. Since ${\text{DI}}_{\mathrm{r}}^{\text{min}}$ was derived from the 1D (plane wave) restitution, the TEG represented an approximate temporal gap relatively far away from the spiral tip (where the spiral wave starts to approximate a plane wave).

The degree of rate acceleration was computed from CL_s averaged at the tissue periphery (CL_sp) as

$$\%\text{Acceleration}=\frac{1/{\text{CL}}_{\text{sp}}^{\text{Multiwave}}-1/{\text{CL}}_{\text{sp}}^{\text{Single}}}{1/{\text{CL}}_{\text{sp}}^{\text{Single}}}\times 100,$$

where ${\text{CL}}_{\text{sp}}^{\text{Single}}$ and ${\text{CL}}_{\text{sp}}^{\text{Multiwave}}$ are the average periods of activation at the tissue periphery during single or multiwave spiral activity, respectively.

Spiral tip and arm dynamics

For all spiral activities, spiral tips were identified from phase maps (Fig. S1 D). Each tip was tracked in time to obtain tip trajectories, intertip distances (for multiple spirals), drift velocities (V_tip), and intrinsic spiral tip cycle lengths (${\text{CL}}_{\mathrm{s}}^{\mathrm{i}}$) (i.e., the revolution period of a spiral arm around its tip). By calculating V_tip and ${\text{CL}}_{\mathrm{s}}^{\mathrm{i}}$, the effects of spiral tip drift and spiral arm rotation could be studied separately (effectively making the spiral tip stationary).

Wavefront curvature

Wavefront curvatures at each point in space were calculated using a modification of the Kay and Gray (19) algorithm. Briefly, a wavefront was defined as a set of points that have activated (reached −30 mV) but have neighboring points that are above and below −30 mV. The scalar curvature value was defined at each node as the derivative of the wavefront's tangent vector with respect to arc distance from the spiral tip. Positive and negative curvature values correspond to convex and concave wavefronts, respectively.

ΔCV_s maps

To distinguish the effects of curvature on CV_s (independent of DI_s), we constructed spatial ΔCV_s maps during single and multiwave spiral activity, as follows. For each location in the tissue and its associated DI, the CV was conceived as being contributed by two terms: a), the velocity of the plane wavefront at this DI (obtained from the 1D restitution curve), and b), the perturbation (ΔCV) due to the presence of wavefront curvature (κ). To construct ΔCV_s maps, each location in the tissue, associated with an average DI_s and average CV_s, was assigned a ΔCV_s value equal to CV_s − CV_r(DI_s). For κ > 0, a negative ΔCV_s was expected, indicating a slower velocity of the positively curved versus plane wavefront, whereas the opposite was expected for κ < 0.

Results

Dependence of single spiral excitable gap on model parameters

The DPS yielded single spirals with a TEG of 16.8 ms. From the DPS, by independently varying the outward current amplitude (%I_so) and the fast inward current conductance (G_fi) or recovery time constant (τ_v1), we were able to obtain a wide range of TEGs between 7 and 167 ms (Fig. S1). As expected, the largest excitable gaps were achieved with a significant decrease in tissue excitability (low G_fi).

Conversion of single to multiwave spirals

Properly timed and positioned point stimulus during single spiral activity (Fig. S2) were used to create multiwave spirals of 1/1 and 2/0 type in 2 × 2 cm² tissue domain and 2/1 type in 3 × 3 cm² domain (see Fig. S4). Although, the multiwave spirals could be induced with this pacing algorithm for a range of G_fi, τ_v1, and %I_so values, we decided to focus on three cases that were within a range of single spiral excitable gaps found in our cardiac monolayers (8–90 ms) (16), i.e., %I_so = 0.85 with TEG = 13 ms, τ_v1 = 100 with TEG = 30 ms, and G_fi = 0.8 with TEG = 51 ms (referred to hereafter as the I_so, τ_v1, and G_fi cases, respectively).

Rate acceleration of multiwave spirals

The stable formation of multiwave spirals was found to yield rate acceleration only in the τ_v1 and G_fi cases that supported a single spiral with a relatively large TEG, but not in the I_so case (Table 1), with a relatively small TEG. Similar to our experimental studies (16), the addition of new spirals (in the τ_v1 and G_fi cases) further accelerated the activation rate in the tissue (Table 1). A maximum rate acceleration of 22% was measured for the τ_v1 3/1 spiral induced by a point stimulus applied during 2/1 spiral activity. In general, the levels of acceleration obtained in simulations were lower than those measured experimentally (10–70%) (16). Furthermore, within each parameter, rate acceleration for a given multispiral type (e.g., a 2/1 spiral) was higher for parameter values resulting in higher single spiral TEG (compare Table S2 and Fig. S3).

Table 1.

Mean cycle length and acceleration for different parameters and spiral types

Parameter		CL (ms)	Acceleration (%)
Iso = 0.85	1/0	160	—
	1/1	160	0.0
	2/0	160	0.0
	2/1	160	0.0
	3/1	-—	—
τv1 = 100	1/0	211	—
	1/1	191	10.5
	2/0	189	11.6
	2/1	179	17.9
	3/1	173	22.0
Gfi = 0.8	1/0	240	—
	1/1	218	10.6
	2/0	220	9.6
	2/1	208	15.9
	3/1	—	—

Analysis of the spiral tip dynamics

To further study the mechanisms of rate acceleration, we focused our analysis on multiwave spirals with the highest number of waves (i.e., 2/1 for G_fi and I_so, and 3/1 for τ_v1). Similar to our experimental studies, multiwave spirals exhibited both separate (stationary) and overlapping (wandering) tip trajectories (Fig. S4). The mean distance between rotating spiral tips (Fig. 1, A and B) remained steady with time (∼15 mm) and similar for different cases (Table 2), regardless of the presence (τ_v1 and G_fi cases) or absence (I_so case) of rate acceleration. The average spiral tip velocity, V_tip, of multiwave spirals was higher than that of the single spiral for the G_fi case but lower for the I_so and τ_v1 cases (Fig. 1 C and Table 2). Therefore, neither the average distance between tips of multiple spirals nor the change in V_tip due to spiral multiplication was found to consistently correlate with the occurrence of rate acceleration.

Figure 1.

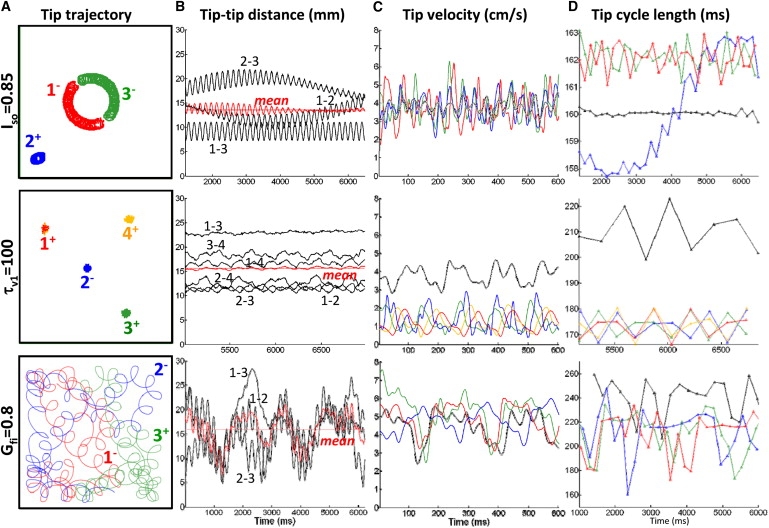
Characteristics of spiral tip dynamics in multiwave spirals. (A) Color-coded tip trajectories. Signs next to the tip numbers denote spiral chiralities. (B) Distances between spiral tip pairs as a function of time. Oscillations in top and bottom rows are due to tip rotations during each cycle. Note that for different cases (rows) the tip-tip distances (black traces) and the mean tip-tip distance (red solid trace) vary distinctly with time, whereas the mean tip-tip distance averaged over the shown time (red dashed line) is comparable among all cases. (C) Tip velocity magnitudes over time, with color coding as in A. (D) Changes in tip cycle length (i.e., period of wave revolution around the tip) over time. Black traces in C and D show corresponding 1/0 cases. The average values from B–D for multiwave and single spiral cases are given in Table 2.

Table 2.

Mean spiral parameter values calculated over the entire tissue domain (excluding boundaries)

Parameter	Iso = 0.85		τV1 = 100		Gfi = 0.8
Spiral type	1/0	2/1	1/0	3/1	1/0	2/1
Tip velocity (cm/s)	3.82	3.77	3.79	1.26	4.41	4.95
Tip-tip distance (mm)	—	13.6	—	15.7	—	15.9
Tip cycle length (ms)	160.0	161.4	209.9	173.5	240.6	211.3
APD (ms)	102.5	104.1	107.6	95.7	99.4	88.3
CV (cm/s)	9.8	10.1	9.7	11.0	9.8	11.27
κ (cm−1)	1.71	1.22	1.68	1.07	1.34	1.10
DI (ms)	57.6	57.8	106.5	77.6	139.3	122.5
TEG (ms)	13.0	13.2	29.8	0.9	51.4	34.6

Parameter values were taken from Figs. 3 and 4.

Rotation rates of individual spirals

Each individual spiral wave within a multiwave spiral was found to rotate with a similar average period (${\text{CL}}_{\mathrm{s}}^{\mathrm{i}}$) around its tip (Fig. 1 D), independent of being stationary (τ_v1), drifting (G_fi and I_so), or at a specific average distance from the boundary or other spiral waves (not shown). In the nonaccelerated multiwave I_so case, these average individual rotation rates were also comparable to that of a single spiral. In contrast, in the accelerated τ_v1 and G_fi cases, the spirals that interacted with each other in a multiwave configuration rotated at an accelerated rate (had shorter average ${\text{CL}}_{\mathrm{s}}^{\mathrm{i}}$) compared to a single spiral in the same tissue (Fig. 1 D and Table 2). As a result, local average activation rates in the tissue were also accelerated either by a repeated activation from the same stationary spiral or by alternate activations from different moving spirals. These local activation rates varied with time (around mean 1/${\text{CL}}_{\mathrm{s}}^{\mathrm{i}}$) due to the movement of individual spirals (Doppler effect (20)) and/or switching to activation by different spirals.

Spatial distribution of spiral parameters

To further elucidate interactions between multiple spirals, we created spatial maps of time-averaged spiral parameters CL_s, DI_s, APD_s, CV_s, and κ (Fig. 2), and derived the average parameters for the entire tissue (Table 2). For the nonaccelerated I_so case, time-averaged CL_s, DI_s, APD_s, and CV_s maps and tissue averages (Table 2) were similar for single and multiwave spirals at sites remote from spiral tips (compare rows 1 and 2 of Fig. 2). In contrast, the formation of multiple waves in the accelerated cases (τ_v1 and G_fi) yielded a decrease in CL_s, DI_s, and TEG in the tissue (Fig. 2, columns 1 and 2, and Table 2). As expected from the monotonic APD restitution curves (Fig. S3), the lower DI_s in multiwave compared to single spirals in τ_v1 and G_fi cases was associated with a lower APD_s (Fig. 2, columns 2 and 3, and Table 2). On the other hand, despite the reduction in DI_s and monotonic CV restitution curves (Fig. S3), CV_s increased rather than decreased (Fig. 2, column 4, and Table 2) suggesting the important roles of wavefront curvature in the interaction of multiple spirals.

Figure 2.

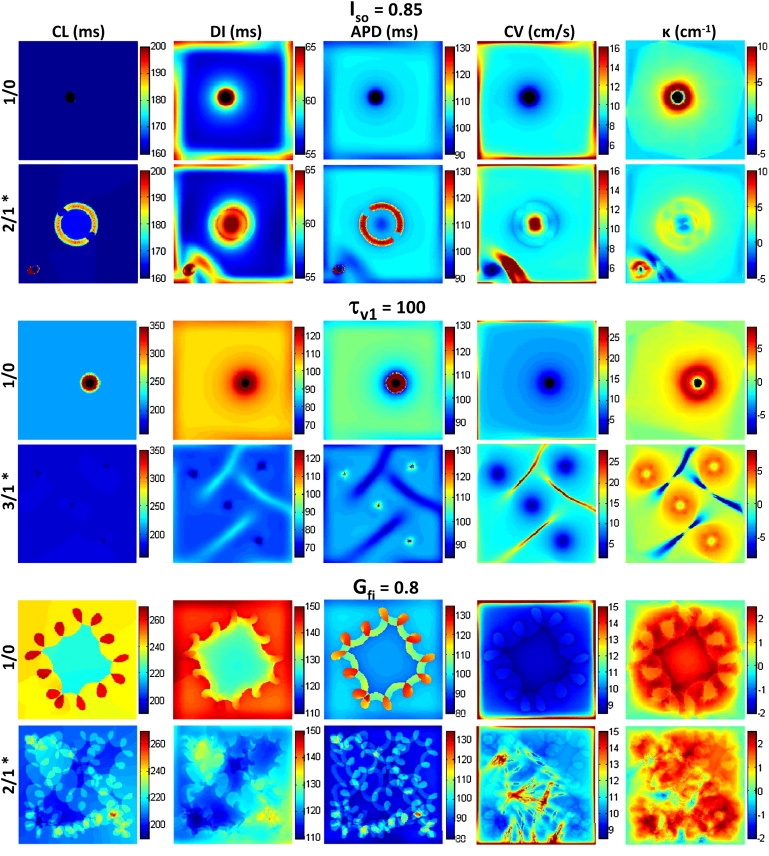
Maps of mean CL, DI, APD, CV, and κ for single and multiwave spirals. Values in the maps are obtained by averaging over the same 10–56 cycles of spiral activity shown in the first column of Fig. S4 for 1/0 cases and in Fig. 1A for 2/1 and 3/1 cases. Color scales are conserved to facilitate comparisons between single (1/0) and multiwave (2/1 and 3/1) spiral maps. The spatially averaged mean values from these maps (ignoring boundaries) are given in Table 2.

By analysis of spatial curvature maps (Fig. 2, column 5), we found that the sites of wave collision in all multiwave spirals introduced highly negative wavefront curvatures, yielding a decrease in the total mean curvature relative to the single spiral (Table 2). As expected from the eikonal relationships (CV and APD versus κ) (21,22), these negative-curvature sites were associated with a local increase in CV_s and decrease in APD_s (most prominent in the relatively stationary I_so and τ_v1 cases; see Fig. 2, rows 2 and 4, and columns 3 and 4). On the other hand, although higher positive curvatures near spiral tips were associated with lower CV_s, APD_s was also reduced (most prominent in 1/0 I_so and τ_v1 maps) rather than increased, due to electrotonic loading by an unexcited tissue area surrounding the spiral tip (23).

Effects of curvature on CV

To further understand the paradoxical increase in CV_s (for decreased DI_s) in accelerated multiwave spirals, we examined the effects of wavefront curvature on CV_s (independent of the effect of varying DI_s) by constructing ΔCV_s maps (Fig. 3 A). In all single spirals, positive wavefront κ values yielded negative ΔCV_s throughout the tissue, as expected (Fig. 3 A). In a similar way, multiwave spirals in the I_so case exhibited predominantly negative ΔCV_s and included small regions of positive ΔCV_s confined only to collision sites with negative curvature (compare Fig. 3 A, row 1, column 2 with Fig. 2, row 2, column 5). In contrast, in the accelerated τ_v1 and G_fi cases, the positive ΔCV_s was not only present at sites of negative curvature, but also spread throughout the tissue where wavefront curvature was positive (compare Fig. 3 A, rows 2 and 3, column 2 with Fig. 2, rows 4 and 6, column 5,). When all ΔCV_s values in the tissue were plotted against corresponding curvatures, the average ΔCV_s versus κ (κ > 0) relationship in the I_so case was similar for single and multiwave spirals (Fig. 3 B). In contrast, the accelerated multiwave τ_v1 and G_fi spirals showed higher average ΔCV_s values than the corresponding single spirals, with positive values measured even for positive curvatures. Therefore, despite having positive curvatures, the wavefronts in accelerated multiwave spirals paradoxically moved at higher velocities than the corresponding plane waves (for the same DI).

Figure 3.

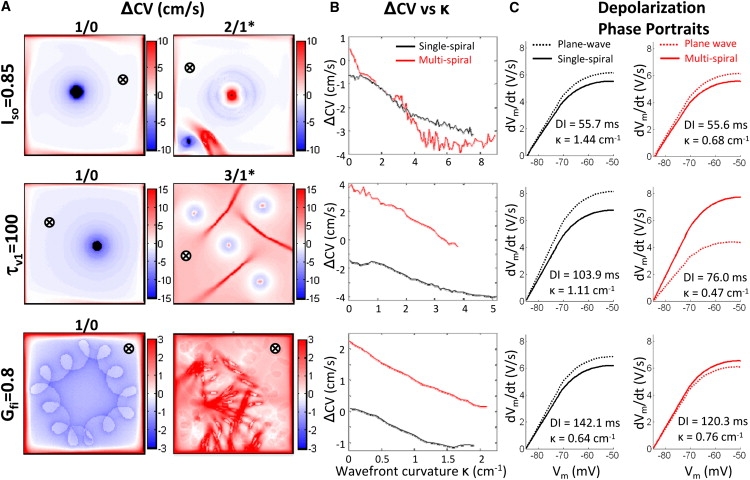
Effects of wave curvature on CV_s and action potential depolarization. (A) Mean ΔCV_s spatial maps. (B) ΔCV_s-curvature relationship for single (black line) and multiwave (red line) spirals. For each point in space, ΔCV_s values represent the difference between the CV_s from Fig. 2 and CV_r from plane-wave restitution curves (Fig. S3) at the corresponding DI from Fig. 2. (C) Assessment of the depolarization phase of the action potential. Representative phase portraits are shown for single (black solid line) and multiwave (red solid line) spirals at a position far from spiral tips and collision sites (denoted by ⊗ in A), as well as corresponding plane waves (dashed lines) at the same DI. Note that despite their positive curvatures, wavefronts in accelerated multiwave spirals (τ_V1 and G_fi) exhibit faster depolarization (including higher (dV_m/dt)^max) compared to plane waves at the same DI.

Effects of curvature on action potential depolarization

To further elucidate the effects of wavefront curvature on propagation, time courses of action potential depolarization were assessed at sites remote from spiral tips, and compared to those measured during plane wave (1D cable) propagation for the same DI. As seen in Fig. 3 C, the take-off potential (V_m^min) was similar in all studied cases. Furthermore, in all single and nonaccelerated multiwave spirals, wavefronts with positive curvature exhibited slower membrane depolarization (lower dV_m/dt at each V_m) and lower maximum upstroke ((dV_m/dt)^max) compared to corresponding plane wavefronts (Fig. 3 C, columns 1 and 2, row 1), as expected. In contrast, the positive curvature wavefronts in accelerated multiwave spirals paradoxically exhibited faster depolarizing action potentials than the corresponding plane wavefronts (Fig. 3 C, column 2, rows 2 and 3). In these cases, the positive wavefront curvature effects were counteracted by the addition of excitatory currents that spread from wavefront collision sites (regions of negative curvature) throughout the available excitable gap to accelerate membrane charging downstream. As a result, spiral wavefronts in these cases rotated faster, yielding an increased activation rate in the tissue.

Role of tissue size and tip proximity in spiral acceleration

When the size of the tissue containing the 3/1 τ_v1 spiral was gradually expanded from 3 × 3 cm² to 8 × 8 cm², the positions and distances of spiral tips slightly changed, with no effects on spiral tip trajectories (Fig. 4, A1), cycle length (Fig. 4, A2), or spatial distribution of wavefront curvatures (Fig. 4, A3) or ΔCV_s (Fig. 4, A4). This result suggests that, although tissue boundaries may be necessary for the point-pacing conversion of a single spiral to certain multispiral patterns (e.g., 1/1 and 2/0 (Fig. S2)), they are not required to maintain accelerated multiwave spiral activity. On the other hand, similar to studies by Zemlin et al. (24), when the same four stable spirals (3/1) were formed in the 8 × 8 cm² tissue remote from one another (Fig. 4, B1), individual spirals rotated independently with no rate acceleration (compare Fig. 4, B2 and Fig. 2, column 1, row 3). In this case, the regions with increased CV_s, including the positive ΔCV_s regions, were confined only to collision sites (Fig. 4, B3 and B4), exerting no effect on spiral rotation.

Figure 4.

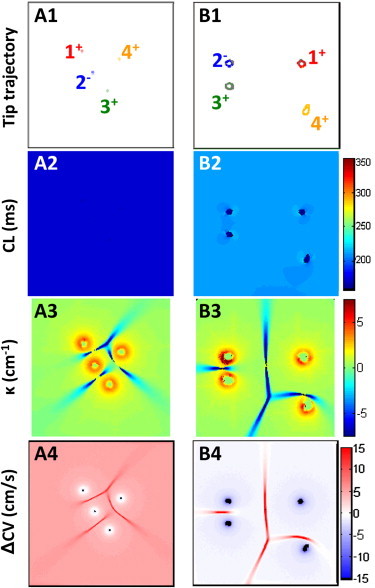
Effect of increased medium size on multiwave spiral activity. (A) The 3 × 3 cm² tissue domain with 3/1 τ_v1 multiwave spiral was gradually expanded to 8 × 8 cm². The resulting tip trajectories and intertip distances (A1) along with the CL_s (A2), κ (A3), and ΔCV_s (A4) distributions remained similar to those in the 3 × 3 cm² domain. As a result, the same degree of rate acceleration persisted. (B) The 3/1 τ_v1 multiwave spiral was reinitiated in an 8 × 8 cm² tissue domain at rest by forming phase singularities at the corners of a 2 × 2 cm² square in the center. The tip trajectories (B1), along with the CL_s (B2), κ (B3), and ΔCV_s (B4) behaved as in the single spiral case, and no rate acceleration occurred. Note that compared to A, the mean intertip distance was increased and the positive ΔCV_s regions were present only at collision sites.

Discussion

Several studies have shown that multiple, coexisting spiral waves can activate a medium at a faster rate than a single spiral. In particular, in double-wave anatomical reentry in atrial or ventricular tissues (11,12) and in multiarm spirals in chemical reactions (25,26) or marginally excitable computational media (27), multiple noncolliding waves rotated in the same direction around a common central core. Although each of the waves had a rotation rate comparable to or lower than that of the single spiral, they activated the tissue in series, yielding an overall acceleration of the activation rate. In this computational study, we described a qualitatively different mechanism of rate acceleration in which each of the multiple spirals rotated around its own tip at a faster rate than the original single spiral. Specifically, the multiple spirals mutually collided, yielding regions with negative wavefront curvature and, consequently, faster conduction velocity. Depending on the ionic properties of the tissue (i.e., size of the single spiral excitable gap) and the proximity of collision sites to spiral tips, these perpetual boosts in conduction velocity effectively propelled each individual spiral to rotate faster and activate the tissue at an accelerated rate. The described mechanism, which we call rotational acceleration, was observed for both stationary (τ_v1 case) and meandering (G_fi case) spirals.

Role of excitable gap in spiral acceleration

As shown in different experimental studies, single spirals (functional reentries) in cardiac tissues are associated with a significant excitable gap. Examples include the 30-ms excitable gap reported in rabbit ventricles (28), the 50-ms gap in canine and sheep ventricles (29), and the 90-ms gap in canine atria (30). In our previous studies in neonatal rat cardiac cell cultures (16), only single spirals with relatively large excitable gaps (70 ms) were accelerated by spiral wave multiplication. In a similar way, in this study, single spirals with a small excitable gap initiated in ratlike tissue domains (2 × 2 or 3 × 3 cm²) were not accelerated by spiral wave multiplication (I_so = 0.85 case). However, when the restitution properties were altered to increase the single spiral excitable gap (τ_v1 = 100 and G_fi = 0.8 cases), spiral wave multiplication yielded accelerated activity. In a similar way, a significant excitable gap was required for spiral acceleration in large computational domains (20 × 20 cm²) with humanlike restitution properties (τ_fi = 0.11 vs. τ_fi = 0.27 case (Fig. S5)).

It is important to note that the majority of computational models, including those of human ventricles (31), support single spirals with a rotation period near the minimum cycle length, beyond which propagation fails. By definition, tissue activated near the minimum cycle length (i.e., break point of the dynamic restitution curve) has little or no temporal excitable gap and will be unable to sustain an accelerated activation rate. Thus, most current computational models permit either studies of VT (if restitution properties of the medium are dynamically stable) or VF (if restitution properties at high activation rates are unstable and yield spiral breakup), but do not allow study of conversions between stable VT and stable accelerated VT or VF. It is possible that a relatively small, nonphysiological excitable gap in simulated spirals is caused by unrealistic mathematical descriptions of fast sodium or different potassium currents (32,33). On the other hand, homogeneous computational media do not contain microheterogeneities inherently present in native cardiac tissues. These heterogeneities may force the spiral tip to trace a tortuous path, causing an increase in the excitable gap in native tissues (16,34).

Realistic conversion of single to multiwave spiral

In previous studies, stable multiwave spirals were induced via nonphysiological methods by creating and subsequently removing a central unexcitable obstacle in the medium (25,26), joining multiple media each containing a stable single spiral (35), or presetting a spatial distribution of multiple excited and recovered regions within a large medium (14,24). In contrast, in this study, we utilized medium boundaries and properly timed and positioned point stimuli to convert single spirals into different multispiral patterns (Fig. S2). We speculate that, similar to this wave multiplication scenario, the endogenously (afterdepolarizations, sympathetic discharge) or exogenously (electrical pulse) induced focal activity in heart tissue may convert simple VT into a more complex activity in the presence of physiological boundaries, such as the atrioventricular groove, blood vessels, or an infarct scar.

Collision-induced negative curvature as a mechanism of rate acceleration

At the site where two spiral wavefronts collide, the resulting negative wavefront curvature (Fig. 5, A2) creates a local excess of depolarization currents relative to the downstream load. These currents will not only increase the CV at the collision site (Fig. 2), but will also tend to spread through the excitable gap toward the tips of the two colliding spirals. When an excitable gap is present along the entire spiral wavefront, and the supplied excess currents are sufficient to excite the recovering tissue downstream of the spiral tip, the rotational phase of the spiral will be advanced (i.e., the spiral cycle will be shortened (Fig. 5, A2)). If this boost in rotation speed repeats every spiral cycle, the average rotational rate of the colliding spirals will stably increase. The condition that spiral tips remain stationary is not required for this process (e.g., G_fi case), provided that collisions continuously propel spiral rotation. A higher number of spirals in the same tissue will produce a higher average number of collisions per spiral cycle to yield ultimately a higher degree of rate acceleration (Table 1). The fact that similar results were found in both small ratlike and large humanlike computational cardiac media (Fig. S5 B) suggests that a common biophysical mechanism may underlie the multiplication-based spiral acceleration in different cardiac tissues.

Figure 5.

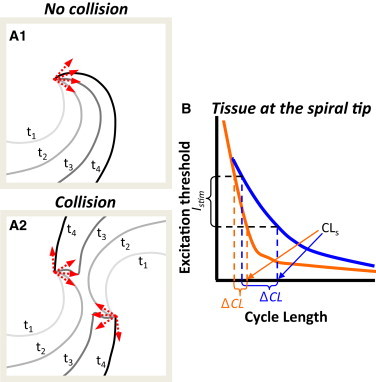
Mechanisms of acceleration in multiwave spirals. (A) Mutual entrainment and advancement of individual spiral phases in multiwave spirals. (A1) Isochrone lines during rotation of a single spiral. Red arrows denote rotational phase of the spiral at times t₁–t₄. (A2) Wavefront collision between two spirals yields faster phase advancement. Isochrones t₁–t₄ show the same time interval as in A1. Note negative curvature at t₃ and the greater advancement of spiral phase between t₂ and t₃ and between t₃ and t₄ compared to A1. (B) Schematic of a spiral CL (CL_s) reduction (rate acceleration) due to the application of external stimulus. Two tissues with different excitation threshold versus premature interval curves at the spiral tip are shown in blue and orange. The negative curvature due to wave collision creates excess depolarizing current, which is equivalent to a suprathreshold stimulus. If I_stim, the current supplied to the spiral tip from the site of collision, is sufficient to excite downstream tissue near the tip, it will advance the spiral phase and decrease the CL. Note that the difference between CL_s and minimum CL at which tissue can be excited represents the available room for rate acceleration. The slope of the curve and the amount of supplied excitatory current, I_stim, determine ΔCL and the resulting degree of rate acceleration (ΔCL/(CL_s − ΔCL)).

The described process of rotational acceleration conceptually resembles well-studied phenomena of reentry resetting and entrainment by a pacing electrode (36,37). Specifically, each wavefront collision is equivalent to a point stimulus with its amplitude determined by the magnitudes of negative curvature and local depolarization currents (Fig. 5 B). Although the location of the pacing (collision) site is generally variable, the stimuli are constantly delivered at the maximum local coupling interval. Pacing at the maximum local coupling interval provides the highest chance for stimulus currents to locally excite the tissue and invade the excitable gap. Whether the stimulus currents will reach and excite downstream tissue at the tip and advance spiral rotation depends on the size of the excitable gap, the amplitude of the stimulus, and the distance from the pacing site to the spiral tip. When the two colliding spirals undergo advancement (e.g., in the G_fi and τ_v1 cases), the return cycle (38) at the pacing site will be shorter than the single spiral cycle. This return cycle determines the mutual entrainment rate for the two spirals. For multiple spirals, the cumulative contribution from all pacing (collision) sites to spiral advancement determines the final degree of rate acceleration.

The role of wavefront curvature in acceleration

According to the eikonal curvature-CV relationship, positive curvature wavefronts will propagate slower (exhibit ΔCV < 0) and negative curvature wavefronts will propagate faster (exhibit ΔCV > 0) than plane waves at the same DI (21,22,39). Although this was generally the case in all single spirals and nonaccelerated multiwave spirals (Fig. 3, A and B), the accelerated multiwave spirals exhibited large tissue regions with both positive curvature and positive ΔCV (Fig. 3, A and B), thus apparently contradicting the eikonal relationship. Analysis of the depolarization phase of the action potential revealed that the charging of membrane capacitance was faster and the action potential upstroke was higher in these regions than during plane-wave propagation at the same DI (Fig. 3 C). We attributed this finding to the presence of excess depolarization currents that spread from the collision sites (with negative curvature) into the excitable gap. If these same currents were somehow added during 1D restitution measurements, the plane-wave CV values would be increased, and paradoxically positive ΔCV values would become negative, as expected. These observations demonstrate that eikonal equations are not directly applicable to tissue regions with altered current source-sink relationships (e.g., near wave collisions, pacing sites, unexcitable boundaries, spiral cores, etc.).

Limitations and perspectives

All of the findings in this study were obtained using phenomenological three- and four-variable models (17,18) that do not reflect the diversity or detail of the realistic cardiac ion currents. The use of 2D homogenous isotropic tissue domains with alternans-free restitution properties represents an additional simplification with respect to native tissues. Nevertheless, we established a framework to systematically study the focally triggered conversion of stable VT to VF by demonstrating, for the first time computationally, to our knowledge, a realistic electrophysiological regime whereby external point stimuli can stably convert a single spiral into accelerated multispiral activity. Future computational studies of how specific ionic currents and tissue structures modulate the impact of negative curvature on multispiral dynamics are expected to further advance our understanding of the VT-to-VF transition. The question remains whether or not these studies can be performed in homogeneous continuous media, or whether more realistic computational cardiac substrates with microscopic heterogeneities and discrete architecture will be needed (40–42). If restitution properties could be tuned to support stable rotation of a single spiral in a homogeneous medium while also supporting dynamic instabilities at activation rates higher than the spiral rate, the conversion from a stable periodic to a stable aperiodic activation regime could, for the first time, be computationally studied in the same homogeneous tissue.

Summary

In this study, we have shown that properly positioned and timed point stimuli can convert a single spiral with an excitable gap into an accelerated multiwave spiral. The resulting acceleration of activation rate is sustained solely by dynamic interactions among multiple spiral waves without a need for micro- or macroscopic tissue heterogeneities. In particular, within the multiwave spiral, individual spirals entrain one another through recurring wave collisions that form regions with negative wavefront curvature near spiral tips. These regions create a surplus of depolarization currents that spread throughout the excitable gap to facilitate the excitation of downstream tissue and accelerate spiral rotation. A higher number of spirals and associated collisions in the same tissue yields a higher degree of rate acceleration. Similar collision-based mechanisms may not only underlie acceleration of functional cardiac reentry, but also yield accelerated activity in closely spaced anatomical reentries (e.g., during atrial flutter or fibrillation (43)).