Monte Carlo Simulation of Buffered Diffusion into and out of a Model Synapse

Abstract

Buffered diffusion occurs when ligands enter or leave a restricted space, such as a chemical synapse, containing a high density of binding sites. This study used Monte Carlo simulations to determine the time and spatial dependences of buffered diffusion without a priori assumptions about kinetics. The synapse was modeled as a box with receptors on one inner face. The exterior was clamped to some ligand concentration and ligands diffused through two sides. Onset and recovery simulations were carried out and the effects of receptor density, ligand properties and synapse geometry were investigated. This study determined equilibration times for binding and the spatial gradient of unliganded receptors. Onset was characterized by a high spatial gradient; equilibration was limited by the time needed for sufficient ligands to enter the synapse. Recovery showed a low spatial gradient with receptor equilibration limited by ligand rebinding. Decreasing ligand association rate or increasing ligand diffusion coefficient reduced the role of buffered diffusion and decreased the spatial gradient. Simulations with irreversible ligands showed larger, persistent spatial gradients. These simulations identify characteristics that can be used to test whether a synaptic process is governed by buffered diffusion. They also indicate that fundamental differences in synapse function may occur with irreversible ligands.

Introduction

Buffered diffusion occurs when high affinity ligands enter or leave a restricted space containing a high density of ligand binding sites. The first quantitative study of buffered diffusion was in 1972. Colquhoun and his colleagues examined the kinetics of labeled tetrodotoxin uptake by nerve bundles (1). Equilibration of toxin with the sodium channels in the nerve bundles containing up to 150 individual nerve cells required hours. Because of the high density of sodium channels present, the rate-limiting step was the time required for sufficient toxin to enter and diffuse through the nerve bundle; individual binding events occurred much more quickly. That study included a mathematical description of the problem and a numerical solution that assumed fast binding kinetics.

In 1979, Armstrong and Lester (2) applied the concept of buffered diffusion to the kinetics of the functional action of (+)-tubocurarine on nicotinic acetylcholine receptors (nAChR) within a single frog neuromuscular junction. Although these kinetics were on the timescale of seconds, the authors showed that the process was limited by buffering rather than binding. Specifically, the kinetics were accelerated when the density of available receptors was reduced with an irreversible antagonist and also when the nerve terminal was removed. A subsequent study (3) examined another prediction of the buffered diffusion model: that the kinetics of equilibration are inversely proportional to the affinity of the ligand for the receptor. Using frog neuromuscular junction, they found this to be valid over a fourfold range of affinity.

Buffered diffusion occurs in other physiological situations as well, particularly those that involve intracellular calcium ions with mobile and stationary buffers. In some cases, the problem was addressed analytically assuming a particular geometry: uniform space (4), a sphere (5), and a hemisphere with a point source of calcium (6,7). Monte Carlo simulation has been used for more complex geometries (8,9).

When the previous studies of buffered diffusion at the neuromuscular junction were carried out, the binding kinetics of nAChR competitive antagonists were unknown. Since then, association and dissociation rate constants have been determined for several antagonists at mouse nAChR (10–12). Using this information, I wanted to calculate the kinetics of receptor occupancy under realistic physiological conditions without making the a priori assumption that binding is fast. This question was addressed using Monte Carlo simulation of ligand entry into and exit from a model synapse. Simulations were carried out using a variety of conditions to assess the effects of ligand kinetics, diffusion coefficient and concentration, receptor density, and synapse dimensions. Situations were addressed in which ligands bind irreversibly to receptors. The results indicate the range of conditions for which buffered diffusion is the rate limiting step, determine combinations of parameters that have complementary effects on diffusion times and identify some unique properties of irreversible ligands.

Methods

Monte Carlo simulations were carried out using MCell 3.1 (http://www.mcell.cnl.salk.edu/) (13,14) running on an Apple MacBook Pro with 2.4 GHz Intel Core 2 Duo (Mac OSX 10.5.6). Ligand and receptor counts were stored in files every 0.01–1.0 ms depending on the duration of the simulation. Visualizations and movies were made from the output of MCell using DReAMM 3.3.0 (http://www.mcell.psc.edu/DReAMM/) and QuickTime Player 7.6.

The model illustrated in Fig. 1 represents a section of a narrow synapse between cells. In this 1 × 2 × 0.05 μm box, the presynaptic cell membrane is on top (+z) and the postsynaptic cell membrane is below (lower x-y surface). The cleft thickness, t_cleft, nominally 0.05 μm, is varied in some simulations. Nondiffusing receptors at a density of ρ are distributed randomly on the 2 μm² postsynaptic surface. The front and rear x-z surfaces are considered to be in contact with an external reservoir of ligands of concentration [C] and diffusion coefficient D. This is achieved with the MCell3 command CLAMP_CONCENTRATION. The two membrane surfaces reflect ligands. The box is considered to be one slice of a synapse that extends further along the x axis. This is modeled by having the right and left surfaces of the box (y-z planes) reflect ligands. The box is divided into 10 numbered segments along the y axis (Fig. 1) for the purpose of counting receptors and ligands at different distances from the clamped surfaces. In the figures, receptors and ligands in sections that are the same distance from a clamped surface are summed (e.g., segments 1 and 10 are denoted as 1 + 10).

Figure 1.

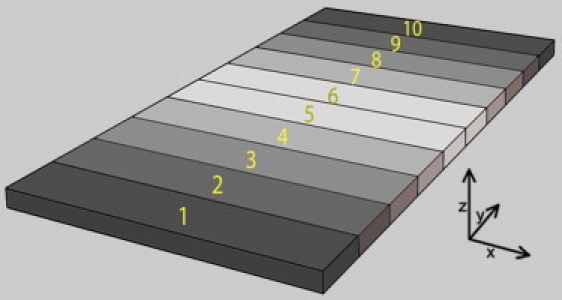
Synaptic model used in the MCell simulations. A simple model in which the synapse is represented by a box with dimensions 1 × 2 × 0.05 μm. Receptors are located on the lower x-y surface (postsynaptic membrane) only. The front and rear x-z surfaces are clamped to the desired ligand concentration and all other surfaces reflect ligand molecules. The box is divided into 10 numbered sections for the purpose of counting receptors and ligands at different distances from the clamped sides. In the figure, sections that have the same distance from a clamped side (e.g., 1 and 10,) are considered together. The synaptic cleft thickness, t_cleft, is varied in some simulations.

This study used a two state kinetic model to describe the binding of ligands, C, to receptors, R with an association rate constant of ${\ell }_{+}$ and a dissociation constant of ${\ell }_{-}$. The dissociation equilibrium constant is L_eq = ${\ell }_{-}$/${\ell }_{+}$,

$$C+R\underset{{\ell }_{-}}{\overset{{\ell }_{+}\left[C\right]}{\rightleftharpoons }}CR\text{.}$$

Simulations were carried out using a set of standard parameter values (Table 1). Subsequently, I varied the parameters individually to test the effects of the parameters on buffered diffusion.

Table 1.

Standard values of the parameters used in the simulations

Parameter	Standard value
Ligand association rate, ${\ell }_{+}$	1 × 108 M−1 s−1
Ligand dissociation rate, ${\ell }_{-}$	3 s−1
Ligand diffusion coefficient, D	1 × 10−6 cm2 s−1
Ligand concentration, [C]	450 nM (15 × Leq)
Receptor density, ρ	104μm−2
Synaptic cleft thickness, tcleft	0.05 μm

A time step of 0.25 μs was used for simulations with the standard parameters. With this value, the average lifetime of every molecule was >50 time steps, the suggested criterion in the MCell3 Reference Guide. For simulations with the ligand association rate increased to 10⁹ M⁻¹s⁻¹ it was necessary to reduce the time step to 0.1 μs.

Simulations were carried out in two phases. In the first phase, onset, the external concentration was clamped to some nonzero value (initially 450 nM), all receptors were unliganded (R = 10⁴ μm⁻² × 2 μm² = 20,000) and there were no free ligands inside the box. The simulation proceeded until equilibrium receptor occupancy $R=\frac{20,000\times L_{\text{eq}}}{\left[C\right]+L_{\text{eq}}}$ and equilibrium free internal ligand count was achieved. Using the standard parameter values (Table 1), there is an average of 27.1 free curare molecules in the box at equilibrium (450 nM). For the onset simulation shown in Fig. 2, 5 s of simulated time required ∼5 min of computation time. In the second phase, recovery, the external concentration was clamped to zero. The simulation proceeded until R > 19,000 and free ligand molecules ≈0. For the recovery simulation shown in Fig. 3, 95 s of simulated time required ∼14 min of computation time.

Figure 2.

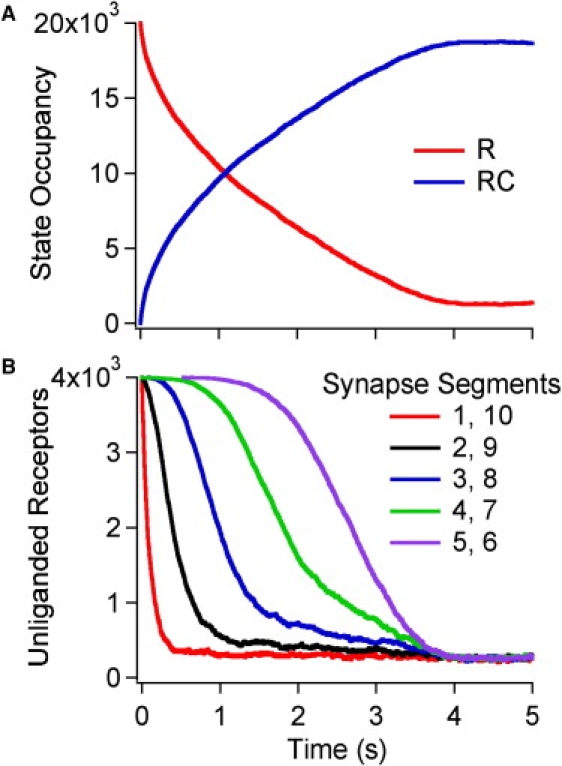
Time dependence of receptor occupancy during the onset phase of buffered diffusion. The standard parameters (Table 1) were used in this simulation. Ligands bind to a single site on each of the 2 × 10⁴ receptors. The ligand concentration external to the synapse was clamped at 15 × L_eq so that at equilibrium, only 6.25% of the receptors were unliganded. The simulation was run using a time step of 0.25 μs; traces show points at 1 ms intervals. Fig. S1 shows the corresponding graphs for free ligands. (A) Unliganded (R) and liganded (RC) receptors as a function of time. (B) Unliganded (R) receptors as a function of time within the different segments of the box synapse. Segments 1 and 10 are nearest to the clamped surface.

Figure 3.

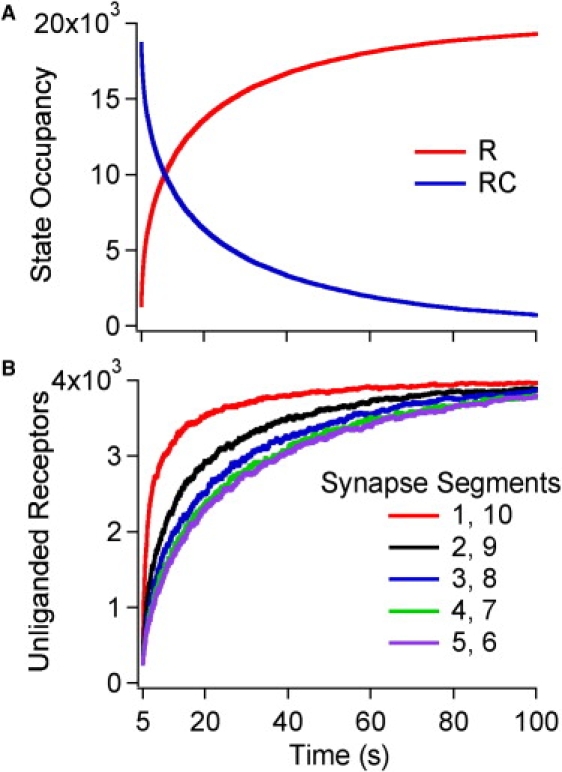
Receptor occupancy and free ligand concentration during the recovery phase of buffered diffusion. Simulation parameters were the same as used in Fig. 2, except that at t = 5 s, the external ligand concentration was clamped to 0. Fig. S2 shows the corresponding graphs for free ligands. (A) Unliganded (R) and liganded (RC) receptors as a function of time. (B) Unliganded (R) receptors as a function of time within the different segments of the box synapse.

Onset and recovery time courses for both receptors and ligands were usually not well fit by one- or two-exponential decay or sigmoid functions. This study characterized the time dependence of unliganded receptors and free ligand number as the time to reach 50% of equilibrium of the onset and recovery simulations (t_0.5). To assess the variability of these measured times, sometimes simulations were repeated using different random number seed values for MCell3. This produces distinct spatial distributions of receptors and different random number sequences to calculate diffusion and reaction probabilities. Multiple seeds were also used for simulations with low receptor densities as indicated in the corresponding figure legends. Spatial differences in receptor occupancy were assessed in two ways: 1), the ratio of t_0.5 values of the central segments (5 + 6) to the edge segments (1 + 10); and 2), a spatial gradient, at t_0.5 for the whole synapse this study assessed the degree of steady-state occupancy at segments 2 + 9, 3 + 8, and 4 + 7 (this omits the central and edge segments), and calculated the absolute value of the slope of these three points versus segment number. If, at t_0.5 during onset, segments 2 + 9 had fully equilibrated with ligands, segments 3 + 8 were half equilibrated, and segments 4 + 7 were still fully unliganded, the slope would be 0.5; the highest spatial gradient possible. A spatial gradient of 0 corresponds to a situation where receptors in all segments equilibrated at nearly the same time. Analysis calculations were done using Igor Pro 6.04 (Wavemetrics, Lake Oswego, OR).

Results

Onset

In this study's standard onset simulation, the ligand concentration around a 0.05 μm high box is suddenly clamped to 450 nM, that is, 15 × L_eq (Table 1). The number of unliganded receptors (Fig. 2 A) declines quickly in the first 0.2 s, then declines more gradually and reaches a steady-state occupancy of 0.06 between 4–5 s. Half-saturation of the receptors occurs at t_0.5 = 0.95 s. This study compared five simulations with different random number seeds and found t_0.5 = 0.95 ± 0.01 s (mean ± SD). Fig. 2 B shows how the number of unliganded receptors progresses at different distances from the concentration clamped surfaces. As expected for a diffusion limited process, the segments closest to the clamped surfaces (segments 1 and 10) equilibrate first. The t_0.5 values were 40-fold slower in the inner segments (5 + 6; 2.63 ± 0.01 s) than the outer segments (1 + 10; 0.065 ± 0.001 s). The spatial gradient, calculated from the fraction of steady-state occupancy at t = t_0.5 in segments 2 + 9, 3 + 8, and 4 + 7 is large; 0.42 (0.5 would signify the largest possible gradient). The time dependence of the free ligand concentration within the box is shown in Fig. S1 A in the Supporting Material. There is a small, fast initial increase, followed by steady increase until 3 s to about half the final value (t_0.5 = 2.82 ± 0.04 s). Fig. S1 B shows how this occurs sequentially through the segments of the box. Movie S1 is a real-time visualization of this onset simulation showing the spatial distribution of unliganded and liganded receptors over time.

Although there were only 27 free ligands in the box at equilibrium (corresponding to 450 nM), during onset nearly 19,000 additional ligands enter the box and ultimately spent 94% of the time bound to the 20,000 receptors. The initial flux of ligands into the box is 200 ms⁻¹ μm⁻². If this rate were maintained, it would require 1 s for 20,000 ligands to diffuse through the 0.1 μm² access surface area. Because the concentration gradient decreases over time, the flux decreases. Given that equilibration requires 4 s (Fig. S2 A), this suggests that the limiting factor for receptor occupancy during the onset of buffered diffusion is the time required for ligand entry.

Recovery

At t = 5 s, the external ligand concentration was clamped to 0 and both the number of liganded receptors (Fig. 3) and free ligands (Fig. S2) began to decrease. The most apparent difference between onset and recovery is a slower timescale for the recovery of unliganded receptors (t_0.5 = 6.81 ± 0.1 s; Fig. 3 A) and faster timescale for the elimination of free ligands (t_0.5 = 0.17 ± 0.03 s; Fig. S2 A). Thus, recovery of unliganded receptors is 7.2-fold slower than onset and recovery of free ligands is 17-fold faster than onset. As with onset, during recovery there remains a sequential change in kinetics in the different segments but it is not as pronounced (Fig. 3 B and Fig. S2 B). The t_0.5 values were only 10.6-fold slower in the inner segments (5 + 6; 13.1 ± 0.04 s) than the outer segments (1 + 10; 1.24 ± 0.04 s). The spatial gradient, calculated from the fraction of steady-state occupancy at t = t_0.5 in segments 2 + 9, 3 + 8, and 4 + 7, is small 0.07 compared to onset. Movie S2 is a visualization of the recovery.

To determine whether diffusion of ligands from the box is the rate limiting step during recovery, a simulation was carried out in which rebinding of ligands could not take place during recovery (${\ell }_{+}$ = 0). In this simulation, t_0.5 was 0.23 s for both unliganded receptors and free ligands. This corresponds to an exponential time constant of 0.33 s, as would be expected for a process limited by the 3 s⁻¹ dissociation rate of the ligand from the receptor. Thus, rebinding rather than diffusion of ligands is the rate-limiting step for recovery. In the simulation of Fig. 3, there was an average of 50 dissociations per receptor during the recovery period (skewed distribution with a mode of 67 dissociations). This contrasts with 11 dissociations per receptor during onset (Gaussian distribution with a mode of 10 dissociations).

Receptor density

These inferences about rate-limiting steps are supported by simulations in which the density of receptors was decreased. Fig. S3 A shows examples of the time courses of onset and recovery simulations with 10, 100, 1000, and 10,000 receptors μm⁻². The t_0.5 values are plotted in Fig. 4 A. As the receptor density was decreased, equilibration time became shorter. At the lowest receptor densities, the onset time is limited by the time needed for tens of ligands to associate with the receptors (1/(${\ell }_{+}$ [C]) = 0.02 s); recovery time is limited by the ligand dissociation rate constant (1/${\ell }_{-}$ = 0.33 s). There is a linear correlation (slope = 1 on log-log plot) between t_0.5 and receptor density ≥1000 μm². Fig. S3 B and Fig. 4 B show the corresponding information for free ligands. At low receptor densities, there is a pronounced fast component in number of free ligands for both the onset and recovery phases and this is what t_0.5 represents. At low receptor density, t_0.5 approaches an asymptote of 2 ms corresponding to the time needed for tens of ligands to diffuse from the box.

Figure 4.

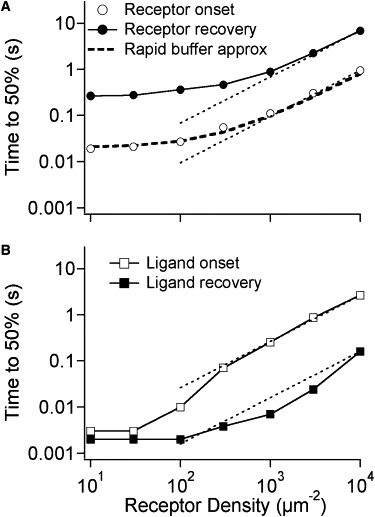
The effect of receptor density on receptor occupancy and free ligand concentration. Parameters are the same as shown in Table 1 except for receptor density. For low receptor density, the simulations were repeated with different random number seeds and the results averaged: 10 μm⁻² (20 simulations), 30 μm⁻² (10 simulations), 100 μm⁻² (5 simulations). Fig. S3 shows individual traces of unliganded receptors and free ligands as a function of time for different receptor density. (A) The time needed to reach 50% of maximum receptor occupancy for onset and recovery simulations with different receptor density. Dashed lines correspond to linear proportionality between time and density. The heavy dashed line corresponds to the predictions of the rapid buffer approximation for a fixed buffer (4) assuming that the t_0.5 ∝ 1/D^eff and t_0.5 has a minimum value of 20 ms. (B) The time needed to reach 50% of maximum free ligand concentration within the synapse for different receptor density. Dashed lines correspond to linear proportionality between time and density.

Binding kinetics and diffusion coefficient

The numerical approximation of buffered diffusion (1) indicates that the time course is a function of the equilibrium binding constant, L_eq, rather than the individual association and dissociation rate constants. Simulations were carried out with different combinations of rate constants to determine the range of validity for this approximation. This study simulated receptor onset (Fig. 5 A) and recovery (Fig. S4 A) as a function of L_eq for different combinations of the binding kinetic parameters. The inverse correlation between time and L_eq is seen with all of the combinations (the slopes of the log-log plots = −1.0). For association rates between 10⁹–10⁷ M⁻¹s⁻¹, the onset and recovery times are nearly independent of binding kinetics. When association is decreased to 10⁶ M⁻¹s⁻¹, however, receptor occupancy is significantly slower. The onset and recovery times are essentially what are expected from a binding-limited process. Consider the 30 nM, ${\ell }_{+}$ = 10⁶ M⁻¹s⁻¹ points: the onset simulation gave 2.6 s (50%) and the binding estimate is 1/(${\ell }_{+}$ [C]) = 2.2 s; the recovery simulation gave 25 s and the binding estimate is 1/(${\ell }_{-}$) = 33 s. In simulations, the time course of free ligand molecules under conditions of slow binding kinetics is fast: ligands enter and leave the box on the 1–10 ms timescale (not shown).

Figure 5.

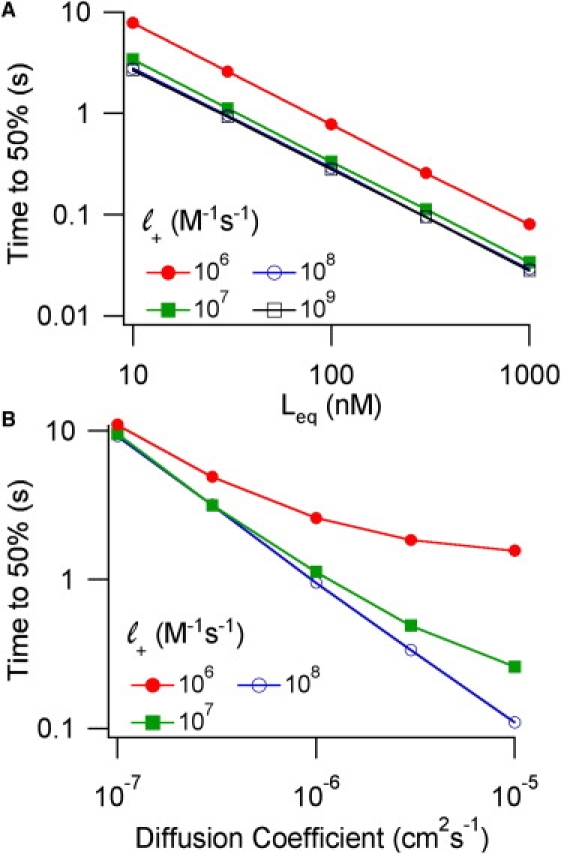
Effect of ligand affinity and diffusion coefficient on the onset kinetics of receptor occupancy during buffered diffusion. Corresponding graphs for the recovery are shown in Fig. S4.

One would expect that the transition from a diffusion-limited process to a binding-limited process depends on the diffusion coefficient as well. This is shown in Fig. 5 B (onset) and Fig. S4 B (recovery). These simulations were carried out with the standard value of L_eq = 30 nM but with diffusion coefficients higher and lower than the standard value of D = 10⁻⁶ cm² s⁻¹. A 10-fold decrease in diffusion coefficient compensates for the 10-fold decrease in binding kinetics seen in going from 10⁷ to 10⁶ M⁻¹s⁻¹. Increases in the diffusion coefficient produce more conditions for which receptor occupancy is binding-limited.

Changes in both binding kinetics and diffusion coefficient also affect the spatial gradient of ligand-bound receptors. For onset, the spatial gradients were 0.44, 0.42, 0.29, and 0.07 for association constants of 10⁹, 10⁸, 10⁷, and 10⁶ M⁻¹s⁻¹ respectively (independent of L_eq). For recovery, the spatial gradients were 0.08, 0.08, 0.07, and 0.02 respectively. Faster diffusion coefficients lead to smaller spatial gradients. Empirically, the ratio of association rate/diffusion coefficient is a good predictor for the spatial gradient (Fig. 6).

Figure 6.

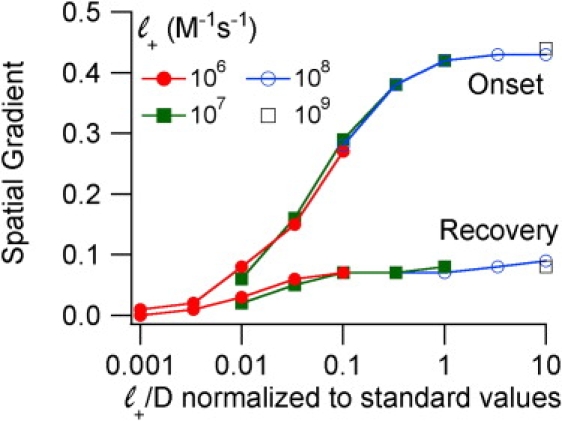
The ratio of ligand association rate to ligand diffusion coefficient determines the spatial gradient of receptor occupancy during buffered diffusion. Standard simulation parameters are given in Table 1; various other combinations of ligand association rate and ligand diffusion coefficient were used as indicated.

Ligand concentration

The ligand concentration dependence of buffered diffusion was investigated by carrying out simulations using the standard parameters (Table 1) for [C]/L_eq between 0.5 and 50. Both onset and recovery became faster at higher ligand concentrations (Fig. 7 A) but the decrease in t_0.5 was more pronounced for onset (46-fold) than for recovery (2.7-fold). A plot of 1/t_0.5 versus [C] was linear (not shown) with a slope of 1.6 × 10⁵ M⁻¹s⁻¹. This is 600 times slower than the ligand association rate; another indication that binding is not rate-limiting during onset. It may seem surprising that recovery at low ligand concentrations is slower than for high concentrations. This is because recovery time is determined by rebinding of ligands and there is a greater opportunity for rebinding when receptor occupancy is low.

Figure 7.

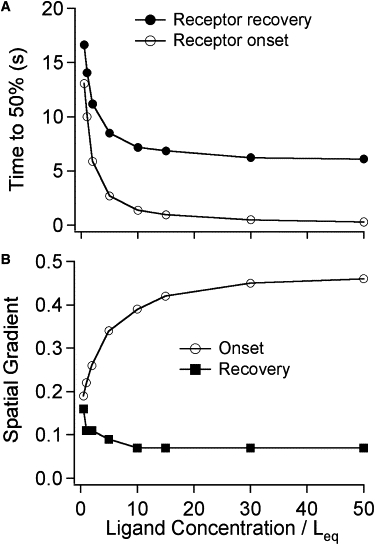
The effect of ligand concentration on diffusion of ligands into and out of the box synapse. Conditions are the same as shown in Table 1 except for the ligand concentration. Concentration is expressed as multiples of the ligand equilibrium binding constant L_eq. (A) The time needed to reach 50% of maximum receptor occupancy for onset and recovery simulations with different ligand concentrations. (B) Spatial gradient.

The size of the spatial gradient is also dependent on ligand concentration (Fig. 7 B). Even at the lowest concentrations simulated, there remains a substantial spatial gradient of unliganded receptors during onset. For the onset simulation with [C]/L_eq = 0.5, at t_0.5 = 13.1 s, the fractional occupancy of segments 2 + 9, 3 + 8, and 4 + 7 were 0.67, 0.48, and 0.29 respectively (spatial gradient = 0.19). The spatial gradient during recovery is generally small (average, 0.01), but at [C]/L_eq = 0.5, it was nearly as large as for onset (0.16).

Cleft width

Fig. S5 summarizes the results of simulations using different cleft widths (t_cleft). As synapse gets wider, more ligands can flow into the box and receptor occupancy becomes faster. For t_cleft < 0.2 μm, the t_0.5 values are inversely proportional to t_cleft. For wider clefts, the additional ligands that enter the box are too far from the receptors to contribute to binding on the 100-ms timescale, and there is less of an effect on t_0.5. The high t_cleft limits (0.1 s for onset, 0.75 for recovery) do not correspond to a binding-limited process (0.01 s for onset, 0.23 s for recovery) because the flow of ligands to and from receptors near the y-z surfaces remains impeded. Additionally, during recovery there remains significant rebinding of ligands: if rebinding is not permitted, t_0.5 = 0.23 s. The spatial gradient during onset (Fig. S5 B) remains high up to a cleft thickness of 0.1 μm, but becomes less steep for wider clefts.

Irreversible ligand

This study simulated buffered diffusion by an irreversible ligand (irreversible at least on the timescale of tens of seconds) by setting ${\ell }_{-}$ = 0 (Fig. 8 and Fig. S6). In this simulation, the clamped ligand concentration was kept at the standard value of 450 nM. The overall time course for receptor occupancy (Fig. 8 A) is similar to the onset simulation with ${\ell }_{-}$ = 3 s⁻¹ (Fig. 2 A); the receptor t_0.5 was 0.98 s (compared to 0.95 s in Fig. 2) but, of course, it proceeds until all receptors are liganded at t ≈ 3.8 s. The t_0.5 values were 44-fold slower in the inner segments than the outer segments (Fig. 8 B). The number of free ligands (Fig. S6 A) rises somewhat more slowly with irreversible ligands (t_0.5 = 3.5 s) compared with reversible ligands (t_0.5 = 2.8 s, Fig. 2 B) and shows a rapid rise after 3.6 s as the last 2% of the receptors become liganded.

Figure 8.

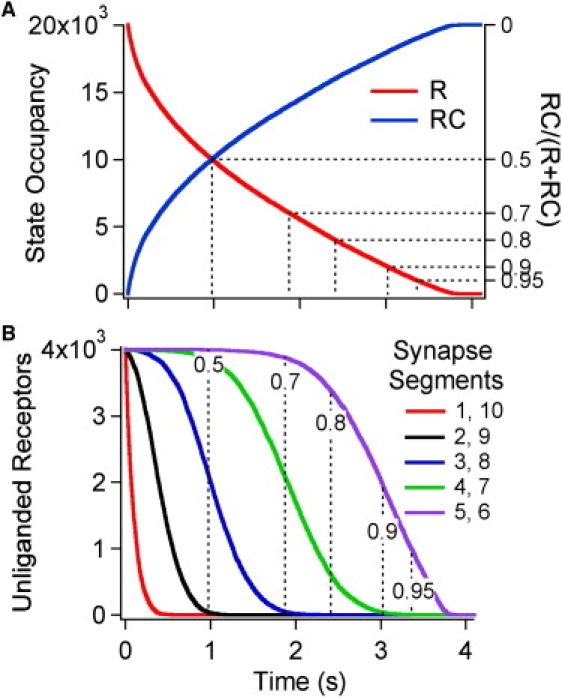
Time-dependence of receptor occupancy during the diffusion of irreversible ligands into the box synapse. This simulation used the parameters from Table 1, except that ${\ell }_{-}$ is set to 0 so that bound ligands do not dissociate. Fig. S6 shows the corresponding graphs for free ligands. (A) Unliganded (R) and liganded (RC) receptors as a function of time. The right hand axis indicates the fraction of liganded receptors. (B) Unliganded (R) receptors as a function of time within the different segments of the box synapse. Segments 1 and 10 are nearest to the clamped surface. The dashed lines indicate the fraction of liganded receptors for the synapse as a whole. Thus, when the overall receptor occupancy is 0.9, segments 5 and 6 have a receptor occupancy of 0.49 but receptors in the other segments are essentially fully occupied.

The spatial gradient seen with the irreversible ligand is larger than for any other simulation described in this study (0.48). The significance of this high spatial gradient can be appreciated in Movie S3 and in Fig. 9. Fig. 9 shows the spatial distribution of receptors states the time when 90% of the receptors are liganded in the simulation of reversible binding (Fig. 9 A, ${\ell }_{-}$ = 3 s⁻¹, t = 3.43 s) and irreversible binding (Fig. 9 B, ${\ell }_{-}$ = 0 s⁻¹, t = 3 s). In the case of reversible binding, unliganded (green) receptors are found throughout the box whereas in the case of irreversible binding, the unliganded receptors are primarily in a band near the center of the box. With irreversible binding, the high spatial gradient is maintained even when lower concentrations of ligand are used (the spatial gradient was 0.48 for every simulation using the same concentrations as shown in Fig. 7 B).

Figure 9.

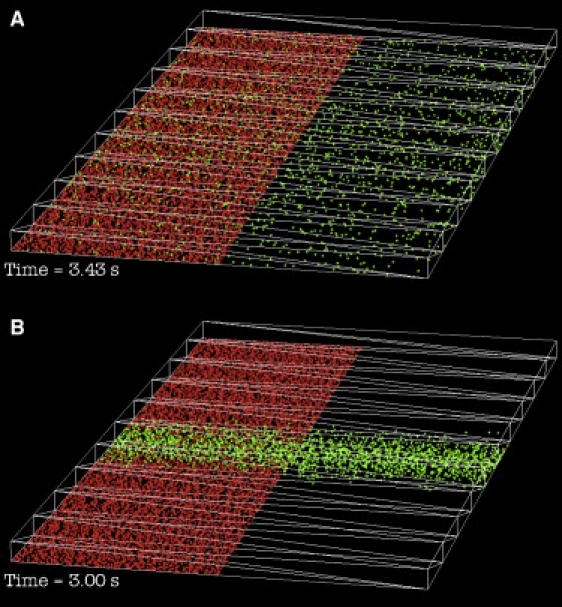
Frames from the movies of onset simulations. Liganded receptors are shown in red, unliganded receptors are shown in green. The liganded receptors are hidden in the right half of each image to show the unliganded receptor distribution more clearly. The frames are from different time points, but both correspond to an overall receptor occupancy of 90%. (A) Reversible ligand (${\ell }_{-}$ = 3 s⁻¹). The unliganded receptors are distributed nearly uniformly across the synapse. (B) Irreversible ligand (${\ell }_{-}$ = 0 s⁻¹). Unliganded receptors are concentrated near the center of the synapse.

Discussion

Buffered diffusion can be described mathematically using a combination of Fick's second law of diffusion and a saturable binding site. The resulting nonlinear equations have been solved numerically for a cylindrical geometry (also including a term for nonsaturable binding) under the simplifying assumption that the kinetics of binding are fast compared to diffusion (1). There have also been analytic solutions for particular geometries that often assume fast binding kinetics, particularly with regard to intracellular calcium buffering (5–7). More recently, there have been numerical solutions of buffered diffusion for calcium using Monte Carlo simulation (8,9). This study used Monte Carlo simulation and applied it to a simple model of a synapse. With this approach, it is not necessary to assume fast binding kinetics. In addition, the method can be used to find the time and spatial dependence of both ligands and receptors during buffered diffusion into any arbitrary geometry.

The standard parameter values (Table 1) were chosen to mimic the diffusion of competitive antagonists of the nicotinic acetylcholine receptor, such as (+)-tubocurarine or pancuronium, into and out of the neuromuscular junction. The box geometry of Fig. 1 resembles a slice of such a synapse in receptor density, synapse thickness and width (the distance from one bulk phase to the other), but, for simplicity, it does not contain junctional folds. The ligand association and dissociation constants, are at the slow kinetic extreme of measured values at room temperature (11,12). The ligand concentration is high relative to L_eq; this is required both experimentally and clinically to overcome the high margin of safety at the neuromuscular junction (15). Some ligands bind with substantial affinity to both binding sites on the acetylcholine receptor (16,17); this could be simulated by increasing receptor density. Although the site-selectivity of competitive antagonists for frog nAChR has not been determined, differences in selectivity may underlie the anomalous result reported for doxacurium (3).

Receptor equilibration

Under the standard condition, and for many other conditions used, the onset phase of ligand binding is limited by the time needed for the large numbers of ligands that must enter the box to bind 94% of the 2 × 10⁴ receptors. The initial flux of ligands into the box (when the concentration gradient is maximal) is ∼2 × 10⁴ s⁻¹ and it takes ∼4 s to reach equilibrium binding. During the recovery phase, ligand equilibration is sevenfold slower. Recovery is dominated by multiple rebinding of ligands to the receptors (on average, >50 rebinding events per ligand).

The simulations carried out at different receptor densities (Fig. 4) suggest that when ρ < 1000 μm⁻², the kinetics of receptor binding begin to limit the rate of receptor occupancy. For ρ < 100 μm⁻², the process is completely binding-limited. Receptor occupancy also becomes binding-limited when binding kinetics are slow (${\ell }_{+}$ = 10⁶ in Fig. 5 A) and when diffusion is fast (D > 10⁻⁶ cm² s⁻¹ in Fig. 5 B). Receptor occupancy is linearly related to synapse thickness until the thickness is >0.5 μm (Fig. S5 A). This did not represent a transition to binding-limited onset/recovery, however. Instead, the impermeable walls of the box in the y-z plane limited the access of ligands to receptors.

The concentration dependence of receptor occupancy (Fig. 7 A) shows that the reciprocal of the onset time varies linearly with ligand concentration as would be expected for the rate-limiting step being the flux of ligands into the box. A surprising finding is that during recovery, the t_0.5 values are concentration-dependent and become shorter at higher concentrations. This is a relatively small effect: twofold occurring over a 20-fold range of concentration (0.5–10 L_eq). It is due to the greater opportunity that ligands have for rebinding when occupancy is low. Measurements of the recovery phase of (+)-tubocurarine out of the frog neuromuscular junction (2), however, showed the same recovery rate at concentrations between 0.2–4 L_eq. This study made simulations of buffered diffusion into the box synapse over this concentration range using the standard parameters except for ${\ell }_{-}$ = 50 s⁻¹ (this gave L_eq = 500 nM, the equilibrium constant used by Armstrong and Lester (2)) and analyzed the recovery time course in several ways. Table 2 shows that the t_0.5 values indicated a 2.1-fold difference in recovery for the two ligand concentrations. The two-exponential fits showed that there is a substantial fast component to recovery and that this was more pronounced at the higher ligand concentration. The slow component of the two-exponential fits differed by only 1.13-fold. Thus, if it is assumed that the fast component of recovery is not easily detected experimentally, this study's simulations are not inconsistent with the experimental measurements. Of course, the box synapse model is an oversimplification of a real neuromuscular junction, but the similarity in recovery time is striking. The onset times are also similar: within a factor of 2 (not shown).

Table 2.

Comparison of recovery from (+)-tubocurarine block of frog nmj and simulations of the box synapse model

	Frog nmj	Simulation of box synapse model
[C]/Leq	τ (s)	t0.5 (s)	τslow (s)	τfast (s)	afast
0.2	2.5	1.14	1.18	0.92	0.30
4.0	2.5	0.55	1.04	0.21	0.37
Ratio	1.00	2.06	1.13	4.46

The τ values for frog nmj were obtained from Armstrong and Lester (2).The standard parameters (Table 1) were used in the simulations except for ${\ell }_{-}$ = 50 s⁻¹ and the indicated values of [C]/L_eq. The half-time for recovery of unliganded receptors, t_0.5, was determined in the usual way. In addition, the time course of recovery was fit to a two-exponential function, R(t)/R(0) = a_fast exp(−t/τ_fast) + (1 − a_fast) exp(−t/τ_slow) where τ_slow and τ_fast are the two time constants and a_fast is the fractional contribution of the fast component. The ratio values compare time measurements at low versus high ligand concentration. Although the t_0.5 values indicate a large concentration dependence for recovery, this arises mostly from the fast component of the decay. The slow component of the simulated R(t) has a much weaker concentration dependence and resembles the experimental data from Armstrong and Lester (2).

nmj, neuromuscular junction.

Ligand equilibration

The comments made above for receptor equilibration are, for the most part, applicable to the equilibration of free ligands in the box synapse model. As can be seen in Fig. 4 B, the time dependence of free ligands is complex and may exhibit up to three distinct phases. Thus, characterization of this in terms of a single value, t_0.5, hides information about the different phases. Nevertheless, some general statements can be made. Ligand equilibration is faster than receptor equilibration. During onset, free ligands are quickly taken up by empty receptors and this delays ligand equilibration. During recovery, free ligands diffuse out quickly due to the concentration gradient (readily apparent in Fig. S2 A). But, the number of free ligands cannot decrease to zero until all of the ligands have dissociated from receptors. Finally, in contrast to receptor equilibration, ligand equilibration during onset is slower than during recovery. Again, this is due to the buffering of the free ligand concentration by receptors during onset.

Spatial gradient

This study introduced the concept of the spatial gradient of unliganded receptors to characterize the sequential equilibration of receptors at different distances from the concentration clamped surfaces. The parameter measures the gradient of ligand occupancy in the vicinity of one-fourth of the way into the synapse (segments 3 + 8) at t_0.5. As defined, the absolute value of the spatial gradient varies from 0 (no gradient) to 0.5. Under the standard conditions of Table 1, the gradient during onset is quite steep, 0.42 but the gradient during recovery is shallow, 0.07. Simulations in which either the association constant was decreased or the diffusion coefficient was increased, lead to less steep spatial gradients (Fig. 6). In these situations, the relative likelihood for ligands to diffuse instead of bind increased and this reduced the distinction between receptors near the clamped surface and receptors further from the clamped surface. The spatial gradient is also decreased as the ligand concentration decreases (Fig. 7 B) and as synapse thickness increases (Fig. 5 B).

An inverse relationship between diffusion coefficient and association constant was also seen in analytic solutions to buffered diffusion equations in the fast binding situation. Junge and McLaughlin (4) derived a rapid buffer approximation for a stationary buffer and found that considered the effective diffusion coefficient of the ligand could be given as $D^{\text{eff}}/D={\left(1+\left[R\right]L_{\text{eq}}/{\left(L_{\text{eq}}+\left[L\right]\right)}^2\right)}^{-1}$. The surface density of receptors can be converted to a concentration by considering them to be uniformly distributed over the volume of the box: when ρ = 10⁴ μm⁻², [R] = 300 μM using the standard box dimensions. The rapid buffer approximation provides a good description of this study's simulated time course of liganded receptors as a function of receptor density (Fig. 4 A, heavy dashed line).

Similarly, several authors (6,7,18) have used the concept of length constant, an average diffusion distance for a ligand entering a sea of mobile buffers: $\lambda =\sqrt{D/\left({\ell }_{+}\left[R\right]\right)}$. For the standard parameters, λ = 0.06 μm, that is, approximately the cleft thickness. Although the buffer in this model, membrane-bound receptors, is not mobile, the inverse relationship between D and ${\ell }_{+}$ remains valid as long as binding is fast.

Irreversible ligand

The highest values of spatial gradient were observed during onset simulations with an irreversible ligand. The spatial gradient was 0.48 independent of ligand concentration. Of course, the equilibrium condition for an irreversible ligand will always be total occupancy, but incubation with the ligand can be halted when some level of overall inhibition is achieved. This is commonly done, for example, in studies with bungarotoxin inhibition of muscle nicotinic acetylcholine receptors (19,20). This study's simulations show that this produces a distinctive distribution of unliganded receptors (Fig. 9, Movie S3). The unliganded receptors are located predominantly in the center of the synapse instead of being distributed randomly as with a reversible ligand at equilibrium. With an irreversible inhibitor present, neurotransmitter molecules released near the center of the synapse would find a near-normal distribution of unliganded receptors.

The results of this investigation provide a framework for determining how specific parameters in a buffered diffusion model affect the time course of liganded receptors and free ligand concentration. The next step is to use a realistic model of a synapse, the neuromuscular junction, to test hypotheses about the mechanism of action of nondepolarizing muscle relaxants that are competitive antagonists for the muscle acetylcholine receptor. In a subsequent study, two issues will be addressed. One issue is whether the observed inverse relationship between muscle relaxant potency and speed of onset is a manifestation of buffered diffusion (3). The other issue concerns the mechanisms of tetanic fade seen in the presence of nondepolarizing muscle relaxants but not in the presence of α-bungarotoxin (20), an irreversible antagonist. Future simulations will be directed toward understanding kinetic phenomena at other chemical synapses.