A Mathematical Analysis of Agonist- and KCl-Induced Ca²⁺ Oscillations in Mouse Airway Smooth Muscle Cells

Abstract

Airway hyperresponsiveness is a major characteristic of asthma and is generally ascribed to excessive airway narrowing associated with the contraction of airway smooth muscle cells (ASMCs). ASMC contraction is initiated by a rise in intracellular calcium concentration ([Ca²⁺]_i), observed as oscillatory Ca²⁺ waves that can be induced by either agonist or high extracellular K⁺ (KCl). In this work, we present a model of oscillatory Ca²⁺ waves based on experimental data that incorporate both the inositol trisphosphate receptor and the ryanodine receptor. We then combined this Ca²⁺ model and our modified actin-myosin cross-bridge model to investigate the role and contribution of oscillatory Ca²⁺ waves to contractile force generation in mouse ASMCs. The model predicts that: 1), the difference in behavior of agonist- and KCl-induced Ca²⁺ waves results principally from the fact that the sarcoplasmic reticulum is depleted during agonist-induced oscillations, but is overfilled during KCl-induced oscillations; 2), regardless of the order in which agonist and KCl are added into the cell, the resulting [Ca²⁺]_i oscillations will always be the short-period, agonist-induced-like oscillations; and 3), both the inositol trisphosphate receptor and the ryanodine receptor densities are higher toward one end of the cell. In addition, our results indicate that oscillatory Ca²⁺ waves generate less contraction than whole-cell Ca²⁺ oscillations induced by the same agonist concentration. This is due to the spatial inhomogeneity of the receptor distributions.

Introduction

Contraction of airway smooth muscle cells (ASMCs) in the walls of the tracheobronchial tree results in a narrowing of the airway and is associated with obstructive lung disease such as asthma. In ASMCs, a change in the cytosolic concentration of calcium ([Ca²⁺]_i) is the primary-signal-regulating contractile function (1–5); an increase in [Ca²⁺]_i activates myosin light chain kinase, which, in turn, phosphorylates myosin, thus stimulating cross-bridge cycling and contraction. In ASMCs, this change in [Ca²⁺]_i does not take the form of a simple increase, but instead occurs as oscillatory Ca²⁺ waves.

Oscillatory Ca²⁺ waves in ASMCs have been observed in different species and cell preparations (6–11) and are usually initiated by contractile agonists such as acetylcholine (ACh), methacholine (MCh), or 5-hydroxytryptamine (5-HT). Surprisingly, Ca²⁺ oscillations can also be initiated in mouse ASMCs by high extracellular K⁺; these Ca²⁺ oscillations usually have a much lower frequency than agonist-induced Ca²⁺ oscillations (10,11). Both types of oscillatory Ca²⁺ waves involve Ca²⁺ release from the internal Ca²⁺ store, the sarcoplasmic reticulum (SR) (4,8,10). Ca²⁺ release from the SR is controlled by either the inositol trisphosphate receptor (IPR) or the ryanodine receptor (RyR), both of which exhibit Ca²⁺-induced Ca²⁺ release (CICR).

Some experimental results suggest that agonist-induced Ca²⁺ oscillations can be mediated by CICR via the RyR (6,7). However, other experimental results have shown no such dependence on the RyR, but instead demonstrate that agonist-induced oscillations depend on Ca²⁺ release through the IPR (10–13). In contrast to agonist-induced Ca²⁺ oscillations, KCl-induced oscillations appear to be initiated by an influx of Ca²⁺ via L-type and/or T-type Ca²⁺ channels (10). The cell appears to compensate for this Ca²⁺ influx by transporting the surplus Ca²⁺ from the cytosol into the SR via SERCA pumps. It was hypothesized in Perez and Sanderson (10) that this Ca²⁺ influx into the SR leads to the overloading of the SR. The consequence of this is an increase in the open probability of the RyR and the triggering of prolonged CICR via the sensitized RyRs to empty the SR and raise the [Ca²⁺]_i.

To understand the mechanisms mediating these two types of Ca²⁺ oscillations and waves in mouse ASMCs, we have constructed and analyzed a model of oscillatory Ca²⁺ waves, based on previously published experimental data (10), which include both the IPR and the RyR. The initial version of the model ignores the spatial aspects of intracellular Ca²⁺ dynamics, assuming instead that the cell is a well-mixed system. The model is then extended by the inclusion of Ca²⁺ diffusion, to simulate oscillatory intracellular waves.

Our ultimate goal is to investigate the role and contribution of oscillatory Ca²⁺ waves to contractile force generation in ASMCs. Therefore, we subsequently combined our model of oscillatory Ca²⁺ waves with our modified cross-bridge model (14) to calculate isometric force generation in response to changes in [Ca²⁺]_i.

The Whole-Cell Model

The model is based on the schematic diagram shown in Fig. 1 and incorporates the dynamics of [Ca²⁺] in both the cytoplasm and the SR, denoted by c and c_s, respectively. An increase in [Ca²⁺]_i can result from entry of Ca²⁺ from the external environment or release from the SR. Ca²⁺ influx from the external environment occurs via voltage-dependent Ca²⁺ channels and arachidonic-acid-operated channels (AAOC). Ca²⁺ release from the SR is through the IPR, the RyR, and a generic leak. [Ca²⁺]_i is reduced by pumping Ca²⁺ out of the cell through an ATPase pump and back to the SR by the SERCA pump.

Figure 1.

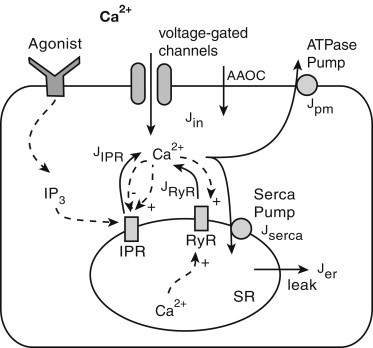
Schematic diagram of the Ca²⁺ model. Ca²⁺ can be released from the sarcoplasmic reticulum (SR) though the inositol trisphosphate receptor (IPR), the ryanodine receptor (RyR), and a generic leak. Binding of agonist to the receptor in the outer cell membrane stimulates IP₃ production. IP₃ binds to the IPR in the SR, thus opening the receptor and leading to Ca²⁺ release. Initially, this has a positive feedback on the IPR and RyR open probabilities, thus triggering the release of more Ca²⁺ into the cytoplasm. At higher [Ca²⁺]_i, this feedback loop becomes negative and closes the IPR. The increase in [Ca²⁺] in the SR also has a positive feedback on the RyR open probability. Ca²⁺ can be pumped into the SR through the SERCA pump and out of the cell via the ATPase pump. Ca²⁺ enters the cell through voltage-gated Ca²⁺ channels or arachidonic-acid-operated channels (AAOC). The Ca²⁺ fluxes are denoted by solid lines. The dashed lines represent the feedback effects on various mechanisms in the cell.

IP₃ receptor

The binding of an agonist to a receptor in the cell's surface membrane triggers a chain reaction leading to the production of the second messenger IP₃. The IP₃ diffuses through the cytosol and binds to the IPR, causing Ca²⁺ to be released from the SR. It was experimentally determined that in ASMCs, Ca²⁺ oscillations are controlled by exerting both positive and negative feedback on the gating of the IPR (15). These feedback loops occur on different timescales. Hence, shorter-period oscillations in ASMCs do not depend on oscillations in [IP₃].

To complicate the situation, Ca²⁺ oscillations and waves have been shown to be the aggregate of a number of stochastic elementary Ca²⁺ release events (16,17). These localized Ca²⁺ release events occur at a single or a small cluster of receptor sites and are termed Ca²⁺ puffs when involving an IPR. Ca²⁺ puffs have been studied in detail in Xenopus oocytes (18) and more recently in SH-SY5Y cells (19). These Ca²⁺ puffs and their propagation during Ca²⁺ waves and oscillations can be modeled using a stochastic Markov process (20).

Although stochastic effects play a major role in intracellular Ca²⁺ dynamics in ASMCs, stochastic simulation of individual or small clusters of IPR is computationally prohibitively expensive. Furthermore, the conditions under which deterministic modeling of Ca²⁺ release via the IPR is insufficient are not fully understood (20,21). Therefore, we used a deterministic approach to model the open probability of the IPR; although this approach will not capture stochastic dynamics, it is sufficient to construct a model with substantial predictive power.

Our model of the IPR is based on the De Young and Keizer model (21–23),

$$P_{\text{IPR}}={\left(\frac{pc\left(1-y\right)}{\left(p+K_1\right)\left(c+K_5\right)}\right)}^3,$$

$$\frac{dy}{dt}={\varphi }_1\left(1-y\right)-{\varphi }_{2}y,$$

$${\varphi }_1=\frac{\left(k_{-4}{K}_2{K}_1+k_{-2}{K}_{4}p\right)c}{K_4{K}_2\left(K_1+p\right)},$$

$${\varphi }_2=\frac{k_{-2}p+k_{-4}{K}_3}{K_3+p},$$

where the variable p denotes [IP₃] in the cytoplasm. As we do not model any of the intervening steps between addition of the agonist and the production of IP₃, we can use p as a surrogate indication of the agonist level. The variable y represents the proportion of IPR that have been inactivated by Ca²⁺. The variables k_i and $K_i=k_{-i}/k_i$ are the receptor binding and dissociation constants, respectively.

Ryanodine receptor

A number of RyR models have been proposed in the relevant literature. However, most models are adapted to studying RyR dynamics in cardiac cells (24) due to its importance in excitation-contraction. Roux and Marhl (25) developed a model to study caffeine-induced Ca²⁺ oscillations in ASMCs. This model assumes a direct dependence of RyR open probability on caffeine concentration, making it unsuitable for our study of KCl-induced [Ca²⁺]_i oscillations.

Friel (26) proposed a simple model to simulate CICR in bullfrog sympathetic neurons. Despite its simplicity, this model provides an excellent quantitative description of Ca²⁺ oscillations over the entire oscillatory cycle. We use a modified version of this RyR model in our work. As previously hypothesized (10), the open probability of the RyR is increased in response to SR overloading (27). We therefore modified the Friel model to include a store-dependent term (28). Hence the open probability of the RyR is

$$P_{\text{RyR}}=\left(k_{\text{ryr}0}+\frac{k_{\text{ryr}1}{c}^3}{k_{\text{ryr}2}^3+c^3}\right)\left(\frac{c_{\text{s}}^4}{k_{\text{ryr}3}^4+c_{\text{s}}^4}\right)\text{.}$$

Other fluxes

The Ca²⁺ flux through the SERCA pump is approximated by a sigmoidal function of c, with a Hill coefficient of 2 as suggested in Lytton et al. (29). Thus

$$J_{\text{serca}}=\frac{V_{\text{e}}{c}^2}{K_{\text{e}}^2+c^2},$$

where V_e is the maximum rate of the pump and K_e is the half-activation for Ca²⁺.

Although we know that agonists cause an increase in Ca²⁺ influx, the exact mechanism between the influx of extracellular Ca²⁺ (J_in) and p remains unknown (30). Therefore, we chose a simple form for Ca²⁺ influx via AAOC as an increasing function of [IP₃]. Hence, we modeled J_in to include a voltage-dependent, an AAOC-dependent, and a constant basal level term, as

$$J_{\text{in}}={\alpha }_0-{\alpha }_1\frac{I_{\text{Ca}}}{2F}+{\alpha }_{2}p,$$

where I_Ca is the current of the Ca²⁺ voltage-gated channel and F is the Faraday constant.

The Ca²⁺ efflux from the cell is maintained by the plasma membrane pump, which is modeled by

$$J_{\text{pm}}=\frac{V_{\text{p}}{c}^4}{K_{\text{p}}^4+c^4}\text{.}$$

Membrane potential

In this model, the voltage-dependent I_Ca current is described by the product of its macroscopic conductance, a voltage-dependent activation gating variable (representing the fraction of current flow for a given membrane potential), and the driving force (31). Hence

$$I_{\text{Ca}}=g_{\text{Ca}}{m}^2{V}_{\text{Ca}},$$

where g_Ca is the conductance and m is the activation-gating variable (32). We modeled m using the sigmoidal relationship

$$m=\frac{1}{1+e^{\frac{-\left(V-V_m\right)}{k_m}}},$$

where V_m represents the voltage at which the current is half-maximally activated. The driving force for Ca²⁺, V_Ca, is obtained from the Goldman-Hodgkin-Katz equation. Therefore,

$$V_{\text{Ca}}=\frac{V\left(c-c_{\text{e}}{e}^{\frac{-2\text{VF}}{\text{RT}}}\right)}{1-e^{\frac{-2\text{VF}}{\text{RF}}}},$$

where c_e is extracellular [Ca²⁺]. R is the gas constant and T is the absolute temperature.

Summary of the model

In our initial model, we assume the SR and all associated pumps and receptors are continuously distributed throughout the cell interior. Furthermore, we assume the buffers are fast, immobile and have low affinities. Hence the model has the conservation equations for [Ca²⁺]_i as

$$\frac{dc}{dt}=J_{\text{release}}-J_{\text{serca}}+\delta \left(J_{\text{in}}-J_{\text{pm}}\right),$$

$$\frac{d{c}_{\text{s}}}{dt}=\gamma \left(J_{\text{serca}}-J_{\text{release}}\right),$$

$$J_{\text{release}}=\left(k_{\text{IPR}}{P}_{\text{IPR}}+k_{\text{RyR}}{P}_{\text{RyR}}+J_{\text{er}}\right)\left(c_{\text{s}}-c\right),$$

where δ scales the net Ca²⁺ flux into the cell. Similarly, γ scales the unit of c_s from moles per liter SR into moles per liter cytoplasm. The values k_IPR and k_RyR represent the densities of the IPR and the RyR, respectively. The value J_release includes fluxes across the IPR, the RyR, and a generic leak given by J_er.

The equations of the Ca²⁺ model and the complete list of parameter values are presented in the Supporting Material.

Results

Agonist-induced oscillations

To simulate an agonist-induced [Ca²⁺]_i oscillation, we solved the system with p = 0.35 μM, indicating the addition of 1 μM acetylcholine (Fig. 2 A). This value of p sets the system to be in an oscillating range (Fig. 2 B). The expanded details of the experimental data and simulations are shown in Fig. 2, C and D. Fig. 2 E shows the corresponding changes in [Ca²⁺] in the SR. [Ca²⁺]_i oscillations caused depletion of the SR, and Ca²⁺ release from the SR was mainly through the IPR (Fig. 2 F). The open probability of the RyR was greatly reduced after an initial transient increase (Fig. 2 G). This is because the initial transient increase in [Ca²⁺]_i via the IPR flux, after the addition of agonist, caused CICR through the RyR. As the SR is depleted by [Ca²⁺]_i oscillations, the RyR open probability decreases in response.

Figure 2.

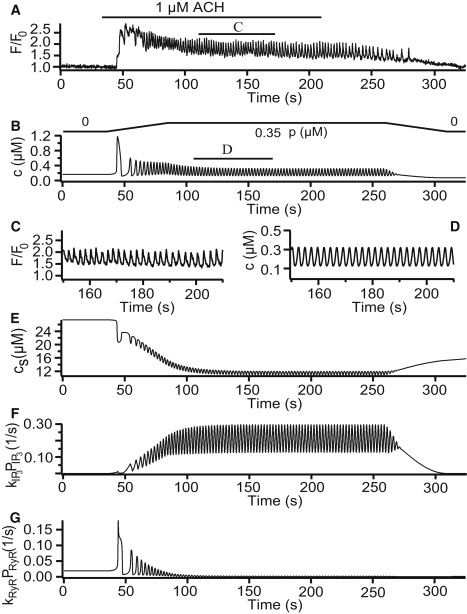
Agonist-induced oscillations. (A) Experimental result from Perez and Sanderson (10), which represents mouse airway smooth muscle cells (ASMCs) stimulated with 1 μM acetylcholine (ACh). (B and D) Numerical simulations of our Ca²⁺ model. (C) Expanded region of 1 min, indicated by the lower bar in panel A. (E) Changes in [Ca²⁺] in the sarcoplasmic reticulum (SR). (F and G) Fluxes from the SR via the inositol trisphosphate receptor (IPR) and the ryanodine receptor (RyR), respectively. To simulate the experimental addition and removal of agonist, the increase and decrease in p required 50 s to reach its maximum level. Parameter values are shown in the Supporting Material with p = 0.35 μM and V = –60 mV.

KCl-induced oscillations

To simulate the [Ca²⁺]_i oscillations caused by membrane depolarization, we solved the system with V = –30 mV, indicating the addition of 100 mM KCl (Fig. 3 A). The simulated [Ca²⁺]_i oscillation is shown in Fig. 3 B. Fig. 3 C shows the corresponding changes in [Ca²⁺] in the SR, indicating there is an obvious overfilling of the SR before its depletion. The overloading of the SR caused the open probability of the RyR to increase (Fig. 3 E), thus leading to the rise in [Ca²⁺]_i. The simulation does not involve agonist, hence the Ca²⁺ release from the SR via the IPR remains zero (Fig. 3 D).

Figure 3.

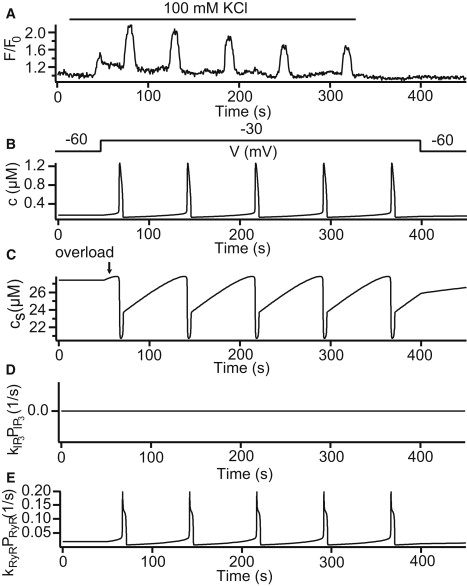
KCl-induced oscillations. (A) Experimental result from Perez and Sanderson (10), which represents mouse airway smooth muscle cells (ASMCs) stimulated with 100 mM KCl. (B) Numerical solution with p = 0 μM and V = –30 mV. (C) Changes in [Ca²⁺] in the SR. (D and E) Fluxes from the sarcoplasmic reticulum (SR) via the inositol trisphosphate receptor (IPR) and the ryanodine receptor (RyR), respectively. Parameter values are shown in the Supporting Material.

The role of extracellular Ca²⁺

[Ca²⁺]_i oscillations can be induced by agonist, but not maintained in the absence of the extracellular Ca²⁺ (10). Both the experimental result and the model simulation are included in the Supporting Material. With zero extracellular Ca²⁺, KCl does not cause a change in [Ca²⁺]_i (10). As expected, numerical simulation of our model in this case did not provide any [Ca²⁺]_i oscillations (result not shown).

Closed-cell model

It has previously been shown that a useful way of understanding the behavior of models such as these is to introduce a new variable related to the total amount of Ca²⁺ in the cell (30). Hence, we introduced the variable c_t (the total number of moles of Ca²⁺ in the cell divided by the cytoplasmic volume), which is defined as c_t = c + (1/γ)c_s. We thus treat c_t as a bifurcation parameter and investigate the behavior of the model for fixed values of c_t. Our result showed that long-period KCl-induced [Ca²⁺]_i oscillations have a very different oscillating range in c_t compared to the short-period agonist-induced oscillations. Higher agonist levels induce [Ca²⁺]_i oscillations in a lower c_t. For a more detailed explanation of this technique and the bifurcation diagram of our model, please see the Supporting Material.

Increased Ca²⁺ load

We first explored the behavior of the oscillation model with the parameter values shown in the Supporting Material by treating p and V as the bifurcation parameters. We then varied the Ca²⁺ load of the system by changing the basal level of J_in flux (α₀). Our result showed that increasing α₀ changes the dynamics of the system. With higher Ca²⁺ load, long-period [Ca²⁺]_i oscillations occur in the low agonist region. This indicates RyR-dominated Ca²⁺ release. In addition, between the short- and long-period [Ca²⁺]_i oscillation regions, the receptors showed strong interaction, and period-doubling bifurcations occur leading to mixed-mode oscillations.

We then performed the two-parameter bifurcation analysis (p versus V) with different α₀ values. By increasing p, the short, mixed-mode and long-period oscillations were observed. The figures indicate no qualitative differences in this analysis between the two Ca²⁺ loads. With Ca²⁺ load increasing, both short- and long-period oscillation regions expand accordingly.

We included these bifurcation diagrams and a more detailed explanation in the Supporting Material.

Model prediction

Based on the two-parameter bifurcation analysis, we predict that long-period KCl-induced Ca²⁺ oscillations are replaced by short-period oscillations when a high concentration of agonist is added to the cell (Fig. 4 A). However, when reversing the order of these two stimuli, we only observe short-period Ca²⁺ oscillations (Fig. 4 D). Fig. 4, B and E, shows the model predictions of [Ca²⁺] in the SR during these two simulations. The prediction has been verified by experiment and results are shown in Fig. 4, C and F. The reason for this result is that agonist always depletes the SR, hence the RyR is unable to open and release Ca²⁺. Therefore, the RyR becomes inoperative and short-period agonist-induced oscillations always dominate.

Figure 4.

Model prediction. (A and B) Numerical simulations of [Ca²⁺] oscillations in the cytosol and sarcoplasmic reticulum (SR), respectively. In this simulation, V = –40 mV and p is set to be 0.35 μM at t = 250 s. (C) Experimental result of [Ca²⁺]_i oscillations induced by 50 mM KCl and 200 nM methacholine (MCh) that were consecutively added to the mouse airway smooth muscle cell (ASMC). (D and E) Numerical simulations with p = 0.35 μM and V set to –40 mV at t = 80 s. (F) [Ca²⁺]_i oscillations corresponding to the reverse order of stimuli. Parameter values are shown in the Supporting Material.

Oscillatory Ca²⁺ waves

Experimental results in Perez and Sanderson (10) indicate that Ca²⁺ oscillations induced by agonist consist of Ca²⁺ waves that propagate along the entire cell (Fig. 5 A). However, KCl-induced waves show elemental Ca²⁺ events that do not propagate through the whole-cell (indicated by arrows in Fig. 5 A). These elemental Ca²⁺ events become more frequent and pronounced immediately before a Ca²⁺ wave. After each Ca²⁺ wave, there is an inhibitory period before the elemental Ca²⁺ events start again.

Figure 5.

Ca²⁺ waves and elemental Ca²⁺ events in ASMCs induced by agonist and KCl. (A) Experimental results of line scans from the longitudinal axes of single mouse ASMC during simulation with 1 μM 5-hydroxytryptamine (5-HT), 1 μM acetylcholine (ACh), and 50 mM KCl (10). The line scans show ∼13 μm along the center of the cell. The elemental Ca²⁺ events in the KCl-induced Ca²⁺ wave are indicated by arrows. It was assumed that a smooth muscle cell is ∼40-μm-long in our model. (B and C) Numerical results showing Ca²⁺ waves close to the center of the smooth muscle cell (15–30 μm) induced by agonist and KCl, respectively. The slopes of the open lines in panel A as well as the colored lines in panels B and C indicate the velocity and direction of the Ca²⁺ waves in the mouse airway smooth muscle cell (ASMC). (D and E) Distributions of inositol trisphosphate receptor (IPR) and the ryanodine receptor (RyR) densities along the cell length u, respectively. Parameter values are shown in the Supporting Material.

The slopes of the open lines in the line-scan plots indicate the velocity (μm/s) and direction of the Ca²⁺ waves in the SMCs. Compared to agonist-induced waves, KCl-induced waves have a slower wave velocity and a longer duration. The initiation site of the agonist-induced Ca²⁺ waves can change and cause the wave to travel in the opposite direction (Fig. 5 A). However, the initiation site of KCl-induced waves seems to be close to the location exhibiting the highest frequency of elemental Ca²⁺ events. The line scans in Fig. 5 A show ∼13 μm along the center of the cell.

Our Ca²⁺ oscillation model was converted into a model for Ca²⁺ waves by including Ca²⁺ diffusion. Experimentally observed intracellular Ca²⁺ waves in mouse-lung-slice preparations exhibit very little, if any, curvature, and thus can effectively be modeled as one-dimensional (see supplemental videos in Perez and Sanderson (10)). Hence, we only consider a model with one spatial variable. Thus

$$\frac{\partial c}{\partial t}=D_{\text{c}}\frac{{\partial }^{2}c}{\partial u^2}+J_{\text{release}}-J_{\text{serca}}+\delta \left(J_{\text{in}}-J_{\text{pm}}\right),$$

where D_c is the diffusion coefficient of Ca²⁺ and the rest of the model remains the same. The spatial variable is u and it was assumed that both IPR and RyR densities are not spatially homogeneous. Parameters k_IPR(u) and k_RyR(u) control the variations in IPR and RyR densities, respectively.

In Fig. 5, B and C, we show Ca²⁺ wave density plots of waves induced by agonist and KCl, respectively. These plots only show an area of 15 μm along the center of the SMC in order to match the experimental data presented in Fig. 5 A. Our agonist-induced simulations are in good agreement with the experimental results and show that waves only change direction close to the center. In both simulations, the wave patterns at the ends of the cell are qualitatively the same as the ones from the middle of the cell (although there are no changes in direction).

There is, however, one important qualitative feature lacking from our model. Because our model is entirely deterministic, our KCl-induced simulations do not exhibit elemental Ca²⁺ events. Prior research (20,21) has shown that the elemental Ca²⁺ events observed experimentally can be reproduced by including stochastic properties of the IPR in the model. Similar methods can be applied for modeling stochastic RyR. It is not clear whether a fully stochastic model would result in qualitatively different predictions, although we believe this unlikely to be the case. In any case, the spatial properties of the elemental events have not yet been studied experimentally in sufficient detail to allow a proper statistical comparison between the model and the data.

Fig. 5, D and E, illustrates the predicted distributions of IPR and RyR densities along the cell. Our model predicts that both IPR and RyR densities are higher at one end of the cell, with RyR density sloping more steeply between the two levels than IPR density. Although we investigated several other hypotheses (included in the Supporting Material), they did not provide satisfactory results in the sense that we were unable to reproduce, even qualitatively, the observed experimental results. In other words, the predicted distributions shown in Fig. 5, D and E, are the only ones we have been able to find that reproduce the experimentally observed results. It is not difficult to find plausible reasons for why this particular receptor distribution should work as observed. Because of the gradient in receptor density, each end of the cell is trying to oscillate at a slightly different frequency. The two ends are able to maintain partial synchronization for a short time, but eventually one end lags too far behind the other. When this happens, the wave cannot then travel the entire length of the cell, but stops halfway (as it hits a refractory region), leaving the slower end of the cell free to initiate the next wave, which thus travels in the opposite direction. Repetition of this process results in waves that regularly change direction.

This conclusion is not based on a rigorous model comparison using a statistical analysis, and hence should be used with caution, but it nevertheless provides a testable prediction of IPR and RyR density distributions in ASMCs. Although this prediction is possibly surprising—it is difficult to think of any physiological reason for such gradients in IPR and RyR density—we know of no a priori reason to believe they are impossible. Only an experimental test will be able to address this question. We are currently developing experiments to test this prediction, but as yet no data are available.

Oscillatory Ca²⁺ waves and force generation

This study is part of a larger project with the goal of developing a distributed multiscale model of the lung to help our understanding of airway hyperresponsiveness. At the cellular level our objective is to understand how these changes in [Ca²⁺]_i are translated into contractile force, and how different Ca²⁺ oscillations can differentially affect contraction, and thus lung impedance.

We studied the role and relative contribution of Ca²⁺ waves versus whole-cell Ca²⁺ oscillations in force generation via the cross-bridge cycle. This was done using a model obtained by combining the wave model and our modified cross-bridge model (14). We only compare the steady-state mean relative force generated for each of these two cases. Although we have previously shown that the isotonic and isometric responses are qualitatively different in terms of transient behavior (14), at the steady state they are qualitatively the same. Due to the computational complexity of isotonic force generation, here we only calculate isometric force. Hence, although this will not generate quantitative predictions valid for the isotonic case, it will still provide the correct qualitative description of the effects on contraction of both oscillation types or spatial heterogeneity of the Ca²⁺ response.

For convenience, we include the equations of the cross-bridge model and the parameter values used in the computations in the Supporting Material.

Our results indicate that whole-cell Ca²⁺ oscillations induce greater contraction than Ca²⁺ waves (Fig. 6 A) for every agonist concentration (referring p). The reason for this is not obvious, as such differences in generated force could be the result of different oscillation frequencies, different mean [Ca²⁺]_i, or other factors.

Figure 6.

Steady-state mean relative force generated by both Ca²⁺ waves and whole-cell Ca²⁺ oscillations represented by stars and circles in all plots, respectively. (A) Relationships between mean relative isometric force and increases in agonist level (p μM). (B and C) Changes in oscillation frequency and average [Ca²⁺]_i corresponding to varied levels of p, respectively. (D) Data are taken from Wang et al. (14), their Fig. 8 C, and shows the contractile response of airway to Ca²⁺ oscillations (i.e., square waves) with different average [Ca²⁺]_i. Note that smaller mean relative airway area corresponds to stronger contraction. For comparison, the area obtained from a constant Ca²⁺ signal of equal average is shown (dashed line). The dot-dashed line gives the mean area for the limit case at high frequency oscillations (for detailed calculation, see Wang et al. (14)). In all panels, Ca²⁺ waves (marked as stars) and whole-cell Ca²⁺ oscillations (marked as circles) induced by p ∼0.32 μM (red) and p ∼0.6 μM (blue). Parameter values are shown in the Supporting Material.

However, Fig. 6, B and C, shows that this is not the case.

First, at each p, Ca²⁺ waves and whole-cell Ca²⁺ oscillations have similar oscillation frequencies (Fig. 6 B, colored stars and circles). Here both whole-cell Ca²⁺ oscillations and Ca²⁺ waves exhibit consistently high frequencies (0.38–0.49 spikes/s in Fig. 6 B). In prior work we demonstrated that increases in frequency above five spikes/min (0.083 spikes/s) for a particular level of average [Ca²⁺]_i cause little additional contraction in ASMCs (14). Hence, any difference in frequency between the two modes of Ca²⁺ oscillations investigated is unlikely to have a significant effect on force generation.

Secondly, Fig. 6 C shows at lower values of p the oscillations have a higher mean [Ca²⁺]_i, whereas the opposite is true at higher values of p. Hence, neither differences in frequency, nor differences in mean [Ca²⁺]_i can explain why oscillations generate greater contraction.

The answer to this puzzle becomes apparent only when we consider previous work. Fig. 6 D (adapted from Wang et al. (14)) illustrates the relationship between mean relative airway area (note that a small area corresponds to large contraction) and average [Ca²⁺]_i, for different wave shapes. We used square-waves (i.e., periodic piecewise linear function), which have the same amplitude, to obtain the high frequency (dot-dashed line) and three spikes/min (solid line) curves. The varying average [Ca²⁺]_i is achieved by changing the spike width (14). For a given mean [Ca²⁺]_i, the shape of the wave is an important determinant of generated force. The greater the frequency, the greater the force, and the least force is generated by a constant [Ca²⁺]_i. Hence, an oscillation with a higher mean [Ca²⁺]_i can generate less force, as long as the oscillation shape is similar to a constant [Ca²⁺]_i.

This explains the results in Fig. 6, A–C. At a lower value of p (p ∼0.32 μM; marked by the red circle and star) the mean [Ca²⁺]_i is higher in the oscillation than in the wave, and both wave shapes lie close to the solid curve in Fig. 6 D. Hence, the mean [Ca²⁺]_i has the greater effect, and the oscillation generates more force.

However, when p ∼0.6 μM (blue circle and star), the shape of the wave has changed dramatically, and looks more similar to a constant [Ca²⁺]_i. Thus, although it has a higher mean [Ca²⁺]_i than the oscillation, its changed shape means that it continues to generate less force.

It is important to note that this difference between waves and oscillations depends crucially on the assumption that the receptor density is not homogeneous—an assumption that is in turn based on the fact that a heterogeneous receptor density is necessary to reproduce the correct qualitative wave behavior. If IPR and RyR are assumed to have a homogeneous spatial distribution, waves and oscillations give the exact same generated force (results not shown). It implies that the heterogeneous distribution of IPR and RyR has a significant effect on ASMC contraction, and it is thus important that these receptor distributions be measured accurately.

Discussion

We have constructed a model to explore the regulatory mechanisms mediating agonist- and KCl-induced [Ca²⁺]_i oscillations in mouse ASMCs. Our model includes both IPR and RyR, interacting via a common SR. Although both receptors are included in the model, a different receptor dominates for each of the oscillation types. Our results show that in ASMCs, Ca²⁺ flux from the SR is mainly through the IPR in the agonist-induced case. However, in the KCl-induced case, Ca²⁺ release from the SR is only through the RyR. This difference in behavior results principally from the fact that the SR is depleted during agonist-induced oscillations, but is overfilled during KCl-induced case. In addition, with zero extracellular [Ca²⁺], agonist-induced [Ca²⁺]_i oscillations cannot be maintained and KCl does not induce any oscillations. Due to the difficulties of fitting one set of parameter values to three separate sets of experimental data (i.e., agonist- and KCl-induced oscillations, and oscillations in the absence of extracellular Ca²⁺), our model does not provide quantitative agreement with the experimental results. Most noticeably, simulated agonist-induced oscillations do not exhibit the raised baseline that can be seen clearly in the data, whereas the simulated KCl-induced oscillations are too thin. It is likely that our highly simplified description of Ca²⁺ influx is to blame for the baseline discrepancies, whereas Ca²⁺ pump rates are probably playing a major role in setting the width of the KCl-induced oscillations. However, despite these quantitative deficiencies, the model does provide testable predictions, all of which were subsequently validated experimentally. Thus, although our model clearly does not capture all the mechanisms underlying the Ca²⁺ oscillations, it does capture many of them, and retains considerable predictive capability.

Membrane depolarization is an important aspect in mediating SMC contractility. The addition of KCl leads to an increase in extracellular [K⁺], thus causing the membrane to depolarize and the Ca²⁺ channels to open, allowing an influx of extracellular Ca²⁺ into the cytoplasm. Our model omits the details of the membrane depolarization process. Hence we can increase V directly in the model to reflect the change in membrane potential induced by the addition of KCl. According to Perez and Sanderson (10), neither L-type nor T-type Ca²⁺ channels can currently be excluded from participating in KCl-induced Ca²⁺ influx. The precise identity, distribution, and physiological role of other types of Ca²⁺ channels in ASMCs is still the subject of ongoing research and beyond the scope of our work (33,34). Therefore we include a nonspecific voltage-gated Ca²⁺ channel in our model. The model could be modified to account for different types of Ca²⁺ channels once more conclusive experimental results become available. However, ASMCs are nonexcitable and thus transmembrane events involving these ion channels are likely less important than in excitable ones such as vascular SMC (34). Therefore, a simple model capturing the major electrophysiological processes such as ours may suffice.

SMCs of various types have been studied extensively. A number of models describing various physiological features of SMC related to cellular Ca²⁺ dynamics have been presented in the literature (35–39). These models, although relevant to their respective cell types, are not directly applicable to ASMCs due to differences in physiological structure and function. In Roux et al. (40), a theoretical model of membrane conductance specific to ASMCs was proposed. In their work they calculate a nonoscillating [Ca²⁺]_i increase and predict the corresponding membrane depolarization and influx of extracellular Ca²⁺. We investigate [Ca²⁺]_i oscillations caused by membrane depolarization, and so we use the approximate steady-state value of membrane potential V = –60 mV as predicted by their model.

With respect to modeling Ca²⁺ release from the internal store in SMCs, Parthimos et al. (35), Koenigsberger et al. (36), and Lemon et al. (39) simulated both CICR from the RyR- and IP₃-induced Ca²⁺ release from the IPR. These models assumed two separate internal stores for the two respective receptor types (i.e., a two-pool model). Other models (38,41) were used to simulate either receptor using a single internal store (i.e., single-pool model). In the literature (25,41) it was assumed that extracellular Ca²⁺ influx is not directly involved in Ca²⁺ signaling (i.e., closed-cell model). However, due to the importance of extracellular Ca²⁺ influx in our model to maintain Ca²⁺ oscillations, we  present an open-cell model here. The RyR model presented in Roux and Marhl (25) simulates caffeine-induced Ca²⁺ oscillations, hence RyR open probability is directly dependent on caffeine concentration, whereas our work focuses on KCl-induced Ca²⁺ oscillations via membrane depolarization. Our model includes both receptor types as necessitated by our experimental results, but uses a single internal store.

Elemental Ca²⁺ signals mediated by single or small clusters of RyR, and termed Ca²⁺ sparks, were initially discovered in cardiac cells and have been studied in a variety of cell types including ASMCs (42–44). Ca²⁺ sparks during agonist-induced Ca²⁺ oscillations have been observed in isolated tracheal SMCs of various species (44–47). Similar behavior has been commonly observed in cardiac myocytes that are overloaded with Ca²⁺ (42). Interestingly, similar experiments with mouse-lung-slice preparations did not produce Ca²⁺ sparks. The only observation of Ca²⁺ sparks was under KCl-induced conditions, where it appeared that Ca²⁺ was leaking into the cell and overloading the internal stores (10,33).

Experimental results from studies of isolated tracheal SMCs presented in the literature (6,7) indicate that agonist-induced [Ca²⁺]_i oscillations are mainly mediated by CICR via the RyR. However, experiments with ASMCs from lung slice preparations do not show this dependence on the RyR, indicating a dependence on the IPR instead (10–13,48). Our results indicate that Ca²⁺ load is a crucial bifurcation parameter. Under increased Ca²⁺ load, the dynamics of the system change to produce a region of agonist-induced Ca²⁺ oscillations dominated by the RyR. We therefore have reason to believe that these experimental results obtained from different cell preparations are not contradictory, but simply correspond to different regions in the bifurcation diagram.

From the two-parameter bifurcation analysis, we predict that no matter in which order agonist and KCl are put into the cell, the resulting [Ca²⁺]_i oscillations will always be the short-period agonist-induced-like oscillations. The experimental results also support this prediction (Fig. 4). Our prediction implies that in ASMCs the addition of agonist will always lead to a decrease of Ca²⁺ in the SR, thus preventing the RyR from releasing Ca²⁺. We also predict that low p can cause Ca²⁺ oscillations that are similar to KCl-induced oscillations. Here the SR can be overfilled as a result of increased Ca²⁺ influx during low p leading to baseline spiking through the RyR. This prediction has been confirmed qualitatively by experiment (results not shown), although the quantitative agreement is poor.

It is important to note that our model is based on the experimental results in Perez and Sanderson (10). We differentiate the receptors using the oscillation frequency based on the nature of our experimental data. However, we do not claim that this distinction is generally applicable to other experimental results or cell types. It is expected that by balancing Ca²⁺ fluxes across the outer plasma membrane, the RyR-mediated CICR could also produce fast oscillations. Ventura and Sneyd (49) presented an in-depth bifurcation analysis to investigate IPR- and RyR-mediated Ca²⁺ oscillations and waves. They concluded that it is not yet clear how changes in the relative effectiveness of IPR and RyR affect Ca²⁺ oscillations. It is not even clear whether or not it is possible to manipulate the receptors pharmacologically with fine enough precision to be able to answer this question.

We studied the spatio-temporal events of Ca²⁺ oscillations induced by agonist and KCl in mouse ASMCs by including the Ca²⁺ diffusion in our Ca²⁺ model to simulate Ca²⁺ waves. Our model only considers one spatial dimension. Due to the nature of the experimental results (10), we deem this to be sufficient for our investigation. Here the use of a more complicated geometry, approximating the actual shape of the cell, would likely be of little benefit, but introduce significant computational overheads. Our simulations provide the correct qualitative behavior when compared with experimental results of agonist-induced waves. However, our model cannot simulate the small elemental Ca²⁺ events in the KCl-induced wave. Our results indicate that both IPR and RyR densities are higher at one end of the cell, with RyR density sloping more steeply between the two levels than IPR density.

Finally, our results also show that oscillatory Ca²⁺ waves cause less contraction than whole-cell Ca²⁺ oscillations induced by the same p. The contraction differences can be attributed to the heterogeneous receptor distributions, decreasing the force generated by an oscillatory wave compared to a spatially homogeneous oscillation. This indicates that the inhomogeneity of the receptor distributions plays an important role in ASMC contraction and the spatial distribution of Ca²⁺ cannot be ignored when computing the force generated by oscillatory Ca²⁺ waves, and hence must be taken into account even in multiscale models. It is currently unclear how best to include this property. Direct numerical simulation is probably computationally prohibitively expensive, but whole-cell models, which are much faster, are quantitatively inadequate. We shall address this issue in later work.