Abstract
Twisting a DNA molecule held under constant tension is accompanied by a transition from a linear to a plectonemic DNA configuration, in which part of the applied twist is absorbed in a superhelical structure. Recent experiments revealed the occurrence of an abrupt extension change at the onset of this transition. To elucidate its origin we study this abrupt DNA shortening using magnetic tweezers. We find that it strongly depends on the length of the DNA molecule and the ionic strength of the solution. This behavior can be well understood in the framework of a model in which the energy per writhe for the initial plectonemic loop is larger than for subsequent turns of the superhelix. By quantitative data analysis, relevant plectoneme energies and other parameters were extracted, providing good agreement with a simple theory. As a direct confirmation of the initial-loop model, we find that for a kinked DNA molecule the abrupt extension change occurs at significantly lower twist than the subsequent superhelix formation. This should allow pinning of the plectoneme position within supercoiled DNA if a kinked substrate is used, and enable the detection of enzymes and proteins which, themselves, bend or kink DNA.
Introduction
DNA supercoiling in living organisms is a direct consequence of the DNA helical structure. It arises during essential cellular processes, such as replication and transcription, when the corresponding cellular factors follow the helical path of the molecule (1,2). Supercoiling needs therefore to be counterbalanced (3), but also fulfills important tasks in genome compaction and transcriptional regulation (4).
To better understand how supercoiling contributes to cellular function, it is essential to know the mechanical response of DNA upon overtwisting. A breakthrough for this topic has been accomplished more than a decade ago, when it become possible to twist a single DNA molecule under an applied tension (5). Up to now, many transitions that DNA undergoes during supercoiling as well as important supercoiling parameters have been carefully characterized and described. This includes, for example, structural transitions of B-DNA during supercoiling (6,7), the torsional rigidity of DNA (8) as well as the twist-stretch coupling (9,10), the direct measurement of torque during supercoiling (11,12), and the dynamics of supercoil release (13).
Upon twisting DNA under constant tension, the DNA length stays approximately constant, as nearly all induced supercoils are stored in the form of twist. Once a critical torque level is reached, the molecule undergoes a transition: it buckles and enters the plectonemic phase in which part of the DNA forms a superhelical structure. Additionally added turns are seen in a linear decrease of the DNA length (Fig. 1 A). The formed superhelix buffers any subsequently applied twist as writhe (14). Although torque increases linearly with the number of added turns before buckling, it remains constant in the plectonemic phase. The transition between linear and plectonemic phase was for a long time thought to occur gradually, based on the shape of the supercoiling curves, i.e., plots of DNA length versus added turns (15). Recently, however, a discrete and abrupt buckling, seen as a sudden, major DNA length change, has been reported (16). Whereas most previous measurements had been carried out using magnetic tweezers, this new study employed optical tweezers, which due to continuous rotation allowed a higher resolution of the supercoiling curves. Though the force dependence of the abrupt buckling transition has been characterized, its exact origin remained unclear and it has been speculated that it reflects the formation of the initial plectonemic loop (16).
Figure 1.
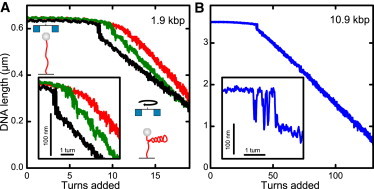
Buckling transition measured for different ionic strengths and DNA lengths. (A) An ∼1.9-kbp DNA molecule held at a constant force of 3.0 pN is continuously twisted with a frequency of 0.5 Hz and its length is recorded simultaneously. Curves are shown for Na+ concentrations of 20 mM, 60 mM, and 320 mM (red, green, and black line). The cartoons illustrate the experimental configuration and the transition from linear to superhelical DNA (red line). The magnetic bead (gray sphere) and the pair of magnets (blue squares) are also shown. (Inset) Enlarged view on the supercoiling curves of the main figure at the buckling transition. (B) Supercoiling curve for a 10.9-kbp DNA molecule twisted with 1 Hz at 3.0 pN force in buffer containing 320 mM Na+. (Inset) Enlarged view on the supercoiling curves of the main figure at the buckling transition. Data were taken at 300 Hz and smoothed to 20 Hz.
Here we investigated the dependence of the abrupt buckling on the concentration of monovalent ions and on the length of the DNA molecule using magnetic tweezers. Although we confirm the presence of an abrupt buckling at increased concentrations of monovalent ions, we find it to become less pronounced and finally to disappear at low (20 mM) concentrations of monovalent ions. In addition, we see a strong dependence of the abrupt buckling on the DNA length. Quantitative analysis of the postbuckling state occupancy during supercoiling shows that the structure formed during buckling is not fixed, but rather variable. It can buffer considerably more than one supercoil in the form of writhe depending on the applied force, the DNA length, and the ionic strength of the solution. As the buckling transition itself is spread over a certain finite range of applied turns, we also see that the buckling structure varies throughout the width of the transition, i.e., more writhe can be accommodated at higher numbers of turns.
This behavior can be well understood within a model in which a higher energy per writhe is required to extrude the initial loop compared to form subsequent turns of the superhelix. Using estimates for the relevant energies, we can reproduce almost quantitatively the dependence of relevant buckling parameters, e.g., the buckling equilibrium point and the associated torque change, on the different conditions. Additionally we investigated a kinked DNA substrate, for which we observe prebuckling (i.e., an abrupt buckling before the actual superhelix formation). This behavior provides independent evidence of the initial-loop model.
Our results provide insight into the energetics of initial-loop formation and reveal, as a consequence, the presence of single and multiplectonemic states of supercoiled DNA. Furthermore, they suggest that the plectoneme position on kinked DNA substrates can be pinned to a fixed position.
Materials and Methods
DNA substrate preparation
The short substrate for the magnetic tweezers experiments was prepared by cutting a custom-made plasmid using the restriction enzymes XhoI and PvuI, providing a linear fragment of 1865-bp length with corresponding sticky ends on either side. Biotin- or digoxigenin-modified attachment handles were made by digesting a 1.2-kbp biotin- and a digoxigenin dUTP-labeled PCR fragment from plasmid pBluescript II SK+ (Stratagene, La Jolla, CA) with XhoI or PvuI, respectively, approximately in the middle of the fragments. The labeled fragments were subsequently ligated to the 1865-bp fragment. The long 10.9-kbp substrate was prepared similarly by digesting an appropriate plasmid and the labeled attachment handles with PciI and SacI. The kinked DNA substrate (1845 bp) was prepared from a plasmid containing five directly repeated BbvCI sites with 16-bp spacing. The plasmid was nicked at the BbvCI sites using Nt.BbvCI and simultaneously cut with BsrGI and PspOMI. The single-stranded gap resulting from the nicking reaction was filled with a DNA single strand containing a 20-bp hairpin (N. Luzzietti, H. Brutzer, and R. Seidel, unpublished). Subsequently the DNA fragment was ligated as described above to labeled attachment handles cut with BsrGI and PspOMI.
Sample preparation
DNA constructs were bound to 1-μm streptavidin-coated superparamagnetic microspheres (MyOne, Invitrogen, Carlsbad, CA) and flushed into a flow cell, whose bottom coverslip was coated with anti-digoxigenin. All measurements were performed at room temperature in 10 mM phosphate buffer at pH 7.5, supplemented with varying amounts of NaCl to achieve the final Na+ concentrations as indicated in the text.
Magnetic tweezers
The basic magnetic tweezers protocol has been described (17,18). The magnetic field was generated using a pair of permanent NdFeB magnets (W-05-N50-G; Supermagnete, Uster, Switzerland). The length of the DNA was monitored by measuring the vertical position of the magnetic microsphere with respect to a nonmagnetic reference microsphere attached to the surface of the flow cell using videomicroscopy and three-dimensional particle tracking. Images of both beads were acquired simultaneously with a frequency of 300 Hz using a fast CMOS-camera (EoSens CL; Mikrotron, Unterschleissheim, Germany) and analyzed in real-time.
DNA supercoiling and data analysis
DNA supercoiling was carried out by rotating the magnetic field (typically at 0.5 Hz) and simultaneously monitoring the DNA length.
The jump size upon abrupt buckling and the postbuckling population was obtained by fitting a double-Gaussian distribution to the histograms of the DNA length (Fig. 2, A and B). The values and (see Results) were obtained by fitting the postbuckling state population with Eq. 11, which provided similar values as Eq. 5. At low forces (<1 pN), where the buckling transition became too fast, was determined from straight line fits to the supercoiling curves. For high forces, both methods were found to produce consistent results.
Figure 2.
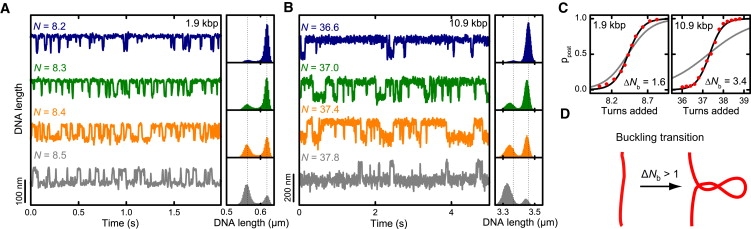
Equilibrium occupancy of pre- and postbuckling state. (A) 1.9 kbp and (B) 10.9 kbp DNA molecules were held at a constant force of 3.0 pN in buffer containing 320 mM Na+. Time traces were recorded at different amounts of added turns N in the vicinity of the buckling transition. Data were taken at 300 Hz. Normalized length histograms are shown on the right. The DNA was observed to rapidly fluctuate between two distinct states, the pre- and the postbuckling state. Dotted lines are centered on the peaks of the uppermost histogram and indicate the shift of the states throughout the transition. (C) Occupancy of the postbuckling state as function of added turns for both DNA lengths (red dots). Experimental conditions are as in panel A. Solid lines are fits to the data according to Eq. 5, where ΔNb was taken to be free (black line, ΔNb of best fit shown in graph) or fixed to ΔNb = 1 (gray). (D) Illustration representing the behavior of DNA at the buckling transition, which can involve the formation of a structure comprising >1 turn of writhe.
Results
Abrupt buckling measured with magnetic tweezers
Abrupt buckling upon DNA supercoiling has only recently been discovered using optical tweezers (16). This technique, however, requires an active feedback to keep the force constant upon changes of the DNA length. To exclude artifacts of the particular measurement technique, we here employed magnetic tweezers, to detect abrupt buckling at the onset of supercoiling. In contrast to optical tweezers, magnetic tweezers can be considered as a constant force device over the length range of interest. For the supercoiling experiments we used a short DNA molecule of ∼1.9 kbp length, similarly to one employed previously (16). In contrast to the standard magnetic tweezers measurements, in which the DNA length is measured at discrete supercoiling steps of full turns, we supercoiled DNA in a continuous fashion, providing a high rotational resolution similar to that used in the optical tweezers experiments (16).
At low amounts of monovalent ions (20 mM Na+) we did not observe an abrupt buckling, but instead a smooth transition from the linear to the plectonemic phase (Fig. 1 A, red line). This is more in line with the traditional picture of DNA supercoiling (15). However, when increasing the ionic strength (to 60 and 320 mM Na+), a sudden jump, i.e., an abrupt buckling, can be observed before plectoneme formation (Fig. 1 A, green and black lines). Notably, with increasing salt the abrupt buckling becomes more pronounced and occurs at fewer added turns, whereas the length change per turn (i.e., the slope) of the supercoiling curve, after the transition, is reduced.
We also tested the abrupt buckling for a long DNA molecule of 10.9 kbp at 320 mM Na+, and found it to be even more pronounced (Fig. 1 B). The jump size increased notably in length. In addition, the buckling transition ranged over several turns, and comprised many fluctuations between the pre- and postbuckling state.
This demonstrates that abrupt buckling is also observed in constant force measurements with magnetic tweezers. In addition to previous observations, we find that the abrupt buckling depends strongly on the ionic strength and on the length of the DNA.
The width of the buckling transition
The transition from pre- to the postbuckling state must coincide with an abrupt reduction of the DNA twist and thus the formation of writhe, because only increasing twist drives the transition. The width of the transition should then provide information about the abrupt twist reduction. We therefore measured the population of pre- and postbuckling state under equilibrium conditions. DNA molecules were held at constant force and time traces were recorded at different discrete numbers of added turns N, distributed over the width of the buckling transition (Fig. 2, A and B). Near the buckling transition, the DNA molecule rapidly fluctuates between a pre- and postbuckling state for a fixed number of added turns. In the histograms of the time traces, this can be seen as two peaks, which are well fit by a Gaussian function. With increasing amount of added turns, the postbuckling state becomes more populated and the corresponding peak becomes relatively larger. From Gaussian fits to the peaks, we determined the probability for the postbuckling state to be populated as function of added turns (Fig. 2 C).
A simple expression for the postbuckling state population can be derived, assuming that for undergoing buckling, a fixed free energy penalty Eb has to be paid. For example, Eb must include the displacement of the magnetic bead and increased DNA bending. The buckling is accompanied by a twist reduction due to the formation of writhe. It occurs when Eb is close to the change in twist energy. Before buckling, the free energy of the DNA upon supercoiling is given by (19,20)
| (1) |
where L0 is the contour length of the DNA and Cs is the effective torsional modulus with (19)
| (2) |
The value C denotes the DNA torsional modulus, p the bending persistence length, and F the applied force. For the torsional modulus and the persistence length, we used values of 100 kBT nm (8) and 45 nm, respectively. Equation 2 accounts for the fact that, due to DNA writhe fluctuations, not all added turns contribute to the twist stored in the DNA.
Upon buckling, the DNA twist energy is reduced. However, the energetic penalty Eb for the formation of the buckling structure has to be overcome, which provides for the free energy of the postbuckling state, as
| (3) |
where ΔNb is the amount of twist, which is transferred into writhe during buckling. Within this simple two-state model, the probability that the postbuckling state ppost is occupied can be calculated using Boltzmann statistics:
| (4) |
Inserting Eqs. 1 and 3 into this expression yields
| (5) |
with Nb being the number of added turns at the point of buckling equilibrium, where the pre- and the postbuckling state are equally populated. The value Nb is then given by
| (6) |
Surprisingly, fits of the experimentally obtained postbuckling state occupancy with Eq. 5 provide values for ΔNb which are considerably larger than one turn (Fig. 2 C). At 3.0 pN and 320 mM Na+, we obtain for the writhe within the buckling structure ΔNb = 1.6 ± 0.1 and 3.4 ± 0.2 turns for the short and the long DNA molecule, respectively. Remarkable also is the DNA length dependence of ΔNb. This suggests that upon abrupt buckling a fixed structure is not formed, such as with a first initial loop, but instead a continuous structure, such as a plectonemic superhelix with multiple turns (Fig. 2 D).
Kinetics of the buckling transition
In addition to studying the equilibrium of the pre- and postbuckling states, we also analyzed the kinetics at the buckling transition. To extract the residence times of the individual states, threshold values were applied to assign each time point to the pre- or postbuckling state. From this a binary step function was reconstructed and residence times were calculated.
The residence times appear exponentially distributed for the short molecules (Fig. 3 A), whereas a minor second exponential component appears for the long DNA (not shown). The mean residence times and change exponentially with added turns (Fig. 3 B) in agreement with a two-state system (Fig. 3 B). The torque in the DNA molecule changes the height of the energy barrier for undergoing the transition. One can describe the torque dependence of and by adding the torque multiplied by the angular distance to the barrier as an additional term into an Arrhenius equation, which results into
| (7) |
where τb is the mean residence time at the buckling transition. The value is substituted by or corresponding to the distance of the transition state to the prebuckling or postbuckling state, respectively. Fitting Eq. 7 to the experimental data, we find the transition state to be approximately half-way between the pre- and the postbuckling state for both molecule lengths (Fig. 3 B). Understanding of the energetic barrier needs further work, as there might not be common transition pathways from prebuckling to postbuckling state and vice versa. At 320 mM Na+ and 3.0 pN force we obtain τb = 35.5 ± 0.5 and 75.7 ± 0.8 ms for the short and the long molecule, respectively. Thus, τb increases with molecular length. This might be due to slower diffusion of the larger plectonemic structure for the long molecule. Furthermore, we find that τb decreases, i.e., transitions become more frequent at lower ionic strength and lower force (data not shown). Generally, we observe that the transition between the pre- and the postbuckling state occurs considerably faster than observed previously with optical tweezers (16). This might be due to different response dynamics for both tweezers systems. The additional potential set by the optical trap leads to different energy landscapes for buckling, which can affect its dynamics.
Figure 3.
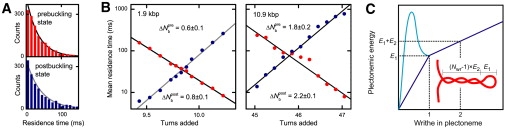
Kinetics of the buckling transition. Data shown is for 4.0 pN and 320 mM Na+. (A) Distributions of the residence times for the pre- and postbuckling state close to the buckling equilibrium (9.8 turns) for the 1.9 kbp DNA molecule. The solid lines represent a single exponential function with the mean residence time as characteristic decay time. (B) Mean residence times of the prebuckling (red solid circles) and the postbuckling states (blue solid circles) as function of added turns for the 1.9 kbp and 10.9 kbp DNA molecule. Solid lines are exponential fits to the data according to Eq. 7. The resulting distances to the transition state and are given in the figure. (C) Schematic drawing of the hypothetical energy landscape for plectoneme formation. Independent of the actual landscape for the initial loop (dark blue straight line and light blue line with transition state), the supercoiling energy attains E1 after one turn and increases with E2 for each subsequent turn. (Inset) Illustration of the plectoneme formation energies E1 and E2.
End-loop model for abrupt buckling
The observations made so far, in particular the length-dependent writhe of the buckling structure, are consistent with a plectonemic superhelix formed upon abrupt buckling. However, so far the structural and energetic basis underlying the observed behavior remains unclear.
For a plectonemic superhelix an apparent discontinuity can be found at the initial loop, which resembles more a planar DNA loop (Fig. 3 C). For a given DNA segment length it is energetically more favorable to form one turn of the superhelix than a circular loop. Therefore, it is reasonable to assume that the energy for the first turn of the superhelix (initial loop) is larger than for any subsequent superhelical turn. This is similar to an approach developed by Daniels et al. (21), which only recently became available.
Let E1 be the free energy for the first turn of writhe in the plectoneme, which comprises the additional energy for the initial loop formation. The value E2 shall denote the free energy of every subsequent writhe within the plectoneme (Fig. 3 C). With Nwr denoting the writhe of the plectoneme, the free energy of the DNA after buckling for Nwr ≥ 1 is given by
| (8) |
The mean writhe Nwr,0 for a given number of added turns N is then obtained by minimizing Eq. 8 with respect to Nwr. Hence, one obtains Nwr,0 and the corresponding postbuckling energy :
| (9) |
| (10) |
Inserting the last equation together with Eq. 1 into Eq. 4 provides now the probability for the DNA to be in the postbuckling state pp within the framework of the initial-loop model:
| (11) |
In analogy to the simple model above, represents the position of the buckling transition, i.e., when pre- and postbuckling state are equally populated:
| (12) |
The value is the average writhe of the abruptly forming plectoneme at the buckling equilibrium point , which can be derived by
| (13) |
In contrast to the simpler model the writhe of the forming plectoneme is now predicted to increase linearly with the added turns, and not to be a constant over the transition (see Eq. 9). This can directly be confirmed by the experiments, because the postbuckling level shifts gradually toward lower DNA length over the transition (see histograms in Fig. 2 and Fig. S1 in the Supporting Material). Note that within our derivation we limit Nwr not to be smaller than 1, as we do not know the actual energy landscape for the initial loop formation (Fig. 3 C). However, as long as ≥ 1, the actual energy landscape for the first turn (e.g., a linear increase with or without an offset, or an additional transition barrier) does not matter, because independent of the actual landscape the same results are obtained (Fig. 3 C). As we find ≥ 1 for our experimental data, this model is well applicable.
Estimating the plectoneme formation energies E1 and E2
If E1 and E2 are known, one can predict the mean torque Γ and the mean DNA length L as a function of the added turns and applied force using the expressions derived above,
| (14) |
| (15) |
where z(F, Γ) is the relative extension of the DNA (19), ΔL1 the length reduction for the initial loop, and dL/dN the slope of the supercoiling curves after the buckling transition (see Supporting Material for full expressions). To estimate the length reduction ΔL1 as well as the energy E1 for the initial loop, we assume it to be a perfect circular loop and calculate its bending energy as well as the energy necessary to shorten the DNA against the applied force. This is similar to the simple-loop model used previously to derive an estimate for postbuckling torque and slope (15), except that here the DNA shortening is corrected by the relative extension of the DNA (22). One then obtains for the initial-loop energy (see Supporting Material):
| (16) |
To obtain an estimate for E2, we use the expression for the postbuckling torque Γ derived within the composite model by Marko (20),
| (17) |
where P is the plectonemic twist stiffness, which is a freely adjustable parameter depending on the ionic strength of the solution. The value P is also related to the postbuckling slope dL/dN (16,20) and can thus be obtained by fitting experimental data (see Supporting Material). We obtained values for P of 31, 28, 24, 21 kBT nm for 30, 60, 170, 320 mM Na+, respectively, in good agreement with previously published data (20,23). We note, however, that the composite model (20) does not provide a satisfactory description of the postbuckling slope over the full range of applied forces (12).
Using Eqs. 11–16, we can now predict the DNA length and the torque upon DNA supercoiling at constant force. Examples of measured and predicted supercoiling curves can be seen in Fig. 4, A and B. Most importantly our model can well describe abrupt buckling. Despite simple estimates for E1 and E2, we obtain remarkable agreement with the experimental data regarding the buckling point, the width of the transition, and the jump length.
Figure 4.
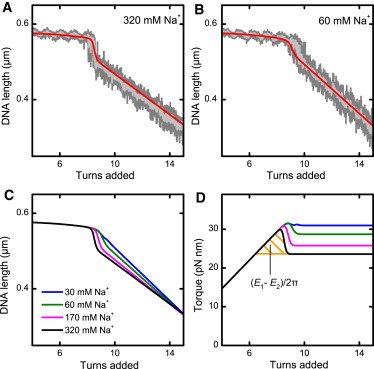
Measured supercoiling curves and predictions from the initial-loop model. (A and B) Supercoiling curves for a 1.9 kbp DNA molecule at 3.0 pN in a buffer containing 320 mM and 60 mM Na+ (as indicated). Data were taken at 300 Hz (dark shading) and smoothed to 20 Hz (light shading). The solid red line is the prediction from the initial-loop model according to Eq. 15 using estimates for the plectoneme formation energies E1 and E2 (Eqs. 16 and 17). (C) Salt dependence of supercoiling curves and (D) torque development as predicted by the initial-loop model. The shaded area between the torque overshoot and the postbuckling torque under the black curve corresponds to the difference between the initial loop energy E1 and superhelix formation energy E2.
We also calculated supercoiling curves and the associated torque at different salt concentrations (Fig. 4, C and D). As for the experimental data (Fig. 1 A), the buckling transition becomes less pronounced at lower salt concentrations. The presence of an abrupt buckling transition is associated with an overshoot of the torque, arising from the sudden writhe formation within the plectoneme (Fig. 4 D). The energetic difference between the initial-loop formation energy E1 and the superhelix-formation energy E2 corresponds to the area enclosed by the torque overshoot and the postbuckling torque (shaded area in Fig. 4 D). Thus, the torsional overshoot and correspondingly the abrupt buckling transition are required to ensure the compensatory work for initial-loop formation. With decreasing ionic strength the electrostatic repulsion between the DNA strands in the plectoneme increases, which is associated with an increase of the postbuckling torque and correspondingly of E2 (Fig. 4 D). For the initial loop, electrostatics plays supposedly a minor role due to the larger DNA-DNA distance within the loop. It should therefore change much less with the ionic strength. Therefore, the difference between E1 and E2 becomes smaller with decreasing ionic strength, which readily explains the disappearance of the abrupt buckling.
Force dependence of the buckling transition
To further support the initial-loop model for abrupt buckling we compared several parameters obtained from experiment and theoretical prediction. Though we use only estimates for E1 and E2, important trends, such as the scaling with the molecule length, should be correctly predicted.
The jump size, , and were obtained as described in Materials and Methods. The plectoneme formation energies E1 and E2 were calculated from and according to the following relations, which were derived from Eqs. 12 and 13:
| (18) |
| (19) |
First we evaluated the force dependence of these parameters at 320 mM Na+ for both the long and the short molecules. The jump size was found to increase with DNA length (Fig. 5 A), which is correctly reflected by the theoretical prediction (see Supporting Material for calculation of the jump size). For the high force regime, the absolute jump length is also well described. However, at low forces, where the jump size is found to remain constant (short molecule) or to decrease slightly (long molecule), a different trend is predicted. Similar behaviors and jump sizes were found for the lower salt concentrations (not shown). We note that Forth et al. (16) reported a large increase of the jump size when decreasing the force and no dependence on the length of the DNA. In our measurements all jump sizes were directly obtained from Gaussian fits to the DNA length distribution at the buckling equilibrium, leaving very little room for ambiguity. Furthermore, the abrupt buckling was especially well resolved for the long DNA molecule. The observed DNA length dependence of the jump size agrees well with the observed length dependence of (i.e., the writhe change during buckling; see Fig. 2 C and below) because a longer plectoneme should also contain more DNA. We currently do not have an explanation for the discrepancy between the different data. We note that small changes in the expression for E1 can remarkably change the force dependence of the jump length, although retaining the trend for the other parameters (21). Beyond simple estimates for E1, a more elaborate theory is required to substantiate the observed jump lengths.
Figure 5.
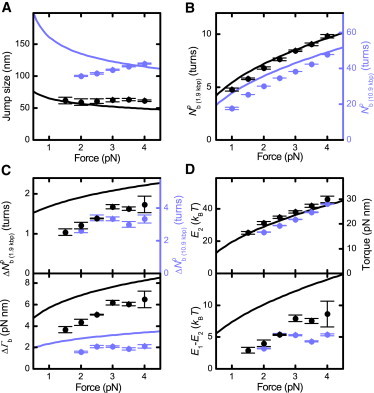
Force dependence of the buckling transition at 320 mM Na+ for the 1.9 kbp (black) and the 10.9 kbp DNA molecule (blue). Experimental values are shown as solid circles, predictions from the end-loop model as solid lines. In the case of an overlap, only the black curve is depicted. (A) Jump size at buckling equilibrium. (B) Position of the buckling equilibrium. To highlight the DNA length dependence, the right axis, corresponding to the 10.9 kbp DNA molecule, was scaled linearly with DNA length compared to the left axis corresponding to the 1.9 kbp DNA molecule. (C) Change of twist transferred into writhe during buckling at buckling equilibrium and corresponding torque change . The expected scaling of with the square root of the DNA length is highlighted by scaling the axes accordingly (Eq. 13). (D) (Top) Superhelix-formation energy E2 and inferred postbuckling torque. (Bottom) Energy difference between the initial-loop formation energy E1 and E2. Error bars represent the statistical error of the data.
For our model predicts a scaling with the square root of the DNA length (Eq. 13). Therefore, does not increase linearly with DNA length but is slightly reduced. To highlight this behavior, we scaled the data for the two DNA lengths linearly in the case of (Fig. 5 B) and with the square root of the DNA length in the case of (Fig. 5 C). Within error we can indeed confirm the prediction. The general trend and magnitude for the two parameters with increasing force are well described, though we somewhat overestimate and the corresponding torque jump upon buckling ΔΓb.
For E2, which is directly related to the postbuckling torque, the data is in agreement with the prediction from Marko (20) (Fig. 5 D, top). Only a slight variation of the postbuckling torque was observed for both DNA lengths, which reflects the experimental error of the procedure. We note that the absolute value of E2 depends directly on the torsional modulus of the DNA, for which we take 100 kBT nm. Thus, using a lower torsional modulus (for example, 94 kBT nm (12)) will reduce the obtained values for E2 and the postbuckling torque.
We also obtained the energy difference between E1 and E2, which can be considered as a nucleation barrier for plectoneme formation. It amounts to several kBT at 320 mM Na+ for the force range considered (Fig. 5 D, bottom), which should strongly favor the existence of only a single plectoneme (see Discussion and Conclusions below). Similar to , the energetic difference between E1 and E2 is also slightly overestimated by the prediction, though the general trend is well described.
Salt dependence of the buckling transition
For the shorter DNA molecule, we also characterized the buckling parameters at different Na+ concentrations in particular 60, 170, and 320 mM (Fig. 6). The general trends are well reproduced by our model. Worth highlighting is the increase of , ΔΓb, and E1 – E2 with increasing ionic strength, which lets the abrupt buckling become more pronounced. Interesting is the measured decrease of E1 with increasing ionic strength (Fig. 6 D), which is not included in the simple theory. However, as argued above, E2 decreases even more strongly, leading to an increase of E1–E2 with increasing ionic strength.
Figure 6.
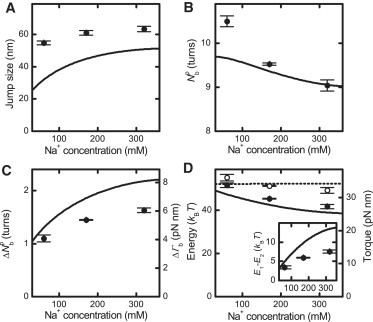
Salt dependence of the buckling transition parameters at 3.5 pN for the 1.9 kbp DNA molecule. Experimental values are shown as circles. Predictions from the initial-loop model are shown as black lines. (A) Jump size at buckling equilibrium. (B) Position of the buckling equilibrium. (C) Change of twist transferred into writhe during buckling at the buckling equilibrium and corresponding torque change ΔΓb. (D) Superhelix-formation energy E2, inferred postbuckling torque (solid circles and solid line), and initial-loop formation energy E1 (open circles and dashed line). (Inset) Energy difference between E1 and E2.
Supercoiling kinked DNA
Generally, the initial-loop model can well describe the observed abrupt buckling at the onset of plectoneme formation. Together with our simple estimates for the plectoneme formation energies, it can well reproduce the scaling and the magnitude of most parameters describing the buckling transition, which provides strong support for the model. For most of the Na+ concentrations considered here, we find E1 > E2, which causes abrupt buckling. However, if one could locally reduce E1 to become smaller than E2, the model would predict the existence of a prebuckling state (i.e., an initial loop would form before the subsequent superhelix is formed).
To test the prediction, a DNA construct was prepared in which a three-arm junction was incorporated (see Materials and Methods). This junction introduces a kink of ∼120° (Fig. 7 A) and should significantly reduce the initial-loop formation energy E1.
Figure 7.
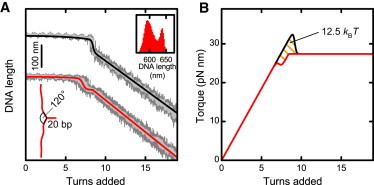
(A) Supercoiling curves for a kinked (lower) and a straight, i.e., unkinked (upper) DNA molecule taken at 3.5 pN and 320 mM Na+. Data are acquired at 300 Hz (dark shaded lines) and filtered to 20 Hz (light shaded lines). Solid red and black lines are calculated according to Eq. 15 with the initial-loop length reduction ΔL1, the initial-loop energy E1, and the superhelix energy E2 taken from fits to the data. The illustration shows the structure of the DNA kink. A 20-bp hairpin was introduced into the substrate, leading to the formation of a small three-arm junction. Neighboring arms should join at an angle of ∼120°. (Inset) Histogram of the DNA length at 7.0 turns for the kinked molecule. (B) Torque development for both molecules as predicted by the model. The shaded area enclosed by the two curves corresponds to the total difference between the initial-loop energies E1 for the straight and the kinked DNA molecule.
Indeed, in supercoiling experiments prebuckling is found for this substrate. After a first length reduction, occurring much earlier than for a straight DNA molecule, the DNA extension remains constant for almost another turn, during which additional torque builds up. Only then does the formation of the superhelix start, causing the linear DNA length decrease with added turns (Fig. 7 A). Interestingly, the transition at the prebuckling point also occurs abruptly, because two distinct DNA lengths can be identified (Fig. 7 A, inset).
Using the expressions derived above for describing DNA length and torque during supercoiling, we can reproduce the supercoiling curves of the kinked DNA. Therefore we have to choose an appropriate E1, which has to be considerably smaller than E2. At a force of 3.0 pN and a Na+-concentration of 320 mM we find E1 to be ∼4 kBT smaller than E2. Using the values for E1 and E2, which best describe the supercoiling curves, we can infer the torque as above from Eq. 14. The prebuckling causes the torque to undershoot compared to the postbuckling torque. The total difference between the initial-loop energies E1 for the straight versus the kinked DNA molecule, corresponding to the area enclosed by the two curves in Fig. 6 B, is 12.5 kBT. This represents an enormous bias for plectoneme nucleation at the DNA kink.
Discussion and Conclusions
Initial loop provides a salt-dependent plectoneme nucleation barrier
In this study we investigated the abrupt buckling before plectoneme formation using magnetic tweezers. In addition to the previously reported force-dependence (16), we found that the abrupt buckling strongly depends on the ionic strength as well as on the length of the DNA molecule. Our data is in agreement with the proposed initial-loop model (21), in which a higher energy per writhe is required to form the initial loop than for subsequent turns in the plectonemic superhelix. Direct support comes from the observed DNA length dependence of the jump size together with the broadening of the transition. Analyzing the transition width (Fig. 2 C) reveals that the writhe of the postbuckling structure scales within error with the square root of the DNA length. This is a direct consequence of our model, independent of particular values for the plectoneme formation energies. Applying estimates for these energies describes well the dependences of the buckling parameters on the applied force and ionic strength, which provides additional support for the model. Qualitatively, the dependence on the ionic strength can be understood by an increased repulsion of the DNA strands in the plectonemic superhelix with decreasing ionic strength. Consequently the energy for superhelix formation E2 increases. Considering that electrostatic interactions within the initial loop should play a minor role due to a larger DNA-DNA distance, the difference between the initial loop energy E1 and E2 decreases and the abrupt buckling becomes less pronounced.
The formation of a second or further plectonemic structures is normally less favorable due to the large initial-loop formation energy E1 compared to the smaller energy E2 required to extend the superhelix. Therefore, plectoneme formation is nucleation-limited (i.e., for a sufficiently large energetic difference, growth of an already existing plectoneme will be more likely than nucleation and maintenance of an additional one). The obtained values for the energy difference between E1 and E2 amount to several kBT for Na+ concentrations ≥60 mM (Figs. 5 D and 6 D). Therefore, under these conditions the presence of only a single plectoneme is much more probable than predicted by a Boltzmann-like distribution for single and multiplectonemic states. By contrast, at low ionic strength, E1 can be equal to or smaller than E2, in agreement with the observed disappearance of the abrupt buckling transition and the appearance of a smooth and broad transition at 20 mM Na+. In this case, the presence of multiple plectonemes will be favored. When E1 is considerably smaller than E2, exclusively initial loops might form. This has been described previously in Monte Carlo simulations of DNA supercoiling at 20 mM monovalent salt, though the applied hard-wall potentials for electrostatic interactions may not allow a quantitative comparison (24). The existence of single, multiple, and more complex plectonemic states needs to be carefully considered for the interpretation of single molecule experiments (13) and the application of theories at low salt concentrations (22,25).
A more quantitative understanding of abrupt buckling will require rigorous theoretical work. Most importantly, the energetics and shape of the initial loop, displaying a teardrop-like configuration (26), should be appropriately considered. Potential kinking of the sharply bent plectoneme tip, as well as the salt dependency of the persistence length and the initial loop energy, need additional attention.
Detecting DNA kinks: plectoneme pinning and energy of DNA bending
By introducing an ∼120° kink into the DNA we were able to achieve a prebuckling state, i.e., buckling that occurred considerably earlier than the actual superhelix formation (Fig. 7 A). This is a direct consequence of the initial-loop model, considering that DNA kinking will reduce E1 to become smaller than E2. Therefore it serves as an independent support for the model. Preferential buckling at kinkable regions and regions with discontinuous stiffness has been predicted in static computational models (27) and is now confirmed experimentally.
In contrast to a reduced E1 at low salt concentrations, the kink acts only locally to favor plectoneme formation at its position. The energetic bias for plectoneme formation at the kink compared to DNA without an artificial kink can reach values of ∼10 kBT at elevated forces and ionic strength (Fig. 7 B). Therefore we predict the plectoneme to be pinned and to stay at the kink position, although this idea still requires independent support. Being able to pin the plectoneme position might be a useful tool, for example, for controlled plectoneme extrusion in rotor bead assays (10).
Generally, supercoiling should allow to measure the energetic differences of bent, kinked, or other structured DNA compared to nonkinked DNA. For example, it might be of interest to see whether nucleosome positioning sequences (28) support pinning of the plectoneme position. In addition, the ability to detect a single kink on a DNA molecule can potentially be used to detect enzymes that kink or bend DNA upon binding to it.
Acknowledgments
This work was supported by Deutsche Forschungsgemeinschaft grant Nos. SE 1646/1-1 and SE 1646/2-1.
Gero Wedemann and Robert Schöpflin are gratefully acknowledged for corrections on the manuscript.
Supporting Material
References
- 1.Harada Y., Ohara O., Kinosita K., Jr. Direct observation of DNA rotation during transcription by Escherichia coli RNA polymerase. Nature. 2001;409:113–115. doi: 10.1038/35051126. [DOI] [PubMed] [Google Scholar]
- 2.Seidel R., Dekker C. Single-molecule studies of nucleic acid motors. Curr. Opin. Struct. Biol. 2007;17:80–86. doi: 10.1016/j.sbi.2006.12.003. [DOI] [PubMed] [Google Scholar]
- 3.Koster D.A., Palle K., Dekker N.H. Antitumor drugs impede DNA uncoiling by topoisomerase I. Nature. 2007;448:213–217. doi: 10.1038/nature05938. [DOI] [PubMed] [Google Scholar]
- 4.Kouzine F., Sanford S., Levens D. The functional response of upstream DNA to dynamic supercoiling in vivo. Nat. Struct. Mol. Biol. 2008;15:146–154. doi: 10.1038/nsmb.1372. [DOI] [PubMed] [Google Scholar]
- 5.Strick T.R., Allemand J.F., Croquette V. The elasticity of a single supercoiled DNA molecule. Science. 1996;271:1835–1837. doi: 10.1126/science.271.5257.1835. [DOI] [PubMed] [Google Scholar]
- 6.Strick T.R., Croquette V., Bensimon D. Homologous pairing in stretched supercoiled DNA. Proc. Natl. Acad. Sci. USA. 1998;95:10579–10583. doi: 10.1073/pnas.95.18.10579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Allemand J.F., Bensimon D., Croquette V. Stretched and overwound DNA forms a Pauling-like structure with exposed bases. Proc. Natl. Acad. Sci. USA. 1998;95:14152–14157. doi: 10.1073/pnas.95.24.14152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bryant Z., Stone M.D., Bustamante C. Structural transitions and elasticity from torque measurements on DNA. Nature. 2003;424:338–341. doi: 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- 9.Lionnet T., Dawid A., Croquette V. DNA mechanics as a tool to probe helicase and translocase activity. Nucleic Acids Res. 2006;34:4232–4244. doi: 10.1093/nar/gkl451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gore J., Bryant Z., Bustamante C. DNA overwinds when stretched. Nature. 2006;442:836–839. doi: 10.1038/nature04974. [DOI] [PubMed] [Google Scholar]
- 11.Deufel C., Forth S., Wang M.D. Nanofabricated quartz cylinders for angular trapping: DNA supercoiling torque detection. Nat. Methods. 2007;4:223–225. doi: 10.1038/nmeth1013. [DOI] [PubMed] [Google Scholar]
- 12.Mosconi F., Allemand J.F., Croquette V. Measurement of the torque on a single stretched and twisted DNA using magnetic tweezers. Phys. Rev. Lett. 2009;102:078301. doi: 10.1103/PhysRevLett.102.078301. [DOI] [PubMed] [Google Scholar]
- 13.Crut A., Koster D.A., Dekker N.H. Fast dynamics of supercoiled DNA revealed by single-molecule experiments. Proc. Natl. Acad. Sci. USA. 2007;104:11957–11962. doi: 10.1073/pnas.0700333104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Strick T.R., Allemand J.F., Croquette V. Behavior of supercoiled DNA. Biophys. J. 1998;74:2016–2028. doi: 10.1016/S0006-3495(98)77908-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Strick T.R., Dessinges M.-N., Croquette V. Stretching of macromolecules and proteins. Rep. Prog. Phys. 2003;66:1–45. [Google Scholar]
- 16.Forth S., Deufel C., Wang M.D. Abrupt buckling transition observed during the plectoneme formation of individual DNA molecules. Phys. Rev. Lett. 2008;100:148301. doi: 10.1103/PhysRevLett.100.148301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Revyakin A., Ebright R.H., Strick T.R. Single-molecule DNA nanomanipulation: improved resolution through use of shorter DNA fragments. Nat. Methods. 2005;2:127–138. doi: 10.1038/nmeth0205-127. [DOI] [PubMed] [Google Scholar]
- 18.Klaue D., Seidel R. Torsional stiffness of single superparamagnetic microspheres in an external magnetic field. Phys. Rev. Lett. 2009;102:028302. doi: 10.1103/PhysRevLett.102.028302. [DOI] [PubMed] [Google Scholar]
- 19.Moroz J.D., Nelson P. Entropic elasticity of twist-storing polymers. Macromolecules. 1998;31:6333–6347. [Google Scholar]
- 20.Marko J.F. Torque and dynamics of linking number relaxation in stretched supercoiled DNA. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:021926. doi: 10.1103/PhysRevE.76.021926. [DOI] [PubMed] [Google Scholar]
- 21.Daniels B.C., Forth S., Sethna J.P. Discontinuities at the DNA supercoiling transition. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:040901. doi: 10.1103/PhysRevE.80.040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Clauvelin N., Audoly B., Neukirch S. Elasticity and electrostatics of plectonemic DNA. Biophys. J. 2009;96:3716–3723. doi: 10.1016/j.bpj.2009.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Klenin K.V., Vologodskii A.V., Frank-Kamenetskii M.D. Computer simulation of DNA supercoiling. J. Mol. Biol. 1991;217:413–419. doi: 10.1016/0022-2836(91)90745-r. [DOI] [PubMed] [Google Scholar]
- 24.Vologodskii A.V., Marko J.F. Extension of torsionally stressed DNA by external force. Biophys. J. 1997;73:123–132. doi: 10.1016/S0006-3495(97)78053-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Neukirch S. Extracting DNA twist rigidity from experimental supercoiling data. Phys. Rev. Lett. 2004;93:198107. doi: 10.1103/PhysRevLett.93.198107. [DOI] [PubMed] [Google Scholar]
- 26.Purohit P.K. Plectoneme formation in twisted fluctuating rods. J. Mech. Phys. Solids. 2008;56:1715–1729. [Google Scholar]
- 27.Goyal S., Perkins N.C. Looping mechanics of rods and DNA with non-homogeneous and discontinuous stiffness. Int. J. Non-linear Mech. 2008;43:1121–1129. [Google Scholar]
- 28.Cloutier T.E., Widom J. DNA twisting flexibility and the formation of sharply looped protein-DNA complexes. Proc. Natl. Acad. Sci. USA. 2005;102:3645–3650. doi: 10.1073/pnas.0409059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


