Abstract
We developed a computer model to simulate associative memory recall of patients with chronic schizophrenia. Model inputs consisted of words derived from normative data that differed in terms of connectivity and network size, with the former quantitatively represented by parametric weights and the latter by the specific number of word associates that formed a particular network. Previous behavioral studies of normal subjects indicated better recall for words of high connectivity-small network (HCSN), followed by low connectivity-small network (LCSN), high connectivity-large network (HCLN), and low connectivity-large network (LCLN). This pattern of recall differed from that observed in behavioral studies of schizophrenic patients, which showed better recall for high connectivity words, regardless of network size. Holding constant network size while manipulating connection weights effectively simulated this schizophrenic pattern of recall. That is, manipulation of parametric weights coupled with a slight increase in noise significantly and reliably elicited the response pattern of abnormal connectivity demonstrated in the prior behavioral study of patients with chronic schizophrenia. An increase in noise was a necessary, but insufficient step in modeling the response pattern of abnormal connectivity. These findings provide support for the use of computational models to investigate dynamics of associative word recall in patients with chronic schizophrenia.
Keywords: Schizophrenia, Computer modeling, Word association, Associative memory, Connectivity
1. Introduction
A hallmark of the neuropsychology of schizophrenic thought disturbance is a breakdown in the associative threads that serve to interweave words, thoughts, and ideas into coherent discourse (Nestor et al., 1998). Bleuler (1911/1950) first observed the intrusion of dominant but contextually inappropriate associations in schizophrenic thought as illustrated by his now classic example of his patient describing her family members as “father, son, and Holy Ghost”. More direct experimental evidence comes from the rigorous work of Chapman and Chapman (1973), who demonstrated a pronounced schizophrenic bias for dominant meanings of homonyms (e.g., “pen” as a writing instrument) even when preceding sentential context called for secondary meanings (e.g., “pen” as an enclosed fence). The locus and mechanisms that underlie schizophrenic associative disturbance have, however, remained elusive. It is unclear, for example, whether the schizophrenic associative disturbance reflects aberrant spread of activation within a presumed lexicon that is widely distributed across frontal and temporal lobes (Nestor et al., 1997, 1998; Caramazza, 1996). Nor has it been established as to whether the disease-related associative disturbance reflects neuronal loss or faulty modulation of pre-existing synapses or connections (Nestor and O’Donnell, 1998).
Connectionist modeling provides a conceptual and empirical vehicle to examine and simulate the dynamics of schizophrenic associative memory, and by extension, associative disturbance. A special, intrinsically parallel architecture lends conceptual definition and neurological plausibility to these models. In their generic and simplest forms, these massively parallel models consist of a number of interconnected units or nodes, each characterized by an activation value. The connections between the units are weighted quantitatively and serve to govern the flow of activation from one unit to the other. These idealized neural elements help to form very “broad abstractions of brain models” of a relatively simple scale that are intended to simulate a very small set of functional characteristics and properties of biological networks (Protopapas, 1999). In reality, however, these generic connectionist or network models are best viewed not even as abstractions of brain models, but as mathematical descriptions of selected sets of dynamic cognitive processes with no clearly established link to underlying neural events and properties.
Such generic models can hypothetically simulate the spread of activation within associative memory, typically using nodes or sets of nodes to represent words and parametric connection weights to represent associative links among nodes. Words and their corresponding nodes are assumed to be organized into networks, which may differ in size, as in number of associates, and in the strength of connections linking these associates. Activation spreads as a function of both size and associative strength of a network, with maximum activation and, hence, better recall for words of small, highly connected networks (Nelson et al., 1993). Connectionist models thus allow for the novel examination of how size and connectivity of word networks govern activation spread in associative memory of schizophrenia. Moreover, these models can address the extent to which schizophrenic recall might be simulated by altering connection weights or by “lesioning” units. By the same token, these models all make provisions for the effect of “noise”, typically defined by adding random error to the implementation program (Hoffman, 1987; Cohen and Servan-Schreiber, 1992; Cohen et al., 1990).
We now present a neural network simulation of a word recall experiment that compared patients with chronic schizophrenia and normal control subjects. In this experiment, subjects studied a list of 32 words, each rated on the dimensions of connectivity (associative strength) and network size (number of associates). The list contained equal proportions of four types of words: high connectivity-small network (HCSN); low connectivity-small network (LCSN); high connectivity-large network (HCLN); and low connectivity-large network (LCLN). Consistent with prior studies, healthy subjects showed a pattern of cued recall of HCSN>LCSN>HCLN>LCLN (Nelson et al., 1993). However, patients with schizophrenia showed a different pattern of recall of HCSN>HCLN>LCSN>LCLN (Nestor et al., 1998). The schizophrenic pattern suggested an abnormal connectivity effect as reflected by the significant statistical interaction of diagnosis and word connectivity, but not word network size. This pattern of word recall occurred against a backdrop of overall reduced recall in patients with schizophrenia as reflected by a statistically significant group effect.
These behavioral data therefore underscored two aspects of performance of associative memory in patients with schizophrenia. First is the overall reduction in word recall, which is hardly surprising and analogous to the near ubiquitous, disease-related generalized impairment seen across a variety of behavioral tasks. To address this robust but general feature of schizophrenic performance, the proposed model incorporates random noise to account for the overall reduced rate of word recall, regardless of connectivity and network size, demonstrated in our prior behavioral study of patients with schizophrenia. In other words, random noise represents a general feature of the proposed schizophrenic model of associative memory, designed to capture the robust empirical finding that patients with schizophrenia generally perform worse than control subjects on virtually all tasks. Second is the more theoretically driven component of the proposed model, which involves the direct manipulation of connection weights that govern or bind activation among network units. Here, the manipulation of connection weights is hypothesized to produce a specific effect that is the schizophrenic pattern of word recall (HCSN>HCLN>LCSN>LCLN) evident in the prior behavioral studies (Nestor et al., 1998). We hypothesize that this pattern of recall is related specifically to the systematic manipulation of connection weights, whereas the expected overall reduced level of performance is related to a general increased level of random noise in the proposed model.
2. Methods
2.1. Control association network
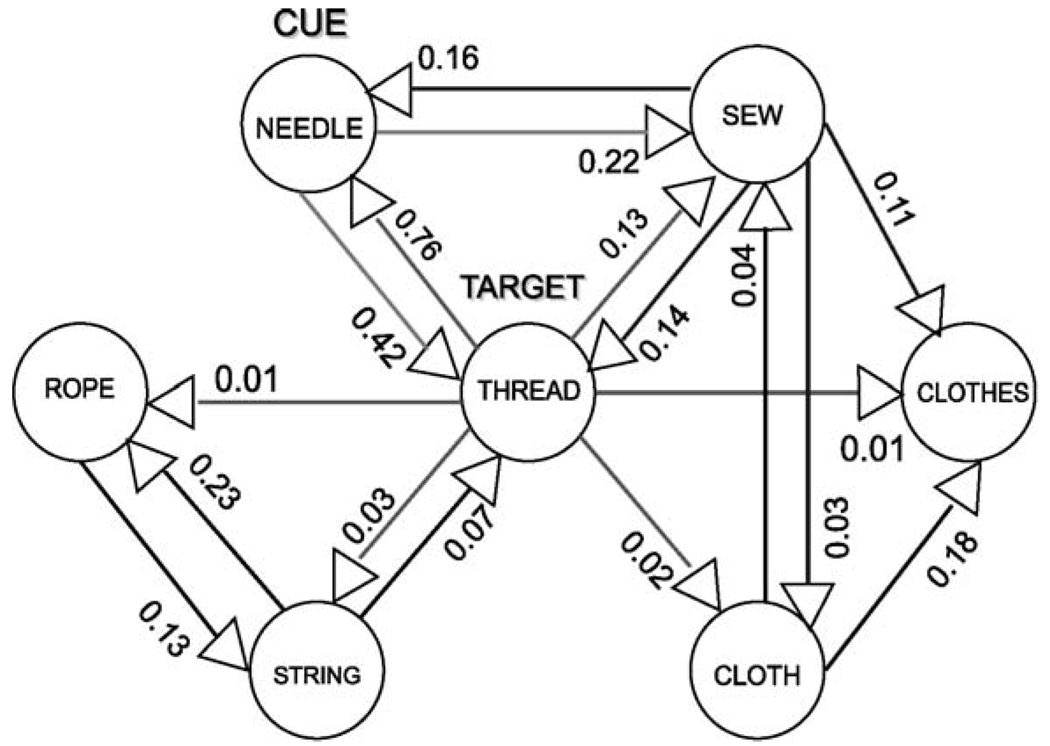
We developed a connectionist computational model of the associative memory cued recall task to provide a controlled, simulated associative memory environment in which to test alternative hypotheses for the schizophrenic associative disturbance. The network architecture was derived by the extensive database developed by Nelson et al. (1998), who have developed a compendium of word association normative data, including factors such as set size and connectivity. As an example, the associative network for the word THREAD taken from the database is illustrated in Fig. 1. Each associative network for each target word included in the list of 32 target-cue word pairs used for the behavioral paradigm was entered into the simulated computational model and comprised the total associative memory network. The total network thus consisted of over 250 nodes, corresponding to words, and over 550 directional weights, corresponding to association strengths or connections.
Fig. 1.
Illustration of the associative network for THREAD.
The behavioral study of the target words was represented by input activations entered into the nodes representing the target words. The activation values then dispersed throughout the network according to the association weighted connections until a steady state was reached, corresponding to the activation of the implicit representations. The cue phase was similarly represented by input activations into the nodes representing cue words. Again, the cue activation values dispersed throughout the network until a steady state was reached. The output of the computational model was the node of highest activation level after the cue steady state was established. A number of other conventional connectionist modeling implementations, such as noise, were also indicative of our model. A more formal description of these is found in Appendix A. Twenty iterations were run corresponding to 20 simulated subjects. The overall rate of recall (approximately 49.5%) observed by Nelson et al. (1993) was achieved by parametrically increasing noise within the system.
2.2. Schizophrenic association network
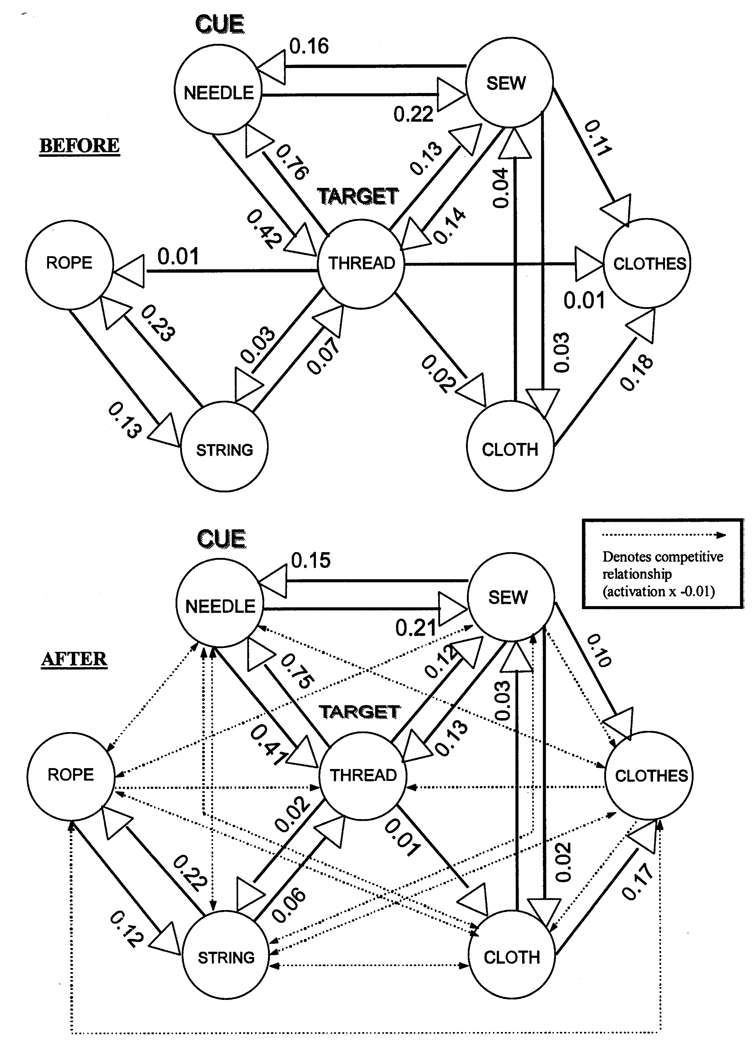
The schizophrenic manipulation was preplanned according to two considerations: (1) a number of researchers have corroborated the notion of an over-activation of more dominant associations and an underactivation of weaker associations using behavioral paradigms (Chapman and Chapman, 1973; Chapman et al., 1964; Nestor et al., 1998), and (2) many researchers have corroborated the notion of aberrant activation and network instability across a variety of converging methodologies, ranging from event-related potentials to behavioral experiments (Lang and Buss, 1965; McGhie and Chapman, 1961; Nestor et al., 1993, 1997; Shenton et al., 1992; Niznikiewicz et al., 1997). In order to employ the most conservative application of this proposed model, each association was individually decremented by the weakest pre-existing association weight within the network (namely 0.01). The manipulation was not selective for pre-existing associations, but rather assumed every node was associated to every other node within the association network. Consequently, pre-existing associations were decremented by 0.01 in strength, and nodes previously unassociated with each other became associated with each other in a weak, negative association (− 0.01). The resulting network is illustrated by the before and after depictions of the THREAD module in Fig. 2.
Fig. 2.
Illustration of THREAD associative network pre- and post-schizophrenic manipulation. After the manipulation, the THREAD associative network is marked by the absence of the weakest associations (formerly weighted 0.01) as well as “competitive” associations between nodes previously unassociated with each other.
The manipulation removed the weakest associations in accordance with the first consideration. The manipulation also established competitive “distracting” relationships between nodes previously unassociated with each other in accordance with the second consideration. These new associations were of particular significance in that they served to disrupt the activation flow between them by drawing activation away from one node in proportion to the activation of the other node. In other words, if there was a distracting association from node A to node B, then the resulting effect on activation is outlined in the following algorithm:
Where
Ba = the activation of B after the competitive effect;
Bb = the activation of B before the competitive effect; and
A = the activation of A.
The disruption in activation flow caused by the manipulation can be seen in Fig. 3.
Fig. 3.
Dispersion of activation throughout the THREAD association network pre- and post-schizophrenic manipulation. After the schizophrenic manipulation, the THREAD associative network is marked by a more erratic dispersion.
Twenty iterations corresponding to 20 subjects were conducted. All other parameters were held constant from the control association network. The overall rate of recall (approximately 37%) observed by Nestor et al. (1998) was achieved by parametrically increasing noise within the system.
3. Results
Results of the control simulation revealed the same pattern of recall as observed for human subjects, namely HCSN>lLCSN>HCLN>LCLN. Repeated-measures ANOVA with word type as within-subject factor again supported the observed pattern as indicated by a significant effect for within-subject factor of word type (F = 8.756; df = 3; p < 0.000). A linear test of within-subject factor of word type again also revealed a significant effect (F = 33.250; df = 1; p < 0.000). Planned categorical comparisons revealed significant differences between HCSN and HCLN (p < 0.000), HCSN and LCLN (p < 0.000), LCSN and HCLN (p < 0.015), and LCSN and LCLN (p < 0.010). To check for model reliability, another 20 simulation iterations were also conducted as a separate experiment, replicating the observed pattern of cued recall.
The schizophrenic simulation involved two manipulations. First, to simulate the overall reduced rate of schizophrenic recall, random noise was subsequently increased (approximately 75%). This resulted in an overall reduced word recall rate, regardless of connectivity and network size similar to that demonstrated in the prior behavioral studies. Though the manipulation reduced overall levels of recall, noise alone failed to produce the hypothesized schizophrenic pattern of recall. Second, as outlined in the foregoing method, to simulate the expected schizophrenic pattern of recall (i.e., HCSN>HCLN>LCSN>LCLN), each association was individually decremented by the weakest existing association weight within the network (namely 0.01). Repeated-measures ANOVA with word type as within-subject factor (HCSN, HCLN, LCSN, LCLN) confirmed the observed pattern as reflected by a highly significant effect for within-subject factor of word type (F = 67.325; df = 3; p < 0.000). Linear (F = 233.266; df = 1; p < 0.000) and cubic (F = 8.274; df = 1; p < 0.010) tests of within-subject factor of word type also revealed highly significant effects. Planned categorical comparisons revealed significant differences between HCSN and LCSN (p < 0.000), HCSN and LCSN (p < 0.000), HCSN and LCLN (p < 0.000), and LCSN and LCLN (p < 0.000). To check for model reliability, another 20 simulation iterations were conducted as a separate experiment, again replicating the observed pattern of cued recall.
Finally, to examine further if the effect of increased noise alone would produce the schizophrenic response, we potentiated the effect of noise within the associative network while disabling the predesigned schizophrenic manipulation. Increased noise alone did not produce the schizophrenic pattern. In fact, we then statistically compared patterns of cued recall produced by the noise potentiation with that produced by the schizophrenic manipulation. A mixed model repeated-measures ANOVA with manipulation as a between factor and word type as a within-subject factor revealed a significant interaction effect (F = 10.188; df = 6; p < 0.000). The pattern of recall produced by the noise manipulation differed significantly from that demonstrated by the schizophrenic manipulation. These tests indicated that the simulated schizophrenic recall pattern could not be attributable to random noise.
4. Discussion
The findings provided support for using computer-generated, connectionist computational models to simulate associative memory performance of control subjects and patients with chronic schizophrenia. The cognitive model implemented here reproduced the recall performance that schizophrenic patients displayed in a prior experiment of associative memory (Nestor et al., 1998). In both the current simulation and previous experiment, words to be studied were specifically selected from a connectionist model because they had been quantitatively rated on two distinct dimensions: connectivity and network set size (Nelson et al., 1993). These two dimensions had considerable appeal and relevance, providing an empirical means to elucidate the dynamics of associative memory and, by extension, associative disturbance in schizophrenia. The connectionist computational model incorporated each of these dimensions in order to provide a direct test of the pattern of findings discussed by Nelson et al. (1992) and the abnormal associative connectivity effect seen in the prior behavioral studies of associative memory in patients with chronic schizophrenia. In addition, the computer-generated model also tested directly the extent, if any, to which random “neural” noise might account for the abnormal schizophrenic pattern of recall observed in the prior behavioral study.
By implementing a conservative algorithmic manipulation designed to alter quantitatively derived parametric weights, while holding constant network size, the simulation provided evidence that converged with prior behavioral findings of an abnormal connectivity effect in the associative memory of schizophrenia. Indeed, the rationale for the manipulation came from prior behavioral studies of patients with chronic schizophrenia that have pointed to a disease-related disturbance in information processing characterized by over-responding of dominant associates, regardless of context, at the expense of weaker associates. The simulation results thus concurred with prior theoretical interpretations that have suggested overactivation of dominant associates and underactivation of weak associations in the schizophrenic lexicon (Chapman et al., 1964; Nestor et al., 2001), as well as aberrant activation and network instability across a variety of methodologies (Nestor et al., 1993, 1997; Shenton et al., 1992; Niznikiewicz et al., 1997).
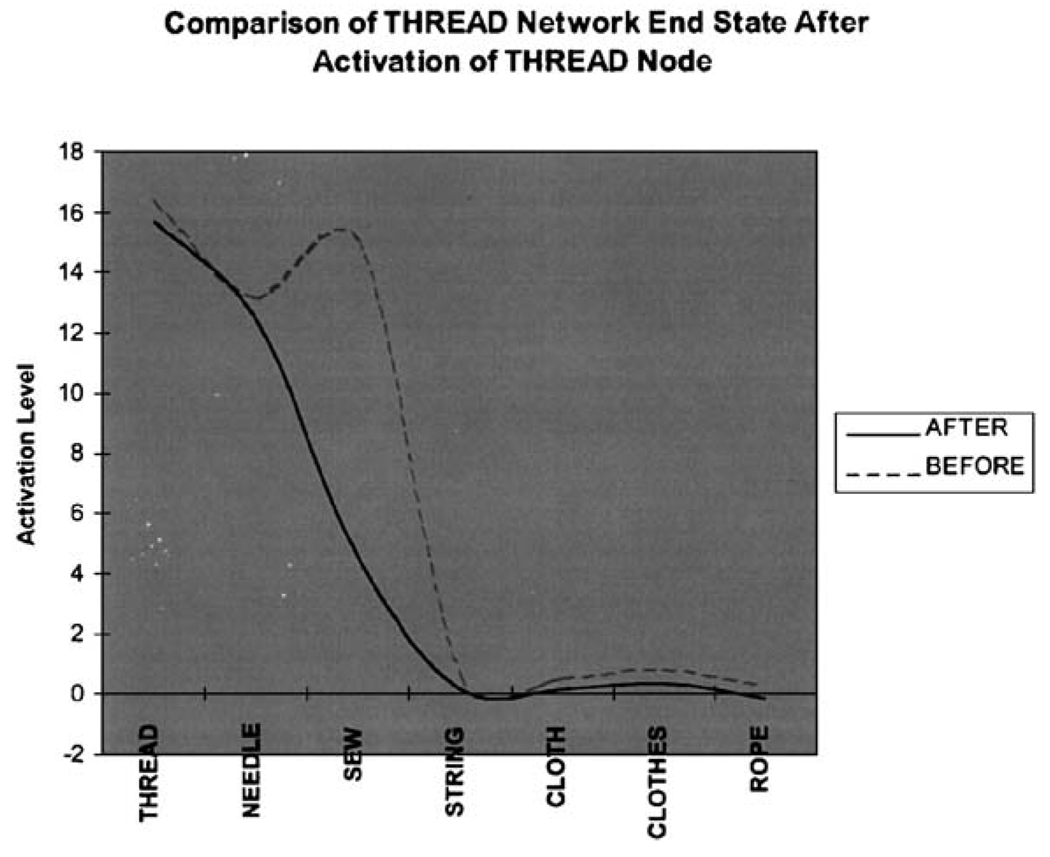
Moreover, the schizophrenic manipulation, which selectively affected weighted connections, resulted in a less cohesive spread of activation within and across local networks of word associates. The once steep gradient of activation that had been characteristic of the normal simulation became decidedly less sharp and focal, and more flat and diffuse, with the implementation of the pivotal manipulation that was designed to not so much “lesion” or “create” connection weights, but to alter or degrade their modulation. This is exemplified by the THREAD network end state illustrated in Fig. 4. The algorithmic manipulation that produced the schizophrenic pattern of associative recall exerted a more pronounced effect on words of low connectivity as opposed to words of high connectivity, with the former proving to be much more vulnerable to the manipulation than the latter. The current simulation extended these findings by suggesting the faulty association modulation might be intimately related to aberrant activation within networks of weakly connected associates.
Fig. 4.
End state activation levels for the nodes of the THREAD association network pre- and post-schizophrenic manipulation. After the schizophrenic manipulation, the THREAD association network is marked by a more flat, less pronounced end state activation pattern.
The simulation of the schizophrenic response pattern thus led to a reduced signal to noise ratio especially evident for words of low connectivity. A similar schizophrenic response pattern could not be simulated by solely manipulating levels of noise, while holding constant all other parameters. Indeed, the noise simulation did not exert a similarly selective effect for words of low connectivity, and thus failed to represent the pattern of associative memory demonstrated in the prior behavioral study of schizophrenic patients. Although other manipulations and certainly other models are likely to be developed to simulate associative memory in schizophrenia, the current findings pointed to the relative specificity of the simulation that targeted association weight modulation in modeling schizophrenic associative memory performance. These findings may very well be viewed as additional evidence of the importance of associative links that bind words within a lexicon widely distributed across frontal and temporal lobes to the neuropsychological disturbance of schizophrenia (Nestor et al., 2001).
A limitation of the present study is the default coupling of two considerations for the schizophrenic manipulation. It remains unclear whether the schizophrenic pattern may be primarily driven by the dominance of strong associations over weak associations, or the implementation of competitive “distracting” relationships for the dispersing activation. While the network’s performance may be of interest in regards to each of these considerations, the technicalities of our current model prevent us from investigating this important question. It is reasonable to hypothesize that the schizophrenic response pattern may be primarily driven by the relative absence of weak associations given the extensive literature that has demonstrated this phenomenon in associative tasks (e.g., Chapman et al., 1964; Nestor et al., 1998). Thus, an important future research contribution would be to investigate the degree to which this affects the presentation of the schizophrenic behavioral response. However, the notion of a competitive or “distracting” relationship is intriguing given the circular, enmeshed quality it produces within an associative network. This mechanism may be a promising avenue of research with regards to the schizophrenic language eccentricities observed by various authors. Regardless, the primary hypothesis of this study was to determine if the schizophrenic response could be attributed to an aberrant associative connectivity as opposed to a simple increase in randomness (a.k.a. noise), and to this end, the simulation was successful.
To summarize, network-modeling principles have only recently begun to be applied to information processing problems of schizophrenia. Among the most influential of these have been the simulations of schizophrenic performance on familiar neuropsychological measures, such as the Stroop and CPT as well as an experimental task designed to isolate the effects of sentence context on processing dominant associates (Cohen and Servan-Schreiber, 1992). In a related vein, Hoffman and McGlashan (1997) simulated hallucinated voices using a model of synaptic pruning as represented by eliminating connections that linked network units. The current study added to these investigations by incorporating relatively precise normative behavioral data to quantify both connection weights and network sizes that together were used to represent key dimensions of associative memory. In so doing, these and related findings underscored the usefulness of network modeling derived from human experimental data and constrained by neurobiology to simulate cardinal features of the neuropsychological disturbance of schizophrenia.
Acknowledgements
This work was supported in part by the 1999 Stanley Foundation Student Fellowship for Research in Mental Illness, supported by a Senior Mentor Award, Stanley Scholars Program, to Martha E. Shenton, PhD, Preceptor: Paul Nestor, PhD, and Margaret Niznikiewicz, PhD. Also supported by MERIT Awards from the Department of Veterans Affairs Medical Research Service (Dr. McCarley and Dr. Shenton), NIMH grants MH-50740, MH-01110 (Dr. Shenton), and MH-40799 (Dr. McCarley), and Young Investigator Awards to Dr. Nestor from the National Alliance for Research on Schizophrenia and Depression.
Appendix A
We provide in this appendix a more thorough and detailed description of the connectionist computational model developed for these sets of experiments. Detailed elements of the model are also described in Nestor et al. (2001), and a full description of the model, including complete syntax and readme file printout, is given in Han (2001).
The model was developed as a simple relaxation network (Ellis and Humphreys, 1999). Each node was considered an idealized representation of a neural population or process that corresponds to a particular word. Activation entered at two points in the association network, at the target node (corresponding to the study phase) and at the cue node (corresponding to the cue phase). Each point of entry allowed for an activation value to enter into the system, and then disperse throughout the network according to the predetermined association weights. Activation dispersed throughout the system in a multidimensional fashion until a steady state was reached. A steady end state was an emergent property of the association network since the association weights were given as a two-digit decimal value below 1. Since only new activation coming into a node would be dispersed to other associated nodes as a function of the weighted connections, the dispersion became less and less until a state of no change was reached.
The output of the model was given in list form with both the correct word response, the model’s output word response, a numerical 0 or 1 corresponding to “incorrect” or “correct”, respectively, and the order in which the words were presented to the model. Algorithms were developed and implemented to ensure a random presentation (activation) of both study and cue words, as well as to constrain activation to the bounds of the system in keeping with the laws of thermodynamics. Recall rates were entered into SPSS for statistical analysis.
References
- Bleuler E. Dementia Praecox of the Group of Schizophrenias. New York: International Univ. Press; 19111950. [Google Scholar]
- Caramazza A. The brain’s dictionary. Nature. 1996;380:485–486. doi: 10.1038/380485a0. [DOI] [PubMed] [Google Scholar]
- Chapman LJ, Chapman JP. Disordered Thought in Schizophrenia. Englewood Cliffs, NJ: Prentice-Hall; 1973. [Google Scholar]
- Chapman LJ, Chapman JP, Miller GA. A theory of verbal behavior in schizophrenia. In: Maher BA, editor. Progress in Experimental Personality Research. New York, NY: Academic Press; 1964. pp. 135–167. [PubMed] [Google Scholar]
- Cohen JD, Servan-Schreiber D. A neural network model of disturbances in the processing of context in schizophrenia. Psychiatric Annals. 1992;22(3):131–136. [Google Scholar]
- Cohen JD, Dunbar K, McClelland JL. On the control of automatic processes: a parallel distributed processing model of the Stroop effect. Psychological Review. 1990;97:332–361. doi: 10.1037/0033-295x.97.3.332. [DOI] [PubMed] [Google Scholar]
- Ellis R, Humphreys G. Connectionist Psychology: A Text With Readings. East Sussex, UK: Psychology Press; 1999. [Google Scholar]
- Han SD. Thesis. Boston, MA: University of Massachusetts Boston; 2001. Word association neural network (WANN): computer simulation of recall in control and schizophrenic subjects. [Google Scholar]
- Hoffman RE. Computer simulations of neural information processing and the schizophrenia-mania dichotomy. Archives of General Psychiatry. 1987;44(2):178–188. doi: 10.1001/archpsyc.1987.01800140090014. [DOI] [PubMed] [Google Scholar]
- Hoffman RE, McGlashan TH. Synaptic elimination, neurodevelopment, and the mechanism of hallucinated “voices” in schizophrenia. American Journal of Psychiatry. 1997;154(12):1683–1689. doi: 10.1176/ajp.154.12.1683. [DOI] [PubMed] [Google Scholar]
- Lang PJ, Buss AH. Psychological deficit in schizophrenia: II. Interference and activation. Journal of Abnormal Psychology. 1965;70:77–106. doi: 10.1037/h0021942. [DOI] [PubMed] [Google Scholar]
- McGhie A, Chapman J. Disorders of attention and perception in early schizophrenia. British Journal of Medical Psychology. 1961;34:103–116. doi: 10.1111/j.2044-8341.1961.tb00936.x. [DOI] [PubMed] [Google Scholar]
- Nelson DL, Schreiber TA, McEvoy CL. Processing implicit and explicit representations. Psychological Review. 1992;99(2):322–348. doi: 10.1037/0033-295x.99.2.322. [DOI] [PubMed] [Google Scholar]
- Nelson DL, Bennett DJ, Gee NR, Schreiber TA, McKinney VM. Implicit memory: effects of network size and interconnectivity on cued recall. Journal of Experimental Psychology. 1993;19(4):747–764. doi: 10.1037//0278-7393.19.4.747. [DOI] [PubMed] [Google Scholar]
- Nelson DL, McEvoy CL, Schreiber TA. The University of South Florida word association, rhyme, and word fragment norms. 1998 doi: 10.3758/bf03195588. http://www.usf.edu/FreeAssociation/. [DOI] [PubMed] [Google Scholar]
- Nestor PG, O’Donnell BF. The mind adrift: attentional dysregulation in schizophrenia. In: Parasuraman R, editor. The Attentive Brain. Cambridge, MA: The MIT Press; 1998. [Google Scholar]
- Nestor PG, Shenton ME, McCarley RW, Haimson J, Smith SR, O’Donnell B, Kimble M, Kikinis R, Jolesz FA. Neuropsychological correlates of MRI temporal lobe abnormalities in schizophrenia. American Journal of Psychiatry. 1993;150:1849–1855. doi: 10.1176/ajp.150.12.1849. [DOI] [PubMed] [Google Scholar]
- Nestor PG, Kimble MW, O’Donnell BF, Smith RS, Niznikiewicz M, Shenton ME, McCarley RW. Aberrant semantic activation in schizophrenia: a neurophysiological study. American Journal of Psychiatry. 1997;154:640–646. doi: 10.1176/ajp.154.5.640. [DOI] [PubMed] [Google Scholar]
- Nestor PG, Akdag SJ, O’Donnell BF, Niznikiewicz M, Law S, Shenton ME, McCarley RW. Word recall in schizophrenia: a connectionist model. American Journal of Psychiatry. 1998;155(12):1685–1690. doi: 10.1176/ajp.155.12.1685. [DOI] [PubMed] [Google Scholar]
- Nestor PG, Han SD, Niznikiewicz M, Salisbury D, Spencer K, Shenton ME, McCarley RW. Semantic disturbance in schizophrenia and its relationship to the cognitive neuroscience of attention. Biological Psychology. 2001;57:23–46. doi: 10.1016/s0301-0511(01)00088-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niznikiewicz M, O’Donnell BF, Nestor PG, Smith L, Law S, Karapelou M, Shenton ME, McCarley RW. ERP assessment of visual and auditory language processing in schizophrenia. Journal of Abnormal Psychology. 1997;106:84–85. doi: 10.1037//0021-843x.106.1.85. [DOI] [PubMed] [Google Scholar]
- Protopapas A. Connectionist modeling of speech perception. Psychological Bulletin. 1999;125(4):410–436. doi: 10.1037/0033-2909.125.4.410. [DOI] [PubMed] [Google Scholar]
- Shenton ME, Kikinis R, Jolesz FA, Pollak SD, LeMay M, Wible CG, Hokama H, Martin J, Metcalf D, Coleman M, McCarley RW. Abnormalities of the left temporal lobe and thought disorder in schizophrenia: a quantitative magnetic resonance imaging study. New England Journal of Medicine. 1992:604–612. doi: 10.1056/NEJM199208273270905. [DOI] [PubMed] [Google Scholar]