Spectral Integration of Dynamic Cues in the Perception of Syllable-Initial Stops

Abstract

The present experiments examine the potential role of auditory spectral integration and spectral center of gravity (COG) effects in the perception of initial formant transitions in the syllables [da]-[ga] and [t^ha]-[k^ha]. Of interest is whether the place distinction for stops in these syllables can be cued by a ‘virtual F3 transition’ in which the percept of a frequency transition is produced by a dynamically changing COG. Listeners perceived the virtual F3 transitions comparably with actual F3 transitions although the former were less salient a cue. However, in a separate experiment, static ‘virtual F3 bursts’ were not as effective as actual F3 bursts in cueing the alveolar-velar place distinction. These results indicate that virtual F3 transitions can provide phonetic information to the perceptual system and that auditory spectral integration (completed by the central auditory system) may play a significant role in speech perception.

Introduction

This paper addresses the role of auditory processes in the perception of speech sounds. Its goal is to assess the possible contribution of a central auditory process known as auditory spectral integration to the phonetic processing of dynamic acoustic events. The interest in auditory spectral integration is common to both psychoacoustic and speech perception research as it concerns auditory processing of spectral information in complex signals.

In psychoacoustics, auditory spectral integration is invoked to explain improvement in detection and discrimination thresholds, or changes in stimulus attributes, as signal bandwidth is increased beyond the width of one ‘critical band’. The critical band is thought to represent the width of one of the presumed bank of adjacent filters used to model basilar membrane mechanics [Fletcher, 1940; Schafer and Gales, 1949; Gassler, 1954; Zwicker et al., 1957]. Several different listening tasks have been interpreted to reflect an empirically determined common value (often called one ‘Bark’) for the width of the critical band at any given frequency [Scharf, 1972]. More recent estimates of this bandwidth using a notched-noise masking paradigm have been called the equivalent rectangular bandwidth [Patterson, 1976; Patterson and Moore, 1986]. The equivalent rectangular bandwidth is systematically smaller (~70%) than the empirically determined critical bandwidth. One interpretation of the critical bandwidth is that it denotes the spectral resolving power of the auditory periphery. However, many studies using complex sounds (with the acoustic signal spread across many auditory filter bands) have shown an improvement in listener performance as the signal bandwidth is increased [e.g., Spiegel, 1979; Green, 1958, 1960, 1988; Hall et al., 1984; Buus et al., 1986; Yost and Sheft, 1989]. This suggests that more central auditory processing is capable of using the output of several peripheral filters, often widely spaced, to extract information and perform the task at hand.

In speech perception, auditory spectral integration has been postulated as a mechanism to account for the apparent integration (or merger) of formants during vowel identification in vowel matching experiments. For example, Delattre et al. [1952] showed that the phonetic quality of simplified back vowels synthesized with only the first two formants could be matched to a vowel containing only a single formant. The success of the match depended on the specific relationship between the frequencies and amplitudes of the two close formants and the peak frequency of the single formant. Variation in the relative intensity ratio between the two close formants in these synthetic back vowels produced a change in the frequency of the single formant to which it was best matched. Specifically, as the ratio of the level of F2 to F1 (L2/L1) was increased, the center frequency of the single-formant vowel whose quality was being matched had to be systematically raised.

Experiments conducted by Chistovich and colleagues [e.g., Bedrov et al., 1978; Chistovich and Lublinskaja, 1979; Chistovich et al., 1979; Chistovich, 1985] showed that the predictable shift in the matching frequency of the single formant occurred when the two close formants fell within a bandwidth much larger than one critical band. It was suggested that in the processing of this type of complex signals, a wider bandwidth of about 3.5 Bark was necessary, which was referred to as a ‘critical distance’ or a ‘critical formant separation’. When two formants differing in relative amplitude were integrated, the frequency of the perceptual formant (F*) was closer to that of the stronger formant. When both formants were of equal strength, F* was located midway between them. This effect disappeared when the frequency separation was larger than 3.5 Bark. In this school of thought, it was proposed that the changes to the relative amplitude ratios between the two formants changed their combined spectral center of gravity (COG) and it was to this spectral COG that the frequency of the single formant was being matched. This COG effect was interpreted as an indication that the auditory system performs auditory spectral summation beyond the level of the cochlea, suggesting that spectral integration may occur at a more central processing level (and within a larger frequency bandwidth).

A concept related to the spectral COG is that of an effective second formant (F2′) explored by the Stockholm group [notably Fant, 1959; Carlson et al., 1970, 1975; Bladon and Fant, 1978; Paliwal et al., 1983]. F2′ represents the frequency of a formant that could replace the second and higher formants of a natural vowel and be matched in terms of phonetic quality [Carlson et al., 1970]. Early modeling of the frequency of F2′ was based primarily on the frequencies of these higher formants, assuming that certain inherent relationships hold among the amplitudes of these formants [e.g., Fant, 1959]. In particular, Carlson et al. proposed that the location of F1, F2 and F3 can be translated to the equivalent spectrum shape parameters: the grave/acute dimension (whereby F1 affects the overall spectrum level and the main spectral balance is determined by F2 which boosts the F1 region when close to F1), plain (F3 is closer to F2 within the F2 F3 F4 cluster) and sharp (F3 is closer to F4). Changes to the frequencies of the higher formants would thus change the COG of the upper portion of the vowel’s spectrum and Carlson et al. [1970, p. 20] concluded that ‘the [spectral] center of gravity would be a possible direct correlate of F2′’. Further modeling of F2′ combined spectral integration within 3.5 Bark and the spectral prominence of F2′ [Bladon, 1983; Escudier et al., 1985; Mantakas et al., 1988; Schwartz and Escudier, 1989], ultimately leading to a model for predicting the organization of vowel systems in human languages, termed the Dispersion-Focalization Theory [Schwartz et al., 1997]. Accordingly, for each vowel in a system, the spectral integration mechanism reduces variation around closely spaced formants. This spectral ‘formant convergence zone’ within 3.5 Bark constitutes a perceptual ‘focal point’ of a vowel. The spectral integration mechanism thus contributes to maintaining perceptual contrast between vowels differing in their focal points, such as /i/ (F3–F4 convergence zone) versus /y/ (F2–F3 convergence zone). Large spectral integration within a 3.5-Bark bandwidth was also found to be effective in signal processing algorithms such as the Perceptual Linear Prediction model for use in automatic speech recognizers [Hermansky, 1990]. From a somewhat different perspective, Syrdal and Gopal [1986] proposed the perceptual model of vowel recognition based on the observation that formant distance measures between F2-F1, F3-F2, F4-F3, F4-F2, and F1-F0 for American English vowels in the Peterson and Barney [1952] study conform to the 3-Bark criterion. Based on whether the Bark-difference values were within or exceeded the 3-Bark distance, they found the F1-F0 dimension corresponding to vowel height and the F3-F2 dimension to the front-back distinction in American English vowels. Thus, the 3-Bark critical distance was shown to play a role in achieving stability in vowel recognition within a whole vowel system of American English.

Over the years, the concept of formant integration in vowel perception encountered numerous criticisms, mostly stemming from the fact that the outcomes of the matching experiments were never convincing. The widely cited study by Chistovich and Lublinskaja [1979] is a representative example. The authors themselves were the only 2 listeners participating in the experiments. The COG effect disappeared with the larger frequency separation for 1 listener who failed to integrate the spectral information beyond the 3.5 Bark (producing a discontinuous pattern of responses) whereas for the same frequency separation, the second listener showed chance performance. This indicates that either the 3.5-Bark critical distance hypothesis is incorrect or that differences in processing reflect differences in the auditory resolution bandwidths for individual listeners as suggested by Xu et al. [2004]. A notorious problem in interpreting the results of early work on spectral integration by Chistovich and colleagues as well as by the Stockholm group is the lack of details regarding selection and number of subjects and the procedures used in the experiments. These reports often do not mention statistical significance of the results. Matching and identification tasks were the most commonly used procedures. However, especially in matching tasks, great variability in the responses posed a problem for interpretation of the results (see Rosner and Pickering, [1994], for a detailed review and criticism of formant integration experiments). Although some of the shortcomings have been addressed subsequently [Beddor and Hawkins, 1990; Assmann, 1991; Hoemeke and Diehl, 1994; Fahey et al., 1996], the skepticism remained, leading to a lack of interest in further exploration of the effect. However, Rosner and Pickering’s [1994, p. 157] conclusion that ‘the determination of an indicator corresponding to F2′ seems unnecessary for vowel identification’ is not surprising, given that the role of such an indicator has not been clearly specified or else has been overestimated in the past. Chistovich [1985, p. 796], speaking of her own work, clarified that ‘the results argue against the hypothesis that the COG of the whole spectrum is the sole determinant of vowel quality of even a restricted class of vowels (back vowels) but that does not mean that this parameter is not used at all in vowel identification’.

Putting aside the unsettled question of integration of vowel formants, insights into this type of auditory filtering can be drawn from early psychoacoustic work by Feth [1974] and Feth and O’Malley [1977]. This research investigated the spectral pitch of complex tones using two-component complex tone pairs that had identical envelopes but differed in fine structure [Voelcker, 1966a, b]. The results were consistent with the COG hypothesis by Chistovich et al. As the separation of the two components increased to 3.5 Bark, their discriminability decreased, which suggested their resolution by the auditory system. Thus, the two-tone resolution bandwidth could play a similar role in auditory signal processing as the integration interval of 3.5 Bark observed by Chistovich et al. in vowel matching tasks. The 3.5-Bark bandwidth may be understood as a limit to the range of auditory spectral integration for processing complex signals (perhaps of a simplified structure), including speech and non-speech sounds. More recently, Xu et al. [2004] replicated both Chistovich and Lublinskaja’s [1979] and Feth’s [1974] results with the two types of signals: two-formant synthetic vowels and two-component complexes. Using the same listeners for both experiments, Xu et al. [2004] found a relationship between the limits of spectral averaging in two-formant vowels and two-tone spectral resolution bandwidth. This suggests that the critical region in vowel-matching tasks and the complex-tone discriminability estimates are linked to a common mechanism, i.e. to an auditory spectral resolving power.

An important limitation of previous research was that the nature of the signals studied could have skewed the results. That is, the averaging effects enhancing the dominant formant in synthetic vowels were observed in stationary sounds, which are unnatural as they normally do not occur in speech. The processing of these static signals is entirely focused on the frequency domain. From the psychoacoustic perspective, dynamic signals (such as speech, bird sounds, and music), prevailing in the ambient environment, are more suitable for studying the integration effects because in these types of signals, some of the auditory processing is typically devoted to tracking the dynamic changes in frequency and some in amplitude. In a landmark study, Lublinskaja [1996] asked whether it would be possible to cause sensation of the non-stationarity of a vowel (i.e., produce the perception of diphthongization) by systematically modifying only the relation (i.e., ratios) of amplitudes of two relatively closely spaced formants over time. That is, does the auditory system attend to a spectral COG that is dynamic, tracking changes in effective frequency over time? Identification experiments reported by Lublinskaja [1996] used two Russian diphthongal vowels [ ij] and [j u]. Listeners identified three-formant fixed-frequency synthetic Russian vowels in which only the amplitudes of F2 and F3 were changed over time so that as the amplitude of one formant increased, the amplitude of the other decreased. When the amplitude of F2 decreased while the amplitude of F3 increased, the resulting percept was phonetically categorized as similar to a diphthongal vowel with a rising F2 [ ij]. A falling F2 as in [j u] was achieved by increasing the amplitude of F2 and decreasing the amplitude of F3 over time. Lublinskaja [1996] reported that such virtual formant changes produced vowels that were perceived as either [ ij] or [j u] (depending on the direction of the effective transition) when F3 − F2 < 3.5; however, these same changes produced a percept of a stationary vowel [u] when F3 − F2 > 4.5 Barks. As the size of the frequency separation was increased from 3.5 to 4.5 Barks, more stationary percepts occurred. Thus, the spectral integration limit for this type of dynamic vowel is between 3.5 and 4.5 Barks, somewhat larger than that obtained for static vowels.

The present experiments were conducted to verify the potential role of a dynamically changing COG in initial CV formant transitions in the syllables [da]-[ga] and [t^ha]-[k^ha]. These formant transitions occur over a much shorter time frame and at a faster rate than the transitions found in diphthongs, which introduces additional demands on auditory processing. Choosing the syllabic context is a natural step toward a better understanding of the dynamic COG as it emphasizes the importance of acoustic transitions arising from coarticulatory effects in speech. In these experiments, the rapid changes in formant transitions affect the percept of a stop consonant (and not the vowel), which has not yet been considered in previous research on auditory spectral integration in speech.

There are several acoustic cues which contribute to the perception of a stop consonant. The closure release bursts and the formant transitions were particularly well studied [e.g., Liberman et al., 1954; Stevens and Blumstein, 1978; Blumstein and Stevens, 1979, 1980; Kewley-Port, 1983; Walley and Carrell, 1983; Furui, 1986; Nittrouer, 1992; Ohde et al., 1995]. The general finding from all these studies is that formant transitions rather than burst spectra alone contribute to the perception of place of articulation of a stop. However, both burst and an initial portion of vowel transitions may form a single integrated cue which is sufficient for the listener to perceive a stop [Stevens and Blumstein, 1978].

Formant transitions in syllables [da]-[ga] are a good example of dynamic properties of speech because they reflect a great degree of influence of both consonant and vowel over time. In particular, when the burst is not present, it is the direction of F3 transition that differentiates the perception of [da] and [ga]: a falling F3 transition gives the percept of [da] and a rising F3 transition leads to the perception of [ga]. That the direction of F3 transition can cue the place of articulation distinction has been well demonstrated with synthetic stimuli [e.g., Whalen and Liberman, 1987; Fox et al., 1997; Gokcen and Fox, 2001].

We have chosen the syllables [da]-[ga] and [t^ha]-[k^ha] for the present investigation of dynamic COG effects because the rapid spectral change in F3 serves as the basis for the alveolar/velar distinction. Of primary interest in this study is whether the place distinction for stops in [da]-[ga] and/or [t^ha]-[k^ha] can be cued by a ‘virtual F3 transition’. If so, we will have evidence that in the perception of dynamic events, the auditory system may use summation (or integration) of information from sources other than frequency changes over time.

Experiment 1: Dynamic Cues to Place of Articulation in Voiced Stops in [da]-[ga]

The goal of experiment 1 was to assess the extent to which the perception of a frequency change in the F3 transition of synthetic [da] and [ga] syllables could be cued by a ‘virtual’ F3 transition produced by the dynamic modification of the amplitudes of two frequency-stationary components.

Stimuli

[da]-[ga] Base Token

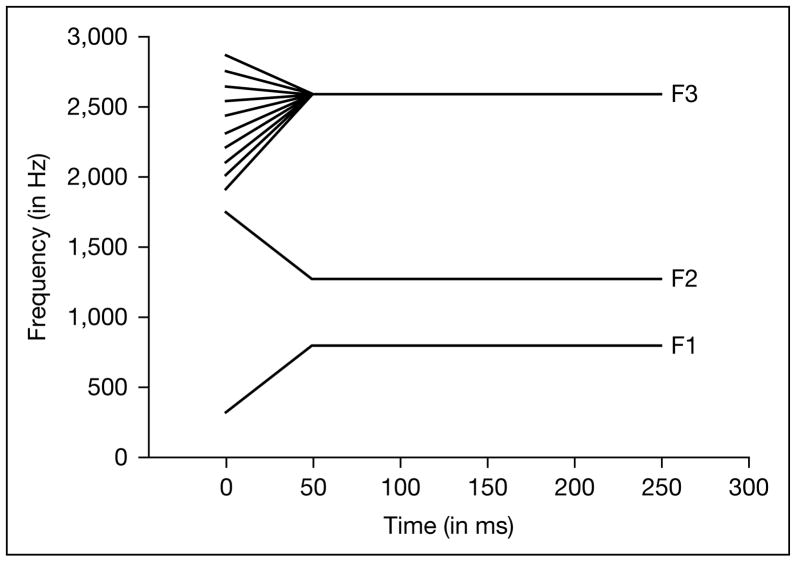
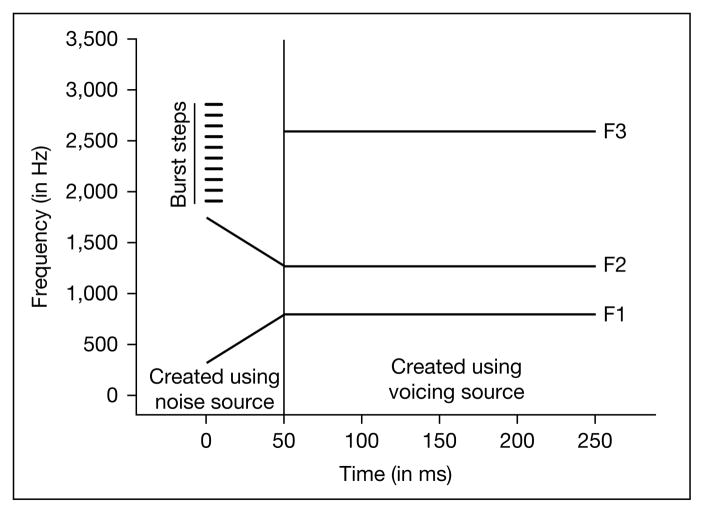
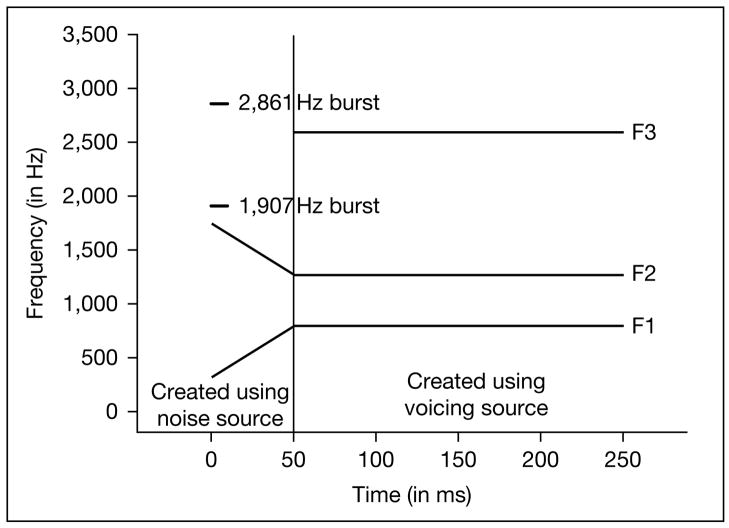
The stimuli were designed so that there were two different [da]-[ga] series which differed only in terms of having an actual or virtual F3 transition. All steps of the series were created by inserting an actual or virtual F3 transition into the first 50 ms of a base CV token. The base CV token was created using the .kld option in the parallel branch of the Klatt synthesizer in HLsyn¹ (Sensimetrics, 1997) with a sampling rate of 11,025 Hz. This base token consisted of a 50-ms transition portion (corresponding to the CV formant transitions) and a 200-ms steady-state vowel portion. The transition portion consisted of the F1 and F2 transitions only, whereas the steady-state portion contained the first three steady-state formants of the vowels. Over the first 50 ms, F1 increased from 318 to 795 Hz and F2 decreased from 1,748 to 1,271 Hz. The frequencies of F1 and F2 then remain unchanged over the final 200 ms of the token. The amplitude of F3 was set to 0 over the first 50 ms of the vowel and was increased to 60 dB. The frequency of F3 for the steady-state portion of the vowel was a constant 2,596 Hz. Fundamental frequency remained steady at 110 Hz for the first 200 ms and was then decreased linearly to 95 Hz over the final 50 ms of the token. None of the stimulus tokens contained stop release bursts. Perceptually, the base token sounded like [da].

Actual F3 Transition Series

Using HLsyn (with the .kld option), ten different 50-ms F3 transitions were created within a 250-ms time frame with a sampling rate of 11,025 kHz. These ten F3 transitions had different onset frequencies that were equally spaced, ranging from 1,907 to 2,861 Hz. The onsets of these F3 transitions in the synthesis frame were synchronized with the onsets of the F1 and F2 formants in the base token. The onset and offset frequencies of these ten F3 transitions are shown in table 1. The bandwidths of F1, F2 and F3 were 80, 90 and 150 Hz, respectively. A sine-squared on-ramp was applied over the first 3 ms of each token, which was abrupt enough to give the impression of a stop onset.

Table 1.

Onset and offset frequencies of F3 transitions and relative amplitudes of onsets and offsets of noise-excited resonances (R1 = 1,907 Hz, R2 = 2,861 Hz) for creation of virtual F3 transitions

Series step	F3 onset target Hz	F3 offset target Hz	R1 relative amplitude onset	R1 relative amplitude offset	R2 relative amplitude onset	R2 relative amplitude offset
1	1,907	2,596	1.00	0.28	0.00	0.72
2	2,013	2,596	0.89	0.28	0.11	0.72
3	2,119	2,596	0.78	0.28	0.22	0.72
4	2,225	2,596	0.67	0.28	0.33	0.72
5	2,331	2,596	0.56	0.28	0.44	0.72
6	2,437	2,596	0.44	0.28	0.56	0.72
7	2,543	2,596	0.33	0.28	0.67	0.72
8	2,649	2,596	0.22	0.28	0.78	0.72
9	2,755	2,596	0.11	0.28	0.89	0.72
10	2,861	2,596	0.00	0.28	1.00	0.72

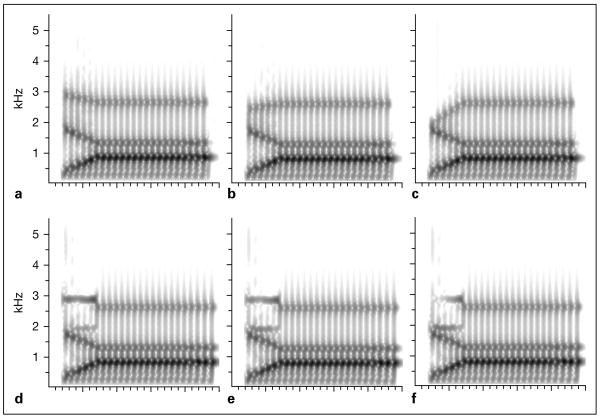
The frequency of all F3 transitions ended at 2,596 Hz (the frequency of the F3 for the steady-state portion of the vowel) and the transitions were created through linear interpolation from the onset frequency to the offset frequency (using a 2-ms frame in the synthesis process). The average rms amplitude of each different F3 transition was measured and the rms values of these transitions were adjusted to be within 1.0 dB of the mean across all ten different transitions. Each of these F3 transitions was then inserted into a copy of the base token using a waveform editor (Adobe Audition). Figure 1 shows a schematic of the final three-formant tokens. Spectrograms of the endpoint stimuli and an intermediate stimulus for the actual F3 transition series can be found in figure 4.

Fig. 1.

Schematic representation of the actual F3 transition series; note that the frequency of the F3 onset varies from 1,907 to 2,596 Hz.

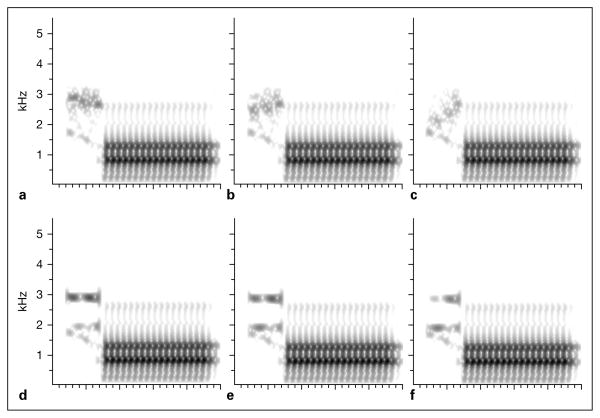
Fig. 4.

Spectrograms of the endpoint stimuli (a, c) and an intermediate stimulus (b) for the actual [da]-[ga] series. The versions of these tokens containing virtual F3 transitions are displayed in d, f and e, respectively.

Virtual F3 Transition Series

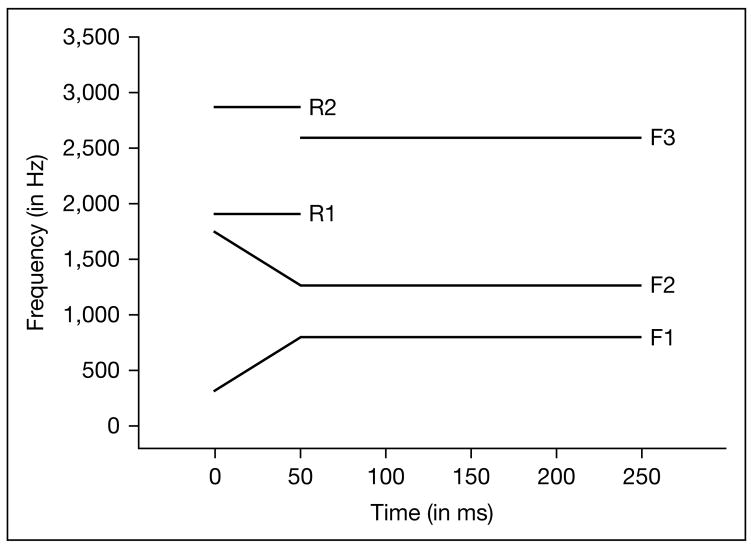
A ten-step virtual F3 transition series was created using the same base token. The virtual F3 transitions were created by changing the relative amplitudes of two 50-ms narrow-band noise-excited resonances with center frequencies at 1,907 and 2,861 Hz (a frequency separation of about 2.5 Bark). We used a narrow-band noise source rather than a periodic signal source in the creation of the virtual formants following Xu et al. [2004], who were concerned that use of a periodic source might introduce distortions in the effective bandwidth. Also, a noise source might encourage subjects to focus on the formant frequencies rather than on the fundamental frequency of the signal. Virtual formants produced with either narrow-band noise or periodic source sound very similar (the narrow-band resonances themselves sound like somewhat noisy pure tones). In creating the virtual transitions, it was our goal that no acoustic energy would occupy most of the range of the F3 frequency transition (particularly in the case of the non-endpoint stimuli). The noise-excited resonances were positioned at the borders of this frequency range: 1,907 and 2,861 Hz (these F3 onset values were selected as they produce unambiguous synthesized [da] and [ga] tokens, respectively). Any perception of frequencies (and/or frequency glides) between these resonances would thus be the result of auditory spectral integration.

These two resonances were produced with Matlab using 100-Hz-wide FIR bandpass filters centered at 1,907 and 2,861 Hz and white noise (fig. 2). The amplitudes of these pairs of resonances were then adjusted (using linear interpolation between the onset and offset amplitudes) so that the movement of the spectral COG of these tokens matched those of the actual F3 transitions. These amplitude adjustments are shown in table 1.

Fig. 2.

The perceived frequency of the actual (left) and the virtual F3 transition (right) as predicted by the IWAIF model. The steady-state portions of F3 are also included.

The spectral COG at each temporal location in the F3 transition was based on the intensity ratio between the lower and higher resonances. The expected change in spectral COG was verified using a program that determined the frequency of the spectral center based on the intensity weighted average of instantaneous frequency (IWAIF) model [Anantharaman et al., 1993; Krishnamurthy and Feth, 1993]. The perceived frequency of the virtual (and the actual) F3 transition as predicted by the IWAIF model is shown in figure 2. If the perceptual system utilizes peripheral auditory filter bands that are limited in their extent (e.g., 3.5-Bark filters), then this might represent the auditory energy summation of a filter centered near the frequency of F3. However, it is clear that listeners will have access to acoustic information across the entire acoustic spectrum and the ultimate goal of a complete perceptual model (not provided here) will need to address the nature of these auditory filters and how they interact in the perceptual process.

These two resonances were then combined in a 250-ms time frame with the onsets of these two resonances synchronized with the onsets of the F1 and F2 formants in the base token. Finally, the overall mean rms of each pair of resonances was adjusted to within 0.1 dB of the average rms value of the actual F3 transitions and was then inserted into a copy of the base token using a waveform editor. Figure 3 shows a schematic of the virtual F3 tokens (amplitude changes are not shown). Spectrograms of the endpoint stimuli and an intermediate stimulus for the virtual F3 series are displayed in figure 4.

Fig. 3.

Schematic representation of the virtual F3 transition series; note that the center frequencies of the two 50-ms noise-excited resonances remain constant.

Listeners

Eleven listeners (6 men and 5 women) aged 19–30 years participated in experiment 1. Eight were students in speech and hearing science or linguistics at the Ohio State University and 2 were undergraduate students at Miami University. All subjects were native speakers of American English. All subjects reported normal hearing. They were paid USD 10 for their participation.

Procedure

Signals were presented diotically via Sennheiser HD600 headphones at a comfortable listening level (70 dB SPL) to a subject seated in a sound-attenuating booth. A single-interval 2AFC identification task was used with the response choices da and ga displayed on two separate halves of the computer monitor. Subjects were asked to indicate whether they heard a da or ga for each token presented by clicking on the mouse button on the appropriate section of the display. There were 200 stimuli presented randomly in each session (10 tokens × 20 repetitions) blocked by the token type (actual and virtual F3 transitions). The presentation order of sessions was counterbalanced across listeners.

In order to familiarize the subject with the stimulus set and the task, prior to the listening task for each blocked set of stimuli, the subject heard each endpoint stimulus for that stimulus series (steps 1 and 10) three times. As each stimulus token was played, the appropriate response area turned red on the computer display. Following the presentation of these examples, the subject was given a practice (with no feedback), consisting of 15 randomly selected tokens. After the practice was completed, the experimenter answered any questions the subject had before the actual testing session. Experiment 1 lasted approximately 40 min. One subject was unable to complete the task and was dropped from the experiment; her data were not included in the analyses to follow. Although the remaining subjects were not interviewed after the experiment as to their impressions about how the stimuli sounded to them, no subject reported a drastic difference between the two stimulus sets.

Results and Discussion

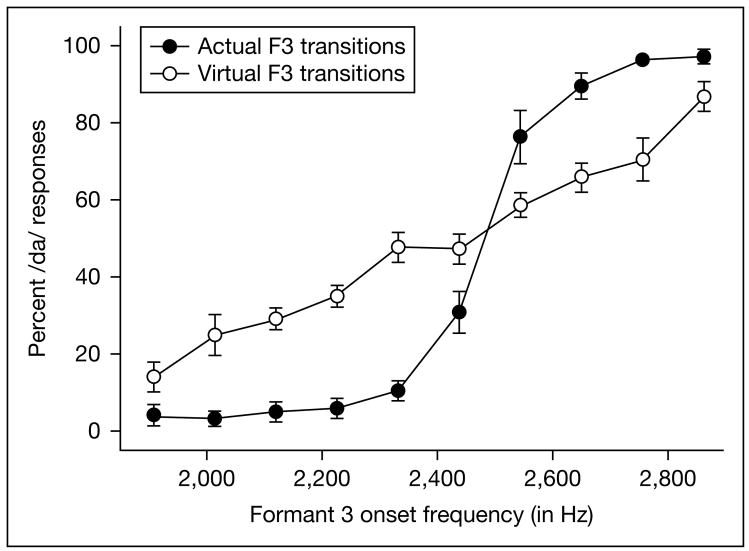
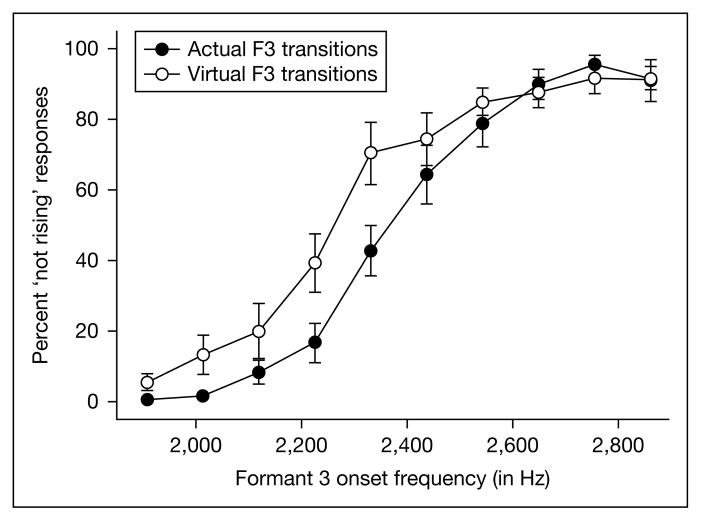
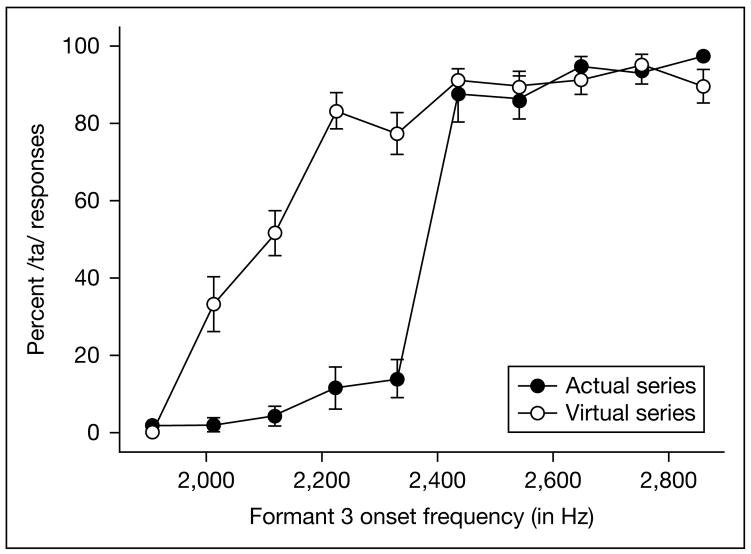
Shown in figure 5 are the identification responses to both the actual and virtual F3 transition series. For the actual frequency series, the identification function is monotonically increasing, indicating primarily ga responses when F3 transition is rising and primarily da responses when it is steady or falling. The slope shows a very abrupt shift from ga to da. For the virtual F3 transition series, the function is again monotonically increasing with the general pattern of responses approximating that for the actual series. However, notable differences can be found in the slopes of both identification functions. In particular, the responses to the virtual series produced a much shallower function, suggesting more uncertainty in labeling the tokens as da and ga.

Fig. 5.

Identification functions of responses to the actual F3 transition and the virtual F3 transition series. Values along the abscissa represent the onset F3 frequency used in the synthesis of the actual formant transition or, for the virtual transitions, the effective onset frequency of the IWAIF-modeled spectral COG for the two noise-excited resonances.

A paired-samples t test showed that there was no significant difference in the total number of da responses given to the two different series [t(9) = 2.21, p = 0.055]. Listeners provided slightly more da responses than ga responses to both the F3 transition series (mean = 58.1%) and the virtual F3 transition series (mean = 52.4%). These results indicate that listeners demonstrated no unexpected response bias difference between the two series. Next, the number of da responses was analyzed using a two-way within-subject ANOVA with the factors F3 transition type (actual and virtual) and F3 onset frequency (series step). There was no significant main effect of transition type [F(1, 9) = 4.877, p = 0.055, η² = 0.351], but there was a significant main effect of F3 onset frequency [F(9, 81) = 154.9, p < 0.001, η² = 0.945]. Most importantly, however, there was a significant F3 transition type-by-F3 onset frequency interaction [F(9, 81) = 28.2, p < 0.001, η² = 0.758]. What the interaction shows is that the slope of the identification function is significantly shallower for the virtual F3 transition series than in the actual F3 transition series. The locations of the [da]-[ga] category boundary (the 50% crossover point) along the F3 onset axis for each individual subject were calculated using Probit Analysis. A paired-samples t test showed that there was no significant difference in the mean category boundary [t(9) = 1.11, p = 0.295] between the actual F3 transition series (2,470 Hz) and the virtual F3 transition series (2,428 Hz).

To better understand the nature of the significant interaction between F3 transition type and F3 onset frequency, two separate ANOVAs with the factors transition type and F3 onset were used as post-hoc tests. The first ANOVA examined the number of da responses for the first six steps which had rising F3 transitions whose slopes were greater than 2 Hz/ms (ranging from 13.8 to 3.2 Hz/ms). The main effect of transition type (actual or virtual) was significant [F(1, 9) = 76.75, p < 0.001, η² = 0.895], as was the main effect of F3 onset [F(5, 45) = 28.37, p < 0.001, η² = 0.759]. The interaction between the transition type and F3 onset was also significant [F(5, 45) = 8.02, p < 0.001, η² = 0.471]. These results indicate that for the rising F3 transitions, the slopes of the actual and the virtual transition series differed from one another, the latter being significantly shallower than the slope for the actual transition. The second ANOVA examined the number of da responses for the last four steps in which the F3 transition was basically flat (with slopes of +1.1 and −1.1 Hz/ms) or falling (with slopes of −3.2 and −5.3 Hz/ms). The main effect of transition type (actual or virtual) was again significant [F(1, 9) = 22.73, p = 0.001, η² = 0.716], as was the main effect of F3 onset [F(3, 27) = 18.3, p < 0.001, η² = 0.670]. However, the interaction between the transition type and F3 onset was not significant. The results of the second ANOVA indicate that for the falling or flat F3 transitions, there were significantly more of da responses for each step of the actual transition series than for the virtual, but the slopes of both functions were comparable.

Overall, these statistical results confirmed what could be inferred from a visual inspection of figure 5 that the primary difference between the two identification functions is in their slopes and not in an unexpected response bias or a different location of category boundary. The continuous albeit significantly shallower function for the virtual series indicates that the listeners were still able to label the tokens systematically as either da or ga, but their identification decisions were not as definite as for the actual transition series. Nonetheless, their response patterns did not show either chance performance or discontinuities in the identification functions. This indicates that the virtual F3 transitions still provided information about the signal, but they were not as salient a cue in comparison with the actual (spectral) F3 transitions.

Experiment 2: Sensitivity to Virtual F3 Transitions

The results of experiment 1 indicate that the actual and, to a lesser extent, virtual F3 transitions provide dynamic cues to identification of the syllables as either [da] or [ga]. The question arises as to whether the listeners were indeed perceiving frequency glides in each case (i.e., using the direction of the F3 transition as a phonetic cue) or were utilizing some other cue (such as the frequency of the F3 onset alone). It may be argued that dynamic cues such as those signaling the direction of F3 transition are not attended to by listeners. Instead, their identification decisions are based on a type of perceptual matching of a spectrum template at CV onset associated with alveolars (a more diffuse spectrum which is dominated by high frequency energy) or velars (a more compact spectrum resulting from the dominant central peak) [Stevens and Blumstein, 1978].

To argue that listeners were attending to the actual or virtual frequency transitions, we must first demonstrate that the F3 transitions – especially the virtual F3 – can be perceived as having a rising or falling frequency. Experiment 2 thus sought to determine whether listeners can accurately report the direction of the frequency transition (either rising as in [ga] or falling as in [da]) when listening to the actual or virtual F3 transitions alone. If listeners are sensitive to these frequency transitions, then we might expect identification functions to be similar to those found in experiment 1.

Stimuli

The stimulus tokens in experiment 2 were the isolated F3 transitions created for the two stimulus series in experiment 1 prior to their insertion into the base CV token. The overall amplitudes of all 20 F3 transitions (10 actual, 10 virtual) were equalized in terms of average rms and were presented to subjects at a comfortable listening level (70 dB SPL). Note: these transitions were presented to listeners at a level considerably higher than the level they had when embedded in the base token.

In addition to these 20 stimuli, two additional stimulus tokens were created for each series. For the actual transition series, static F3 formants (which were 50 ms in duration) were created that had a steady-state frequency of either 2,013 or 2,755 Hz. These were not-rising. For the virtual transition series, two 50-ms steady-state signals were composed of the two noise-excited resonances with a COG equivalent to 2,013 or 2,755 Hz. These additional tokens were included to ensure that listeners did not make their rising/not-rising decisions merely on the onset frequency of the token. There were 250 stimuli presented randomly in each session, blocked by the token type (actual and virtual F3 transitions). The presentation order of sessions was counterbalanced across listeners.

Listeners

Nine listeners (4 men and 5 women), aged 19–38 years old, with no known history of hearing impairment participated in experiment 2. Six of them participated in experiment 1 and 3 were new. A comparison of individual plots indicated no systematic differences in the performance of listeners who participated in experiment 1 and the ones who were new. All were native speakers of American English and were graduate students in speech and hearing science at the Ohio State University or undergraduate students at Miami University. They were paid USD 10 for their participation.

Procedure

The testing procedure was similar to that utilized in experiment 1. A single-interval 2AFC identification task was administered with the response choices rising and not rising displayed on the computer screen. Listeners were asked to identify each token as either a rising glide (corresponding to a rising transition) or a not-rising one (corresponding to either a falling transition or steady-state sound). The familiarization and practice procedure was as in experiment 1. Experiment 2 lasted approximately 40 min.

Results and Discussion

Shown in figure 6 are the identification responses to both the actual and virtual F3 transitions alone. Listeners had no difficulty in completing the task and were generally able to recognize the direction of the transitions, as indicated in the number of responses as rising and not-rising. The slope of the identification function for the actual F3 transition is still ‘categorical’, although it is not as abrupt as in experiment 1. The function for the virtual transition series is again shallower, although, unlike in experiment 1, the slopes of both functions run clearly in parallel to one another and even overlap for the last three stimuli.

Fig. 6.

Identification functions (rising/not rising) of responses to the actual F3 transitions and the virtual F3 transition series. Values along the abscissa represent the onset F3 frequency used in the synthesis of the actual formant transition or, for the virtual transitions, the effective onset frequency of the IWAIF-modeled COG for the two noise-excited resonances.

A paired-samples t test showed that there was no significant difference in the total number of not-rising responses given to the two different series [t(8) = 2.27, p = 0.053], although there was a tendency for listeners to give more not-rising responses to the actual F3 transitions (mean = 51.0%) than to the virtual F3 transitions (mean = 42.1%). Next, the number of not-rising responses was analyzed using a two-way within-subject ANOVA with the factors transition type and F3 onset frequency. The main effect of transition type was not significant [F(1, 8) = 5.137, p = 0.053, η² = 0.391], indicating no response bias difference between the actual and virtual series. There was a significant main effect of F3 onset frequency [F(9, 72) = 96.5, p < 0.001, η² = 0.923]. Again, there was a significant transition type-by-F3 onset frequency interaction [F(9, 72) = 3.2, p = 0.003, η² = 0.285], which indicated that the slope of the identification function for the virtual F3 transition series was not parallel to the slope of the actual F3 transition series. A paired-samples t test on the Probit means showed that there was no significant difference in the mean category boundary [t(8) = 2.25, p = 0.055] between the actual series (2,400 Hz) and the virtual series (2,299 Hz).

Two separate ANOVAs, of the same nature as in experiment 1, were used to examine the significant interaction between the transition type and F3 onset. For the first six steps examined in the first ANOVA, the main effect of transition type (actual or virtual) was significant [F(1, 8) = 9.64, p = 0.015, η² = 0.546], as was the main effect of F3 onset [F(5, 40) = 56.65, p < 0.001, η² = 0.876]. The interaction between the transition type and F3 onset was not significant. Thus, for the rising F3 transitions, the number of not-rising responses for each step was significantly greater for the virtual series than for the actual, but the slopes for these two functions were equally steep. The second ANOVA showed very different results for the last four steps. There was a significant small effect of F3 onset [F(3, 24) = 3.82, p = 0.023, η² = 0.323] but neither the main effect of transition type nor the interaction between the two factors were significant. These results suggest almost no difference in response pattern to either the actual and virtual series.

Altogether, the results of the statistical analyses for experiment 2 indicate that the differences between the responses to the virtual and the actual glide series were found merely for the first six steps of both series, in which listeners gave more not-rising responses to stimuli with a rising glide. However, the slopes of the two functions were comparable through the whole series. It is clear that the listeners perceived frequency glides in each case, which was the main question asked in this experiment. However, the results also show that when F3 transitions were presented in isolation from the base token, there was a bias toward not-rising responses. This may suggest that the subjects tended to label as not-rising the stimuli with a very small frequency change, which remained unnoticed (or perhaps too small to detect) when they assigned phonetic labels to the same transitions in the syllabic context.

Experiment 3: Dynamic Cues to Place of Articulation in Voiceless Stops in [t^ha]-[k^ha]

Experiment 1 demonstrated that a virtual F3 transition could cue a [da]-[ga] distinction just as earlier experiments [e.g., Mann and Liberman, 1983; Feth et al., 2006; Gokcen and Fox, 2001] had shown that one could successfully substitute a frequency-modulated tone for this voiced F3 transition. However, in real speech the initial formant transitions are often voiceless and aspirated (which occurs when the formants are excited by the noise produced by air turbulence at the open glottis) when voiceless stops are produced. Can a virtual glide also cue these voiceless transitions? The experiment reported here compares the phonetic processing of voiceless frequency transitions (i.e., noise-excited or ‘aspirated’ formants) and amplitude-modulated noise-excited resonances (representing the virtual F3 transitions) in cueing place of articulation distinctions in [t^ha] vs. [k^ha] CV syllables in English. In particular, the experiment was designed to determine whether one could successfully ‘mimic’ a voiceless F3 transition (excited by an unvoiced ‘hiss’ source) by changing the relative amplitudes of (and thus, the spectral COG between) two noise-excited resonances whose frequencies are held constant. Again, we are also interested in determining the relative perceptual salience of the virtual F3 transitions in comparison to actual aspirated formant transitions.

Stimuli

[t^ha]-[k^ha] Base Token

As in experiment 1, the stimuli were designed so that there were two different [t^ha]-[k^ha] series whose steps differed only in terms of having an actual or virtual F3 transition. The [t^ha]-[k^ha] base token was created in a fashion identical to the [da]-[ga] base token except that the source of acoustic energy used in the parallel synthesis in the first 50 ms was a noise source rather than a voice source. This produced a very weak F1 transition, but a fairly strong F2 transition. None of the stimulus tokens contained stop release bursts. Perceptually, the [t^ha]-[k^ha] base token sounded like [t^ha].

Voiceless F3 Transition Tokens

Using the HLsyn software (with the .kld option), ten different voiceless F3 transitions that were 50 ms in duration were created within a 250-ms time frame. The formant values used in the synthesis of these voiceless actual F3 transitions were identical to the ones used in experiment 1 (table 1). The onsets of these F3 transitions were synchronized with the onsets of F1 and F2 in the base token. The frequency of all F3 transitions ended at 2,596 Hz (the frequency of the F3 for the steady-state vowel) and the transitions were created through linear interpolation from the onset frequency to the offset frequency (using 2-ms windows in the synthesis process). The average rms amplitude of each different F3 transition was measured and the rms values were within 1.0 dB across the ten different transitions. Each of these F3 transitions was then inserted into a copy of the [t^ha]-[k^ha] base token using a waveform editor.

Virtual Voiceless Transition Series

A ten-step virtual F3 transition series was created using the same [t^ha]-[k^ha] base token. Again, the voiceless virtual F3 transitions were created by changing the relative amplitudes of two 50-ms narrow-band noise-excited resonances with center frequencies at 1,907 and 2,861 Hz (a frequency separation of about 2.5 Bark). The virtual voiceless F3 transitions were created in a slightly different manner than in experiment 1. In particular, these two resonances were produced with Matlab using 100-Hz-wide FIR bandpass filters centered at 1,907 and 2,861 Hz and white noise (fig. 2). As in experiment 1, a waveform editor was used to adjust the amplitudes of each pair of resonances (using linear interpolation between the onset and offset amplitudes) so that the movement of the spectral COG of these tokens matched those of the voiceless actual F3 transitions. These amplitude adjustments were the same as those shown in table 1.

These two resonances were then combined in a 250-ms time frame, with the onsets of these two resonances synchronized with the onsets of the F1 and F2 formants in the base token. Finally, the overall mean rms of each pair of resonances was adjusted to stay within 1.0 dB of the average rms value of the actual voiceless F3 transitions and was then inserted into a copy of the base token using a waveform editor. These voiceless transitions (both the actual and the virtual) were less intense than their voiced counterparts in experiment 1. Figure 7 shows spectrograms of the endpoint stimuli and an intermediate stimulus for both the actual and virtual [t^ha]-[k^ha] series.

Fig. 7.

Spectrograms of the endpoint stimuli (a, c) and an intermediate stimulus (b) for the actual [t^ha]-[k^ha] series. The versions of these tokens containing virtual F3 transitions are displayed in d, f and e, respectively.

Listeners

Listeners were 13 native speakers of American English (4 men and 9 women), aged 19–38 years, students at the Ohio State University, and with no known history of hearing impairment. They were paid USD 10 for their participation.

Procedure

The testing procedure was as in experiment 1. The only difference was that listeners were asked to identify each token as either a ta or ka. Experiment 3 lasted approximately 40 min.

Results and Discussion

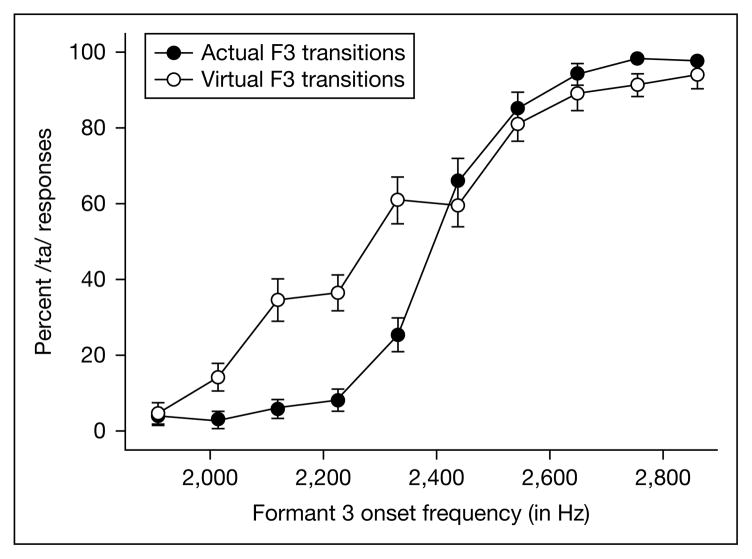
Shown in figure 8 are the identification responses to both the actual and virtual voiceless transition tokens. As for the first six stimuli with the rising F3 transition, both identification functions are relatively close reflections of the pattern seen in experiment 1. However, the responses to the last four stimuli line up rather closely, showing very little difference between the two functions. This suggests that, for the tokens with the falling transitions, listeners had no apparent difficulty in labeling the virtual stimuli as instances of ta.

Fig. 8.

Identification functions of responses to the actual F3 transition voiceless series and the virtual F3 transition voiceless series. Values along the abscissa represent the onset F3 frequency used in the synthesis of the actual formant transition or, for the virtual transitions, the effective onset frequency of the IWAIF-modeled spectral COG for the two noise-excited resonances.

A paired-samples t test showed that there was a small but significant difference in the total number of ta responses given to the two different series [t(12) = 2.646, p = 0.021]. Listeners responded with more ta responses to the virtual series (mean = 56.7%) than to the actual series (mean = 48.8%). Since it is the ka response that depends on listeners hearing a rising F3 transition, this again indicates that although the amplitude changes of the two resonances may produce a virtual frequency glide, the glide percept is not as salient as that perceived when there is an actual formant transition (whether the transition is voiced or voiceless).

Next, the number of ta responses was analyzed using a two-way within-subject ANOVA with the factors transition type and F3 onset frequency. There was a significant main effect of transition type [F(1, 12) = 7.00, p = 0.021, η² = 0.368] as well as a significant main effect of F3 onset frequency [F(9, 108) = 215.1, p < 0.001, η² = 0.947]. There was also a significant transition type-by-F3 onset frequency interaction [F(9, 108) = 11.65, p < 0.001, η² = 0.493]. The significant interaction was obtained because the identification functions were not parallel for the stimulus steps in the first part of the series. Prior to the [t^ha]-[k^ha] category boundary there were more ta responses to the virtual F3 transition than to the actual F3 transition series. Again, the slope of the identification function for the actual series resembles the typical ‘categorical perception’ shape whereas the slope for the virtual series is much shallower in the first part of the series.

As before, the locations of the [t^ha]-[k^ha] category boundary (the 50% crossover point) along the F3 onset axis for each individual subject were calculated using Probit Analysis. A paired-samples t test showed a small (88 Hz) but nonsignificant difference in the mean category boundary [t(12) = 2.25, p = 0.055] of the actual series (2,397 Hz) and the virtual series (2,309 Hz). The difference between the two series in responses to steps 2–5 (more ta responses to the virtual series) indicates that listeners were less often perceiving a rising F3 transition when the transition was virtual. This again suggests that the virtual transition was less salient as a cue to place of articulation than was the actual formant transition.

To closer examine each identification function, two separate ANOVAs were used as in experiments 1 and 2. For the first six steps, the first ANOVA revealed a significant main effect of transition type [F(1, 12) = 16.9, p = 0.001, η² = 0.585]) and a significant main effect of F3 onset [F(5, 60) = 75, p < 0.001, η² = 0.862]. The interaction between the transition type and F3 onset was also significant [F(5, 60) = 12.27, p < 0.001, η² = 0.506]. These results confirmed that the source of the differences between the two functions was in the significantly shallower function for the virtual series. The second ANOVA examining the last four steps showed no significant effect of transition type. There was a significant effect of F3 onset [F(3, 36) = 11.44, p < 0.001, η² = 0.488], but the interaction between the two factors was not significant. These results indicate that, for the stimuli with flat or the falling F3 transitions, there were no differences in the response pattern to either the actual or virtual series.

Experiment 4: Static Burst Cues to Place of Articulation in Voiceless Stops in [t^ha]-[k^ha]

Stop bursts can cue the place distinction in initial stop consonants as can formant transitions, although in real human speech one normally expects these two cues to provide redundant information regarding place of articulation. In experiments 1 and 3, one might argue that listeners were paying attention to the onset of the F3 transition (as a ‘burst’ cue) rather than the perceived frequency modulation in the transition itself. Experiment 4 examined this possibility by creating two different stimulus series each of which provided short, static acoustic cues to F3 and, therefore, to place of articulation. In these stimuli there were no frequency or amplitude modulations over time in the F3 cue.

Stimuli

Two new series of stimuli were created, which both utilized the [t^ha]-[k^ha] base token from experiment 3.

Actual F3 Burst Stimuli

Using Matlab, 10 different F3 ‘bursts’ were created. Each burst was 10 ms in duration and was created by adding together 51 sine waves (of equal amplitude) 1 Hz apart in frequency in random phase. These 10 bursts had center frequencies equal to the transition onsets listed in table 1. The onsets and offsets of these bursts were ramped to full intensity over 1 ms. The overall amplitudes of these burst were then adjusted to stay within 1.0 dB of the mean amplitude of the voiceless F3 transitions. Each burst was then inserted into a copy of the [t^ha]-[k^ha] base token producing ten steps of a [t^ha]-[t^ha] voiceless burst series. These tokens are schematically shown in figure 9, which illustrates all 10 different burst locations.

Fig. 9.

Schematic representation of the actual F3 burst series; each stimulus token in the series uses the [t^ha]-[k^ha] base token.

Virtual F3 Burst Stimuli

Ten virtual F3 bursts were created by adjusting the amplitudes of the lowest and highest frequency bursts (the bursts centered at 1,907 and 2,861 Hz) so that the spectral COG of these two bursts matched the center frequencies of the ten steps of the actual F3 burst series (these amplitude adjustments matched the R1 and R2 relative amplitude onsets listed in table 1). The overall amplitude of each pair of bursts was then adjusted to stay within 1.0 dB of the mean amplitude of the voiceless F3 bursts and was inserted into a copy of the [t^ha]-[k^ha] base token. Figure 10 is a schematic representation of the virtual burst stimuli (amplitude adjustments are not shown).

Fig. 10.

Schematic representation of the virtual F3 burst series; each stimulus token in the series uses the [t^ha]-[k^ha] base token.

Listeners and Procedure

Listeners and procedure were the same as in experiment 3.

Results and Discussion

Shown in figure 11 are the identification responses to both the actual and virtual voiceless burst tokens. Unlike in the first three experiments, the slopes of the two identification functions are very different. The responses to the actual voiceless bursts show an abrupt change from ka to ta near the middle of the series, produced by about the same proportion of ta and ka responses (mean = 56.7% ta responses). However, the virtual F3 burst tokens were identified far more often as ta (mean = 70%). Only the first step (when the amplitude of the lower burst was relatively high) was consistently identified as ka.

Fig. 11.

Identification functions of responses to the actual and virtual F3 burst series. Values along the abscissa represent the onset F3 frequency used in the synthesis of the actual F3 burst or, for the virtual F3 bursts, the effective onset frequency of the IWAIF-modeled spectral COG for the bursts centered at 1,907 and 2,861 Hz.

It must be pointed out that, unlike experiments 1–3 (in which there were linear amplitude transitions from the onset amplitudes to the offset amplitudes resonances), the first and final steps of the virtual burst series were exactly the same tokens as the first and final steps of the actual burst series. Only steps 2–9 in the virtual series had both endpoint bursts present (albeit at systematically different amplitude levels). It is important to note that as soon as both bursts were present in the virtual tokens in step 2, the number of ka responses began to decline. Except for step 1, only steps 2 and 3 of the virtual series produced any significant number of ka responses. It is difficult to argue that listeners were performing auditory spectral integration with these very short bursts. Certainly the virtual burst cues in steps 2 and 3 were not providing the same cue as the actual bursts.

The same types of statistical analyses were used in experiment 4. The results from the t test revealed that the difference between the two series in the number of ta responses over all stimulus steps was significant [t(12) = 4.27, p = 0.001]. The ANOVA on the number of ta responses showed a significant main effect of stimulus type [F(1, 12) = 84.5, p < 0.001, η² = 0.876] as well as a significant main effect of burst frequency [F(9, 108) = 150.7, p < 0.001, η² = 0.926]). There was also a significant stimulus type-by-burst frequency interaction [F(9, 108) = 45.5, p < 0.001, η² = 0.791]. The significant interaction was obtained because the two identification functions for steps 2–5 were very different. Examining the locations of the [t^ha]-[k^ha] category boundary, a paired-samples t test showed a large (246 Hz) and significant difference in the mean category boundary [t(12) = 9.92, p < 0.001] between the actual (2,394 Hz) and the virtual burst series (2,148 Hz). Again, it is clear that the responses of the listeners to the virtual burst tokens were very different from their responses to the actual burst series.

As may be expected, the separate ANOVA for the first five steps revealed large significant effects of stimulus type [F(1, 12) = 191.3, p < 0.001, η² = 0.941], burst frequency [F(4, 48) = 70.2, p < 0.001, η² = 0.854], and stimulus type-by-burst interaction [F(4, 48) = 35.3, p < 0.001, η² = 0.746]. For the last five steps of both series, the second ANOVA showed no significant effects.

It is important to compare the results of experiment 3 for the voiceless [t^ha]-[k^ha] transitions (both actual and virtual) and experiment 4 for the actual and virtual bursts in addressing the question of the relative importance of each cue for each stimulus type. Using the same two-way ANOVA model on the ta responses comparing the voiceless actual F3 transition series to the actual F3 burst series we found no significant main effect of F3 cue type (transition or burst) [F(1, 12) = 0.042, p = 0.841, η² = 0.003]. However, there was a significant main effect of F3 onset frequency [F(9, 108) = 323.4, p < 0.001, η² = 0.964] and a significant F3 cue type-by-F3 onset frequency interaction [F(9, 108) = 3.80, p < 0.001, η² = 0.241]. This significant interaction stems from the fact that although the two actual series had about the same category boundary, the identification function for the actual F3 transition series did not change from ka to ta responses as abruptly as for the actual F3 burst series (i.e., had a shallower slope).

For the virtual series, there was a large (161 Hz) and significant difference in the mean category boundary [t(12) = 4.62, p = 0.001] for the virtual F3 transition series and the virtual burst series. It is clear that the responses of the listeners to the virtual F3 burst tokens were significantly different from their responses to the virtual transition series. A two-way ANOVA on the ta responses comparing the voiceless virtual F3 transition and virtual burst series showed significant main effects of both F3 cue type [F(1, 12) = 18.0, p = 0.001, η² = 0.599] and F3 onset frequency [F(9, 108) = 99.3, p < 0.001, η² = 0.892]. The F3 cue type-by-F3 onset frequency interaction was also significant [F(9, 108) = 11.5, p < 0.001, η² = 0.488]. This indicates that the virtual burst cues were not providing as much information about place of articulation as the virtual transitions.

General Discussion

The four experiments presented here assessed whether the perception of the initial stops in synthetic [da]-[ga] and [t^ha]-[k^ha] tokens could be cued by virtual F3 transitions or virtual F3 bursts in a manner comparable with actual F3 transitions or bursts. In the virtual signals, the actual relevant frequency information was mimicked by spectral COG effects produced by modification of the amplitudes of two stationary-frequency components. In the first three experiments, these F3 transitions – dynamic cues to place of articulation – were examined for their ability to cue place differences in both voiced and voiceless stops. These F3 transitions were also presented in isolation separately from the base token in order to determine listeners’ ability to detect the direction of change (rising or not-rising). The final experiment examined the perceptual salience of both virtual and actual F3 bursts alone as cues to the alveolar-velar place distinction. These bursts were nondynamic F3 cues which did not involve dynamic frequency changes (either actual or virtual).

Overall, the results demonstrated that listeners were able to perceive the alveolar/velar place-of-articulation distinction on the basis of the virtual F3 transitions in a manner comparable, although not identical, to the actual F3 transitions. This was true for both voiced and voiceless series in experiments 1 and 3. In addition, listeners were able to determine the direction of the both virtual and actual F3 transitions in experiment 2. We will begin a review and discussion of the obtained results to experiments 1–3 by examining our expectations of the pattern of responses to two separate groups of stimuli: (1) tokens with clearly rising (actual or virtual) F3 transitions, and (2) tokens with relatively flat or falling transitions.

One might suggest that the patterns of listener responses to stimuli with rising F3 transitions (the first five to six steps of both the actual and virtual series in experiments 1–3) are somewhat more critical to the questions addressed in the present study than their responses to stimuli with relatively flat or falling transitions (the last four steps). This is because the synthetic base tokens alone (which were used in the construction of the virtual tokens and had no F3 transitions or bursts) are heard as beginning with an alveolar stop. If listeners cannot extract and/or utilize distinctively the F3 cue from a given stimulus token, their ‘default’ response will likely be da or ta. Inability to utilize the F3 cue in identifying the tokens may thus result either in (1) a preponderance of alveolar responses across all steps or (2) chance-level responses as the listeners strive to balance their responses between the two perceptually indistinguishable alternative choices. However, if listeners do extract the dynamic F3 cue appropriately, their expected responses to the first five to six steps with a rising F3 transitions are either ga or ka (but since the slope of the F3 rise decreases from step 1 to step 6, we expect the number of velar responses to decline).

This leads us to the question of whether we can make strong claims about listener’s ability to extract the F3 as a dynamic cue for the last four tokens, since the expected response to the stimuli with the flat or falling F3 transition (or the base token alone) is either da or ta. Again, if the response patterns represent chance-level performance, then we can argue that listeners are unable to use the F3 cue in making their identifications. Only if the slope of identification function from steps 7 to 10 is rising (going from fewer to more alveolar responses) can we infer that listeners are, in fact, extracting relevant F3 information.

Turning to the results, we find that, for both series in experiments 1 and 3, the tokens with clearly rising F3 transitions (steps 1–6) were more often identified as [ga] or [k^ha]. The number of velar responses decreased (and the number of alveolar responses increased) as the slope of the rising transition decreased. This indicates that listeners were able to use the F3 transition cue (in both series) to identify place of articulation of the initial stop. In both experiments, there were significantly fewer velar responses in the virtual series as compared to the actual series. Nevertheless, these data indicate that the virtual F3 transitions provided the same type of phonetic information regarding place of articulation as did the actual F3 transitions, but we may infer from the differences in the shapes of the two identification functions that the strength of the virtual phonetic cue was less salient than that of the actual F3 transition. The identification responses to the last four tokens (steps 7–10) show a rising slope for both series, and are thus also producing the response patterns expected if listeners were utilizing the F3 transition cue. The responses in experiment 3 were almost identical for the actual and virtual series, although there were somewhat fewer da responses in experiment 1 for the same steps. This suggests that listeners were, in fact, extracting relevant phonetic information from both the actual and virtual F3 transitions.

When transitions only were presented to the listeners in experiment 2, asking them to indicate whether they heard a rising or a not-rising sound, there were no significant differences in the basic shapes of the two identification functions. Although the number of not-rising responses for each step was greater for the virtual series than for the actual series, the slopes of two identification functions were basically equivalent. This suggests that, for the rising F3 transition, the differences in responses to the virtual and actual frequency transitions were minimized when listeners were not required to assign phonetic labels to the tokens. The pattern of responses from experiment 2 conforms to our expectations assuming that listeners are able to perceive a frequency glide when hearing the F3 transitions alone. Their not-rising responses increased monotonically as the slope of the F3 transition (actual or virtual) decreased.

In experiment 4, the actual and virtual F3 bursts served as static cues to the alveolar-velar place distinction in voiceless stops. Experiment 4 established that actual F3 bursts can provide consistent perceptual cues to place of articulation. The responses for the actual bursts gave rise to a strongly categorical, almost discontinuous identification function. Comparing the slopes for the actual bursts and actual F3 transitions, it became clear that the differences were primarily in the responses to the midstimuli, i.e., steps 5 and 6. A more continuous function for the actual F3 transitions was a result of a greater number of mixed responses to these two tokens whereas for the actual burst series, these two stimuli tended to be identified as either ka or ta, respectively.

Since our stimuli did not provide conflicting cues such as mismatch between the frequency of transitions and the burst frequency for a particular place distinction in stops, the present results do not provide evidence whether dynamic cues (in the form of F3 transitions) or static cues (in the form of release bursts) are more important in the perception of the place of articulation of the stop consonant [e.g., Stevens and Blumstein, 1978; Walley and Carell, 1983; Francis et al., 2000]. In the stimulus sets presented here, the use of F3 transitions and F3 bursts were mutually exclusive, and the results clearly indicate that both types of cues were comparable in terms of providing information about the place distinction in stops. The identification function for the burst as compared to the voiceless F3 transition was less ‘categorical’, suggesting that, for the latter, listeners were not paying attention to the onset of the F3 transition (as a ‘burst’ cue). Rather, they did perceive the dynamic frequency transition.

Turning to the virtual F3 bursts, our results indicate that they simply did not supply the same quality of information and certainly do not reflect as strong a phonetic cue to place of articulation as the actual F3 burst (or the virtual or actual F3 transitions). It appears that the listeners choose the ‘default’ ta response to most stimuli. One must remember that step 1 of the virtual burst series is identical to step 1 of the actual burst series (and requires no spectral integration of the F3 cue), so it is no surprise that listener response to this token is almost completely ka. However, only two other tokens in the virtual burst series (steps 2 and 3) provide any significant number of ka responses, and the identification function itself is not at all categorical. Consequently, not only was there a significant difference in the mean category boundary between the actual and virtual F3 burst series but the category boundary difference was also significant for the virtual F3 bursts and virtual F3 transitions. As argued above, this would indicate that subjects are unable to utilize the virtual F3 burst as a phonetic cue appropriately.

One possible explanation for the sharp discrepancy between the virtual F3 bursts and the other three series is very likely a function of the short duration (10 ms) of the bursts. Although brief information in the burst for the actual burst was adequate to cue the place-of-articulation distinction (in a manner comparable to the F3 transitions), the virtual burst was insufficient to provide the same place of articulation information. Certainly, given the pattern of responses in experiment 4, it can be argued that listeners did not demonstrate auditory spectral integration in the processing of these short virtual bursts. It may be that listeners are unable to complete the auditory spectral integration necessary to utilize the virtual F3 cue in such a short time. The extent to which auditory spectral integration is limited by the duration of the signal is, in fact, a question to be addressed in future research.

Based on the overall results of this study we may conclude that although the responses to the dynamic cues in virtual transitions were not always as strong as for actual transitions, we nonetheless obtained compelling evidence that listeners do hear frequency glides when attending to the virtual F3 transitions and respond predictably to the direction of their frequency transition (either rising or falling). In the case of the cues in virtual bursts, their brief durations may limit listeners’ ability to process it as a strong phonetic cue to place of articulation.

The present results bear on several questions related to the COG effect in speech perception research. Most importantly, is the COG effect a demonstration of an auditory mechanism responsible for integration of information in vowel formants at a more central level of signal processing? As pointed out in the ‘Introduction’, the concept of auditory spectral integration comes from psychoacoustic research and is based on a number of reports on improvement of listener’s responses to spectral information in complex signals which contain energy spanning more than one critical band. This argument was also used by Chistovich and colleagues, who introduced the concept of a larger spectral integration bandwidth, that of the 3.5 Bark, to vowel perception research. The present results provide evidence that some form of auditory spectral integration is used in processing the short virtual transition. Listeners’ responses to stimuli which produced movement of the spectral COG (i.e., a dynamic virtual frequency change) are an indication that the auditory system can combine amplitude and frequency information in the perception of formant transitions.

Reflecting on past research on the COG effects in closely spaced formants in static back vowels, we must admit the possibility that the spectral COG in this vowel region may not necessarily represent exclusively the dominant information in closely spaced formants. What the experiments by Chistovich and others showed was that a form of auditory spectral integration took place, which was evident when the COG of the two-formant speech-like signal was shifted. Listeners perceived this shift as a vowel quality change as indicated in their identification responses in a phonetic labeling task. Research still needs to be done to determine the nature of the dominant information in closely spaced formants, which may not require appealing to the spectral COG in making identification decisions.

The experiments with dynamic signals, on the other hand, point to the importance of spectral integration effects within a larger frequency bandwidth and not simply to the COG effects per se. In the stimuli at hand, the rapid COG movement within the bandwidth of 2.5 Bark was created experimentally to mimic that of a F3 transition. This frequency range is, of course, narrower than the 3.5-Bark limit reported in the past for quality differences of static two-formant vowels and it is also substantially narrower than that found in virtual diphthongs [Lublinskaja, 1996; Jacewicz et al., 2006]. However, the current experiments were not attempting to determine limits to the bandwidth over which such integration occurs. Moreover, since the amplitude adjustments utilized here were a product of systematic manipulation rather than a reflection of measured acoustic variation seen in normally produced CV tokens, we do not know whether similar amplitude changes may occur in natural speech. It may even be the case that this exact form of COG movement does not take place in naturally produced coarticulated vowels. However, it should be noted that even slight changes in the frequencies of a vowel’s formants will produce amplitude changes in the harmonics of the source (and we assume, the spectral COG of the resulting signal). Given these considerations, the specific methodology used here should be regarded as a testing ground for determining whether the auditory system is capable of using a variety of cues within a larger bandwidth and does not require exclusive presence of formant frequencies per se. We observed that when dynamic frequency information in the actual F3 transitions was unavailable to the listeners, the dynamic amplitude cues in the virtual transitions successfully substituted for them. This outcome can be interpreted in reference to the summation of spectral information by the central auditory system.

It is often assumed that the 3.5-Bark bandwidth obtained in static vowel quality experiments represents some anatomical limit imposed by the auditory system. Our work to date indicates that it may be the type of signal and specific task that determines auditory resolving power [Fox et al., 2007a, b]. This position is in accord with psychoacoustic research, which gives an indication that the improvement in listener performance [as predicted by the multi-band energy detector model; Green, 1958, 1960] may depend on the psychoacoustic task or even signal manipulation [e.g., Grose and Hall, 1997]. The two perspectives on the width of the integration bandwidth, i.e. coming from psychoacoustics and from past work on COG in relation to 3.5 Bark in speech perception research, need to be reconciled in light of future research. Variation in the bandwidth of auditory spectral integration as a function of both the experimental task and the nature of the stimulus (e.g., static vs. dynamic) serve as the topic of continuous research in our lab.