Monte Carlo dose mapping on deforming anatomy

Abstract

This paper proposes a Monte Carlo-based energy and mass congruent mapping (EMCM) method to calculate the dose on deforming anatomy. Different from dose interpolation methods, EMCM separately maps each voxel’s deposited energy and mass from a source image to a reference image with a displacement vector field (DVF) generated by deformable image registration (DIR). EMCM was compared with other dose mapping methods: energy-based dose interpolation (EBDI) and trilinear dose interpolation (TDI). These methods were implemented in EGSnrc/DOSXYZnrc, validated using a numerical deformable phantom and compared for clinical CT images. On the numerical phantom with an analytically invertible deformation map, EMCM mapped the dose exactly the same as its analytic solution, while EBDI and TDI had average dose errors of 2.5% and 6.0%. For a lung patient’s IMRT treatment plan, EBDI and TDI differed from EMCM by 1.96% and 7.3% in the lung patient’s entire dose region, respectively. As a 4D Monte Carlo dose calculation technique, EMCM is accurate and its speed is comparable to 3D Monte Carlo simulation. This method may serve as a valuable tool for accurate dose accumulation as well as for 4D dosimetry QA.

1. Introduction

Recent advances in four-dimensional (4D) imaging and image-guided radiation therapy have highlighted the need to map and sum dose distributions over deformed anatomy. The dose mapping has been investigated by multiple groups in the recent years (Yan et al 1999, Chetty et al 2003, Olivera et al 2004, Schaly et al 2004, Rosu et al 2005, Coolens et al 2006, Flampouri et al 2006, Seco et al 2007, Zhong et al 2008). The majority of dose mapping processes use a displacement vector field (DVF) from a deformable image registration (DIR) algorithm to identify locations in the dose delivery image which correspond to the points of interest in a fixed reference image where the dose is to be mapped to. Dose values interpolated in the delivery image are then mapped to the reference image which represents a deformed state of the delivery image. Note that dose is the energy deposited per unit mass. In each reference voxel, the energy deposited and mass could come from multiple source voxels. Consequently, the accuracy of dose mapping will depend on how accurate energy deposition and mass are individually calculated within each reference voxel, instead of interpolation of the doses in source voxels. It has recently been shown that dose interpolation methods (DIMs) have inherent errors with the deviations largest in dose gradient regions where tissue voxels have expanded or compressed between the dose delivery and reference images (Siebers and Zhong 2008).

Heath and Seuntjens avoided the dose interpolation problem by utilizing a Monte Carlo dose calculation algorithm that used the DVF to map the regular rectilinear voxel boundaries in the reference image directly onto the dose delivery source image, resulting in irregular dodecahedral voxels in the source image (Heath and Seuntjens 2006). The mass density in each dodecahedral voxel is then adjusted based on the voxel’s volume variation before and after the DVF mapping. In this voxel warping method (VWM), dose interpolation is not required since the voxel contents (mass and then energy deposited) are counted on a voxel by voxel basis between the dose delivery and reference images. The downside of the VWM is that the MC ray-tracing algorithm needs to detect the irregular voxel boundaries to calculate the energy deposited during the MC particle transport simulation, and therefore the VWM is time consuming.

Recently, we proposed an energy transfer method (ETM) to map energy deposited between deformed anatomies (Siebers and Zhong 2008). In the ETM, particle transport is simulated within a typical rectilinear grid in the dose delivery source image, but the energy deposited is mapped using the DVF to regular voxels on the reference image. The dose in each reference voxel is calculated as the ratio of the mapped energy deposited and the mass in the reference image. Given a correctly mapped mass density matrix, both VWM and ETM can accurately calculate the mapped dose, but the ETM does not need to detect irregular voxel boundaries, thereby achieving a speed comparable to that of a regular 3D MC dose calculation.

The correctness of the mapped mass density could be compromised by errors in DIR. For VWM, the density of the deformed voxel can be derived by scaling the density of the reference voxel (Health and Seuntjens 2006). Due to DIR errors, Heath et al showed that there is an average of 2% difference between the mass density of the source image and that scaled from the reference image. If the warped voxel’s density is assigned directly from that of its correspondent reference voxel without density scaling, the dose difference between VWM and the trilinear DIM is within 1% (Heath et al 2008). However, the density assignment without scaling contradicts to the underlying physics of a mass-conserved compressional deformation. A typical example of this is the intra-fractional lung deformation where the mass of the tumor and surrounding tissues does not change during a respiratory cycle and the lung volume variation is mainly due to air exchange (Simon 2000). In this case, the energy deposited and its associated mass can be exactly mapped from the source image to reference image.

Like VWM, ETM may also suffer from DIR errors, especially when its mass density is directly assigned from the reference image. To minimize the consequence of the potential errors in the mapped dose distributions, the mass mapping should be congruent to the mapping of particle interaction events. In this study, we will present different mass mapping strategies, explore their dosimetric consequences and demonstrate their clinical application to a lung IMRT case.

2. Material and methods

To map dose for deforming anatomy, in this paper the energy deposited is transferred from a radiation delivery (source) dose grid (S) to a fixed reference dose grid (R) using the ETM method. Briefly, in the ETM method, MC particle transport takes place in a rectilinear voxelization of the S. Locations of individual energy deposition events in S are mapped to the rectilinear voxels in R via application of a deformation vector field from a DIR algorithm. For each voxel in R, a dose is equal to energy deposited mapped to that voxel divided by the voxel mass. Since the ETM requires the reference voxel mass, mass nonconservation errors due to DIR errors will directly relate (propagate) to errors in voxel dose. To address the DVF error-related issues, this study will incorporate different mass mapping methods into ETM and then investigate their dosimetric consequences in clinical applications.

2.1. Concept of dose mapping on deforming anatomy

Due to tissue deformation, the material contents of a single voxel in S can be deformed into multiple voxels in R. Similarly, each R voxel could have its mass mapped from multiple S voxels. To clarify the representation of the energy deposition and mass mapping information, let s represent the index of a source voxel in S, ν for the index of a reference voxel in R and l for the index of an energy deposition event. The total energy deposited in a source voxel s is denoted by E_s and the total mass by M_s.

Suppose e_s(ν) and m_s(ν) represent the energy deposited (probably from multiple events) and the mass physically deformed from the source voxel s to the reference voxel ν, respectively. The mapped dose can then be represented as

$$d_{\mathrm{EMCM}}\left(\nu \right)=\frac{\sum _{s\in V\left(\nu \right)}{e}_s\left(\nu \right)}{\sum _{s\in U\left(\nu \right)}{m}_s\left(\nu \right)}=\frac{\sum _{s\in V\left(\nu \right)}{q}_s\left(\nu \right)E_s}{\sum _{s\in U\left(\nu \right)}{p}_s\left(\nu \right)M_s},$$ (1)

where $q_s\left(\nu \right)=\frac{e_s\left(\nu \right)}{E_s}$, and $p_s\left(\nu \right)=\frac{m_s\left(\nu \right)}{M_s}$. U(ν) is the set of the source voxels which have mass mapping points (i.e. the center of subvoxels) mapped to the voxel ν. V(ν) is the set of all the source voxels which have particle energy deposition events mapped to the reference voxel ν. The definitions of U(ν) and V(ν) are illustrated in figure 1. Given a large number of subvoxels, for each particle energy deposition event, there exists a subvoxel whose mass is mapped to the same target voxel as that the particle’s energy is warped to. This method is called the energy and mass congruent mapping (EMCM) method. By direct mapping, mass conservation between the source and reference images is guaranteed.

Figure 1.

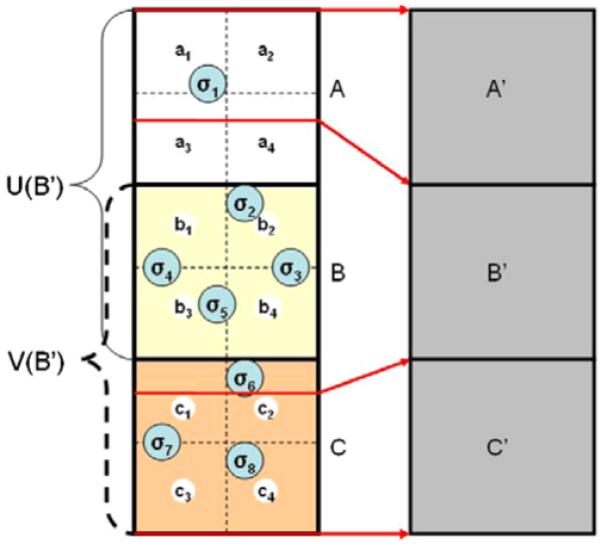
Three source voxels {A, B and C} are mapped to the target voxels {A’, B’, C’} via the DVF indicated by the red arrows. Each source voxel can be subdivided into multiple smaller subvoxels ({a₁, . . . , a₄}, {b₁, . . . , b₄}, . . .). Consider voxel B’. V(B’) is the set of source voxels which contribute energy deposition events {σ₂, . . ., σ₆} to voxel B’, therefore V(B’) = {B, C}. U(B’) is the set of source voxels which contribute mass from the center of their subvoxels to voxel B’. Therefore, U(B’) = {A, B}. As the number of subvoxels tends toward infinity, V(B’) ⊆ U(B’).

In Monte Carlo simulations, each dose computation voxel is assumed to have a uniform mass density, but the particle energy deposition events could be unevenly distributed within this voxel. Consequently, we have $\frac{e_s\left(\nu \right)}{m_s\left(\nu \right)}\ne \frac{E_s}{M_s}$. This difference will be greatest at beam edges or in beam build-up regions. EMCM maps individual particle incident events located within each voxel and therefore is more accurate than voxel-based DIMs. For the dose calculated by convolution/superposition algorithms, the energy deposition distribution within each source voxel s is not available. When part of the voxel s is mapped to a reference voxel ν, dose interpolation approaches assume that the dose d_s(ν) contributed from the same source voxel s to the target voxel ν satisfies $\frac{e_s\left(\nu \right)}{m_s\left(\nu \right)}=d_s\left(\nu \right)=\frac{E_s}{M_s}$. Consequently, $m_s\left(\nu \right)=\frac{e_s\left(\nu \right)}{E_s}{M}_s$. In this case, equation (1) can be approximated by

$$d\left(\nu \right)=\frac{\sum _{s\in V\left(\nu \right)}{e}_s\left(\nu \right)}{\sum _{s\in U\left(\nu \right)}{m}_s\left(\nu \right)}=\frac{\sum _{s\in V\left(\nu \right)}{q}_s\left(\nu \right)E_s}{\sum _{s\in V\left(\nu \right)}{q}_s\left(\nu \right)M_s}$$ (2)

where $q_s\left(\nu \right)=\frac{e_s\left(\nu \right)}{E_s}$, and V(ν) is the set of the source voxels which have particle events mapped to voxel ν. This is called an energy-based dose interpolation (EBDI) method.

In contrast to EMCM, general DIMs such as the center of mass (Flampouri et al 2006, Paganetti et al 2004) or trilinear dose interpolation (TDI) method (Rosu et al 2005) usually have DIR performed from the reference image to the source image (the ETM utilizes a DVF in the opposite direction). Consequently, making a general comparison between DIM and EMCM without involving the effect of the DVF’s self-inverse inconsistencies is difficult. To address this issue, we employed a self-consistent inverse DVF generation technique so that EMCM and EBDI can be compared with other DIMs in clinical CT images (Yan et al 2008).

2.2. EMCM

The dose in each reference voxel ν is the ratio of the total energy deposited $E_{\nu }^R={\sum }_{s\in V\left(\nu \right)}{e}_s\left(\nu \right)$ and the total mass $M_{\nu }^R={\sum }_{s\in U\left(\nu \right)}{m}_s\left(\nu \right)$ mapped to the voxel ν. In Monte Carlo simulation, e_s(ν) can be accumulated on a particle-by-particle basis. When particle l deposits its energy $e_s^{\left(l\right)}\left(\nu \right)$ in the source voxel s, it is immediately scored in the reference voxel ν by application of the DVF. Each e_s(ν) can be obtained by accumulating $e_s^{\left(l\right)}\left(\nu \right)$ for all particles l during Monte Carlo simulation. Without the necessity of classifying its source voxel index s for each mapped particle in implementation, the total energy deposited mapped to the voxel ν is simply denoted by $E_{\nu }^R={\sum }_{l\in L\left(\nu \right)}{e}^{\left(l\right)}\left(\nu \right)$, where e^(l)(ν)is the energy deposited to the voxel ν by the l-th tracked particle, and L(ν) is the set of all such tracked particles events which are mapped to the reference voxel ν. The detail of its implementation was described in Siebers and Zhong (2008).

The dose grid and its mass density matrix are generated from CT images, and the dose grid size is set to 4 × 4 × 4 mm³ which is larger than CT image’s resolution. To determine the mapped mass $M_{\nu }^R$ precisely, an equi-space mass mapping approach, which pushes mass from the source image to the reference image, is utilized. It partitions each source dose voxel s into n³ subvoxels, each having 1/n³ of the voxel mass M_s. The mass of each source subvoxel is mapped to a reference dose voxel pointed by the displacement vector of the source subvoxel’s center. The mass $M_{\nu }^R$ in the reference voxel ν is the sum of the mass contributed from all the source subvoxels t_s to the voxel ν, represented as

$$M_{\nu }^R=\sum _{t_s\in \Gamma \left(\nu \right)}{m}^{\left(t_s\right)}\left(\nu \right),m^{\left(t_s\right)}\left(\nu \right)=M_s∕n^3,$$ (3)

where Γ(ν) represents the set of all the subvoxels whose center is mapped to the reference voxel ν. The dose defined in (1) is then calculated by

$$d_{\mathrm{EMCM}}\left(\nu \right)=\frac{1}{M_{\nu }^R}\sum _{l\in L\left(\nu \right)}{e}^{\left(l\right)}\left(\nu \right).$$ (4)

It should be mentioned that if n in (3) is not large enough, part of the source mass might not be mapped to a target voxel that the associated particle events are mapped to. The resultant mass inaccuracy may cause some errors in dose interpretation (see section 3.2).

2.3. EBDI

For the energy deposition-based dose interpolation, the parameter q_s(ν) given in (2) must be calculated for each of source and reference voxel pairs (s, ν). The procedure to update q_s(ν) is described as follows.

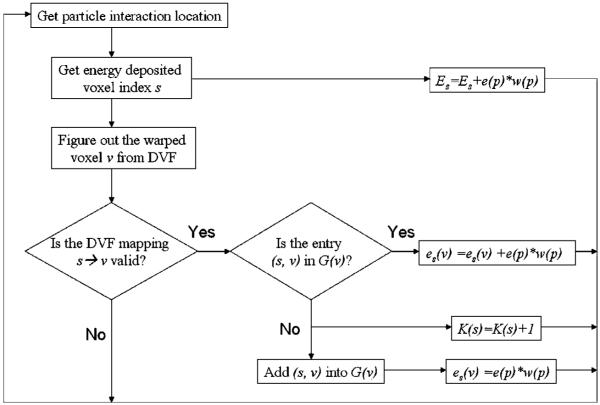
When the particle p interacts in voxel s in the source dose grid, its deposited energy e(p) multiplied by the particle’s weight w (p) is added to the total energy E_s deposited in this voxel. The particle’s energy deposition location is mapped to a voxel ν in the reference dose grid by the DVF, and the deposited energy e(p) weighted by w(p) is added to e_s(ν) which represents the energy deposited mapped from the source voxel s to the reference voxel ν. Through all the particle transport simulation and event mapping operations, a look back table G(ν) is established to record all the pairs of s and ν. The size of V(ν) is denoted by K(ν). The flowchart for updating these variables in Monte Carlo simulation is illustrated in figure 2.

Figure 2.

Flow of the EBDI method which updates mass and energy deposition mapping variables is based on the particle interaction location and its mapped position.

After all the particle transport simulations are done, each of E_s, e_s(ν) and K(ν) has been determined. As the ratio of e_s(ν) and E_s, the obtained parameter q_s(ν) combined with E_s and M_s can be used to perform the EBDI at the reference voxel ν as described by (2). Note that in the energy deposition event mapping process, each particle’s energy deposition location is taken as a mass mapping point and the same weight q_s(ν) is used to accumulate both the energy deposited and the mass. This approach avoids the additional mass mapping step required for EMCM, but it may sacrifice its computational precision. Mass mapping that should use equally spaced sampling points within each voxel is actually sampled at the unevenly distributed energy deposition locations, and this may cause 2% mass mapping errors in EBDI (see table 1). The number of the entries in the table G is less than k × H, where H is the dose grid size,and k = max{|G(ν)| : ν ∈ R}. Given any reference voxel ν, the number of its source voxels is small, and in our implementation, k is chosen to be 100. So, for a 100 × 100 × 100 dose grid, the table may contain 100 million entries which is not a challenge to most computers’ memory.

Table 1.

The mass and energy deposited calculated by DOSXYZnrc, EMCM, EBDI and TDI for the phantom in figure 3 where M, E and D represent mass, energy and dose, respectively. The energy deposited unit is μJ MU⁻¹ and mass is in the density of g cm⁻³

		DOSXYZnrc in source (y)	EMCM in reference (Y)	EBDI in reference (Y)	TDI in reference (Y)
Layer 8	M	0.5	1.5	1.478
	E	0.684	1.734	1.734
	D	1.368	1.156	1.173	1.221
Layer 9	M	2.0	1.0	1.022
	E	2.148	1.098	1.098
	D	1.074	1.098	1.074	1.074
Layer 12	M	2.0	1.0	1.031
	E	2.103	1.086	1.086
	D	1.052	1.086	1.053	1.052
Layer 13	M	0.5	1.5	1.469
	E	0.671	1.688	1.688
	D	1.342	1.125	1.149	1.197

In the current implementation, the validation of the DVF mapping shown in figure 2 is default to Yes, and we have not yet implemented a mechanism to discard particles’ deposited energy. However, this framework keeps the capability of discarding energy deposition due to any physical mass loss or DVF errors, thereby allowing more accurate dose mapping if mass replacement or loss in a voxel can be detected.

2.4. TDI

In TDI, image registration is performed from a reference image to a source image and the resultant DVF is used to warp the dose delivered on the source image to the reference image (Rosu et al 2005). In our implementation, each reference dose voxel is partitioned into 27 subvoxels, each mapped to a dose delivered source voxel with the DVF. The dose averaged on these source voxels will be assigned as a mapped dose to the reference voxel.

Since the image registrations in TDI and EMCM are performed in opposite directions, to validly compare their results, the DVFs utilized must be inversely consistent, i.e., the composition of their back-and-forth mappings should be an identity mapping. The implementation details of the method to create the inverse-consistent DVF is described in (Yan et al 2008). To allow comparison of the TDI with EMCM, the DVF used in TDI is generated from the EMCM’s DVF using the inverse-DVF generation technique.

2.5. Implementation and evaluation of dose mapping methods

The above-mentioned dose mapping methods are implemented in our in-house integrated Monte Carlo dose calculation system (Siebers et al 2002), which utilizes several components of the BEAMnrc/EGSnrc systems (Rogers et al 2007, Walters et al 2007). Source particles for the simulation are sampled from a previously commissioned rotationally symmetric phase space generated from a BEAM simulation for the 6 MV mode of a Varian Cl21EX treatment machine (Siebers et al 1999, Keall et al 2004). These particles are then transported through the treatment head and jaws using BEAMnrc (Rogers et al 2007). For IMRT test cases, a pseudo-MC method is utilized to transport particles through the MLC (Siebers et al 2002). For the patient case, CT images are converted to material–mass–density phantoms using the CTCREATE program where a 55 material ramp is used in the Hounsfield unit (HU)-to-density conversion (Siebers 2005, Dogan et al 2006). The resultant phantom is represented as a uniform dose grid of 4 × 4 × 4 mm³. Sufficient source particles are sampled from the initial phase-space file to result in a statistical precision of <1% in the dose at D_max in the source geometry with 4 × 4 × 4 mm³ voxels.

Particle transport in patient/phantom is simulated with a modified version of DOSXYZnrc (Walters et al 2007). In the modified version, energy deposition-related variables are updated during the particle transport simulation and those of the mass-related variables are created after the simulation. The scoring matrices are duplicated to hold values in both the source and reference images with their correlation variables created to track the mapping records. In DOSXYZnrc, the EXACT boundary crossing algorithm is employed, thus, single elastic scattering is used to cross the boundaries. ECUT and PCUT are set to 0.7 MeV and 0.01 MeV. XIMAX is 0.5 as default and ESTEPE is 25% except where explicitly specified.

Since the DVF mapping mimics tissue deformation, the Monte Carlo dose mapping method treats energy re-deposition as a natural extension of particle transport simulation. The statistical uncertainty of its mapped dose due to the stochastic energy deposition is defined by

$${\delta }_w\left(\nu \right)=\frac{1}{M_{\nu }^R}\sqrt{\frac{1}{N-1}\left\{\sum _{l\in L\left(\nu \right)}{\left({\mathrm{e}}^{\left(l\right)}\left(\nu \right)\right)}^2-\left(\sum _{l\in L\left(\nu \right)}{\mathrm{e}}^{\left(l\right)}\left(\nu \right)∕N\right)\left(\sum _{l\in L\left(\nu \right)}{\mathrm{e}}^{\left(l\right)}\left(\nu \right)∕N\right)\right\}}$$ (5)

where L(ν) is the set of all the particle interaction events mapped into the voxel ν, and N is the number of the independent histories. $M_{\nu }^R$ is the mapped mass in the voxel ν. The normalized uncertainty is

$${\sigma }_w\left(\nu \right)={\delta }_w\left(\nu \right)∕d_w\left(\nu \right),$$ (6)

where d_w (ν) is the mapped dose in the voxel ν, defined as the total mapped energy divided by the total mapped mass. Since both the dose and the uncertainty (5) have mass as their denominator, the normalized uncertainty defined by (6) is independent of mass mapping strategy. Consequently, the doses calculated by (1) and (2) have the same normalized statistical uncertainty, but their absolute uncertainties are determined by different mass mapping strategies.

For the evaluation of the resultant dose distributions, a χ²-correlation is introduced as

$${\chi }^2=\frac{1}{H}\sum _j{\left(\frac{d_1\left(j\right)-d_2\left(j\right)}{{\sigma }_1\left(j\right)+{\sigma }_2\left(j\right)}\right)}^2,$$ (7)

where d_i and σ _i, i = 1, 2, are the calculated dose and the statistical uncertainties from two dose mapping methods, respectively, and H is the dimension of the dose grid. This correlation quantifies the similarity of two dose sets with χ² ≤ 1 indicating a good agreement between the two datasets (Babcock et al 2008).

3. Tests and results

In this section, different dose mapping approaches presented above will be demonstrated using a deforming phantom and clinical CT images, and their dose differences are characterized by different metrics. The implementation of DOSXYZnrc for these approaches is validated with the numerical phantom under a given deformation map.

3.1. Validation of dose mapping methods on a deformable phantom

The purpose of this test is to verify that the mass and energy deposition mapping procedures implemented in the previous sections can be performed as expected on a numerical phantom with an analytically invertible deformation mapping. A 10 × 10 × 10 cm³ digital phantom that consists of 0.5 × 0.5 × 0.5 cm³ voxels is created. The phantom is converted to a material density matrix m(S) for the source image. Let y specify the voxel index in the source image and Y the voxel index in the fixed reference image. The material density of each voxel in the layers of y = 8–13 is specified in figure 3 and those in the other layers have their density equal to one. The voxels of y = 9, 12 are evenly split by a given DVF, that is, the displacement d_y=9 = −0.25 and d_y=12 = 0.25. Consequently, the density matrix m(W) of the warped phantom (the reference image) can be derived analytically from m(S) and the deformation map, and their results are shown in the right column of figure 3.

Figure 3.

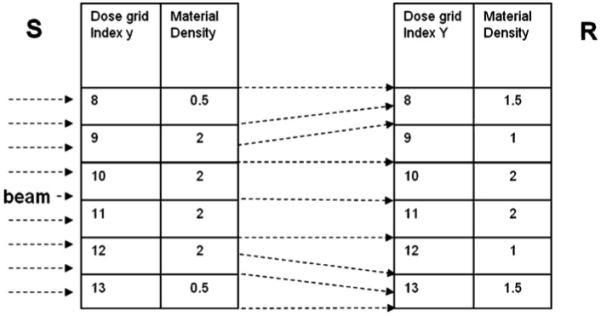
A heterogeneous phantom is deformed under a given map where the voxels of y = 9, 12 are evenly split and all the voxels with the same y index share the same displacement.

A 6 × 6 cm² 6 MV photon beam whose direction is perpendicular to the tissue deformation is directed from the left of the phantom.

Under the specified DVF mapping, the mass and energy deposited calculated by EMCM and EBDI in the reference image (Y) can be compared with those from DOSXYZnrc recorded in the source image (y). From figure 3, the mass in the voxel y = 9, 12 are evenly split to their neighbors. The masses mapped by EMCM and EBDI are validated through comparing their calculated values (table 1) with the analytical results listed in figure 3 (right). The mass precisions of EMCM are above 99.95%.

The energy deposited accuracy of EMCM is validated through the energy conservation condition, that is

$$\begin{array}{c}{E}_{Y=8}^{\mathrm{EMCM}}+E_{Y=9}^{\mathrm{EMCM}}=E_{y=8}^{\mathrm{DOSXYZ}\mathit{nrc}}+E_{y=9}^{\mathrm{DOSXYZ}\mathit{nrc}}=2.832,\hfill \\ E_{Y=12}^{\mathrm{EMCM}}+E_{Y=13}^{\mathrm{EMCM}}=E_{y=12}^{\mathrm{DOSXYZ}\mathit{nrc}}+E_{y=13}^{\mathrm{DOSXYZ}\mathit{nrc}}=2.774.\hfill \end{array}$$

The mapped energy deposited from EBDI is exactly equal to that from EMCM, consistent to the energy conservation, but their mapped masses are different, with 2.0% and 3.0% discrepancies at Y = 9 and Y = 12, respectively, for the EBDI calculated dose.

With the TDI, the reference voxels Y = 8 and Y = 13 have their dose evenly contributed from the source voxels y = 8, 9, and y = 12, 13, respectively. Consequently $D_{Y=8}^{\mathrm{TDI}}=\left(D_{Y=8}^{\mathrm{DOSXYZ}\mathit{nrc}}+D_{Y=9}^{\mathrm{DOSXYZ}\mathit{nrc}}\right)∕2=1.221$, $D_{Y=13}^{\mathrm{TDI}}=\left(D_{Y=12}^{\mathrm{DOSXYZ}\mathit{nrc}}+D_{Y=13}^{\mathrm{DOSXYZ}\mathit{nrc}}\right)∕2=1.197$. Compared with the known analytic solution, TDI has the dose errors of 6.4% at Y = 8 and 5.6% at Y = 13, respectively. This test has validated the implementation of the different mass and energy deposited mapping procedures with an analytically invertible DVF. The rest of this paper will focus on the use of the proposed dose mapping methods with DVFs derived from clinical CT images.

3.2. Convergence of EMCM

For the EMCM method, the mapped energy deposited is accumulated during the particle transport simulation. The mapped mass is determined by mapping the n³ subvoxels from the source to reference phantoms. The accuracy of the reinterpreted dose depends on the statistics of the MC simulation as well as the mass approximation. Different from the above well-designed DVF, those generated from DIRs may suffer from volumetric singularities which may affect the accuracy of the mapped dose. Since intensity driving image registrations often fail in low image-contrast regions, such as those encountered in areas surrounding the prostate, this section will evaluate the convergence of the proposed dose mapping method with image registrations performed between a region selected from two prostate CT images. These images were registered by ITK demons algorithm as described in Zhong et al (2008). For the sake of computational efficiency, the size of these images is reduced by removing the regions far from prostate. The obtained sub-images consist of 160 × 160 × 36 voxels whose volume is 0.97 × 0.97 × 3 mm³. The dose grid consists of 36 × 36 × 25 voxels, each of which is 4 × 4 × 4 mm³. A single 6 MV beam is set at a 30° angle for a 10 × 10 cm² open field. Note, although this reduced image set and single beam is clinically unrealistic, it provides a sufficient test to demonstrate the convergence of our method in low contrast regions.

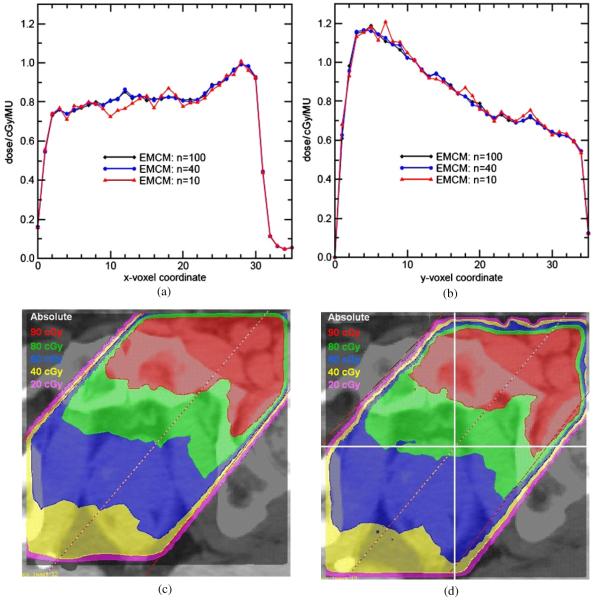
The test results show that the mass constructed by EMCM with n = 10 (1000 subvoxels) differs by as much as 7.7% from that with n = 100 (1 000 000 subvoxels). This mass error directly translates to a dose error. Figure 4 shows beam profiles for n = 10, 40 and 100, demonstrating the convergence with increasing n. Over the entire dose distribution, the average difference of n = 10 to n = 100 decreases from 2.1% to 0.56% and the χ² decreases from 1.83 to 0.18, as n increases to 40. The DOSXYZnrc calculated dose and the EMCM (n = 100) warped dose are shown in figures 4(c) and (d), respectively. The dose profiles in figures 4(a) and (b) cross the center of the dose region as illustrated in figure 4(d).

Figure 4.

Dose profiles calculated by EMCM with n = 10, 40 and 100, respectively, (a) X profiles and (b) Y profiles cross the center of the dose grid. (c), (d) The dose paintings of the original and EMCM warped dose distributions, respectively.

Note that if an insufficient number of points are used to determine the mass mapping, the distinction between these mass mapping points and particle energy deposition locations may cause some hot spots in the mapped dose profiles. Increasing the number n improves the precision of the mass mapping in the EMCM dose calculation, and consequently enhances the congruence between the mass and energy mappings. Theoretically, with a correct DVF map and a large mass sampling number n, this approach will interpret dose accurately on the reference dose grid. These EMCM convergence tests show that from n = 40 to 100, the dose difference is small. In the following discussion, we take EMCM with n = 100 as a standard to evaluate other dose mapping methods.

3.3. MC dose mapping on lung CT images

Dose mapping is a basic step in 4D IMRT which will be an important technique for the radiation treatment of lung cancer patients (Suh et al 2008). The purpose of this section is to compare the results of different dose mapping methods for a sample lung IMRT case. A 10 phase 4D CT image is employed with a free-breathing IMRT treatment plan developed on the inhale image with Pinnacle treatment planning system® (Philips Medical systems, Fitchburg, WI). The tumor size is about 2 cm in diameter and its center moves down about 2.5 cm from exhale to inhale. Image registrations are performed from exhale to inhale by the ITK demons algorithm. For this test, only the two phases of exhale and inhale are considered. Beam delivery is simulated on the exhale image, with the dose being mapped to the inhale image. The same phase space file after the DMLC simulation is used for all the following dose calculation methods to maximize the correlation in the results. Consequently, the normalized statistics of these simulations can be directly compared.

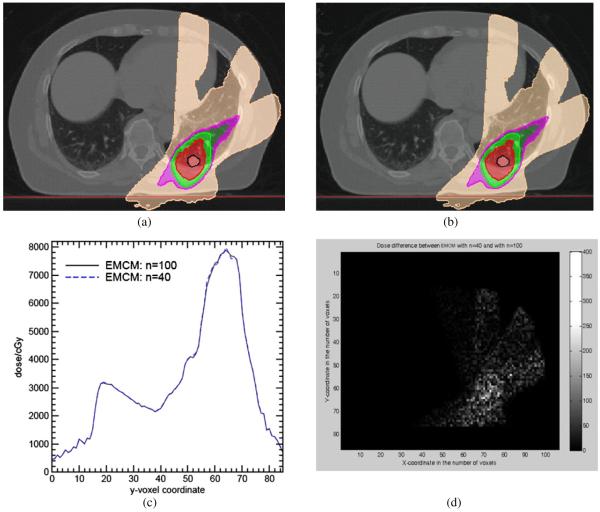
Each particle deposited energy and its associated mass are mapped to its target position in the inhale image by EMCM with n = 40, 100 using a DVF generated by the ITK demons algorithm. The mapped doses are loaded back to the treatment plan on the inhale image set as shown in figures 5(a), (b). Their profiles across the CTV region (X = 70, Z = 17) are illustrated in figure 5(c), and their absolute differences on a transverse slice are illustrated in figure 5(d). Compared with the result of n = 100, the dose calculated by EMCM with n = 40 is stable. The mean difference over the whole dose region in figure 5(d) is only 0.57%, and their overall χ² correlation is only 0.009.

Figure 5.

Dose distributions with dose calculated by EMCM at (a) n = 40 and (b) n = 100, respectively, with ITK demons DVF; (c) their Y dose profiles at X = 70 in the slice of Z = 17, and (d) their absolute differences (cGy) on a transverse slice.

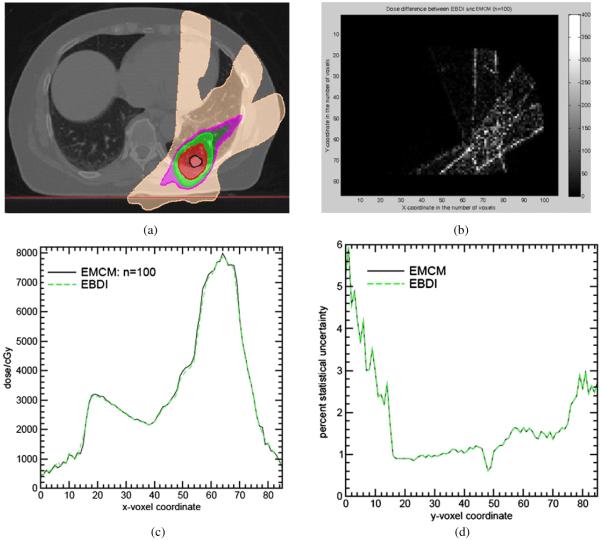
After verifying the convergence of EMCM, the dose distributions of EBDI (figure 6(a)) are compared with EMCM with n = 100. The 90% isodose regions (red) are smaller than that of EMCM (figure 5(b)). The absolute dose difference between EBDI and EMCM are shown in figure 6(b) with the mean difference 11.45 cGy out of the total dose 583 cGy averaged over the whole dose region. The overall χ² correlation between EBDI and EMCM is 0.042. From figure 6(b), it can be observed that a relatively large discrepancy appears at the beam penumbra as expected.

Figure 6.

(a) The dose distributions calculated by EBDI; (b) their differences from EMCM, (c) their Y dose profiles at X = 70 in the slice of Z = 17; (d) statistical uncertainties of EMCM and EBDI. (Note: given a DVF, EMCM and EBDI have the same statistical uncertainty.)

Figure 6(d) illustrates the statistics of doses calculated by EMCM and EBDI with the DVFs from the ITK demons algorithm. The same dose statistical curves are generated by the two algorithms as expected. In general, the 4D Monte Carlo simulations are statistically stable and their statistical uncertainties are less than 2% as shown in figure 6(d).

EMCM (n = 40) and EBDI are compared with EMCM at n = 100, and their DVHs are illustrated in figures 7(a) and (b). Their average deviations from EMCM (n = 100) in the whole dose region are 3.3 cGy (0.57%) and 11.45 cGy (1.96%), respectively.

Figure 7.

The DVHs of EMCM with n = 100 are compared with the DVHs of: (a) EMCM with n = 40; (b) EBDI and (c) TDI. The dose difference between EMCM and trilinear dose interpolation is shown in (d)

TDI is also employed to warp the dose calculated by DOSXYZnrc on the exhale image. With a DVF generated by the self-consistent inversing technique, TDI warps the DOSXYZnrc calculated dose from the exhale image to the inhale image. The mean difference between the doses mapped by EMCM and TDI is 42.7 cGy or 7.32% with respect to the total dose 583 cGy averaged over the whole dose region. The largest difference again appeared at beam edges as shown in figure 7(d). Note that the DVFs used in TDI and EMCM are in opposite directions. However, the inconsistency between the two DVFs is minimized by using the self-inverse consistent DVF generation technique.

The error observed for the lung IMRT case is from mapping the dose from one breathing extreme (exhale) to the other (inhale). This is where the maximum DIR and dose mapping error is expected. Including additional breathing phases and summing all of the doses mapped to inhale would likely reduce the overall error. The extent of this needs to be quantified in future studies.

4. Discussion

Heterogeneity exists in both mass and energy deposition event distributions. Traditional DIMs cannot cope with the two types of heterogeneities, simultaneously. The separation of the radiation transport and dose scoring grids during Monte Carlo particle transport simulation allows the two heterogeneous distributions to be mapped independently on the reference image. Given a DVF, the EMCM method maps the energy deposited from the particle interacted location to a reference voxel during the particle transport simulation, and then determines the warped mass in each reference voxel from all the source voxels using the equi-space mass mapping approach. To prevent any dose discrepancy caused by the incongruence of the two mappings, the number of subvoxels partitioned from each source voxel must be large enough so that there is a number of sampling points which are mapped to the same reference voxel as each particle’s energy deposition location is mapped to. This allows EMCM to accurately interpret the warped dose defined on deforming anatomies for different physiological cases.

When the underlying physical deformation has mass conserved, the dose mapped by EMCM, represented in (1), is exactly equal to an analytic solution. However, if mass is not conserved during the physical deformation, neither the traditional dose interpolation nor the EMCM takes into account the lost mass in the dose mapping, and consequently, they will have a similar dose discrepancy. For example, suppose two adjacent voxels A and B are mapped to a target voxel C, but the mass in voxel A is lost. TDI still assigns the warped dose in C by d_C = (d_A + d_B)/2. In this case, EMCM interprets the warped dose as d_C = (M_Ad_A + M_Bd_B)/(M_A + M_B). If M_A = M_B, EMCM also has the warped dose d_C = (d_A + d_B)/2. Consequently, EMCM will have the same error as TDI. This example shows that neither TDI nor the current implementation of EMCM can solve the mass loss-related issue during dose mapping. However, when the number of voxels which lose mass during a deformation is limited, then EMCM is more accurate than other DIMs, especially for intra-fractional motion.

For dose calculated by convolution/superposition methods, dose is imputed to a point, instead of to a voxel volume, and there is no energy distribution available within each voxel. Consequently, DIMs must be adopted for its dose warping. However, TDIs generally suffer from inherent discrepancy. Compared with EMCM, for our test cases, it has 6.0% errors for dose mapped on an analytically deformed phantom and 7.3% errors in a lung patient’s IMRT case. In this study, we employed a self-consistent DVF generation technique so the side effect of their DVF difference on the mapped doses is minimized. EBDI is similar to the TDI, but they have thousands of sampling points in each voxel for energy and mass mapping, respectively, so they have much higher sampling resolutions than other DIMs such as the center of mass mapping (one sampling point) or octant-based TDI (eight sampling points).

The statistical precision of the 4D Monte Carlo dose calculation, given by (5) and (6), is inherited from the original 3D MC simulation. Theoretically, the 4D precision could be compromised by the DIR. However, with the DVF generated by the demons algorithm, the statistical precision is almost unchanged as shown in figure 6(d) where the statistical uncertainty of the 3D MC simulation was set to 1%. In our present, unoptimized implementation, EBDI requires about 10% more computation time than the conventional 3D DOSXYZnrc. EMCM’s energy event mapping is same as EBDI, but it requires an extra procedure to map the mass. In out tests, for a 106 × 86 × 35 dose grid with each voxel partitioned into 125 000 subvoxels, the mass mapping takes about 45 min. However, like DIR, mass mapping does not need to be performed for each beam, and it is required only once for each deformation case.

Like DIMs, the implemented Monte Carlo dose mapping framework may have dose mapping errors if the underlying tissue deformation is mass or energy inconsistent. To address this issue, the mass physically changed or replaced must be quantified so that its associated particles’ energy can be processed correctly during the mass and energy mapping processes. In the developed 4D MC framework, the mechanism of discarding a particle’s energy deposited and its associated mass has been implemented, and its further analysis and validation will be performed in future studies.

5. Conclusion

In this study, we developed a Monte Carlo dose mapping framework to accurately interpret the dose on a deforming anatomy. This method does not need to detect the irregular boundary of each deformed voxel during particle transport simulation. With this system, users may calculate 4D dose distributions to account for intra-fraction organ deformation and perform daily dose accumulation for clinical adaptive planning and for treatment outcome evaluation.