Probabilistic Model for Listeria monocytogenes Growth during Distribution, Retail Storage, and Domestic Storage of Pasteurized Milk

Abstract

A survey on the time-temperature conditions of pasteurized milk in Greece during transportation to retail, retail storage, and domestic storage and handling was performed. The data derived from the survey were described with appropriate probability distributions and introduced into a growth model of Listeria monocytogenes in pasteurized milk which was appropriately modified for taking into account strain variability. Based on the above components, a probabilistic model was applied to evaluate the growth of L. monocytogenes during the chill chain of pasteurized milk using a Monte Carlo simulation. The model predicted that, in 44.8% of the milk cartons released in the market, the pathogen will grow until the time of consumption. For these products the estimated mean total growth of L. monocytogenes during transportation, retail storage, and domestic storage was 0.93 log CFU, with 95th and 99th percentiles of 2.68 and 4.01 log CFU, respectively. Although based on EU regulation 2073/2005 pasteurized milk produced in Greece belongs to the category of products that do not allow the growth of L. monocytogenes due to a shelf life (defined by law) of 5 days, the above results show that this shelf life limit cannot prevent L. monocytogenes from growing under the current chill chain conditions. The predicted percentage of milk cartons—initially contaminated with 1 cell/1-liter carton—in which the pathogen exceeds the safety criterion of 100 cells/ml at the time of consumption was 0.14%. The probabilistic model was used for an importance analysis of the chill chain factors, using rank order correlation, while selected intervention and shelf life increase scenarios were evaluated. The results showed that simple interventions, such as excluding the door shelf from the domestic storage of pasteurized milk, can effectively reduce the growth of the pathogen. The door shelf was found to be the warmest position in domestic refrigerators, and it was most frequently used by the consumers for domestic storage of pasteurized milk. Furthermore, the model predicted that a combination of this intervention with a decrease of the mean temperature of domestic refrigerators by 2°C may allow an extension of pasteurized milk shelf life from 5 to 7 days without affecting the current consumer exposure to L. monocytogenes.

L. monocytogenes is an important safety concern for the dairy industry. Several listeriosis outbreaks have been associated with the consumption of dairy products, including pasteurized milk (13, 22). An effective control of L. monocytogenes in pasteurized milk should be based on the selection of raw milk and the controls of the processing, packaging, distribution, and storage conditions. In general, the pathogen is effectively controlled during pasteurization. However, its presence in the finished product is possible as a result of postpasteurization contamination from sources in the plant environment. Considering that the levels of postpasteurization contamination are usually very low, the extent of L. monocytogenes growth during distribution, retail storage, and domestic storage is of major significance for the safety status of pasteurized milk at the time of consumption.

The growth of L. monocytogenes during distribution and storage of pasteurized milk can be evaluated using the available predictive models. During the last decade, a large number of mathematical models for L. monocytogenes growth have been published (9, 11, 16, 19, 21, 24, 26, 31, 38), and some of them have been targeted to pasteurized milk (1, 40, 49). However, since the available data show that conditions that prevail during the chill chain vary significantly (8, 17, 23, 27, 28, 34, 44, 45, 48), the value of a deterministic application of these models as a tool in safety management of pasteurized milk would be limited.

In recent years the need for taking into account the variabilities of the various factors in predictive microbiology has been increasingly recognized, leading to a more sophisticated modeling approach called probabilistic or stochastic modeling. The main characteristic of probabilistic modeling is the specific quantification of variabilities using probability distributions for the input data rather than point estimates. The importance of characterizing variability was stressed by Nauta (41), who illustrated the differences in decisions that could result if variability is ignored. Probabilistic modeling is being used with increasing frequency in the area of food safety. It has been extensively applied in quantitative microbial risk assessments (12, 18, 20), in quality and safety management systems (25, 30, 32), and recently for more specific topics, such as the evaluation of the effects of food processing (39) and the compliance of food products to safety criteria set by regulations (33).

In the present study a probabilistic modeling approach was applied for evaluating the growth of Listeria monocytogenes in pasteurized milk from production to the time of consumption based on a Monte Carlo simulation. The objectives of the study were (i) to estimate the growth of the pathogen at the various stages of the chill chain, including transportation to retail, retail storage, and domestic storage, (ii) to analyze the importance of the chill chain factors, (iii) to evaluate the effects of selected intervention scenarios related to the improvement of the chill chain and handling conditions, and (iv) to evaluate the effect of a potential extension of milk shelf life on the growth of Listeria monocytogenes.

MATERIALS AND METHODS

Collection of data on chill chain conditions of pasteurized milk.

A survey on the time-temperature conditions of the Hellenic chill chain of pasteurized milk, including transportation to retail, retail storage, and domestic storage, was performed.

Transportation to retail.

Time-temperature data during transportation of pasteurized milk from a distribution center of a large Greek dairy company in Athens to retailers were collected. The temperature in trucks was recorded using electronic temperature-monitoring data loggers (Cox tracer; Cox Technologies, Belmont, NC). Temperature was recorded for five working days in 12 to 15 different trucks for each day (n = 83). Transportation time was monitored by using a form in which the driver of the truck completed the time and quantity (number of cartons) in every delivery. In total, the transportation times of 64,904 milk cartons were recorded.

Retail refrigeration storage.

The temperatures of retail cabinets for dairy products were recorded for 5 to 7 days by using electronic temperature-monitoring data loggers. In total, 60 retail cabinets from supermarkets in five different cities (Athens, Patra, Iraklio, Thessaloniki, and Larisa) in Greece were tested. The storage time of pasteurized milk in retail was discussed with experts from the Greek dairy company.

Domestic refrigeration storage.

One hundred domestic refrigerators were surveyed in northern Greece. The data loggers were programmed to record the temperature every 5 min for 24 h and were located at the top, middle, lower, and door shelves of a refrigerator. In addition, the investigators interviewed a family representative and completed a questionnaire in order to collect information on (i) characteristics of participants (age, profession, income, number of family members, and region), (ii) the position in the refrigerator where they store the milk, and (iii) the storage time of pasteurized milk in the domestic refrigerator.

Model for L. monocytogenes growth in pasteurized milk.

Growth of L. monocytogenes in pasteurized milk was calculated using a three-phase linear model (10): log(N_t) = log(N₀) for t ≤ lag; log(N_t) = log(N₀) + [μ_max/ln(10)](t − t_lag) for t_lag < t < t_max; and log(N_t) = log(N_max) for t ≥ t_max. For these equations, N_t is the population density at time t (in CFU/g); N₀ is the initial population density (in CFU/g); N_max is the maximum population density (in CFU/g); t is the elapsed time (in h); t_lag is the time when the lag phase ends (in h); t_max is the time when the maximum population density is reached (in h); and μ_max is the maximum specific growth rate (expressed as h⁻¹).

A maximum population density of 10^8.5 CFU ml⁻¹ was assumed (49), while the maximum specific growth rate at a certain temperature was calculated based on the square root model for the effect of temperature developed by Xanthiakos et al. (49): (μ_max)^½ = 0.024(T − T_min), where T is the temperature and T_min is the theoretical minimum temperature for growth. In order to take into account the strain variability in the latter model, a normal distribution N(−2.47, 1.26) was used for T_min, as proposed by Pouillot et al. (43). The lag time at a certain temperature was calculated based on the physiological state parameter h₀. The latter parameter characterizes the amount of “adaptation work” that the cells have to perform in order to adapt to their new environment and is calculated from the product of μ_max and the lag (5). In the present work an h₀ value of 1.34 was used, based on the findings of Xianthiakos et al. (49): h₀ = μ_max lag ⇒ lag = [1.34]/[0.024(T − T_min)].

The prediction of growth under changing storage temperatures was based on the time-temperature conditions of the chill chain, T_t, in conjunction with the square root model for the estimation of the “momentary” μ_max and the cumulative approach for calculating the total lag, as presented by Koutsoumanis (29): 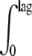(1/lag_T)dt = 1 ⇒ 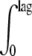[0.024(T_t − T_min)/1.34]dt = 1, where lag is the total lag and lag_T is the lag time assuming a constant temperature time interval, dt.

Probabilistic modeling approach.

The time-temperature data collected from the chill chain surveys were fitted by various distributions using @RISK 4.5.2 (Palisade Corporation, Newfield, NY). The goodness of fit was evaluated using the χ² test. The best-fitted distributions describing the chill chain conditions during transportation, retail storage, and domestic storage were used as an input to the growth model described in the previous section. The concentration of L. monocytogenes in pasteurized milk at the time of consumption was calculated using the Monte Carlo simulation technique with 10,000 iterations, using the @RISK 4.5.2 software.

An importance analysis was also performed to provide a quantitative measure for identification of the most important factors of the chill chain affecting the concentration of L. monocytogenes in pasteurized milk at the time of consumption. The importance analysis was performed using rank correlations based on Spearman rank correlation coefficient calculations. With this analysis, the rank correlation coefficient is calculated between the selected output variable and the samples for each of the input distributions.

Based on the developed model, several intervention scenarios related to the improvement of the chill chain were evaluated. The tested interventions were introduced to the model by appropriate adjustment of the distributions describing the respective chill chain factor, and the effect on growth of L. monocytogenes in pasteurized milk was evaluated by running a Monte Carlo simulation with the new distributions.

RESULTS AND DISCUSSION

Mapping the chill chain of pasteurized milk.

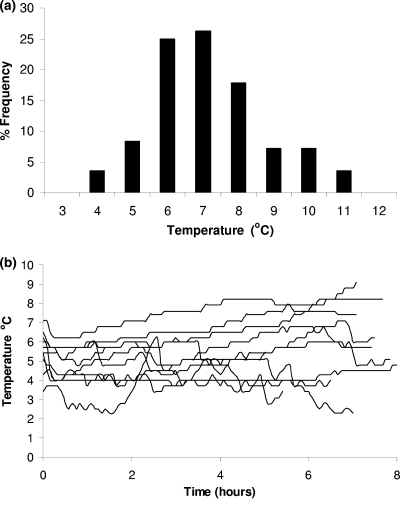
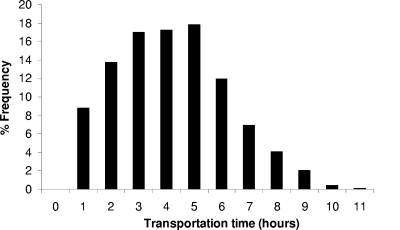
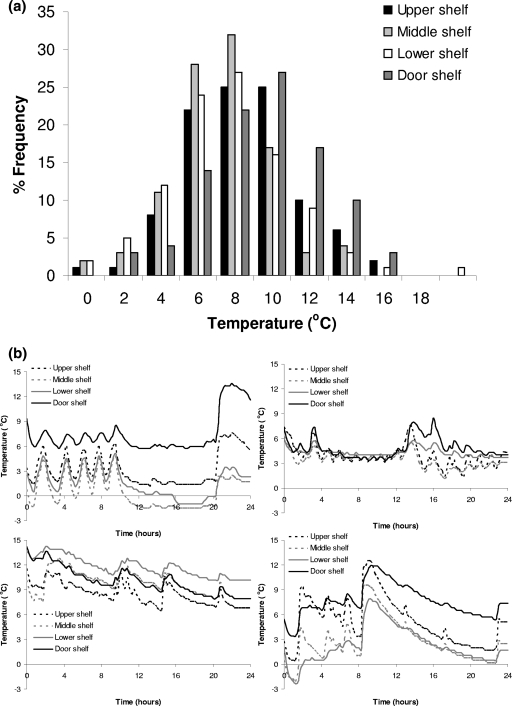
The chill chain data were collected through an extensive survey of time and temperature conditions and consumer handling practices of pasteurized milk during transportation to retail, retail storage, and domestic storage. The distribution of the mean temperature together with 10 representative temperature profiles during transportation are shown in Fig. 1a and b, respectively. The temperature in the truck during transportation ranged from 3.6 to 10.9°C, with a mean value of 6.7°C, median of 6.5°C, and standard deviation 1.6°C. The transportation time (Fig. 2) ranged from 0.2 to 10.2 h, with an overall mean of 3.7 h, median of 3.6 h, and standard deviation of 2.0 h. Although the conditions during transportation depend on the distribution system of each company, the data collected in this study can be characterized as representative, since the majority of pasteurized milk distributors are large-scale dairy firms. In general, time-temperature conditions during transportation showed relatively high variability, but the transportation time was rather short (<12 h) in all cases.

FIG. 1.

Distribution of mean temperature (a) and representative temperature profiles (b) in trucks during transportation of pasteurized milk.

FIG. 2.

Distribution of transportation times of pasteurized milk.

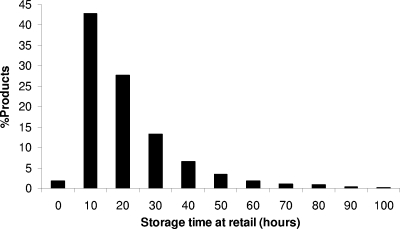
The distribution of temperatures in retail cabinets for dairy products is presented in Fig. 3a. Retail storage temperature ranged from 0 to 11.7°C with a mean of 4.98°C, median of 5.44°C, and a standard deviation of 2.90°C. The available data on retail storage temperatures in the literature, although limited, are in agreement with the results of the present survey. Pierre (42) reported a mean temperature of 4°C in retail refrigerators in France, while Likar and Jevsnik (37) examined 1,286 retail refrigerators in Slovenia and found that the temperature ranged between −2.2 and 12.2°C with an average value (weighted mean) of 4.6°C. In the present study, a significant variation of temperature with time was also observed in retail cabinets. As shown in the representative temperature profiles of Fig. 3b, in most cases periodic upshifts of temperature occurred and were probably due to the defrost systems of the refrigerators. Based on expert opinion from the Greek dairy industry, the storage time of pasteurized milk cartons at retail locations can be described using a log normal distribution with a mean of 20 h and a standard deviation of 20 h, which is truncated on the right side at 96 h. Truncation was based on the fact that the shelf life of fresh pasteurized milk in Greece is by law 5 days (120 h) after pasteurization, and the products are removed from the market 1 day before the expiration date. A simulation of retail storage time distribution based on the latter assumption is shown in Fig. 4. Based on this, 50% of the cartons remain at the retail market for less than 14 h, while the 5th and 95th percentiles of retail storage time are 3.6 and 51.5 h, respectively.

FIG. 3.

Distribution of mean temperature (a) and representative temperature profiles (b) in retail cabinets for dairy products.

FIG. 4.

Simulation of pasteurized milk storage time at retail sites.

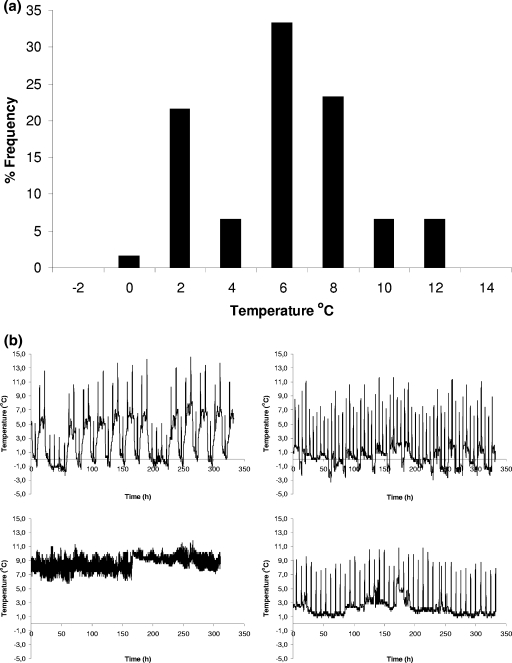
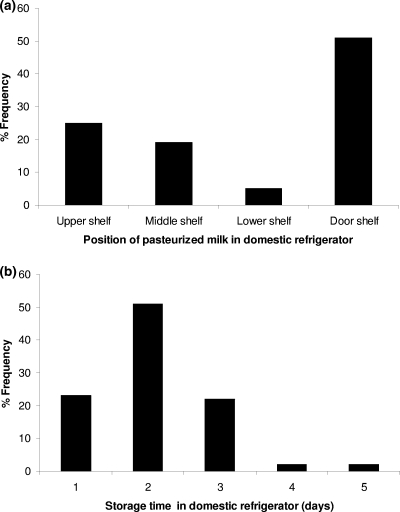
The results of the survey on the temperature of domestic refrigerators are presented in Fig. 5 and Table 1. Significant differences (P < 0.05) in temperatures between the different positions of the refrigerators tested were observed (Table 1). The highest temperature was observed at the door shelf (8.4°C), followed by the upper shelf (7.6°C), while the middle (6.3°C) and lower (6.7°C) shelves were the coldest positions. The latter observation is in agreement with other published surveys. Bakalis et al. (4) also found the warmest place was the refrigerator door. Laguerre and Flick (35) reported that most of the time the higher temperatures were observed at the top of the refrigerators; however, in their study the door shelf was not tested. In general, the temperatures of domestic refrigerators observed in the survey of the present study were similar to those reported in several European surveys. The results of nine survey studies conducted in the United Kingdom, France, Ireland, and Greece (2, 8, 17, 23, 27, 28, 35, 44, 45, 48), with a total of 1,171 refrigerators tested, showed a weighted mean temperature of 6.4°C with 64.1% of the refrigerators operating at a temperature of >5°C. It needs to be noted that domestic storage temperatures in Europe are significantly higher than in the United States. In a survey of 939 domestic refrigerators in the United States (3) the mean temperature was 4°C, while in only 27.5% of the tested refrigerators did the temperature exceed 5°C. The results for the temperatures at the different positions of domestic refrigerators are very important for pasteurized milk, considering that the door shelf, where the higher temperatures were observed, is the most frequent position used for storage of this product. Indeed, the answers of the consumers related to the position where they usually stored pasteurized milk (Fig. 6a) showed that in total 76% of the consumers stored the milk in the door (51%) or the upper shelf (25%) of the refrigerator, while only 24% of the consumers used the colder middle (19%) and lower (5%) shelves. Consumers' answers related to storage time showed that most of them (96%) stored pasteurized milk in the refrigerator for up to 3 days (Fig. 6b).

FIG. 5.

Distribution of mean temperature (a) and representative temperature profiles (b) in domestic refrigerators.

TABLE 1.

Temperature data for domestic refrigerators

Statistical parameter	Temp (°C) for indicated shelf locationa
	Upper	Middle	Lower	Door
Mean	7.57A	6.31B	6.69B	8.40C
SD	2.95	2.66	3.29	3.00
Minimum	−1.77	−0.70	−2.69	1.18
Maximum	14.47	13.03	18.08	14.94
Median	7.60	6.29	6.40	8.32

^aValues with different superscript capital letters are significantly different from each other (P < 0.05).

FIG. 6.

Consumer answers regarding the position (a) and storage time (b) of pasteurized milk in domestic refrigerators.

Probabilistic modeling of L. monocytogenes growth in pasteurized milk.

For prediction of L. monocytogenes growth in pasteurized milk, the square root model developed by Xanthiakos et al. (49) was used. The model (see Materials and Methods) was targeted to pasteurized milk (developed based on data from pasteurized milk) and has been successfully validated under both static and dynamic temperature conditions, showing a better performance than other available models developed in laboratory media (49).

Several investigations have demonstrated the growth variation among L. monocytogenes strains (6, 7, 36). The strain effect is an important source of microbial growth variability (14), and thus it should be taken into account in a probabilistic growth modeling approach. In order to take into account growth variations among strains in the present study, the T_min parameter of the square root model was described with a normal distribution, N(−2.47, 1.26). This variability of T_min was estimated by Pouillot et al. (43) from 124 growth curves of L. monocytogenes in milk and using Bayesian inference. The mean value of the above distribution was close to the T_min value (−2.32°C) reported by Xianthiakos et al. (49).

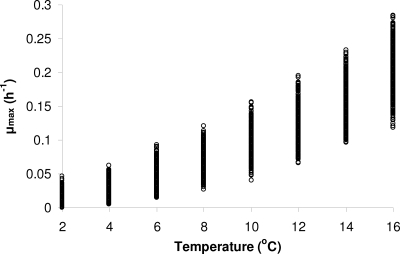
The effect of storage temperature on the μ_max of L. monocytogenes in pasteurized milk predicted by the square root model described above is presented in Fig. 7a. As shown in the figure, the description of the model parameter T_min with a distribution results in variation of the predicted μ_max at each storage temperature, representing the variability of the kinetic behavior among strains of L. monocytogenes. It needs to be noted that based on this approach the variation of the predicted μ_max is affected by the storage temperature. For example, the coefficient of variation of the predicted μ_max increases from 13.8% at 16°C to 53.8% at 2°C. This is in agreement with the kinetic behavior we have observed for other pathogens, showing that strain variability increases as the growth environment becomes more stressful (data not shown). Growth variation among strains refers not only to the growth rate but also to the lag time (7, 36). With the model used in this study, the variation of μ_max results in a corresponding variation of lag time, since the latter is predicted based on the ratio between the physiological state parameter h₀ and μ_max.

FIG. 7.

Effects of storage temperature and strain variability on the maximum specific growth rate of L. monocytogenes in pasteurized milk, predicted by the square root model (see text). Values for each temperature were calculated using a Monte Carlo simulation (1,000 iterations).

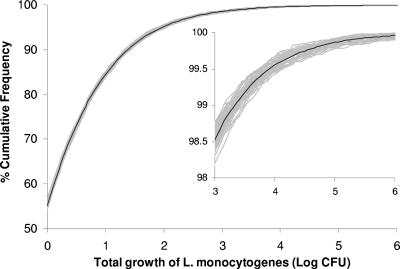
The chill chain data obtained from the surveys were described with the appropriate distributions (Table 2) and used as an input to the growth models (see the equations in Materials and Methods) in order to estimate the total growth of L. monocytogenes in pasteurized milk from production to the time of consumption by using a Monte Carlo simulation. The cumulative frequency of the predicted total growth of L. monocytogenes in pasteurized milk during transportation, retail storage, and domestic storage is shown in Fig. 8. The model predicted growth of the pathogen in 44.8% of milk cartons. For these products the estimated mean total growth of L. monocytogenes was 0.93 log CFU, with 95th and 99th percentiles of 2.68 and 4.01 log CFU, respectively. The total growth, which was used as the output of the model, is the difference between the initial concentration and the concentration at the time of consumption, and it could be translated as the concentration at the time of consumption in log CFU per ml or per 1-liter carton, assuming an initial contamination level of 1 cell per ml or per 1-liter carton (−3 log CFU/ml), respectively.

TABLE 2.

Pasteurized milk chill chain variables used as model inputs

Variable	Description	Units	Distributional assumption(s)
TT	Temp during transportation to retail	°C	Normal (6.66; 1.64)
tT	Transportation time	h	Weibull (1.98; 4.33; shift [0.096])
TR	Retail storage temp	°C	Normal (4.98; 2.9)
tR	Retail storage time	h	Log normal (20; 20; truncate [96])
PD	Position in domestic refrigerator		Discrete (1\2\3\4; 0.25\0.19\0.05\0.51)a
TD-U	Domestic storage temp (upper shelf)	°C	Normal (7.57; 2.95)
TD-M	Domestic storage temp (middle shelf)	°C	Normal (6.31; 2.66)
TD-L	Domestic storage temp (lower shelf)	°C	Normal (6.69; 3.29)
TD-D	Domestic storage temp (door shelf)	°C	Normal (8.40; 3.00)
tD	Domestic storage time	h	Cumulative (0; 120; 0\24\48\72\96\120; 0\0.23\0.74\0.96\0.98\1; truncate [120-tT-tR])

^aValues are for the upper, middle, lower, and door shelves, respectively.

FIG. 8.

Cumulative frequency of the total growth of L. monocytogenes in pasteurized milk from production to the time of consumption. The gray lines show results from 50 simulations (10,000 iterations each), and the black line shows the mean cumulative frequency.

According to EU regulation 2073/2005, pasteurized milk produced in Greece belongs to the category of products which do not support growth of L. monocytogenes, due to a shelf life of 5 days. As shown in Fig. 8, however, the present model predicted that in almost half of the milk cartons released in the market the pathogen will grow during the period from production to consumption. These results indicate that a limit of 5 days for the shelf life cannot ensure stopping L. monocytogenes growth in pasteurized milk under current chill chain conditions. It needs to be noted, however, that the probability of growth of L. monocytogenes during the shelf life is strongly affected by the lag phase, which depends on the physiological state of the cells that contaminated the product (15, 47). In the present work, a constant value of the physiological state parameter was used in the model, which was derived from a study with artificially contaminated cells (49). The “true” physiological state, however, is expected to vary depending on the environment in which the cells are exposed before contamination. Information on the “true” physiological state and its variability requires studies on the growth of naturally contaminated L. monocytogenes in milk, which are not available.

The probabilistic model can be used to estimate the probability of exceeding the safety criterion of EU regulation 2073/2005 (100 cells/ml) for L. monocytogenes, assuming a certain level of initial contamination. The simulation results showed that the percentage of cartons initially contaminated with 1 cell per 1-liter carton (−3 log CFU/ml) in which the concentration of the pathogen at the time of consumption exceeded the safety criterion was 0.14%. In fact, this percentage refers to products in which the total growth of the pathogen exceeded 5 log CFU. The probability of exceeding the safety criterion, however, depends on the initial contamination level (Table 3). For example, an increase in the initial contamination from 1 to 100 cells per 1-liter carton results in a corresponding increase in the number of cartons exceeding the safety criterion, from 0.14 to 1.47%. Nevertheless, considering that the initial concentration of L. monocytogenes in contaminated pasteurized milk is expected to be very low (18, 20), these results indicate that in general the level of noncompliance to the safety criterion for this product is low, mainly due to the its limited shelf life.

TABLE 3.

Effects of initial contamination (at packaging) on probability of L. monocytogenes level exceeding the safety criterion (100 cells/ml) in pasteurized milk at time of consumption

Initial contamination (at packaging stage)		Meana (SD) probability of exceeding safety criterion at time of consumption
No. of cells/1-liter carton	Log CFU/ml
1	−3	0.0014 (0.0003)
5	−2.3	0.0032 (0.0005)
10	−2	0.0045 (0.0006)
50	−1.3	0.0104 (0.0009)
100	−1	0.0147 (0.0012)
500	−0.3	0.0339 (0.0017)
1,000	0	0.0486 (0.0021)

^aMeans of 50 simulations with 10,000 iterations each.

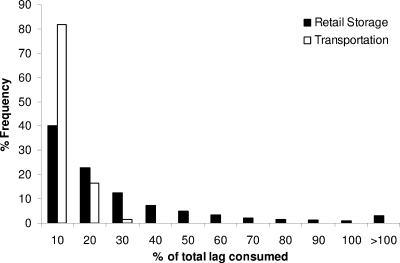
Moreover, the structure of the developed probabilistic model allows the evaluation of L. monocytogenes growth in pasteurized milk during the each stage of the chill chain (transportation, retail storage, and domestic storage) separately. The estimated probability of growth during milk transportation was 0, indicating that the time-temperature conditions of this stage do not allow the pathogen to pass the lag phase. The lag time consumed during transportation ranged from 0 to 54.7% of the total lag, with a mean of 6.4% (Fig. 9). During retail storage the percentage of total lag consumed ranged from 0 to 51% with a mean value of 23.1% (Fig. 9). Based on the model used (the cumulative approach of Koutsoumanis [29]; see Materials and Methods), L. monocytogenes will start growing in a milk carton during retail storage when the sum of the percentage of total lag consumed during transportation and retail storage exceeds 100%. The estimated percentage of cartons allowing growth during retail storage was 3.2%, while the mean and the 95th and 99th percentiles of the predicted growth in these products were 0.59, 1.89, and 3.03 log CFU, respectively. The results of the Monte Carlo simulation showed that the majority of the total growth of L. monocytogenes during transportation, retail storage, and domestic storage occurs during the last stage of the chill chain. Indeed, the estimated percentage of cartons allowing growth during domestic storage was 44.5%. The mean growth of the pathogen in the latter products was 0.87 log CFU with 95th and 99th percentiles of 2.53 and 3.90 log CFU, respectively.

FIG. 9.

Percentages of total lag time of L. monocytogenes that occur during transportation and retail storage of pasteurized milk.

Importance analysis: evaluation of potential intervention and shelf life extension scenarios.

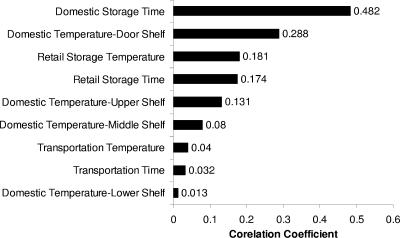
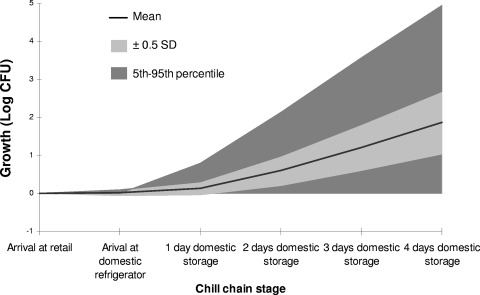
Figure 10 shows a Tornado graph with the Spearman rank correlation between the estimated concentration of L. monocytogenes in pasteurized milk at the time of consumption and the chill chain factors used in the model. Tornado graphs provide a pictorial representation of the sensitivity analysis of the model and illustrate the degree to which the model output is affected by the individual input variables within the model (46). In this study, the total growth of the pathogen during the chill chain was most sensitive to the domestic storage time. This can be also seen in Fig. 11, which presents the total growth of the pathogen and its variance at the various stages of the chill chain. The mean growth of L. monocytogenes during the first day of domestic storage is 0.12 log CFU and increases to 0.46, 0.61, and 0.66 log CFU for the second, third, and fourth days of storage, respectively. The second most important factor was the temperature at the door shelf of the domestic refrigerator, which was found to be higher than the other positions, while this shelf is most frequently used for storage of pasteurized milk. The time-temperature conditions during retail storage were also important, with a correlation coefficient above 0.15. Lower correlations (<0.05) were observed for transportation temperature and time and the temperature of the lower shelf, mainly due to the limited transportation period and the rare use of the lower shelf for storage of pasteurized milk.

FIG. 10.

Spearman rank correlation between the estimated concentration of L. monocytogenes in pasteurized milk at the time of consumption and the chill chain factors used in the model.

FIG. 11.

Growth of L. monocytogenes in pasteurized milk at various stages of the chill chain.

The results of the importance analysis can be used as the basis for the identification of effective intervention strategies for controlling the growth of L. monocytogenes in pasteurized milk. In this study the developed probabilistic model was applied to evaluate the effects of potential interventions in the chill chain on the total growth of L. monocytogenes in pasteurized milk as they related to the improvement of the retail and domestic storage conditions. The following three intervention scenarios were evaluated: intervention I, better control of retail storage temperature, which was introduced to the model by changing the distribution for retail storage temperature from normal (4.98; 2.9) to normal (4.00, 1.5); intervention II, excluding the door shelf from domestic storage of pasteurized milk (changing the distribution for the position in domestic refrigerators from discrete (1\2\3\4; 0.25\0.19\0.05\0.51) to discrete (1\2\3; 0.51\0.39\0.10); intervention III, a combination of intervention II with a decrease of the mean domestic temperature by 2°C (reducing the mean of the distributions for upper, middle, and lower shelf temperatures by 2°C).

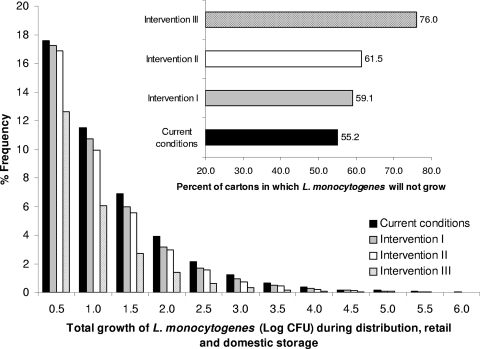
Figure 12 shows the effects of the tested interventions in comparison to the current chill chain conditions. Under the current chill chain conditions, 44.8% of cartons allow growth, while in 1.51% of these products the total growth of the pathogen exceeds 3 log CFU. Intervention I resulted in a limited reduction of the total growth. Products allowing growth were reduced to 40.9%, and the percentage of those exceeding 3-log CFU growth was reduced to 1.13% (25.4% reduction compared to current conditions). Excluding the door shelf from domestic storage (intervention II) was more effective, with cartons allowing growth reduced to 38.5% and those exceeding 3-log CFU growth to 0.90% (40.4% reduction). When the latter intervention was combined with a decrease of the mean domestic temperature by 2°C (intervention III), the cartons allowing growth were reduced to 24.0%, with L. monocytogenes total growth exceeding 3 log CFU in 0.26% (82.6% reduction). The above results indicate that a simple intervention, such as excluding the door shelf for pasteurized milk storage, can be effective in controlling the growth of the pathogen. In addition, the results showed that the domestic storage temperature is the most important factor affecting the concentration of L. monocytogenes at the time of consumption. This is in agreement with the conclusions of the available risk assessment studies of L. monocytogenes in ready-to-eat foods (18, 20), which stress the importance of refrigerated storage temperature in consumer exposure to L. monocytogenes at the time of food consumption. In this study we showed that for pasteurized milk better control of domestic refrigerators, compared to retail storage, is much more effective, while consumer handling practices, such as the position of milk cartons in the refrigerator, are also significant. Thus, an improvement in handling and storage conditions at the domestic level can be very effective in reducing consumer exposure to the pathogen. This improvement could be achieved by the application of a consumer education program and/or a change in the technology of refrigerators. Although these are not easy tasks, the lower domestic storage temperatures observed in the United States show that better control is achievable.

FIG. 12.

Effects of selected interventions on the total growth (during transportation, retail storage, and domestic storage) of L. monocytogenes in pasteurized milk. Intervention I, better control of retail temperature; intervention II, exclude door shelf from domestic storage; intervention III, intervention II and a decrease in the mean domestic refrigeration temperature by 2°C.

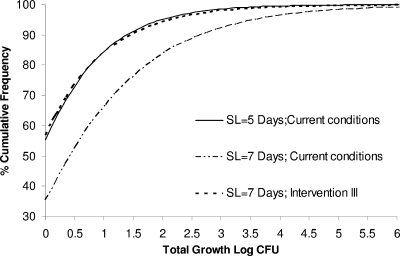
The probabilistic model was also used for evaluating the effect of a potential extension of the shelf life of pasteurized milk on the growth of L. monocytogenes. As mentioned previously, the shelf life of pasteurized milk in Greece has been defined by law to be 5 days. Recently, however, a discussion between the regulatory authorities and the Greek dairy industry on a potential extension of the shelf life of pasteurized milk has been in progress (http://www.gge.gr/7/sub.asp?1926). The problem is that the latter discussion is not supported by any scientific data for the evaluation of the effects of a shelf life extension on the safety and quality status of the product. In this study the developed model was applied to evaluate the effects of a shelf life increase from 5 to 7 days on the total growth of L. monocytogenes in pasteurized milk. The increase in shelf life was introduced to the model by appropriate adjustment of storage times, assuming that it would lead to a corresponding increase in retail and domestic storage times. In particular, the distributions of retail and domestic storage times were adjusted to log normal (30, 20; truncate [168]) and cumulative (0, 168; {0, 33.6, 67.2, 100.8, 134.4, 168}, {0, 0.23, 0.74, 0.96, 0.98, 1}; truncate [168 − t_T − t_R]), respectively. A comparison between the total growth of L. monocytogenes in pasteurized milk with shelf lives of 5 versus 7 days is shown in Fig. 13. As expected the extension in shelf life resulted in a significant increase of the total growth of the pathogen. The percentage of cartons that allowed growth of L. monocytogenes increased from 44.8% to 65.5%, and the mean growth in these cartons increased from 0.93 to 1.47 log CFU/ml. In addition, the shelf life extension resulted in a 13-fold increase of cartons (initially contaminated with 1 cell/1-liter carton) exceeding the safety criterion of 100 cells/ml (from 0.14% to 1.8%). Figure 13 also shows the effects of intervention III on the total growth of L. monocytogenes in pasteurized milk when a shelf life of 7 days is used. Intervention III resulted in a decrease of products allowing growth from 65% to 43.2%, with the mean total growth in these products decreased from 1.47 to 0.98 log CFU. These results indicate that by excluding the door shelf from domestic milk storage and improving the temperature of domestic refrigerators by 2°C, the shelf life of pasteurized milk can be extended from 5 to 7 days without affecting the current consumer exposure to L. monocytogenes.

FIG. 13.

Comparison of L. monocytogenes total growth in pasteurized milk with a shelf life of 5 and 7 days under current chill chain conditions versus total growth in pasteurized milk with a shelf life of 7 days after the application of intervention III (excludes the door shelf from domestic storage and decreases the domestic refrigeration mean temperature by 2°C).

The total growth of L. monocytogenes in pasteurized milk which was used as the output of the developed probabilistic model cannot provide information on the risk in terms of probability of illness. For this, additional data related to the prevalence and concentration of the pathogen at the time of packaging and the dose-response are required. However, it is well known that the available dose-response relationships are characterized by high uncertainty while the data on the initial prevalence and concentration of the pathogen are very limited. For example, in the available risk assessment studies of L. monocytogenes in pasteurized milk (18, 20) the initial concentration of the pathogen was described based on data from retail due to absence of data at the stage of packaging. The use of these data in the model can increase significantly the uncertainty of the output. On the contrary, the total growth of the pathogen can be predicted based on more accurate data and thus lead to more effective evaluation and comparison of different intervention strategies. Furthermore, the risk assessments studies of L. monocytogenes in ready-to-eat foods (18, 20) have stressed the great impact of the growth between manufacture and consumption on the rates of listeriosis. Consequently, the evaluation of the effect of the various chill chain factors on the growth of the pathogen in a probabilistic way would be very important in decision making for the improvement of product's safety.

Probabilistic modeling approaches that take into account the variability of the factors affecting microbial behavior can provide more realistic estimation of the food quality and safety. Most importantly, probabilistic models can be used as effective tools for identifying, evaluating and comparing potential intervention scenarios and mitigation strategies. It is expected that new developments in predictive microbiology related to the physiological state of microbial cells and single cell behavior that are now under investigation will further improve the effectiveness of probabilistic models and make them a powerful tool for food safety management.