High b-value q-space Diffusion Weighted MRI of the Human Cervical Spinal Cord in vivo: Feasibility and Application to Multiple Sclerosis

Abstract

Q-space analysis is an alternative analysis technique for diffusion weighted imaging (DWI) data in which the probability density function (PDF) for molecular diffusion is estimated without the need to assume a Gaussian shape. Although used in the human brain, q-space DWI has not yet been applied to study the human spinal cord in vivo. Here we demonstrate the feasibility of performing q-space imaging in the cervical spinal cord of eight healthy volunteers and four patients with multiple sclerosis. The PDF was computed and water displacement and zero-displacement probability maps were calculated from the width and height of the PDF, respectively. In the dorsal column white matter, q-space contrasts showed a significant (p<0.01) increase in the width and a decrease in the height of the PDF in lesions, the result of increased diffusion. These q-space contrasts, which are sensitive to the slow diffusion component, exhibited improved detection of abnormal diffusion compared to perpendicular apparent diffusion constant measurements. The conspicuity of lesions compared favorably with magnetization transfer (MT) weighted images and quantitative CSF-normalized MT measurements. Thus q-space DWI can be used to study water diffusion in the human spinal cord in vivo and is well suited to assess white matter damage.

INTRODUCTION

In white matter (WM), the axonal membrane and myelin sheath present barriers to water displacement, resulting in anisotropic diffusion (1–4). WM damage is known to affect tissue microstructure and diffusion weighted MRI (DWI) has been used to measure changes in diffusion properties (both parallel and perpendicular to WM fiber bundles) in a number of WM diseases in humans (5) as well as animal models of myelin deficiency (6,7). In general, however, conclusive assignment of diffusion changes observed with DWI to axonal and/or myelin damage is not straightforward, in part because the biophysics of diffusion in vivo is not fully understood and because axonal and myelin loss are histopathologically related. Additionally, the technique selected to analyze diffusion weighted images (DWIs) is an important consideration and has an impact on the quantitative interpretation of diffusion experiments. DWIs are typically analyzed with a mono-exponential tensor model that characterizes the observed signal decay according to the Stejskal-Tanner equation (8)

$$\text{ln}(\mathrm{S}/{\mathrm{S}}_0)=-{\mathrm{\gamma }}^2{\mathrm{\delta }}^2(\mathrm{\Delta }-\mathrm{\delta }/3)\mathbf{G}·\mathbf{D}·\mathbf{G}=-\mathbf{b}:\mathbf{D}$$ [1]

where S/S₀ is the normalized signal intensity, γ is the proton gyromagnetic ratio, δ,G, and Δ are the duration, magnitude and leading edge separation time of the diffusion weighting gradient vector, respectively, and D is the diffusion tensor. Diffusion tensor imaging (DTI) has been applied in the brain (5,9–12) and spinal cord (10,13–15) and is typically performed in the low b-value (< 1500 s/mm²) regime where the signal decay is, to a reasonable approximation, monoexponential. The degree to which diffusion is reduced in the CNS, compared to free water, is the result of micro-structural barriers, which generally includes multiple compartments in vivo and the diffusion time that molecules have to explore their environment. If restrictions between compartments are sufficiently large so that exchange is slow on the MR timescale, the signal attenuation will become non-monoexponential. This effect becomes apparent at higher b-values (> 1500 s/mm²) in cell systems (16,17), animal models (18,19) and the human brain (20,21) and may be useful in detecting micro-structural changes due to WM damage. To improve the fit to the data, multi-component models can be used (19–22). Though bi-exponential fits approximate the observed signal behavior, a quantitative interpretation in terms of fast and slow diffusion components and corresponding assignment to extra- and intra-cellular water fractions has not been straightforward (19). This is not surprising, as cellular systems are comprised of many compartments of multiple sizes and shapes, many of which are connected through exchange. The use of relaxation agents in combination with diffusion studies (23) may aid the quantitative assignment of water diffusion populations.

An alternative approach to characterize diffusion is q-space analysis (24–27), which, unlike conventional DTI and DWI analysis, does not assume a Gaussian shape for the underlying probability density function (PDF) of molecular diffusion. The PDF is the conditional probability that a spin diffuses a distance R = r−r₀ from its initial position r₀ during the allowed diffusion time. At a given diffusion time, a tall, narrow PDF suggests a low diffusion constant and/or restricted diffusion, whereas a low, broad PDF suggests a high diffusion constant and/or more unrestricted diffusion. Q-space analysis allows experimental determination of the PDF and has been used in animal models to study the effects of reduced blood flow (28), myelin development (29), WM damage due to crush injury (30), myelin deficiency (31), and hypertension induced neurodegeneration (32). Structural information derived from q-space DWI in fixed rat spinal cords has also correlated well with axon diameters obtained from histological examination (33).

Recently, q-space DWI has been used to study experimental allergic encephalomyelitis in excised swine spinal cord (34) and multiple sclerosis (MS) in the human brain (35–37). MS is characterized by heterogeneous pathological changes in the CNS including demyelination, axonal loss and inflammation. Even though conventional MRI has emerged as a powerful tool to diagnose and prospectively monitor MS in clinical practice (38), some histopathological lesions appear normal on MRI examinations. To address this challenge, new MRI methods have been developed to assess axonal damage and myelin loss, including magnetization transfer (MT) (39) and DWI techniques. MS involvement in the spinal cord is of particular interest because the prevalence of abnormalities is high (40) and because functional deficits can be associated with MRI indications of damage to the dorsal and lateral column WM, which convey sensory and motor information, respectively. The anatomical organization of the spinal cord, with densely packed, myelinated axons, oriented predominantly in one direction, makes it an ideal model system to investigate the effects of restricted diffusion. This a priori information allows diffusion weighting gradients to be oriented perpendicular to the WM fiber bundles, which is difficult to achieve in the brain due to its complex fiber architecture. The average diameter of axons in cervical spinal cord WM is approximately 1–1.5µm, increasing to approximately 1.7µm in MS lesions (40), which could be due to cell death of small axons and/or enlargement of surviving axons.

We hypothesized that the PDF of water diffusion perpendicular to the spinal cord’s long axis may serve as a sensitive marker of disease-related damage. Here we demonstrate the ability of q-space DWI to delineate WM and gray matter (GM) and compare it to the apparent diffusion constant perpendicular to the WM fiber orientation (ADC_⊥), as well as to quantitative MT measurements.

MATERIALS AND METHODS

Theory

DWIs were acquired with a pulsed magnetic field gradient spin-echo (PGSE) experiment in which G is stepped while holding δ constant. The quantity q = γδG/(2π)[cm⁻¹] is independent of Δ, but the effective diffusion time t_dif = Δ − δ/3 should be stated for a given q-space experiment as it will affect the average displacement measured. The relationship between the measured signal attenuation E_tdif(q), the PDF P̅_s(R,t_dif), and the loss of phase coherence due to spin displacement is:

$$E_{tdif}(\mathbf{q})={\displaystyle \int {\overline{P}}_s(\mathbf{R},t_{dif})\text{exp}(i2\pi \mathbf{q}·\mathbf{R})d\mathbf{R}}$$ [2]

The key principle in q-space analysis is that a Fourier transform (FT) of the signal attenuation with respect to q provides the PDF for diffusion:

$${\overline{P}}_s(\mathbf{R},t_{dif})=FT\{E_{tdif}(q)\}.$$ [3]

The shape of the computed PDF can be characterized by the full width at half maximum (FWHM) and the maximum height (zero displacement probability, P₀) (29). In the specific case of unrestricted Gaussian diffusion, the diffusion constant D and the root mean square displacement (RMSD) for one-dimensional diffusion can be computed from the FWHM (27):

$$FWHM=2\sqrt{4D{t}_{dif}\text{ln}(2)}$$ [4]

$$RMSD=\frac{FWHM}{2\sqrt{2\text{ln}(2)}}=\sqrt{2D{t}_{dif}}.$$ [5]

For consistency and ease of comparison with results from previous studies, the displacement values in this study are reported in terms of RMSD (0.425 × FWHM).

Subjects

The local institutional review board approved the study and informed consent was obtained from each subject. Eight healthy volunteers (6 males, 2 females, average age 32 ± 7 years) with no history of neurological disease and four individuals diagnosed with MS (two with relapsing remitting (RRMS) and two with secondary progressive (SPMS) forms of the disease) were enrolled in the study. Table 1 provides relevant clinical information. Follow-up datasets were acquired in 3 of the 4 patients as part of an ongoing longitudinal study.

Table 1.

Clinical information for patients studied

Patient	MS Subtype	Age (years)	Gender	Evaluations	Disease Duration (years)	EDSS	Affected Systems (FSS>= 2)
A	RR	25	male	initial	1	3.5	V, C, B
B	RR	31	female	initial	8	3.5	P, C, B, S
				4 months	8	5.5	P, C, B
C	SP	43	female	initial	15	3.5	P, C
				4 months	15	3.5	P, C
D	SP	41	male	initial	6	5.5	P, C, S, CL
				2 months	6	5.5	P, C, S, CL

Expanded disability status scale (EDSS); functional system score (FSS). Affected system abbreviations: visual (V), cerebellar (C), bowel and bladder (B), pyramidal (P), sensory (S), cerebral (CL)

MRI

Data were acquired on a 3T MR scanner (Philips Medical Systems, Best, The Netherlands), capable of producing 62mT/m magnetic field gradient strength. The body coil was used for transmission, while reception was accomplished with a 2-element surface coil placed bi-laterally around the neck. Pillows, sandbags and a head strap were used to minimize gross subject motion during scanning.

DWIs were acquired using spin-echo single-shot echo-planar imaging (EPI, SENSE factor = 1.8, TR/TE = 7000/112 ms). Thirty axial slices were acquired perpendicular to the long axis of the spinal cord covering approximately C1 to C7 (nominal resolution = 1.3 × 1.3 × 3.0 mm, field of view = 62 × 62 × 90 mm, scan matrix = 48 × 48, reconstructed matrix = 128 × 128). EPI-based geometric distortion can lead to anatomical mismatch between structural images and DWIs, especially in the spinal cord. To decrease the prevalence of susceptibility related artifacts, second order shimming was performed and a small acquisition matrix was used to decrease the length of the EPI echo train. To suppress foldover artifacts from surrounding tissue, saturation slabs were applied in the phase encoding direction (patient right-left axis) extending half the field of view outside the imaged volume. Diffusion weighting was applied perpendicular to the long axis of the spinal cord using both sets of transverse gradient coils to achieve the maximum gradient strength, thereby minimizing TE at the largest b-value. Gradient length (δ = 16ms) and leading edge spacing (Δ = 74.5ms) were kept constant, giving t_dif = 69.2ms. Gradient strength was increased up to G_max = 60.855 mT/m (b_max = 4685 s/mm²) to achieve 31 linearly spaced q-values from 0 to 414 cm⁻¹ (Table 2). The q-space DWI dataset was acquired in two separate blocks (b₀, b₁, b₃, b₅ … b₂₉) and (b₀, b₂, b₄, b₆ … b₃₀) where b₃₀ = b_max and b₀ is the k-space average of three scans with b = 0 s/mm². To improve SNR, each block was collected with diffusion weighting along two orthogonal directions ([G_x, G_y, G_z] = [1,1,0] and [1,−1,0]) with a total acquisition time of approximately 10 min.

Table 2.

Acquired b-values and corresponding q-values at t_dif = 69.2ms

b-value s/mm2	q-value cm−1	b-value s/mm2	q-value cm−1
0	0.0	1333	220.9
5	13.8	1504	234.7
21	27.6	1687	248.5
47	41.4	1879	262.3
83	55.2	2082	276.2
130	69.0	2296	290.0
187	82.8	2520	303.8
255	96.7	2754	317.6
333	110.5	2998	331.4
422	124.3	3254	345.2
521	138.1	3519	359.0
630	151.9	3795	372.8
750	165.7	4081	386.6
880	179.5	4378	400.4
1020	193.3	4685	414.2
1171	207.1

Sagittal short-tau inversion recovery (STIR) images and high-resolution MT (41) datasets were also acquired for anatomical reference and lesion localization. For the latter, gradient echo volumes, consisting of 40 slices, were acquired with and without a 24ms sinc-shaped MT prepulse (8.5 µT played at 1.5 kHz off-resonance with respect to water at a nominal resolution of 0.69 × 0.69 × 2.25 mm). The acquisition with RF saturation is denoted as MT weighted (MTw). As reported previously (42), the MTw signal is largely sensitive to changes in macromolecular content (e.g. demyelination) and shows excellent contrast between healthy tissue and lesions in MS. Scan time for STIR and MT acquisitions was approximately 12 minutes.

Data Processing and Image Analysis

Processing was done offline on a Sun Fire V880 server (Sun Microsystems Inc., Santa Clara, CA). The b₀ images from all blocks were co-registered using FLIRT (FMRIB’s Linear Image Registration Tool, Oxford, UK) (43) employing a rigid body 2 degrees of freedom (in plane translation only) model. This restrictive model was selected because through-plane motion can be particularly difficult to identify in the spinal cord, especially in DWIs, which typically suffer from both low SNR and low tissue contrast. A further confounding factor is that the spinal cord, in contrast to the brain, has limited visual anatomical differences from slice to slice (given the limitations of MRI resolution). The same transformation was applied to the remaining DWIs of the same block. For each b-value, the coregistered images with G = [1,1,0] and [1,−1,0] were averaged to increase SNR. The four co-registered b₀ volumes were also averaged.

Q-space and statistical analyses were performed with in-house MATLAB (The Mathworks, Natick, MA) routines. For SNR calculations, average and difference images of DWIs with G = [1,1,0] and [1,−1,0] were computed at each b-value. The SNR was computed as the mean value in the dorsal column region of interest (ROI) in the average image divided by the standard deviation over the voxels in the same ROI within the difference image. For the data for q-space analysis (i.e. average of 4 b₀s and the average of 2 DWIs at each b-value), the mean SNR, averaged over the 8 controls and all slices, was 24±2:1, 8.8±1:1, 6.5±0.9:1 and 4±0.4:1 at b-values of 0, 83, 1020, and 4685 s/mm², respectively. For estimation of the noise floor, the standard deviation over all voxels in the difference image, at each b-value, was computed. The mean over a b-value range of 3519 to 4685 s/mm² was used as the noise floor and was subtracted from all data before processing. Signal falling below this artificial noise floor in magnitude images was set to zero. For each voxel, a bi-exponential fit was applied to the signal decay as a function of b-value for the sole purpose of extrapolating the signal decay to 1% of the value measured at b = 0 s/mm², to reduce truncation artifacts in the subsequent Fourier transform. The extrapolated signal decay was then zero-filled to q = 6150 cm⁻¹ to improve resolution. The resulting curve was Fourier transformed with respect to q (Eq. 3), giving a PDF for each voxel. FWHM, P₀ and RMSD maps were computed on a voxel-by-voxel basis. In order to compare q-space and conventional DWI analysis, an ADC_⊥ map was computed by fitting the mono-exponential form of Eq. 1 to the signal attenuation at b-values up to 1020 s/mm².

Diffusion data were further analyzed by manually delineating ROIs in the dorsal column WM on the RMSD maps in each slice. Care was taken to exclude voxels of cerebrospinal fluid (defined as having a ADC_⊥ > 3 µm²/ms). It should be noted that, due to the small size of spinal cord structures with respect to the acquired resolution, some partial volume effects are unavoidable. These effects were reduced further by removing the outermost layer of voxels from the perimeter of each ROI. Each ROI consisted of approximately 60 to 70 voxels. The same ROIs were then applied to the P₀ and ADC_⊥ maps, and the mean value and standard deviation over all voxels within the ROIs were computed for the three contrasts.

To prevent anatomical mismatch (due to EPI-based image distortion) from confounding the comparison of results, MT data were coregistered and analyzed independently from the DWI data. The two volumes of the MT dataset were coregistered using a three degrees of freedom model (in plane translation and rotation) and were resliced, with sinc interpolation, to the match the number of slices and slice thickness of the DWI data. Magnetization transfer ratio (MTR) maps were computed on a voxel-by-voxel basis according to:

$$\text{MTR}=1-\frac{\mathrm{S}(\mathrm{\omega })}{{\mathrm{S}}_0}$$ [6]

where S₀ and S(ω) are the signal intensities in the absence and presence of RF irradiation, respectively. For MT analysis, a separate set of ROIs was manually delineated in the dorsal column WM on the MTw images. The ROIs were then applied to the MTR images and the mean value and standard deviation over all voxels within the ROIs were computed. The mean MTw signal in each ROI was normalized by the mean CSF signal on the same slice in the MT image without RF saturation to provide MTCSF measurements (41).

Acquired data covered approximately the same anatomical extent of the cervical spinal cord in all subjects. To compare results across subjects, the resultant ROI-based RMSD, P₀, ADC_⊥, MTR and MTCSF data were normalized to a consistent anatomical coordinate system based on cervical vertebral levels. This was accomplished by identifying the slices at the superior aspect of the C2 and C6 vertebral bodies (anatomical landmarks) for each subject, as visualized on the overlay of the q-space DWI slice stack on the sagittal STIR image. Inspection of the data for 8 healthy controls showed that, on average, 21 slices were necessary to traverse the distance between these landmarks. Slices outside the landmarks were discarded as these areas were not visualized for all subjects. The mean and standard deviation values from the ROI-based analysis between the landmarks were interpolated to 21 equally spaced points spanning four complete vertebral segments (C2, C3, C4 and C5) and the RMSD, P₀, ADC_⊥, MTR and MTCSF results were partitioned accordingly. The average and standard deviation of the ROI-based measures from the eight controls were computed for each contrast and displayed as a function of slice level.

In addition to the voxel-by-voxel q-space analysis, PDFs and ADC_⊥ measurements were also obtained for ROIs in WM and MS lesions. This was done by computing the average diffusion weighted signal in each ROI as a function of b-value prior to taking the Fourier transform in q-space analysis and fitting for ADC_⊥.

Statistical Analysis

To determine the contrasts (RMSD, P₀, ADC_⊥, MTCSF and MTR) that show the most significant differences between MS patients and healthy controls, a slice-wise statistical analysis was performed. For each anatomically normalized slice level a distribution of approximately 600 data points was obtained by pooling the signal intensities from all voxels within each of the ROIs from all healthy controls. As the number of controls was small, this method provides a robust estimation of the true variance. At the same slice level, corresponding distributions were obtained for each MS patient (approximately 60 to 70 voxels per slice). Two-tailed and one-tailed Student’s t-tests, assuming unequal variance, were performed to test the null hypothesis that the control distribution and distribution from a subject with MS had equal means (at a significance level of α = 0.01). Separate tests were performed for each contrast at each anatomical slice level. An approximate measure of sensitivity to WM damage was defined as the number of slice levels (out of 21, expressed as a percentage) identified as significantly different from the control cohort. For the one-tailed t-tests, it was expected that RMSD, ADC_⊥, and MTCSF increase, while P₀ and MTR decrease in MS lesions.

RESULTS

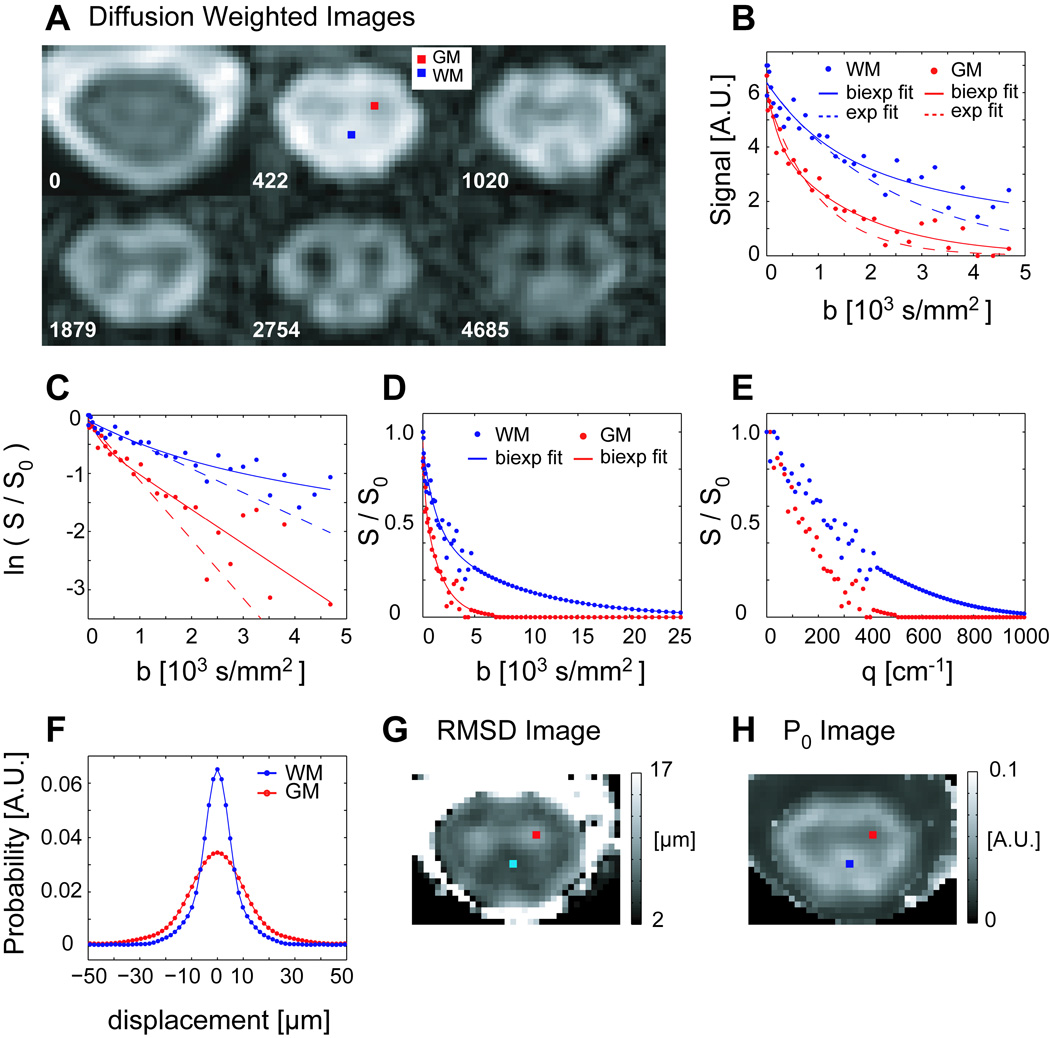
Figure 1 shows typical DWIs as a function of b-value at the level of C4 in a healthy spinal cord. Because the diffusion weighting was applied perpendicular to the long axis of the spinal cord, WM signal is preserved even in the high b-value range, whereas GM signal drops off rapidly with b-value. Notably, the monoexponential fit, from which ADC_⊥ is calculated, describes the data well only at low b-values while the biexponential fit can fit the data reasonably well. The computed PDFs in WM are narrower and taller (decreased RMSD and increased P₀) than those for GM, and the GM horns and surrounding WM can be visually appreciated on the maps of RMSD and P₀.

Figure 1.

A) DWIs (axial cross section, average of 2 diffusion weighting directions) through C4 spinal cord in a healthy 25 year old female volunteer. All DWIs (b>0) have the same windowing level. B) Measured signal decays for representative WM and GM voxels as a function of b-value, with bi-exponential (solid line) and mono-exponential (dashed line) fits. C) Natural log of the normalized signal showing departure from mono-exponential signal attenuation. D, E) The normalized signal, extrapolated and zero-padded (partial) data series as a function of b- and q- value, respectively. F) PDFs computed for GM and WM voxels. G, H) Maps of the RMSD and height (P₀) of the PDF computed for each voxel at the slice level, with the location of the representative voxels indicated.

Figure 2A shows three slices of the RMSD, P₀, and ADC_⊥ images for the healthy volunteer in Fig. 1. The GM-WM differentiation corresponds well to the anatomy shown in the MTw images at the same levels. As a first clinical example, RMSD, P₀ and ADC_⊥ images computed for a 43-year old female with SPMS are also shown (Fig. 2B). There is a signal hyperintensity in the dorsal column on the MTw image. The RMSD and ADC_⊥ images also show hyperintensity, indicating increased diffusion in the transverse plane, whereas hypointensity is apparent on the P₀ image, indicating lower probability for no net water displacement during the diffusion time. Additionally, differential involvement in the right and left dorsal columns can be easily appreciated: an increased involvement of the right dorsal column is noted over the slices shown.

Figure 2.

Comparison of MTw, RMSD, P₀, and ADC_⊥ maps. A) The healthy female volunteer in Figure 1. Three contiguous slices from C5 to C4 shown (left to right) clearly demonstrate the shape of the GM horns and surrounding WM in all image types. B) 43 year old female with SPMS. Contiguous slices extending from C4 to approximately mid level of C3 (left to right in the figure). On all four images, MS-related abnormality in the right dorsal column is evident. For visual display, voxels outside the cord are set to zero for the RMSD, P₀ and ADC_⊥ maps.

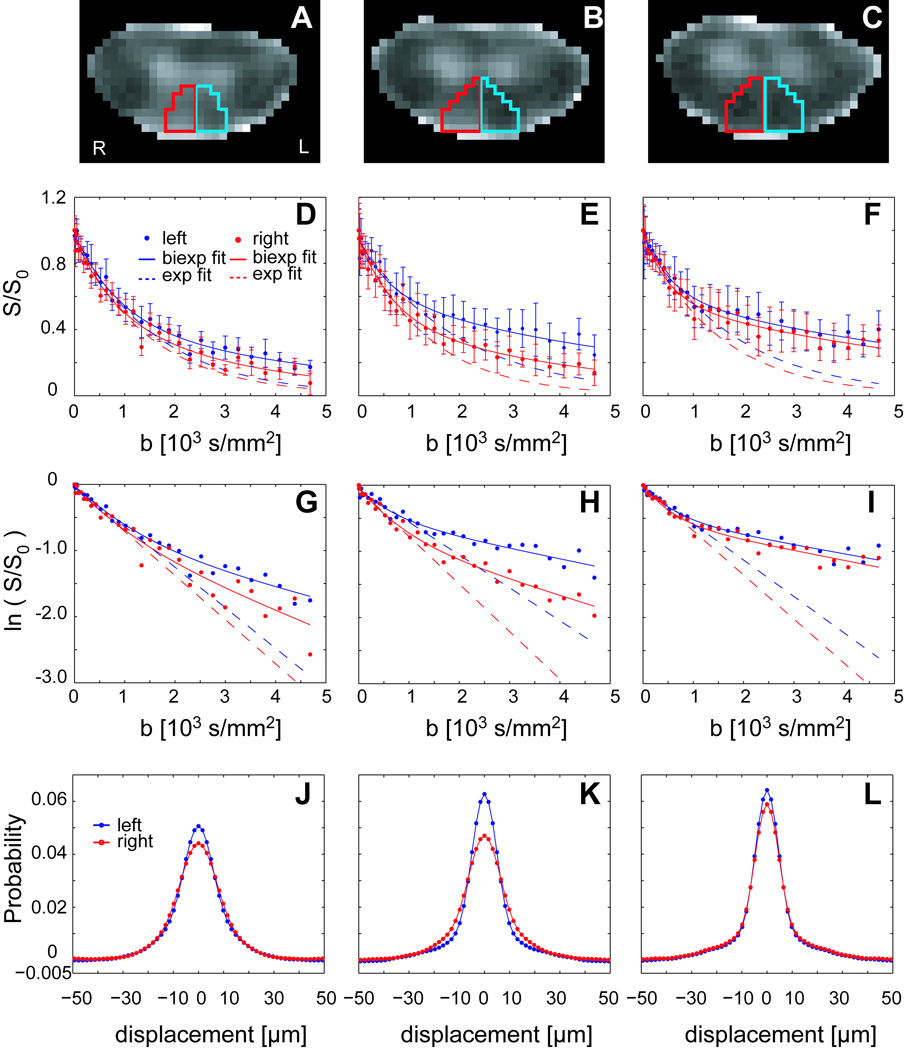
Figure 3 shows ROI-based q-space analysis for three slices through the dorsal column of the individual with SPMS shown in Figure 2. A qualitative decrease in tissue abnormality in the right dorsal column (red ROI and data) is noted in the panels from left to right (inferior to superior in the cord). It is readily apparent that the signal decay in grossly damaged WM (Panels D and E) is different from that observed in more normal-appearing WM (Panel F). The natural log of the signal attenuation as a function of b-value becomes more linear in regions of WM damage and approaches the mono-exponential fit. ROI-based PDFs are broader and lower in the lesion than in normal-appearing WM.

Figure 3.

ROI analysis for the three contiguous slices for the SPMS patient in Figure 2. A–C) ROI definition in the right (red) and left (blue) dorsal columns overlaid on RMSD images. D–F) Average signal intensity (± SD over ROI voxels) plotted as a function of b-value. G–I) The natural log of average signal intensity as a function of b-value. J–L) computed PDFs.

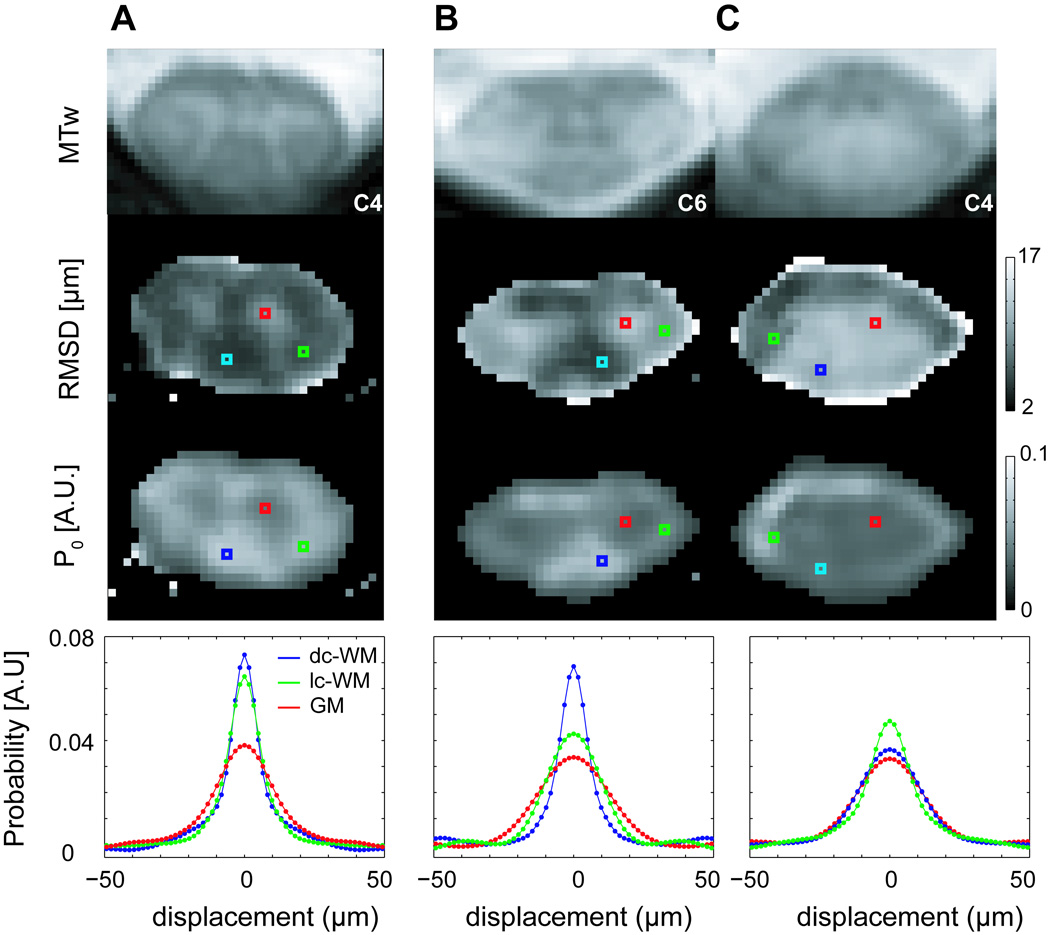
Figure 4 compares results from a healthy volunteer with those from a patient with RRMS with both lateral and dorsal column involvement as seen on the MTw images. The single-voxel PDFs illustrate the sensitivity of PDF shape to WM damage, which produces a broader, shorter PDF, approaching that of GM.

Figure 4.

MTw, RMSD, and P₀ images and voxel-based PDFs for a healthy 25-year old male volunteer at the C4 level (A) and for a 25 year old male with RRMS at slice levels C6 (B) and C4 (C). Lesion involvement in the lateral (lc-WM) and dorsal column WM (dc-WM) is visible, with lesions appearing hyperintense on the RMSD image, hypointense on the P₀ image, and hyperintense on the MTw image.

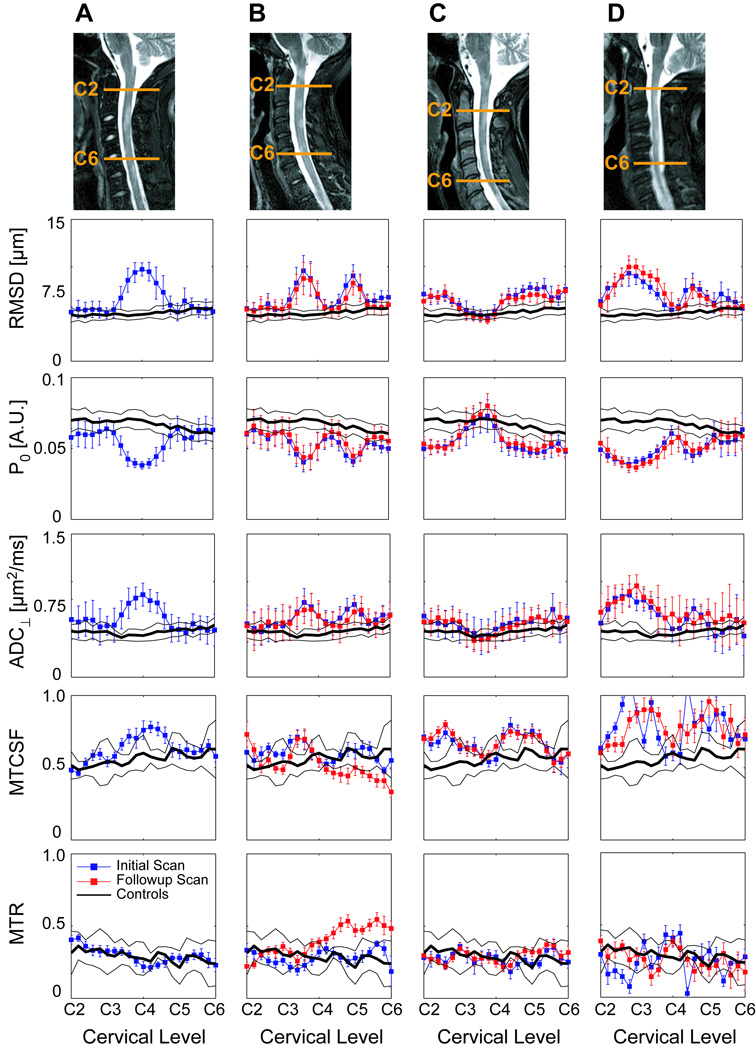
Figure 5 compares quantitative diffusion and MT measurements in ROIs in the dorsal column WM for 4 patients from the superior aspect of C2 to the superior aspect of C6. Areas of MS lesion involvement are indicated by increased RMSD, ADC_⊥, and MTCSF, and decreased P₀, relative to controls. MTR values were difficult to determine accurately, probably due to motion sensitivity in the ratio determination (note irregular values in Panels B and D, due to image artifacts), and did not change appreciably in most lesions due to the large error margins. The sensitivity of the q-space metrics to the presence of lesions is well demonstrated in Panel C where the deviation of ADC_⊥ relative to controls is minimal (well within one standard deviation), but quite noticeable (well outside one standard deviation) in RMSD and P₀ plots. Statistical analysis showed that, compared to ADC_⊥, ROI analysis of RMSD and P₀ identified more slices as significantly different from the control cohort (Table 3). While MTCSF proved to be quite sensitive to WM damage, the changes observed in MTR were generally small and within the standard deviation of controls, but at some locations appeared statistically significant due to the small standard deviation of MTR within an individual subject’s ROI. Three of the four individuals with MS (Panels B, C, D) were scanned in a follow-up study, and good reproducibility of the q-space and ADC_⊥ results was found in all three instances. More detailed examinations of the reproducibility of results in healthy controls and correlations with MS disease progression in a longitudinal study are ongoing.

Figure 5.

RMSD, P₀, ADC_⊥, MTCSF and MTR within ROIs in the dorsal column WM (mean ± standard deviation over the voxels in the ROI), plotted as a function of cervical level. Results for four patients, A) 25 year old male with RRMS, B) 31 year old female with RRMS, C) 43 year old female with SPMS and D) 41 year old male with SPMS, are compared with the average results (solid black line, ± one standard deviation) from 8 healthy controls. Initial and follow-up results are shown for three of the MS patients. Sagittal STIR images show slice and lesion localization for the initial exam of each patient.

Table 3.

Percentage of anatomical slice levels (out of 21 slices) identified as significantly different from controls at a significance level of α = 0.01.

	Percent of slices significantly different from controls
Patient	A		B		C		D
t-test type	Two|	one sided	Two	one sided	Two	one sided	Two	one sided
RMSD	76	67	93	93	86	79	86	86
P0	71	71	95	95	83	79	86	86
ADC⊥	67	62	86	86	55	50	79	76
MTCSF	86	76	90	43	95	81	95	93
MTR	86	52	88	43	79	57	88	57

Results from initial and follow-up evaluations are averaged. Values are reported for two-sided and one-sided t-tests for the four cases (A–D) shown in Figure 5.

DISCUSSION

The results of this feasibility and initial clinical study show that it is possible to apply q-space imaging in the human cervical spinal cord in vivo, and that displacement (RMSD) and probability (P₀) maps provide useful contrasts to visualize spinal cord anatomy and WM damage. The degree to which diffusion is reduced in the CNS, compared to free water, is a product of micro-structural barriers, such as axonal and myelin membranes, as well as the experimentally chosen diffusion time that water molecules have to explore the local environment. These physical properties are conveyed in the diffusion properties measured perpendicular to the spinal cord’s long axis with DTI (radial diffusion, ADC_⊥) or the RMSD and P₀ of the PDF in q-space DWI. The observed diffusivity is a complex combination of the volume fractions and diffusion constants of all compartments contributing to the voxel as well as of the exchange occurring between them. Obviously, the number of observed quantities is too limited to draw many inferences about this microstructural environment. However, analytical models of restricted diffusion (22) have provided valuable insights into the interpretation of signal attenuation curves and allow extraction of some quantitative parameters.

Postmortem histopathology has shown marked morphological changes in spinal cords affected by MS, with increases in the mean axon diameter and axonal spacing, together with decreases in axon and myelin densities (40). These changes would necessarily affect the diffusion properties of water in the spinal cord. Even though precise correlations between diffusion measurements and morphology are not straightforward, DTI and the q-space approach can be used to obtain information about the average state of cellular systems and whether they are healthy or diseased. In healthy controls, PDFs in dorsal and lateral column WM (narrow, tall) are similar and are both distinct from the PDFs in GM (broad, short). When myelin and/or axonal damage occurs, the magnitude and number of restrictions is expected to decrease, resulting in increased diffusion. While the RMSD and P₀ can be expressed in terms of each other for a Gaussian PDF, this is not the case, in general, for non-Gaussian PDFs, and thus it is possible that the information provided by these contrasts could be different.

The results in this study showing that that the PDF shape is sensitive to WM damage, are consistent with previous studies in animals (29–32,34) and the human brain (35–37). However, we caution that comparison of quantitative values between in vivo studies and those using fixed tissue can only be qualitative, because tissue fixation and lower temperature will decrease the measured diffusion constant (44). The results for RMSD in healthy WM, and GM and in WM affected by MS are in good agreement with values reported in the literature (Table 4). Additionally, the observed increase in ADC_⊥ from 0.52–0.61±0.09 µm²/ms (across the C2 to C6 levels) in healthy WM to 0.65–1.0 µm²/ms in MS lesions (see Fig. 5) is in excellent agreement with the range of values reported for healthy WM (10,14,15) and the elevation of ADC_⊥ in the spinal cord (13) and corticospinal tract of patients with MS (45). Areas that appeared abnormal on q-space contrasts appeared abnormal (hyperintense) on the MTw images, which are sensitive to changes in macromolecular (i.e. myelin) content.

Table 4.

RMSD values for diffusion measured perpendicular to the long axis of WM fibers in the brain and spinal cord with q-space DWI.

Study Type	RMSD (µm)			δ/tdif	Disease / Model	Ref.
				(ms)
	WM Control	GM Control	WM Lesion
Humana
Spinal Cord	5.2−6.3 ± 0.9+	8.5−10	7−10	16/69	MS	This study
Brain	9	11.9*	13	20/81	MS	(37)
Brain	3.8 ± 0.2	5−9	6.9 ± 0.6	65/49	MS	(36)
Brain	3.3 ± 0.8	7−9	8.1 ± 2.4	65/49	MS	(35)
Swine
Spinal Cordc	5.83 ± 0.06*	7−8†	7.3 ± 0.4*	10/200	EAE	(34)
Rat
Spinal Cordb	2−3	9−10	6.6 ± 0.6‡	2/150	Development	(29)
Spinal Cordc	2.2 ± 0.3	6.1 ± 1.3	3.8 ± 0.6	2/150	Hypertension	(32)
Spinal Cordd	6.6 ± 0.1†	8.2 ± 0.6†	7.5 ± 0.5†	2/50	Myelin deficient	(31)
Spinal Cordd	2.7 ± 0.1	9.7 ± 0.3	3.9 ± 0.3	2/150	Crush trauma	(30)

^a)in vivo studies.

^b)Excised tissue, no fixation.

^c)Formalin fixed tissue,

^d)paraformaldehyde fixed tissue.

⁺across the C2 to C6 levels,

^*computed from data in supplied tables.

^†estimated from figure.

^‡7 day old rat (compared to WM and GM control in 77 day old mature rat).

Experimental allergic encephalomyelitis (EAE).

It is important to evaluate whether we have used sufficiently high b-values to reliably detect the slow diffusion component in vivo. Our results show that a departure from mono-exponential signal attenuation was apparent at b > 1000 s/mm². This is in excellent agreement with Assaf et al (18) who showed detection of the slow diffusing component at b > 1000 s/mm² in the rat spinal cord. These authors also reported, via simulation studies, that in heavily diffusion weighted images (b > 2000 s/mm²) the majority of the signal represents the slow diffusing component. Our DWIs at high b-value (Fig. 1) support this finding in that the signal in GM (predominantly monoexponential fast diffusion) is largely attenuated while signal in WM remains due to spatial restrictions.

Another important point is whether q-space analysis provides additional information or improved lesion detection compared to conventional measures of the fast diffusion component (ADC_⊥). Using the number of slices identified as significantly different from controls as an approximate measure of sensitivity to WM damage, statistical analysis showed that RMSD and P₀ were more sensitive to abnormal diffusion than ADC_⊥ (Table 3), even though it should be noted that the q-space dataset had inherently higher SNR due to the 10 minutes of data acquisition vs 5 minutes for the low b-value DWI dataset. While direct comparison of the sensitivity of diffusion and MTCSF measures to WM damage is not straightforward given the differences in resolution, SNR, and scan time, it is encouraging that the location and extent of WM damage compares favorably in both the images and the ROI analysis as a function of cervical level. Given the potential for detecting different pathological changes, a combined MT and diffusion approach may be useful in quantitatively assessing WM damage in MS lesions. High b-value q-space DWI is well suited to evaluate WM damage through its effects on both the fast and slow diffusion components, which may provide different correlations with pathological changes.

Overall, the change in the shape of the PDF in MS lesions in the spinal cord can probably be explained by the loss of axonal and/or myelin barriers to diffusion, which offers the opportunity to use this technology to study the different pathologies presented by neurodegenerative diseases such as MS, and possibly amyotrophic lateral sclerosis and adrenoleukodystrophies.

Technical Considerations

The main drawback of q-space DWI is the requirement of heavy diffusion weighting, which reduces available SNR and may be impractical on some clinical scanners due to hardware limitations. This study, performed at 3T, benefited from the availability of a gradient strength of 62mT/m, permitting b-values of approximately 4700 s/mm² with a TE = 112 ms. This was possible even though the long TE and the high resolution needed to discern spinal cord structures limited SNR. This was accomplished by using a small field of view and a small imaging matrix, made possible by the availability of a phased-array surface coil setup to shorten the length of the EPI echo train (with the additional benefit of decreasing susceptibility related distortions). Previously, the effects of t_dif, δ and TE on q-space DWI indices have been investigated (46). Q-space theory requires δ ≪ Δ, but this condition is difficult to fulfill on clinical scanners because the maximum magnetic field gradient strength is limited. Theoretical simulations (47) and studies in the rat spinal cord (46) and sciatic nerve (35) have shown that when δ is not negligible compared to Δ, the PDF obtained by q-space analysis is narrowed, resulting in an underestimate of the RMSD. Consequently, parameters derived from q-space DWI in this study should be interpreted as apparent values, and direct comparison between studies should be made with care.

A second condition in q-space analysis is that t_dif is long enough to allow spins sufficient time to encounter barriers to diffusion (i.e. t_dif > a²/2D, where a is the compartment radius in the case of cylindrical symmetry). The average diameter of axons in healthy human spinal cord WM is approximately 1 to 1.5µm (40). Taking the diffusion constant of water to be approximately 2×10⁻⁹ m²/s, the one-dimensional RMSD of a spin would exceed 1 µm after a t_dif of 0.25 ms. Thus the t_dif of 69ms in this study clearly satisfies the long diffusion time criterion. Previous studies have shown that while the PDF of perpendicular diffusion in mature rat spinal cord WM is largely independent of t_dif, diffusion in developing tissue is not (29). Consequently, improved GM-WM contrast has been demonstrated in the rat spinal cord by increasing t_dif (46). This approach may improve detection of WM damage, where diffusion is less restricted, and longer diffusion times could be achieved by the use of stimulated echo sequences. At the cost of increased scan time, additional SNR could be achieved by increasing the number of averages and implementing appropriate cardiac gating to minimize instability-based noise due to cardiac pulsation and respiratory motion. It is also feasible that the total scan time for a q-space DWI dataset could be reduced by acquiring DWIs at fewer b-values and employing a fitting and interpolation procedure. It is tremendously encouraging that DWIs of the quality reported here can be obtained even without these additional considerations in a scan time that is clinically feasible.

CONCLUSION

Diffusion-weighted imaging with q-space analysis can be used to study the diffusion properties of water in the human spinal cord in vivo in both healthy and diseased tissue.