Muscle moment arms of the gibbon hind limb: implications for hylobatid locomotion

Abstract

Muscles facilitate skeletal movement via the production of a torque or moment about a joint. The magnitude of the moment produced depends on both the force of muscular contraction and the size of the moment arm used to rotate the joint. Hence, larger muscle moment arms generate larger joint torques and forces at the point of application. The moment arms of a number of gibbon hind limb muscles were measured on four cadaveric specimens (one Hylobates lar, one H. moloch and two H. syndactylus). The tendon travel technique was used, utilizing an electro-goniometer and a linear voltage displacement transducer. The data were analysed using a technique based on a differentiated cubic spline and normalized to remove the effect of body size. The data demonstrated a functional differentiation between voluminous muscles with short fascicles having small muscle moment arms and muscles with longer fascicles and comparatively smaller physiological cross-sectional area having longer muscle moment arms. The functional implications of these particular configurations were simulated using a simple geometric fascicle strain model that predicts that the rectus femoris and gastrocnemius muscles are more likely to act primarily at their distal joints (knee and ankle, respectively) because they have short fascicles. The data also show that the main hip and knee extensors maintain a very small moment arm throughout the range of joint angles seen in the locomotion of gibbons, which (coupled to voluminous, short-fascicled muscles) might help facilitate rapid joint rotation during powerful movements.

Introduction

The functional importance of muscle moment arms

Muscles contribute to skeletal movement by exerting moments about joints. The magnitude of a joint moment is dependent on the activation level of the muscle, its contractile properties [fascicle length, fibre type, pennation angle (PA) and physiological cross-sectional area (PCSA)] and its moment arm (MA) at the joint (Zajac, 1992). The muscle MA is defined as the shortest perpendicular distance between the joint centre of rotation (CoR) and the line of action of the muscle-tendon unit (Németh & Ohlsén, 1985; Rugg et al. 1990; Spoor & van Leeuwen, 1992). Larger MAs are associated with larger joint moments (as moment = F × MA) but slower contraction velocities [as angular velocity = Tan⁻¹ (Δcontraction distance/MA)/time; see also Lieber & Friden, 2001]. Because of these relationships, muscles with long fascicles are not necessarily associated with large ranges of motion or rapid joint rotation (McClearn, 1985; Gans & Gaunt, 1991; Lieber & Friden, 2001) and neither are short-fascicled muscles inherently associated with slow angular joint velocity (e.g. short-fascicled muscles can rotate joints rapidly utilizing a small MA). These force- and contraction-velocity-modulating capacities of MAs illustrate the important influence of MAs on muscle function.

Clearly, data on MAs represent crucial information when estimating muscle function and predicting muscle forces and moments, and are thus essential to obtain a full insight into the functional morphology of an animal (Gans & Gaunt, 1991; Zajac, 1992; Pandy, 1999; Azizi et al. 2008). In addition, accurate MA data can be used in musculoskeletal modelling to predict the magnitude of joint moments and hence ground reaction forces produced by virtual models (Crompton et al. 1996; Sellers et al. 2005; Hirasaki et al. 2006; Sellers & Manning, 2007; Kramer, 1999). Such computational models are a very powerful and promising tool for understanding locomotor evolution and performance, yet they rely heavily on the availability of accurate anatomical data.

Methods of measuring moment arms

Muscle MAs can be measured in a number of ways. Traditional methods include the direct measurement of the MA as the distance between the line of action of the muscle-tendon unit and the joint CoR (McClearn, 1985; Németh & Ohlsén, 1985; Graichen et al. 2001; Meershoek et al. 2001). However, the position of the joint CoR can change during flexion and extension due to the irregular morphology of skeletal joints (e.g. the knee joint). Use of the tendon travel technique is often favoured because it requires no direct knowledge of the joint CoR, although this is implied through the calculation of joint angle (see Pandy, 1999 for implications of changes in the CoR on MA measurements), and it is also relatively cost effective (Visser et al. 1990; Thorpe et al. 1999; Payne et al. 2006b; Williams et al. 2007). By measuring the joint angle and the amount of tendon travel that the muscle-tendon unit undergoes and subsequently taking the first derivative of tendon travel divided by angular excursion of the joint, an estimate of MA can be made. Tendon travel is traditionally measured using threads or cords attached to the muscle belly and running through loops that represent the muscle’s insertion or origin. Tags on known reference points and scales are used to calculate the absolute travel distance. Photographs are taken (although video recordings can also be used) at different stages through the flexion/extension cycle of the joint and the images are digitized to yield joint angle and tendon travel. A polynomial curve is fitted, and then differentiated, to give MA (Visser et al. 1990; Thorpe et al. 1999; Payne et al. 2006b). Dissection is an unavoidable requirement of traditional techniques to ascertain an accurate measurement of the muscle’s line of action or tendon travel. The dissection of deeper musculature related to the study muscle can change the MA of the study muscles through the elimination of wrapping effects (Murray et al. 1995; Ackland & Pandy, 2009). When using more advanced methods, such as magnetic resonance imaging (Rugg et al. 1990; Spoor & van Leeuwen, 1992) and computed tomography, MAs can be measured on living or undissected specimens. These imaging methods have the advantage of measuring the MAs in situ, i.e. the MA of the Muscle Tendon Units (MTUs) in their actual configuration, and so conserve muscle wrapping effects and the effects of sesamoid bones on joint morphometry (Delp et al. 1994; Murray et al. 1995; Pandy, 1999; Krevolin et al. 2004). Further, these techniques allow the analysis of MAs in different planes, especially applicable at the shoulder and hip joints, where circumduction occurs (Garner & Pandy, 2001; Ackland & Pandy, 2009). Non-invasive imaging techniques are, however, subject to the limitation of lacking complete determination of joint CoRs (a parameter not required for the tendon travel technique), although mathematical analysis of surface geometry can be used to estimate the CoR position within a given confidence interval (Yamaguchi & Zajac, 1989; Wretenberg et al. 1996; Pandy, 1999; Sheehan, 2007). An optimization-based approach can be used to ascertain instantaneous joint axes in dynamic systems (Caravaggi et al. 2009). Other limitations of these techniques include the expense of the apparatus involved and/or time-consuming and technically difficult analyses. The tendon travel technique, however, is relatively straightforward, inexpensive and fast, allowing multiple specimens to be tested. Its reliability is limited by the accuracy of approximation of the site of the origin or insertion and of the estimated line of action of the muscle (due to the need for dissection) and the accuracy of digitization of the photographs. Further, the shape of the MA curve is heavily dependent on the type of curve used to fit the raw data (see below). Agreement between magnetic resonance imaging and tendon travel techniques is generally good, although for some muscles it can differ substantially [Spoor & van Leeuwen (1992) attributed this to a number of reasons including tension in accessory muscles causing changes in MA of the object muscle]. Pandy (1999) provides a comprehensive review of MA measurement techniques, derivation mathematics and sources of error. In this study, we use a modified tendon travel technique based on cubic spline functions to ascertain the MAs of hind limb muscles in gibbons, using cadaveric material.

Why use cubic splines?

Traditionally, MAs have been derived from differentiation of polynomial approximations of the tendon travel–joint angle relationship. However, the type of curve used to fit these data has a marked bearing on the parameters of the curve that describes the MA, i.e. if a quadratic function is used to approximate the tendon travel–joint angle relationship, the shape of the MA curve will be linear, whereas it will be constant when a linear function is used. The decision to opt for a quadratic or higher order function is often based on ‘visual’ best fit or on R² values, which have not proven to be very accurate (Angilletta, 2006). One way of avoiding this problem is to use a mathematical spline.

Cubic splines use a third-order polynomial to interpolate between data points, providing a smooth curve (Reinsch, 1967; Craven & Wahba, 1978; Hou & Andrews, 1978; Späth & Meier, 1988). Splines of varying complexity are used throughout scientific research and are favoured for allowing large data sets to be smoothed without susceptibility to Runge’s phenomenon (where high-order polynomials approximate extreme regions of the data more poorly than lower order alternatives) (Reinsch, 1967; Späth & Meier, 1988).

Muscular properties of the gibbon hind limb

As mentioned above, quantitative anatomical data on mechanically relevant parameters are often lacking for ape species, especially for the lesser apes. Although several functional anatomical studies have been conducted on the gibbon hind limb (Sigmon & Farslow, 1986; Vereecke et al. 2005; Payne et al. 2006a), to date there is only one study presenting detailed MA data, based on a single white-handed gibbon specimen (Hylobates lar) (Payne et al. 2006b).

Gibbons are highly agile apes, capable of traversing gaps in the forest canopy of up to 15 m by leaping or brachiating (Fleagle, 1974, 1976; Gittins, 1983). Their locomotor repertoire also includes bipedalism (walking), climbing and orthograde clambering (Sati & Alfred, 2002; Vereecke et al. 2005, 2006a,b), and this locomotor versatility is likely to place contrasting pressures on the musculoskeletal anatomy of the gibbon hind limb. Recent studies have highlighted how the musculo-tendinous anatomy of gibbons may be suited to performing this range of locomotor activities (Payne et al. 2006a; Channon et al. 2009). The gluteal and quadriceps femoris muscle groups have large PCSAs and thus can produce high levels of force but their short muscle fascicles may limit contraction distance and velocity (Zajac, 1992). The hamstrings and long hip flexors [sartorius (Sar) and gracilis (Gra)], by contrast, appear suited for producing relatively modest levels of force but over a much greater range of joint motion (although this depends on a plethora of other variables including MA, fibre type and the proximity and properties of surrounding muscles). The distal hind limb is characterized by short-fascicled, highly pennate muscles suitable for high force production (Vereecke et al. 2005; Payne et al. 2006a). However, accurate information on the MAs of the hind limb muscle groups is needed to better assess the role of these muscles in gibbon locomotion.

In a previous study (Channon et al. 2009), we suggested that the voluminous knee extensor muscles of gibbons may contribute to propulsion generation in leaping when associated with short MAs. In other studies, we have pointed to some potential elastic energy stores in the gibbon hind limb (Vereecke et al. 2006b; Vereecke & Aerts, 2008). Gibbons have very short-fascicled triceps surae with a long and well-developed Achilles tendon (Payne et al. 2006a; Vereecke et al. 2006b; Channon et al. 2009), which might act as an elastic energy store during locomotion. However, the long digital flexor and patellar tendons might also function as elastic springs during locomotion (Vereecke et al. 2006b; Vereecke & Aerts, 2008). A detailed understanding of the architectural make-up, MA variation and functional link between the two is essential to achieve greater insight into the potential adaptations of the gibbon hind limb for energy storage and power production during locomotion.

In this study, we measure the MAs of a selection of gibbon hind limb muscles using a modified tendon travel technique. These data are used in conjunction with data from previous research (Channon et al. 2009) to assess the function of specific muscle groups and their contribution to the range of locomotor modes used by gibbons. In addition, we compare the spline-based technique used here and the traditional, polynomial-based technique to assess the efficacy of the modified methodology for measuring MAs in cadaveric specimens.

Materials and methods

Subject data

The material used in this study comprises four gibbon cadavers of known age and sex (Table 1), i.e. one white-handed gibbon (H. lar), one silvery gibbon (H. moloch) and two siamangs (H. syndactylus). The relatively small sample analysed here is inevitable when dealing with endangered species (IUCN, 2008) but the hind limb MA data presented are very valuable as they contribute to a quantitative database of the architecture of the gibbon and enhance our understanding of the quantitative functional anatomy of gibbons (Vereecke et al. 2005; Payne et al. 2006a,b; Channon et al. 2009). The specimens were obtained from The Royal Zoological Society of Antwerp (H. lar and one H. syndactylus) and The National Museums of Scotland, Edinburgh (H. moloch and one H. syndactylus), and were kept frozen until required for this study. Cadavers were eviscerated during post-mortem examination and body mass (prior to evisceration) was hence not available for all specimens. Therefore, segment length was used to normalize MAs to remove the effect of body size, following Alexander (1977; see also Table 1). All specimens died under natural circumstances and none of the specimens exhibited any obvious musculoskeletal pathology.

Table 1.

Details of the four cadavers used in this study.

Specimen	Hylobates lar	Hylobates moloch	Hylobates syndactylus 1	Hylobates syndactylus 2
Sex	M	M	F	F
Age at death (years)	6	19	32	–
Mass at death (kg)	6.3	7.2	12.5	–
Femur length (cm)	20.5	20.5	21.5	22.7
Tibia length (cm)	16.9	19.8	21.4	19.8
Foot length (cm)	8.8	8.7	9.8	9.3
Source	RZSA	NMS	RZSA	NMS

RZSA, Royal Zoological Society of Antwerp; NMS, National Museums of Scotland; –, data were unavailable.

Moment arm measurements

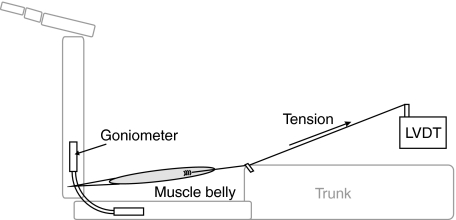
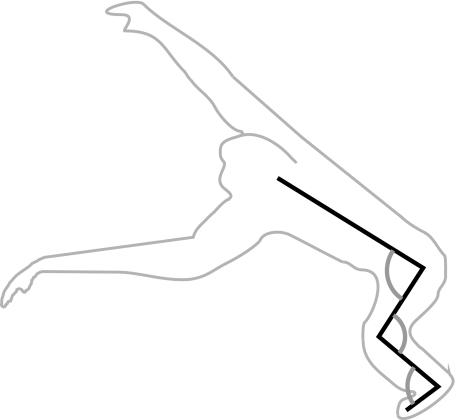
The MAs were measured using a modified version of the tendon travel technique (Spoor & van Leeuwen, 1992). A biaxial electro-goniometer (Biometrics, Gwent, UK) was positioned across the joint, secured using zip ties and connected to a differential thermocouple module and data acquisition base (sample frequency, 3 Hz; National Instruments, TX, USA) to measure joint angle. The goniometer gave readings in two perpendicular planes. Modelling the goniometer following the technique of Legnani et al. (2000) allowed the joint angle to be ascertained even when the bases were not parallel (i.e. twisted). Tendon travel was measured using a linear voltage displacement transducer (LVDT) (Celesco, Chatsworth, CA, USA), which acts like a tensioned drawstring and provides an output voltage linearly correlated to the length of wire drawn from it. The muscle was removed at its origin and a nylon fishing line (strength, 30 lb or 13.6 kg; minimal elasticity) was sutured into the muscle belly. The fishing line was passed through a zip tie positioned at the muscle’s site of origin and tied to the free end of the LVDT. The tension maintained on the line by the LVDT was adequate to keep the muscle taut during the experiment. Data from the goniometer and LVDT were collected by separate modules in a data acquisition base and using custom-written software in LabVIEW (version 8.2; National Instruments) (see Fig. 1 for apparatus set-up). Five trials per muscle were recorded, where each trial represented distal segment motion from fully flexed to fully extended and back to full flexion. Hip angle was defined as the angle enclosed between the ventral side of the trunk and the anterior aspect of the femur (range, 7–178°; Fig. 2), knee angle as the angle between the posterior aspect of the femur and the posterior of the calf (7–202°, the removal of proximal muscles allowed the knee joint to be hyper-extended; it is to be noted that this exceeds the in-vivo range of joint motion), and ankle angle as the angle between the anterior of the tibia and the dorsum of the foot (16–171°; Fig. 2). For biarticular muscles, the secondary joint was kept at a constant angle, representative of joint extension (hip ∼ 170°, knee ∼ 175°, ankle ∼ 160°; cf. Payne et al. 2006b; Thorpe et al. 1999; Williams et al. 2007). Unfortunately, we were not able to collect MA data for all of the muscles in all animals for various reasons, such as damaged muscle bellies (due to skinning by a taxidermist, Table 2).

Fig. 1.

The apparatus used for data collection. LVDT, Linear voltage displacement transducer.

Fig. 2.

The joint angles used in the analyses.

Table 2.

Muscles for which no moment arm (MA) data could be collected.

Hylobates lar	Hylobates moloch	Hylobates syndactylus 1	Hylobates syndactylus 2
Tibialis anterior		Gluteus medius	Gluteus medius
		Semimembranosus

Curve fitting

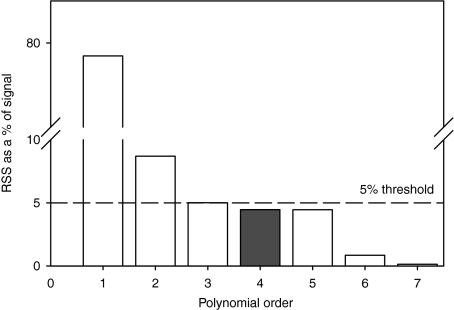
Tendon travel was plotted against joint angle and a cubic spline was used to smooth the data (LabVIEW 8.2; National Instruments). The spline could be modified by changing a balance parameter, within the boundaries 0–1, where 0 interpolates using a linear relationship and 1 interpolates between the points exactly. Traditional curve-fitting statistics (Jeffrey, 2005; Angilletta, 2006) were not useful in determining which balance parameter should be used, as the large number of degrees of freedom (due to the large number of data points per trial) always resulted in a very high significance value (1 × 10⁻¹⁸ < P < 1 × 10⁻¹⁴) regardless of the shape of the curve. Instead, the residual sum of squares (RSS) was used to choose a spline to describe our data. RSS decreases with increasingly complex curves (see Fig. 3 for the effect of polynomial complexity on RSS) and we chose the least complex spline curve where the RSS fell within 5% of the sample range, effectively yielding a signal-to-noise ratio of 19 : 1. This threshold represented a good compromise between fitting the data accurately and providing a realistically noise-free MA (however, again, this was difficult to test statistically because of the large number of data points per trial; see Fig. 3 for the technique being used to choose a polynomial curve). The splined data were then differentiated to give the instantaneous MA (as a function of joint angle).

Fig. 3.

Decreasing residual sum of squares (RSS) values for increasing orders of polynomial used to fit data from the rectus femoris at the hip. The filled bar represents the least complex model, which has an RSS of less than the 5% threshold.

One disadvantage of spline fitting is that no F(x) coefficients are given (i.e. no y = ax² + bx + c is produced), so it is not possible to calculate the instantaneous MA for a given joint angle. A polynomial curve was therefore fitted to the splined MA data, in order to provide a means of recreating the curves mathematically and allowing comparison with other studies on different species. The polynomial curves were used only for this purpose, whereas splined data were used exclusively for analysis. The same RSS-based curve-fitting technique was used to choose which polynomial we report. For example, in Fig. 3 a fourth-order polynomial is the least complex curve with an RSS value of < 5% of the signal range, so this curve was chosen. Where a sixth-order polynomial was not sufficient to go below this threshold a linear curve was described (Appendix 1).

Fascicle strain model

A simple geometric model was used to estimate fascicle strain (ΔFL/FL) during contraction. The role of the model was to estimate the fascicle strain that each respective muscle, with a specific MA and PA, undergoes during flexion or extension through the range of motion tested. Estimating fascicle strain yields insight into muscular function during locomotion by illustrating which muscles are likely to require excessive strain to rotate the joint through the range of motion seen. It also allows enquiry into the extent to which muscles with short fascicles are compensated by short MAs, to increase joint range and velocity.

The fascicle strain model for a given change in joint angle (Δθ) is formulated as:

As TanΔθ = ΔFL/MA and ΔFL is dependent on the cosine of PA

hence ΔFL/FL = [(MA × TanΔθ)/Cos(PA)]/FL.

The parameters were inserted into the model and the predicted fascicle strain for the range of motion seen during data collection was calculated. The model assumes that the muscle fascicles were at their longest, and fascicle strain = 0, when the joint started its movement. For example, for the vastus knee extensor the model assumes that the fascicles were at their longest when the knee was fully flexed and for the soleus (Sol) that the fascicles were at their longest when the ankle was maximally dorsiflexed (see also Discussion).

Hind limb kinematics

We executed a preliminary kinematic study of squat-jumping (i.e. jumping from a deep crouched position) in a group of captive white-handed gibbons (n = 4 gibbons, 12 jumps analysed; Chester Zoo, UK) to measure the actual range of motion of the hind limb joints. Squat-jumping offered the largest range of motion for the hind limb joints and is used here as an example of maximal in-vivo range of joint motion. This information is used to estimate the muscle fascicle length ranges during normal activities of gibbons. The (untrained) gibbons were recorded during spontaneous jumping bouts using two orthogonally positioned (one lateral and one frontal) high-speed video cameras (125 Hz; AOS Technologies, Switzerland) and the joint centres were digitized using custom-written software (LabVIEW, National Instruments) to calculate two-dimensional joint angles. The cranial view was used solely to ensure that the jumps were parallel to the field of view of the lateral camera, from which all of the joint angles were measured.

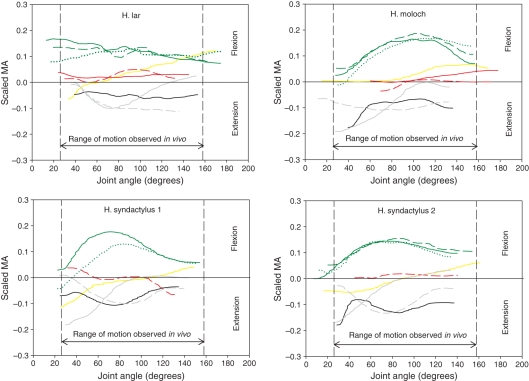
The range of motion observed at the hip, knee and ankle during squat-jumping was 26–158°, 34–143° and 58–164°, respectively (Figs 4–6). Joint angles are defined as explained above.

Fig. 4.

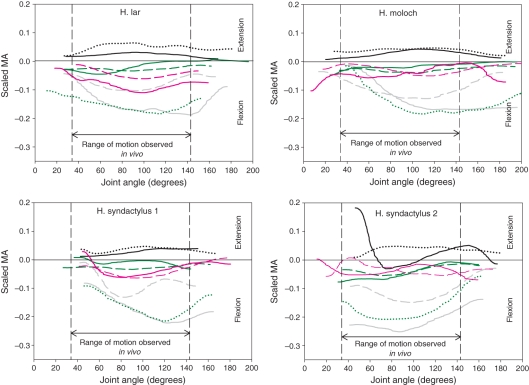
Scaled moment arms (MAs) at the hip for the four specimens. Solid yellow line, adductor magnus; solid red line, gluteus medius; dashed red line, gluteus superficialis; solid black line, rectus femoris; solid grey line, gracilis; dashed grey line, sartorius; solid green line, biceps femoris; dashed green line, semimembranosus; dotted green line, semitendinosus. The vertical black dashed lines indicate the range of joint motion used during jumping (see Materials and methods for jumping data collection).

Fig. 6.

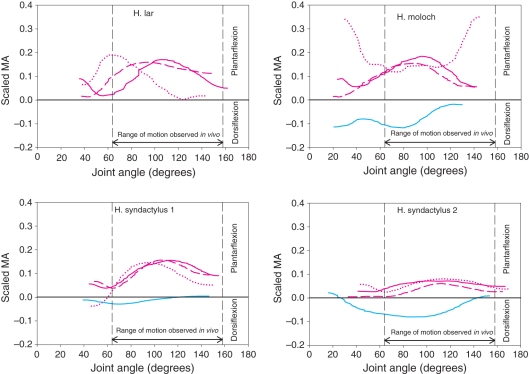
Scaled moment arms (MAs) at the ankle for the four specimens. Solid pink line, gastrocnemius lateralis; dashed pink line, gastrocnemius medialis; dotted pink line, soleus; cyan line, tibialis anterior. The vertical black dashed lines indicate the range of joint motion used during jumping (see Materials and methods for jumping data collection).

Results

Muscle moment arms

At the hip

The semimembranosus (SeM), Gra, biceps femoris (BiF) and semitendinosus (SeT) had the largest MAs of the (tested) muscles crossing the hip joint [maximal MA interspecific mean: Gra, 3.41 ± 0.85 cm; SeM, 3.41 ± 0.64 cm; BiF, 3.41 ± 0.21 cm; SeT, 2.98 ± 0.42 cm; scaled MA values are presented in Fig. 4]. The shape of these MA curves was consistent in all specimens, except for the white-handed gibbon, where there was a more-or-less linear relationship between MA and joint angle for the hamstrings instead of the bell-shaped curve that was found in the other specimens. The gluteal muscles had the smallest MAs [maximal MA interspecific (mean ± SD): gluteus superficialis (GSu), 0.85 ± 0.43 cm; gluteus medius (GMe), 0.85 ± 0.21 cm] of all hip muscles. In all specimens, the MA–joint angle curve of adductor magnus (AdM) crossed the x-axis, implying a change of function from flexion to extension; the same phenomenon was also seen for the Gra in all but one specimen (the silvery gibbon) where it approached but never reached zero (minimum value 0.06). The MA–joint angle curve of GMe also crossed the x-axis in two specimens (silvery gibbon and siamang 1) but the change in function was reversed in the two specimens: in the silvery gibbon the change in function was from flexion to extension and in the siamang it was from extension to flexion. The rectus femoris (RFe) MA varied greatly in magnitude, particularly at the extreme joint angles measured.

At the knee

The Gra (4.10 ± 0.78 cm) and SeT (3.90 ± 0.78 cm) had the largest MAs of the tested muscles crossing the knee joint (Fig. 5), the shape of the MA curve for these muscles being broadly similar in all specimens. The hamstrings (BiF, 0.98 ± 0.39 cm; SeM, 0.78 ± 0.20 cm) and the quadriceps [vastus lateralis (VaL), 0.05 ± 0.01 cm; RFe, 0.78 ± 0.20 cm] had the smallest interspecific mean MAs of the knee joint muscles. The MAs of the two gastrocnemius heads [gastrocnemius medialis (GaM), 1.17 ± 0.20 cm; gastrocnemius lateralis (GaL), 1.76 ± 0.39 cm] remained small throughout the full range of motion of the knee and crossed the x-axis at the extreme joint angles in two specimens (siamangs 1 and 2), indicating a change of function. The MA–joint angle curve of BiF also crossed the x-axis in two specimens (siamang 1 and the white-handed gibbon) but the change in function was reversed in the two specimens, i.e. in the siamang the change in function was from extension to flexion and in the white-handed gibbon it was from flexion to extension. The MA–joint angle curve of RFe of siamang 2 was unusually shaped in comparison to the other specimens, especially at extreme joint angles; it was also the only specimen where the MA of RFe at the knee crossed the x-axis.

Fig. 5.

Scaled moment arms (MAs) at the knee for the four specimens. Solid black line, rectus femoris; dotted black line, vastus lateralis; solid grey line, gracilis; dashed grey line, sartorius; solid green line, biceps femoris; dashed green line, semimembranosus; dotted green line, semitendinosus; solid pink line, gastrocnemius lateralis; dashed pink line, gastrocnemius medialis. The vertical black dashed lines indicate the range of joint motion used during jumping (see Materials and methods for jumping data collection).

At the ankle

The Sol (1.75 ± 0.92 cm, maximal interspecific mean MA) had the largest MA of the ankle joint muscles (Fig. 6) and GaM and GaL had similar MAs throughout the entire range of motion of the ankle joint (1.38 ± 0.46 cm and 1.20 ± 0.46 cm, respectively). The tibialis anterior (TiA) had the smallest MA (0.74 ± 0.37 cm) and crossed the x-axis in two specimens, implying that the insertion passed the joint CoR during extreme plantarflexion.

Fascicle strain model

The fascicle strain model estimates how much strain the muscle fascicles must undergo (shortening distance during contraction relative to the fascicle rest length) to move the joint through the observed range of motion. Vertebrate muscle fascicle strain data from in-vivo activity is widespread but variable between ∼0.20 and ∼0.36, depending on the species, activity and measurement technique (Griffiths, 1991; Kawakami et al. 2002; Daley & Biewener, 2003; Lichtwark et al. 2006; Wakeling et al. 2006). As no fascicle strain data for gibbons are available to date, our estimated strains will be compared with the values shown here.

Muscles at the hip

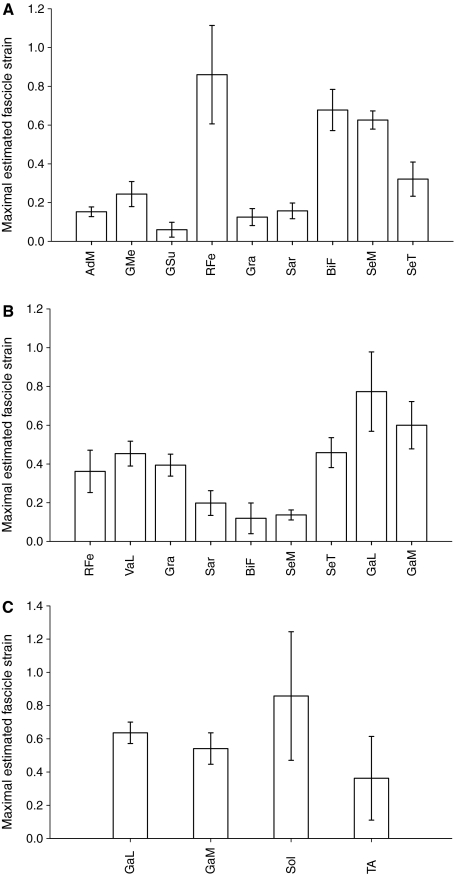
The RFe was predicted to exhibit the largest fascicle strain (0.86 ± 0.25 cm, Fig. 7A), although BiF and SeM were also predicted high strains (0.68 ± 0.11 cm and 0.63 ± 0.05 cm, respectively). SeT and GMe were predicted to have strains of 0.32 ± 0.09 cm and 0.24 ± 0.06 cm, respectively. The lowest strains were predicted for Sar, AdM, Gra and GSu (0.16 ± 0.04 cm, 0.15 ± 0.03 cm, 0.12 ± 0.04 cm and 0.06 ± 0.04 cm, respectively).

Fig. 7.

Estimated fascicle strain during the range of motion tested for muscles at the hip (A), knee (B) and ankle (C). AdM, adductor magnus; BiF, biceps femoris; SeM, semimembranosus; SeT, semitendinosus; Sol, soleus; GMe, gluteus medius; GSu, gluteus superficialis; Gra, gracilis; Sar, sartorius; RFe, rectus femoris; VaL, vastus lateralis; GaL, gastrocnemius lateralis; GaM, gastrocnemius medialis; TiA, tibialis anterior.

Muscles at the knee

The GaL and GaM were predicted to have the highest fascicle strains crossing the knee (0.77 ± 0.20 cm and 0.60 ± 0.12 cm, respectively, Fig. 7B). SeT, VaL, Gra and RFe were predicted to have strains of 0.46 ± 0.08 cm, 0.45 ± 0.06 cm, 0.39 ± 0.06 cm and 0.36 ± 0.01 cm, respectively. The lowest strains were predicted for BiF, SeM and Sar (0.12 ± 0.08 cm, 0.14 ± 0.03 cm and 0.20 ± 0.06 cm, respectively).

Muscles at the ankle

The highest predicted strains across the ankle were in Sol (0.86 ± 0.39 cm, Fig. 7C). GaL and GaM were predicted to have strains of 0.64 ± 0.06 cm and 0.54 ± 0.09 cm, respectively. The lowest predicted strains were in TiA (0.36 ± 0.25 cm).

Discussion

Muscle function

By combining the MA data with quantitative information about muscle properties from previous studies we can assess the function of different hind limb muscle groups. Our fascicle strain model gives additional insight into muscle function by predicting the strains occurring in the muscle fascicles during joint motion. Although this model is quite simple and makes several assumptions (see below), the predicted fascicle strains can be used as rough estimates in evaluating muscle function. In-vivo strain values have been published for several animals (cats: Griffiths, 1991; humans: Lichtwark et al. 2006; Kawakami et al. 2002; Wakeling et al. 2006; guinea fowl: Daley & Biewener, 2003; see also above). Predicted strain values that fall outside the reported range of in-vivo values are considered ‘unrealistic’.

Hip extension

The gluteal muscles had relatively small MAs in all animals tested (Fig. 4) and the fascicle strain model estimated that they would undergo moderate fascicle strains during the range of in-vivo motion (Fig. 7A). Small MAs require large muscle forces to produce high joint torques but do not require long fascicles for rapid joint rotation (Gans & Gaunt, 1991; Alexander, 1996; Lieber & Friden, 2001). The gluteal muscles of gibbons have been shown to possess a large PCSA, which is proportional to force production, and short fascicles (Channon et al. 2009). The glutei have MAs of ∼0.025× femur length, i.e. 2–8× smaller MAs than other muscles crossing the hip, but possess 4–10× as much PCSA as other muscles crossing the hip (Channon et al. 2009) and are therefore likely to maintain equal or greater moment production capabilities than other hip muscles. Having muscles with a small MA and a large PCSA probably reduces thigh mass, and hence thigh inertia, contributing to efficient locomotion (Witte et al. 1991; Crompton et al. 1996; Steudel, 1996; Schoonaert et al. 2007). This particular muscle architecture enables the production of large amounts of joint power without high thigh muscle mass (as would be the case for long-fascicled, voluminous muscles).

Powerful hip extension is useful for a variety of locomotor tasks including clambering, climbing (Preuschoft, 2002; Isler, 2005) and leaping (Alexander, 1995; Scholz et al. 2006), and the gross architecture of gibbon gluteals is similar to that of the bonobo, a very proficient (yet atypical) leaper (Payne et al. 2006a; Scholz et al. 2006; note, however, that the studies on bonobos utilized a polynomial-based approach and digitized photographic images). Our results also indicate that the MAs of the gluteals are relatively smaller in gibbons than in the great apes (except bonobos; Payne et al. 2006b), facilitating increased angular velocity and excursion at the hip (Scholz et al. 2006) for a given distance of muscular contraction (Gans & Gaunt, 1991). There were no outstanding differences in MA of the hip extensors between gibbon species, despite a difference in the prevalence of leaping (∼6% locomotor time for siamangs vs. ∼15% for white-handed gibbons; Whitmoor, 1975). Differences in muscle architecture between species are very subtle (Channon et al. 2009) and interspecific analyses are hampered by the small sample size analysed here.

The large MAs of the hamstrings at the hip (Fig. 4) and the unrealistically high fascicle strains (interspecific hamstring mean 0.56) predicted by the fascicle strain model (Fig. 7A) suggest that, despite the relatively long fascicles (and hence sarcomeres in series) of BiF and SeT, these muscles are unlikely to be involved in powerful hip extension during jumping. This hypothesis is supported by their small PCSA (Channon et al. 2009), which precludes them from producing large amounts of force (although, even with a small PCSA, large moment production might be achieved thanks to the large MA). Instead, they may be involved in producing a modest hip extension force during bipedalism, as in humans (Hase & Stein, 1999), or may play a fine-tuning or stabilizing role during terrestrial locomotion (see below). The advantage of using the glutei instead of the hamstrings as powerful hip extensors is twofold. First, high muscle powers require large muscle volume and locating that volume on the femur shaft would increase the limb inertia and hence the metabolic costs of other (leg swinging) activities such as walking (Witte et al. 1991; Crompton et al. 1996; Steudel, 1996; Schoonaert et al. 2007). Second, the hamstrings are biarticular (see below for how secondary MA might affect estimates of fascicle strain) and, during powerful movements such as jumping, extending the hip might (depending on both joint positions) require muscular effort (and hence metabolic energy) from an antagonist (here the knee extensors) to prevent energy wastage through knee flexion (the hamstrings’ other role).

Hip flexion

Activities that require hip flexion, i.e. swinging the leg forward during terrestrial locomotion or lifting the legs during brachiation, do not require high levels of muscular force (Bertram & Chang, 2001) but call for a wide range of motion instead. The biarticular muscles Sar and Gra (which flex both hip and knee) had large MAs (Figs 4 and 5) that, thanks to their long fascicles, facilitate a large range of motion at both joints as predicted by the fascicle strain model (Fig. 7A,B). This large range of motion is probably useful in achieving the wide range of joint angles used during leg-lift brachiation (Usherwood & Bertram, 2003; Channon et al. 2009) and during quadrumanous clambering, where limb placement is highly variable. They also have very small PCSAs but can increase torque production by using a large MA. This has the added benefit of decreasing the muscle mass and, hence, the rotational inertia of the thigh, saving metabolic energy during locomotion (Steudel, 1996).

The short fascicles of RFe and relatively large MA lead to unrealistically high strains to obtain the range of hip flexion seen in vivo, as predicted by the model (interspecific mean, 0.86). This implies that RFe does not act as a primary hip flexor but is probably synergistic to the other quadriceps muscles (i.e. the vasti) in knee extension (see below).

Thigh adduction

The MA of AdM was small throughout the tested range of hip flexion/extension and presented a change of role from flexion to extension with decreasing joint angle. This is due to a change in position of the muscle’s insertion relative to its origin. When the hip joint angle is larger than 90°, the line of action of the muscle suggests that it acts as a flexor (second to an adductor) but when the hip is flexed (0° < hip angle < 90°) its line of action indicates hip extension. However, its main role is undoubtedly thigh adduction (Sigmon & Farslow, 1986). In all specimens, the fascicle strain model predicted small fascicle length changes through the flexion/extension cycle. As the MA was not measured during adduction/abduction, it is not possible to accurately suggest what the result in adduction would have been. However, the origin of AdM is approximately circular in shape (it covers the obturator foramen; see also Sigmon & Farslow, 1986), which makes it unlikely that the MA, and hence the fascicle strain model, would be radically different from the flexion/extension results seen here. Further data are, however, desirable to support or refute this hypothesis.

Knee extension

The fascicle strain model indicates that the short fascicles of RFe are more adept at knee extension than hip flexion. Unpublished work on the fibre type composition of gibbon quadriceps supports this hypothesis; RFe is made up almost entirely of type 2 (both a and b) fast-twitch fibres (as in galagos; Ariano et al. 1973) without a significant proportion of type 1 slow-twitch fibres (as in humans; Saltin et al. 1977; A.J.C., personal observation). As type 2 muscle fibres are associated with fast, powerful movements it seems likely that RFe has a primary role in knee extension. In gibbons, RFe probably acts in concert with the powerful vasti to obtain knee extension (although the anatomical approach taken here would not differentiate between the functions of these muscles, as they share an insertion). Muscle volume dedicated to knee extension is likely to be associated with powerful movements, such as jumping and climbing, at both of which gibbons are very proficient (Fleagle, 1974; Gittins, 1983). The voluminous VaL has a small MA at the knee that, according to the fascicle strain model, allows its short fascicles (Channon et al. 2009) to execute the range of knee motion observed in vivo. The other vasti (vastus medialis and vastus intermedius) were not measured in this study but are likely to have similar fascicle strain estimates to VaL as they share an insertion, originate from a similar position and have a similar muscle architecture (Channon et al. 2009). Again, there were no outstanding differences in MA of the knee extensors between gibbon species (see above), which is probably due in part at least to the small sample size analysed here.

The short fascicle/small MA combination seen in the quadriceps femoris (RFe and vasti) may also facilitate elastic energy storage during locomotion, in the well-developed patellar tendon (Vereecke et al. 2006b). Recent studies on human ankle morphology have suggested that the size of the MA is more important than tendon stiffness in facilitating storage of elastic strain energy in tendons during cyclical locomotor modes, with a small ankle MA leading to enhanced energy storage and recoil, and hence more economical locomotion (Scholz et al. 2008). When extrapolated to the knee joint, this could mean that the small MA of the quadriceps might, together with appropriate tendon properties, facilitate elastic energy recovery via the patellar tendon.

Knee flexion

All knee flexors located on the thigh had long fascicles, small PCSAs (Channon et al. 2009) and relatively large MAs. The fascicle strain model predicted that none would require unrealistically high strains to flex the knee joint fully. As with hip flexion, activities involving knee flexion do not require large amounts of force production and so it is not surprising that the main knee flexors have neither small MAs nor large PCSAs. Again, having large MAs may allow the long-fascicled muscles to produce relatively larger knee torques but adding relatively little mass to the thigh.

The gastrocnemius was predicted to be a poor knee flexor by the fascicle strain model, which is not surprising as many previous studies have indeed indicated that it is the main ankle plantarflexor in a range of mammalian taxa (Wickiewicz et al. 1983; Alexander, 1995, 1996; Vereecke et al. 2005; Payne et al. 2006a).

Ankle plantarflexion

Interestingly, the triceps surae were predicted to undergo very high muscle strains at the ankle (group average, 0.68). This observation is surprising as the group is considered to be the primary plantarflexor (see above). It may be that the group is involved primarily in isometric contraction during cyclical locomotion, where elastic energy may be stored in the well-developed Achilles tendon (Vereecke et al. 2006b), as in several other species (Alexander, 1984). A potential candidate for large joint excursion at the ankle is the digital flexor group, which has fascicles of a similar length as the triceps surae but acts via an MA that is probably smaller, given its site of insertion (the insertion tendon passes down the medial side of the calcaneus close to the talocrural joint), and therefore elicits smaller fascicle strains (note that the digital flexor MA was not measured in this study).

Payne et al. (2006b) found that the triceps surae MA at the ankle in gibbons was short but of a similar size to that seen in other apes. However, the mass-specific fascicle length of the calf muscles was considerably shorter in gibbons compared with the other apes (1.6 cm for gibbons vs. 2.2 cm interspecific mean for other apes; Payne et al. 2006a), indicating a functional difference between lesser and great ape species.

Ankle dorsiflexion

The MA of TiA was highly variable between specimens (Fig. 6) and, as a result, the fascicle strain estimates also vary widely. It is likely that the presence of retinaculae contributed to the variability of these data even though the retinaculae at the ankle were left intact or reconstructed during data collection. The (superior and inferior) retinaculae reduce the MA of the TiA (and of other muscles running through the retinaculae, e.g. digital flexors and extensors) and avoid ‘bowstringing’ of the tendons, i.e. prevent the tendon taking a direct line between its origin (on the proximomedial tibia) and its insertion (on the lateral cuneiform of the foot).

Large moment arms for fine control, small moment arms for angular velocity and elastic energy storage

One could predict that, in order to maximize torque production, long-fascicled muscles will be associated with large MAs, whereas short-fascicled muscles will have small MAs to allow a full range of motion and high angular velocity. However, our model shows that such a clear correlation between fascicle length and MA is not observed in all muscles. One reason for this could relate to control. In a short-fascicled/small-MA muscle a very small change in fascicle length elicits a large change in joint position. If, however, a large MA is used (for the same fascicle length), the movement is smaller and a finer degree of control is possible. This may be especially advantageous if the muscles are involved in stabilization (rather than realizing a large range of motion) or if there are synergists that can help elicit extreme joint angles (as with RFe when acting at the hip).

In gibbons, the short-fascicled/small-MA muscles may use short fascicles to reduce the amount of muscle mass on the hind limb and reduce locomotor cost. By reducing fascicle length, muscles can increase PCSA (and hence propensity for force production) with no penalty in limb inertia. The trade-off of having short fascicles is that the range of motion and angular joint velocity (limiting work and power, respectively) may be compromised but using a small MA increases the range of motion and angular joint velocity.

Short fascicles and small MAs may also be advantageous for eliciting strain and hence elastic energy storage in tendinous tissues (Scholz et al. 2008). Channon et al. (2009) showed that the major tendons in the gibbon hind limb (Achilles and patellar) are both associated with short-fascicled muscle groups (triceps surae and quadriceps femoris, respectively). Short-fascicled muscles with long, well-developed tendons are often associated with elastic energy storage, where the muscle fascicles act mainly isometrically, eliciting tendon strain and elastic energy storage. Here we found that the quadriceps femoris possesses a small MA and short fascicles coupled in series with a well-developed tendon (patellar) and so is a likely candidate for elastic energy storage during gibbon locomotion. The short-fascicled triceps surae had a relatively large MA and appeared to require relatively high fascicle strains to elicit a large range of motion. The substantial Achilles tendon associated with the group may also be used as an elastic energy store. This would explain the short-fascicled nature of the triceps surae, as during cyclical locomotion the muscle fascicles could act isometrically, storing strain energy in the tendon. Further biomechanical studies into tendon properties and gibbon locomotor kinematics are required to enhance our understanding of these mechanisms during the different locomotor modes of gibbons.

Comparison of techniques, spline vs. polynomial

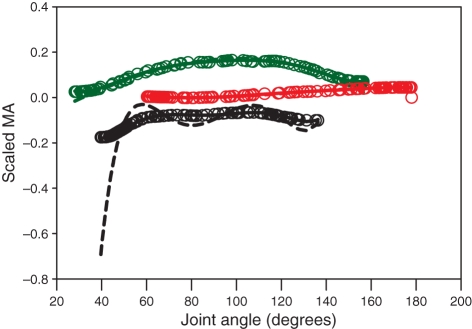
The differences in MAs obtained with the traditional, polynomial-based technique and the spline-based technique were inconsistent between individual muscles and specimens (Fig. 8). In some muscles, the two methods predicted very similar MAs (Fig. 8; GMe), whereas in others (Fig. 8; RFe) there were large differences, particularly at extreme joint angles, leading to MAs that fluctuate excessively and/or increase in magnitude to a size that we would consider unrealistic given our knowledge of the joint geometry. This is probably attributable to fitting a polynomial to the large and varied dataset and then differentiating the resulting curve. The differentiation stage amplifies the small inflections made by the original function, resulting in unrealistically high MA values. Fitting a polynomial directly to the spline gave a very close fit, which deviated little at extreme values; the coefficients of these polynomials are given in Appendix 1.

Fig. 8.

The differences in predicted moment arm (MA) for polynomial-based and spline-based techniques for three muscles. Black, rectus femoris muscle; green, biceps femoris muscle; red, gluteus medius muscle. Dashed lines, traditional (polynomial-based) technique; open circles, spline based technique; solid lines, polynomial fitted to the splined data.

The cubic splines used in this investigation produced MA curves that were at least as feasible, given the basic joint geometry, as their polynomial counterparts and in many cases the cubic spine method gave more feasible results. Polynomial interpolation is particularly susceptible to erratic behaviour at the extremes of the data set (as seen in Fig. 8; RFe). This tendency, termed Runge’s phenomenon (Epperson, 1987), is caused by the high sensitivity of high-order polynomials to small changes in the dependent variable (in this case tendon travel).

One of the disadvantages of smoothing by spline interpolation is that there is no definitive curve output, i.e. an F(x) is not produced. Having a definite function has several advantages: the curve can be reproduced exactly, y can be calculated for a given x and curves can be compared more easily. The output of a spline function is a vector of y-coordinates for the x-coordinate input vector. We have presented polynomial functions approximating the spline-smoothed data to yield an approximate F(x) to allow others to replicate the curves produced by our spline functions for comparison with other studies only (Appendix 1).

Without reanalysing the raw data it is difficult to estimate the effect that the use of spline fitting would have on the results of past studies that used polynomial interpolation. Many previous studies used digitized photographs to attain tendon travel and so the number of data points per trial was much smaller than in this study (n ∼ 10–30 compared with n = 150 per trial), so that polynomial approximation may have behaved less erratically. When data from this study are compared with the study of Payne et al. (2006b) of gibbon MAs the results are mixed, with some muscles similar in shape and magnitude to the previous study (RFe at the hip, VaL, BiF, SeT, Gra, GaM and GaL across the knee), some muscles similar in magnitude only (AdM, SeT across the hip, SeM across hip and knee), some in curve shape only (GSu, GMe), and some not similar in either attribute (BiF at the hip). It can be argued that MAs derived through magnetic resonance imaging or computed tomography may be more accurate (Rugg et al. 1990; Spoor & van Leeuwen, 1992; Wretenberg et al. 1996), as they allow the avoidance of dissection damage to the muscle’s line of action and direct measurement of the joint CoR (and hence joint angle). They are, however, expensive to perform and require technical expertise and complex analyses to yield usable results. The tendon travel technique, however, is intuitive, simple and cost effective. Our modifications to it do not change any of these properties; the equipment used was of modest value and the analysis can be performed in many basic computer packages. The most pertinent advantages of the technique outlined here are its repeatability (by removing subjective measurements in digitizing and curve fitting) and plasticity (by changing the curve-fitting parameters or thresholds). These characteristics make the modified tendon travel technique a favoured method of MA derivation when using cadaveric material.

Assessment of the fascicle strain model

The simple model presented here combines MA and muscle architecture data and attempts to estimate fascicle strain in vivo but there are several sources of error associated with our model’s calculation of fascicle strain. The measurement of initial (resting) fascicle length is taken from cadaveric gibbon muscles and so may not be identical to in-vivo resting length. However, to obtain the best possible estimates, the specimens were slowly defrosted at room temperature before dissection and exhibited no obvious muscle tension in the form of rigor (Jungk et al. 1967). A second potential source of error is that the model does not account for the effect of secondary MA on fascicle strain for biarticular muscles, several of which exhibited unrealistically high strains. We used fixed and consistent secondary joint angles during measurements but there is likely to be some unaccountable change in primary MA (and hence fascicle strain) with secondary joint angle. MacFadden & Brown (2007) quantified the effect of secondary joint angle on primary MA in cats and found quite substantial effects for biarticular muscles. Our model also assumes that there is no change in PA during contraction but several studies have shown the PA to vary between 18° and 30° during contraction of mammalian muscle, which would, however, only reduce the model’s denominator from 1 to 0.95–0.87 and thus have little effect on the majority of strain estimates (Lichtwark & Wilson, 2005; Azizi et al. 2008; McGowan et al. 2008). Our fascicle strain estimates were calculated using joint angle attained during the MA data collection and there is likely to be a small error associated with this (see above). Finally, our model assumes fascicle homogeneity throughout the muscle belly and recent studies have shown this not to be the case (Carroll et al. 2008. Our model predicted fascicle strains in excess of what we would consider feasible for several muscles. Despite these limitations, we believe that the model is adequate to estimate muscle function, even if numerical values of fascicle strain are not exact. A more complex version of the model, e.g. with incorporation of force-strain data, could provide additional insight and might indicate that muscles use short MAs to allow them to remain at an optimal length for longer, or otherwise explain the results shown here.

Conclusions

This study shows that the gibbon hind limb displays a functional specialization of the muscles to different locomotor tasks. The hip and knee extensor muscles (with large PCSAs coupled to small MAs) are probably advantageous for powerful movements such as leaping and climbing. Conversely, the slender hip and knee flexors (with large MAs and long fascicles) are probably useful in providing a wide range of limb placement for support or for leg lift during brachiation. Muscles with short fascicles coupled to long MAs may represent a method of increasing control during precise limb placement. The triceps surae and quadriceps femoris muscle groups may provide some means of storing elastic energy in the substantial Achilles and patellar tendons, respectively. Additional in-depth biomechanical studies could further elucidate the relationship between morphology and locomotor biomechanics in gibbons.

Appendix

Appendix 1a: Polynomial approximations to describe the scaled MA curves of H. lar. The curve is described as an nth order polynomial and describes y (scaled MA) in terms of hx⁷ + gx⁶ + fx⁵ + ex⁴ + dx³ + cx² + bx + a; x is joint angle in degrees. Where it was not possible to obtain a polynomial that minimized the RSS to within 5% of the range, a linear curve is quoted (see text for curve-fitting methodology)

		Coefficients
Muscle	Polynomial order	RSS/range (%)	g	f	e	d	c	b	a
Hip
Adductor magnus	3	3.2					−4.7E−06	2.3E−03	−1.3E−01
Gluteus medius	4	1.2				−9.7E−08	2.8E−05	−2.5E−03	8.4E−02
Gluteus superficialis	6	1.2		2.8E−10	−1.1E−07	1.6E−05	−1.1E−03	3.2E−02	−3.3E−01
Rectus femoris	4	3.1				1.4E−07	−3.8E−05	2.9E−03	−1.1E−01
Gracilis	6	1.1		2.6E−10	−1.2E−07	2.2E−05	−1.7E−03	6.0E−02	−7.3E−01
Sartorius	4	2.8				−2.9E−07	9.4E−05	−1.0E−02	2.8E−01
Biceps femoris	Lin.	2.7						−5.9E−04	1.8E−01
Semimembranosus	6	4.7		1.7E−11	−8.0E−09	1.4E−06	−1.0E−04	3.1E−03	1.0E−01
Semitendinosus	Lin.	41.7						2.4E−04	7.9E−02
Knee
Rectus femoris	3	1.9					−3.5E−06	6.3E−04	4.0E−04
Vastus lateralis	4	2.2				8.0E−08	−3.0E−05	3.5E−03	−6.2E−02
Gracilis	7	1.1	−2.0E−12	1.2E−09	−3.0E−07	3.6E−05	−2.2E−03	6.4E−02	−7.1E−01
Sartorius	5	1.9			−3.1E−09	1.1E−06	−1.1E−04	3.0E−03	−6.0E−02
Biceps femoris	4	4.0				−1.0E−07	3.1E−05	−2.4E−03	1.6E−02
Semimembranosus	3	4.2					1.9E−06	−2.7E−04	−2.1E−02
Semitendinosus	4	1.2				1.2E−07	−1.8E−05	−1.2E−04	−1.0E−01
Gastrocnemius lateralis	6	3.1		−7.1E−11	3.0E−08	−4.6E−06	3.4E−04	−1.3E−02	1.4E−01
Gastrocnemius medialis	3	2.0					1.2E−05	−2.5E−03	7.2E−02
Ankle
Gastrocnemius lateralis	6	3.8		1.8E−10	−7.3E−08	9.7E−06	−4.4E−04	−1.1E−03	3.6E−01
Gastrocnemius medialis	5	3.1			1.3E−08	−4.7E−06	5.8E−04	−2.5E−02	3.8E−01
Soleus	6	4.4		−5.3E−10	2.4E−07	−4.0E−05	3.0E−03	−9.9E−02	1.2E+00

Appendix 1b: Polynomial approximations to describe the MA curves of H. moloch

			Coefficients
Muscle	Polynomial order	RSS/range (%)	g	f	e	d	c	b	a
Hip
Adductor magnus	4	2.4				−1.2E−07	3.6E−05	−2.4E−03	4.3E−02
Gluteus medius	Lin.	4.8						4.0E−04	−2.5E−02
Gluteus superficialis	4	3.6				1.2E−07	−5.3E−05	7.6E−03	−3.5E−01
Rectus femoris	5	4.5			−5.6E−09	2.2E−06	−3.6E−04	2.6E−02	−7.9E−01
Gracilis	4	1.4				−6.1E−07	1.4E−04	−6.9E−03	−8.9E−02
Sartorius	3	2.1					1.1E−05	−1.6E−03	−4.3E−02
Biceps femoris	4	4.5				−7.2E−08	−1.0E−05	4.3E−03	−9.8E−02
Semimembranosus	5	0.6			6.1E−09	−2.4E−06	3.0E−04	−1.3E−02	2.2E−01
Semitendinosus	3	1.9					−2.6E−05	6.0E−03	−1.8E−01
Knee
Rectus femoris	3	4.6					−4.4E−06	9.3E−04	−1.2E−02
Vastus lateralis	3	3.4					−3.3E−06	6.2E−04	1.7E−02
Gracilis	5	2.1			−1.9E−09	8.5E−07	−1.2E−04	3.8E−03	−2.4E−02
Sartorius	4	3.8				3.8E−08	2.5E−06	−1.8E−03	−7.3E−03
Biceps femoris	4	3.4				3.0E−08	−1.1E−05	1.5E−03	−7.6E−02
Semimembranosus	5	1.2			−9.0E−10	3.9E−07	−5.7E−05	3.2E−03	−8.7E−02
Semitendinosus	4	2.4				−7.4E−08	4.6E−05	−8.1E−03	2.5E−01
Gastrocnemius lateralis	6	2.7		1.6E−11	−1.0E−08	2.2E−06	−2.0E−04	7.8E−03	−1.5E−01
Gastrocnemius medialis	5	1.3			−1.3E−09	5.9E−07	−8.8E−05	4.7E−03	−9.0E−02
Ankle
Gastrocnemius lateralis	6	2.0		1.9E−10	−6.8E−08	7.7E−06	−3.0E−04	1.6E−03	1.4E−01
Gastrocnemius medialis	5	0.9			1.2E−08	−3.8E−06	4.0E−04	−1.3E−02	1.5E−01
Soleus	7	4.3	−1.6E−11	8.5E−09	−1.7E−06	1.8E−04	−9.5E−03	2.4E−01	−1.9E+00
Tibialis anterior	6	3.3		−3.6E−10	1.2E−07	−1.4E−05	7.3E−04	−1.6E−02	−1.6E−03

Appendix 1c: Polynomial approximations to describe the MA curves of H. syndactylus 1

			Coefficients
Muscle	Polynomial order	RSS/range (%)	f	e	d	c	b	a
Hip
Adductor magnus	3	4.8				−9.3E−06	2.8E−03	−1.8E−01
Gluteus superficialis	4	4.8			−4.6E−07	1.1E−04	−8.4E−03	2.2E−01
Rectus femoris	5	2.2		−1.5E−08	4.8E−06	−5.2E−04	2.2E−02	−3.7E−01
Gracilis	4	4.4			−2.6E−07	4.5E−05	4.9E−04	−2.4E−01
Sartorius	5	0.6		−1.0E−08	3.3E−06	−3.4E−04	1.1E−02	−9.9E−02
Biceps femoris	5	4.0		2.6E−09	−4.2E−07	−5.5E−05	1.1E−02	−2.2E−01
Semitendinosus	5	0.8		5.7E−09	−1.8E−06	1.6E−04	−1.7E−03	−7.4E−02
Knee
Rectus femoris	Lin.	4.0					3.0E−04	−1.3E−03
Vastus lateralis	5	2.0		3.1E−09	−1.4E−06	2.2E−04	−1.4E−02	3.3E−01
Gracilis	3	4.8				2.0E−05	−5.3E−03	1.3E−01
Sartorius	6	0.3	5.4E−10	−2.7E−07	5.1E−05	−4.5E−03	1.9E−01	−2.8E+00
Biceps femoris	4	3.3			−2.6E−07	6.8E−05	−5.8E−03	1.5E−01
Semitendinosus	5	2.8		−4.4E−09	2.1E−06	−3.2E−04	1.8E−02	−4.2E−01
Gastrocnemius lateralis	4	3.9			−3.5E−07	1.3E−04	−1.5E−02	4.6E−01
Gastrocnemius medialis	3	4.4				1.2E−05	−2.4E−03	6.1E−02
Ankle
Gastrocnemius lateralis	5	1.3		1.3E−08	−5.6E−06	8.5E−04	−5.1E−02	1.1E+00
Gastrocnemius medialis	5	4.1		2.4E−08	−1.0E−05	1.5E−03	−9.5E−02	2.1E+00
Soleus	5	3.3		2.4E−08	−8.9E−06	1.1E−03	−5.6E−02	8.7E−01
Tibialis anterior	4	1.4			−1.9E−07	5.7E−05	−5.1E−03	1.2E−01

Appendix 1d: Polynomial approximations to describe the MA curves of H. syndactylus 2

			Coefficients
Muscle	Polynomial order	RSS/range (%)	h	g	f	e	d	c	b	a
Hip
Adductor magnus	Lin.	4.3							8.8E−04	−8.1E−02
Gluteus superficialis	5	2.4				7.0E−09	−2.6E−06	3.4E−04	−1.8E−02	3.6E−01
Rectus femoris	7	3.3		7.8E−12	−3.7E−09	6.8E−07	−5.9E−05	2.4E−03	−3.2E−02	−2.4E−01
Gracilis	3	2.2						−1.9E−05	4.9E−03	−3.0E−01
Sartorius	5	1.3				−1.4E−08	4.0E−06	−3.8E−04	1.1E−02	−1.1E−01
Biceps femoris	5	1.6				4.5E−09	−1.2E−06	8.2E−05	1.1E−03	−2.4E−02
Semimembranosus	5	1.9				3.8E−09	−1.2E−06	1.1E−04	−1.9E−03	5.0E−02
Semitendinosus	5	3.3				1.1E−08	−3.2E−06	2.9E−04	−7.4E−03	8.0E−02
Knee
Rectus femoris	8	1.8	2.0E−13	−1.6E−10	5.3E−08	−9.5E−06	1.0E−03	−6.0E−02	1.9E+00	−2.5E+01
Vastus lateralis	4	3.1					9.6E−08	−3.9E−05	5.0E−03	−1.5E−01
Gracilis	3	3.9						1.5E−05	−2.4E−03	−1.5E−01
Sartorius	5	0.5				−5.1E−09	2.2E−06	−3.1E−04	1.6E−02	−3.7E−01
Biceps femoris	4	3.1					−1.3E−07	3.7E−05	−2.5E−03	−2.5E−02
Semimembranosus	4	2.2					−1.6E−07	5.1E−05	−4.7E−03	8.1E−02
Semitendinosus	3	3.8						2.7E−05	−4.5E−03	−2.1E−02
Gastrocnemius lateralis	4	3.6					−2.7E−07	6.7E−05	−4.8E−03	5.3E−02
Gastrocnemius medialis	Lin.	69.5							−4.6E−05	−3.1E−02
Ankle
Gastrocnemius lateralis	5	1.5				4.0E−09	−1.7E−06	2.5E−04	−1.4E−02	2.8E−01
Gastrocnemius medialis	6	1.3			8.6E−11	−4.0E−08	6.7E−06	−5.1E−04	1.8E−02	−2.3E−01
Soleus	5	4.7				4.9E−09	−2.3E−06	3.8E−04	−2.5E−02	6.1E−01
Tibialis anterior	3	3.0						2.3E−05	−3.9E−03	8.5E−02

Lin., Linear fit; RSS, residual sum of squares.