Skip to main content
PMC home page
Journal of Anatomy logoLink to Journal of Anatomy
. 2010 Apr;216(4):463–469. doi: 10.1111/j.1469-7580.2009.01196.x

Architectural properties of the first dorsal interosseous muscle

Benjamin W Infantolino 1, John H Challis 1
PMCID: PMC2849523  PMID: 20070422

Abstract

Muscle architecture is considered to reflect the function of muscle in vivo, and is important for example to clinicians in designing tendon-transfer and tendon-lengthening surgeries. The purpose of this study was to quantify the architectural properties of the FDI muscle. It is hypothesized that there will be consistency, that is low variability, in the architectural parameters used to describe the first dorsal interosseous muscle because of its clear functional role in index finger motion. The important architectural parameters identified were those required to characterize a muscle adequately by modeling. Specifically the mass, cross-sectional area, and length of the tendon and muscle were measured in cadavers along with the muscle fiber optimum length and pennation angle, and the moment arm of the first dorsal interosseous at the metacarpophalangeal joint. These parameters provide a characterization of the architecture of the first dorsal interosseous, and were used to indicate the inherent variability between samples. The results demonstrated a large amount of variability for all architectural parameters measured; leading to a rejection of the hypothesis. Ratios designed to describe the functioning of the muscles in vivo, for example the ratio of tendon to fiber optimum lengths, also demonstrated a large variability. The results suggest that function cannot be deduced from form for the first dorsal interosseous, and that subject-specific architectural parameters may be necessary for the formulation of accurate musculoskeletal models or making clinical decisions.

Keywords: cadaver, first dorsal interosseous, muscle architecture

Introduction

In 1667, Niels Stensen developed models of muscle which accounted for the architectural features of muscle (Kardel, 1990). Gans & Bock (1965) highlighted how the architecture of a muscle indicates its function in vivo. Indeed, insights into the function of muscle have been gained by examining muscle architecture (e.g. Alexander & Vernon, 1975; Otten, 1988; Lieber & Friden, 2000). These architectural features are important parameters for musculoskeletal models (Zajac, 1989), and can be clinically important, for example, in guiding clinicians performing tendon-transfer surgeries (e.g. Lieber, 1993), and there is a presumed link between the architecture and function of a muscle.

A number of studies have examined how the architecture of a muscle indicates its function, which would imply within a species a consistent architectural pattern across different individuals. For example, Alexander & Bennet-Clark (1977) demonstrated that the ratio of muscle tendon length to fiber length indicates the potential for elastic energy storage within muscle. Alexander & Ker (1990) were able to classify muscles into one of three groups based on this ratio and the thickness of the tendon. In one group the fiber length was greater than the tendon length, whereas in the other two groups the tendon length was greater than the fiber length with either relatively thick or thin tendons. Elliott & Crawford (1965) demonstrated in rabbit muscle that the ratio of muscle to tendon cross-sectional area was consistent, with this ratio giving a measure of the maximum stress the tendon would experience. In human forearm muscles, Cutts et al. (1991) examined this ratio and presented a consistent area ratio. The stress in the tendon has implications for both the control of movement (Rack & Westbury, 1984) and the role of elastic energy storage (Alexander, 1988). The operating range of the fibers making up a muscle are a function of the length of the fibers and the moment arm of the joint(s) over which they cross; therefore the ratio of fiber optimum length to moment arm has been identified as an important ratio indicating muscle function in vivo (Loren et al. 1996). These studies indicate that the function of muscle will be reflected in its architecture; in the current study, the architectural features of the first dorsal interosseous (FDI) were determined to examine to what extent there is consistency across specimens in these architectural features.

The FDI muscle is well suited for the examination of the relationship between muscle function and architecture because it is an example of the rare instance of only one muscle being responsible for a particular joint motion (it abducts the index finger metacarpophalangeal joint). Due to its unique role in joint motion the FDI has been frequently used for the investigation of muscle properties, for example motor unit recruitment (e.g. Milner-Brown et al. 1973; Kornatz et al. 2005), strength training (e.g. Davies et al. 1985), and tendon stiffness (e.g. Cook & McDonagh, 1996). Data on the architecture of the FDI are limited. Brand et al. (1981) reported muscle fascicle rest lengths for 15 muscles, and Jacobson et al. (1992) reported muscle mass, muscle belly length, pennation angle, and physiological cross-sectional area (PCSA) for nine muscles. None of these studies specifically examined whether there was an architectural consistency across samples of the FDI.

The purpose of this study was to quantify the architectural properties of the FDI muscle. It is hypothesized that there will be consistency, that is low variability, in the architectural parameters used to describe the FDI because of its clear functional role in index finger abduction. The important architectural parameters were identified as those required to characterize a muscle adequately by modeling (Zajac, 1989). Specifically the mass cross-sectional area, and length of the tendon and muscle were measured in cadavers along with the muscle fascicle optimum length and pennation angle, and the moment arm of the FDI at the second metacarpophalangeal joint. These parameters will provide a characterization of the architecture of the FDI, and be used to indicate the inherent variability between samples and therefore assess the consistency of its architecture.

Methods

Nine embalmed cadavers were dissected (Table 1), and the FDI muscle was removed using blunt dissection from each hand of each cadaver. For each sample all measurements were made three times, to reduce noise influences, and the mean of the three samples was used for all subsequent calculations using that sample.

Table 1.

Cadaver characteristics of the nine cadavers in the current study.

Cadaver Gender Height (cm) Age at death (years) Cause of death
1 Male 177 82 Lung cancer and severe dementia
2 Female 157 70 Metastatic pancreatic carcinoma
3 Male 181 88 Sepsis
4 Male 175 74 Congestive heart failure
5 Female 167 76 Possible pulmonary embolism
6 Female 161 68 Interstitial pulmonary fibrosis
7 Male 180 55 End stage liver disease
8 Male 174 56 Bronchogenic carcinoma
9 Female 169 37 Metastatic breast cancer
Open in a new tab

The mass of each muscle (Mmt) was measured to the nearest 0.01 g immediately after dissection. Muscle belly length (Lmb), and external tendon length (Lt) were measured to the nearest 0.5 mm using a standard rule and a stereo dissecting microscope at 5× magnification. Blunt dissection was used to expose the internal tendon or aponeurosis. The internal tendon was traced from where it joined the external tendon to the distinct location where it disappeared into the muscle belly. Once the internal tendon was fully exposed, its length (Lti) was measured. The external tendon was removed from the muscle and its mass (Mt) recorded. Muscle volume (Vm) was measured to the nearest 0.8 mL using water displacement.

The force-length properties of muscle dictate that there is a length at which a muscle can produce maximal force (Ramsey & Street, 1940); this length is referred to as the optimal length. As the FDI has two heads, one originating from the first metacarpal and one from the second metacarpal, to determine the optimum fascicle length, two muscle fascicles were therefore removed from each head of each FDI muscle. These samples were placed in 20% nitric acid to digest the connective tissue surrounding the muscle fibers (Close, 1964; Friederich & Brand, 1990). Fascicle length (Lf) was determined using a standard rule and the stereo dissection microscope. After acid digestion, forceps were used to remove individual fibers with the aid of a stereo dissection microscope at 25× magnification. Sections of fiber, approximately 5 mm in length, were mounted on a microscope slide using isotonic saline. Digital images of the fiber sections were taken from a light microscope. In the images the sarcomeres were clearly visible, and custom-written matlab code counted the number of sarcomeres in each digital image, and measured the sample length. This gave the average sarcomere length (Ls) in the sample. Therefore, for each fascicle the optimal fascicle length (Lfopt) could be calculated using

graphic file with name joa0216-0463-m1.jpg (1)

where Lsopt is the optimal sarcomere length for human muscle fibers (2.7 μm from Walker & Schrodt, 1974). Based on the recommendation of Langenderfer et al. (2004) at least 60 sarcomeres were counted for each fiber section.

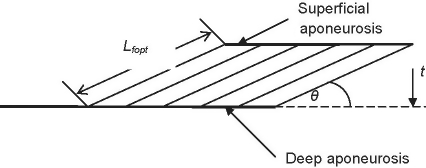
Pennation angles were measured in both heads using a standard goniometer. Pennation angle varies with changes in muscle length (Loram et al. 2006), therefore any reported pennation angles should be referenced to a specified muscle fascicle length. In this study the pennation angle for each head was reported for the optimal fascicle length. As pennation angle was measured at a fascicle length which varied between cadavers, these had to be adjusted to that angle which would be achieved at optimum fascicle length. To make this adjustment a planimetric model of muscle geometry was used (Fig. 1), in which muscle thickness was assumed to remain constant irrespective of fascicle length (Otten, 1988). Based on simple geometry, muscle thickness (t) was calculated from

graphic file with name joa0216-0463-m2.jpg (2)

Fig. 1.

Fig. 1

Open in a new tab

A planimetric representation of a pennated muscle. Pennation angle (θ) is assumed to be measured at optimal fascicle length in musculoskeletal models. The superficial and deep aponeuroses are a muscle thickness (t) apart and a muscle fascicle of optimal length Lfopt spans the distance between the two aponeuroses.

where θ is the pennation angle of the muscle measured upon removal from the cadaver. Given the muscle thickness, the pennation angle can be calculated with respect to optimal fascicle length

graphic file with name joa0216-0463-m3.jpg (3)

where θopt is the pennation angle at the optimum fascicle length.

The moment arm of the FDI was estimated using the tendon-excursion method (e.g. An et al. 1983) in eight hands. The moment arm can be computed using this method, as moment arm is the first derivative of tendon excursion with respect to joint angle; therefore, tendon excursion was measured with changes in joint angle. A rig was constructed to hold the wrist and thumb at a fixed joint angle while the second metacarpophalangeal joint was moved through a physiologic range of motion of 20° of abduction (Kendall et al. 1993). To track tendon excursion once the FDI was removed from the cadaver, a linear cable extensometer was attached to the insertion of the FDI muscle. The extensometer cable was passed through an eye hook screwed into the second metacarpal to ensure that the cable followed the path of the tendon and did not ‘bowstring’ during movement through the range of motion. The cable extensometer was connected to a data acquisition device with ten bit resolution that recorded at 29 Hz. A clear plastic goniometer was used to measure the joint angle, with the axis of the goniometer placed over the exposed joint center. The operator moved the finger from full adduction to full abduction in 5 s and back in another 5 s. Polynomials of varying order were fit to the joint angle tendon excursion data. In all cases, polynomials higher than a first order polynomial had residuals to the fit which were smaller than the noise level in the measurements, therefore the first order polynomials were used for subsequent analysis. The first derivative of the polynomials with respect to joint angle gives a constant moment arm for the joint range of motion investigated.

For a pennated muscle the force the muscle exerts on its tendon is directly proportional to the muscle’s physiological cross-sectional area (PCSA). For the pennated FDI the PCSA was computed from (Challis, 2000):

graphic file with name joa0216-0463-m4.jpg (4)

The FDI tendon was approximately circular in cross-section, therefore its cross-section area (TCSA) was computed from

graphic file with name joa0216-0463-m5.jpg (5)

where ρ is the density of tendon (1120 kg m−3; Ker, 1981).

In addition to the above calculated parameters, the ratio of the PCSA to the TCSA was calculated, as this ratio should stay relatively constant for all FDI muscles because the force applied to the tendon (PSCA) should be associated with the size of the tendon (Elliott & Crawford, 1965). The ratio of Lt to Lfopt was calculated; a larger ratio would indicate a greater capacity to store energy in the tendon rather than the muscle fibers (Alexander & Bennet-Clark, 1977). Finally, the ratio of Lfopt to r was calculated to give an indication of the potential excursion of the muscle with joint motion.

Simple descriptive statistics of all data were computed. Some measurements could not be made on all 18 muscles; therefore, throughout the Results section the number of samples obtained for each measurement is noted.

Results

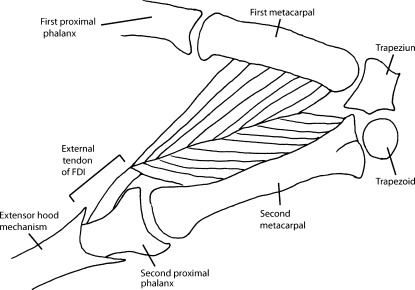
During dissection of the FDI a large amount of variability was observed. The proximal attachment of the muscle went directly from muscle belly to the bone with no external tendon on either the first or second metacarpal (Fig. 2); in five specimens there was no external tendon at the distal attachment. The FDI showed variability in its insertion with the dissected muscles falling, in equal proportions, into one of three groups: FDI inserting onto the second proximal phalanx, inserting onto the extensor hood mechanism, and inserting onto both the second proximal phalanx and extensor hood mechanism. In one sample the external tendon was 40 mm long, approximately an order of magnitude longer than the mean length of the remainder of the tendons, although in all other respects this muscle was similar to the other samples. For subsequent analyses this tendon was ignored when computing the descriptive statistics.

Fig. 2.

Fig. 2

Open in a new tab

A sketch of the first dorsal interosseous and relevant skeletal structures.

There was no consistent pattern in the measured architectural parameters (Table 2). The parameters had large coefficients of variation, ranging from 11%, for muscle belly length, to 100%, for external tendon mass. Optimal fascicle lengths were computed for both heads of the FDI but a paired t-test demonstrated that there was no statistically significant difference between the lengths for the two heads of the muscles (P > 0.05); therefore, the mean of two heads was used. Optimal fascicle length also demonstrated a large amount of variability (coefficient of variation 30%).

Table 2.

The mean (± SD) of the first dorsal interosseous of architectural parameters (minimums and maximums are also listed). All values are based on 18 muscles unless noted otherwise parenthetically.

Parameter Mean ± SD Minimum value Maximum value
Mmt (g, n = 17) 5.62 ± 1.79 3.26 9.47
Mt (g, n = 13) 0.06 ± 0.06 0 0.18
Vm (mL) 5.2 ± 1.6 3.0 8.0
Lmt (mm, n = 17) 63.6 ± 11.7 45.0 105.0
Lmb (mm) 58.6 ± 6.7 45.0 80.0
Lt (mm, n = 13) 4.5 ± 6.5 0 25.0
Lti (mm) 26.0 ± 4.7 15.0 34.0
Lfopt (mm, n = 17) 29.9 ± 9.1 20.6 61.0
Open in a new tab

Pennation angles were computed for both heads of the FDI (Table 3); a paired t-test demonstrated that pennation angle was not statistically significantly different between the between the two heads of the muscle (P > 0.05). The range of pennation angles which could be reasonably expected for the muscles was computed by assuming the muscle fibers did not shorten to <50% of the optimum length or lengthen by more 50% of the optimal length. This analysis gave a range of pennation angles for both heads of <15 degrees.

Table 3.

The mean (± SD) of the first dorsal interosseous pennation angles calculated at optimal, maximum and minimum fascicle lengths for 18 muscles.

Muscle head Pennation angle at Lfopt (degrees) Pennation angle at Lfmax (degrees) Pennation angle at Lfmin (degrees) Mean range of Pennation angle (degrees)
First metacarpal 10.0 ± 5.0 6.6 ± 3.3 20.8 ± 11.8 14.9 ± 8.5
Second metacarpal 11.7 ± 7.6 7.7 ± 4.9 21.4 ± 11.9 14.6 ± 8.3
Open in a new tab

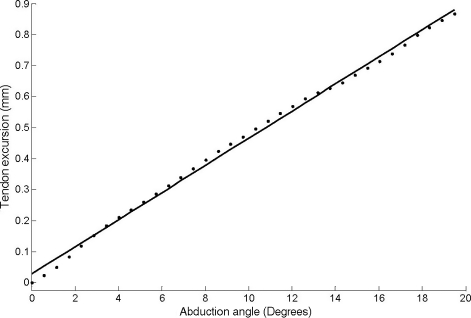
The relationship between joint angle and tendon excursion data was linear for the FDI of all cadaver hands analyzed (n = 8) for the range of joint motion examined (Fig. 3). Given this linear relationship, the moment arm of the FDI at the second metacarpophalangeal joint was constant, 2.1 ± 0.5 mm; once again, even for this architectural parameter the coefficient of variation was high (24%). If the moment arm is normalized to index finger length or breadth the moment arm is 4.0 ± 0.9% and 6.4 ± 2.6%, respectively; again, the coefficients of variation are high, at 22 and 41%, respectively.

Fig. 3.

Fig. 3

Open in a new tab

Plot of index finger abduction angle against tendon excursion for the first dorsal interosseoeus for a typical sample, where the dots are the raw data and the line represents the fit to that data.

The force a muscle exerts on the tendon in series varies with its PCSA; this architectural parameter varied between samples, as did TCSA (Table 4). The ratio of PCSA to TCSA had a large coefficient of variation (121%), even though it would be expected that these two parameters would co-vary. The ratio of tendon length to fascicle optimum length also had a large coefficient of variation (150%). Finally, as a measure of the potential excursion of the muscle fibers, the ratio of fascicle optimum length to moment arm was computed, once again showing high variability (56%).

Table 4.

The mean (± SD) of the first dorsal interosseous muscles physiological cross-sectional area (PCSA), tendon CSA (TCSA), and the ratios of PCSA/TCSA, Lt/Lfopt, and Lfopt/r, where r is the moment of the muscle. The number of samples for each parameter is given in parentheses.

Parameter Mean ± SD
PCSA (cm2) (n = 17) 1.8 ± 0.6
TCSA (cm2) (n = 12) 0.2 ± 0.2
PCSA/TCSA (n = 12) 21.7 ± 26.3
Lt/Lfopt (n = 13) 0.2 ± 0.3
Lfopt/r (n = 8) 16.5 ± 9.2
Open in a new tab

Not all measures were completed for all samples, but complete datasets were available for eight samples (Table 5). These data reflect the trends seen throughout the whole dataset.

Table 5.

The architectural parameters of the eight first dorsal interossi for which complete datasets were available.

Cadaver (L/R) Lfopt (mm) Lt (mm) PCSA (cm2) TCSA (cm2) Pennation angle at Lfopt (degrees) Moment arm (mm)
6 (R) 22.1 3.0 1.7 0.4 16.6 1.8
6 (L) 33.1 2.0 0.9 0.1 13.3 2.6
7 (R) 30.0 5.0 2.0 0.2 16.0 2.2
7 (L) 31.9 7.0 1.8 0.2 12.9 2.5
8 (R) 24.8 0 2.6 0 13.7 1.9
8 (L) 61.0 4.0 0.9 0.2 9.1 1.6
9 (R) 33.8 2.0 2.3 0.1 14.5 2.3
9 (L) 28.1 2.0 2.6 0.8 20.3 1.9
Open in a new tab

Discussion

The gross architectural parameters measured in this study had a large amount of variability between specimens. This finding should not be too surprising given the variability seen in the cadavers themselves. However, it was unexpected that the ratios that were used to attempt to normalize the architectural parameters, for example PCSA/TCSA and Lt/Lfopt, also had a large amount of variability. The hypothesis that there would be consistency in the architectural parameters describing the FDI because of its clear functional role in index finger motion was rejected. This implies either that the functional abilities of the muscles from different cadavers were different or that, at least for this muscle, the function is not indicated by its form. Obviously with a cadaver study such as this, it is impossible to examine how the muscle was used in vivo. Interestingly, in a small sample of greyhounds Williams et al. (2008) had high coefficients of variation for many muscle architectural parameters determined for the muscles of the legs, yet the examined muscles represent an animal with ‘extreme specialization’ for fast sprinting. These data lend some support to the idea that the relationship between form and function for muscle is not always as strong as is sometimes assumed (Thompson, 1942).

The ratio of PCSA to TCSA reflects the stress experienced by the tendon, as the force the muscle produces and therefore exerts on the tendon is directly proportional to the muscle PCSA (Challis, 2000). In this study the variability of this ratio was high, in contrast to the study of Cutts et al. (1991) where the coefficient of variation was low for this ratio, although the mean values from the two studies are comparable. In Cutts et al. (1991) multiple muscles were examined but from one specimen only. This raises the question of whether this ratio is relatively constant for all muscles within a specimen but variable for the same muscle from different specimens.

The ratio of Lt to Lfopt was calculated and indicates the capacity to store energy in the tendon rather than the muscle fibers (Alexander & Bennet-Clark, 1977). In this study there was a large variability in the FDI in the ratio of Lt to Lfopt. Other muscles in man have more important roles for elastic energy storage, for the example the gastrocnemius (Alexander, 1988), so it could be anticipated that variability in this ratio may be smaller for such muscles in comparison with the FDI. In the three-category model of Alexander & Ker (1990) different specimens within this study fall into each of the categories, indicating that there is no across-subject-specific specialization of muscle.

High variability was found in the ratio of Lfopt to r, which is an indication of the working range of the muscle. These data parallel those of Maganaris et al. (2006), who examined the in vivo relationship between fiber length to muscle moment arm for the gastrocnemius medialis, gastrocnemius lateralis, soleus, vastus lateralis and vastus intermedius in man. All of their correlations between fiber length and moment arm were low, therefore one parameter predicted only a small amount of variability in the other parameter. Their study was unable to measure optimum length but made measurements at specified joint configurations. The present study has the same finding, with the advantage that the cadaver preparation permitted a precise determination of parameters.

The measured architectural parameters were in agreement with previously published values of fascicle length (Brand et al. 1981; Jacobson et al. 1992), muscle mass, muscle belly length, average pennation angle, and PCSA (Jacobson et al. 1992). The moment arms differ to some extent from those measured by An et al. (1983), where the range of motion was five times greater than the physiologic range of motion; however, the data were comparable when considering only the range of motion used in the present study. Many of the measurements in the current study have not been previously reported in the literature and therefore no comparisons with existing literature could be made.

The observations of the anatomy in this manuscript correspond with those made by Masquelet et al. (1986). They identified the actions of the FDI as adduction of the first carpometacarpal joint, and abduction of the index finger metacarpophalangeal joint. Eyler & Markee (1954) also described the FDI as a second proximal interphalangeal joint flexor. An et al. (1983) showed that the FDI had a moment arm at the second metacarpophalangeal joint as a flexor. In the present study the moment arm for abduction of the index finger metacarpophalangeal joint was assessed; unfortunately, the other potential moment arms of this muscle were not assessed. This would be an interesting future study. In studies examining FDI muscle properties in vivo its role in abduction of the second metacarpophalangeal joint is predominantly exploited (e.g. Milner-Brown et al. 1973; Davies et al. 1985; Cook & McDonagh, 1996; Kornatz et al. 2005).

The study did not examine a number of factors which are important for understanding the functioning of muscle in vivo; primary among these factors are tendon elasticity, muscle-specific tension, and fiber type distribution. A more compliant tendon compared with a stiffer tendon would increase the working range of the muscle fibers. In this study, tendon cross-sectional area was assessed based on the assumption that tendon elasticity varies with tendon cross-sectional area (Ker, 1981). The specific tension of muscle is the force it can develop per unit area; the greater this value, the greater the potential for stretching the tendon, which once again changes the potential operating range of the muscle. There is no indication that the specific tension of muscle varies between samples from the same species (Powell et al. 1984). Of course there are some expected sources of variation in the muscle-specific tension, for example, the reduction that occurs in old age (Brooks & Faulkner, 1988), and differences between fiber types (Harridge et al. 1996). Although muscle fiber type distribution was not assessed in this study, Johnson et al. (1973) did examine this for the FDI in six cadavers, and demonstrated the muscle has approximately equal proportions of fast twitch (type II) and slow twitch (type I) muscle fibers.

As the FDI is the only muscle responsible for second metacarpophalangeal joint abduction it is relatively easy to examine its function in vivo if the thumb is immobilized. Measuring the architecture of the muscle in vivo is technically more challenging but imaging techniques (e.g. Infantolino et al. 2007), and elegant experimental procedures (e.g. tendon properties –Cook & McDonagh, 1996; moment arm –Lee et al. 2008) can allow determination of many architectural parameters in vivo. An investigation combining analysis of function and form in vivo would permit a more detailed examination of the relationship between form and function for this muscle. Such an investigation would allow the examination of how subjects use their FDI, and then examine the correlation with form; such an approach would permit the examination of the hypothesis formulated in this study in vivo. Such a study is feasible for the FDI but it would also be useful to examine other muscles to determine how generalizable the results of this study, particularly in terms of variability, are to other muscles. Future work could extend the measures made in this study to other muscles of the human body, for example the muscles involved in locomotion. Some limitations to this study include the applicability of cadaver measurements to live subject research, and the high mean age of the cadavers (67 years old at death). Both of these limitations hinder the ability to generalize the current study findings. Such data limitations are common, for example cadaver-based muscle architectural parameters are the norm in human musculoskeletal models (e.g. Delp et al. 1990).

It was hypothesized that there would be consistency, that is low variability, in the architectural parameters used to describe the FDI because of its clear functional role in index finger motion. The results of the present study demonstrated large variability and do not indicate a strong link between form and function for this muscle. These results also speak to the need for subject-specific musculoskeletal parameters for musculoskeletal models, which would therefore permit the use of these models to gain insight into muscle properties and the production of movement. They also suggest that clinicians performing tendon-transfer surgeries should consider patient-specific muscle architecture.

References

  1. Alexander RM. Elastic Mechanisms in Animal Movement. Cambridge: Cambridge University Press; 1988. [Google Scholar]
  2. Alexander RM, Bennet-Clark HC. Storage of elastic strain energy in muscle and other tissues. Nature. 1977;265:114–117. doi: 10.1038/265114a0. [DOI] [PubMed] [Google Scholar]
  3. Alexander RM, Ker RF. The architecture of leg muscles. In: Winters JM, Woo SLY, editors. Multiple Muscle Systems: Biomechanics and Movement Organization. New York: Springer-Verlag; 1990. pp. 568–577. [Google Scholar]
  4. Alexander RM, Vernon A. The dimensions of knee and ankle muscles and the forces they exert. J Human Mov Stud. 1975;1:115–123. [Google Scholar]
  5. An KN, Ueba Y, Chao EY, et al. Tendon excursion and moment arm of index finger muscles. J Biomech. 1983;16:419–425. doi: 10.1016/0021-9290(83)90074-x. [DOI] [PubMed] [Google Scholar]
  6. Brand PW, Beach RB, Thompson DE. Relative tension and potential excursion of muscles in the forearm and hand. J Hand Surg Am. 1981;6:209–219. doi: 10.1016/s0363-5023(81)80072-x. [DOI] [PubMed] [Google Scholar]
  7. Brooks SV, Faulkner JA. Contractile properties of skeletal muscles from young, adult and aged mice. J Physiol. 1988;404:71–82. doi: 10.1113/jphysiol.1988.sp017279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Challis JH. Muscle-tendon architecture and athletic performance. In: Zatsiorsky VM, editor. Biomechanics in Sport. Oxford: Blackwell Science Inc; 2000. pp. 33–55. Olympic Encyclopaedia of Sports Medicine Vol. IX) (ed. [Google Scholar]
  9. Close R. Dynamic properties of fast and slow skeletal muscles of the rat during development. J Physiol. 1964;173:74–95. doi: 10.1113/jphysiol.1964.sp007444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cook CS, McDonagh MJ. Measurement of muscle and tendon stiffness in man. Eur J Appl Physiol. 1996;72:380–382. doi: 10.1007/BF00599700. [DOI] [PubMed] [Google Scholar]
  11. Cutts A, Alexander RM, Ker RF. Ratios of cross-sectional areas of muscles and their tendons in a healthy human forearm. J Anat. 1991;176:133–137. [PMC free article] [PubMed] [Google Scholar]
  12. Davies CT, Dooley P, McDonagh MJ, et al. Adaptation of mechanical properties of muscle to high force training in man. J Physiol. 1985;365:2772–2784. doi: 10.1113/jphysiol.1985.sp015771. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Delp SL, Loan JP, Hoy MG, et al. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng. 1990;37:757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
  14. Elliott DH, Crawford GNC. The thickness and collagen content of tendon relative to the strength and cross-sectional area of muscle. Proc R Soc Lond B Biol Sci. 1965;162:137–146. doi: 10.1098/rspb.1965.0033. [DOI] [PubMed] [Google Scholar]
  15. Eyler DL, Markee JE. The anatomy and function of the intrinsic musculature of the fingers. J Bone Joint Surg Am. 1954;36:1–18. [PubMed] [Google Scholar]
  16. Friederich JA, Brand RA. Muscle fiber architecture in the human lower limb. J Biomech. 1990;23:91–95. doi: 10.1016/0021-9290(90)90373-b. [DOI] [PubMed] [Google Scholar]
  17. Gans C, Bock WJ. The functional significance of muscle architecture – a theoretical analysis. Ergeb Anat Entwicklungsgesch. 1965;38:115–142. [PubMed] [Google Scholar]
  18. Harridge SD, Bottinelli R, Canepari M, et al. Whole-muscle and single-fibre contractile properties and myosin heavy chain isoforms in humans. Pflugers Arch. 1996;432:913–920. doi: 10.1007/s004240050215. [DOI] [PubMed] [Google Scholar]
  19. Infantolino BW, Gales DJ, Winter SL, et al. The validity of ultrasound estimation of muscle volumes. J Appl Biomech. 2007;23:213–217. doi: 10.1123/jab.23.3.213. [DOI] [PubMed] [Google Scholar]
  20. Jacobson MD, Raab R, Fazeli BM, et al. Architectural design of the human intrinsic hand muscles. J Hand Surg Am. 1992;17A:804–809. doi: 10.1016/0363-5023(92)90446-v. [DOI] [PubMed] [Google Scholar]
  21. Johnson MA, Polgar J, Weightman D, et al. Data on the distribution of fibre types in thirty-six human muscles. Can J Neurol Sci. 1973;18:111–129. doi: 10.1016/0022-510x(73)90023-3. [DOI] [PubMed] [Google Scholar]
  22. Kardel T. Niels Stensen’s geometrical theory of muscle contraction (1667): a reappraisal. J Biomech. 1990;23:953–965. doi: 10.1016/0021-9290(90)90310-y. [DOI] [PubMed] [Google Scholar]
  23. Kendall FP, McCreary EK, Provance PG. Muscles, Testing and Functions. Baltimore: Lippincott Williams & Wilkins; 1993. [Google Scholar]
  24. Ker R. Dynamic tensile properties of the plantaris tendon of sheep (Ovis aries) J Exp Biol. 1981;93:283–302. doi: 10.1242/jeb.93.1.283. [DOI] [PubMed] [Google Scholar]
  25. Kornatz KW, Christou EA, Enoka RM. Practice reduces motor unit discharge variability in a hand muscle and improves manual dexterity in old adults. J Appl Physiol. 2005;98:2072–2080. doi: 10.1152/japplphysiol.01149.2004. [DOI] [PubMed] [Google Scholar]
  26. Langenderfer J, Jerabek SA, Thangamani VB, et al. Musculoskeletal parameters of muscles crossing the shoulder and elbow and the effect of sarcomere length sample size on estimation of optimal muscle length. Clin Biomech. 2004;19:664–670. doi: 10.1016/j.clinbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
  27. Lee SSM, Lewis GS, Piazza SJ. An algorithm for automated analysis of ultrasound images to measure tendon excursion in vivo. J Appl Biomech. 2008;24:75–82. doi: 10.1123/jab.24.1.75. [DOI] [PubMed] [Google Scholar]
  28. Lieber RL. Skeletal muscle architecture: implications for muscle function and surgical tendon transfer. J Hand Ther. 1993;6:105–113. [PubMed] [Google Scholar]
  29. Lieber RL, Friden J. Functional and clinical significance of skeletal muscle architecture. Muscle Nerve. 2000;23:1647–1666. doi: 10.1002/1097-4598(200011)23:11<1647::aid-mus1>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
  30. Loram ID, Maganaris CN, Lakie M. Use of ultrasound to make noninvasive in vivo measurement of continuous changes in human muscle contractile length. J Appl Physiol. 2006;100:1311–1323. doi: 10.1152/japplphysiol.01229.2005. [DOI] [PubMed] [Google Scholar]
  31. Loren GJ, Shoemaker SD, Burkholder TJ, et al. Human wrist motors: biomechanical design and application to tendon transfers. J Biomech. 1996;29:331–342. doi: 10.1016/0021-9290(95)00055-0. [DOI] [PubMed] [Google Scholar]
  32. Maganaris CN, Baltzopoulos V, Tsaopoulos D. Muscle fibre length-to-moment arm ratios in the human lower limb determined in vivo. J Biomech. 2006;39:1663–1668. doi: 10.1016/j.jbiomech.2005.04.025. [DOI] [PubMed] [Google Scholar]
  33. Masquelet AC, Salama J, Outrequin G, et al. Morphology and functional anatomy of the first dorsal interosseous muscle of the hand. Surg Radiol Anat. 1986;8:19–28. doi: 10.1007/BF02539704. [DOI] [PubMed] [Google Scholar]
  34. Milner-Brown HS, Stein RB, Yemm R. Changes in firing rate of human motor units during linearly changing voluntary contractions. J Physiol. 1973;230:371–390. doi: 10.1113/jphysiol.1973.sp010193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Otten E. Concepts and models of functional architecture in skeletal muscle. Exerc Sport Sci Rev. 1988;16:89–137. [PubMed] [Google Scholar]
  36. Powell PL, Roy RR, Kanim P, et al. Predictability of skeletal muscle tension from architectural determinations in guinea pig hindlimbs. J Appl Physiol. 1984;56:1715–1721. doi: 10.1152/jappl.1984.57.6.1715. [DOI] [PubMed] [Google Scholar]
  37. Rack PM, Westbury DR. Elastic properties of the cat soleus tendon and their functional importance. J Physiol. 1984;347:479–495. doi: 10.1113/jphysiol.1984.sp015077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ramsey RW, Street SF. The isometric length-tension diagram of isolated skeletal muscle fibers of the frog. J Cell Comp Physiol. 1940;15:11–34. [Google Scholar]
  39. Thompson DW. On Growth and Form. Cambridge: Cambridge University Press; 1942. [Google Scholar]
  40. Walker SM, Schrodt GR. I segment lengths and thin filament periods in skeletal muscle fibers of the rhesus monkey and the human. Anat Rec. 1974;178:63–82. doi: 10.1002/ar.1091780107. [DOI] [PubMed] [Google Scholar]
  41. Williams SB, Wilson AM, Rhodes L, et al. Functional anatomy and muscle moment arms of the pelvic limb of an elite sprinting athlete: the racing greyhound Canis familiaris. J Anat. 2008;213:361–372. doi: 10.1111/j.1469-7580.2008.00961.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. CRC Crit Rev Bioeng. 1989;17:359–411. [PubMed] [Google Scholar]

Articles from Journal of Anatomy are provided here courtesy of Anatomical Society of Great Britain and Ireland

RESOURCES