One-dimensional representation of a neuron in a uniform electric field

Abstract

The neocortex is the most common target of sub-dural electrotherapy and non-invasive brain stimulation modalities including transcranial magnetic stimulation (TMS) and transcranial current simulation (TCS). Specific neuronal elements targeted by cortical stimulation are considered to underlie therapeutic effects, but the exact cell-type(s) affected by these methods remains poorly understood. We determined if neuronal morphology predicted responses to subthreshold uniform electric fields. We characterized the effects of subthreshold electrical stimulation on identified cortical neurons in vitro. Uniform electric fields were applied to rat motor cortex brain slices, while recording from interneurons and pyramidal cells across cortical layers, using whole cell patch clamp. Neuron morphology was reconstructed following intracellular dialysis of biocytin. Based solely on volume-weighted morphology, we developed a simplified model of neuronal polarization by sub-threshold electric field: an electrotonically linear cylinder that further predicts polarization at distal dendritic tree terminations. We found that neuronal morphology correlated with somatic sub-threshold polarization. Layer 5/6 pyramidal neuron somata (individually) and dendrites (averaging across neurons) were most sensitive to sub-threshold fields. This analysis was extended to predict a terminal polarization of a human cortical neuron as 1.44 mV per mV/mm electric field.

I. INTRODUCTION

Fundamental questions remain regarding the cellular targets of transcranial direct current stimulation (tDCS), including the relative activation of morphologically and functionally diverse groups of inhibitory interneurons and excitatory pyramidal cells. Neuronal segments closest to the stimulating anode (virtual anode for TMS) have been shown to hyperpolarize, and concomitantly the segments closest to the (virtual) cathode depolarize [1]. In response to the unique electric fields induced by tDCS [2], neuronal membranes are considered to polarize in a “compartment” specific manner; the polarized compartments interact according to the electrotonic decay along the neuron [3, 4]. Neuronal modeling [5–8] and in vitro [9] studies of electric field stimulation have identified morphological features which govern the polarization of (interacting) neuronal compartments, including branching patterns and membrane space constants,. Changes of compartment angle relative to an applied electric field (e.g. activating function), branch terminations, or changes in inter-compartment impedance can determine the locations of entry and exit of induced transmembrane currents that lead to polarization [5, 8]. The neuronal space constants (λ), and related diameter of axons and dendrites, govern the axial distribution of these induced transmembrane polarizations, and therefore regulate the degree to which neuronal compartments interact [8, 10]. Concurrent polarization of individual segments of a neuronal tree can lead to complex changes in overall neuronal function by modulating cellular biophysics [11] including non-linear voltage-gated conductances, synaptic efficacy, and AP threshold or timing [1].

The goal of the present study was to determine if the distinct morphological features of cortical cell types affect their response to stimulation by electric field.

II. METHODS

Coronal slices (300 µm) of primary motor cortex (M1) were prepared from male P21-25 Sprague-Dawley rats as previously described [12, 13]. Conventional whole-cell patch clamp recording techniques were used to measure activity from neurons in M1. Uniform electric fields were generated across individual slices by passing current between two parallel Ag/AgCl electrodes [14] placed on the bottom of a customized submerged chamber. The convention of electric field polarity used in the present report refers to the anode on the pial side of the cortex. The somatic steady-state transmembrane voltage response to ~ 5 mV/mm electric field steps, up to ~ +/−30 mV/mm, were linearly fit (Fig. 1), the slope of which was used as the subthreshold polarization per unit electric field applied, which is described in mV of polarization per mV/mm of electric field. Post-recordings, biotin-avidin-HRP histochemistry was performed as previously described [15]. The tracing was aligned so the direction of the electric field traversed along the 90° line from the top of the tracing to the bottom. NeuroExplorer (Microbrightfield, Williston, VT, USA) branched structure analyses were used to determine segment angle (φ_seg), length (l_seg), diameter (d_seg), and volume information for each segment of each individual neuron’s tracing.

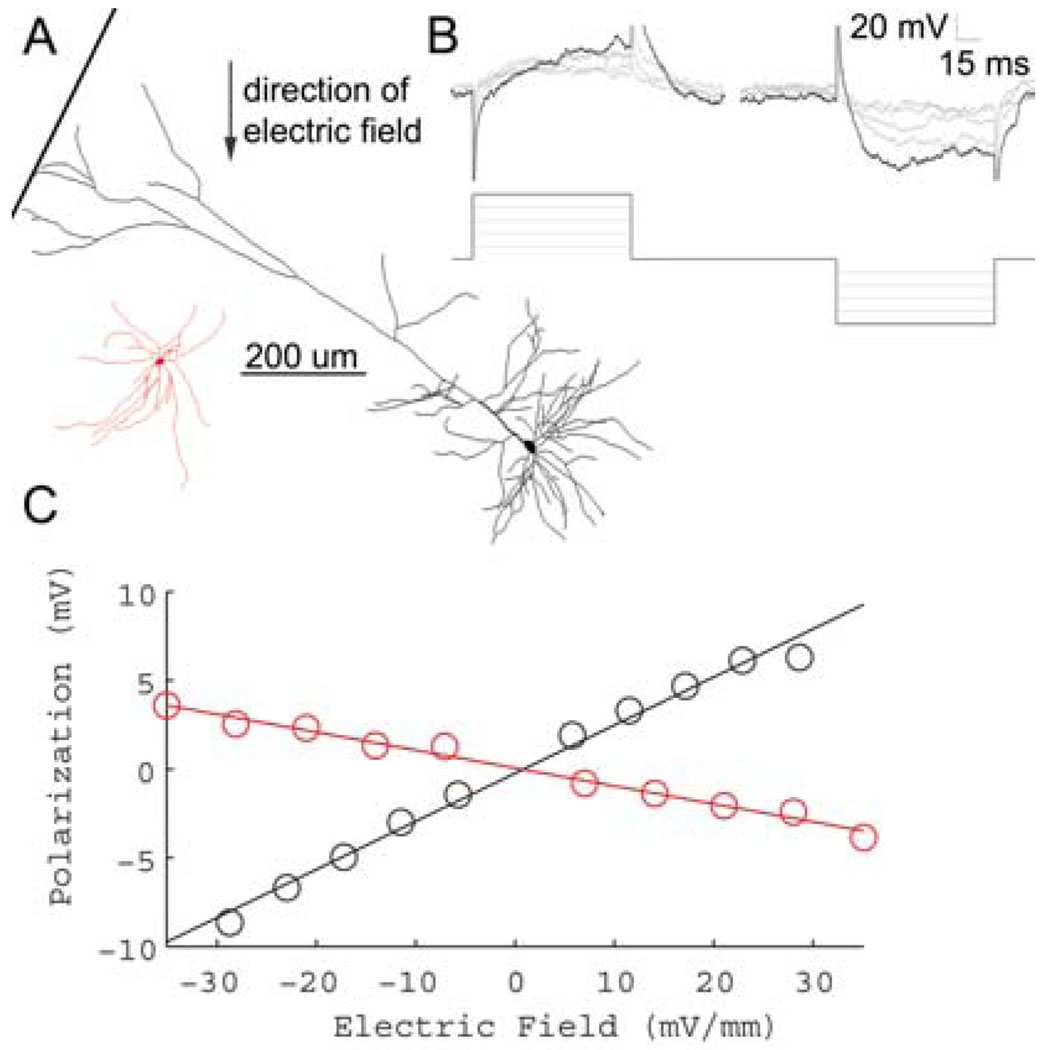
Fig. 1.

Sub-threshold electric fields polarize cortical neuronal soma linearly. A, Example morphological reconstruction of a L5 pyramidal neuron (black), and L5 fast-spiking interneuron (red) B, Incrementing electric field steps of 5.8 mV/mm (bottom) linearly polarize cell soma (top). Reconstructions shown are from L5 regular spiking pyramidal neuron of A (top). C, Summary of the polarization per electric field for the neurons shown in A. The slope of the fitted line determines the sub-threshold field polarization sensitivity for each neuron. LV pyramidal neuron (black) = .27 mV*(mV/mm)⁻¹, LV fast-spiking interneuron (red) = −.02 mV*(mV/mm)⁻¹.

For each cortical neuron, an electrotonically 1-dimensional cylinder was created integrating all segments of a neuronal tree, based on the diameter of each segment and its angle relative to the uniform electric field. We assumed a linear and symmetric distribution of electric field-induced polarization, maximal and of opposite polarity at each cylinder terminal (e.g. the dendrite tufts). The cylinder was divided into “apical” (towards the anode) and “basal” (towards the cathode) sub-cylinders, anchored around the soma, such that the polarization of the soma was predicted by the relative sub-cylinder lengths (Figure 2A, B).

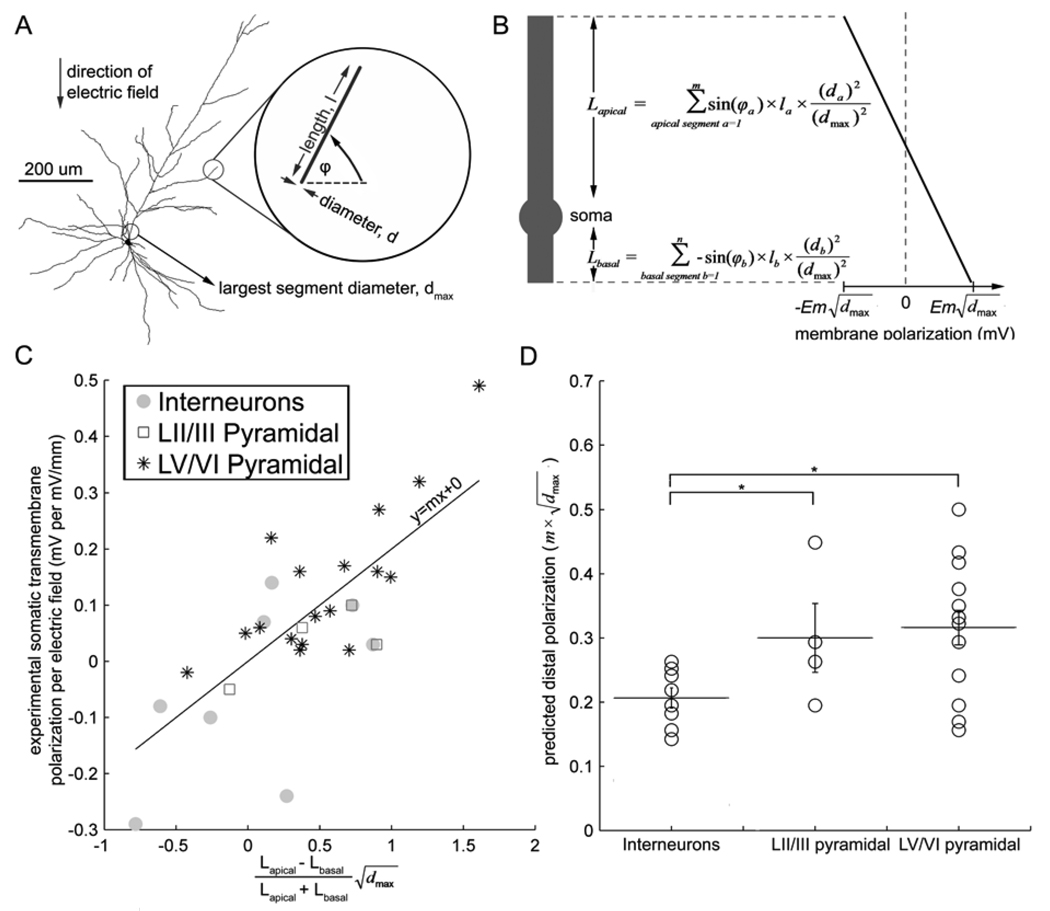
Fig. 2.

Electrotonically linear 1-D model: Neuronal morphology predicts somatic and dendritic tuft sensitivity to sub-threshold electric fields. A, Example morphological reconstruction of a L5 regular spiking pyramidal neuron with electric field induced somatic polarization of 0.14 mV*(mV/mm)⁻¹. The left circle indicates the largest segment diameter for this neuron’s segments, d_max. The right circle and inset illustrates a sample segment length, l; segment diameter, d; and angle with respect to the electric field, φ; used to construct the 1-D cylinder in B. B, 1-D cylinder model of transmembrane polarization. Schematic (left) represents construction of equivalent neuron with apical and basal combined cylinders and soma. Linear distribution of polarization along the equivalent neuron is plotted (right), with maximal polarization of +/− E_m √d_max at the distal ends of the neuron. Equations represent construction of apical and basal cylinders, using variables illustrated in A. C, For all reconstructed neurons, the 1-d model of B is applied to predict somatic polarization (x-axis), and correlated to experimentally recorded somatic transmembrane polarization (p < .05, r² = .55, n=30). D, The slope, m, of the best fit line in C is then used as a general membrane property constant (see Methods) that is multiplied by each individual neuron’s √d_max to predict terminal polarization. 1-D cylinder model predictions of terminal polarization, separated according to cortical cell type, yields a statistically significant difference between interneurons and L5/6 pyramidal neurons (p < .02) as well as between interneurons and L2/3 pyramidal neurons (p < .03).

The effect of the uniform electric field to each segment was weighted by the sine of the segment angle (φ_seg) relative to the electric field, multiplied by that segment’s length (l_seg) (Equation 1).

$$l_{\mathit{\text{proj}}}=\text{sin}({\phi }_{\mathit{\text{seg}}})\times l_{\mathit{\text{seg}}}$$ (Eq. 1)

The resulting projected length along the direction of the field (l_proj), was further adjusted to replace the original diameter (d_seg) with the largest diameter segment in the neuronal tree (d_max), but maintaining the same volume of the original segment, using the assumption of cylindrical segments (Equation 2).

$$l_{\mathit{\text{eq}}}=l_{\mathit{\text{proj}}}\times \frac{{(d_{\mathit{\text{seg}}})}^2}{{(d_{\text{max}})}^2}$$ (Eq. 2)

All apical and basal segments (·a, ·b) were weighted and summed to give two respective combined cylinders (L_apical, L_basal):

$$\begin{array}{c}{{\displaystyle L}}_{\mathit{\text{apical}}}={\displaystyle \sum _{\mathit{\text{apical segment}}a=1}^j{{\displaystyle l}}_{eq•a}}\\ ={\displaystyle \sum _{\mathit{\text{apical segment}}a=1}^j\text{sin}({{\displaystyle \phi }}_{seg•a})\times {{\displaystyle l}}_{seg•a}\times \frac{{{\displaystyle ({{\displaystyle d}}_{seg•a})}}^2}{{{\displaystyle ({{\displaystyle d}}_{\max })}}^2}}\end{array}$$ (Eq. 3)

$$\begin{array}{c}{{\displaystyle L}}_{\mathit{\text{basal}}}={\displaystyle \sum _{\mathit{\text{basal segment}}b=1}^i{{\displaystyle -l}}_{eq•b}}\\ ={\displaystyle \sum _{\mathit{\text{basal segment}}b=1}^i\text{sin}({{\displaystyle \phi }}_{seg•b})\times {{\displaystyle l}}_{seg•b}\times \frac{{{\displaystyle ({{\displaystyle d}}_{seg•b})}}^2}{{{\displaystyle ({{\displaystyle d}}_{\max })}}^2}}\end{array}$$ (Eq. 4)

Finally, we assumed an induced polarization, varying linearly along the cylinder from $-E\mathit{(}\sqrt{d_{\text{max}}}m\mathit{)}$ at the apical cylinder (anode proximal) terminal to $+E\mathit{(}\sqrt{d_{\text{max}}}m\mathit{)}$ at the basal (cathodal proximal) terminal. The ratio of the difference of the apical and basal cylinders (L_apical, L_basal) to their sum represents the location of the soma, such that the voltage of the soma may be simply predicted as:

$$V_{\mathit{\text{soma}}}=E\times (m\times \sqrt{d_{\text{max}}})\times \frac{L_{\mathit{\text{apical}}}-L_{\mathit{\text{basal}}}}{L_{\mathit{\text{apical}}}+L_{\mathit{\text{basal}}}}$$ (Eq. 5)

This holistic model is analogous to 1-dimensional cable theory predicting a peak terminal polarization, of a homogeneous equivalent cylinder with infinite-resistance terminals in a uniform field, of +/− Eλ mV for cylinders of length L >> λ [1, 8, 16]. λ is the cylinder’s length constant equal to $\sqrt{d_{\text{max}}}\times \sqrt{R_m}÷\sqrt{4R_i}$ [3, 4], L is the total equivalent cylinder length, R_m is the membrane resistivity, and R_i is intracellular resistivity. We incorporated an experimentally derived variable m, determined from fitting Eq. 5 to all morphologically reconstructed neurons; m approximates the relations of the membrane (R_m) and axial (R_i) resistivity in the equation for space constant $(\lambda ):,\sqrt{d_{\text{max}}}\times \sqrt{R_m}÷\sqrt{4R_i},\text{thus}\lambda \approx \sqrt{d_{\text{max}}}\times m$. We then used this value of m to estimate the theoretical distal terminal polarization of Eλ as $E\mathit{(}\sqrt{d_{\text{max}}}m\mathit{)}$.

III. RESULTS

A. Neuronal morphology, relative to applied electric field, correlates induced subthreshold polarization: one-dimensional transformation of neuronal morphology and predictions of distal terminal polarization

A total of 51 neurons from M1 were recorded, 36 of which were identified by cortical layer and cell type. The direction of cortical sub-threshold somatic polarization increased linearly with increasing electric field steps, and reversed polarity with the direction of the applied electric field (Fig. 1).

One dimensional electrotonic approximations of neuronal branching have previously been proposed for simplified structures [4, 8]. We developed an automated transformation, for any morphologically reconstructed neurons, into an electrotonically 1-dimensional cylinder with a linear distribution of polarization; the polarization varying from $-Em\sqrt{d_{\text{max}}}$ at the distal apical (closest to the anode) terminal, to $+Em\sqrt{d_{\text{max}}}$ at the distal basal (closest to the cathode) terminal. For each neuron, all segment volumes were weighted according to the segment’s angle to the electric field, and all apical and basal segments where then combined into respective cylinders with diameter equal to the maximal diameter (d_max) of the original neuronal tree (see Methods). The position of the soma was determined at the junction of apical and basal cylinders, such that somatic polarization may be predicted (Fig. 2A and B, and methods equations 1–5). The cylinder’s space constant, λ, was estimated as the square root of the diameter of the cylinder, , d_max, scaled by a variable, m. The scaling variable m is common across all neurons, and derived from the best fit of the electrotonically 1-dimensional predictions of somatic polarizations, to experimentally recorded values (variable m=.21, p < .05, r² = .55, n=30, Fig. 2C). Analytical models predict a maximal polarization of +/− Eλ at the distal terminals of an homogenous cylinder in a uniform electric field , when L >> λ; where L is the total equivalent cylinder length [8, 16]. Approximating λ using $m\sqrt{d_{\text{max}}}$ (see methods), we predicted distal terminal subthreshold polarization sensitivities of $\mathit{\text{E m}}\sqrt{d_{\text{max}}}$. A significant difference was found between predicted distal subthreshold polarization ($m\sqrt{d_{\text{max}}}$) of interneurons across layer, compared to either L2/3 (p < .03) or L5/6 (p < .02) pyramids (T-test, Fig. 2D).

IV. DISCUSSION

A. Response to subthreshold fields, implication to tDCS

Our results indicate that based only on volume-weighted neuronal morphology (without considering cell/compartment specific membrane biophysics) the polarity of cortical neuron somatic membrane polarization by uniform fields can be predicted with high fidelity, and the magnitude of polarization approximated, using the 1-dimensional cylinder transformation of neuronal morphology.

Human cortical neurons can be longer, with a larger maximal segment diameter, than the rat cortical neurons investigated here [17]. Assuming the ratio between the sum of apical and basal neuronal elements is similar, between rat and human cortical neurons, despite differences in overall size, our metrics predict a similar distribution of somatic polarization differences across species (Figure 2). If we consider a maximal segment diameter of an illustrative human layer 5 neuron to be 10 µm [17], the electrotonically 1-D model of terminal polarization, $\mathit{\text{Em}}\sqrt{d_{\text{max}}}$, predicts a terminal polarization sensitivity of ~ .66 mV per mV/mm of electric field induced. This value is moderately higher than the maximal predicted terminal polarization predicted for rat cortical neurons (up to .5 mV*(mV/mm)⁻¹). Note we are making the assumption that the experimentally derived variable m, dependent on the cell specific axial and membrane resistance, is the same across these species. During conventional tDCS, peak cortical fields may be of magnitudes from .43 to 1.09 mV/mm per 1 mA of total surface electrode current [18] across human cortex, resulting in a predicted terminal polarization of ~ .28 to .72 mV per 1 mA. Up to 2mA are commonly used in tDCS experiments, thus the peak terminal polarization prediction is 1.44 mV. Small changes in membrane polarization may be amplified through non-linear neuronal processes. Previous models [7] show somatic polarization of .17 mV per 1 mV/mm electric field applied. Their maximum terminal polarization is .46 mV per mV/mm electric field. In summary, these results demonstrate the importance of cortical neuronal morphology and cortical cell type during sub- and suprathreshold electric field stimulation