Identifying single-cell molecular programs by stochastic profiling

Abstract

Cells within tissues can be morphologically indistinguishable yet show molecular expression patterns that are remarkably heterogeneous. Here, we describe an approach for comprehensively identifying coregulated, heterogeneously expressed genes among cells that otherwise appear identical. The technique, called “stochastic profiling”, involves the repeated, random selection of very-small cell populations via laser-capture microdissection, followed by a customized single-cell amplification procedure and transcriptional profiling. Fluctuations in the resulting gene-expression measurements are then analyzed statistically to identify transcripts that are heterogeneously co-expressed. We stochastically profiled matrix-attached human epithelial cells in a three-dimensional culture model of mammary-acinar morphogenesis. Of 4,557 transcripts, we identified 547 genes with strong cell-to-cell expression differences. Clustering of this heterogeneous subset revealed several molecular “programs” implicated in protein biosynthesis, oxidative-stress responses, and nuclear factor-κB signaling, which were independently confirmed by RNA fluorescence in situ hybridization. Thus, stochastic profiling can reveal single-cell heterogeneities without measuring individual cells explicitly.

INTRODUCTION

Cell-to-cell variations in gene and protein expression play an important role in the development and function of many tissues^{1, 2}. Fluctuations at the single-cell level can be masked or completely misrepresented when analyzed at the population level³. This makes heterogeneities problematic for interpreting bulk measurements from large numbers of cells, such as from tumors or developing organs. Yet, such non-uniformities often uncover interesting molecular patterns that can reveal important mechanisms for the regulation of cell fate^{4, 5}. Identifying heterogeneities is thus key for gaining a deeper understanding of tissue physiology.

The challenge in discovering heterogeneities is that cells of the same type may appear phenotypically indistinguishable. Heterogeneities at the molecular level can be uncovered by immunochemistry, but the markers must be selected a priori and analyzed in small groups. While more parameters can be screened simultaneously with flow cytometry³, this involves substantial tissue processing to isolate single cells from solid tissues. Extraction of individual cells is possible in situ using laser-capture microdissection⁶, but aside from large cells such as neurons and cardiomyocytes^{7, 8}, there is usually not enough biological material to measure the expression of all but the most-abundant transcripts.

Last and most importantly, there is the conceptual hurdle of interpreting measurements from a single cell. Regulated cell-to-cell heterogeneities will appear as fluctuations in one-cell measurements. However, fluctuations will also be observed because of random biological variation, which may be functionally inconsequential⁹, and measurement error, which can be enormous¹⁰. The inability to separate contributions from these different sources has precluded using single-cell approaches to study the coordination of pathways that are heterogeneously activated.

We sought to address these challenges by developing an approach, called stochastic profiling, which is based on small-population averaging of randomly chosen cells. As a first application, we examined single-cell gene expression in a three-dimensional culture model of mammary acinar morphogenesis¹¹. The sensitivity, precision, and quantitative accuracy of stochastic profiling make it an attractive technique for studying endogenous transcriptional heterogeneities in development and cancer.

RESULTS

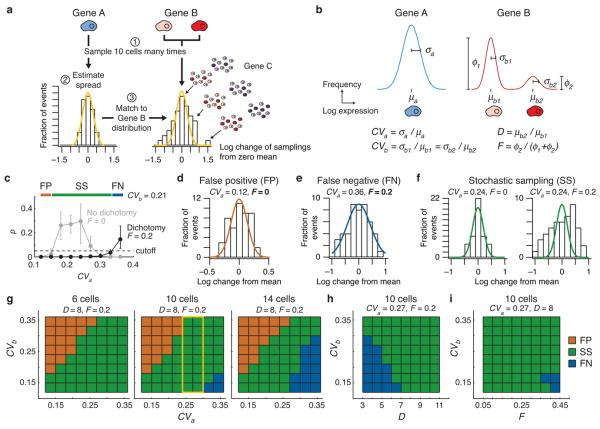
To reveal the dichotomous expression of a gene (“Gene B”), which is expressed at high levels in one population and at low levels in another (Fig. 1a), we repeatedly select very-small cell populations at random and measure the average gene expression from each random sampling (Step 1). Then, we construct a reference histogram from homogeneously expressed genes (“Gene A”), which estimates the sampling fluctuations when no dichotomy is present (Step 2). Last, we compare the estimated reference distribution to fluctuations of candidate genes measured from the same stochastic samplings (Step 3). The Gene-B distribution will deviate from the Gene-A reference because of differences in the proportion of subpopulations that were collected at each sampling (Fig. 1a). In addition, dichotomously expressed genes that are coregulated at the single-cell level (“Gene B” and “Gene C”) will have deviations that correlate across repeated samplings. Therefore, we can in principle reveal heterogeneous expression programs composed of multiple genes by clustering patterns of sampling fluctuations.

Figure 1. Small-cell profiling by stochastic sampling can distinguish transcriptional heterogeneities from normal biological variation.

(a) The statistical and empirical steps of stochastic sampling, as described in the main text. The distributions shown were based on 48 simulated samplings with the following model parameters: CV_a = 25%, CV_b = 25%, D = 8, F = 0.2 (as defined in the main text). (b) Theoretical population distributions of a constitutively expressed gene (Gene A) and a dichotomy with two subpopulations (Gene B). (c) Identifying false positives (FP, brown), false negatives (FN, blue), and effective stochastic sampling (SS, green) through Monte Carlo simulations. Stochastic-sampling experiments were simulated as described in the Online Methods with the indicated parameters and D = 8. Data are shown as the median p value for the χ² goodness of fit between the test and reference distributions ± 90% nonparametric confidence intervals from 50 simulations of 48 samplings. (d-f) Examples of false positives (brown), false negatives (green), and effective stochastic sampling (blue) for D = 8 and CV_b = 0.21. (g) Effective stochastic sampling with up to 10 averaged cells. Note that when 10 cells are averaged and CV_a = 25–30% (yellow box), stochastic sampling is effective for all values of CV_b. (h) Effective stochastic sampling for dichotomies with expression differences greater than fivefold. (i) Stochastic sampling is not strongly dependent on the relative proportion of subpopulations in a dichotomy.

Theoretical validation of stochastic sampling

We used computer simulations to help define the required sampling conditions and characterize the expression heterogeneities that stochastic sampling detects. Cells transcribe genes in exponential “bursts”¹², which give rise to log-normal distributions of mRNA species in the population¹³ (see below). Single-cell gene-expression levels were thus modeled as log-normal probability distributions with coefficients of variation (CVs) proportional to the log-standard deviation (Fig. 1b). Together, the model described the reference and dichotomous distributions with four parameters: the CV of the reference distribution (CV_a), the CV of the distributions in the gene that is dichotomously expressed (CV_b), the magnitude of the expression difference between the dichotomous subpopulations (D), and the fraction of cells with high expression for the gene that is dichotomously expressed (F) (Fig. 1b).

After selecting values for CV_a, CV_b, D, and F, we simulated the experiments and centered the sampling fluctuations of each gene on their respective log mean (Fig. 1a). Next, the sampling fluctuations of the dichotomously expressed gene were compared against a log-normal distribution using the log-standard deviation calculated from the reference distribution. The discrepancy between the log-normal reference and the sampling fluctuations of the dichotomously expressed gene was then assessed for statistical significance by a χ² goodness-of-fit test (see Online Methods).

As a control for the modeled stochastic samplings, we simulated a parallel set of control samplings, where all the parameters were the same but F was set to zero (i.e., no dichotomy). These control samplings identified false positives, which were scored as different from the reference simply because the model CVs were poorly matched (CV_a << CV_b; Fig. 1c,d). When the reference and dichotomy CVs were poorly matched in the opposite direction (CV_a >> CV_b), there was the danger of false negatives, because a dichotomous sampling distribution could be misinterpreted as a log-normal distribution with a larger CV (Fig. 1c,e). Effective stochastic sampling occurred when the reference and dichotomy CVs were roughly comparable, so that significant deviations from the reference were observed only when F ≠ 0 (P < 0.05, Fig. 1c,f).

We first sought to determine the maximum number of cells that, when averaged, could confidently identify heterogeneities across a wide range of CV_b. Direct estimates of transcriptional noise are not available, but studies in yeast have found that protein levels can fluctuate with CVs ranging from ~12-38% (Ref. ¹⁴). We independently varied CV_a and CV_b over this range for different numbers of cells sampled and then identified the CV combinations that gave false positives, false negatives, and effective stochastic sampling. When CV_a was very low (< 20%), we found that there was a substantial likelihood of false positives, which was independent of the number of cells sampled (Fig. 1g). Conversely, when CV_a was very high (> 30%), there was a danger of false negatives, which increased dramatically when more than 10 cells were sampled (Fig. 1g). With 10-cell samplings and an intermediate reference distribution (CV_b ~25–30%), we were able to achieve effective stochastic sampling across nearly all CV_b values (Fig. 1g). Furthermore, using these parameters, stochastic sampling could successfully identify dichotomies as small as 5–6 fold (Fig. 1h), with relatively little dependence on the dichotomy fraction above ~5% (Fig. 1i). When F < 0.05, the dichotomy is too rare to detect reliably in 10-cell samplings, and we observed a sharp increase in false negatives (Supplementary Fig. 1). We conclude that stochastic sampling of up to 10 cells is sufficient to detect many dichotomies when given a reference for the “average” non-dichotomous sampling fluctuations.

Optimization of small-cell PCR for stochastic profiling

Based on the simulation-derived estimates, we then developed a poly(A)-PCR amplification procedure for accurately profiling gene expression in 10 microdissected cells. Poly(A) PCR can amplify large quantities of polyadenylated transcripts from minute samples¹⁵. This technique has previously been modified to improve either single-cell representation of genes or detection sensitivity for low-abundance transcripts^{10, 16}. To optimize the technique for stochastic sampling, we designed a “small-cell” poly(A) PCR that maximizes both the reproducibility between measurement replicates and the quantitative accuracy of genes measured from 10 cells (Supplementary Fig. 2 and Online Methods). Accuracy and precision were validated by serially diluting microdissected cells before the amplification and then quantifying high- to low-abundance genes post-amplification by real-time quantitative PCR (RT-qPCR). The dilutions are critical to ensure that quantitative differences in transcript levels are not artificially increased or decreased during the procedure. To date, this quantitative accuracy has only been shown when amplification is omitted entirely¹⁷, which substantially limits the number of transcripts that can analyzed from the same sample.

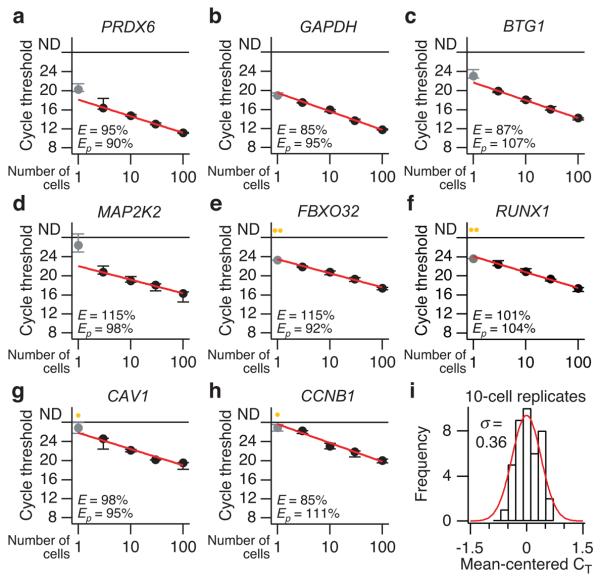
For a large panel of genes with varying abundances, we found that small-cell poly(A) PCR was highly accurate and reproducible for 3–100 cells (Fig. 2a–h and Supplementary Fig. 3). The median amplification efficiency (E) across all genes measured was 99.5%, and for individual genes, the efficiency was comparable to that of the RT-qPCR primers themselves (E_p). This suggested that the poly(A)-PCR procedure was not skewing changes in the abundance of individual genes. Overall 10-cell reproducibility as measured by RT-qPCR was 0.36 cycle thresholds (C_T), which corresponds to an amplification precision of ~28% if E = 100% (2^0.36 – 1 = 28%, Fig. 2i). Importantly, we found for many genes that the accuracy and precision of poly(A) PCR decreased substantially when single-cell equivalents of RNA were used (Fig. 2a–h and Supplementary Fig. 3). Several genes were not reproducibly detectable (e.g., Fig. 2e–h), whereas others deviated from the log-linear standard predicted from the 3–100-cell dilution series (e.g., Fig. 2a,c,d). These results were obtained from microdissected breast-epithelial cells with an average diameter of ~10 μm. Therefore, many more cell types should be quantifiable using a small-cell (rather than single-cell) approach together with stochastic profiling.

Figure 2. Quantitative and reproducible small-cell amplification of high- to low-abundance transcripts from 3–100 cells.

(a–h) The RT-qPCR cycle threshold for each gene is plotted as a function of starting cellular material and is shown as the median ± range of three replicate small-cell amplifications. Amplification efficiencies (E) based on a log-linear fit of the 3–100-cell dilutions (red line) are listed along with primer efficiencies (E_p) calculated by serially diluting the template before RT-qPCR. Genes are ordered a through h in the order of increasing median cycle threshold from the 10-cell replicates, which was used as an approximation of relative abundance (lower cycle thresholds suggest increased relative abundance). Note that the one-cell amplifications (gray) of higher-abundance transcripts (a-d) often deviate from the log-linear fit, and the one-cell amplification of lower-abundance transcripts (e-h) are frequently not detectable (yellow, ND). (i) Reproducible small-cell amplification of 10 cells. The cycle thresholds from 10-cell amplification replicates of all genes were mean centered, grouped, and fit to a normal distribution. The standard deviation (σ) of the mean-centered cycle thresholds (C_T) was 0.36, corresponding to a coefficient of variation of 28%, assuming that amplicons double after each cycle (i.e., 100% efficiency, 2^0.36 – 1 = 0.28).

Adapting small-cell PCR to oligonucleotide microarrays

A key step toward accurate 10-cell quantification was limiting the number of amplification cycles in small-cell poly(A) PCR to no more than 30 (Supplementary Fig. 2). With 10 microdissected cells, a 30-cycle amplification typically yielded ~10 ng of unlabeled cDNA, which was insufficient for oligonucleotide microarrays. We therefore reamplified a fraction of the poly(A) cDNA and added aminoallyl-dUTP for subsequent fluorophore labeling, yielding ~1.5 μg of labeled cDNA per 10-cell sample. The conditions for reamplification differed from small-cell poly(A) PCR (see Online Methods) and were carefully monitored with real-time pilot experiments to identify the maximum number of cycles that kept all samples in the exponential phase of amplification. We found that doing so maintained the quantitative accuracy toward high- and low-abundance transcripts (Supplementary Fig. 4). Furthermore, repeat reamplifications using the same starting cDNA pool confirmed that reamplification added little measurement error to the final microarray measurements (Supplementary Fig. 5). Hybridization of reamplified samples to Illumina HumanRef-8 microarrays consistently detected 7,000–8,000 transcripts (median detection P < 0.1). This result compares favorably with an earlier study from our group¹⁸, in which ~8,700 transcripts were detected by standard profiling approaches using RNA extracted from large populations of the cells used here. We conclude that our experimental platform is sufficiently accurate and sensitive to quantify much of the transcriptome for stochastic profiling.

Stochastic profiling of epithelial acinar morphogenesis

As a proof of principle, we tested the feasibility of stochastic profiling in a three-dimensional (3D) culture model of mammary-epithelial acinar morphogenesis¹¹. For this culture model, individual MCF10A mammary-epithelial cells are seeded in reconstituted basement membrane and develop to form proliferation-arrested, hollow acinar structures comprised of 50–100 cells when fully mature. Each acinus is clonal and thus isogenic, but many signaling and cell-fate dichotomies nonetheless emerge during morphogenesis. For example, matrix-attached cells of the outer acinus appear grossly similar but show variable expression of phospho-Akt¹⁹, phospho-myosin light chain²⁰, and the CDK inhibitor p27 (Ref. ²¹). The overall extent of such cell-to-cell heterogeneities and their role in morphogenesis has not been defined.

We focused the stochastic profiling on matrix-attached cells in developing 3D cultures, because these cells comprise the final acinar structure that resembles the lobular unit of the breast in vivo¹¹. Matrix-attached cells are also readily identified in cryosections of 3D structures and can be microdissected as single cells with high accuracy (Supplementary Fig. 6 and Online Methods). We obtained transcriptional profiles for 16 independent 10-cell samplings of matrix-attached cells along with 16 measurement controls. The control samples consisted of independent amplifications from a common starting pool of 160 microdissected cells. These amplification replicates were used to gauge the measurement error associated with profiling gene expression from 10 “average” cells.

Our analysis focused on the 4,557 transcripts that were clearly identified in all 32 microarrays (16 samplings plus 16 controls, P < 0.1). First, we identified the subset of transcripts whose sampling CV was significantly higher than the corresponding control CV in amplification replicates (see Online Methods). We reasoned that the independent samplings of such transcripts would provide a good estimate for normal biological variation with only a minor contribution from measurement noise. Many transcripts were eliminated from the subset because their independent 10-cell sampling measurements were highly reproducible. For example, 1,332 genes had a sampling CV < 20%, meaning that the corresponding control CV would have needed to be < ~10% to be included in the analysis. We presume that the majority of these transcripts are homogeneously expressed or show heterogeneities too small or infrequent to be detected experimentally.

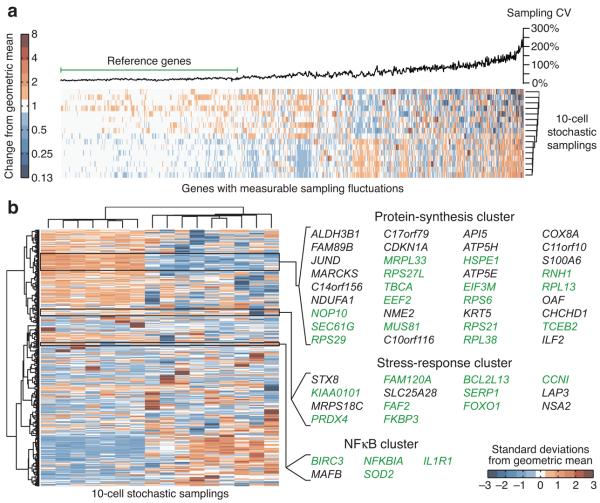
Next, we clustered the independent measurements of the 1,003 genes in the subset, using Euclidean distance as a metric to sort transcripts roughly by sampling CV (Fig. 3a). We observed a plateau of low and consistent sampling CVs, followed by an abrupt increase where sampling fluctuations seemed to become more irregular and less random. We defined the transcripts in the early plateau as the reference-gene set (Fig. 3a) and found that the median sampling CV in this set was 19% with an interquartile range of 14–26% (Supplementary Fig. 7a). We fed these empirically derived parameters into our earlier model and found that stochastic profiling should be effective across the entire interquartile range of CVs (Supplementary Fig. 7b). Last, we compared sampling fluctuations of individual transcripts against a log-normal reference distribution with CV_a = 0.19 at a false-discovery rate of 0.05 (Supplementary Fig. 7c). Overall, stochastic profiling identified 547 genes whose expression was predicted to be strongly heterogeneous (12% of all transcripts consistently detected).

Figure 3. Stochastic profiling of matrix-attached cells at day 10 of MCF10A morphogenesis.

(a) Hierarchical clustering of unscaled sampling fluctuations for transcripts with measurable biological variation. Genes with sampling variations greater than measurement error were clutered using a Euclidean distance metric and average linkage. The genes with consistent CV values (left) were used as the reference subset for calculating an appropriate reference distribution used to test for heterogeneous expression. (b) Hierarchical clustering of scaled sampling fluctuations for transcripts predicted to be heterogeneously expressed by stochastic profiling. Candidate heterogeneities were scaled to unit variance and clustered using a Euclidean distance metric and Ward's linkage. Selected clusters were examined for enriched biological functions. Genes consistent with the assigned functions are highlighted in green.

Discovery of heterogeneous single-cell programs

We standardized and reclustered the sampling data for the candidate heterogeneities to organize genes by their pattern of sampling fluctuations (Fig. 3b). The analysis identified multiple clusters that had strong links to recognized biological processes. The first cluster contained many genes involved in protein synthesis, including ribosomal subunits (RPS6, RPL38, etc.), initiation-elongation factors (EIF3M, EEF2), and chaperones (SEC61G, TBCA). This cluster also contained the basal-progenitor markers, KRT5 (Ref. ²²) and an ALDH isoform²³, and the JUND transcription factor. The second cluster was comprised of several transcripts connected with oxidative-stress responses and proliferative suppression, such as PRDX4, FAM120A²⁴, SERP1 (Ref. ²⁵), and FOXO1²⁶. The third cluster was the smallest but contained a large proportion of genes known to be initiators (ILIR1), effectors (NFKBIA), or markers (BIRC3, SOD2) of nuclear factor-κB (NF-κB) signaling²⁷. NF-κB signaling heterogeneity was also observed posttranslationally by localization of the p65 subunit of NF-κB and expression of IκBα, an upstream inhibitor of NF-κB (Supplementary Fig. 8). Taken together, the correlated sampling fluctuations and shared biological function within clusters suggested these were molecular programs that were induced heterogeneously in single cells.

We next sought to validate the stochastic-profiling predictions by an independent method. We developed an RNA fluorescence in situ hybridization (FISH) procedure for dual tracking of gene-expression variation in individual cells (see Online Methods). Our two-color RNA FISH protocol was optimized for specificity (Supplementary Figs. 9 and 10) and for reliably detecting single-cell coregulatory patterns between selected transcripts (Fig. 4a-c). Using RNA FISH, we observed pronounced cell-to-cell expression heterogeneities for nearly all transcripts identified by stochastic profiling that were examined (Fig. 4a-c, Supplementary Fig. 11, and Supplementary Note 1). Conversely, we observed more-uniform expression for two genes, GAPDH and HINT1, whose stochastic-sampling fluctuations were not different than the reference distribution (Supplementary Fig. 12). Thus, stochastic profiling can separate acute single-cell heterogeneities from transcripts with normal expression variability.

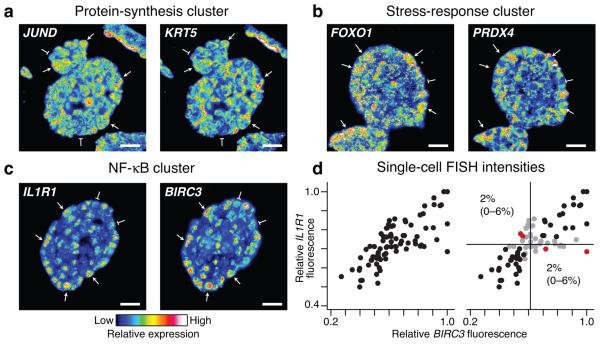
Figure 4. Stochastic profiling identifies clusters of heterogeneously coexpressed transcripts.

Two-color RNA FISH images were collected at day 10 of MCF10A morphogenesis for (a) JUND and KRT5 in the protein-synthesis cluster, (b) FOXO1 and PRDX4 in the stress-response cluster, and (c) IL1R1 and BIRC3 in the NF-κB cluster. Images are pseudocolored to highlight quantitative differences in fluorescence intensity, and single cells showing strong coexpression are highlighted with arrows (high expression) or flat markers (low expression). Two-color images for 3–4 additional gene pairs within each cluster are shown in Supplementary Figure 11. (d) BIRC3–IL1R1 images were segmented to quantify average fluorescence intensities in single cells as described in the Online Methods. Data are shown from cells in four independent acini after normalization to the maximum observed cellular fluorescence signal in each image. Gates were defined as the 25^th percentile centered on the median fluorescence intensity (black lines) for each gene. Observations that were within the range of the gates were scored as neither positive nor negative (gray). Single positive cells (red) are shown as the percentage of the overall cell population with 90% confidence intervals in parentheses. For a-c, scale bar is 20 μm.

In addition, for gene pairs in the same cluster, we found highly concordant patterns of strong and weak expression among individual cells (Fig. 4a-c, Supplementary Fig. 11, and Supplementary Note 2). Analysis of cell-to-cell fluorescence intensities revealed that matrix-attached cells were almost exclusively “double negative” (weakly expressing both genes) or “double positive” (strongly expressing both genes) (Fig. 4d). Cells that strongly expressed one gene but not the other (“single positive”) were too rare to constitute a meaningful subpopulation and were likely filtered out by stochastic profiling (Fig. 4d and Supplementary Fig. 1). Together, this indicates that clusters of genes with similar stochastic-sampling fluctuations are heterogeneously coexpressed with high probability.

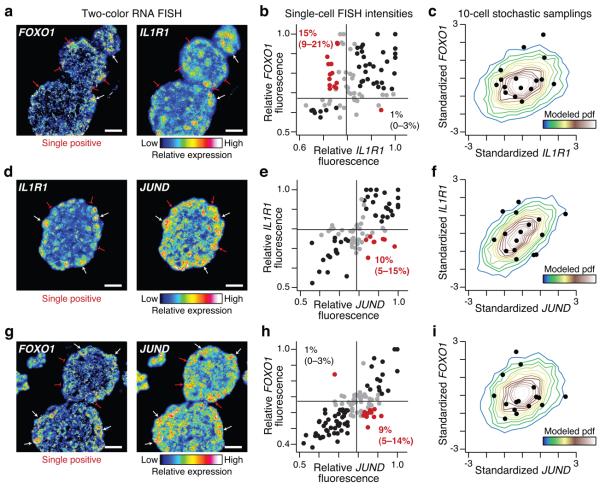
As a final validation, we checked whether genes in separate stochastic-profiling clusters were distinguishable on the single-cell level by RNA FISH. The observed concordance between clusters ranged from no discernable correlation (Fig. 5a-c) to pairs with stronger covariation (Fig. 5d-i). Nevertheless, for each gene pairing, we repeatedly identified single-positive cells at frequencies that should be detected by stochastic profiling (> 9–10%, Figs. 1i and 5b,e,h). Inclusion of these single-positive cells during stochastic sampling would be sufficient to perturb any correlated fluctuations, providing an explanation for the distinct clusters shown in Figure 3b. Indeed, using the RNA FISH measurements as the basis for simulated stochastic samplings, we estimated probability distributions that largely captured the stochastic-profiling measurements (Figs. 3b and 5c,f,i).

Figure 5. Stochastic profiling distinguishes heterogeneous expression patterns that are not exclusively coexpressed.

Two-color RNA FISH images were collected at day 10 of MCF10A morphogenesis and compared to the stochastic-profiling data for (a-c) FOXO1 and IL1R1, (d-f) IL1R1 and JUND, and (g-i) FOXO1 and JUND. (a,d,g) Representative pseudocolored images, containing single-positive cells highlighted with red arrows (high expression) or flat markers (low expression) Scale bar is 20 μm. (b,e,h) Fluorescence intensities are shown from cells in four independent acini after normalization to the maximum observed cellular fluorescence signal in each image. Gates were defined as the 25^th percentile centered on the median fluorescence intensity (black lines) for each gene. Observations that were within the range of the gates were scored as neither positive nor negative (gray). The percentages of single-positive cells (red) in the overall cell population are shown with 90% confidence intervals in parentheses. (c,f,i,) RNA FISH distributions of b,e,h were resampled as 10-cell averages, standardized, and the resulting probability density function (pdf) was compared to the standardized sampling fluctuations from stochastic profiling (black circles) shown in Figure 3b.

DISCUSSION

Transcriptional heterogeneities can emerge from purely stochastic cell-fate decisions^{1, 2, 28}, but they can also be instructed by differences in the microenvironment²⁹. Stochastic profiling does not make a distinction between these heterogeneities but provides a means for identifying them so that the underlying mechanisms can be studied thereafter. The biggest advantage of stochastic profiling is its improved accuracy and reproducibility, which becomes possible when 10 cells are measured instead of one (Fig. 2). Although measurements are not explicitly single cell, the entire procedure requires only a few hundred cells, meaning that stochastic profiling should be amenable to most ex vivo tissue specimens in the future.

Our first application of stochastic profiling uncovered many genes not previously suspected to show heterogeneous regulation during morphogenesis. MCF10A cells have a basal-progenitor expression profile³⁰, suggesting that some heterogeneities could be due to partial differentiation of single cells in 3D. The existence of a heterogeneous stress-response program is particularly intriguing, because it raises the possibility that individual cells might occupy stressful niches caused by local cell-cell interactions and basement-membrane composition.

Another interesting question raised by the study here is whether the single-cell programs identified by stochastic profiling are coordinated during morphogenesis. For the gene clusters imaged simultaneously by RNA FISH, we found that the single-positive populations were not equally populated. For example, high JUND expression could be found in cells with low IL1R1 or FOXO1 expression, but cells with the opposite pattern were extremely rare (Fig. 5e,h). Future work will focus in greater depth on these dependencies and their possible role during morphogenesis.

The extent to which heterogeneously activated pathways in vivo might obscure phenotypes or create patterns in tissues is only beginning to be studied¹. The bottleneck is not in studying the role of heterogeneities, but rather in identifying them in the first place. Stochastic profiling provides a valuable tool for analyzing the coordination of such pathways quantitatively and systematically.

ONLINE METHODS

Monte Carlo simulations

Stochastic sampling simulations (Fig. 1) were performed in MATLAB (Mathworks) with the statistics toolbox. For each simulation, the model assumed a binomial distribution for the cellular dichotomy and log-normal distribution of measured transcripts^{13, 31}. CV_a and CV_b were varied between 12–38% to approximate biologically plausible values¹⁴ and then re-run with empirically derived values (Supplementary Fig. 7a,b). The distribution of 48 population-averaged samplings was log-mean centered and compared to a log-normal distribution with a standard deviation estimated from 48 reference samplings. The χ² goodness of fit between the dichotomous and reference distributions was done using the chi2gof function with 10 bins. The χ² test directly evaluates the relative differences between observed and expected values on the sampling histogram and is a robust, conservative test for this application³². Bins were pooled if the observed or expected value in a bin was less than five. Each CV_a, CV_b, D, and F parameter set was run 50 times to measure the median P values and the associated nonparametric confidence intervals. Stochastic sampling was deemed effective when the median P value for F ≠ 0 was less than 0.05 and the median P value for F = 0 was greater than 0.05. The source code for the simulations is available in the Supplementary Software.

For the simulation of probability density functions (Fig. 5c,f,i), the single-cell FISH intensities from Fig. 5b,e,h were randomly combined as 10-cell averages for each gene pair for 5,000 iterations. These bootstrapped estimates were standardized and then compiled as two-dimensional histograms by using the hist2 function with 20 bins.

Cell lines

The MCF10A-5E clone was isolated by limiting dilution of the parental MCF10A line (ATCC) and selected for its homogeneous behavior in 3D. MCF10A-5E cells were maintained as described previously for MCF10A cells³³.

Frozen sectioning of 3D cultures

To allow embedding of 3D cultures, a plastic coverslip was cut to size and placed at the base of an 8-well chamber slide (BD Biosciences) before starting. Coverslipped chamber slides were then coated with Matrigel (BD Biosciences), and 3D culture of MCF10A-5E cells was performed as described previously³³. For fresh frozen sections (used for laser capture microdissection), coverslips were washed with PBS and then embedded directly in NEG 50 on a dry ice-isopentane bath. For fixed frozen sections (used for RNA FISH), coverslips were washed in PBS and fixed in 3.7% paraformaldehyde for 15 min. After three 5 min washes in PBS, samples were cryopreserved in 15% sucrose for 15 min, 30% sucrose for 15 min, and then embedded in NEG 50 as described above. Sectioning was performed at −24°C on a cryostat (Leica). Embedded specimens and cryosections were stored at −80°C until further use.

Laser capture microdissection

8 μm sections were cut on plain glass slides and kept at −24°C during sectioning and −80°C during storage. After removing from −80°C, slides were fixed immediately in 75% ethanol for 30 sec, followed by distilled water for 30 sec. Fixed slides were stained for 30 sec with nuclear fast red (Vector Laboratories) containing 1 U ml⁻¹ RNAsin Plus (Promega), then washed twice in distilled water for 15 sec. Stained slides were dehydrated with an ethanol series (30 sec each of 70%, 95%, and 100% ethanol) and cleared with xylene for 2 min. After air drying for 5–10 min, slides were stored in a dessicator and used immediately.

Before microdissection, slides were cleaned with a PrepStrip (Arcturus) to remove loosely adherent material. Microdissection was performed on a Pixcell II instrument (Arcturus) using Capsure HS LCM caps (Arcturus). 750 μs laser shots were used at 50–65 mW power to achieve single-cell resolution (Supplementary Fig. 6). For this study, matrix-attached cells were sampled at 3–4 random positions across ~3 acini to focus on matrix-dependent (rather than acinus-dependent) heterogeneities. After microdissection, LCM caps were cleaned with an adhesive note to remove biological material adjacent to the dissected cells.

Small-cell quantitative mRNA amplification

Samples were eluted from the microdissection caps by adding 4 μl digestion buffer (1.25× MMLV RT buffer [Invitrogen], 100 μM dNTPs [Roche], 0.08 OD ml⁻¹ oligo(dT)₂₄, and 250 μg ml⁻¹ proteinase K [Sigma]) and incubating at 42°C for 1 hr. Digested samples were spun into PCR tubes and quenched with 1 μl of digestion stop buffer (1.5 U ml⁻¹ Prime RNAse inhibitor [Eppendorf], 1.5 U ml⁻¹ RNAguard [Amersham], and 5 mM freshly prepared PMSF). The quenched samples were then processed by using poly(A) PCR¹⁵ that was heavily modified to allow quantitative amplification of high- and low-abundance transcripts.

4.5 μl of the quenched samples were transferred into thin-walled 0.2-ml PCR tubes, and 0.5 μl of Superscript III (Invitrogen) was added. The first-strand synthesis reaction was incubated at 50°C for 15 min and then heat-inactivated at 70°C for 15 min. The samples were placed on ice and spun for 2 min at 14,000 rpm on a benchtop centrifuge at 4°C. Next, 1 μl of RNAse H solution (2.5 U ml⁻¹ RNAse H [USB Corporation],12.5 mM MgCl₂) was added, and the reaction was incubated at 37°C for 15 min. After RNAse H treatment, the reaction was poly(A) tailed with 3.5 μl of 2.6× tailing solution (80 U terminal transferase [Roche], 2.6× terminal transferase buffer [Invitrogen], 1.9 mM dATP) for 15 min at 37°C and then heat-inactivated at 65°C for 10 min. The samples were placed on ice and spun for 2 min at 14,000 rpm on a benchtop centrifuge at 4°C. To each sample, 90 μl of ThermoPol PCR buffer was added to a final concentration of 1× ThermoPol buffer (New England Biolabs), 2.5 mM MgSO₄, 1 mM dNTPs (Roche), 100 μg ml⁻¹ BSA (Roche), 10 U AmpliTaq (Applied Biosystems), and 5 μg AL1 primer¹⁵. Each reaction was split into three thin-walled 0.2-ml PCR tubes and amplified according to the following thermal cycling scheme: four cycles of 1 min at 94°C (denaturation), 2 min at 32°C (annealing), and 6 min plus 10 sec per cycle at 72°C (extension); 21 cycles of 1 min at 94°C (denaturation), 2 min at 42°C (annealing), and 6 min 40 sec plus 10 sec per cycle at 72°C (extension). The reaction was cooled, placed on ice, and the three tubes from each sample were pooled and amplified according to the following thermal cycling scheme: five cycles of 1 min at 94°C (denaturation), 2 min at 42°C (annealing), and 6 min at 72°C (extension). Further thermal cycling led to overamplification and loss of quantitative accuracy (K.A.J. and J.S.B., unpublished observations). Samples were stored at −20°C until use.

Real-time quantitative PCR (RT-qPCR)

RT-qPCR of amplified material from stochastic sampling was measured as described previously³⁴, except that tenfold less of each amplified sample was used as the starting cDNA template. Primer sequences and concentrations are shown in Supplementary Table 1.

Small-cell reamplification and microarray hybridization

Amplified small-cell samples were reamplified and aminoallyl labeled in a 100 μl reaction containing 1× High-Fidelity buffer (Roche), 3.5 mM MgCl₂, 200 μM dATP, dCTP, and dGTP, 40 μM dTTP (Roche), 160 μM aminoallyl-dUTP (Ambion), 100 μg ml⁻¹ BSA (Roche), 5 μg AL1 primer, and 1 μl amplified cDNA. Each reaction was amplified according to the following thermal cycling scheme: 1 min at 94°C (denaturation), 2 min at 42°C (annealing), and 3 min at 72°C (extension). In pilot experiments, 20 μl of this reaction for each stochastic sampling was monitored in the presence of 0.25× SYBR Green on a LightCycler II real-time PCR instrument (Roche). The number of amplification cycles (~20) was selected to ensure that all samples remained in the exponential phase during amplification³⁵. Samples were purified on a PureLink column (Invitrogen), ethanol precipitated, and labeled with Alexa 555 amine-reactive dye (Invitrogen) according to the manufacturer's recommendation. Labeling efficiency was ~2 dye molecules per 100 bases.

For microarray hybridization, 1 μg Alexa 555-labeled cDNA (total volume: 5 μl) was mixed with 10 μl GEX hybridization buffer (Illumina). Samples were denatured at 94°C for 4 min and then added directly to HumanRef-8 Expression BeadChips (Illumina) prewarmed at 58°C. Slides were incubated at 58°C for 20 hr and washed according to the manufacturer's recommendations. After drying, slides were scanned on a BeadArray reader (Illumina) with a scan setting of “Direct hybridization 1”. Samples were normalized to their mean overall fluorescence intensity relative to the overall dataset and then to the median fluorescence intensity of all transcripts detected (P < 0.1) on each sample for subsequent analysis.

Riboprobe synthesis

A 175–225 bp fragment of each gene was cloned by PCR into pcDNA3 (Invitrogen) from an MCF10A cDNA library generated by first-strand synthesis with Superscript III (Invitrogen) and an oligo(dT)₂₄ primer. Plasmids were linearized with the appropriate restriction enzymes and purified by phenol-chloroform extraction and ethanol precipitation. Riboprobes were synthesized from the linearized template by using the MAXIscript Sp6/T7 kit (Ambion) as recommended, except that in vitro transcriptions were incubated for 2 hr and Sp6 in vitro transcriptions were performed at 40°C to increase yield. Digoxigenin (DIG)- and dinitrophenyl (DNP)-labeled riboprobes were synthesized with 35% DIG–UTP (Roche) or DNP–UTP (Perkin Elmer) and 65% unlabeled UTP. After DNAse digestion, riboprobes were ethanol precipitated, resuspended in RNAse-free water to 0.2 μg ml⁻¹, and stored at −80°C.

Multicolor RNA fluorescence in situ hybridization (RNA FISH)

5 μm frozen sections of day 10 structures were cut on Superfrost Plus slides (Fisher), air dried, and stored at −80°C until further use. Slides were thawed at room temperature until completely dry, treated with 0.2 N HCl for 10 min, and washed in PBS for 5 min. Slides were then postfixed in 3.7% paraformaldehyde for 15 min, washed 2 × 10 min in PBS, and once in freshly prepared 0.1 M triethanolamine (pH 8.0) for 10 min. Samples were next acetylated with 0.25% acetic anhydride in freshly prepared 0.1 M triethanolamine (pH 8.0) for 5 min and washed in 2× SSC for 10 min. Slides were dehydrated with an ethanol series (2 min each of 70%, 95%, and 100% ethanol), and sections were covered with hybridization solution (1 mg ml⁻¹ yeast tRNA, 10% dextran sulfate in 2× SSC, 50% formamide) containing 50–500 ng ml⁻¹ of each riboprobe. Sections were covered with Parafilm, sealed with rubber cement, and incubated at 42°C in a humidified chamber for 14–16 hr.

After hybridization, slides were soaked in 2× SSC at 37°C for 5 min, the Parafilm was removed, and slides were washed in 2× SSC, 50% formamide for 30 min at 55°C, followed by 0.1× SSC for 30 min at 55°C. Slides were equilibrated in PBS for 10 min and then blocked for 1 hr at room temperature with 1× Western Blocking Reagent (Roche) in PBS + 0.3% Tween-20. After blocking, slides were incubated 1 hr at room temperature with 1× Western Blocking Reagent (Roche) in PBS + 0.3% Tween-20 containing anti-digoxin (1:500, Jackson ImmunoResearch) and anti-DNP (1:1,000, Invitrogen). Slides were washed 3 × 5 min in PBS and incubated for 1 hr at room temperature with 1× Western Blocking Reagent (Roche) in PBS + 0.3% Tween-20 containing Alexa 488-conjugated goat anti-rabbit (1:200, Invitrogen) and Alexa 555-conjugated goat anti-mouse (1:200, Invitrogen). Slides were washed 3 × 5 min in PBS and cell membranes were labeled with 20 μg ml⁻¹ Alexa 350-conjugated wheat-germ agglutinin for 5 min at room temperature. After two 5 min washes in PBS, autofluorescence was quenched with 10 mM CuSO₄ in 50 mM NH₄Ac (pH 5.0) for 10 min³⁶. Slides were washed with PBS for 5 min and mounted with 0.5% n-propyl gallate in PBS + 90% glycerol³⁷.

Immunofluorescence

5 μm sections of day 10 structures were cut on Superfrost Plus slides (Fisher), air dried, and stored at −80°C until further use. Slides were thawed at room temperature until completely dry, hydrated 3 × 5 min in PBS, and then blocked for 1 hr at room temperature with 1× Western Blocking Reagent (Roche) in PBS + 0.3% Tween-20. After blocking, slides were incubated overnight at room temperature with 1× Western Blocking Reagent (Roche) in PBS + 0.3% Tween-20 containing anti-p65 (A) (1:100, Santa Cruz) or anti-IκBα (C-21) (1:500, Santa Cruz). Slides were washed 3 × 5 min in PBS and incubated for 1 hr at room temperature with 1× Western Blocking Reagent (Roche) in PBS + 0.3% Tween-20 containing Alexa 555-conjugated goat anti-rabbit (1:200, Invitrogen). Slides were washed 3 × 5 min in PBS and counterstained with 0.5 μg ml⁻¹ DAPI (Sigma) for 5 min at room temperature. After two 5 min washes in PBS, autofluorescence was quenched with 10 mM CuSO₄ in 50 mM NH₄Ac (pH 5.0) for 10 min³⁶. Slides were washed with PBS for 5 min and mounted with 0.5% n-propyl gallate in PBS + 90% glycerol³⁷.

Microscopy

Frozen sections and coverslips were imaged with a 40× 1.3 NA oil objective on an BX51 upright fluorescence microscope (Olympus) with the following filter sets: ET-DAPI (excitation: 325–375 nm, dichroic: 400 nm, emission: 435–485 nm), ET-FITC (excitation: 450–490 nm, dichroic: 495 nm, emission: 500–550 nm), ET-CY3 (excitation: 520–570 nm, dichroic: 565 nm, emission: 570–640 nm), and ET-CY5 (excitation: 590–650 nm, dichroic: 660 nm, emission: 665–735 nm). Images were captured with an Orca R2 CCD camera (Hamamatsu) at 2×2 binning and exposure times that filled 90% of the camera bit depth, with the exception of the RNA FISH sense controls (Supplementary Figs. 9 and 10) where the exposure time was matched to the antisense image. Displayed images were rainbow pseudocolored with a linear lookup table that covered the full range of the data for each fluorescence channel.

Image segmentation and quantification

Single cells from RNA FISH images were segmented by hand based on wheat-germ agglutinin staining (DAPI channel), and traced image segments were then applied to the DIG- and DNP-labeled riboprobe stainings (FITC and Cy3 channels). Median fluorescence intensities per cell for each riboprobe were calculated, and individual images were normalized to the maximum observed intensity in each channel for comparison across multiple images.

Statistical analysis

Statistical analyses of RT-qPCR measurements were performed on the cycle thresholds of the measured genes. This is equivalent to a log₂ transformation, which allows log-normal distributions to be treated as normal distributions^{13, 31}. Estimation of the coefficient of variation for amplification replicates (Fig. 2i) was done in Igor Pro (WaveMetrics) by nonlinear least-squares curve fitting of the mean-centered cycle thresholds to a normal distribution with a mean of zero. Confidence intervals on CVs were calculated with McKay's transformation³⁸, and non-overlapping 90% confidence intervals were considered significantly different. χ² goodness-of-fit tests for sampling fluctuations were performed in MATLAB with the chi2gof function, a mean of zero, and a standard deviation equal to the reference distribution (false-discovery rate = 0.05). Nonparametric confidence intervals for the RNA FISH subpopulations were based on a binomial distribution.