Abstract
The adverse effect of co-inheritance linkage of a large number of sites on adaptation has been studied extensively for asexual populations. However, it is insufficiently understood for multi-site populations in the presence of recombination. In the present work motivated by our studies of HIV evolution in infected patients, we consider a model of haploid populations with infrequent recombination. We assume that small quantities of beneficial alleles preexist at a large number of sites and neglect new mutation. Using a generalized form of the traveling wave method, we show that the effectiveness of recombination is impeded and the adaptation rate is decreased by inter-sequence correlations, arising due to the fact that some pairs of homologous sites have common ancestors existing after the onset of adaptation. As the recombination rate per individual becomes smaller, site pairs with common ancestors become more frequent, making recombination even less effective. In addition, an increasing number of sites become identical by descent across large samples of sequences, causing reversion of the direction of evolution and the loss of beneficial alleles at these sites. As a result, within a 10-fold range of the recombination rate, the average adaptation rate falls from 90% of the infinite-recombination value down to 10%. The entire transition from almost maximum to almost zero may occur at very small recombination rates. Interestingly, the strong effect of linkage on the adaptation rate is predicted in the absence of average linkage disequilibrium (Lewontin's measure).
Keywords: multi-locus, recombination, selection, HIV, genealogy
1. Introduction
Adaptation rate and other evolutionary properties are strongly affected by co-inheritance linkage, i.e., the fact that many genomic sites are passed to progeny all together, as a set. Studies of few-site models showed that linkage has adverse effects on progressive evolution, including much slower fixation of beneficial alleles (Felsenstein, 1974; Fisher, 1930; Hey, 1998; Hill and Robertson, 1966; Muller, 1932; Otto and Barton, 1997) and Muller's ratchet (Charlesworth and Charlesworth, 1997; Felsenstein, 1974; Gordo and Charlesworth, 2000; Haigh, 1978; Stephan et al., 1993).
Using a very simple analytic approximation (neglecting new mutations within already growing clones), Maynard Smith argued that the effect of linkage on adaptation should increase with the number of evolving sites (Maynard Smith, 1971). The prediction was confirmed recently by development of quantitative analytic theory of asexual evolution in the multiple-mutation regime (Brunet et al., 2008; Desai and Fisher, 2007; Rouzine et al., 2003; Rouzine et al., 2008; Tsimring et al., 1996). The basic idea is to consider dynamics of classes of genomes with the same fitness. All the fitness classes, with the exception of the best-fit class, are treated deterministically. The best-fit class is subject to strong stochastic effects. Originally, the idea of treating a single, fittest class stochastically was used in the limit of either large selection coefficients or very large population sizes (Charlesworth and Charlesworth, 1997; Gordo and Charlesworth, 2000; Haigh, 1978; Stephan et al., 1993) when the distribution is nearly always close to mutation-selection equilibrium, and infrequent loss of the fittest class, Muller's ratchet (Felsenstein, 1974), takes place. The cited recent papers considered a more general case of non-equilibrium populations to describe relatively fast accumulation of favorable or deleterious mutations. The fittest class was described by various approximations, starting from a simple cutoff at one copy (Tsimring et al., 1996), a more accurate diffusion approach (Rouzine et al., 2003; Rouzine et al., 2008), or a branching process theory (Brunet et al., 2008; Desai and Fisher, 2007). Overall, this work showed that the fitness distribution represents a traveling solitary wave, whose speed is determined by stochastic processes occurring at the edge, and predicted the substitution rate over a broad parameter range.
In the asexual case, the importance of considering evolution at many sites at once is especially clear. The best illustration is provided by comparison with the “clonal interference” approximation (Gerrish and Lenski, 1998; Orr, 2000; Wilke, 2004), which considers competition between two clones with different selection coefficients emerging due to consecutive beneficial mutations at two randomly chosen sites. In this approach, emergence of new clones at other sites, within already existing clones, is neglected. The substitution rate is predicted to saturate, at large population sizes, at a value much smaller than predicted by a model considering a single evolving site (single-site model, limit of infinite recombination). By contrast, the cited multi-site theory allows for new mutations within already growing clones. Competition between sequences occurs due to different numbers of beneficial alleles, rather than variation of selection coefficient. The substitution rate increases slowly (logarithmically) with the population size up to extremely large population sizes, when different sites become statistically independent. The population size at which the independent-site limit is reached increases exponentially with the total site number.
Recombination has been broadly discussed as a mechanism that evolved to compensate for the adverse effects of linkage (Barton, 1995; Barton and Charlesworth, 1998; Charlesworth, 1990; Fisher, 1930; Kondrashov, 1993; Maynard Smith, 1971; Muller, 1932; Otto and Barton, 1997; Pamilo et al., 1987). Recombination of two genomes generates progeny with fitness, which varies below and above the average fitness of parents. The better-fit progeny is amplified by selection, the less-fit progeny is selected against. Thus, recombination can collect beneficial alleles from different genomes within the same genome, counteracting the Fisher-Muller effect (Felsenstein, 1974; Fisher, 1930; Hey, 1998; Hill and Robertson, 1966; Muller, 1932; Otto and Barton, 1997) and restoring highly-fit genomes lost due to Muller's ratchet. When recombination is sufficiently frequent, or population size is very large, linkage is no longer important, and the single-site model is expected to apply. In keeping with the cited findings for asexual populations, recent simulations confirm that the advantage of recombination and sex to evolution, as well as the maximum population size at which recombination confers advantage, increase with the total number of sites (Iles et al., 2003; Keightley and Otto, 2006).
It is especially instructive to consider the role of recombination in the evolution of organisms that have both asexual and sexual modes of reproduction. Examples of organisms with occasional recombination between some pairs of genomes include yeast, corals, and some viruses, including HIV. (Cohen et al., 2005) applied the solitary wave approach to bacteria which, instead of recombination, exchange small genomic segments. Previously, we considered a multi-site model applicable to HIV populations, in the simple approximation that beneficial alleles are distributed randomly within a genome of given fitness (Rouzine and Coffin, 2005). Incomplete compensation of linkage effects by recombination was shown to cause shrinking of fitness distribution and decrease of the substitution rate below the single-site model prediction at small population sizes N or small recombination rates, r. The single-site limit was demonstrated to occur at large N or r; unless r is extremely small, the corresponding value of N is much smaller than in the case of asexual model.
A recent Monte-Carlo study (Gheorghiu-Svirschevski et al., 2007) demonstrated that site-site correlations between genomes neglected in the previous approach (Rouzine and Coffin, 2005) decrease the effect of recombination and impede the adaptation process significantly. The aim of the present work is to explain these results and to show that identity by descent is the likely reason for these correlations. When mutation events are rare, homologous sites in parental genomes that have common ancestors usually carry identical alleles and do not contribute to the diversifying effect of recombination. Correlations, which gradually accumulate in time, are especially strong at small recombination rates, when fitness classes comprise a small number of large clones, so that the probability for two ancestor genomes to fall within same clone is relatively high.
Our findings confirm the evolutionary advantage of recombination in finite haploid populations in the absence of epistasis demonstrated previously for models restricted to a small number of sites [(Barton and Charlesworth, 1998) and references therein]. In contrast to the predictions of few-site models, the adaptation time and the effective population size depend on the recombination probability per individual but not on the average crossover number or on the distance between adjacent variable sites. The transition of the adaptation rate from the asexual regime to the limit of “infinitely frequent” recombination may occur at very small recombination rates.
2. Methods
2.1. Model
We consider a haploid population of N genomes with a large number of linked sites L. Each site can carry either a better-fit (beneficial) allele or a less-fit (deleterious) allele. The dominant mode of reproduction is asexual: After each discrete generation, most genomes are replaced with their copies. The progeny number for a genome obeys Poisson distribution, subject to the restriction that the total population size N is constant (multinomial distribution, broken stick). The average progeny number relative to that of the best-fit sequence that could possible evolve, is given by e-sk, where k is the number of deleterious alleles, and s is the selection coefficient, s ≪ 1. The best-fit genome that could possible evolve has k = 0 and fitness 1. Thus, we assume that all the sites have identical multiplicative effect on genome fitness, and epistasis is absent.
A small fraction of the genomes, r, are not copied directly to progeny but undergo recombination with another randomly sampled genome. The two recombinants replace their parents in a population. The number of crossovers per genome M is assumed to be large, so that a new genome is composed of random half-and-half mixture of parental sequences. (Surprisingly, M is not a parameter of theory. The standard recombination rate between adjacent sites, r2site, is related to our recombination parameter r, as r2site = rM/L. The results of our multi-site theory, however, depend only on r.)
At the initial moment t = 0, beneficial alleles exist at all sites at low frequency and are distributed randomly among sites and genomes. The number of allele copies per site is sufficiently large, so that the loss of alleles in the beginning of evolution due to random drift can be neglected. Mutation is absent.
2.2. HIV populations
The choice of a model (above) and the range of parameter values (below) are dictated by a particular biological system under consideration. The present work is primarily motivated by evolution of HIV populations within infected individuals. In the case of HIV, an individual genome is represented by a proviral DNA sequence integrated into a cellular chromosome. Each infected cell produces virus particles that carry pairs of RNA copies of the genome and can infect new cells. During persistent infection, on the average, one new cell is infected for each infected cell in the previous generation. If an infected cell is co-infected with another virus particle, the probability of which event we denote 2r, a half of particles budding from the cell will carry heterologous pairs of genomic RNA. Upon entry into a cell, the two RNAs are reverse-transcribed to a new DNA provirus. Only one RNA template is copied at a time. Recombination between the two genomes occurs due to 10-20 switches of reverse transcriptase between the two RNA templates (Levy et al., 2004).
L sites considered in the model are the sites that are less-fit at the beginning of evolution due to random transmission of virus from a previous individual (Rouzine and Coffin, 1999). Beneficial alleles pre-exist in small quantities at these sites in the beginning of long-term evolution, because they are generated by frequent mutation events during the virus peak in acute infection. Although new beneficial mutations are expected to emerge frequently during persistent infection as well, we neglect this effect, because, for high adaptation rates studied in this work, recombination is much more efficient for forming new highly fit recombinants than mutation. (Our preliminary estimates based on results of the present work and measurements of inter-sequence correlations for a group of untreated patients show that a typical patient has an average adaptation rate only several-fold smaller than the maximum rate predicted for infinite recombination; results not shown). Asexual adaptation due to addition of new beneficial alleles to the existing clones by mutation is much slower [see estimates in (Rouzine and Coffin, 2005)].
2.3. Parameter range
In the case of HIV, the population size N entering the model as an input parameter is the total number of proviruses that produce infectious virus particles able to reach new cells. The model itself is based on the panmixia assumption and, in general, does not apply to non-panmictic populations (e.g., to metapopulations consisting of many weakly connected demes). In some simple cases of a non-panmictic population, the model can still apply. For example, if a significant fraction of infected cells is located in tissue regions where new virions have poor access to fresh susceptible cells, we still can use the model by including in population size N only proviruses infecting cells at more favorable locations. In this case, parameter N can be smaller than the census provirus number. (Note that our definition of N differs from definitions of the “effective” population size based on various observables predicted by simple models, such as measures of random drift, diversity, or genealogy, and applied to more complex situations than these models are designed to describe. The effective population size based on these definitions and estimated from data depends on an observable and a model used.)
The estimate of N in an average untreated patient is still a subject of debates among HIV researchers. The maximum estimate is given by the census number of virus-producing cells, 107 - 108 (Haase, 1999). The multi-site theory presented in this work is not convenient for estimating N, because all its results change with N very slowly (logarithmically). On the bright side, the same fact implies that obtaining an accurate estimate of N is not critically important for overall properties of a multi-site population. The estimate of N is important and can be obtained from evolution of rare single sites with unusually large s, such as the primary drug-resistant mutations. In the framework of a single-site model, the extrapolated variation in the frequency of drug-resistant alleles between patients under monodrug therapy is consistent with N roughly on the order of 106 (Frost et al., 2000). For the purpose of our work, it is sufficient to restrict N to the realistic range 104-108.
The selection coefficient varies broadly among bases. In our simplified model, this variation is neglected, and all sites are assigned the same characteristic value s. The relevant range of s can be anticipated from the time scale of a particular experiment based on a single-site model (Rouzine and Coffin, 1999). For sites with s ∼ 10-3 or smaller, adaptation would take more than 104 virus generations and exceed duration of an average HIV infection (2 to 12 years, one generation per day). Such loci can be safely considered as neutral. Larger values, s > 0.1, are expected to be relevant for evolution early in infection (first weeks or months) or for evolution of drug-resistance. In the present work, we focus on the long-term adaptation in untreated patients, which implies an intermediate range of the selection coefficient, s = 0.1 to 0.01.
The characteristic number of sites, L, also depends on the particular experiment. In accumulation of beneficial alleles in untreated patients, the number of strongly polymorphic (allele frequency between 5% and 95%) sites per genome is estimated as L ∼ 200 (Rouzine and Coffin, 1999). In experiments on fixation of drug-resistant mutants under multiple drugs, L is much smaller and on the order of the number of drug-binding sites. In current drug regiments, L = 2 to 3, which is outside of the range of the present theory.
The effective frequency of cell co-infection, 2r, is difficult to measure directly. While an estimate r ∼ 1 has been obtained in some untreated patients based on the sampling of double HIV DNA positive cells (Jung et al., 2002), conclusive experimental measurements of the rate r in productively infected (RNA positive) cells for given N have yet to be performed. The above estimate of r may be too high if most coinfecting virions originate in neighboring cells and therefore are genetically uniform. If a population of infected cells is very dilute in the tissue, and effective recombination occurs between genomes coming from distant infected cells, the frequency of co-infection r is not an independent parameter of the model, but is itself proportional to the infected cell number N, as given by r(N) = N/N0, where new independent parameter N0 depends on the tissue properties. However, below we treat N and r as independent parameters.
In the present work that aims at investigating the effect of virus depletion on the evolution rate, we consider the region of one order of magnitude in r centered at r ∼ s[L/ln(Nr)]1/2 ≪ 1, where the adaptation rate is in the middle between the maximum value predicted for infinite recombination and zero (see Results and Derivation). Our preliminary estimates obtained from sequence data for untreated patients imply that most patients are in this parameter region (not shown).
2.4. Fitness of a recombinant and inter-sequence correlation
We need to specify the effect of recombination on fitness. We consider two parental genomes with mutation loads k1 and k2, where k1 and k2 ≫ 1. Mutation load k of a specific progeny genome cannot be expressed in terms of k1 and k2 alone, because it depends on location of specific alleles in each parental genome and on location of crossovers points. However, if k1 and k2 are large, and we have some additional information about the distribution of alleles within and between genomes, we can predict distribution of k in the statistical sense, which is sufficient to describe the average adaptation rate.
In the simplest approximation, when alleles are distributed completely randomly given their mutation loads k1 and k2, the distribution of recombinant progeny over k is a Gaussian with the maximum at k = k̄ ≡ (k1 + k2)/2 and the variance , where
| (1) |
is a half of the pairwise genetic distance (number of differences) between the parental genomes. Eq. (1) can be derived either from the general hypergeometric distribution (Barton and Shpak, 2000; Shpak and Kondrashov, 1999), or assuming k ≫ 1 and noting that the contributions to k from the two parents are statistically independent and obey Gaussian distribution [for the case 1 ≪ k ≪ L, see (Rouzine and Coffin, 2005)].
We can generalize Eq. (1) to account for inter-genome correlations. We define C as the average fraction of homologous sites per pair of genomes that descend from the same ancestor which existed after the onset of evolution, t > 0. Based on this definition, correlations are absent in the beginning of adaptation, C = 0 at t = 0, and increase gradually as more pairs of homologous sites have a common ancestor. Because we neglect new mutations in our model, homologous sites identical by descent must carry alleles of the same type. Therefore, pairs of sites with common ancestors are excluded from the genetic distance and, hence, from the fitness variation of recombinants, as given by
| (2) |
When C approaches 1, which, as we show below, happens at small recombination rates in the end of adaptation, a significant proportion of sites have common ancestors not only for samples of two, but also for larger samples and, eventually, across the entire population. We denote the frequency of these completely correlated sites Closs. These sites are monomorphic in either the beneficial allele (lose all deleterious alleles) or the deleterious allele (lose all beneficial alleles). According to Monte-Carlo simulation results (Gheorghiu-Svirschevski et al, 2007), in the relevant parameter range, it is the second type of sites that are important in the traveling wave regime. The loss of deleterious alleles occurs when the traveling wave has already arrived at its final destination and is rapidly collapsing to a clone (Appendix E).
We exclude the sites that lost beneficial alleles from consideration, as given by replacements L → L – LCloss, k̄ → k̄ – LCloss. Then, the genetic half-distance in Eq. (2) takes a more general form
| (3) |
| (4) |
where f1=k̄ / L is the average frequency of less-fit alleles. As one check, q is always smaller than f1(1-f1). The genetic half-distance is thus decreased by a factor of 1-C due to pairwise correlations and, in addition, by a factor of q/[f1(1-f1)] due to full-population correlations. Inter-genome correlations enter the derivation below only through the genetic distance w2. In particular, correlations for samples of size larger than 2 but less than N are irrelevant.
2.5. Dynamics of inter-genome correlations
Correlation parameter C depends on time. As it follows from its definition, C(t) is the probability of having the time to the most recent common ancestor for two homologous sites TMRCA smaller than current time t. Therefore, C(t) monotonously increases in time as more pairs of sites acquire common ancestors. The initial sequences are not correlated, as given by C(0) = 0. To describe dynamics of C(t), we introduce “effective population size for genealogy” Nanc(t), where 1/Nanc(t) is defined as the probability that two homologous sites in two randomly sampled sequences have a common ancestor in the previous generation (i.e., the average density of coalescent events in time for genealogy). In the simplest selectively neutral model, we would have Nanc(t) = N (Kingman, 1982a; Kingman, 1982b). In the case with directional selection, based on few-site models, Nanc(t) is expected to be smaller than N. Dynamics of correlations is then described by
| (5) |
In general, Nanc(t) does not have to depend only on the current state of a population at time t, but can also depend on population history. Below we show that, in the regime of stationary traveling wave, Nanc(t) is, in a good approximation, a function of the current state of population only (Appendix E). Specifically, Nanc(t) is expressed in terms of the current genetic distance, 2w2(t), and the four constant model parameters, N, s, r, and L. The substitution rate V=−dk̄ / dt is shown below to be approximately equal to sw2. Therefore, Eq. (5) can be written as
| (6) |
Because Nanc depends on a single time-dependent variable w2, and w2 is expressed in terms of C, Closs, and f1, as given by Eqs. (3) and (4), the right-hand side of Eq. (6) also depends only on C, Closs, f1, and the model parameters.
We still need to describe evolution of Closs in time. The proper treatment is difficult, because it would be based on an infinite system of coupled differential equations written for the distribution functions of time intervals between adjacent coalescent events, with Nanc(t) as a time-dependent parameter. Hence, we take a shortcut. We will assume that Closs can be expressed in terms of C using a relation following from a stationary neutral model. This approximation, valid in a broad parameter range, is explained in Appendix E. The dependence of Closs on C can be conveniently represented by an interpolation formula (Fig. 1)
Fig. 1.
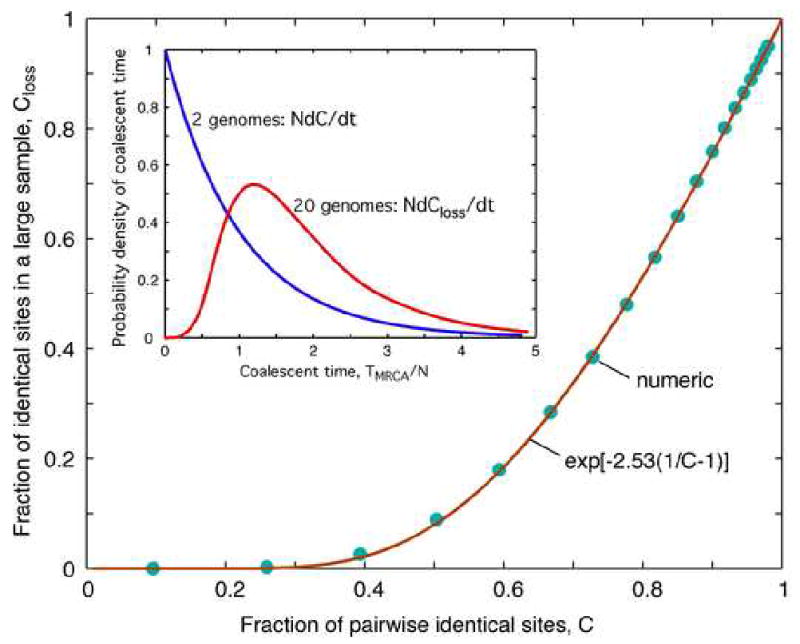
Relation between the fractions of homologous sites identical by descent for a sample of two individuals and a large sample, C and Closs, based on a selectively neutral model.
Dots: Relation between the cumulative probability distribution of the coalescent time for samples of 2 and 20 individuals, C and Closs, calculated numerically for the neutral model from the inset. Smooth line: Interpolation formula, Eq. (7). Inset: Rescaled probability density of the coalescent time for samples of 2 and 20 sites, dC/dt and dCloss/dt for the neutral model.
| (7) |
2.6. Traveling wave with a stochastic edge
Developing a full description of a population as a collection of 2L-1 possible sequences is hopeless. On the bright side, we do not need evolution of all haplotypes. Our aim is only to predict average characteristics, such as the average adaptation rate and the correlation parameter. Following the recently developed approach (Barton and Shpak, 2000; Rouzine et al, 2003; Rouzine and Coffin, 2005; Shpak and Kondrashov, 1999; Tsimring et al., 1996), we group genomes according to their fitness or, for a model with constant selection coefficient, considered here, according to their mutation load k. We introduce the fitness distribution function f(k,t), defined as the probability that a randomly sampled genome has mutation load k. All fitness classes are treated deterministically, with the exception of the smallest, best-fit class at the edge, which requires stochastic treatment. The justification of the semi-deterministic approximation, tested carefully for the asexual model, is that the fitness distribution decays rapidly towards its high-fitness edge, so that the next-to-best-fit class is already large enough to be roughly considered as deterministic. In the asexual model, the best-fit class and the next-best class are directly adjacent in k; in the present model, they are separated by a random gap of empty classes (Appendix A).
Shortly after evolution starts, fitness distribution f(k,t) assumes a form of a traveling wave with a slowly changing profile (Fig. 2). The wave speed (the average substitution rate) is also changing slowly. The overall shift of the wave to higher fitness values occurs due to selection of better-fit genomes which are produced by recombination. The speed cannot be found from purely deterministic consideration: It is determined by stochastic generation of new best-fit recombinants. As a result, the adaptation rate depends on the population size and the recombination rate. Monte-Carlo simulation (Gheorghiu-Svirschevski et al., 2007) shows the existence of three time intervals: (i) a relatively short transitional period when a distribution over k is formed, (ii) a long traveling wave interval, and (iii) rapid collapse of the wave into uniform population, at which point evolution stops. In the present work, we consider only the traveling wave interval (ii), because it is limiting for the overall speed of adaptation.
Fig. 2.
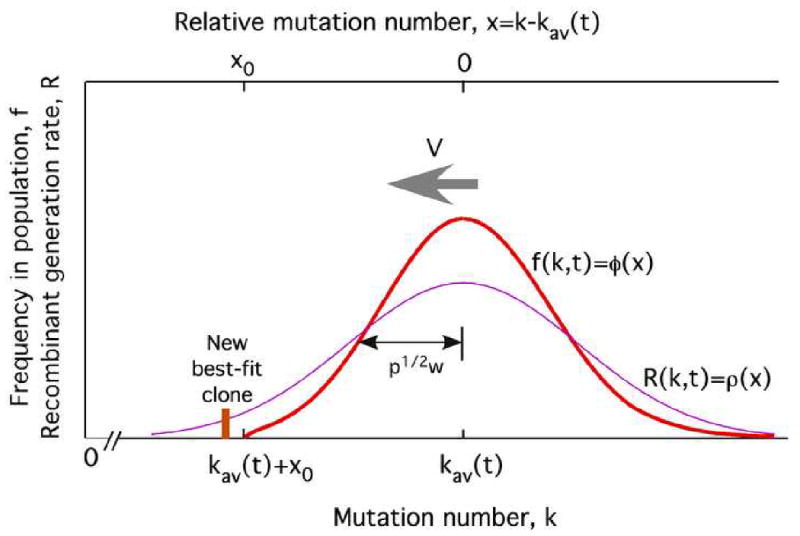
Fitness distribution (“solitary wave”) and the recombinant generation profile.
Thick red line: Average frequency of genomes with k less-fit alleles. Thin magenta line: Normalized generation rate of recombinants. Parameters V, |x0|, and wp1/2: Substitution rate, the high-fitness tail length, and the standard deviation of k, respectively.
The deterministic part of fitness distribution, f(k,t), is described by the balance equation
| (8) |
| (9) |
where kav≡ ∫ dk kf(k,t) is the mutation load averaged over a population. The first term on the right-hand side of Eq. 8 describes the asexual reproduction and the death. The terms rR(k,t) and −rf(k,t) describe, respectively, the generation and the loss of genomes with k alleles due to recombination. The form of function R(k,t) is based on the discussion above. Functions f and R are normalized, as given by ∫ dk f(k,t) = ∫ dk R(k,t) = 1.
The half-distance w2 in the integrand in Eq. (9) is expressed in terms of C, Closs, and the average mutation load of two parental genomes of a recombinant, k̄ = (k1 + k2)/2, as given by Eqs. (3) and (4). In the stationary traveling wave regime we study in the present work, fitness distribution f(k, t) is relatively narrow, i.e., located far from the best-fit possible sequence, k = 0. Therefore, for any relevant parent loads k1 and k2, their average can be approximated with the population average of the mutation load, as given by k̄ ≈ kav. Below, we use Eqs. (3) and (4) in this approximation.
The effects of selection and recombination are described in Eq. (8) by additive terms; effects of genome fitness on its chance to recombine are neglected. This approximation is valid, if both the recombination rate and the selection coefficient are sufficiently small, as given by r ≪ 1 and s|k - kav| ≪ 1 for all relevant k. The condition on r implies that most genomes reproduce asexually. The condition on s implies that the best-fit genome has a small selective advantage as compared to the average genome. Eqs. (8) and (9) can also be used to calculate the clone structure of a population (Appendix C).
Eqs. 8 and 9 have a solution in the form of a localized traveling wave, as given by f(k, t) = φ[k − kav(t)], R(k,t) = ρ[k − kav(t)]. In this case, Eqs. (8) and (9) are reduced to a simpler form with the relative mutation load x = k-kav(t) as the only independent variable (Rouzine and Coffin, 2005)
| (10) |
| (11) |
Although the wave profile φ(x) is not quite constant due to the time dependence of genetic half-distance w2, Eq. (3), the partial time derivative of φ can be neglected if the wave is far from the boundaries, i.e., |k-kav| ≪ kav for all relevant k.
As we already mentioned, the substitution rate V and the width of the fitness distribution cannot be found from purely deterministic consideration, because it is controlled by stochastic processes at the high-fitness edge of fitness distribution. The treatment of the stochastic edge is explained in Appendix A.
2.7. Procedure outline
To summarize our method, we will incorporate inter-genome correlations into the solitary wave approach using a self-consistent procedure, as follows:
The variance of fitness of recombinant offspring is calculated, assuming that parental fitnesses and intersequence correlations (C and Closs) are known (Eqs. 3 and 4).
The effective population size for genealogy, Nanc(t), which determines the average density of coalescent events in time, is introduced to describe how C increases in time or with average allelic frequency (Eqs. 5 or 6). A numeric interpolation formula relating Closs to C is presented (Eq. 7).
The traveling wave equation in the presence of recombination (Eqs. 10 and 11 and Appendix A) is solved. The result is dependent on C and Closs through the genetic distance 2w2.
This solution is used to calculate Nanc(t), based on recent results on the clone composition of fitness classes and the ancestor fitness distribution (Rouzine and Coffin, 2007).
Now we have a self-consistent equation for dynamics of C and Closs and all other variables. We solve this equation and describe various ways to summarize the overall effect of recombination on the adaptation rate.
3. Derivation and results
3.1. Validity conditions
The following results obtained below for the traveling wave regime are valid in the parameter range, as follows. (i) Both the total number of sites L and the average mutation load kav should be much larger than ln(Nr). The condition ensures that the traveling regime exists, i.e., that the high-fitness edge is far from the best-fit genome that could evolve, k = 0. (ii) To ensure that the leading tail of the distribution is long, |x0| ≫ w, the population size should be large, as given by Ns ≫ 1 and Nr ≫ 1. The first inequality represents the classical limit of “strong selection” in few-site models. (iii) Both the recombination rate per genome and the selection coefficient should be sufficiently small, as given by r ≪ sL1/2 ≪ ln-1/2 (Nr). The first inequality ensures that, in the main region of interest r ∼ s[L/ln(Nr)]1/2, the total number of recombination events per population Nr is large. The right inequality implies that the fitness advantage of the best-fit individuals compared to an average individual is small. Then, in Eq. (8), we can expand fitness in mutation load k and approximate the difference f(k,t+1) - f(k,t) with the time derivative.
3.2. Distribution of genomes in fitness
Although Eqs. (10) and (11) are difficult to evaluate exactly, asymptotically accurate solutions for different parameter regions can be obtained. In the next two subsections, we review our previous results (Rouzine and Coffin, 2005; Rouzine and Coffin, 2007) for two important overlapping intervals of the recombination rate.
Small recombination rates
If r is much less than s[L/ln(Nr)]1/2, Eqs. (10) and (11) for centered fitness distribution φ(x) have a Gaussian solution with a cutoff (Rouzine and Coffin, 2005; Rouzine and Coffin, 2007)
| (12) |
| (13) |
where p is the normalized adaptation rate V. The negative cutoff point x0 < 0 is the high-fitness edge of the distribution, beyond which genomes are absent. We will refer to the distance between the edge and the center of the wave, |x0|, as the “lead” of distribution (Desai and Fisher, 2007). The fraction p and the lead determined from the stochastic edge consideration (Appendix A) are given by
| (14) |
| (15) |
Here we introduced notation we will use in the rest of our work
| (16) |
| (17) |
| (18) |
These results apply if the recombination rate is sufficiently small, r ≪ sw2/|x0|, which is equivalent to 1-p ≫ 1/Λ1 and β≪ 1, and ensures that the condition Λ2 ≫ 1 is met. The case of arbitrary β is considered below. Throughout this work, we also assume a large total number of recombination events per population per generation, Nr ≫1, which ensures Λ1 ≫ 1. Note that Eqs. (16) and (17) define Λ1 and Λ2 recursively. Because the dependencies of the right-hand sides on Λ1 and Λ2 are slow (logarithmic), the two values can be calculated by consecutive iterations, with two iterations giving a fair accuracy even at moderately large Λ1 and Λ2. The recombinant generation profile ρ(x) introduced in Eq. (11) is also a Gaussian
| (19) |
Note that the profile is broader than the fitness distribution given by Eq. (12) due to p < 1 and does not have a cutoff at large negative x (Fig. 2).
Thus, the normalized adaptation rate p monotonously increases with the population size and the recombination rate combined together into parameter Λ1 ≈ ln(Nr), Eq. (14). As ln(Nr) becomes on the order of (sw/r)2 ∼ L(s/r)2, which value is large according to condition (iii) above, we have Λ2 ∼ 1 and p is close to 1, as given by 1-p ∼ 1/ln(Nr). Then, if intersequence correlations were absent, C = Closs= 0, the substitution rate V would be
| (20) |
where V1site is a well-known deterministic result of the single-site model. At smaller ln(Nr), we have p < 1 and V < V1site. Thus, factor p reflects the adverse effect of co-inheritance linkage on adaptation, partly compensated by recombination, when correlations between sequences are neglected. Adaptation is impeded due to a synergetic effect of finite population size and finite recombination rate, as follows. (i) Finite population size causes the fitness distribution to have a high-fitness cutoff. Note that the lead |x0| diverges with ln(Nr), Eq. (15). (ii) Finite generation rate of new recombinants at the edge limits the wave speed.
The relative roles of parameter p and inter-sequence correlations are easy to understand in terms of Fisher's Theorem, V = sVar[k], where Var[k] is the variance of the mutation load among sequences. Our results are consistent with that theorem: From Eqs. (12) and (13), we have Var[k] = pw2 and V = spw2, respectively. Neglecting, for a second, the loss of alleles, Closs = 0, we can write
| (21) |
Factor kav(1−kav/L) in Eq. (21) is the variance in the case of the binomial distribution, which takes place in the single-site limit (very large recombination rate or population size, when sites evolve independently). Factors p and 1-C describe shrinking of fitness distribution caused by two different types of correlation between genomes, both existing due to the combined effect of co-inheritance linkage, selection, and finite population size, but acting in a different way. Factor p describes correlation in the total mutation load k existing due to the fact that genomes compete with each other (selection) as whole sequences (linkage) and the high-fitness cutoff (finite N). Because the fitness distribution has an edge with limited extension speed, selection squeezes the distribution of k against the edge. As a result, Var[k] is decreased without changing the genetic half-distance w2. In contrast, correlations on the level of individual sites, represented by factor 1-C, decrease Var[k] by decreasing the genetic half-distance w2. The loss of variable sites, Closs > 0, further decreases w2. As we show in the end of this section, the effect of sequence correlations is stronger than the effect of correlations in k.
Intermediate recombination rates
As we show in the following subsections, the most significant changes in the correlation factor C and the substitution rate V occur at the border of the interval of r considered in the previous subsection, r ∼ sw2/|x0|, when β ∼ 1 and parameter p is still close to 1. In this region, the fitness distribution deviates from the Gaussian form, Eq. (12). We developed another approach, which does not rely on strong inequality r ≪ sw2/∣x0, but instead assumes 1-p to be much less than 1 and treats it as a small parameter. In this approximation, the fitness distribution φ(x) has a form (Rouzine and Coffin, 2007)
| (22) |
| (23) |
In the exponential in Eq. (22), the term x2/2w2 corresponds to the single-site limit, p = 1. The term εβhβ(u) ∼ 1 is an important non-Gaussian correction for finite r and N. The values of εβ and hβ(u) are determined by parameter β defined in Eq. (18), as discussed in Appendix B. The lead of the distribution |x0| is given by
| (24) |
The adaptation rate is given by V = sw2[1−(w2/x02) εβ], where the second term is a small negative correction, 1-p. The decrease of adaptation rate V below the single-site model value, Eq. (20), is mostly due to the effect of correlations on w2 (see below).
In the limit of small recombination rates, r ≪ s|x0|/w2, which corresponds to β ≪ 1, we have
| (25) |
so that φ(x) matches Eq. (12), as it should. In the opposite limit β ≫ 1, εβ is exponentially small.
In the same work (Rouzine and Coffin, 2007), we studied the fitness distribution of a remote ancestor of a site, φ(x). Because that distribution is conditioned on leaving progeny in the far future, it differs strongly from the unconditional fitness distribution φ(x). It can be rescaled as φ(x) ≡ (1/|x0|)yβ(x/|x0|), where function yβ(u) depends on single external parameter β (Appendix B and Fig. 8).
Fig. 8.
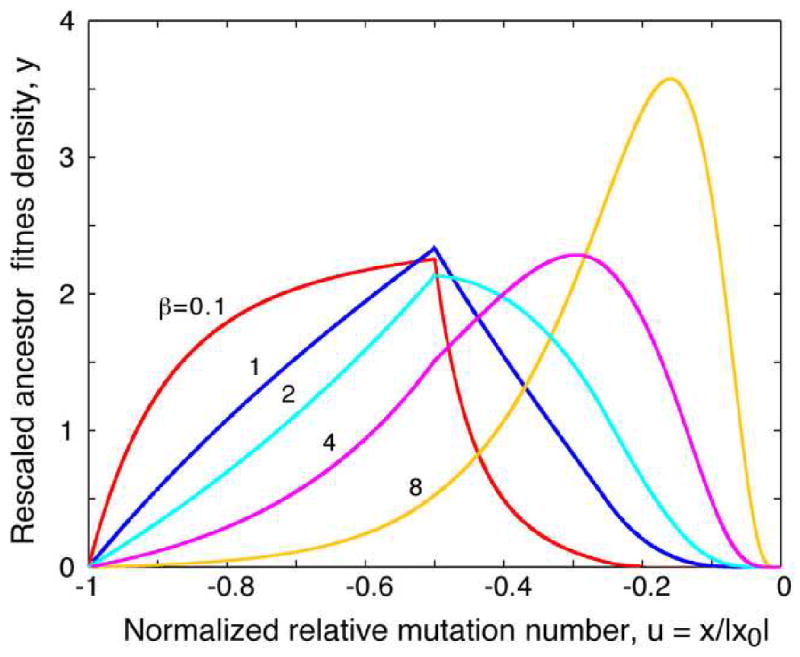
Fitness distribution of remote ancestors (Rouzine and Coffin, 2007).
Solid lines: Rescaled probability density of the centered mutation load of a remote ancestor, yβ(u) (values of β on the curves). Results are obtained numerically from Eqs. (B4) and (B2).
3.3. Genealogy and the effective population size
Now we derive an expression for the effective population size Nanc, which determines the density of coalescent events in time, Eq. (6). Consider two homologous sites in two randomly sampled genomes in current generation t. By definition, 1/Nanc is the probability of having these two sites descend from a common ancestor site in a genome in an earlier generation, which can be written as
| (26) |
The term φ2(x) is the probability that the two ancestors of two sampled sites belong to the same fitness class x. The term Pcl(x) is defined as the probability that two genomes in fitness class x also belong to the same clone of identical sequences. The accuracy of Eq. (26), which implies that 1/Nanc depends locally on time through genetic half-distance w2(t) and is a function of the current state of population, is discussed in Appendix E.
Derivation of Pcl(x) based on calculation of the clone structure of a population (Rouzine and Coffin, 2007) is given in Appendix C. The final result has a form
| (27) |
Substituting Pcl(x) from Eq. (27) into Eq. (26) and using the rescaled form for the ancestor fitness distribution, φ(x) = (1/|x0|)yβ(x/|x0|), we get
| (28) |
Eq. (28) represents the central result of the present work: It shows that the effective population size of genealogy is a product of wΛ′13/2 and a universal function of parameter β. At very small or very large β, asymptotic expressions for the integral in Eq. (28) can be derived analytically (Appendix D). At β ∼ 1, we calculated the integral in Eq. (28) numerically based on Eq. (27) for Fβ(u) and results for εβ, hβ(u), and yβ(u) given in Appendix C. The final result can be represented either graphically (Fig. 3) or by an interpolation formula
Fig. 3.
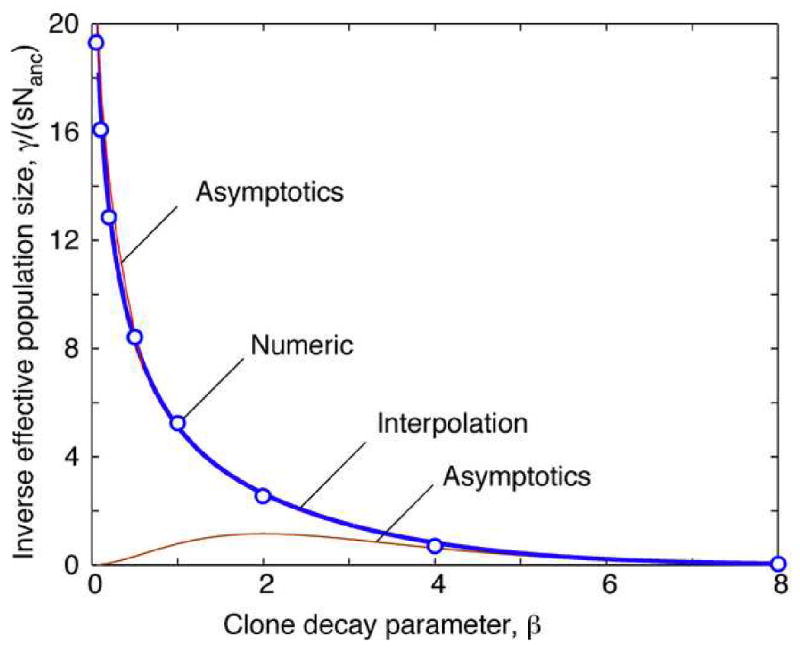
Dependence of the effective population size on the clone decay parameter β.
Open circles: Numeric results for from Eqs. (28), (27), (B2), and (B4). Red and brown thin lines: Asymptotics at small and large β, Eq. (D3). Thick blue line: Interpolation formula, Eq. (29).
| (29) |
where 15.0 is the value of the (only) fitting parameter used for interpolation. The interpolation formula has correct asymptotics at small β and large β and has the accuracy of 1% in the entire interval of β, as compared to the numeric result based on Eq. (28).
We observe that the value of the effective population size depends monotonously on the current value of parameter β (Fig. 3), which represents the degree of clone decay affecting the clonal structure of a population. At small β, a typical fitness class comprises a few large clones born at the high-fitness edge of a population, so that the time to common ancestor is short, i.e., Nanc is small. At large β, a fitness class is broken into many small clones, and the time to common ancestor is exponentially large.
3.3. Dynamics of inter-genome correlations
Now, we are ready to calculate the dynamics of the correlation parameter C from Eqs. (6) and (29). Quantities w2, β, and Nanc defined in Eqs. (3), (18) and (29) can be expressed in terms of variables C, Closs, and f1 = kav/L as
| (30) |
| (31) |
where Closs is related to C by Eq. (7), q is given by Eq. (4), and we introduced two new constants
| (32) |
| (33) |
The intuitive meaning of the time-dependent parameter β as the degree of clone decay has already been explained. Eq. (30) shows that β is a product of a single composite model parameter β′ and a parameterless function of the current level of correlations and allelic frequency. At the intermediate or small level of correlations and in the middle of adaptation, as given by C ∼ f1 ∼ 0.5, we have q ∼ 1, and parameters β and β′ are of the same order of magnitude. The condition β′ ∼ 1 determines the characteristic value of recombination rate at which Hill-Robertson interference becomes important (for γ ∼ 1), r ∼ s(L/Λ1)1/2. The composite parameter γ defined in Eq. (33) characterizes the relative strength of selection, given the number of sites and the population size, analogous to product Ns in few-site models.
Substituting Eq. (31) into Eq. (6), we arrive at the desired self-consistent equation for C
| (34) |
The right-hand side of Eq. (34) depends on variables C and f1 and two constant external parameters, β′ and γ. The initial condition is C(f0) = 0, where f0, such that 1-f0 ≪ 1, is the starting frequency of less-fit alleles. Specific choice of a small value of 1-f0 has minor effect on the results.
We solved Eq. (34) for C(f1) at different β′ and γ= 10 numerically (Fig. 4a). At large β′, the magnitude of inter-genome correlations is modest, and the loss of alleles is very small. At small β′, correlations accumulate to high levels, and adaptation fails at a significant fraction of sites fend given by
Fig. 4.
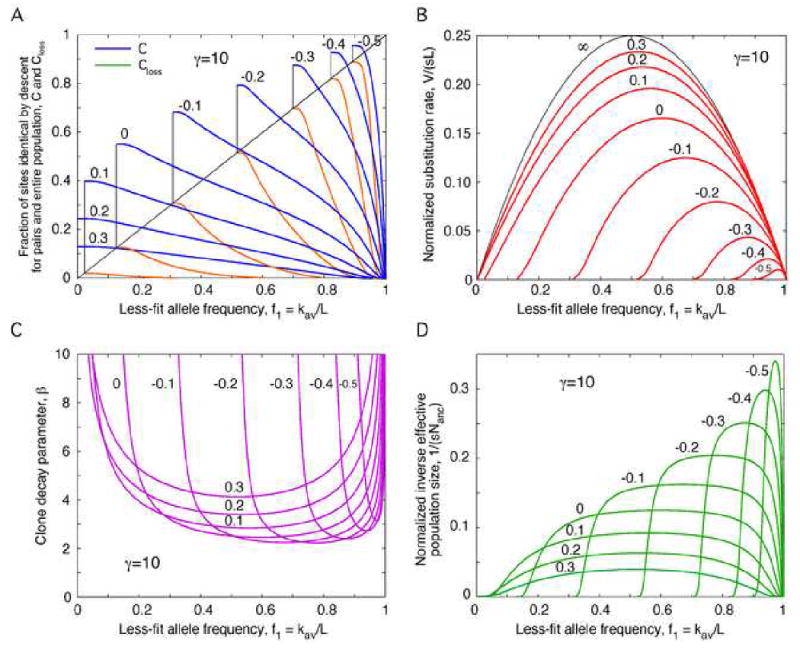
Evolution of inter-genome correlations, the substitution rate, parameter β, and the effective population size with the current frequency of less-fit alleles.
(a) Blue: Fraction of homologous sites identical by descent for a genome pair, C, at different values of parameter β′ defined in Eq. (32). Brown: Fraction of sites that have lost beneficial alleles, Closs. Vertical black lines: End point of evolution. (b) Red: Normalized substitution rate V/(sL) as a function of f1. Black: Same in the limit of infinite N or r. (c) Clone decay parameter β defined in Eq. (18). (d) Normalized inverse effective population size 1/(sNanc). (a-d) Parameters: ; values of log10 β′ are on the curves. Numeric results are obtained by solving Eq. (34) with the use of Eqs. (4), (7), (30), and (31).
| (35) |
The value of fend represents the final, minimum frequency of less-fit alleles. As β′ decreases, the normalized substitution rate
| (36) |
decreases in magnitude and vanishes at finite f1 = fend. In addition, the dependence of the substitution rate on f1 deviates from the elliptical shape predicted by the single-site model (Fig. 4B).
The current value of the clone decay parameter β given by Eq. (30) has a broad minimum in f1 (and in β′) and diverges in the beginning and end of adaptation, f1 = 1 and f1 = fend (Fig. 4c). The divergence of β is caused by slow speed of the wave (formally, small q), which gives more time to clones to recombine with other clones and decay. As a result of this behavior of β, the density of coalescent events 1/Nanc has a flat maximum at intermediate f1 and sharply declines towards the beginning and the end of adaptation [Eq. (31) and Fig. 4D]. These results are valid only at those values of f1 where 1/Nanc ≫ 1/N. The opposite inequality would imply that an ancestral clone consist of less than one individual. (Practically, for correct evaluation of dynamics of C, the average of 1/Nanc over time has to be much larger than 1/N.)
After the wave stops at f1 = fend, it rapidly collapses to a uniform population, and the value of C rapidly increases to 1. The value of Closs does not change. The collapse, evident in simulation, is beyond the scope of our theory.
3.4. Averaging over time
The adaptation rate V and the effective population size Nanc depend on the average frequency of less-fit alleles (Fig. 4), which itself depends on time, df1/dt = - V/L. To show the overall effect of linkage and inter-genome correlations on the adaptation rate, we need an intuitively clear method to average it over the adaptation process. Below we use below three intuitively clear methods and show that they produce essentially the same result.
Method 1
The first method is based on the concept of effective selection coefficient seff (Gheorghiu-Svirschevski et al, 2007). We compare the predicted substitution rate, Eq. (36), to a crude approximation
| (37) |
where q is defined in Eq. (4) and seff < s is a constant. Eq. (37) has the form of the single-site model result, V1site = seffLf1(1-f1), but with a smaller selection coefficient and with exclusion of monomorphic sites by including Closs in Eq. (4). We will treat seff as a fitting parameter adjusted to ensure best fit, in the mean-square sense, of the actually predicted V(t) with Vcrude(t). As one can show, the best-fit value of seff is given by
| (38) |
Changing the integration variable in Eq. (38) from t to f1, as given by df1 = −(V/L)dt, and substituting V from Eq. (36), we obtain
| (39) |
Thus, seff/s represents the harmonic average of 1-C over the less-fit allele frequency. We calculated numerically seff/s and fend for different β′ and γ from Eq. (39) (Fig. 5a). The results shown in Fig. 5b agree with Monte-Carlo simulation from Ref (Gheorghiu-Svirschevski et al., 2007) much better than the results of the random-allele approximation (Rouzine and Coffin, 2005).
Fig. 5.
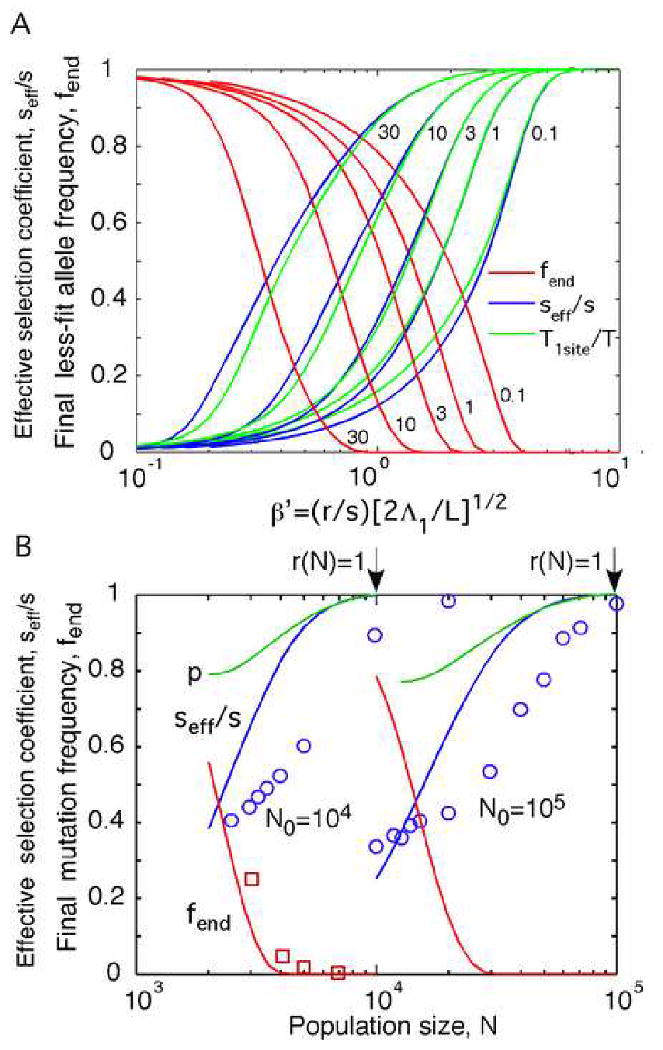
Total adaptation time T and the frequency of sites that fail adaptation fend.
(a) Blue: Normalized effective selection coefficient seff/s calculated from Eq. (38) as a function of normalized recombination rate β′. Green: Inverse normalized adaptation time T1site/T. Red: Final value of the less-fit allele frequency, fend. Values of γ are on the curves. (b) Quantities seff/s and fend as a function of the population size N for the dilute virus case, r = N/N0. Green curves: values of 〈p〉f1 calculated from Eqs. (47) and (B3), results for εβ (Fig. 7), and dynamics of β (Fig. 4). Open symbols: Monte-Carlo simulation results from (Gheorghiu-Svirschevski et al., 2007). Parameters L,s, and N0 are shown.
Method 2
Another convenient measure is the normalized total time of adaptation T/T1site, given by
| (40) |
where 1−f0 ≪ 1 is the initial frequency of beneficial alleles, and
| (41) |
is the value of T in the single-site model limit. For the sake of symmetry, we consider beneficial alleles fixed when their frequency averaged over the L(1−fend) sites that complete adaptation is equal to f0. We notice that the integral in Eq. (40) would diverge logarithmically on both limits if not for finite 1−f0. [The issue did not arise with the integrals in Eq. (39).] Using the fact that the integral in Eq. (40) is mostly contributed from the two divergence regions, we obtain an approximate expression
| (42) |
where C(fend) is the final value of C, and we assumed |ln(1−fend)| ≪|ln(1−f0)|, which condition is met when β′ is not too small. Interestingly, the two measures of the linkage effect, seff/s and T1site/T, although expressed differently in terms of C, are numerically similar in a broad range of β′ and γ (Fig. 5a).
Method 3
A measure convenient for direct comparison with the experimentally measured genetic distance (Eqs. 2 or 3) is the arithmetic average of 1-C over time
| (43) |
Approximating the integral in f1 in the same way as in Eq. (40), we obtain
| (44) |
Average effective population size
We also need to average the effective population size of genealogy, Nanc. Integrating Eq. (5), we can express correlation parameter at the end of adaptation, C(fend), in terms of the harmonic average in time, N̄anc, as given by
| (45) |
Eq. (45) has the formal appearance of the cumulative distribution of the coalescent time in a stationary process, with N̄anc replacing the average time to the most recent common ancestor, 〈TMRCA〉. In fact, we do not have a stationary process, and the average coalescent time is not defined, because a population does not exist at t < 0, and a fraction of site pairs do not have common ancestors at t > 0. We will use the harmonic average in time, N̄anc, as an average measure of Nanc and a substitute for 〈TMRCA〉.
Note that N̄anc depends on the initial condition 1−f0 and is proportional to (1/s)|ln(1−f0)|, because the time interval T over which 1/Nanc has been averaged is proportional to this factor [the second of Eqs. (45)]. To isolate this factor and show dependence of N̄anc on the recombination rate and the log population size (or on composite parameters β′ and γ), we normalize N̄anc to two different values: Either to T, which itself depends on β′ and γ, or to T1site. Using Eqs. (42) and (45), both ratios can be expressed in terms of final correlation parameter C(fend) alone, as given by
| (46) |
The ratio N̄anc/T decreases monotonously with the final level of correlations C(fend) and, therefore, increases monotonously with β′ and γ, Fig. 6a. At small recombination rates (small β′ or γ), correlations are strong, and N̄anc/T is small. At large recombination rates (large β′ or γ), correlations are weak, and N̄anc/T is large.
Fig. 6.
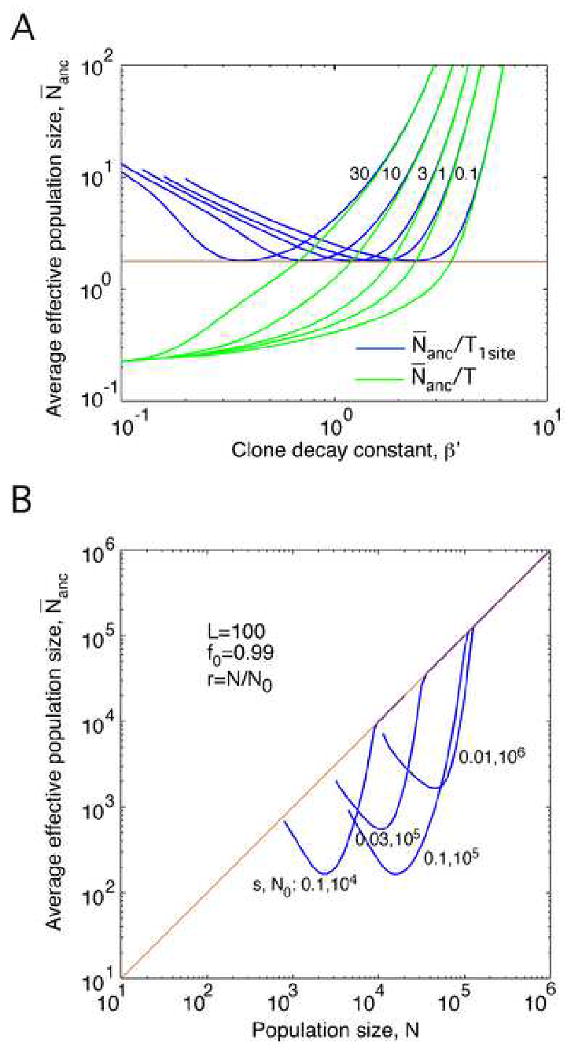
Average effective population size for genealogy.
(a) Blue: Harmonic average N̄anc normalized to the total adaptation time in the deterministic limit T1site as a function of β′ at different γ (on the curves). Green: N̄anc normalized to the total adaptation time T. Brown line: Minimum value of N̄anc/T1site. (b) N̄anc as a function of population size N in the dilute virus case, r = N/N0. Parameters are shown. (a, b) Results are obtained from Eqs. (46).
The ratio N̄anc/T1site (and, hence, the average effective population size itself), has a more complex dependence on C(fend): It diverges at the end of interval in C(fend) and has a minimum in the middle at C(fend) = 0.72. As a result, N̄anc has a minimum in either β′ or γ, where N̄anc/T1site =1.80 and T1site/T = 0.44 (Fig. 6a). The increase of the effective population size at small β′ is caused by the increasing loss of variable sites, Closs, which decreases the genetic distance (q ≪1) and hence increases the clone decay parameter β (cf. divergence of β in Fig. 4c).
We also calculated the raw value of N̄anc as a function of population size N for the dilute virus model, r = N/N0 and parameter values relevant for HIV populations (Fig. 6B). In a window of N values, N̄anc can be much less than the neutral model prediction, N̄anc = N, provided N0, s, or L is sufficiently large. At the minimum of N̄anc, the condition is N ≫ 1.8T1site, i.e., Ns ≫ 4 |ln(1-f0)|. (As we already pointed out, our derivation does not apply when it predicts N̄anc >N.)
We assumed everywhere that the fraction p = V/sw2 characterizing fitness correlations between whole sequences is approximately equal to 1, based on the small parameter 1/ln(Nr). To test this approximation for representative parameter values, we averaged p over the adaptation period with a weight function equal to the substitution rate V, which is equivalent to weightless averaging in f1, as given by
| (47) |
In the region shown in Fig. 6b, we found 1 − 〈p〉f1 < 0.2, so that the approximation is fair.
Summary of results
We showed that the dynamics of inter-sequence correlations, the total adaptation time T, and the harmonic average of the effective population size N̄anc normalized to T depend monotonously on two composite model parameters: Parameter β′ ≈ (r/s)[2ln(Nr)/L]1/2 characterizing the strength of recombination, and parameter γ ≈ s[L ln3(Ns)/2]1/2 characterizing the strength of selection. The two parameters replace the scaled parameters of a two-site model in the diffusion limit, Nr2site and Ns, respectively, where r2site is the recombination rate per pair of sites. At large β′ or γ, correlations are weak, and the adaptation time T saturates at its single-site model minimum, T1site. At small β′, correlations are strong, adaptation fails at many sites (due to reversion of the direction of evolution and eventual loss of beneficial alleles) and is slow for the successful sites. The transition between the two limits occurs within one order of magnitude in β′: The fraction of failed sites fend and the ratio T1site/T change from 0.9 to 0.1 and from 0.1 to 0.9, respectively, when β′ increases by less than 10-fold (Fig. 5a).
The rapid change in the outcome and rate of adaptation with r reflects rapid changes in the clone structure of a population affecting, in their turn, the effective population size N̄anc. At small β′, each fitness class represents a single clone born at the high-fitness edge of a population N̄anc ≪T. At large β′, many small clones form a fitness class, and N̄anc ≫T (Fig. 5a).
4. Discussion
We considered simultaneous fixation of preexisting beneficial alleles at a large number of sites, driven by the combined effect of selection and infrequent recombination. Our findings confirm the evolutionary advantage of recombination in finite haploid populations in the absence of epistasis demonstrated previously (Barton and Charlesworth, 1998; Iles et al., 2003; Keightley and Otto, 2006). In addition, we specified the incidence of recombination events required for recombination to have an essential effect on the speed of evolution.
We showed that the multi-site adaptation is impeded by inter-sequence correlations arising due to ascendance of some homologous sites from common ancestors existing after the onset of fixation. Using a recently developed method, the “traveling wave”, we determined the fitness distribution and the clone structure of fitness classes. From the clone structure and a previously derived distribution of fitness of ancestors, we calculated the effective population size Nanc, which determines the density of coalescent events per generation. Finally, we derived and solved numerically a self-consistent equation for the dynamics of inter-sequence correlations. Our results are summarized in Figs. 4 to 6.
One important result is that the transition to the case of “very frequent recombination” occurs at r ∼ s[L / ln(Nr)]1/2, which may correspond to rather modest recombination rates, provided s is small and L is not too large. For example, for N = 106, L = 100, s = 0.01, r=0.05, the adaptation time exceeds its single-site model limit by only 10% (γ ≈ 2, β′ ≈ 2.5, Fig. 5a). Thus, at only 5% of sexual reproduction, a population can adapt at 90% of the maximum rate. In view of this result, why fully sexual reproduction, on the grand evolutionary scale, is preferable to partly sexual reproduction remains an open question.
Our prediction that strong effects of co-inheritance linkage on the adaptation rate are not related to LD, but act through inter-sequence correlations, is another difference from predictions of the few-site models. Our previous simulation results (Gheorghiu-Svirschevski et al., 2007) show that, although separate site pairs have strong LD in the parameter region of interest (Fig. 6b), its sign is apparently random, and the average Lewontin's measure of LD is zero even for adjacent sites. One possible reason for zero LD is that association between favorable alleles may be randomly positive or negative, depending on whether alleles are on the same sequence (where they help each other to grow) or different sequences (where they interfere with each other grows). In our future work, we will try to derive LD analytically using the same method of clonal decomposition of fitness classes used in the present work to derive the level of inter-genome correlations.
Note that, although, in few-site models, Fisher-Muller-Hill-Robertson effect is tightly related to negative LD, there is no such requirement in the many-site limit. According to Fisher's Fundamental Theorem, the decrease in the adaptation rate due to co-inheritance linkage is proportional to the decrease in the variance of the mutation load (fitness) among sequences. As we discussed in Results, the decrease of variance is due to two independent mechanisms and represents a product of two factors, p and 1-C (pp. 18-19). The first mechanism is that selection in the presence of linkage an finite N trims fluctuations of the total number of favorable alleles between sequences below the value given by the binomial distribution (Rouzine and Coffin, 2005). The second mechanism is the decrease of the genetic distance due to site-site correlations, calculated in the present work. Neither mechanism implies non-zero LD. Indeed, the first mechanism requires only a slight adjustment of total k at various sequences, which does not put much restriction on sequences if k and L-k are large. The correlation factor C is calculated for a single site and averaged over sites. In contrast, LD is calculated for a pair of sites and averaged over pairs. One can have C > 0 and yet zero LD. In the case of a small number of sites and, hence, a few alleles per sequence, the two mechanisms are not mutually independent and may imply non-zero average LD. Thus, relation between negative LD and the Hill-Robertson effect is a specific feature of few-site models.
As for asexual population models in the multiple-mutation regime, all our results depend on population size N only logarithmically. The prediction is in contrast to the predictions of two-site models with recombination. Another difference is that results of two-site models depend on parameter Nr2site, where r2site = rM/L is the recombination rate per pair of adjacent sites, and M is the average number of crossover points per genome. In the many-site model, the value of M does not enter the problem, as only the average probability of recombination per genome, r, matters. It is quite possible that it is important for LD, which, as we stated, does not appear in our derivations.
At very small recombination rates, such that β′ is much less than 1, most sites revert the direction of evolution and lose beneficial alleles. To predict continuous adaptation of all sites, we would have to include in the model new beneficial mutations compensating for the loss of alleles. In this regime, both recombination and mutation are equally important. At even smaller recombination rates, recombination will no longer be important, and asexual evolution will set in.
We obtained a closed expression for the effective population size Nanc representing a local-in-time analogue of the average time to the most recent common ancestor, <TMRCA> [Eq. (30), Fig. 3]. The statistical treatment of <TMRCA> (the coalescent) (Kingman, 1982a; Kingman, 1982b) is one of the most powerful tools of neutral theory, whose generalization to the case with selection proved to be rather challenging. The papers addressing this issue used Monte-Carlo simulation, models with a single selected site, or assumed infinite population size. For example, the “background selection” approach (Charlesworth et al., 1993) developed for infinite steady-state populations under purifying selection, predicted reduction of the coalescent time by a factor equal to the frequency of genomes free of deleterious alleles. There has been some numeric effort on calculating the coalescent time for many-site models at finite N. (Krone and Neuhauser, 1997; Neuhauser and Krone, 1997) proposed an “ancestral selection graph”, from which the true coalescent tree had to be recovered numerically by going back and, then, forward in time. Because the size of the graph increases exponentially with Ns, these authors were able to study interval Ns < 2, observing a slight decrease in the coalescent time in the case of mutation-selection balance. (Williamson and Orive, 2002) applied direct Monte-Carlo simulation to extend this result, in the infinite-allele formulation with deleterious mutation, to large Ns. They predicted a maximum two-fold decrease of the coalescent time at s on the order of the mutation rate per sequence. The statistical shape of the phylogenetic tree changed very slightly. (Wilke et al., 2002), who simulated a more complex case of the random correlated fitness landscape, observed three different regimes for the phylogenetic tree depending on the mutation rate. Analytic work for a model with one selected site and two alleles was carried out by Hudson and Kaplan (Hudson and Kaplan, 1988; Kaplan et al, 1988) and Barton et al (Barton and Etheridge, 2004; Barton et al., 2004). The general approach was to combine a Markov jump process, including mutation between the two allelic classes and coalescent events within each class, with a backward diffusion equation. The focus of numeric calculations was on the stationary population in the case of balancing selection, such as acting on diploid organisms in the case of allelic over-dominance. These authors demonstrated a considerable increase in <TMRCA> at Ns ≫ 1 and Nμ ≪ 1, as compared to the neutral prediction <TMRCA> = N. The value of <TMRCA> within each allelic class is given by the class size instead of the total population size. The average over population <TMRCA> is much longer, on the order of 1/μ. At moderate Ns, the overall <TMRCA> returns back to the neutral result N due to genetic drift causing fluctuation of allelic class sizes. For mutation-selection balance under purfying selection, a mild decrease of <TMRCA> due to selection was predicted at Ns ≫ 1 and s ∼ μ, in agreement with previous simulation (Williamson and Orive, 2002). Using a numerical method based on the conditional ancestral selection graph, Wakeley (Wakeley, 2008) showed that this result is valid for random samples; for rare samples containing more than one deleterious allele, he found that the effect of selection on genealogy at Ns > 10 can be very strong.
The cited papers addressed an equilibrium population. Hermisson and Pennings (Hermisson and Pennings, 2005; Pennings and Hermisson, 2006a; Pennings and Hermisson, 2006b) considered (analytically and by simulation) a non-stationary process of adaptation of a two-allele site under changed environmental conditions at large Ns. The focus was on the transition from the regime of “hard selection sweep” at small μN, when a single beneficial mutation spreads to the entire population, to the regime of “soft selection sweep” at μN ∼ 1 or μN ≫ 1, when multiple clones originating either from preexisting variation or from additional mutation events during a sweep arise to share the final population. Applying the approach of Hudson and Kaplan, these authors analyzed the structure of phylogenetic tree and the sequence structure for the final population. In the two limits of μN, they predicted <TMRCA> equal to the full adaptation time T1site and N, respectively. The last result is due to the existence of multiple ancestors of a final population before the beginning of the sweep.
Our results can be compared with these findings, even for selection sweeps, only tentatively. Firstly, the value of <TMRCA> is not defined in our case: An HIV population does not exist before the moment of infection, i.e., beginning of adaptation, and the fraction 1-C of site pairs do not have common ancestors. Secondly, we operate with the effective population size Nanc, which determines the density of coalescent events in time. In the traveling wave regime, Nanc is local in time, because even modest recombination mixes classes effectively, and we have not two, but a very large number of classes forming a population. As a result, Nanc averages over all classes and over a period of time much smaller than the adaptation time. In the two-allele, one-site model, analogous local-in-time density of coalescent events does not exist: One can introduce it only within an allelic class, where it is equal to the inverse class size. Thirdly, we predict that the value of Nanc becomes very large near the beginning and the end of adaptation (Fig. 4d), so that most coalescent events occur in the middle of the sweep. This result is in striking contrast to the two-allele model, where most coalescent events for individuals sampled after adaptation occur in the beginning of adaptation when the better-fit class size is small (Pennings and Hermisson, 2006a; Pennings and Hermisson, 2006b). Fourthly, the average value of Nanc is very sensitive to the recombination rate (Fig. 6a), which is not relevant for a model with a single selected site (recombination was considered in all the cited works only between the selected site and a linked neutral site used as a measurement tool).
All these differences stress the importance of application of the multi-site theory to systems where many sites adapt in the same time frame. For HIV, the number of strongly variable sites can reach 200-300 per genome (Rouzine and Coffin, 1999). We are not aware of direct estimates of L, e.g., for yeast or any higher organisms, but it is quite possible that L is large for these systems as well. The next step would be to consider of evolution of single sites existing against the background of multi-site evolution. Examples of important problems are the random variation of the adaptation rate among L sites, and evolution of neutral sites linked to one of these sites.
To summarize, we derived the adaptation rate and an analogue of the time to most recent common ancestor for a model of mostly asexual reproduction, with a small recombination rate per individual, r ≪ 1. We showed that even rare recombination is a much more effective for adaptation than mutation in the asexual model, but that the results depend strongly on the recombination rate. One may expect the existence of an intermediate regime at small r, when new beneficial mutations are important, because they compensate for the long-term loss of beneficial alleles predicted by our theory in this region. Among other potential generalizations of the present theory is evolution of recombination, which would require introduction of an additional locus, which controls the value of parameter r. An important particular limit is the case of fully sexual reproduction. Although many important results are expected to change in this case due to the lack of clone growth, the basic method considering a deterministic traveling wave with stochastic front can be generalized for this case. We hope to address these important applications of our theory elsewhere.
Table 1.
Parameters and variables.
| Model parameters | ||
| N | Population size | |
| s | Selection coefficient | |
| r | Recombination rate per genome | |
| L | Number of evolving sites | |
| Other notation | ||
| k | Mutation load (number of less-fit alleles) in a genome | |
| f1 = k/L | Frequency of less-fit alleles per site | |
| kav | k averaged over population | |
| x = k-kav | Relative mutation load | |
| x0 | High-fitness edge location | |
| u = x/|x0| | Normalized relative mutation load | |
| t | Time (generation number) | |
| V = -dkav/dt | Average substitution rate | |
| w2 | Pairwise genetic half-distance | |
| p = V/(sw2) | Parameter of correlation of fitness between genomes | |
| C | Pairwise identity by descent for homologous sites | |
| Closs | Fraction of sites that lost beneficial alleles | |
| Nanc, N̄anc | Effective population size of genealogy and its harmonic average in time | |
| f(k,t) = φ(x) | Frequency of genomes with given k (or x) | |
| R(k,t) = ρ(x) | Normalized generation rate of genomes with given k (x) | |
| φ(x) = y(u)/|x0| | Probability density of x for an ancestor of a site | |
| n(x′,x) | Size of a clone established at x′ and measured at x | |
| m(x)dx | Number of clones established in interval [x, x+dx] | |
| Pcl(x) | Probability that two genomes in fitness class x are in the same clone | |
| β= r|x0|/V | Clone decay parameter | |
|
|
Clone decay constant (constant factor in β) | |
|
|
Second constant controlling correlation dynamics | |
| T | Total adaptation time | |
| T1site | T in the limit of very frequent recombination | |
| seff | Effective selection coefficient (average linkage effect on adaptation) | |
| Λ1 ≈ ln[Nr/2(πΛ1)1/2] | Logarithmic factors treated as large dimensionless parameters | |
| Λ2 ≈ ln(2Λ2/β) | ||
|
|
Acknowledgments
We are thankful to E. Goubankova, R. Batorsky, H. Levine, M. Slatkin, R. Sergeev, M. Turelli, J. Wakeley, and C. Wilke for useful comments. The work was supported by National Institutes of Health grants R01 AI 063926 to I.M.R. and R01 CA 089441 to J.M.C. J.M.C. was an American Cancer Society Research Professor with support from the George Kirby Foundation.
Appendix A: Stochastic edge treatment
Stochastic edge
In the high-fitness tail of the distribution, deterministic equations (10) and (11) predict the existence of a finite cutoff in x, beyond which there are no genomes, φ(x) = 0 at x < x0, where x0 < 0 (Rouzine and Coffin, 2005). The position of the cutoff x0 can be expressed in terms of V (or p), w2, and four model parameters. However, the substitution rate V remains unspecified. It cannot be found from purely deterministic consideration. The biological reason behind the cutoff is that, initially, very highly fit genomes do not exist. As a population evolves, they are generated infrequently and randomly near the high-fitness edge by recombination. Thus, the deterministic cutoff coincides with stochastic edge of the wave, which gradually advances towards higher fitness (Fig. 2). In order to keep the wave profile constant, the edge must advance at the same average speed as the deterministic part of the wave, which yields the condition
| (A1) |
The three terms on the left-hand side of Eq. (A1) are, respectively: (i) The generation rate of recombinants within interval of mutation load [x0-Δx, x0], where Δx is the typical distance of a new recombinant from the existing edge in x; (ii) the survival probability of a new recombinant in the presence of random drift, based on the single-site, two-allele model with the effective selection coefficient s|x0|; (iii) Δx. The value of Δx is given by the exponential slope of the recombinant generation function ρ(x) near the edge x0. As it follows from Eqs. (10) and (11), ρ(x) depends exponentially on speed V as a parameter. (Note that Eq. (A1) is written within the accuracy of unknown numeric factor at N. Fortunately, all final results depend on N logarithmically, and N is usually very large.) The results for the fitness distribution and the adaptation rate cited in the two subsections on small and intermediate recombination rates in the main text are obtained with the use of Eq. (A1).
Appendix B: Intermediate recombination rates
Substituting Eq. (22) into Eq. (11) for the recombinant generation profile ρ(x), and evaluating the integral over x1 and x2, we obtain
| (B1) |
where we neglected small terms ∼ 1/ln(Nr). Substituting Eq. (B1) into (A1), we obtain Eq. (24) for the lead |x0| where we, again, neglected the term ∼1/ln(Nr) in the brackets. From Eqs. (22) and (10), we get
| (B2) |
where β is defined by Eq. (18) in the text.
We solved Eq. (B2) numerically with respect to εβhβ(u) at different β (Rouzine and Coffin, 2007). Results are shown in Fig. 7. We checked that, for each β, there exist a unique value εβ, such that solution εβhβ(u) is positive and diverges at u = −1. The latter condition follows from the definition of cutoff point x0, φ(x0) = 0. At β ≪ 1, Eq. (B2) can be solved analytically, which yields asymptotics given by Eq. (25).
Fig. 7.
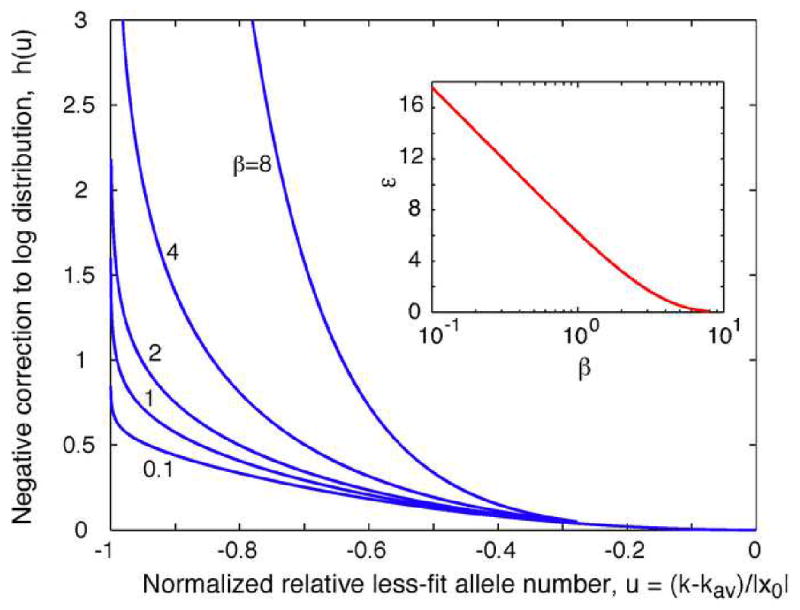
Correction to the fitness distribution profile and to the adaptation rate due to finite recombination rate in the intermediate recombination rate regime (Rouzine and Coffin, 2007).
Solid lines: Normalized negative correction to the logarithm of fitness distribution hβ(u) defined in Eq. (22), as a function of the normalized relative mutation load u at different values of clone decay parameter β defined in Eq. (18). Inset: Normalized negative correction to 1−p, parameter εβ defined in Eq. (23), as a function of β. Results are obtained numerically from Eq. (B2).
Note that the validity regions of the derivations for small and intermediate recombination rates (Derivation and Results) overlap in the interval 1/ln(Nr) ≪ 1-p ≪ 1. Using this fact, at 1-p ≪ 1, Eqs. (14) and (23) for p can be interpolated by an expression
| (B3) |
Ancestor fitness distribution
Consider a remote ancestor of a chosen site in a genome and the probability density of its relative mutation load, φ(x). After rescaling, φ(x) ≡ (1/|x0|)yβ(x/|x0|), the ancestor fitness distribution satisfies an equation of the form (Rouzine and Coffin, 2007)
| (B4) |
where u = x/|x0|. Eq. (B4) applies only for ancestors that existed earlier than β/r generations ago. For more recent ancestors, a more general expression has to be used, with yβ(u) depending on fitness values of the two sampled genomes and the time to ancestor (Rouzine and Coffin, 2007). As it follows from the definition of β, Eq. (18), characteristic time β/r = |x0|/V is the time in which the fitness distribution moves by its lead |x0|.
Numeric solution of Eq. (B4) for yβ (u) at different β is shown in Fig. 4. As compared to the fitness distribution, φ(x), which is centered at x = 0 and has the width w, the ancestor distribution φ(x) is broader by a factor of ln1/2(Nr) and located in the leading tail of φ(x). Thus, an individual has to be exceptionally fit to leave progeny in the distant future.
Appendix C: Clone structure of fitness classes
To calculate the probability Pcl(x) of two individuals to be found within the same clone, we need to address the clone composition of fitness classes. Each group of genomes with mutation number k is comprised of subgroups of identical sequences (clones). Although all clones within a class have the same fitness, different clones are born and established (i.e. exceed the characteristic random drift threshold) at different times. Earlier clones have a larger size. The relative mutation number of a clone x = k−kav(t) increases in time due to the decrease in the average mutation number kav(t). It is convenient to label each clone with the mutation load k born at time t′ by its relative mutation number at birth, x′ = k − kav(t′). We denote the total number of clones established while in the interval [x′, x′+dx′] as m(x′)dx′. The function m(x′) can be obtained from the third term in the right-hand side of Eq. (10), which describes the generation of new recombinants within a fitness class (Rouzine and Coffin, 2007)
| (C1) |
Here product Nrρ(x′) is the generation rate of recombinants per unit time per population in class x′. The second factor, s|x′|, is the survival probability of a new recombinant in the presence of random drift, based on the single-site, two-allele model with the effective selection coefficient s|x′|. The third factor, 1/V, connects units of time and x. It represents the time interval during which the relative mutation load of class k, given by x′ = k-kav(t), stays within interval [x′, x′+1].
Now we consider a clone with mutation number k, which was established at time t′, when it had the relative mutation load x′ = k-kav(t′). We wish to know its size, n(x′,x), at later time t, when it has the relative mutation load x = k-kav(t). The clone dynamics can be obtained from Eq. (10) by ignoring the third term in the right-hand side. Changing variable t to x, dx/dt = V, and integrating in x, we obtain
| (C2) |
where the prefactor is the initial size of an established (deterministic) clone. (Note that in Eqs. C1 and C2, product s| x′| is defined up to numeric factors ∼1 which, however, are mutually consistent and cancel later, see below.) At x′ < x < 0, the first term in the brackets is positive, because it describes the growth of a clone due to positive selection, and the second term is negative, because it describes the loss of genomes due to recombination with genomes from other fitness classes (the chance of recombination with other clones in the same fitness class is small per condition x0 ≫ 1). The fitness distribution φ(x) can be expressed as an integral over x′, as given by
| (C3) |
The integrand in Eq. (C3) determines the clone structure of fitness class x. Evaluating it at small recombination rates, r ≪ s|x0|/V, with the use of Eqs. (C1), (C2), (19), and the normalization condition ∫ dxφ(x) = 1, we obtain Eq. (12) of the main text. In other words, the same expression for the fitness distribution can be obtained either directly from Eqs. (10) and (11), or as an integral over clones comprising fitness classes. This test also confirms the mutual consistency of numeric factors at s|x′| in Eqs. (C1) and (C2).
Now we can calculate the probability of two individuals to be found within the same clone, Pcl(x). If we use the continuous approximation in x′, as we did in Eq. (C3), we obtain
| (C4) |
Here n(x′,x)/[Nφ(x)] is the fraction of class x taken by a clone born at location x′. However, there are two reasons the continuous-in-x′ approximation is not correct, both following from the fact that n(x′,x) enters the integrand of Eq. (C4) as a second power. In the integrand of Eq. (C4), at large negative x′, m(x′) is proportional to exp(-x′2/2w2), and n2(x′,x) to exp(x′2/w2). Therefore, the integrand in Eq. (C4) increases towards the lower limit as exp(x′2/2w2). The rapid increase has two effects, as follows.
Firstly, expanding the net exponential near the edge x′ = x0, as given by x′2 = x02 − 2(x′-x0)|x0|, we observe that the integral in x′ is mainly contributed from a narrow region near the edge, . The region is of the same order as the typical distance between the birth locations in x of adjacent highest-fitting clones, Δx, Eq. (A1). Thus, Pcl is mainly contributed from a small number of edge-born clones, and their contribution to Pcl differs significantly. Therefore, we need to write a discrete sum over these clones instead of an integral and, then, average it out over their birth locations.
The second effect of the divergent integrand simplifies this procedure greatly. In Eq. (C4), we assumed that the lower limit in x′ is given by the average location of the edge x0 determined from Eq. (A1) and leading to Eq. (24). Yet, the value of Pcl is extremely sensitive to fluctuation of the birth location of the largest clone x′ = x0′, because it enters a large exponential in Eq. (C2). Rare clones that are born ahead of the average edge contribute much more to Pcl than typical largest clones born near x0. Therefore, Pcl (x) is mostly contributed from rare realizations (or rare times), in which the entire fitness class x consists of a single large clone born far ahead the average distribution edge. Its birth location x0′ can be estimated as
| (C5) |
Eq. (C5) implies that x0′ depends on x. Then, the probability of two genomes belonging to the same clone is given by the probability to have the largest clone born that far out
| (C6) |
which replaces Eq. (C4). Substituting φ(x) and n(x′,x) from Eqs. (22) and (C2) into Eq. (C5), for x0′ we obtain
| (C7) |
Next, substituting m(x) from Eqs. (C1) and (B1) into Eq. (C6), we get
| (C8) |
Finally, solving Eq. (C7) for x0′ and substituting into Eq. (C8), we arrive at Eqs. (27) of the main text.
Appendix D: Asymptotics at small and large β
We can derive analytically asymptotic expressions of Fβ(u) at small and large β. At β ≪ 1, asymptotic expressions for hβ(u) and εβ are determined by Eqs. (25). At β ≫ 1, the value of εβ is exponentially small (cf. Fig. 7), and the second term in the exponential in Eq. (27) for Fβ(u) can be neglected. Based on this information, we obtain
| (D1) |
Asymptotics of yβ(u) can also be derived analytically from Eq. (B4)
| (D2) |
Substituting Eqs. (D1) and (D2) into Eq. (28), we obtain asymptotic expressions for 1/Nanc
| (D3) |
where numeric coefficient 0.53 is obtained by solving numerically Eq. (D2) for σ(v) and calculating the integral in v in Eq. (D3).
Appendix E: Main approximations
Neglecting the loss of deleterious alleles
Based on our previous simulation, we assumed that sites, which have a common ancestor for large samples, typically carry deleterious alleles. From the one-site model perspective, the assumption is counter-intuitive: Better-fit sites have more chances to leave progeny in the far future. In a many-site system, however, the importance of this factor is not obvious, because it is fitness of the entire genome, which is important (Fig. 8).
The two reasons for the asymmetry in favor of the loss of beneficial alleles observed in simulation (Gheorghiu-Svirschevski et al., 2007) is that deleterious alleles are much more abundant in the initial population (1-f0 ≪ 1), and that the coalescent time tends to be several-fold longer for large samples of sequences than for samples of two [cf. neutral model, (Kingman, 1982a; Kingman, 1982b)]. Therefore, at moderately small recombination rates, when the coalescent time for pairs tends to be several-fold less than the elapsed adaptation time, so that pairwise correlations are already strong, C > 0.7, the extrapolated large-sample coalescent time of sites is still either longer or somewhat shorter than the adaptation time. If it is longer, a site does not have a common ancestor and remains polymorphic. If it is somewhat shorter, a site is monomorphic, but the common ancestor is still at early stages of adaptation and is likely to carry a deleterious allele. The asymmetry is enhanced by a relatively narrow distribution of the large-sample correlation time. Only at very small recombination rates, when the coalescent time for large samples is much shorter than the adaptation time, C close to 1, the common ancestors carrying beneficial alleles emerge.
Effective population size is local in time
For a non-stationary process (adaptation) considered in the present work, the effective population size Nanc introduced in Eq. (5) depends on time through the genetic half-distance w2. Eq. (5) does not include a time delay and, hence, is based on the assumption that Nanc is a local variable depending on the current state of population. For the thoughtful reader, this approximation might appear to contradict Eq. (26), which expresses Nanc at current time t in terms of φ(x), which is fitness distribution of remote ancestors. Firstly, the ancestor fitness distribution φ(x) depends on the time elapsed between the ancestor and progeny, τ, and on the fitness value of the genome to which the sampled site belongs. Secondly, φ(x) and Pcl(x), which depend on time through w2, must refer to an earlier state of a population.
However, as we have shown previously (Rouzine and Coffin, 2007), the ancestor fitness distribution becomes independent on τ and the progeny fitness, when τ is larger than β/r = |x0|/V. Here |x0|/V has a meaning of the time interval in which a wave moves by its lead |x0|. We can neglect coalescent events that might occur in this time interval, and we can neglect the time delay, provided |x0|/V is much less than both Nanc and the characteristic adaptation time T ∼ L/V. In the parameter region of interest where C is neither small nor close to 1, β ∼ 1, Nanc is on the order of T. Therefore, the validity condition of Eqs. (5) and (26), under which they are asymptotically accurate, is |x0| ≪ L or Λ1 ≪ L. This strong inequality is equivalent to Condition (i) stated in beginning of Derivation and Results: It ensures the existence of the traveling wave regime.
We did not include in the integrand in Eq. (26) the term representing the probability that the two ancestors known to be within the same clone are also identical individuals. Once the two ancestors are in the same clone, they will coalesce to the same individual in less than |x0|/V generations back with probability equal to 1. As we just showed, additional time |x0|/V can be neglected as compared to the characteristic coalescent time ∼ Nanc.
Neutral stationary relation between Closs and C
As we show in Fig. 4d, in the parameter range of interests, 1/Nanc depends on time rather sharply: It declines rapidly towards the beginning and the end of adaptation, but does not change much in an interval in the middle of adaptation. Hence, coalescent events occur mostly in this time interval. Therefore, the statistical shape of the phylogenetic tree is roughly similar to that in a stationary neutral model (Kingman, 1982a; Kingman, 1982b), with Nanc replacing N. The only modification is that the earliest and latest branches are elongated by constant time intervals. The relation between Closs and C, which represent the cumulative distributions of the coalescent time for an infinite sample and a pair of genomes, respectively, are not affected by this modification and can be approximated by the neutral relation [Fig. 1, Eq. (7)].
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Barton NH. A general model for the evolution of recombination. Genet Res, Camb. 1995;65:123–144. doi: 10.1017/s0016672300033140. [DOI] [PubMed] [Google Scholar]
- Barton NH, Charlesworth B. Why sex and recombination? Science. 1998;281:1986. [PubMed] [Google Scholar]
- Barton NH, Etheridge AM. The effect of selection on genealogies. Genetics. 2004;166:1115–31. doi: 10.1093/genetics/166.2.1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton NH, Etheridge AM, Sturm AK. Coalescence in a random background. Ann Appl Prob. 2004;14:754–785. [Google Scholar]
- Barton NH, Shpak M. The stability of symmetric solutions to polygenic models. Theor Popul Biol. 2000;57:249–63. doi: 10.1006/tpbi.2000.1455. [DOI] [PubMed] [Google Scholar]
- Brunet E, Rouzine IM, Wilke CO. The stochastic edge in adaptive evolution. Genetics. 2008;179:603–20. doi: 10.1534/genetics.107.079319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B. Mutation-selection balance and the evolutionary advantage of sex and recombination. Genet Res, Camb. 1990;55:199–221. doi: 10.1017/s0016672300025532. [DOI] [PubMed] [Google Scholar]
- Charlesworth B, Charlesworth D. Rapid fixation of deleterious alleles can be caused by Muller's ratchet. Genet Res. 1997;70:63–73. doi: 10.1017/s0016672397002899. [DOI] [PubMed] [Google Scholar]
- Charlesworth B, Morgan MT, Charlesworth D. The effect of deleterious mutations on neutral molecular variation. Genetics. 1993;134:1289–303. doi: 10.1093/genetics/134.4.1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen E, Kessler D, Levine H. Recombination dramatically speeds up evolution of finite populations. Phys Rev Lett. 2005;94 doi: 10.1103/PhysRevLett.94.098102. Art. No. 098102. [DOI] [PubMed] [Google Scholar]
- Desai MM, Fisher DS. Beneficial mutation selection balance and the effect of linkage on positive selection. Genetics. 2007;176:1759–98. doi: 10.1534/genetics.106.067678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. The evolutionary advantage of recombination [review] Genetics. 1974;78:737–756. doi: 10.1093/genetics/78.2.737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. The genetical theory of natural selection. Clarendon Press; Oxford, United Kingdom: 1930. 1958. [Google Scholar]
- Frost SD, Nijhuis M, Schuurman R, Boucher CA, Brown AJ. Evolution of lamivudine resistance in human immunodeficiency virus type 1-infected individuals: the relative roles of drift and selection. J Virol. 2000;74:6262–8. doi: 10.1128/jvi.74.14.6262-6268.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102/103:127–144. [PubMed] [Google Scholar]
- Gheorghiu-Svirschevski S, Rouzine IM, Coffin JM. Increasing sequence correlation limits the efficiency of recombination in a multisite evolution model. Mol Biol Evol. 2007;24:574–86. doi: 10.1093/molbev/msl189. [DOI] [PubMed] [Google Scholar]
- Gordo I, Charlesworth B. The degeneration of asexual haploid populations and the speed of Muller's ratchet. Genetics. 2000;154:1379–1387. doi: 10.1093/genetics/154.3.1379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haase AT. Population biology of HIV-1 infection: viral and CD4+ T cell demographics and dynamics in lymphatic tissues. Annu Rev Immunol. 1999;17:625–56. doi: 10.1146/annurev.immunol.17.1.625. [DOI] [PubMed] [Google Scholar]
- Haigh J. The accumulation of deleterious genes in a population - Muller's ratchet. Theor Popul Biol. 1978;14:251–267. doi: 10.1016/0040-5809(78)90027-8. [DOI] [PubMed] [Google Scholar]
- Hermisson J, Pennings PS. Soft sweeps: Molecular population genetics of adaptation from standing genetic variation. Genetics. 2005;169:2335–2352. doi: 10.1534/genetics.104.036947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J. Selfish genes, pleiotropy and the origin of recombination. Genetics. 1998;149:2089–2097. doi: 10.1093/genetics/149.4.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Robertson A. The effect of linkage on limits to artificial selection. Genet Res. 1966;8:269–294. [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL. The coalescent process in models with selection and recombination. Genetics. 1988;120:831–40. doi: 10.1093/genetics/120.3.831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iles MM, Walters K, Cannings C. Recombination can evolve in large finite populations given selection on sufficient loci. Genetics. 2003;165:2249–58. doi: 10.1093/genetics/165.4.2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung A, Maier R, Vartanian J, Bocharov G, Jung V, Fisher U, Meese E, Wain-Hobson S, Meyerhans A. Multiply infected spleen cells in HIV patients. Nature. 2002;418:144. doi: 10.1038/418144a. [DOI] [PubMed] [Google Scholar]
- Kaplan NL, Darden T, Hudson RR. The coalescent process in models with selection. Genetics. 1988;120:819–29. doi: 10.1093/genetics/120.3.819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Otto SP. Interference among deleterious mutations favours sex and recombination in finite populations. Nature. 2006;443:89–92. doi: 10.1038/nature05049. [DOI] [PubMed] [Google Scholar]
- Kingman JFC. On the genealogy of large populations. J Appl Probability. 1982a;19A:27–43. [Google Scholar]
- Kingman JFC. The coalescent. Stochastic Processes and Applications. 1982b;13:235–248. [Google Scholar]
- Kondrashov AS. Classification of hypotheses on the advantage of amphimixis. J Hered. 1993;84:372–387. doi: 10.1093/oxfordjournals.jhered.a111358. [DOI] [PubMed] [Google Scholar]
- Krone SM, Neuhauser C. Ancestral processes with selection. Theor Popul Bio. 1997;51:210–237. doi: 10.1006/tpbi.1997.1299. [DOI] [PubMed] [Google Scholar]
- Levy DN, Aldrovandi GM, Kutsch O, Shaw GM. Dynamics of HIV-1 recombination in its natural target cells. Proc Natl Acad Sci U S A. 2004;101:4204–4209. doi: 10.1073/pnas.0306764101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith JM. What use is sex? J Theor Biol. 1971;30:319–335. doi: 10.1016/0022-5193(71)90058-0. [DOI] [PubMed] [Google Scholar]
- Muller HJ. Some genetic aspects of sex. Am Nat. 1932;66:118–128. [Google Scholar]
- Neuhauser C, Krone SM. The genealogy of samples in models with selection. Genetics. 1997;145:519–534. doi: 10.1093/genetics/145.2.519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA. The rate of adaptation in asexuals. Genetics. 2000;155:961–968. doi: 10.1093/genetics/155.2.961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto S, Barton N. The evolution of recombination: removing the limits to natural selection. Genetics. 1997;147:879–906. doi: 10.1093/genetics/147.2.879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pamilo P, Nei M, Li WH. Accumulation of mutations in sexual and asexual populations. Genet Res, Camb. 1987;49:135–146. doi: 10.1017/s0016672300026938. [DOI] [PubMed] [Google Scholar]
- Pennings PS, Hermisson J. Soft sweeps II--molecular population genetics of adaptation from recurrent mutation or migration. Mol Biol Evol. 2006a;23:1076–84. doi: 10.1093/molbev/msj117. [DOI] [PubMed] [Google Scholar]
- Pennings PS, Hermisson J. Soft sweeps III: the signature of positive selection from recurrent mutation. PLoS Genet. 2006b;2:e186. doi: 10.1371/journal.pgen.0020186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine I, Wakeley J, Coffin J. The solitary wave of asexual evolution. Proc Natl Acad Sci U S A. 2003;100:587–592. doi: 10.1073/pnas.242719299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine IM, Brunet E, Wilke CO. The traveling-wave approach to asexual evolution: Muller's ratchet and speed of adaptation. Theor Popul Biol. 2008;73:24–46. doi: 10.1016/j.tpb.2007.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine IM, Coffin JM. Search for the mechanism of genetic variation in the pro gene of human immunodeficiency virus. J Virol. 1999;73:8167–78. doi: 10.1128/jvi.73.10.8167-8178.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine IM, Coffin JM. Evolution of human immunodeficiency virus under selection and weak recombination. Genetics. 2005;170:7–18. doi: 10.1534/genetics.104.029926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine IM, Coffin JM. Highly fit ancestors of a partly sexual haploid population. Theor Popul Biol. 2007;71:239–50. doi: 10.1016/j.tpb.2006.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shpak M, Kondrashov AS. Applicability of the hypergeometric phenotypic model to haploid and diploid populations. Evolution. 1999;53:600–604. doi: 10.1111/j.1558-5646.1999.tb03794.x. [DOI] [PubMed] [Google Scholar]
- Stephan W, Chao L, Smale JG. The advance of Muller's ratchet in a haploid asexual population: approximate solutions based on diffusion theory. Genet Res. 1993;61:225–31. doi: 10.1017/s0016672300031384. [DOI] [PubMed] [Google Scholar]
- Tsimring LS, Levine H, Kessler D. RNA virus evolution via a fitness-space model. Phys Rev Lett. 1996;76:4440–4443. doi: 10.1103/PhysRevLett.76.4440. [DOI] [PubMed] [Google Scholar]
- Wakeley J. Conditional gene genealogies under strong purifying selection. Mol Biol Evol. 2008;25:2615–26. doi: 10.1093/molbev/msn209. [DOI] [PubMed] [Google Scholar]
- Wilke CO. The speed of adaptation in large asexual populations. Genetics. 2004;167:2045–2053. doi: 10.1534/genetics.104.027136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke CO, Campos PRA, Fontanari JF. Genealogical process on a correlated fitness landscape. J Exp Zool (Mol Dev Evol) 2002;294:274–284. doi: 10.1002/jez.10146. [DOI] [PubMed] [Google Scholar]
- Williamson S, Orive ME. The genealogy of a sequence subject to purifying selection at multiple sites. Mol Biol Evol. 2002;19:1376–84. doi: 10.1093/oxfordjournals.molbev.a004199. [DOI] [PubMed] [Google Scholar]


