Time preference and its relationship with age, health, and survival probability

Abstract

Although theories from economics and evolutionary biology predict that one's age, health, and survival probability should be associated with one's subjective discount rate (SDR), few studies have empirically tested for these links. Our study analyzes in detail how the SDR is related to age, health, and survival probability, by surveying a sample of individuals in townships around Durban, South Africa. In contrast to previous studies, we find that age is not significantly related to the SDR, but both physical health and survival expectations have a U-shaped relationship with the SDR. Individuals in very poor health have high discount rates, and those in very good health also have high discount rates. Similarly, those with expected survival probability on the extremes have high discount rates. Therefore, health and survival probability, and not age, seem to be predictors of one's SDR in an area of the world with high morbidity and mortality.

1 Introduction

People generally prefer to receive a reward sooner rather than later. The present value of a future reward is often discounted when there is a delay to receiving the reward. Many terms are used to describe this phenomenon, such as time preference, positive rate of intertemporal substitution, impatience, and impulsivity. “Delay discounting” will be used in this paper to refer to the phenomenon that an individual discounts the value of a reward to be received in the future relative to receiving the reward immediately, and the degree to which an individual discounts the future reward will be measured as the subjective discount rate or SDR (which we define formally below).

Although delay discounting is a common assumption in models of intertemporal choice, the literature is relatively incomplete when it comes to why people discount the future in general and why some people discount more than others. Among the various factors associated with delay discounting proposed in the literature (which we review in detail in the next section on Theory and Background), age has emerged as one key factor.¹ Although existing theoretical models of delay discounting often explicitly specify mortality risk (which reduces opportunity for consumption in the future) and morbidity risk (which reduces utility from consumption in the future) as determinants of delay discounting, most existing empirical tests of the theoretical models rely mostly on age as a proxy for those risks. The distinction between age and mortality/morbidity may be important. If the determinants of SDR are known and if such determinants can be changed, many potentially bad outcomes related to impatience could in theory be prevented, if the willingness to wait for some future reward could be enhanced. While one's age is not changeable, one's mortality and morbidity risks can be changed, either through investment in one's own health capital or through public health interventions. If mortality and morbidity risks are causally related to one's SDR, changes in these risks can potentially lead to changes in one's SDR. Our study complements the existing literature by adding health and survival probability — in addition to age — to empirical specifications. In environments such as southern Africa with high prevalence of HIV/AIDS, age is no longer a good proxy for mortality and morbidity risks; here, health and survival probability may play more important roles than age in determining people's SDRs.

1.1 Theory and background

Below we describe research that tries to explain why people discount the future. We begin by more precisely stating the individual's decision problem. Using discounted utility theory (see reviews by Frederick et al., 2002 and Read, 2003), we can represent the individual's intertemporal utility function as follows:

$$U(c_t,c_{t+1},\dots ,c_{t+d},\dots ,c_T)=\sum _{d=0}^{T-t}F(d)u(c_{t+d}),$$ (1)

where U is the utility derived from consumptions, (c_t, c_t+1,…, c_t+d,…, c_T), that regularly occur from time period t up to the final time period T of the individual's life; u(c_t+d) is the individual's instantaneous utility from consumption c in time period t+d; t is the time period when evaluation of this utility occurs; d is the amount of delay since time period t, and F(d) is a discount function. Because the present value of future consumption is often discounted when there is a delay, F(d) is usually represented by some declining function with respect to delay, with F(0)=1 when there is no delay. Corresponding to each discount function is a discount rate or r(d), which is defined as the proportional change in value of F(d) per period of time interval (such as a day or a year):

$$r(d)=-\frac{F(d)-F(d-1)}{F(d-1)}.$$ (2)

In this paper, we call the individual's discount rate the subjective discount rate or SDR.

The most common discount function in the literature is the exponential discount function:

$$F{(d)}_{\mathit{\text{exponential}}}={\left(\frac{1}{1+\rho }\right)}^d,$$ (3a)

where ρ is a discount parameter per period of time interval (such as per day or per year), and d is the number of time intervals in the delay (measured in number of days or number of years). Greater ρ means greater per-period discounting; also, the longer the delay, the greater the total discounting applied to the delayed consumption. Based on Equation 2, the exponential discount rate is:

$$r{(d)}_{\mathit{\text{exponential}}}=\frac{1}{1+\rho },$$ (3b)

which is independent of the amount of delay.²

Although the exponential discount functional form has been used traditionally in studies of delay discounting, a hyperbolic discount function has also gained acceptance and has been found in some studies to fit empirical data better than exponential functional forms (e.g., Rachlin, 1989; Green et al., 1994; Kirby & Marakovic, 1995; Kirby, 1997; and recently by neuroeconomists, Kable & Glimcher, 2007). One hyperbolic discount function is:

$$F{(d)}_{\mathit{\text{hyperbolic}}}=(\frac{1}{1+kd}),$$ (4a)

where k is a per-period discount parameter, and d is the number of such periods in the delay. Higher values of k imply greater discounting. Because the delay d is in the denominator of the hyperbolic discount function, the impact of an additional unit of delay, from d to d+1, will be greater when the original delay d is short than when the delay is long (see Read, 2003; Ainslie, 1975). The corresponding hyperbolic discount rate can be derived using Equation 2 and is:

$$r{(d)}_{\mathit{\text{hyperbolic}}}=(\frac{k}{1+kd}).$$ (4b)

Regardless of the functional form, a future reward will be discounted more the greater the individual's SDR.

We use the discrete exponential discount rate, as in Equation 3b, for all of the results presented in this paper. The results obtained from using a hyperbolic discount rate as in Equation 4b or the hyperbolic discount parameter k remain essentially the same.³ To calculate each person's SDR such as in Equation 3b or 4b, one needs to find that person's value for ρ or k (depending on the assumed discount function), and this can be done by having the person perform a series of delay discounting tasks (i.e. make a series of trade-offs between less money in an earlier time period and more money later). Suppose an individual has won a reward A to be received at some future date t+d. With the future reward as part of his new budget constraint, the individual derives utility U from a new string of per period consumption stream as follows:

$$U=U(c_t,c_{t+1},\dots ,c_{t+d}+A,\dots ,c_T).$$ (5)

Suppose this individual is given the choice of receiving an alternate reward V today (when d=0) in lieu of receiving A in the future. The amount V that would make him indifferent between receiving V today relative to receiving A in time t+d is the equivalent present value of A (see Loewenstein and Prelec, 1992, for a more general exposition),⁴ such that

$$\begin{array}{l}U(c_t+V,c_{t+1},\dots ,c_{t+d},\dots ,c_T)=\\ U(c_t,c_{t+1},\dots ,c_{t+d}+A,\dots ,c_T),\end{array}$$ (6)

which when substituted into Equation 1, results in:

$$u(c_t+V)-u(c_t)=F(d)(u(c_{t+d}+A)-u(c_{t+d})).$$ (7)

This essentially says that the value of the marginal utility derived from receiving an award today of amount V is equivalent to the discounted present value of the marginal utility derived from receiving a future award of magnitude A with a delay d.

Although not an entirely innocuous assumption, most delay discounting tasks used to elicit discount parameters in the literature also make a further assumption that the utility function u(.) in Equation 7 is related to the quantity of consumption goods by a multiplicative constant (see Read, 2003). This linearity assumption essentially reduces Equation 7 to:

$$V=AF(d),$$ (8a)

or

$$V=A{(\frac{1}{1+\rho })}^d$$ (8b)

for an exponential discount function, and

$$V=A(\frac{1}{1+kd})$$ (8c)

for a hyperbolic discount function.

1.2 Existing theories of delay discounting

We next present the relevant literature on why delay discounting occurs, and specifically, why age may be a determinant of delay discounting. Early researchers' attempts at explaining the underlying mechanisms of delay discounting have been well summarized by Frederick et al. (2002). Rae (1834) viewed intertemporal choice behavior as a joint product of factors that promoted delay of consumption (such as the bequest motive and a social norm of self-restraint) and hastening of consumption (such as the uncertainty of human life, the reduction in ability to enjoy pleasure with ageing, and the discomfort from delaying gratification). The uncertainty of life carries the risk that postponed consumption might not be realized, and this has been further modeled by Yaari (1965) and later Halevy (2005) as to why delay discounting may change with age. In addition to mortality risks, age is also associated with morbidity risks. Börsch-Supan and Stahl (1991) modeled how deteriorations in health of the elderly constrained their consumption, and, more recently, Trostel and Taylor (2001) using state-dependent utility functions theorized that as people's ability to enjoy consumption declines at an increasing rate over time due to ageing, people should increasingly discount the future since the marginal utility of consumption will decline with age. Reductions in marginal utility from declines in health have been found empirically by Finkelstein et al. (2008).

In addition to the models from economics, evolutionary biology approaches have also been used to explain how the discount rate should change with age (Rogers, 1994; Sozou & Seymour, 2003). Because successful reproduction to propagate one's genes requires expending resources and because reproductive potential varies with age, these models also link SDR with age. Rogers (1994) identified three determinants of delay discounting, namely an expectation of rising consumption, declining reproductive value, and bequest possibilities. Rogers predicted an inverted U-shaped SDR-age profile for a 5–10 year investment horizon: sexually immature youngsters should save resources for use later for reproduction (low SDR), sexually mature adults should expend resources pursuing reproduction and not save, since they face the threat of mortality with time as well as fertility decline with ageing (high SDR), and old people with little prospects for propagating their genes by reproduction should save resources and transfer them to an offspring with genes like their own (low SDR). Sozou and Seymour (2003) used similar reasoning as that of Rogers but also allowed for uncertain exogenous environmental hazard and no bequests. (Also, their model did not include sexually immature youngsters, in contrast with that of Rogers.) They predicted a U-shaped relationship between one's SDR and one's age: young sexually mature adults, not knowing when they will die, should expend resources to reproduce (high SDR), middle-aged adults with reproductive prowess, but with low mortality hazard given that those with high mortality hazards have all died, could take a longer-term view (low SDR), and old adults, with low environmental hazard but rapidly declining fertility and rapidly rising ageing-related mortality, should act as if there is no tomorrow (high SDR). Sozou and Seymour further suggested that genes for “visceral pleasures” such as eating, drinking, and partying, proxy for reproduction and should face similar time preference functions.⁵

Therefore, theories from both economics and evolutionary biology, although they disagree on the form of the relationship and the reasons for it, all share one important prediction — age should bear (some kind of) a relationship with the SDR.

1.3 Previous empirical studies

Empirically, there is some support for a relationship between age and the SDR, but the exact shape of the relationship differs by study. Trostel & Taylor (2001) tested their model using micro-level longitudinal consumption data in the U.S. to empirically support their theory and found a statistically significant negative relationship between age and consumption growth (where higher consumption growth was assumed to reflect a lower discount rate). The study further tested for a nonlinear effect of age on consumption growth and found that the effect of the linear and the quadratic terms for age were jointly significant in determining consumption growth, but the terms were individually insignificant (see footnote 19 in Trostel and Taylor, 2001).

Instead of measuring SDR indirectly through consumption changes over time, a few studies have measured SDR directly by posing questions similar to those as depicted in Equation 6. Green et al. (1994) surveyed 36 participants in the U.S. drawn from 3 age brackets (sixth graders, college students, and older adults with mean age around 68), by presenting them with a hypothetical reward to be received in the future (as the variables A in Equation 6) and asking them their equivalent present value (V in Equation 6) when the delay (d) ranged from 1 week to 25 years. Using a hyperbolic discount function, they found that the older adults had a discount parameter (k in Equation 8c) that was much lower than that found for college students, whose discount parameter in turn was much smaller than sixth graders — suggesting an inverse SDR-age relationship.

Using a slightly different experimental procedure, Harrison et al. (2002) elicited discount rates among 268 people between the ages of 19 and 75 drawn from a nationally representative sample in Denmark. The participants were asked to choose between a smaller sooner reward to be received with a one-month front end delay and a larger later reward to be received in 7, 13, 15, or 37 months. The delay discounting task was also incentive compatible, because the participants had a chance to win an actual reward as chosen in the delay discounting task. The results showed that the average discount rate among those aged 41 to 50 was lower than the discount rate among those either younger than 41 or older than 50, indicative of a U-shaped relationship between SDR and age (as predicted by Sozou & Seymour, 2003). Nevertheless, having controlled for other demographic characteristics, the regression results showed no statistically significant differences in discounting between people in different age brackets. The regression did show, however, that those who were retired (and hence among the oldest in the sample) had significantly greater discount rates than those still working.

Read and Read (2004) conducted a study designed specifically to test the relationship between SDR and age, by surveying 123 U.K. respondents selected using a quota sample of three distinct age groups consisting of the young (mean age of 25), middle-aged (44), and elderly (75). Using either a larger later hypothetical reward (such as A in Equation 6) and asking for the equivalent present value (V) or a smaller sooner hypothetical reward (V) and eliciting the equivalent future value (A), the study examined discounting over various time horizons (from 1 to 10 years, with front end delays that ranged from 0 to 7 years). In addition to hypothetical monetary rewards, the study also examined discounting with respect to receiving holiday time or getting the flu. To test for a curvilinear relationship between SDR and age, linear and quadratic versions of the variable age were included in the analyses. The study mostly confirmed the theoretical predictions of Sozou and Seymour (2003) and the empirical findings of Harrison et al. (2002), that the middle aged group had the lowest discount rate, followed by the young, and with the elderly discounting the most. This U-shaped relationship between SDR and age was significant for monetary rewards in the 0–10 and 7–10 year time horizons. After having controlled for other demographic variables, the signs of the regression coefficients for age and for age squared reflected a U-shaped relationship between SDR and age, but the linear term for age in the 0–10 year horizon and the quadratic term for age in the 7–10 year horizon became insignificant. The paper did not report whether the linear and quadratic terms were jointly significant.

Age, therefore, has been studied as a determinant of delay discounting, both theoretically and empirically. However, age as modeled by both the evolutionary biology and the economics approaches was merely a proxy for factors that affected propagation of one's genes and one's ability to enjoy pleasure, respectively. Two key factors implicitly important in determining reproductive fitness and felicity are mortality risks (which reduce the time available for reproduction and for fun) and morbidity risks (which reduce the ability to reproduce and to consume and enjoy fun activities).

However, the direct effects of mortality and morbidity on delay discounting have received relatively little attention in the empirical literature. Existing studies that include only age cannot separate out the different effects contributed by morbidity and mortality risks from other age-related factors that influence preferences and behavioral patterns over the lifespan. The very few studies that did examine the impact of mortality and morbidity risks on delay discounting have also found mixed results. For instance, Trostel and Taylor (2001) found no effect from mortality risk (measured by life table estimates of survival probability based on the demographics of the respondents) or morbidity (measured by the health-related absenteeism) on consumption growth, although it is unclear whether these mortality and morbidity measures were insignificant because they indeed had no effect, or whether the measures were poor proxies for actual risks. The few studies that have included proxies for health have mostly included only dichotomous or linear terms for health, which may not be sufficient if health like age could be non-linearly related to the discount rate. Kirby et al. (2002) found no relationship between body mass index and SDR.⁶ Read and Read (2004), using two dichotomous variables for health (good vs. bad health; disease in last year vs. not), found poor health to be unrelated to discounting for monetary rewards but related to discounting of a vacation reward.⁷

Our paper makes a contribution to this ongoing debate by examining SDR and its associations with not just age, but also with the respondents' level of morbidity (as measured by a health status instrument) and their mortality risks (as measured by their subjective survival probability). Our main hypotheses are that morbidity and mortality (or health and survival expectations) are systematically related to the SDR. Rather than make assumptions and build a theory about the exact shape of this relationship, we examine empirically the relationship between age, health, and survival expectations, allowing for both linear and non-linear relationships, as well as controlling for other variables that may potentially impact delay discounting. In contrast to prior studies that have found age to be a factor associated with delay discounting, we find that health and survival expectations but not age are significant factors associated with the SDR. We discuss our method, followed by our results and findings, then we speculate on the underlying mechanisms of delay discounting that could account for our findings, and we conclude with some potential implications of our findings.

2 Method

2.1 Participants and procedures

This study is part of a larger study on the impact of poor health and HIV/AIDS on micro and small enterprises (MSEs) around Durban, South Africa. The sample is described in detail elsewhere (Chao et al., 2007). Surveys were conducted over a three year period in six randomly selected townships stratified by income around Durban, with information on health, business activity, and general demographics. Questions on delay discounting were asked during the third year of the survey. This paper is based on the results from the total of 175 individuals that had completed the delay discounting task. The Results section presents descriptive statistics of this sample.

2.2 Measures

Five parts of the questionnaire were used to measure the respondent's SDR, physical and mental health, subjective probabilities of one-, five-, and ten-year survival, planning and savings behavior, and expectations of future economic condition.

2.2.1 Subjective discount rate

We adopted the time preference instrument originally developed by Kirby and Marakovic (1995) and Kirby et al. (1999), by using the South African Rand (which had an exchange rate at the time of survey of about 6.7 rand to the dollar). This instrument presented the participants with a set of hypothetical choices between smaller immediate rewards (V) and larger later rewards (A), as in Equation 6. The delay discounting task essentially asked the respondents whether they wanted the reward on the right side of Equation 6 or the reward on the left side of Equation 6, when V, A, and d were varied. Table 1 lists, for each trial, the smaller immediate reward (V), the larger later reward (A), the amount of the delay (d), the calculated exponential discount rate when the respondent is indifferent between the immediate and the future rewards (as in Equation 3b), the calculated hyperbolic discount rate (as in Equation 4b), and the calculated hyperbolic discount parameter (k). Although Table 1 tabulates the individual trials in increasing ranks of discount rates, the order of the presentation of the trials in the actual choice task was random with respect to the ranking of the discount rates, but the sequence was the same for all participants. The delays ranged from 1 week to 6 months and were presented as number of days from today.⁸ An example of one of the choices in this instrument was “Would you prefer R54 today or R80 in 30 days?” To prevent the participants from anchoring to one fixed larger later reward, the amount A also varied by plus R5 to minus R5 from the larger later reward of R80. The exact numbers of days of delay and the possible smaller immediate rewards were also varied. Although the combinations of V, d, and A were varied for each of the delay discounting trials, they were designed to give 9 possible discount rates when the respondent became indifferent between the left and the right side of Equation 6.

Table 1.

Values of delay discounting task rewards and associated discount rates and parameters.

Discount rate ranking	Reward today V	Future reward A	Delay in days d	Exponential discount rate if indifferent (equation 3b)	Hyperbolic discount rate if indifferent (equation 4b)	Hyperbolic Discount Parameter if indifferent (k)
1	78	80	162	0.00016	0.00015	0.00016
2	80	85	157	0.00039	0.00037	0.00040
3	67	75	119	0.00095	0.00090	0.00100
4	69	85	91	0.00229	0.00207	0.00255
5	55	75	61	0.00507	0.00437	0.00596
6	54	80	30	0.01302	0.01083	0.01605
7	41	75	20	0.02974	0.02267	0.04146
8	33	80	14	0.06129	0.04196	0.10173
9	31	85	7	0.13419	0.09076	0.24885

The respondent's SDR can be estimated from his choices in these trials. For instance, a respondent who prefers “R80 in 30 days” over “R54 today” (trial rank #6) can be inferred to have an exponential SDR of less than 0.01302. If this same respondent also prefers “R55 today” over “R75 in 61 days” (trial rank #5), his SDR can be inferred to be greater than 0.00507. The combined information from these two trials suggests that this respondent's actual SDR is bounded between 0.00507 and 0.01302. In this paper, following Kirby et al. (1999), we take the geometric mean between these two numbers as the SDR for this particular participant.⁹

A respondent who always chooses the larger later reward for each of the 9 trials can be inferred to have an SDR that is smaller than 0.00016 (but we do not know how much smaller); similarly, a respondent who always chooses the smaller sooner reward has an SDR that is greater than 0.13419 (but we do not know how much greater). For these respondents, we use the end point SDR, but in the regression analysis, we utilize Tobit regressions to take care of the left and right censoring in the data (explained further below).

Because we were unable to make a 100% guarantee of delivery of the future reward to our participants (due to logistical issues), we did not use real rewards in the delay discounting task.¹⁰

2.2.2 Health measures

We used the SF12 health status instrument, which consisted of 12 questions that assessed symptoms, functioning, and quality of life along two dimensions: mental and physical health (Ware et al., 1995). Examples of questions included in the SF12 are “Please tell me if your health now limits you in carrying out moderate activities that you might do during a typical day, such as walking to transport or helping at home? If so, how much?” and “How much of the time during the past 4 weeks did you have a lot of energy?” Also, one of the 12 questions was a self-assessed general health question in which the respondent was asked to rate his/her health into five categories, ranging from excellent to poor. Separate scores for physical health (PCS12) and for mental health (MCS12) were obtained by weighting each question according to a formula (Ware et al., 1995). This instrument has been validated in many developing countries in various languages including Zulu speaking populations in South Africa (available from QualityMetric.com) and was designed to be easily administered and answerable even by respondents who could not read.

2.2.3 Subjective probabilities of survival

The next set of questions asked individuals to rate their subjective probabilities of survival between 0% to 100% to measure how certain the respondent was that he/she would not die in the next 1, 5, or 10 years. A similar question was asked in the Health and Retirement Study (HRS) in the United States. A study by Smith et al. (2001) demonstrated that respondents not only could answer these questions, but also that their answers indeed predicted their own mortality.

2.2.4 Planning and savings behavior

We asked questions about the respondents' planning behavior and savings behavior. For the planning behavior, we asked whether the respondents classified themselves as planning ahead all the time or living from day to day. Similarly, for savings behavior, we asked whether the respondents classified themselves as preferring to spend money to enjoy life today or to save more for the future. These questions were modeled after the US Panel Study of Income Dynamics. We also asked about the time horizon (ranging from a few months, a year, to the next several years) in the respondents' planning and savings behavior.

2.2.5 Expectations of economic and business situation in the next two years

Because current versus future marginal utility of the hypothetical reward depends on the baseline income level in the two time periods, we asked all respondents whether they expected the economic situation of their community to improve a lot, improve a little, remain the same, decline a little, or decline a lot in the next two years.

2.3 Data analysis

Because the main papers that studied the relationship between age and SDR used different discount functions to calculate the SDR (Green et al., 1994 used a hyperbolic function but Read & Read, 2004, and Harrison et al., 2002, used exponential discount functions), we calculated SDR using both the hyperbolic and the exponential discount functions (as depicted in Equations 3 and 4, respectively).

Using the calculated SDR for each participant, we analyzed the bivariate relationships between the SDR and the respondents' demographic characteristics, age, health, and expectations of subjective survival probability to live a certain number of years. We then performed a series of multivariate regressions using the natural log of the SDR as the dependent variable, because the SDR is highly skewed without the log transformation. Given that the SDRs elicited by the hypothetical monetary tradeoffs are censored between 0.00016 and 0.13419, we used two-sided Tobit regressions to account for the left- and right-side censoring of the calculated SDR.¹¹

To check the robustness of our results, we performed various regression diagnostics to flag potential outlier and influential observations, compared results derived from regressions using both the full sample as well as the subsample after having deleted observations flagged by the regression diagnostics, examined results derived from OLS and Tobit regressions, and compared regression results when the dependent variable was the (log of) the exponential SDR, the hyperbolic SDR, or the hyperbolic discount parameter (k). The main results and conclusions did not differ among these various alternative specifications. Therefore, we present below the results obtained from two-sided Tobit regressions with ln(SDR) as the dependent variable, and briefly summarize the findings from these other alternative specifications.

Given that the delay discounting task used the number of days as the delay, all the discount rates are measured as discount rate per day.

3 Results

3.1 Descriptive statistics

Table 2 presents the mean and median SDRs for the full sample and for the subsamples defined by various sociodemographic variables. The first column also presents the mean and standard deviation for sociodemographic variables with a continuous distribution. The full sample consisted of 175 individuals, with 73% female and 46% married or cohabiting, and a mean age around 47 years, with a range from 18 to 91. Over 80% of the sample consisted of current or former small business owners. The respondents' mean physical and mental health scores for the SF12 were 47.48 and 51.90, respectively, with standard deviations of 12.1 and 10.9. The mean health scores in our population are similar to those in the United States (which have a normalized score of 50 and a standard deviation of 10) (Ware et al., 1995). Twenty-five percent of respondents reported their health to be fair or poor (instead of excellent, very good, or good). In terms of the respondents' expectations regarding their one-year survival probability, 38% (67 out of 175) said they were 100% confident that they would “live to this time next year,” and 21% stated at least a 60% chance of not living until the next year. The mean response was an 82% confidence of living to the next year. When we asked individuals their expectations to living to this time in five years (not shown in Table 2), 25% expressed a 100% confidence that they would live to this time in 5 years, and 31% of respondents expressed a 50–50 chance of living to the next 5 years. A similar pattern was found when we considered individuals' expectations to live 10 years. While 19% of respondents were 100% confident that they would be alive, 48% of respondents expressed a 50–50 percent chance or lower of being alive in 10 years.

Table 2.

Mean and median subjective discount rate (SDR), by sociodemographic variables (continued on next page).

					Kruskal difference b Wallis test etween gro of ups
	N	Arithmetic mean SDR	Geometric mean SDR	Median SDR	χ2	df	p
Full Sample	175	0.040	0.017	0.020
Age (mean age = 46.52; s.d.=15.09)
Lowest Quintile	28	0.037	0.021	0.026	1.43	4	0.84
2nd Quintile	34	0.040	0.020	0.020
3rd Quintile	37	0.039	0.016	0.008
4th Quintile	40	0.041	0.012	0.019
Highest Quintile	36	0.044	0.018	0.019
Physical Health (mean = 47.48; s.d.=12.06)
Lowest Quintile	34	0.046	0.016	0.027	3.99	4	0.41
2nd Quintile	36	0.042	0.013	0.008
3rd Quintile	35	0.035	0.016	0.008
4th Quintile	43	0.035	0.016	0.019
Highest Quintile	27	0.046	0.027	0.043
Mental Health (mean = 51.90; s.d.=10.86)
Lowest Quintile	35	0.040	0.014	0.043	0.88	4	0.93
2nd Quintile	34	0.031	0.013	0.019
3rd Quintile	35	0.0407	0.020	0.187
4th Quintile	35	0.040	0.016	0.020
Highest Quintile	36	0.049	0.021	0.019
1-Year Survival Probability (mean = 81.83; s.d.=19.71)
0 - 60%	36	0.063	0.028	0.043	16.77	3	0.00
70 - 80%	48	0.029	0.011	0.008
90%	24	0.018	0.010	0.008
100%	67	0.044	0.020	0.043
Overall business environment in 2 years
Improve a lot	10	0.029	0.014	0.020	2.86	4	0.58
Improve a little	52	0.040	0.020	0.043
The same	59	0.038	0.016	0.019
Decline a little	33	0.050	0.018	0.008
Decline a lot	10	0.024	0.008	0.008
Gender
Male	48	0.033	0.014	0.020	0.10	1	0.92
Female	127	0.043	0.018	0.019
Marital Status
Married or Cohabiting	80	0.046	0.015	0.020	0.26	1	0.61
Single, divorced, widowed	95	0.036	0.018	0.019
Education Completed
None	11	0.090	0.062	0.134	11.92	5	0.04
Some primary	34	0.042	0.013	0.013
Primary completed	23	0.041	0.016	0.043
Some secondary	51	0.030	0.012	0.008
Secondary completed	37	0.037	0.019	0.020
Beyond secondary	19	0.041	0.020	0.020
Income
High Income	55	0.041	0.019	0.019	0.44	2	0.18
Middle Income	66	0.033	0.015	0.0187
Low Income	54	0.048	0.0164	0.040
Area dummies
Area N (high income)	25	0.033	0.012	0.008
Area A (high income)	30	0.048	0.027	0.031	8.07	5	0.15
Area J (middle income)	30	0.030	0.011	0.008
Area K (middle income)	36	0.036	0.020	0.043
Area C (low income)	26	0.058	0.025	0.043
Area G (low income)	28	0.038	0.011	0.008
Business Ownership
Business Owner or Past Owner	143	0.041	0.017	0.020	0.01	1	0.91
Never Owner	32	0.036	0.016	0.019
Know where to borrow R100
No	86	0.039	0.014	0.008	3.34	1	0.07
Yes	89	0.042	0.019	0.043

The overall mean and median for the SDR (calculated using Equation 3b) for the full sample are 0.040 and 0.017 (per day).¹² Because of the censoring of the SDRs due to the nature of the monetary delay discounting tasks used, (with a lower bound of 0.00016 and an upper bound of 0.134), there is also a significant number of individuals displaying the lowest SDR (7 in 175) and a large number of respondents displaying the highest SDR (24 in 175).

Table 2 also presents the mean and median SDRs grouped by sociodemographic variables and by health and survival expectations, and the Kruskal-Wallis test for significance in difference between groups. It is interesting to note that gender, marital status, business ownership, and income level of the respondent's area of residence were not significantly related to SDR. Respondents with no education had significantly higher SDRs than those with some education.

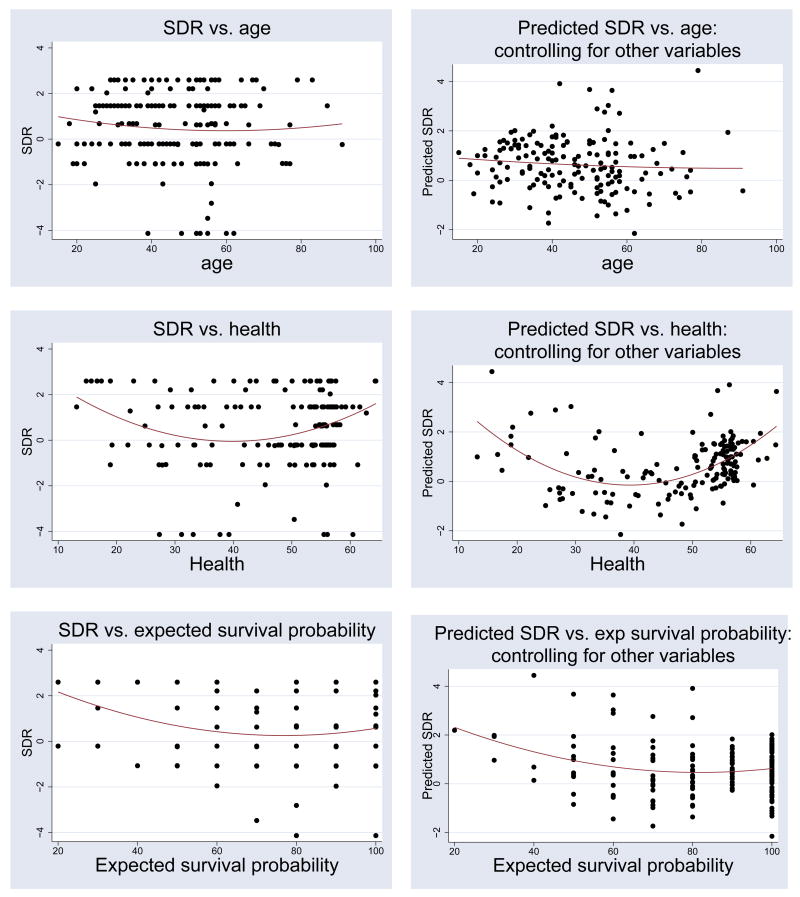
We next examined the bivariate relationship between the SDR and age, physical health, mental health, and subjective survival probability. Spearman rank correlation was insignificant between SDR and all of these variables (not shown in the table). This could either be because a relationship between these variables and the SDR does not exist, or the relationship is non-linear. Because the theoretical predictions (see Introduction above) suggest that the relationship between age and SDR may be nonlinear and perhaps U-shaped, we next divided the sample into approximate quintiles.¹³ It is interesting to note that older respondents do not have higher SDRs than the younger respondents. Figure 1 presents a plot of the raw and predicted values of SDR plotted against age, physical health, and expected survival probability, with and without controlling for other variables, respectively. Older people do not seem to have a higher discount rate than younger people, while health and survival expectations seem to have a U-shaped relationship with SDR.

Figure 1.

Plot of raw and predicted subjective discount rate (SDR) as a function of age, health, and survival probability. Note that the vertical axis is ln(SDR·100).

We also examined the relationship between SDRs and several behavioral variables that are often linked with time preference, such as willingness to plan for the future and to save money, and the results are shown in Table 3. We found that respondents who claimed that they had one year or longer planning or savings horizons had significantly lower SDRs than those with short horizons. Because planning and savings for long horizons require a preference for waiting for a larger reward in the future, the results in Table 3 suggest that the level of “patience” as measured by SDR is consistent with the self-reported planning and savings behavior in our sample.¹⁴

Table 3.

Mean discount rate, by selected self-reported behavioral variables

					Kruskal Wallis test of difference between groups
	N	Arithmetic mean SDR	Geometric mean SDR	Median SDR	χ2	df	p
Planning Behavior
Plan ahead all the time	145	0.036	0.015	0.020	1.425	1	0.2326
Live from day to day	30	0.059	0.023	0.027
Savings behavior
Prefer saving money	148	0.037	0.016	0.019	3.901	1	0.0482
Prefer spending money	25	0.063	0.026	0.043
Planning horizon
Next few months	58	0.054	0.024	0.043	5.433	2	0.0661
Next year	71	0.033	0.018	0.019
Next few years or longer	46	0.034	0.010	0.013
Saving horizon
Next few months	35	0.068	0.034	0.043	11.239	2	0.0036
Next year	79	0.034	0.015	0.020
Next few years or longer	61	0.033	0.013	0.008

In addition to bivariate relationships, we next explored the relationship that SDR has with age, health, and survival expectations, while controlling for other potential confounders. Using two-sided Tobit regression, we first regressed ln(SDR) on age and then also with age squared, but neither variable was significant (shown in Columns 1a and 1b of Table 4, respectively). We next included other demographic covariates plus area-specific dummy variables, and the results are shown in Column 1c. It is worth noting that Sozou and Seymour (2003) predicted a U-shaped relationship of the SDR and age, and empirical support for such a relationship was found by Read and Read (2004). However, in our study, this relationship was not statistically significant for either age alone or with both age and age squared jointly (test of joint significance, F(2, 144) = 0.34, p > 0.71). Gender and marital status were also insignificant, but those who had no education had a significantly higher SDR than those with at least some primary school education. Some of the area specific dummy variables were also significant.

Table 4.

Double sided Tobit regression, full sample (dependent variable = ln(SDR·100)).

	1a	1b	1c	2a	2b	2c	3a	3b	3c
AGE
Age	−0.001 [0.009]	−0.033 [0.046]	−0.055 [0.049]	−0.036 [0.048]	−0.017 [0.050]	0.014 [0.050]	−0.019 [0.042]	−0.001 [0.042]	0.035 [0.042]
Age Squared		0.000 [0.000]	0.001 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]
HEALTH
Physical Health Score(PCS12)				−0.268 [0.102]**	−0.277 [0.104]**	−0.198 [0.108]+	−0.202 [0.098]*	−0.208 [0.100]*	−0.16 [0.104]
Physical Health Score Squared (PCS12ˆ2)				0.003 [0.001]**	0.004 [0.001]**	0.003 [0.001]*	0.003 [0.001]*	0.003 [0.001]*	0.002[0.001]+
Mental Health Score (MCS12)					−0.008 [0.131]	0.003 [0.131]		−0.038 [0.120]	−0.052 [0.127]
Mental Health Score S quared (MCS12ˆ2)					0.000 [0.001]	0.000 [0.001]		0.001 [0.001]	0.001 [0.001]
SURVIVAL
One-Year Survival Probability Expectation						−0.160 [0.059]**			−0.135 [0.057]*
One-Year Survival Probability Expectation Squared						0.001 [0.000]**			0.001 [0.000]*
ECONOMY IN NEXT 2 YEARS
Dummy for Economy Improves A Lot (Reference = Economy Declines A Lot)							0.762 [0.760]	0.773 [0.748]	0.782 [0.765]
Dummy for Economy Improves A Little							1.329 [0.601]*	1.368 [0.602]*	1.438 [0.637]*
Dummy for Economy Remains The Same							1.183 [0.609]+	1.139 [0.600]+	1.136 [0.607]+
Dummy for Economy Declines A Little							1.083 [0.632]+	1.078 [0.635]+	1.036 [0.632]
SOCIODEMOGRAPHICS
Dummy for Female Gender			0.323 [0.365]	0.364 [0.358]	0.346 [0.353]	0.359 [0.341]	0.175 [0.332]	0.145 [0.326]	0.134 [0.316]
Dummy for Married/Cohabiting			−0.085 [0.344]	−0.151 [0.339]	−0.175 [0.339]	−0.243 [0.335]	−0.004 [0.316]	−0.029 [0.316]	−0.076 [0.315]
Dummy for No Education			2.314 [0.761]**	2.169 [0.745]**	2.178 [0.733]**	2.305 [0.700]**	2.93 [0.666]**	2.832 [0.653]**	2.88 [0.622]**
Dummy for High Income Area N (Reference = High Income Area A)			−1.049 [0.493]*	−1.145 [0.482]*	−1.061 [0.478]*	−1.096 [0.464]*	−0.957 [0.501]+	−0.893 [0.496]+	−0.943 [0.485]+
Dummy for Middle Income Area J			−1.129 [0.494]*	−1.167 [0.487]*	−1.101 [0.465]*	−1.261 [0.459]**	−1.069 [0.455]*	−1.013 [0.439]*	−1.168 [0.431]**
Dummy for Middle Income Area K			−0.387 [0.398]	−0.406 [0.390]	−0.406 [0.413]	−0.578 [0.401]	−0.136 [0.399]	−0.155 [0.416]	−0.32 [0.414]
Dummy for Low Income Area C			−0.407 [0.555]	−0.408 [0.551]	−0.335 [0.559]	−0.315 [0.547]	−0.339 [0.477]	−0.245 [0.474]	−0.255 [0.475]
Dummy for Low Income Area G			−1.133 [0.530]*	−0.976 [0.526]+	−0.874 [0.498]+	−0.979 [0.496]+	−1.315 [0.542]*	−1.241 [0.510]*	−1.31 [0.505]*
INTERCEPT	0.708 [0.395]+	1.403 [1.019]	2.234 [1.078]*	5.916 [2.154]**	5.125 [3.737]	8.06 [3.966]*	3.072 [2.134]	3.109 [3.673]	6.514 [4.001]
Likelihood Ratio	0.017	0.397	22.318	33.065	35.599	44.628	44.952	46.445	53.463
Prob > LR	0.896	0.82	0.014	0.001	0.001	0.000	0.000	0.000	0.000
Cragg-Uhler R Square	0	0.002	0.122	0.176	0.188	0.23	0.245	0.252	0.284
Observations	175	175	175	175	175	175	164	164	164

[Robust standard errors in brackets].

⁺significant at 10%;

^*significant at 5%;

^**significant at 1%

We next examined the relationship between health and survival probability and the SDR, and these results are presented in Columns 2a, 2b, and 2c in Table 4. Physical health, but not mental health, was significantly associated with the SDR. Given that health may be associated with the SDR through its effect on mortality risk, we next added the one-year subjective probability of survival to the regression.¹⁵ Interestingly, as shown in specification 2c of Table 4, survival was not only highly significant, but inclusion of the survival variables reduced both the magnitude and the significance level of the physical health variables — suggesting that part of the effect of the health variable on SDR was via the relationship between health and survival. In regressions not reported in Table 4, we also included one-year survival without the health variables; the coefficient magnitude and significance level of the survival variables were not reduced with the inclusion of the health variables. This suggests that the effect of survival on discounting is not via health, but part of the effect of health on discounting is via survival.

From specification (2c) in Table 4, it is apparent that the relationship between the SDR and both health and survival in our sample is U-shaped. This suggests that those in very poor health have high SDRs, but those in very good health also have high SDRs. Similarly, those with both high and low survival probabilities (but not those in between) display high SDRs. In fact, the nadir of the U-relationship between SDR and health occurred when PCS12 was 33, or less than one standard deviation below the mean physical health level of the sample. The nadir for the U-shaped relationship between the SDR and the one-year survival probability occurred at around 80%, or slightly below the mean subjective survival probability for the sample.

Because expanding income in the future may reduce the marginal utility of consumption in the future (and hence lead to greater discounting of the future), we next included a variable on the respondent's subjective outlook for the overall economic environment in their community in the next two years.¹⁶ (Eleven respondents did not answer this question and were excluded from subsequent analysis.) This variable is only a crude proxy for the respondents' subjective outlook for their own future consumption opportunity, so the results should be interpreted with caution. Columns 3a, 3b, and 3c show that those who thought the economy was going to worsen a lot in the next two years (the omitted dummy) had the lowest SDR. The U-shaped effect from survival probability on SDR continues to be significant. Under specification 3c, the linear term for physical health is no longer significant but the quadratic term remains significant at the 10% level. The two variables are jointly significant (F(2,144) = 3.34, Prob > F = 0.0381), suggesting that physical health still bears a U-shaped relationship.

To control for any effect from business ownership (compared to never owning a business) and liquidity constraints (which was crudely proxied for with a question that asked the respondent if he/she knew where to go if he/she needed to borrow 100 Rand), we included two dummy variables, which were found to be insignificant, while health and survival expectations continued to be significantly U-shaped with respect to SDR (not reported in Table 4). A likelihood-ratio test shows that the model that includes the dummy variables for business ownership and liquidity constraints is no better than the more parsimonious model 3c, (likelihood ratio test chi-square (2 df) = 3.39, Prob > chi-square = 0.1838). We consider 3c to be the correct model for our analysis.

As a robustness check for our results, Table 5 presents regressions using different methods and using samples after removal of observations flagged by regression diagnostics. The first column of Table 5 is a repeat of specification 3c in Table 4, using double-sided Tobit and the full sample. The second column uses the same full sample but with ordinary least squares (OLS) as the regression method; the results are similar to those obtained from using Tobit. We next performed outlier diagnostics using Studentized residuals and influence diagnostics using Cook's D and DFITS (Belsley et al., 1980) to test whether our results are driven by specific observations. Interestingly, eight observations were flagged by all three diagnostics. Removal of these problematic observations and then using Tobit (3^rd column Table 5) or OLS (4^th column Table 5) showed that not only are our results still robust with these observations removed, but also our main variables of interest (age, health, and survival) increased in statistical significance while remaining the same in magnitude. The similarity in the results derived from the Tobit and the OLS estimations suggests that any inconsistency in coefficient estimates due to violations of Tobit assumptions (heteroscedasticity and non-normality of errors) does not bias the Tobit estimates beyond the inconsistent estimates from OLS.¹⁷ Columns 5 and 6 of Table 5 present the Tobit and OLS regressions results using the full sample but using ln(k·100) as the dependent variable. The results are very similar to those with the exponential form ln(SDR·100) as the dependent variable.

Table 5.

Double-sided Tobit and OLS regressions, by sample (dependent variable = ln(SDR·100)).

	SDR = Exponential Discount Rate Full S ample		SDR = Exponential Discount Rate (with 8 outliers deleted)		SDR = Hyperbolic Discount Parameter (k) Full Sample
	1. Tobit	2. OLS	3. Tobit	4. OLS	5. Tobit	6. OLS
AGE
Age	0.035 [0.042]	0.025 [0.038]	0.050 [0.034]	0.043 [0.032]	0.040 [0.047]	0.030 [0.047]
Age Squared	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.000]	0.000 [0.0004]
HEALTH
Physical health score (PCS12)	−0.160 [0.104]	−0.115 [0.081]	−0.155 [0.084]+	−0.121 [0.069]+	−0.180 [0.116]	−0.130 [ 0.091]
Physical health score squared (PCS12ˆ2)	0.002 [0.001]+	0.002 [0.001]+	0.002 [0.001]*	0.002 [0.001]*	0.003 [0.001]+	0.002 [0.001]+
Mental health score (MCS12)	−0.052 [0.127]	−0.014 [0.107]	–0.017 [0.101]	0.008 [0.089]	−0.064 [0.138]	−0.022 [0.116]
Mental health score squared (MCS12ˆ2)	0.001 [0.001]	0.000 [0.001]	0.000 [0.001]	0.000 [0.001]	0.001 [0.002]	0.000 [0.001]
SURVIVAL
One-year survival probability expectation	−0.135 [0.057]*	−0.112 [0.046]*	−0.130 [0.053]*	−0.115 [0.046]*	−0.151 [0.064]*	−0.126 [0.051]*
One-year survival probability expectation square	d 0.001 [0.000]*	0.001 [0.000]*	0.001 [0.000]**	0.001 [0.000]**	0.001 [0.000]*	0.001 [0.000]*
ECONOMY IN NEXT 2 YEARS
Dummy for economy improves a lot(Reference = Economy declines a lot)	0.782 [0.765]	0.726 [0.699]	1.094 [0.613]+	1.059 [0.577]+	0.858 [0.836]	0.796 [.761]
Dummy for economy improves a little	1.438 [0.637]*	1.238 [0.543]*	1.421 [0.595]*	1.311 [0.542]*	1.593 [0.695]*	1.374 [ 0.589]*
Dummy for economy remains the same	1.136 [0.607]+	1.010 [0.503]*	1.293 [0.584]*	1.207 [0.525]*	1.254 [0.664]+	1.116 [0.548]*
Dummy for economy declines a little	1.036 [0.632]	0.831 [0.512]	0.998 [0.600]+	0.890 [0.530]+	1.155 [0.694]+	0.931 [0.560]+
SOCIODEMOGRAPHICS
Dummy for female gender	0.134 [0.316]	0.014 [0.278]	−0.235 [0.221]	−0.292 [0.204]	0.145 [0.347]	0.014 [0.305]
Dummy for married/cohabiting	−0.076 [0.315]	−0.146 [0.270]	0.098 [0.252]	0.038 [0.227]	−0.056 [0.349]	−0.132 [0.299]
Dummy for no education	2.880 [0.622]**	1.996 [0.368]**	2.382 [0.567]**	1.840 [0.381]**	3.195 [0.695]**	2.234 [0.415]**
Dummy for high income area N (Reference = High income area A)	−0.943 [0.485]+	−0.860 [0.424]*	−0.664 [0.396]+	−0.624 [0.366]+	−1.032 [0.536]+	−0.941 [0.468]*
Dummy for middle income area J	−1.168 [0.431]**	−1.005 [0.371]**	−0.910 [0.344]**	−0.814 [0.312]*	−1.289 [0.476]**	−1.112 [0.410]**
Dummy for middle income area K	−0.320 [0.414]	−0.174 [0.356]	−0.175 [0.338]	−0.082 [0.303]	−0.365 [0.461]	−0.208 [0.396]
Dummy for low income area C	−0.255 [0.475]	−0.142 [0.394]	−0.032 [0.408]	0.025 [0.363]	−0.261 [0.529]	−0.139 [0.440]
Dummy for Low Income Area G	−1.310 [0.505]*	−1.127 [0.450]*	−0.792 [0.347]*	−0.713 [0.331]*	−1.432 [0.556]*	−1.231 [0.496]*
INTERCEPT	6.514 [4.001]	4.499 [3.105]	5.556 [3.478]	4.159 [2.918]	7.648 [4.416]+	5.444 [3.428]
Cragg-Uhler R Square	0.28		0.33		0.29
Adjusted R Square		0.16		0.22		0.16
Observations	164	164	156	156	164	164

[Robust standard errors in brackets].

⁺significant at 10%;

^*significant at 5%;

^**significant at 1%

Finally, both the adjusted R-square in the OLS model and the Cragg-Uhler R-square in the Tobit model are between 0.16 and 0.33, which is comparable to the adjusted R-squares in the OLS models by Read and Read (2004) that range from 0.04 to 0.24, depending on the time horizon used in the discounting task.

4 Discussion

Several of our findings are new. Our first main finding is that age is not a significant predictor of time preference, which is in contrast to the findings in Green et al. (1994) and Read and Read (2004). Our findings may differ from those of these authors for at least two reasons. One is that only 25% of our sample consists of people over the age of 55 and that our sample may not contain enough older people to show an age effect, whereas Read and Read (2004) concentrated their sample selection based on three age strata, with the oldest strata around age 70. Notably, we are comparing different kinds of people in very different environments. The other reason is that health and especially survival probability, not age, may be a true underlying determinant of people's SDRs. In populations where age does correlate well with health and survival probability, the effect of these other variables on SDRs can be well-manifested by the effects of age. However, because causes of morbidity and mortality in South Africa are not necessarily related to age, age is no longer a strong predictor of health and expected survival and, hence, of SDRs.

Our second main finding is the U-shaped relationship between physical health and the SDR. Although the relationship is attenuated both in magnitude and in significance with the inclusion of survival probability, the linear and the quadratic terms for physical health remain jointly significant at the 5 percent significance level for all specifications. The few studies that did examine the relationship between health and the SDR did not find evidence of such a relationship probably because of the crude health measures used and because of the lack of a non-linear term in these other studies' regressions. Respondents in our sample with average health have a lower discount rate than those who are very healthy or very sick, and this could be due to several reasons. We note that we find a higher SDR among people with very poor health, while simultaneously controlling for expected survival probability (and hence “wanting to deplete resources before death” cannot completely explain this finding). According to Trostel and Taylor (2001), Olsho (2006), and Finkelstein et al. (2008), the ability to enjoy consumption depends on an individual's health, and the healthier an individual, the greater the marginal utility of consumption. Because health generally declines over the life cycle, individuals should have a high SDR when healthy and, thus, enjoy consumption while they still can. Alternatively, people with very poor health may have more immediate need for cash to pay for medical care or for daily survival (perhaps because they are too sick to work), hence the unwillingness to wait for the larger reward. Unfortunately, our data set limits us from testing these explanations, which must await future studies.

Our third main finding is a very robust U-shaped relationship between the SDR and survival probability after controlling for current physical and mental health status. It is reasonable for people with low expected survival to have a high SDR, because their future consumption may never come. It is somewhat perplexing as to why those with a very high expected survival probability also highly discount the future; an explanation for this finding must also await future studies.

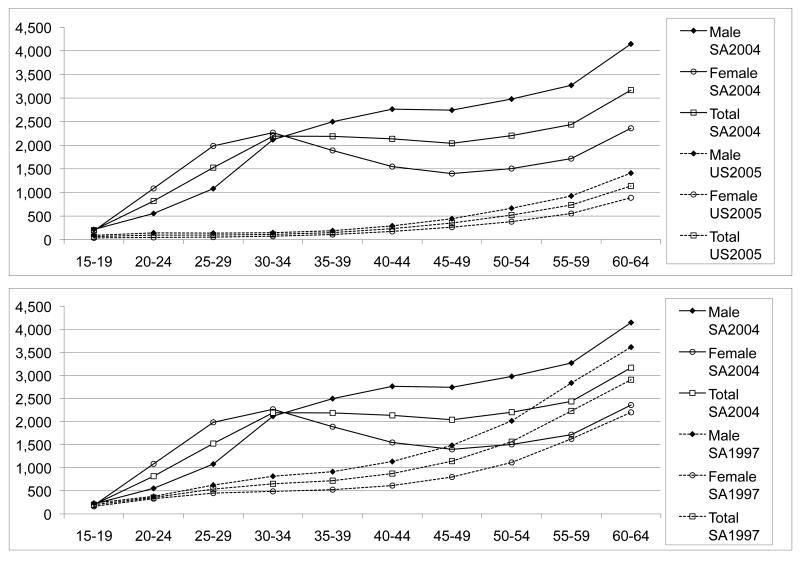
In spite of our inability to dig deeper into the many mechanisms by which health and survival probability should have U-shaped relationships with SDR, the potential importance of health and survival probability as determinants of delay discounting is a novel finding. The inclusion of comprehensive measures of health status and expected survival probability is an important contribution. The inclusion of these variables is already implicit in the theories that we reviewed, but we think it is important to include these variables more explicitly in empirical specifications in order to tease apart the contributions of each of these variables and to understand the true factors that determine the SDR. From the empirical standpoint, the use of the SF12 instrument as a comprehensive measures of health status is less subject to systematic measurement error than single question health status measures (Dow et al., 1997) and may be what contributed to our capturing the U-shaped relationship between health and the SDR. Furthermore, incorporating subjective survival probabilities as a determinant of time preference is important because age proxies for a lot of factors in life, with mortality risk being only one such factor. In particular, many studies confound the differential effects of age and expected survival probability on discounting. Although age is correlated with health and expected survival probability in developed economies, in South African townships where morbidity and mortality risks are very high and where disease profiles are not necessarily related to ageing, age may not be a good proxy for morbidity and mortality. Figure 2 presents the age-specific number of deaths per 100,000 people, by gender, for South Africa in 2004 and the United States in 2005 as well as for South Africa in 2004 and in 1997. In 1997 when the AIDS mortality is just beginning to rise, the age-specific deaths per 100,000 in South Africa had a monotonically increasing relationship with respect to age. However, in 2004, with a maturing AIDS epidemic in South Africa, age-specific mortality rates no longer monotonically increased with age. This is especially evident among females of child-bearing age in South Africa, who have higher HIV prevalence and AIDS deaths than males (Shisana et al., 2005).¹⁸

Figure 2.

Comparison of age-specific death rates per 100,000: S.A. 2004 vs. U.S. 2005 and S.A. 2004 vs. S.A. 1997. (Source: Statistics South Africa, 2006, and Kung et al., 2008.)

4.1 Limitations

The study is subject to several limitations and the results must be interpreted with caution. The first limitation is that we had a small sample that consisted of mostly business operators. While this gave us confidence that the answers to questions involving monetary tradeoffs were less likely to be subject to the problems of low mathematical literacy, it is unclear whether our results from a mostly mathematically-literate population are generalizable to other populations in the developing world. Nevertheless, as shown in Table 2 and in regressions that included business ownership as a dummy variable (not reported in the tables), business owners did not have significantly different SDRs than non-owners.

The second limitation is that we did not have good measures of household assets and income; we only have measures of the income strata where the respondents resided. Relative to the highest income area, the fixed effects for low and middle income areas were consistently negative and some statistically significant and negative, which indicates that respondents in the lower income areas have lower SDRs than those from the highest income area. This finding is opposite to that found by Green et al. (1996), who found that income, not age, was associated with SDR, and that found by Read and Read (2004), who also included income strata for their time preference study among populations of the United Kingdom and found that high income strata were associated with a lower SDR. This seeming contradiction may be because all of our respondents are poor, just that some are less poor than others. Even our “high income” strata would be considered below the lowest income strata in the study populations of these other authors.

4.2 Study implications

The relationship between individual characteristics and delay discounting is an important area for future research. Given the robust relationship that survival probability has with the SDR and the marginally significant relationship between health and the SDR, there may be a role for the inclusion of health and survival probability into delay discounting models and empirical studies. The possibility of non-linear relationships that the SDR has with age, health, and survival probability should also be taken into consideration in future empirical specifications.