Abstract
This paper presents Respondent-Driven Sampling (RDS) as a viable method of sampling and analyzing social networks with survey data. RDS is a network based sampling and analysis method that provides a middle ground compliment to ego-centric and saturated methods of social network analysis. The method provides survey data, similar to ego-centric approaches, on individuals who are connected by behaviorally documented ties, allowing for macro-level analysis of network structure, similar to that supported by saturated approaches. Using racial interaction of university undergraduates as an empirical example, the paper examines whether and to what extent racial diversity at the institutional level is reflected as racial integration at the interpersonal level by testing hypotheses regarding the quantity and quality of cross-race friendships. The primary goal of this article, however, is to introduce RDS to the network community and to stimulate further research toward the goal of expanding the analytical capacity of RDS. Advantages, limitations, and areas for future research to network analysis using RDS are discussed.
Introduction
While discussions of social networks in sociology have steadily increased over the past several decades, methods of sampling and analyzing the network structure of real world networks have remained largely under-developed. Marsden (1990) identifies two primary sampling and analysis approaches commonly used to study social networks, those relying on ego-centric data and those using saturated network data.
First, the ego-centric approach relies on questionnaires and surveys pertaining to a node's attributes, direct personal ties, and attributes of those ties and is ideal for studying the local effects of social networks on individuals. For example, Ratcliff and Bogdan (1988) look at the social support structures in the personal networks of unemployed women. Similarly, Cornwell and Waite (2009) find social disconnectedness and perceived isolation have distinct associations with health outcomes in older adults. A major advantage of ego centric analysis is its focus on the individual as the unit of analysis. This allows statistical inference on nodes in a population based on data collected and analyzed using standard survey procedures. The approach does, however, have several limitations. First, the method often relies on name generators which ask respondents to list the names of ties in a given category. For example, the General Social Survey network questions ask respondents to name “people with whom you discuss important matters” (Burt 1984). In many cases, researchers are not able to contact a respondent's ties directly and must rely on proxy reports from respondents about their alters’ characteristics. Unfortunately, there is much potentially relevant information that respondents simply do not know about their social connections. Laumann (1969) finds that while proxy reports of observable characteristics such as race and age are often accurate, alters’ political views are often unknown to respondents. More generally, in a study of adolescent sexual views and behavior, Wilcox and Udry (1986) find that egos often project their own views onto their alters when responding to questions asking for proxy reports. This tendency, termed the “false consensus effect” by Ross (1977), has been the focus of over a decade of research confirming projection of ego's views onto alters (see Marks and Miller (1987) for an extensive review). Therefore, proxy reports on alters’ attributes not only limit the scope of analysis, but may also provide misinformation on the similarity of connected individuals. For many large networks, few, if any, named alters will be present as respondents in the data, limiting inferences on overall structural properties of the network. For studies interested in connectivity, such as the spread of information, culture, or disease, it is important to collect data “extending beyond ego-centric networks, for it is only by learning directly about the behavior of partners’ partners that we can map the structure of connectivity through which disease must flow” (Bearman et al. 2004, p .59). Additionally, some human subjects review boards have blocked ego-centric studies on ethical grounds, suggesting that solicitation of information on alters requires informed consent from those alters (Kadushin 2005; Klovdahl 2005).
Overall network structure is best studied with saturated data that includes information on all nodes and connections in a network (Marsden 1990; Wasserman and Faust 1994; Bearman et. al. 2004). Saturated network data consist of survey data for all nodes in a population with either self-report or behavioral data on ties connecting the nodes. Such data do not technically constitute a “sample” because all members of the population of interest are measured. Saturated data represent the ideal case for all survey research because statistical estimation of population level measures is not necessary. For example, using saturated data of high school student sexual relationships, Bearman et al. (2004) are able to directly calculate overall network parameters such as density and network centralization. However, for large networks, the saturated data approach quickly becomes problematic. First, observational data, even for relatively small networks, can be costly and time consuming. Newcomb (1961), for example, observed the formation of two small (n < 20) social networks over a one-year period. The project involved nine graduate students who “devoted large portions of their time” (p. vi) and provided a house, free of charge, to participants for the duration of the study. While immensely valuable, such data cannot be obtained for the vast majority of network questions. Thus, self-report data on social ties are often used in saturated network studies. While ego-centric studies have often used name generators (Marsden 1990), saturated network studies often use a reciprocation method, where each respondent provides information on his or her connections to every potential alter in the population. A tie is then considered present when both members of a given dyad provide symmetric information. However, while more capable of dealing with larger networks than observational methods, respondents cannot be expected to accurately report their connections within populations of hundreds or thousands of nodes.
Recently, social network researchers have focused on computer-based networks, such as email networks and the internet. This approach has proved immensely valuable to the study structure of naturally occurring networks, including social networks, because all connections in the network, often with thousands or millions of nodes, are automatically documented. While highly effective for analyzing network structure, such data often lack demographic information on nodes or content information on emails and thus cannot be used to study common sociological questions, such as those pertaining to race or gender. In addition, as the popularity of networking websites grows, users are increasingly able to manipulate their network characteristics. For example, a desire to be linked to the maximum number of “friends” may lead users to include alters with whom they have little or no contact as ties. Such behavior not only inflates the users’ degree, but also transitivity and clustering because alters who are socially closer, e.g. friends of friends, are more likely to make their way onto friend lists of egos they do not know directly.
In summary, ego-centric approaches provide a means for studying sociological questions regarding the effect of social networks on individuals, but the lack of direct data on both ego and alter limits the range of research questions and makes insight into the global structure of a network difficult. On the other hand, saturated approaches are ideal for all types of structural network analysis, but are limited to very small populations or electronic data that often lack key sociological variables. The goal of this paper is to present Respondent-Driven Sampling (RDS) as a viable compliment to these approaches that allows researchers studying social networks to make sociological inferences regarding individuals and global social network structure using survey data.
RDS is a chain referral or “snowball”-type sampling and analysis methodology originally developed for studying hidden or hard to reach populations (Heckathorn 1997). The method goes beyond other snowball sampling techniques by incorporating sampling procedures and analytical tools that allow for the calculation of unbiased population estimates. Consequently, RDS utilizes the reach of snowball sampling while maintaining the ability to make unbiased statistical inference (Salganik and Heckathorn 2004). Now widely used in studies of hidden populations, RDS data provide a wealth of information and potential for social network analysis by shifting the unit of analysis from nodes to ties in the network. Below I introduce the analytical techniques available for social network analysis with RDS, provide a comparison of RDS for social network analysis (RDS-SN) and RDS for studying hidden populations (RDS-HP), and demonstrate RDS-SN by considering whether, and to what extent, racial categories (Whites, Asians, and under-represented minorities (URM)) are socially integrated within the student body using an RDS sample of 150 undergraduate ties from a large (> 13,000 students), selective university. Advantages, limitations, and areas for further development of RDS-SN are also discussed. RDS is now widely used to study hidden populations throughout the globe (Malekinejad et al. 2008). While some RDS studies have conducted network analysis (e.g. Spiller et al. 2008), RDS has yet to be applied in studies where social networks are a primary focus.
Substantive Importance
Before describing the analytical procedures of RDS-SN, it is important to enumerate the questions that can be addressed with them. RDS-SN allows for social analysis at three levels of the network. First, through homophily and affiliation analyses, RDS-SN can identify global network structure based on respondent characteristics. Thus RDS-SN can structurally identify network clusters and the socially salient characteristics associated with the clusters. Second, because RDS provides a representative sample of network ties from a connected population, analyses in which the tie is the unit of analysis are possible. Such analyses are useful for comparison of tie characteristics, such as in-group vs. bridging ties. Finally, the presence of survey data from respondents allows for analyses of nodes, similar to that performed using ego-centric data.
Conducting analysis at three levels of the network is currently only possible with saturated data. However, the practical limitations of collecting saturated survey data make such approaches virtually impossible for all but the smallest populations. RDS-SN allows similar analysis based on an easily collected sample of the network. Alternately, ego-centric approaches can be used to conduct analyses at the structural and node levels, but not the tie level. Furthermore, while homophily and affiliation can be calculated using ego-centric data, the methods are data intensive and less robust due to their reliance on self-reports. Ego-centric approaches, however, remain the best method of conducting node based analyses. While RDS-SN is capable of such analysis, the RDS-HP weighting schemes are needed for unbiased estimation, complicating and limiting the analysis.
Simultaneous analysis at three levels make RDS-SN especially well suited to empirical investigation of research questions related to spread or contagion through a network. In fact, because respondents recruit each other for participation through the network, the sampling process itself can be viewed as a model of contagion within a network. With a single RDS study, researchers can answer questions such as: what are the salient clustering agents within the population that serve as barriers to spread? What characterizes the individuals and ties that serve as bridges that connect clusters? How are bridging ties or individuals different from non-bridging ties and individuals? And, how do the network characteristics of observed clusters differ? These questions have far reaching applications to fields such as sociology and public health by providing important insight into the pathways to disease, information, social norms, or cultural spread throughout a population. Identifying and understanding the boundaries and bridges within a network can provide more efficient methods of containing disease spread or saturating a population with important information.
One application especially noteworthy is in the field of public health, specifically those studies focused on the spread of diseases, such as HIV/AIDS in high-risk populations. For studies of these populations, which are often hidden or hard to reach with traditional sampling methods, RDS combines the ability to provide a probability sample safely and efficiently and collect behavioral network data. While Bearman et al. (2004) argue that snowball and ego-centric network sampling methods can not provide a complete understanding of a network's structure and its interaction with disease, these methods can provide valuable information regarding network constraints to disease spread in large populations. For example, Laumann and Youm (1999) find that high rates of select STDs among African Americans, compared to other groups, can be explained by differences in association patterns between high and low risk members of various racial/ethnic groups. The advantages of RDS over ego-centric data are the random sample of behaviorally documented social ties and the presence of both ego and alter in the data which greatly simplifies network analysis and reduces data requirements. Additionally, RDS is already widely used to study these populations in over 100 countries studying studies of HIV/AIDS and other infectious diseases; in these cases, the relevant question is not “why use RDS to study networks,” but “why is such a rich source of information in pre-existing data often left untapped?”
Currently, research regarding contagion and information spread in social networks is conducted primarily using simulation and digital networks (Centola and Macy 2007). RDS-SN compliments this work by providing an empirical way to test and apply computationally derived theories empirically in real world social networks. Thus while RDS-SN does not provide direct insight into causality, it provides an empirical means to test theoretical and causal claims backed by computational work.
Respondent-Driven Sampling
RDS consists of an enhancement of network or “snowball” sampling, in which data on who recruited whom and individual degree provide the basis for calculation of relative inclusion probabilities, population indicators of minimal bias, and the variability of these indicators (Heckathorn 2002; 2007; Salganik and Heckathorn 2004; Volz and Heckathorn 2008). Unlike standard snowball samples, in which respondents provide researchers with a list of contacts that researchers then use to contact new respondents, RDS recruitment is done by the respondents themselves by passing recruitment coupons with unique serial numbers from recruiter to recruit. RDS is implemented the same way for both the study of hidden populations (RDS-HP) and social networks (RDS-SN), however, each application presents different advantages and challenges. For example, RDS-HP benefits from the recruitment of new respondents by previous respondents by more easily reaching populations that may be dangerous to or suspicious of researchers in the field, as is common in hidden populations. On the other hand, peer recruitment benefits RDS-SN by ensuring observed ties are behaviorally documented.
RDS theory is based on two observations (Heckathorn 2002). First, if the chain-referral process consists of enough cycles of recruitment, or waves, the composition of the final sample with respect to critical characteristics and behaviors will become independent of the seeds from which it began. After a certain number of waves, usually less than five, the sample composition becomes stable and ties are drawn randomly from the network providing a representative sample of network ties for network analysis and all members of the target population a non-zero probably of selection that is independent of seed composition (Heckathorn 2002; Salganik and Heckathorn 2004). The second observation upon which RDS is based is that information gathered during the sampling process can provide the means for making inferences about the underlying network structure, which in turn provide the means for calculating unbiased population estimates.
RDS-HP employs a two stage estimation procedure where data is collected and used to make inferences about the underlying social network. These network inferences are then used in the second step to make inferences about the population (Salganik and Heckathorn 2004). By focusing primarily on network structure, RDS-SN removes this second step. In both cases, RDS analysis is based on two pieces of information gathered during the sampling process (Heckathorn 2002; Salganik and Heckathorn 2004). First, each recruiter-recruit dyad is documented, providing behaviorally documented data on network ties and the basis for controlling for bias introduced by the tendency of individuals to form social ties in a non-random way. Second, respondents are asked how many other members of the target population they know and interact with. In a network-based sample the inclusion probability of an individual is proportional to his or her degree (Volz and Heckathorn 2008). Similarly, Salganik and Heckathorn (2004) show that, in the absence of differential recruitment, once a sample reaches equilibrium all ties within the target population have equal probability of being used for recruitment. Consequently the sample may be biased toward high degree individuals. Salganik and Heckathorn (2004) derive an average group degree estimator that is asymptotically unbiased with bias on the order of n−1, where n is the sample size (see also Cochran 1977).In addition to providing important network information, the degree estimator (described below) plays a key role in the RDS-HP estimator for proportional group size, (Salganik and Heckathorn 2004, p.218; see also Heckathorn 2002):
| (1) |
where is the proportion of recruitments from group X to group Y and is the estimated average degree of group X. In RDS analysis a “group” is defined as a set of individuals who share a common characteristic, such as gender or race. While groups may exhibit network structural characteristics such as high density or connectedness, group members may also avoid each other or form connections randomly with respect to membership (Wasserman and Faust 1994). Detailed discussions of estimation procedures employed by RDS-HP are presented elsewhere (Heckathorn 2002; 2007; Salganik and Heckathorn 2004; Volz and Heckathorn 2008; Wejnert 2009).
Measuring Network Structure with RDS
A typical RDS data set includes several recruitment chains, each originating from a single seed. Seeds are selected for diversity, status within the population, and convenience (Wejnert and Heckathorn 2008; Heckathorn and Magnani forthcoming) In the absence of differential recruitment, that is if all groups recruit with equal efficiency, the final sample composition is independent of initial recruits and provides a random sample of ties from the network (Salganik and Heckathorn 2004). Therefore, the unit of analysis for RDS-SN is one “recruitment”. Each recruitment is assumed to be a behaviorally documented tie between recruiter and recruit because a recruitment coupon must be physically transferred to the recruit. While recruitment of strangers is possible, respondents are encouraged to recruit friends and acquaintances. Furthermore, RDS protocol includes several means for promoting recruitment of alters with whom the respondent is already associated with. First, respondents are compensated for each successful recruitment they make. Second, each respondent is limited to a small number of recruitments, usually three. In combination, these factors make recruitment coupons both valuable and scarce, such that respondents are unlikely to waste coupons on strangers whom they cannot monitor or encourage to participate (Heckathorn 1997; Heckathorn and Magnani forthcoming). In most RDS studies, while the specific type of tie used for recruitment can vary within and across samples, respondents report being recruited by “friends” with whom they interact frequently. While beyond the scope of the paper, recruitment can be guided so that respondents recruit along specific ties defined by the researcher. Additionally, multiple ties can be collected using different types of coupons. For example an HIV study of injection-drug users (IDU) can provide different colored coupons for recruiting other injectors, those ego has shared syringes with, or romantic partners to provide more detailed data on these specific connections. Further research is needed to evaluate the statistical properties of such samples.
The directed nature of recruitment poses further complications for network analysis of RDS data. Specifically, because respondents don't know who they will recruit until after the interview, they can be asked backward-looking questions about the nature of their relationship with their recruiter but not their recruits. Consequently, tie information is only gathered from one node in each dyad. While many respondents have more than one recruit, information on each of these ties is provided by different individuals.
RDS has several advantages that make it especially efficient for social network analysis. First, it allows analysis of social network structure based on a sample of the network so that structural inferences can be made using survey data. Second, every respondent has at least one documented behavioral tie to another respondent in the data1. Including respondents’ alters in the data allows for analysis of network structure based on private characteristics unknown to a respondent's immediate ties, avoiding what Erickson (1979) calls masking. It also provides greater range of analysis because tie and node characteristics can be collected independently and combined during analysis. Finally, because respondents are only asked information about themselves or their recruiter, who has already provided informed consent through his or her own participation, many ethical human subjects concerns are avoided.
Tie Strength and Transitivity
In his work on social capital, Coleman (1990) writes that closure in a network provides increased potential for amplifying returns to the actor. While RDS data cannot be used to measure overall network closure, transitive closure for the recruiter-recruit dyad can be estimated. Recruits are asked about the nature of their relationship with their recruiter. These data are then used to analyze differences between in-group and out-group ties. Because respondents can only be recruited into the survey once, transitivity can not be measured directly; however, respondents are asked how many of their contacts are connected to their recruiter. The ratio of this measure to the respondent's degree is then used to provide a measure of transitive closure (TC), which can be compared across categories of ties.
| (2) |
where the number of actual triangles is estimated by the number of the respondent's daily contacts that are known to her recruiter and the number of possible triangles is measured by the total number of contacts the respondent reports. That is if all the respondent's contacts are also known to the recruiter, there is complete transitive closure.
Such reliance on self-reports for network analysis, especially ones that can not be cross-checked with both members of a dyad, is a limitation that impacts the reliability of certain analyses more than others. Specifically, the data are best suited for relative comparisons within the network and not general statements about the population. For example, conclusions from an analysis comparing the strength of same-race ties to cross-race ties will be more reliable than conclusions regarding overall tie strength within the network.
Average Group Degree
Salganik and Heckathorn (2004) derive an average group degree estimator that is the ratio of two Hansen-Hurwitz estimators, which are known to be unbiased (Brewer and Hanif 1983). The ratio of two unbiased estimators is asymptotically unbiased with bias on the order of n−1 , where n is the sample size (Cochran 1977; Salganik and Heckathorn 2004). Thus, the estimator provides an unbiased measure of group centrality.
| (3) |
where is the average degree of group X, nX is the sample size of nodes in group X, and di is the self reported personal degree of individual i (Salganik and Heckathorn 2004 pp. 218). While not immune to problems associated with self-report data, the RDS degree estimator is less susceptible to such problems than other network measures because it relies on the inverse of self-reported degrees. Thus, the estimator is minimally affected by large outliers in the degree distribution.
Homophily
As stated above, network-based samples, like RDS, are biased by the non-random nature of social network ties used to make recruitments. RDS-SN makes use of this bias to measure a common friendship tendency constraining social network structure: the tendency for individuals to associate with specific alters based on the characteristics of those alters. A special form of this tendency, termed homophily, concerns “the principle that contact between similar people occurs at a higher rate than among dissimilar people” and has been shown to be a powerful mechanism by which affiliations deviate from random mixing (McPherson et al. 2001, p.416).
Evidence for the homophily effect is extensive across a wide range of variables. Strong instances of homophily have been found according to race and ethnicity (e.g. Marsden 1987; Mollica et al. 2003), age (e.g. Feld 1982; Fischer 1982a), gender (e.g. Tuma and Hallinan 1979; Marsden 1987), educational aspiration (e.g. Tuma and Hallinan 1979; Kandel 1978), drug use (e.g. Heckathorn and Rosenstein 2002; Kandel 1978), musical tastes (Mark 1998), political identification, religion, and behavior (see McPherson et al. 2001 for an extensive review).
RDS homophily can be calculated by comparing a standardized measure of the difference between affiliation patterns observed among respondents and the affiliation patterns that would result from random mixing (Heckathorn 2002). Specifically, homophily is calculated from the estimated proportion of in-group ties and that which would be expected from random mixing, in which in-group ties would merely reflect the group's proportional size (Heckathorn 2002).
| (4) |
where is the transition probability or proportion of in-group recruitments made by group X, is the estimated proportion of the population contained in group X, and is the homophily of group X. The measure was first introduced by Coleman (1958) as what he termed an index of “inbreeding bias” and later independently derived by Fararo & Sunshine (1964) as part of their work on biased net theory. RDS homophily can be calculated for any partition of categorical variables and ranges from negative one to positive one. Positive homophily indicates a group with disproportionate in-group ties, suggestive of preference. Homophily near zero indicates a non-group, i.e. the variable in question is not of social importance to the network. Negative homophily, or heterophily, indicates disproportionately few in-group ties, suggestive of avoidance (Heckathorn 2002). The measure can be calculated without additional data, providing an advantage over other network analysis techniques. For example, in order to calculate racial and gender homophily using ego-centric network data, each participant would need to provide information on the racial and gender composition of her personal networks. RDS homophily can be calculated without such additional data.
The RDS homophily measure depends on the population proportion of each group, providing a better measure of departure from random mixing than earlier methods, such as Krackhardt and Stern's (1988) E-I index, which depend on the proportion of in-group ties compared to that of out-group ties. In studies where groups represent equal portions of the population these methods are not problematic; however, in populations where group sizes differ, random mixing will generate more ties to individuals in larger groups than smaller groups.
In RDS-SN, the homophily estimator reflects the strength of association to one's own group beyond random mixing. A generalization, termed affiliation, expresses the strength of association between differing groups, where a positive value for two groups indicates a greater proportion of cross-linking ties than random mixing would produce, and a negative value indicates fewer cross-linking ties (Heckathorn 2002). Hence, the affiliation estimator provides a measure of preference or avoidance for any cell in the matrix. It can measure, for example, not only whether Whites prefer or avoid other Whites (homophily or heterophily), but whether and to what extent they interact with Blacks, Asians, or Hispanics. RDS network measures differ from other indices, which identify groups by structural measures, such as density and transitivity (Wasserman and Faust 1994), by focusing on actor characteristics and identifying which characteristics significantly influence the network.
| (5) |
where is the affiliation preference of X for Y and is as defined above. In calculating homophily, the term is simply the transition probably from group X to itself observed in the data. In calculating the affiliation, RDS’ assumption of reciprocity (see below) between recruiter and recruit becomes significant for the term. Under the reciprocity assumption, if all groups recruit equally effectively, the number of recruitments from group X to group Y should equal that of those from group Y to group X. Heckathorn (2002) presents an adjustment for differential recruitment by data-smoothing the recruitment matrix such that the number of recruitments of group X is equal to the number of recruitments by group X and calculating the transition probability based on this new data-smoothed recruitment matrix. Note that because data-smoothing does not alter the diagonal entries of the transition matrix, it does not alter calculation of homophily.
RDS-SN Implementation
Implementation procedures for RDS in general, which are the same for all analysis applications, are described in detail elsewhere (Heckathorn 1997; Wejnert and Heckathorn 2008; Wejnert and Heckathorn in press). Here I discuss issues of relevance to network analysis, including sample size, missing data, and organization of data.
First, calculation of sample size for RDS-HP analysis is often complicated by unknown design effects associated with the method. Salganik (2006) recommends a sample size twice that of a simple random sample, consistent with a design effect of two. Wejnert (2009), finds design effects larger than two, suggesting a sample size three to four times larger than what would be needed with a simple random sample. These design effects, however, apply to estimates of population properties of nodes. While RDS samples of nodes are biased by the non-random nature of network ties, RDS produces a representative sample of ties from the network. Consequently, RDS-SN analyses that focus only on the network ties do not suffer from high design effect. Regardless, a sample size twice that of a simple random sample is recommended to allow analysis of nodal properties and be on the safe side in tie analyses until further research is conducted. Also, it is important to note that since the unit of analysis is a tie and each tie is made up of recruiter and recruit, the actual sample size of an RDS study excludes the initial seeds, who have no recruiter.
Second, missing data is especially problematic for RDS-SN analysis for the same reason: data from both recruiter and recruit are combined to form information about each tie. Thus, missing data for one respondent can result in a loss of multiple data points in analysis. For example, missing data for a respondent who makes three recruitments result in lost data for the tie connecting him to his recruiter and the three ties connecting him to his recruits. Consequently, all possible steps should be taken to avoid missing data. RDS-SN's sensitivity to missing data is another reason why doubling sample size is recommended. If they can not be avoided, there are several ways to treat missing data: 1) code the data as missing, excluding it from analysis, 2) code missing data as a separate group to test if data are missing for any systematic reasons, or 3) data imputation based on non-missing data. Further research is needed to confirm the best approach.
Finally, RDS-SN analysis does not require any elaborate formatting of network data beyond that necessary for loading into RDSAT (Volz et al. 2007)2. To conduct RDS-SN analysis the researcher needs to record the coupon numbers each respondent is given to recruit with and the coupon number she is recruited with. If coupon numbers are recorded accurately, there is no need to record each respondent's recruiter. Additionally, as with all RDS data, each respondent's degree must be recorded.
RDS Assumptions
RDS sampling and estimation relies on five assumptions (Heckathorn 2007):
Respondents maintain reciprocal relationships with individuals who they know to be members of the target population.
Respondents are all linked into a single component in the network.
Sampling is with replacement.
Respondents can accurately report their personal network size or equivalently, their degree.
Peer recruitment is a random selection of the recruiter's peers.
With the exception of assumption three, these assumptions are necessary for both RDS-HP and RDS-SN. However, in some cases the interpretation and relevance of an assumption differs across the two applications. A detailed discussion of these assumptions and how they relate to unbiased estimation of hidden populations (RDS-HP) is presented elsewhere (Wejnert and Heckathorn 2008). Here I provide a brief summary and discuss how the assumptions relate to RDS-SN.
The first two assumptions specify the population conditions required to successful application of RDS. First, in order for recruitment to occur, respondents must have access to other members of the population and be able to identify which of their peers qualify for recruitment. Additionally, RDS analyses assume reciprocal ties between recruiters and recruits (Heckathorn 2002, Heckathorn and Salganik 2004). For RDS-HP, the interpretation is if A recruits B, then there must be a non-zero probability that B could have recruited A. RDS-SN, however, requires a stricter interpretation because self-report data on recruitment ties are provided by only one node in each dyad. Consequently, reciprocal ties are interpreted as not only existing in both directions, but as being equivalent in both directions. Second, the population is assumed to form a single connected component such that any member of the target population is reachable from any other member through the network (Salganik and Heckathorn 2004, see also Heckathorn 2007). Consequently, RDS is best suited for populations structured around social interaction, a requirement that is easily met in research focusing on a single social network.
In RDS-HP, the third assumption, that sampling occurs with replacement3, is necessary for estimation. Sampling with replacement, however, is not directly assumed in RDS-SN. Furthermore, the measure of transitivity presented above explicitly assumes sampling without replacement. If sampling occurred with replacement, transitivity could be calculated directly.
The final assumptions are equally relevant to both RDS applications. First, respondents are assumed able to provide accurate information on their personal degree that is used in the calculation of average group degree and sampling weights. Fortunately, Wejnert (2009) suggests degree indicators currently employed in most RDS studies are among the most effective at yielding accurate population estimates. Finally, recruitment patterns are assumed to reflect personal network composition within the network. In other words, RDS assumes respondents recruit as though they were selecting randomly from their personal networks (Heckathorn 2002). This assumption is necessary for a representative sample of ties and calculation of sampling weights.
Lastly, while the interpretation of RDS assumptions differs based on application, it is important to note that in cases where the RDS population proportion estimate (equation 1) is used in affiliation and homophily calculations, both RDS-HP and RDS-SN interpretations of assumptions apply.
Empirical Example of Social Network Analysis with RDS
RDS provides a random sample of ties based on behavioral network data, i.e. recruitments (Salganik and Heckathorn 2004), that can be used to make social network inferences of tie characteristics by comparing characteristics of certain types of ties with others, node characteristics through estimates of average group degree, and structural network characteristics through homophily and affiliation analysis. I now demonstrate these techniques with an empirical example that tests five hypotheses regarding racial integration among undergraduates at a large, selective university.
Hypotheses
In their study of undergraduates at selective universities, Bowen and Bok (2000) argue that integration is “extremely high” at U.S. universities because “the large majority of all kinds [of students] ‘knew well’ two or more individuals in many different categories” (p. 231, emphasis original). Furthermore, less than one in ten white students knew no black students or did not answer the question. While suggesting that selective campuses are not entirely segregated, these findings show a high degree of exposure to diversity on campus, but do not directly speak to the level of interpersonal integration present within the social structure. Specifically, while most U.S. universities maintain a strong commitment to diversity within the student body, few studies ask whether racial diversity at the institutional level is necessarily reflected as racial integration at the interpersonal level. In this paper, five hypotheses consistent with the assumption that there is no gap between racial diversity at the institutional level and integration at the interpersonal level are tested using RDS-SN.
At the institutional level, diversity reflects the extent to which individuals of different types are present or absent in the population. At the interpersonal level, however, a failure of racial integration can manifest itself in several ways. First, for a network to be racially integrated, cross-race ties must exist in proportionately equal quantity to same-race ties. That is, patterns of association should resemble random mixing and no group(s) should favor interaction with itself or any other specific group(s). Second, cross-race ties should be of equal quality to same race-ties in terms of frequency of interaction, strength of relationship, and transitive closure. Finally, members of each group should have similar structural standing within the network. That is, no group(s) should occupy a more central position than any other group(s).
Quantity of Cross-Race Ties
First and foremost, a racially integrated network not only must include cross-race ties, but must not display an overall pattern of preference or avoidance of any group(s) by any group(s). That is, the overall pattern of ties should resemble random mixing within the population and racial homophily and affiliation should be trivial. This is especially important for ruling out the possibility of perceived integration due to tokens who physically appear to be of one race, but are culturally of another. For example, one could imagine a population of White students who all “know well” at least one Asian student. However, if they all know the same Asian student and that student is “White” in her interests, behaviors, and ideas, the benefit of this tie in terms of exposure to diversity is minimized.
Hypothesis One: Racial homophily and affiliation are not significantly different from random mixing.
Quality of Cross-Race Ties
I compare the quality of same-race and cross-race ties using three measures of tie strength: self-reported tie strength (close friend, friend, or acquaintance), frequency of interaction (how often ego, the recruit, interacts with alter, her recruiter), and transitive closure with the recruiter.
First, if the closeness of cross-race ties is less than that of same-race ties, then friendships across racial boundaries are more likely to be strained, difficult to maintain, and viewed differently from same-race ties.
Hypothesis Two: Average self-reported tie strength of same-race ties is not different from average self-reported tie strength for cross-race ties.
Unfortunately, self-reported data on friendship closeness can be problematic because the distinction between “friend” and “close friend” may vary across individuals and groups (Fischer 1982b). An alternate way of measuring tie strength is through the frequency of interaction between nodes in the dyad.
Hypothesis Three: Frequency of interaction among same-race ties is not different from frequency of interaction among cross-race ties.
In his work on social capital, Coleman (1990) writes that closure in a network provides increased potential for amplifying returns to the actor by strengthening social norms. Similarly, transitive ties have higher potential for returns to an actor than non-transitive ties; thus, if the population is racially integrated, same-race ties should not have higher transitive closure that cross-race ties.
Hypothesis Four: Transitive closure among same-race ties is not different from transitive closure among cross-race ties.
Group Status
Finally, in a racially integrated population, no race should occupy a higher structural standing than any other race. In segregated populations, minority groups are likely to make and maintain less ties on average than majority groups because there are fewer of them to interact and form connections with. One way to measure the structural standing of groups is to compare the average degree of individuals within each group. Other, more sophisticated methods would compare the number of very high degree individuals, or socio-metric stars, within each group or to compare degree distributions across groups (Wasserman and Faust 1994). However, such approaches require data that is independent of individual degree, which RDS does not provide (see above). Consequently, I restrict my analysis to the average group degree across race calculated using the RDS degree estimator.
Hypothesis Five: There is no difference in average network size across racial groups.
Data and Methods
A sample of 150 recruitments from a selective, residential university population with over 13,000 undergraduates was collected in 2004. Including nine seeds, the sample size was 159 students. Demographic information for the final sample is presented in Table 1. Due to low sample prevalence of under-represented minorities (URM), race is divided into three categories: White, Asian, and URM. The URM category includes two African American students, seven Hispanic/Latino students and 11 students describing themselves as “Other”. Analyses presented here focus on these three categories and network differences between them.
Table 1.
Demographic Characteristics of Network Data
| Seeds | |||
|---|---|---|---|
| n = 9 | n = 159 | Percent | |
| Gender | |||
| Male | 5 | 95 | 59.7 |
| Female | 4 | 64 | 40.3 |
| Race | |||
| White | 6 | 81 | 50.9 |
| Asian | 2 | 58 | 36.5 |
| URM | 1 | 20 | 12.6 |
| Year | |||
| Freshman | 0 | 13 | 8.2 |
| Sophomore | 4 | 51 | 32.1 |
| Junior | 2 | 40 | 25.2 |
| Senior | 3 | 51 | 32.1 |
| 5+ | 0 | 4 | 2.5 |
Overall, 55.3% (n=88) of the 159 respondents recruited peers for the study. Six of the 88 respondents who recruited were seeds. While only 88 respondents recruited, the average number of recruits for successful recruiters was 1.69, resulting in a sample of 150 ties. This is consistent with other RDS studies and the geometry of RDS recruitment networks. That is, if each recruiter averages two recruits, then only half of the respondents will have recruited (Heckathorn 2002).
The study was conducted using WebRDS, an online version of RDS with email-based recruitment coupons and an internet survey. Sampling began on a Friday morning and was completed in 72 hours. A detailed discussion of the data and WebRDS procedures is presented elsewhere (Wejnert and Heckathorn 2008).
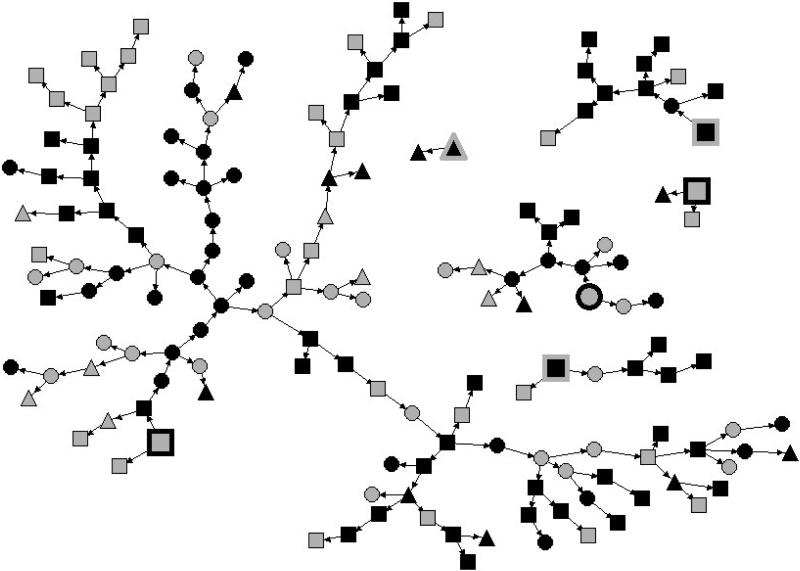
Figure 1 illustrates recruitment chains by all productive seeds from the sample. It includes a single long chain that makes up over 70% of the data and five smaller chains that make up the remaining 30%. Recruitment in RDS is often dominated by large recruitment chains initiated by respondents who can be termed “super seeds” (e.g. Heckathorn 1997; Heckathorn et al. 1999; Heckathorn et al. 2002; Ramirez-Valles et al. 2005). This does not reflect special characteristics of the individual, because it results from a positive feedback process in which the larger a recruitment chain grows, the greater is the number of respondents working to make it grow even larger, so a “rich-get-richer” dynamic is produced in which the larger chains grow ever more quickly than the smaller chains. Hence, any reasonably productive seed stands a good chance of becoming a “super seed”.
Figure 1.
RDS recruitment chains of all 6 productive seeds (enlarged and highlighted with opposite color borders). The nodes are color-coded for gender (male = black, female = gray) and shape-coded for race/ethnicity (White = square, Asian = circle, URM = triangle).
Wasserman and Faust (1994) define “degree” as the union of out-degree, the number of individuals ego knows, and in-degree, the number of individuals ego is known to. RDS solicits out-degree data from respondents, however, under the reciprocity assumption; in-degree equals out-degree. Consequently, RDS out-degree is referred to and treated as equivalent to “degree”. The data include two measures of individual degree: a “buddy list” measure, which solicits the number of “buddies” a student has on her instant messenger “buddylist” and a standard self-report measure that asks for the “number of undergraduates you know by name who know you by name with whom you have interacted with in the past 30 days”.
In earlier work with these data Wejnert and Heckathorn (2008) use the buddylist degree measure for RDS estimation. At the time of sampling, instant messenger programs (IM) were the primary means of communication among students on campus and many respondents reported contacting potential recruits using IM before sending them a recruitment email. Additionally, these programs store users’ buddylists and display the number of contacts, reducing recall bias in degree estimates. However, the buddylist measure has several limitations. First, not all students may use IM regularly or at all. Second, it is unclear how many respondents included IM contacts not attending the university. Finally, buddylists may include former contacts with whom the respondent no longer interacts.
Furthermore, this study included additional network questions regarding the standard measure, but not the buddylist measure. Specifically, respondents were asked “Of those undergraduates you know by name who know you by name with whom you have interacted with in the past 30 days, how many are: White? Asian? African-American, Hispanic/Latino? Other race?” Similarly, to assess transitivity, respondents were asked “How many of your daily contacts do you think your recruiter knows?” While “daily contacts” are clearly distinct from those “with whom you have interacted with in the past 30 days,” this transitivity measure is more consistent with the standard degree measure than buddylist degree. Consequently, this paper uses the standard self-report degree measure to promote consistency and comparability within the analysis.
Due to the non-hidden nature of this population, institutional data is available for several variables of interest, including race (Cornell 2004). In these cases institutional population proportions are used in calculations of homophily and affiliation. Consequently, calculations of homophily and affiliation (equations 4 and 5) presented here are based on true institutional values for PX and do not rely on the RDS-HP population proportion estimate. A comparison of RDS population estimates with institutional data is presented elsewhere (Wejnert and Heckathorn 2008; Wejnert 2009).
Following the assumption that RDS provides a random sample of ties from the network, hypothesis one is tested by calculating affiliation and homophily from the data and testing it against the expectation of random mixing. Hypotheses two through four are tested using basic hypothesis-testing methods. Finally, results for hypothesis five are calculated using the RDS degree estimator described above.
Results
Before considering results it is necessary to show that the sample reached equilibrium. This is done by simulating the number of waves required to reach equilibrium for each variable and then comparing it with the actual number of waves reached in the sample (See Heckathorn et al. 2002 Appendix for equilibrium and waves required calculations). The standard RDS interpretation is that if equilibrium is reached within a single chain, then equilibrium is reached for the entire sample because all individuals have a non-zero probability of selection (Heckathorn 2002). For this analysis, the highest simulated number of necessary waves is six. The longest chain in the sample has more than 18 waves, satisfying the equilibrium requirement. For a detailed discussion of equilibrium and out-of-equilibrium data effect on RDS estimation with this sample, see Wejnert (2009).
Raw and data-smoothed matrices for recruitment and transition probabilities for race are presented in Table 2. Table rows represent recruiters and columns represent recruits. For example, 13 of the 75 recruitments made by Whites were of Asians, corresponding to a transition probability from Whites to Asians of 0.173 in the transition matrix. When the data are smoothed, there are 12.7 White to Asian recruitments, corresponding to a smoothed transition probability of 0.163. The similarities between raw and data-smoothed versions of each matrix suggest that differential recruitment, beyond that expected from stochastic variation in such a small sample, did not occur and recruitments likely represent a random sample of ties from the network. Due to the small number of recruitments involving URMs, this analysis pools all data and compares same-race and cross-race ties across all categories, the data includes 97 same-race ties and 53 cross-race ties. Where possible, analysis is performed in multiple ways to show consistency across minor tweaking in the analytical procedure.
Table 2.
Recruitment and Transition Matrices by Race
| Recruitment Matrix | Data-Smoothed Recruitment Matrix | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| White |
Asian |
URM |
Total |
White |
Asian |
URM |
Total |
||
| White | 55 | 13 | 7 | 75 | White | 57.24 | 12.70 | 8.12 | 78.06 |
| Asian | 14 | 39 | 9 | 62 | Asian | 12.70 | 33.06 | 6.80 | 52.55 |
| URM | 6 |
4 |
3 |
13 |
URM | 8.12 |
6.80 |
4.47 |
19.39 |
| Total | 75 | 56 | 19 | 150 | Total | 78.06 | 52.55 | 19.39 | 150 |
| Raw Transition Matrix | Data-Smoothed Transition Matrix | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| White |
Asian |
URM |
Total |
White |
Asian |
URM |
Total |
||
| White | 0.733 | 0.173 | 0.093 | 1 | White | 0.733 | 0.163 | 0.104 | 1 |
| Asian | 0.226 | 0.629 | 0.145 | 1 | Asian | 0.242 | 0.629 | 0.129 | 1 |
| URM | 0.462 |
0.308 |
0.231 |
1 |
URM | 0.419 |
0.351 |
0.231 |
1 |
Quantity of Cross-Race Ties
Table 3 shows the institutional population proportions (Cornell 2004)4 and affiliation preference for race based on the data-smoothed5 recruitment and transition matrices shown in Table 2. Results show that affiliation is governed by in-group selection and not random racial mixing. White students display a significant preference for other Whites and small but non-significant avoidance of other groups. Asian students display significantly high preference for other Asians and avoidance of Whites, and associate randomly with URM. Finally, while URM affiliation patterns are non-significant, likely due to low sample size, URM students follow a pattern similar to Asian students, avoiding Whites and preferring Asians and other URM.
Table 3.
Recruitment-Based Racial Affiliation Preference
| Racial Population Proportions | |||
|---|---|---|---|
| White | Asian | URM | |
| 0.594 | 0.164 | 0.111 | |
| Racial Affiliation Based on Data-Smoothed Recruitment | |||
|---|---|---|---|
| White | Asian | URM | |
| White | 0.342* | −0.006 | −0.063 |
| Asian | −0.593*** | 0.556*** | 0.020 |
| URM |
−0.295 |
0.224 |
0.135 |
p < 0.05
p < 0.001
It is important to note that affiliation patterns are not symmetric. For example, Asian students avoid Whites, while Whites appear to interact with Asian students randomly. This result is due to large differences in racial proportions observed in the population that make it easier to avoid some groups and harder to avoid others. For example, because Asian students make up only 16.4% of the population, significantly less than 16.4% of all White students’ ties must be to Asian students in order for Whites to be said to be “avoiding” interaction with Asians. Conversely, the window for Asians to avoid Whites is much wider because Whites make up the majority of the population. For the same reasons, it is much more difficult for Whites to differently associate with other Whites than it is for Asians to prefer Asians.
The analysis presented in Table 3 operates under the assumption that recruitment provides a random selection of students’ network ties. However, it is possible that recruitment occurs through a network that is related, but different from the overall social network in the population. For example, the online nature of the study may have excluded individuals who rarely check their email6. To test this theory, respondents were asked how many of their recent contacts are White, Asian, or URM (see Appendix for question wording). The ratio of the sum of these values to the sum of the overall number of respondents’ resent contacts in each racial category is then used as a self-report measure of racial transition probabilities, which are then used to calculate racial affiliation. If recruitment occurred via a different network, racial affiliation calculated in this way will differ substantially from that presented in Table 3. Additionally, because such an analysis is possible with ego-centric approaches, it serves as a comparison of the two methods. In the case of racial affiliation, where individual categories are easily observable, affiliation patterns calculated in each way should converge. However, for variables that are not easily observable, such as opinions or stigmatized behaviors, the ego-centric approach is not feasible. Furthermore, even for observable variables, the ego-centric approach requires much more data than the RDS-SN approach.
Table 4 shows racial affiliation preference based on these self-report transition probabilities. Statistically, the results are equivalent to those of Table 3. However, some important, though non-significant, differences exist. First, affiliation of Whites to Asians and URMs is more negative, more clearly compensating for in-group preference. Next, Asian affiliation to URMs is more negative. Finally, URMs display a greater preference for other URM than other groups, with which they affiliate randomly. It is difficult to say whether these differences are due small sample size or a bias in recruitment, however, the overall consistency of affiliation direction (positive or negative) and statistical significance suggests that both measures provide reliable evidence against hypothesis one.
Table 4.
Self-Report-Based Racial Affiliation Preference
| Self-Reported Racial Transition Probability | |||||
|---|---|---|---|---|---|
|
|
White |
Asian |
URM |
Overall |
|
| White (n = 80) | Mean | 54.64 | 10.25 | 6.84 | 71.91 |
| Sum | 4371 | 820 | 547 | 5753 | |
| Transition Probability |
0.760 | 0.143 | 0.095 | 1.000 | |
| Asian (n = 58) | Mean | 25.38 | 35.74 | 5.43 | 66.53 |
| Sum | 1472 | 2073 | 315 | 3859 | |
| Transition Probability |
0.381 | 0.537 | 0.082 | 1.000 | |
| URM (n=20) | Mean | 63.20 | 23.05 | 27.10 | 113.25 |
| Sum | 1264 | 461 | 542 | 2265 | |
| Transition Probability |
0.558 |
0.204 |
0.239 |
1.000 |
|
| Racial Affiliation Based on Self-Report Network Composition | ||||
|---|---|---|---|---|
|
|
White |
Asian |
URM |
|
| White | 0.408* | −0.131 | −0.143 | |
| Asian | −0.358** | 0.446*** | −0.265 | |
| URM |
−0.061 |
0.047 |
0.144 |
|
p < 0.05
p < 0.01
p < 0.001
Quality of Cross-Race Ties
Table 5 shows frequency tables for overall self-reported strength of respondents’ relationship with recruiters and their frequency of interaction. Consistent with the assumption that a reciprocal relationship between recruiter and recruit exists, the data suggest that recruitment occurred along strong ties; 97% of recruits referred to their recruiter as at least a “friend” and over 90% reported interacting with their recruiter at least once a week. For the purposes of this paper, tie strength and frequency of interaction are dichotomized so that the results compare ties that are considered “close friends” versus others and interactions which occur “daily” versus others. Table 5 also shows that, on average, respondents reported approximately 25% of their network contacts know their recruiter.
Table 5.
Descriptive Statistics for Tie Strength Variables
| Relationship with Recruiter | |||
|---|---|---|---|
| Frequency | Percent | Cumulative Percent | |
| Close Friend | 70 | 0.47 | 0.47 |
| Friend | 75 | 0.50 | 0.97 |
| Acquaintance |
5 |
0.03 |
1.00 |
| Total | 150 | 1.00 | |
| Frequency of Interaction with Recruiter | |||
|---|---|---|---|
| Frequency | Percent | Cumulative Percent | |
| Daily | 83 | 0.55 | 0.55 |
| Several times a week | 34 | 0.23 | 0.78 |
| Once a week | 18 | 0.12 | 0.90 |
| Once every other week | 9 | 0.06 | 0.96 |
| Once a month |
6 |
0.04 |
1.00 |
| Total | 150 | 1.00 | |
| Transitive Closure | |||
|---|---|---|---|
| N | Mean | Variance | |
| 148 | 0.245 | 0.057 | |
Table 6 shows a comparison of dichotomized tie strength and interaction frequency and mean transitive closure for same-race and cross-race ties used to test hypotheses two, three, and four. There is little difference between same-race ties and cross-race ties and no statistically significant difference in means for same-race and cross-race ties for self-reported tie strength, interaction frequency, or transitive closure. Thus, while the analysis does not directly support hypotheses two, three, or four, there is an overwhelming lack of evidence against them. Consequently, the analysis shows that when close cross-race ties are formed, there is little evidence to suggest that they are any different in terms of tie strength, interaction frequency, or transitive closure than same-race ties.
Table 6.
Comparison of Same-Race and Cross-Race Tie Strength Variables
| Mean Tie Strength by Type of Tie | ||||
|---|---|---|---|---|
| N | Mean | Std. Error Mean | ||
| Tie Strength | Same-Race Tie | 97 | 0.505 | 0.051 |
| Cross-Race Tie | 53 | 0.396 | 0.068 | |
| Interaction Frequency | Same-Race Tie | 97 | 0.557 | 0.051 |
| Cross-Race Tie | 53 | 0.547 | 0.069 | |
| Transitive Closure | Same-Race Tie | 95 | 0.257 | 0.024 |
| Cross-Race Tie | 53 | 0.225 | 0.033 | |
| Comparison of Mean Difference | ||||
|---|---|---|---|---|
| Mean Difference | Std. Error | p-value* | df | |
| Tie Strength | 0.109 | 0.085 | 0.202 | 108.7 |
| Interaction Frequency | 0.010 | 0.085 | 0.911 | 148 |
| Transitive Closure | 0.032 | 0.041 | 0.432 | 146 |
Independent-Samples t-test
Group Status
Table 7 shows arithmetic and RDS mean group degree by race. Hypothesis five states that if the population was not integrated, we would expect minority groups to be marginalized and therefore have smaller average degree than larger groups. Based on the results, it is clear that this is not the case and that if there are any differences in average group degree, they favor the minority groups. Thus, there is little evidence against hypothesis five or racial integration at the group level.
Table 7.
Average Group Degree
| RDS Average Degree* | Arithmetic Mean Degree | Median | N | Minimum | Maximum | |
|---|---|---|---|---|---|---|
| White | 39.09 | 71.89 | 50 | 80 | 4 | 300 |
| Asian | 40.09 | 66.50 | 50 | 58 | 10 | 400 |
| URM |
52.34 |
113.95 |
80 |
20 |
20 |
450 |
| Overall | 40.79 | 75.22 | 50 | 158 | 4 | 450 |
Calculated using RDSAT 6.01
Conclusion
The results of this study suggest that racial diversity at the institutional level is reflected as diversity at the interpersonal level in terms of the quality of interracial interaction, but not quantity (at this university). Specifically, this study finds that 1) overall patterns of racial interaction are governed by in-group preference that deviates significantly from random mixing, 2) when they exist, cross-race ties are not significantly different from same-race ties in terms of tie strength, frequency of interaction, or transitive closure, 3) there is little evidence to suggest that, on average, members of minority groups pay a social cost in terms of the number of ties they can maintain. Therefore, significant, but permeable, racial boundaries to tie formation exist, but, once a cross-race tie is formed, it is treated as any other tie.
While the results are not generalizable beyond the study university, they have promising policy implications for colleges dedicated to student diversity. While a fully racially integrated society is the ultimate goal of race-relations, historical racial tensions, and cultural differences provide strong barriers to racial integration (Quillian and Campbell 2003). Research on friendship formation and the homophily effect suggest that while these differences remain, friendship selection will favor the in-group for a variety of social and structural reasons (Newcomb 1961; Mouw and Entwisle 2006). Consequently, in a network exhibiting random racial mixing, the racial differences that benefit the population by bringing new ideas and experiences may not exist. The finding that cross-race ties are not qualitatively different from same-race ties suggests that students are experiencing a primary benefit of diversity through their connections with different types of people despite differentially associating with similar individuals.
More generally, the above serve as an empirical example of RDS-SN. By focusing on race, the RDS affiliation analysis is validated through comparison of affiliation analysis based on self-report network composition. Essentially, it is a comparison of RDS and self-report (i.e. ego-centric) approaches to affiliation analysis. As expected for an easily identifiable characteristic that does not suffer from masking (see above), the results are convergent. In addition to being applicable to other characteristics than race, which may not be easily identifiable to respondents, the RDS method is much less data intensive than its self-report counterpart. In addition to standard RDS data7, the RDS affiliation analysis only requires data on respondents’ race. Similar analysis based on ego-centric approaches, however, requires not only respondents’ racial data, but also their individual network composition by race. The second set of analyses (Table 6) uses network ties as the unit of analysis and allows for comparison of within and across group ties based on a representative sample of network ties that is not possible with ego-centric data. The final analysis, a comparison of average group degree based on self-report degrees is not unique to RDS-SN analysis. A similar study on such a large population could not feasibly be conducted using saturated survey data. A saturated approach using digital network data, such as an email network, would provide information regarding network structure, but lack socially relevant variables, such as race. Consequently RDS-SN provides a more efficient method of describing the social network structure of large real world populations than ego-centric data and more extensive breadth of analysis than saturated methods with respect to socially relevant factors such as race.
Limitations of RDS-SN and Directions for Future Research
The primary limitations of RDS-SN, and RDS in general, are the complex nature of RDS data and its youth as a statistical method. While the presence of network ties connecting respondents provides valuable network data, it also violates a key assumption of many statistical analysis techniques that observations are independent of each other. Thus, new analytical methods specific to RDS data are required for most analyses. While much progress has been made in the decade since RDS’ introduction in 1997 (Heckathorn 1997), much work remains to be done and researchers looking to apply their favorite statistical analyses to RDS data will likely find RDS analysis underdeveloped. For example, current RDS-SN methods can provide information on affiliation patterns and relative differences between groups, but cannot provide general network information such as density or average distance between nodes. What is presented here is the current state of the art in RDS social network analysis, further research and development of statistical analysis for RDS data is required.
In addition, RDS-SN has several other limitations. First, while RDS-SN's reliance on self-report data is lower than in many other methods of sampling and analyzing real world networks, RDS–SN does rely on self-report data for some network properties such as individual degree, tie strength, and transitive closure. A significant amount of research on self-report network characteristics suggests that “people simply do not know, with any degree of accuracy, with whom they communicate” (Killworth and Bernard 1976, p. 283). Recent research on network estimation techniques in which respondents are asked to estimate their number of alters in a network, has found significant forgetting of friends (Bell, Belli-McQueen, and Haider 2007). However, the work suggests differences in recall error are primarily associated with network and not demographic or other key sociological attributes of respondents (Brewer 2000). Researchers have found moderate positive correlation between degree and number of forgotten alters (Brewer and Webster 1999) moderate negative correlation between degree and tie strength (Brewer 2000). Fortunately, if recall error in self-report network data is independent of most key respondent attributes and demographics, inferences on relative network differences, such as those presented in the example above, remain valid. Furthermore, improved recall of strong ties, compared to weak ties, benefits RDS-SN because the method appears to favor recruitment along strong ties (see below).
In order to gage sensitivity of RDS to varying measures of degree, Wejnert (2009, p.108)) compared RDS-HP estimates based on multiple degree measures to known population proportions and concluded that “while the standard [self-report] degree measure, which is commonly used in RDS studies, does not produce the best estimates..., it does quite well.” This work suggests RDS’ reliance on self-report data does not negate the method's ability to provide unbiased stimulation. While reliance on self-report data is not unique to RDS-SN, further research is needed to explore the affect of informant inaccuracy in general and on RDS-SN in particular. Specifically how sensitive are RDS-SN inferences to errors in self-report data and whether alternative methods of generating self-report network data provide improved results?
Second, the analysis presented here relies heavily on the assumption that RDS provides a random sample of ties from the social network which breaks down if recruits are not recruited randomly from each recruiter's entire pool of social ties. Wejnert and Heckathorn (2008) present a method of testing this assumption for easily observable variables. However, Wejnert (2009) points out the test's results, which rely on self-report data, may be more indicative of the quality of self-reports rather than the representativeness of recruitment. Non-random recruitment can affect network analysis differently depending on whether non-random recruitment occurs based on respondent or tie characteristics. For example, if recruitment favors white respondents, then the inferences regarding racial affiliation and homophily may be biased. However, if recruitment favors strong ties, then inferences regarding global network tie characteristics can be affected. However, if a similar bias exists across all groups, then comparisons of one group relative to another remain valid.
While more research is needed, some evidence exists suggesting that RDS recruitment favors strong ties beyond any other variable. Wejnert (2009) finds a disproportionately large number of respondents being recruited by those with whom they discuss important matters. Furthermore, the incentive structure employed by RDS to exclude recruitment of strangers by making recruitment rights both valuable and scarce likely favors stronger ties over weaker ties. Finally, if respondents simply recruit the first eligible peer they interact with, recruitment will also favor strong ties due to frequency of interaction. If it is confirmed that RDS recruitment predominantly favors strong ties, then network inferences would apply primarily to networks of strong ties.
Third, the nature of the recruitment process and reciprocity model requires recruiter and recruit to be status equals within the population (Heckathorn 1997). Thus, the method can not be used to study ties across a status gradient, such as employer-employee relations. Furthermore, RDS-SN assumes recruitment ties are equivalent in each direction and that accurate self-report information about each tie can be accurately gathered from one node in each dyad. While falling short of the network analysis standard of verifying information with responses from both dyad members, the presence of a physical recruitment by the recruiter guarantees the presence of a multi-directional tie between recruiter and recruit. Further research is needed to develop methods of gathering network information from recruiters and test the accuracy of recruit self-reports regarding tie properties between recruiter and recruit.
Fourth, RDS is an organic sampling method, making it difficult to know which respondent characteristics and, more importantly, which types of tie will be over or under sampled. This study suggests recruitment favors strong ties, making RDS-SN better suited for strong tie networks. A simple solution could be to restrict recruitment to specific types of ties through eligibility criteria, such as recruiting only those with whom you discuss important matters. However, it is unclear what effect restricting recruitment would have on the data. Specifically, any restrictions on recruitment risk recruitment chains dieing out prematurely. Furthermore, RDS-SN assumptions would apply to the restricted network. For example, if recruitment is limited to strong ties only, then RDS-SN requires the network to be fully connected through strong ties only. Further research is needed to test the effects and severity of limiting recruitment in any way on network analysis.
Finally, currently available RDS-SN analyses lack the ability to address causality. For example, homophily can occur in two ways: First, similar people are more likely to interact by virtue of having similar interests and participating in similar events. Alternately, individuals who spend a large portion of time together are likely to become more similar by adopting interests and characteristics from each other and developing new ones together. Consequently, while RDS-SN can measure homophily, it is not capable of discerning its causes or consequences. However, multiple RDS samples collected over time can be used to gain a longitudinal perspective on changes in the network and the factors related to it.
Discussion
Despite these limitations, RDS offers several major advantages for studying social networks over currently employed methods. First, RDS provides a way of sampling and analyzing network structure of real world networks within a social context. Current methods for studying network structure rely on either self-report descriptions of alters, which are limited to respondents’ knowledge of their alters’ traits and their recall of these traits, or database data, such as email networks, which often lack socially relevant information on node characteristics, such as gender and race. Second, RDS-SN provides a sample of nodes connected by behaviorally documented ties. By sampling both members of the dyad, the methodology allows for greater range of analyses from a single dataset.
While the substantive focus of this paper is to present RDS-SN as an approach distinct from RDS-HP and as a compliment to other methods of social network analysis, the analytical procedures presented here can also be used in conjunction with these approaches. First, RDS-SN can be combined with ego-centric data by starting with an ego-centric sample of nodes and allowing the recruitment of a small number of waves from each node. The initial ego-centric sample will allow node based analyses and the recruitments will allow tie based analysis. Such an approach is problematic for RDS-HP because a representative sample of seeds can not be collected and thus the sample needs multiple waves to become independent of its starting point and reach equilibrium. However, if the initial sample is representative, then it is initiated at or very close to equilibrium, making RDS-SN analysis techniques applicable to the data even if only a small number of waves are recruited in each chain (Wejnert and Heckathorn, in press). Second, RDS-SN can be used in conjunction with online networking sites, such as MySpace or Facebook, to study social networks and the propagation of information through them. While the existence of such sites and their direct data on social connections has proven invaluable to network researchers, the data suffer from a high degree of false positives. That is, many individuals are listed as “friends” of others who they may not associate with currently, directly, or at all. By applying RDS-SN recruitment to such networks, researchers guarantee that only active ties are being sampled. RDS adjustments can then be applied to data and comparisons to complete network data can be made to gain a richer understanding of the network structure and how information, in the form of recruitment, propagates through it. Finally, as discussed above, a network component can be added to any RDS-HP project with minimal additions to survey instrumentation to enrich the analytical capacity of studies of hidden populations.
Conclusion
This paper presents RDS-SN as a viable means of sampling and analyzing real world social networks. While the analytical techniques described here are substantial, the full potential of RDS-SN is far from realization. The primary goal of this article is to introduce RDS-SN to the network community and to stimulate further research toward the goal of expanding the analytical capacity of RDS-SN and, more generally, the statistical toolset available to network researchers.
Appendix: Survey Questions for Network Analysis
Degree Measures
How many undergraduates at [this university] do you know personally (i.e., you know their name and they know you, and you have interacted with them in some way in the last 30 days)? ______
How many of these ____ students that you know are: (please answer “0” if you do not know anyone in a given group)
White _______
African American _______
Hispanic or Latino _______
Asian ______
Native American ______
Other race ______
Tie Strength and Transitivity
Which of the following best describes your relationship with your recruiter?
-
g.
Close friend
-
h.
Friend
-
i.
Acquaintance
-
j.
Stranger
How often do you usually interact with your recruiter in person, by phone, by e-mail, by instant messaging, or by other means?
-
k.
Daily
-
l.
Several times a week
-
m.
Once a week
-
n.
Once every other week
-
o.
Once a month
-
p.
Once every other month
-
q.
Less than every two months
Think of those students you have contact with on a daily or near daily basis, how many of these people does your recruiter know? _______
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
This research was made possible by grants from the Centers for Disease Control and Prevention, the National Institutes of Health, the National Institute on Drug Abuse, and the National Endowment for the Arts. I thank Douglas D. Heckathorn, Katherine E. Wejnert, Jason Perelshteyn, Michael Prentice, Michael W. Spiller III, and Barbara Wejnert for helpful comments and advice.
Non-recruiting seeds are not tied to any other respondents and are generally excluded from the analysis.
The RDS Analysis Tool (RDSAT) and documentation are available for download at: RespondentDrivenSampling.org.
Because respondents are only allowed to participate once, RDS always occurs without replacement. The assumption is considered met if the sampling fraction remains small enough for such a model to be appropriate (Salganik and Heckathorn 2004; Heckathorn 2007).
Institutional population proportions for race do not sum to 100% because they do not include two categories, “foreign national” and “US Citizen, Unknown”, which make up approximately 13% of the institutional data (Cornell 2004).
Results are unchanged if raw data is used in place of data-smoothed data.
For a complete discussion of potential biases in this data, see Wejnert and Heckathorn (2008).
All RDS analysis requires documenting who recruited whom in the form of a recruitment matrix and a measure of individual degree.
References
- Abdul-Quader AS, Heckathorn DD, McKnight C, Bramson H, Nemeth C, Sabin K, Gallagher K, Des Jarlais DC. Effectiveness of Respondent Driven Sampling for Recruiting Drug Users in New York City: Findings from a Pilot Study. Journal of Urban Health. 2006;83:459–476. doi: 10.1007/s11524-006-9052-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bearman PS, Moody J, Stovel K. Chains of Affection: The Structure of Adolescent Romantic and Sexual Networks. American Journal of Sociology. 2004;110:44–91. [Google Scholar]
- Bell DC, Belli-McQueen B, Haider A. Partner Naming and Forgetting: Recall of Network Members. Social Networks. 2007;29:279–299. doi: 10.1016/j.socnet.2006.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brewer DD. Forgetting in the Recall-based Elicitation of Personal and Social Networks. Social Networks. 2000;22:29–43. [Google Scholar]
- Brewer DD, Webster CM. Forgetting of Friends and its Effects on Measuring Friendship Networks. Social Networks. 1999;21:361–373. [Google Scholar]
- Brewer KRW, Hanif M. Sampling with Unequal Probability. Springer-Verlag; New York, NY: 1983. [Google Scholar]
- Bowen WG, Bok D. The Shape of the River. Princeton University Press; Princeton, NJ: 2000. [Google Scholar]
- Burt RS. Network Items and the General Social Survey. Social Networks. 1984;6:293–339. [Google Scholar]
- Centola D, Macy M. Complex Contagion and the Weakness of Long Ties. American Journal of Sociology. 2007;113:702–734. [Google Scholar]
- Cochran WG. Sampling Techniques. 3d ed. Wiley; New York, NY: 1977. [Google Scholar]
- Coleman JS. Relational Analysis: The Study of Social Organization with Survey Methods. Human Organization. 1958;17:28–36. [Google Scholar]
- Coleman JS. Foundations of Social Theory. Harvard University Press; Cambridge, MA: 1990. [Google Scholar]
- Cornell University . Enrollment at a Glance. Cornell University, Division of Planning and Budget; Ithaca, NY: 2004. [May 5, 2004]. Available at: http://dpb.cornell.edu/F_Undergraduate_Enrollment.htm. [Google Scholar]
- Cornwell EY, Waite LJ. Social Disconnectedness, Perceived Isolation, and Health among Older Adults. Journal of Health and Social Behavior. 2009;50:31–48. doi: 10.1177/002214650905000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erickson BH. Some Problems of Inference from Chain Data. Sociological Methodology. 1979;10:276–302. [Google Scholar]
- Fararo TJ, Sunshine MH. A Study of a Biased Friendship Net. Syracuse University Youth Development Center; Syracuse, NY: 1964. [Google Scholar]
- Feld SL. Social structural determinants of similarity among associates. American Sociological Review. 1982;47:797–801. [Google Scholar]
- Fischer CS. To Dwell Among Others. University of Chicago Press; Chicago, IL: 1982a. [Google Scholar]
- Fischer CS. What Do We Mean by ‘Friend’? An Inductive Study. Social Networks. 1982b;3:287–306. [Google Scholar]
- Heckathorn DD. Respondent-Driven Sampling: A New Approach to the Study of Hidden Populations. Social Problems. 1997;44:174–199. [Google Scholar]
- Heckathorn DD. Respondent-Driven Sampling II: Deriving Valid Population Estimates from Chain Referral Samples of Hidden Populations. Social Problems. 2002;49:11–34. [Google Scholar]
- Heckathorn DD. Extensions of Respondent-Driven Sampling: Analyzing Continuous Variables and Controlling for Differential Degree Sociological Methodology. 2007;37:151–208. [Google Scholar]
- Heckathorn DD, Jeffri J. Finding the Beat: Using Respondent-Driven Sampling to Study Jazz Musicians. Poetics. 2001;28:307–329. [Google Scholar]
- Heckathorn DD, Magnani R. Snowball and Respondent-Driven Sampling. Behavioral Surveillance Surveys: Guidelines for Repeated Behavioral Surveys in Populations at Risk for HIV. Forthcoming.
- Heckathorn DD, Rosenstein JE. Group Solidarity as the Product of Collective Action: Creation of Solidarity in a Population of Injection Drug Users. Advances in Group Processes. 2002;19:37–66. [Google Scholar]
- Heckathorn DD, Broadhead RS, Anthony DL, Weakliem DL. AIDS and Social Networks: Prevention through Network Mobilization. Sociological Focus. 1999;32:159–79. [Google Scholar]
- Heckathorn DD, Semaan S, Broadhead RS, Hughes JJ. Extensions of Respondent-Driven Sampling: A New Approach to the Study of Injection Drug Users Aged 18-25. AIDS and Behavior. 2002;6:55–67. [Google Scholar]
- Kadushin C. Who benefits from network analysis: ethics of social network research. Social Networks. 2005;27:139–153. [Google Scholar]
- Kandel DB. Homophily, selection, and socialization in adolescent friendships. American Journal of Sociology. 1978;84:427–436. [Google Scholar]
- Killworth PD, Bernard HR. Informant Accuracy in Social Network Data. Human Organization. 1976;35:269–286. [Google Scholar]
- Kissinger P, Liddon N, Longfellow L, Curtin E, Schmidt N, Salinas O, Cleto J, Heckathorn DD, Parrado EA. HIV/STI risk among Latino Migrant Workers in New Orleans Post-Hurricane Katrina.. Paper presented at the Annual Meeting of the National STD Prevention Conference; Chicago, IL. 2008. [Google Scholar]
- Klovdahl AS. Social network research and human subjects protection: Towards more effect infectious disease control. Social Networks. 2005;27:119–137. [Google Scholar]
- Krackhardt D, Stern R. Informal Networks and Organizational Crises: An Experimental Simulation. Social Psychology Quarterly. 1988;51:123–140. [Google Scholar]
- Laumann EO. Friends of urban men: and assessment of accuracy in reporting their socioeconomic attributes, mutual choice, and attitude agreement. Sociometry. 1969;32:54–69. [Google Scholar]
- Laumann EO, Youm YM. Racial/Ethnic Group Differences in the Prevalence of Sexually Transmitted Diseases in the United States: A Network Explanation. Sexually Transmitted Diseases. 1999;26:250–261. doi: 10.1097/00007435-199905000-00003. [DOI] [PubMed] [Google Scholar]
- Malekinejad M, Johnston LG, Kendall C, Kerr LGFS, Rifkin M, Rutherford GW. Using Respondent-Driven Sampling Methodology for HIV Biological and Behavioral Surveillance in International Settings: a Systematic Review. AIDS and Behavior. 2008;12:105–130. doi: 10.1007/s10461-008-9421-1. [DOI] [PubMed] [Google Scholar]
- Mark N. Beyond individual Differences: social differentiation from first principles. American Sociological Review. 1998;63:309–330. [Google Scholar]
- Marks G, Miller N. Ten Years of Research on the False-Consensus Effect: An Empirical and Theoretical Review. Psychological Bulletin. 1987;102:72–90. [Google Scholar]
- Marsden PV. Core Discussion Networks of Americans. American Sociological Review. 1987;52:122–131. [Google Scholar]
- Marsden PV. Network Data and Measurement. Annual Review of Sociology. 1990;16:435–463. [Google Scholar]
- McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: Homophily in Social networks. Annual Review of Sociology. 2001;27:415–444. [Google Scholar]
- Mollica K, Gray B, Trevino L. Racial Homophily and Its Persistence in Newcomers’ Social Networks. Organization Science. 2003;14:123–136. [Google Scholar]
- Mouw T, Entwisle B. Residential Segregation and Interracial Friendship in Schools. American Journal of Sociology. 2006;112:394–441. [Google Scholar]
- Newcomb TM. The Acquaintance Process. Holt, Rinehart & Winston; New York, NY: 1961. [Google Scholar]
- Quillian L, Campbell ME. Beyond Black and White: The Present and Future of Multiracial Friendship Segregation. American Sociological Review. 2003;68:540–566. [Google Scholar]
- Ramirez-Valles J, Heckathorn DD, Vázquez R, Diaz RM, Campbell RT. From Networks to Populations: The Development and Application of Respondent-Driven Sampling among IDUs and Latino Gay Men. AIDS and Behavior. 2005;9:387–402. doi: 10.1007/s10461-005-9012-3. [DOI] [PubMed] [Google Scholar]
- Ratcliff KS, Bogdan J. Unemployed Women: When “Social Support” is Not Supportive. Social Problems. 1988;35:54–63. [Google Scholar]
- Ross L. The ‘False Consensus Effect’: An egocentric Bias in Social Perception and Attribution Processes. Journal of Experimental Social Psychology. 1977;13:279–301. [Google Scholar]
- Salganik MJ. Variance Estimation, Design Effects, and Sample Size Calculations for Respondent-Driven Sampling. Journal of Urban Health. 2006;83:i98–i112. doi: 10.1007/s11524-006-9106-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salganik MJ, Heckathorn DD. Sampling and Estimation in Hidden Populations Using Respondent Driven Sampling. Sociological Methodology. 2004;34:193–239. [Google Scholar]
- Spiller MW, Heckathorn DD, Jeffri J. Above Ground: Information on Artists III: Special Focus on New York City Aging Artists. Research Center for Arts and Culture; New York, NY: 2008. The Social Networks of Aging Visual Artists.”; pp. 49–69. [Google Scholar]
- Tuma NB, Hallinan NZ. The effect of sex, race, and achievement on schoolchildren's friendships. Social Forces. 1979;57:1265–1285. [Google Scholar]
- Volz E, Heckathorn DD. Probability-Based Estimation Theory for Respondent-Driven Sampling. Journal of Official Statistics. 2008;24:79–97. [Google Scholar]
- Volz E, Wejnert C, Deganii I, Heckathorn DD. Ithaca, NY: 2007. Respondent-Driven Sampling Analysis Tool (RDSAT) Version 6.0.1. [Google Scholar]
- Wasserman S, Faust K. Social Network Analysis. Cambridge University Press; Cambridge, MA: 1994. [Google Scholar]
- Wejnert C. An Empirical Test of Respondent-Driven Sampling: Point Estimates, Variance, Measures of Degree, and Out-of-Equilibrium Data. Sociological Methodology. 2009;39:73–116. doi: 10.1111/j.1467-9531.2009.01216.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wejnert C, Heckathorn DD. Web-Based Network Sampling: Efficiency and Efficacy of Respondent-Driven Sampling for Online Research. Sociological Methods and Research. 2008;37:105–134. [Google Scholar]
- Wejnert C, Heckathorn DD. Respondent-Driven Sampling: Operational Procedures, Evolution of Estimators, and Topics for Future Research. In: Williams M, Vogt P, editors. The Handbook of Methodological Innovations in the Social Sciences. SAGE Publications; In press. [Google Scholar]
- Wilcox S, Udry JR. Autism and accuracy in adolescent perceptions of friends’ sexual attitudes and behavior. Journal of Personality and Social Psychology. 1986;10:371–374. [Google Scholar]