Phylogenetic Tree Reconstruction Accuracy and Model Fit when Proportions of Variable Sites Change across the Tree

Abstract

Commonly used phylogenetic models assume a homogeneous process through time in all parts of the tree. However, it is known that these models can be too simplistic as they do not account for nonhomogeneous lineage-specific properties. In particular, it is now widely recognized that as constraints on sequences evolve, the proportion and positions of variable sites can vary between lineages causing heterotachy. The extent to which this model misspecification affects tree reconstruction is still unknown. Here, we evaluate the effect of changes in the proportions and positions of variable sites on model fit and tree estimation. We consider 5 current models of nucleotide sequence evolution in a Bayesian Markov chain Monte Carlo framework as well as maximum parsimony (MP). We show that for a tree with 4 lineages where 2 nonsister taxa undergo a change in the proportion of variable sites tree reconstruction under the best-fitting model, which is chosen using a relative test, often results in the wrong tree. In this case, we found that an absolute test of model fit is a better predictor of tree estimation accuracy. We also found further evidence that MP is not immune to heterotachy. In addition, we show that increased sampling of taxa that have undergone a change in proportion and positions of variable sites is critical for accurate tree reconstruction.

Commonly used phylogenetic models assume a homogeneous, time-reversible stationary process, at each site, throughout the tree. However, it is known that these assumptions are a simplification of the true evolutionary process. In particular, a site can display lineage-specific rates of substitution, an observation that has been termed heterotachy (Philippe and Lopez 2001). This type of variation appears to be a prevalent feature of molecular sequence data (Fitch and Markowitz 1970; Lopez et al. 2002; Ane et al. 2005; Lockhart et al. 2006); however, some evolutionary processes that can cause heterotachy are not accounted for in phylogenetic models. Such model misspecification can mislead model-based tree reconstruction (Inagaki et al. 2004; Gruenheit et al. 2008).

Heterotachy arises from different evolutionary processes including changes in 1) the overall rates of substitutions 2) the positions of variable sites, and/or 3) the proportions of variable sites. These processes are likely to be correlated and reflect variations, over time, in the underlying evolutionary constraints that are acting on the sequences. Importantly, the later 2 processes, which can be biochemically explained by changes in evolutionary constraints that are acting on secondary and tertiary structures, can explain the observed changes in overall rates as well as variations in rates across sites.

Here, we focus on changes in the proportions and positions of variable sites and their effect on model fit and tree reconstruction. Although such changes are known to occur over time independently in different lineages (Fitch and Markowitz 1970; Germot and Philippe 1999; Lopez et al. 2002; Ane et al. 2005; Lockhart et al. 2006) and have been shown to mislead tree reconstruction (Lockhart and Steel 2005; Gruenheit et al. 2008; Kolaczkowski and Thornton 2008), the extent of their effects on phylogenetic reconstruction is still uncertain. Using simulated data, we measured and compared tree reconstruction accuracies of 5 current models of nucleotide sequence evolution in a Bayesian Markov chain Monte Carlo (MCMC) framework, as well as the accuracy of maximum parsimony (MP), when applied to data containing increasing levels of change in the proportions of variable sites (Pvar) with and without additional changing positions of variable sites.

We explore the effect of taxon sampling on the estimation of the innermost branch. The number of possible trees increases superexponentially with the number of taxa. Therefore, phylogenetic analysis using a large number of taxa is computationally difficult. However, the inclusion of appropriate additional taxa has previously been found to increase the reconstruction accuracy of underlying relationships particularly when the additional taxa break up long branches (Holland et al. 2003; Shavit et al. 2007).

We also examine the relative and absolute adequacy of these models for such data. It is important to note that the best-fit model is not necessarily adequate for tree reconstruction (Minin et al. 2003). Model selection methods chose a model, from a given set of models, that maximizes the likelihood of the data given the tree (considering and in some cases penalizing for the number of parameters). Model-adequacy assessment methods (such as Goldman 1993 and Bollback 2002) evaluate how well a certain model performs in predicting future observations. This is usually done by simulating predictive observations under the model in question and comparing these to the original data using some test statistic. Unlike model selection methods, these evaluate the absolute adequacy of the model and can reject the best-fit model if some component of the evolutionary process is not accounted for in the set of models tested (Posada and Buckley 2004).

MATERIAL AND METHODS

Simulations

We generated data using our newly developed simulator LineageSpecificSeqgen (Shavit Grievink et al. 2008); an extension to the Seq-Gen program (Rambaut and Grassly 1997) that allows generation of sequences with both changes in the proportions of variable sites (Pvar) and changes in the variable/invariable switch rate of the covarion model (Tuffley and Steel 1998). One hundred DNA data sets of 10,000 nucleotides each were generated along the 4-, 6-, 8-, and 16-taxon trees depicted in Figure 1. We used the default option of LineageSpecificSeqgen where branch lengths are defined as the expected number of substitutions per variable site, as opposed to the expected number of substitutions per site (which is averaged over all sites, including invariable sites). The advantage of this setting is that it is more intuitive; the input branch lengths are used directly and the rate of variable sites is not increased (rescaled) to compensate for the invariable sites when the data are generated. This results in simulation of more moderate rates than in the alternative setting of branch lengths being the expected number of substitutions per site (see Shavit Grievink et al. 2008 for further detail). The setting used does not affect tree estimation, as the expected number of substitutions per site will be estimated from the data.

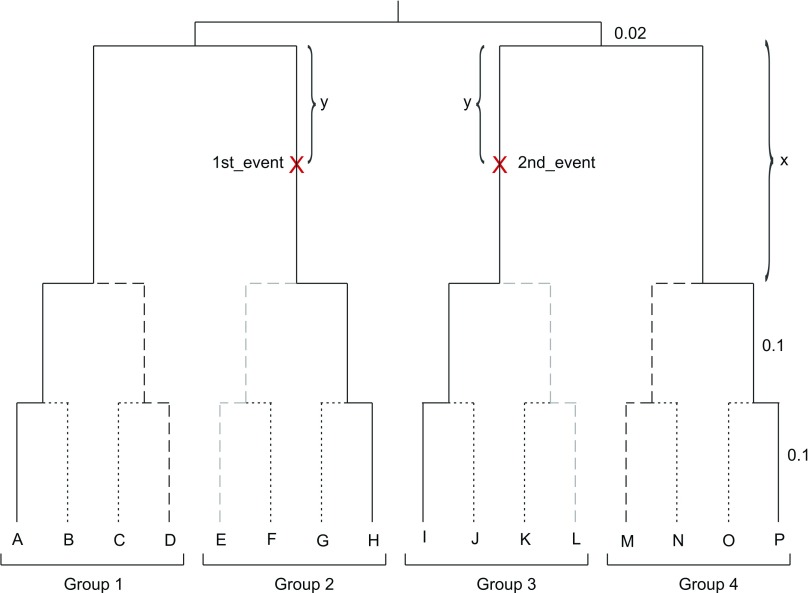
FIGURE 1.

Simulations were done on a 4-taxon tree: T₄=((A,H),(I,P)) (solid lines), two 6-taxon trees: $T_{6a}=($(A,(E,H)),((I,L),P)) (solid and light dashed lines) and $T_{6b}=($((A,D),H),(I,(M,P))) (solid and dark dashed lines), an 8-taxon tree: $T_8=\left(\right($(A,D),(E,H)),((I,L),(M,P))) solid and both light and dark dashed lines, and a 16-taxon tree: T₁₆=((((A,B),(C,D)),((E,F),(G,H))),(((I,J),(K,L)),((M,N),(O,P)))) (all lines). At the root, 80% of the sites were set as invariable. Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50) percent of the invariable sites were reset to be variable in 2 events marked as “1st_event” and “2nd_event.”

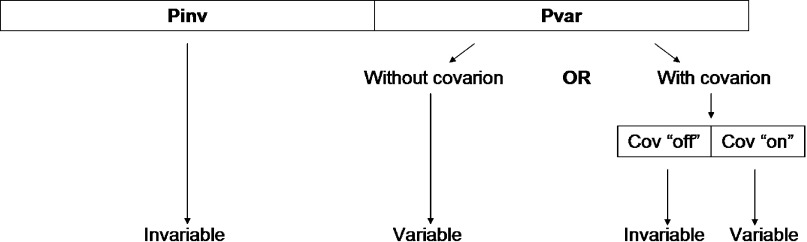
The Jukes–Cantor (JC) model (Jukes and Cantor 1969) of nucleotide substitution was used both with and without the covarion model of Tuffley and Steel (1998; the proportion of sites that are variable under the covarion model was set to 0.6 and the rate of change from variable to invariable and vice versa was set to 0.1). As illustrated in Figure 2, a site can be invariable at a certain section of the tree if 1) it is part of the proportion of sites that are invariable (Pinv) or 2) it is part of the proportion of sites that are variable (Pvar) but is invariable (“off”) under the covarion model. At the root, 80% of the sites were set as invariable (i.e., $\text{Pinv}=0.8$ and $\text{Pvar}=0.2$). Changes in the proportion of variable sites (Pvar), “events”, were introduced in 2 positions on the trees marked as “1st_event” and “2nd_event” (Fig. 1); ${\text{Pvar}}^{+}=(0,5,10,15,20,25,30,35,40,45,50)$ percent of the invariable sites were reset to be variable in these 2 events. Unless otherwise stated, these 2 events were set to be correlated, so that the positions of sites that switch state are identical.

FIGURE 2.

A description of the variable and invariable sites in the simulated data. When sequences are simulated without the covarion model, the number of variable sites is equal to the proportion of variable sites (Pvar) multiplied by the number of sites and thus the number of invariable sites is equal to the proportion of invariable sites (Pinv) multiplied by the number of sites. However, when sequences are simulated with the covarion model, the number of variable sites is equal to the proportion of variable sites (Pvar) multiplied by the proportion of sites that are “on” (i.e., variable) under the covarion model (Cov “on”) and the number of sites; the number of invariable sites is then equal to the proportion of invariable sites (Pinv) multiplied by the number of sites plus the proportion of variable sites (Pvar) multiplied by the proportion of sites that are “off” (i.e., invariable) under the covarion model (Cov “off”) and the number of sites. A site can therefore be invariable at a certain time if a) it is part of Pinv or b) it is part of Cov “off.”

Although the simulation tree used is very specific, we believe that the parameters used are of great relevance to phylogenetic studies. By choosing to have 2 events on nonsister branches, we are of course deliberately selecting a situation that we expect to be problematic for phylogenetic methods, but it seems more important to focus attention on cases where phylogenetic methods may be mislead than situations (e.g., events on sister taxa) where there may be a positive bias toward getting the correct tree. We chose a high proportion of sites to be invariant at the root of the tree based on the suggestions of Fitch and Markowitz (1970) who found that (in the case of mammalian cytochrome c) when a single species is considered, more than 90% of the codons are invariant. We have considered both fully correlated and uncorrelated events to demonstrate the effect this setting has on the results (accuracy still decreases although slower than in correlated events). Of course, many other interesting settings are possible.

Phylogenetic Analyses

For each simulated data set, we conducted a Bayesian analysis using MrBayes version 3.1 (Ronquist and Huelsenbeck 2003) under 5 different models: JC, JC with invariable sites (JC + I), JC with a gamma distribution of rates across sites (JC + G), JC with invariable sites and a gamma distribution (JC + I + G), and JC with the covarion model (JC + Cov). Four chains (3 heated) were run for 2,000,000 generations with the default settings. Pilot runs using the more complex models (JC + I + G and JC + Cov) were examined for convergence in Tracer version 1.4 (Rambaut and Drummond 2007) and used to choose an appropriate burn-in (sump and sumt $\text{burn-in}=5000$; this equals 50,000 generations). MP analysis was conducted using PAUP${}^{*}$ version 4.0b10 (with default settings except for HSearch $\text{NBest}=1$).

For the model incorporating covarion evolution (JC + Cov), we used the covarion model of Tuffley and Steel (1998). Huelsenbeck (2002) described an extension to this model with an underlying variable rates across sites (a rate for each site is first drawn from a gamma distribution) and an overlaying covarion process. Under this model, a site can be variable, in which case its rate is taken from the gamma distribution, or invariable; an invariable site can become variable and vice versa. This model is implemented in a Bayesian framework in MrBayes. However, we encountered problems when using JC with variable rates across sites and covarion (JC + Hue). In many cases, the application of both these models to our data resulted in convergence on positive log likelihoods! Similar problems with MCMC using parameter-rich models have been previously reported (Smedmark et al. 2006). We reported these problems in April 2008 using the MrBayes bug report tool (http://sourceforge.net/tracker/index.php?func=detail&aid=1945304&group_id=129302&atid=714418).

Reconstruction Accuracy

We evaluated the accuracy of the different analyses in reconstructing the tree T=((Group 1, Group 2),(Group 3, Group 4)), that is, the innermost edge splitting Groups 1 and 2 from Groups 3 and 4 (see Fig. 1). The tree T is one of 3 possible trees splitting the 4 groups into 2 bipartitions (1 + 2 vs. 3 + 4, 1 + 3 vs. 2 + 4, and 1 + 4 vs. 2 + 3). For the Bayesian analyses, the support for each of the 3 possible trees was calculated as the number of data sets for which the tree had the highest frequency in the posterior distribution. For MP, the support for each of the 3 possible trees was calculated as the number of data sets for which the tree was inferred.

Model Fit

There is no agreed-upon method for objective model selection in a Bayesian framework (Huelsenbeck et al. 2002). Therefore, we used several procedures to determine the best-fit model: 1) direct comparison of the harmonic mean of the estimated marginal likelihoods 2) Bayes factors (BFs) applied to the harmonic mean of the estimated marginal likelihoods, 3) The Akaike information criterion (AIC; Akaike 1974) applied to the arithmetic mean of the estimated marginal likelihoods (as in Strugnell et al. 2005), 4) the AIC applied to the maximum likelihood (ML) found for the cold chain, and 5) Bayesian information criterion (BIC; Schwarz 1978) applied to the ML found for the cold chain. The adequacy of each of the models was also evaluated using our own implementation of the method described by Bollback (2002), which uses the posterior predictive distributions to account for uncertainty in the phylogeny and model parameters (the code is available from l.shavit@massey.ac.nz). This method assumes that an adequate model should perform well in predicting future observations. In absence of future observations (which is generally the case), predicted observations are simulated under the model in question by sampling from the joint posterior density of trees and parameters as approximated using MCMC. A test statistic is then used to evaluate the difference between the simulated and the original data. This is a Bayesian equivalent of frequentist methods such as the classic parametric bootstrap (Bollback 2002). We used the multinomial test statistic $T\left(X\right)=\left({\sum }_{\xi \in S}{N}_{\xi }ln\left(N_{\xi }\right)\right)-Nln\left(N\right)$, where S is the set of (unique) possible site patterns, N is the number of sites, and $N_{\xi }$ is the number of sites in which pattern ξ was observed. This is a general statistic that is used to test the overall predictive performance of the model rather than the performance of a specific aspect of the model. As in the phylogenetic analysis, the first 50,000 generations were discarded from the posterior distribution before conducting this analysis.

RESULTS AND DISCUSSION

We evaluated tree reconstruction accuracies of Bayesian analyses using each of the 5 models (JC, JC + I, JC + G, JC + I + G, and JC + Cov) when applied to data where Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50) percent of the invariable sites were reset to be variable in 2 events defined on the tree (Fig. 1).

Tree Reconstruction Accuracy with Changing Proportions of Variable Sites—4 Taxa

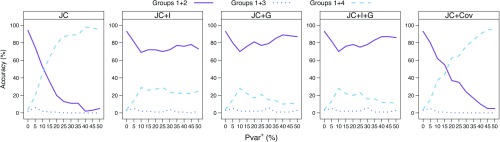
Figure 3 shows the ability of the analyses to reconstruct the correct phylogeny for data that was simulated under JC without the covarion model for the 4-taxon simulations. The only change in the evolutionary process is introduced (at the 2 events; see Fig. 1) by an increased proportion of variable sites. In general, the higher the percentage of sites that become variable in the 2 events (Pvar⁺) the less accurate the tree reconstruction is. None of the 5 models used for phylogenetic inference describe the data accurately (they do not account for the changing Pvar). Nevertheless, one might consider the JC + Cov model as the closest to the simulated data, as the changing proportions of variable sites are expected to produce covarion-like site patterns. However, the accuracy with which Bayesian analysis using this model (as well as JC) reconstructs the correct phylogeny is strongly impaired when Pvar⁺ increases. For Pvar⁺≥ 20%, the wrong tree (where the 2 nonsister lineages H and I, in which the change in Pvar occurred, are grouped together) is chosen most often. This may be, in part, due to the proportion of sites that are invariable across all taxa that is not accounted for by this model. For the JC + I model, the correct tree is chosen most often, although decreased accuracy is observed. The models allowing for variable rates across sites (JC + G and JC + I + G) are the most accurate in reconstructing the correct phylogeny for the parameters used in this simulation. Nevertheless, tree reconstruction under these models has been shown to be inconsistent when applied to other types of heterotachy (Kolaczkowski and Thornton 2004; Ruano-Rubio and Fares 2007).

FIGURE 3.

Tree reconstruction accuracy for the 4-taxon simulations without the covarion model. Bayesian analysis was done using JC, JC with invariable sites (JC + I), JC with a gamma distribution (JC + G), JC with invariable sites and a gamma distribution (JC + I + G), and JC with the covarion model (JC + Cov). For each model, the sum of the proportional frequencies of each of the 3 possible splits of the groups (1 + 2 vs. 3 + 4, 1 + 3 vs. 2 + 4, and 1 + 4 vs. 2 + 3) is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50) percent of the invariable sites that were reset to be variable in the 2 events.

When branch lengths are defined as the expected number of substitution per variable site, a simulated increase in Pvar enforces an increase in branch length. In order to test whether the observed decrease in accuracy is due to the increased Pvar or simply due to the increase in branch lengths per se, we have simulated additional data in which branch lengths were defined as the expected number of substitutions per site. No change in Pvar was introduced in this data. Instead, the branch lengths of taxa H and I were increased in a manner that corresponds to the increase that was enforced by the increased Pvar in our original simulations (see Supplementary Data, available from http://www.sysbio.oxfordjournals.org/, for a detailed description of this simulation setting). Under this setting, tree reconstruction under the JC + Cov model results in 100% accuracy. The observed decrease in accuracy is therefore a result of the increased proportion of variable sites and cannot be explained by increased branch lengths alone.

Correlated versus Uncorrelated Events

Next we tested the effect of the correlation between the 2 events. Correlated events, where the positions of sites that switch state are identical, might occur if a similar change in function (and therefore functional constraints) takes place in separate lineages. Conversely, uncorrelated events, where the positions of sites that switch state are independent, might occur when the change in constraints acting on the lineages is different. Tree reconstruction accuracies for the 4-taxon trees T₄ in the case of correlated events (Fig. 3) were compared with the case of uncorrelated events (results not shown). We found that the effect of changing Pvar is much less pronounced in the case of uncorrelated events. In fact, the tree reconstruction accuracy of Bayesian analysis using any of the 5 models tested was higher than 86% for all values of Pvar⁺. These results are expected, as the positions of sites that become variable at the events, in the 2 nonsister lineages (taxa H and I), are likely to be much less similar in this case (compared with the identical positions in the correlated case).

Adding the Covarion Model

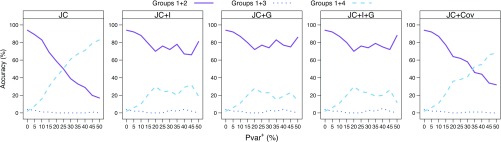
Under the settings used in our simulations, having sites evolve under the covarion model raises the overall number of invariable sites (see Fig. 2). This is done in a random manner (effectively reducing the correlation between the events) and therefore decreases the similarity between the positions of invariable sites in the 2 nonsister taxa H and I. This can be seen as an intermediate case between correlated and uncorrelated events. We compared the tree reconstruction accuracies for data that were simulated with and without the covarion model (Figs. 3 and 4). The results show that when data are simulated without the covarion model (Fig. 3), the effect of change in Pvar on phylogenetic inference is twice as strong as that when data are simulated with the covarion model (Fig. 4). The inclusion of the covarion models delays, but does not change the nature of, the effect of changes in Pvar on tree reconstruction accuracy.

FIGURE 4.

Tree reconstruction accuracy for the 4-taxon simulations with the covarion model. Bayesian analysis was done using JC, JC + I, JC + G, JC + I + G, and JC + Cov. For each model, the sum of the proportional frequencies of each of the 3 possible splits of the groups (1 + 2 vs. 3 + 4, 1 + 3 vs. 2 + 4, and 1 + 4 vs. 2 + 3) is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50).

Model Fit

Reconstructing trees under the best-fit model found using selection methods (e.g., as implemented in ModelTest [Posada and Crandall 1998]) is a common procedure in phylogenetic inference. However, model selection in a Bayesian framework is not straightforward. BFs evaluate the evidence provided by the data in favor of one model over another (Kass and Raftery 1995). Such pairwise comparisons are useful, but model selection from a larger set of models is difficult for the following 2 main reasons. First, the interpretation of BF is subjective. Second, BFs are usually interpreted by comparison to some standard scale; the results in this case might depend on the order of pairwise comparisons (the same problem is encountered when using likelihood ratio tests in a ML framework; Sullivan and Joyce 2005). We therefore used direct comparison of the harmonic means of the estimated marginal likelihoods, AIC, and BIC, in addition to BF, to determine the best-fit model for each data set and compared their outcomes.

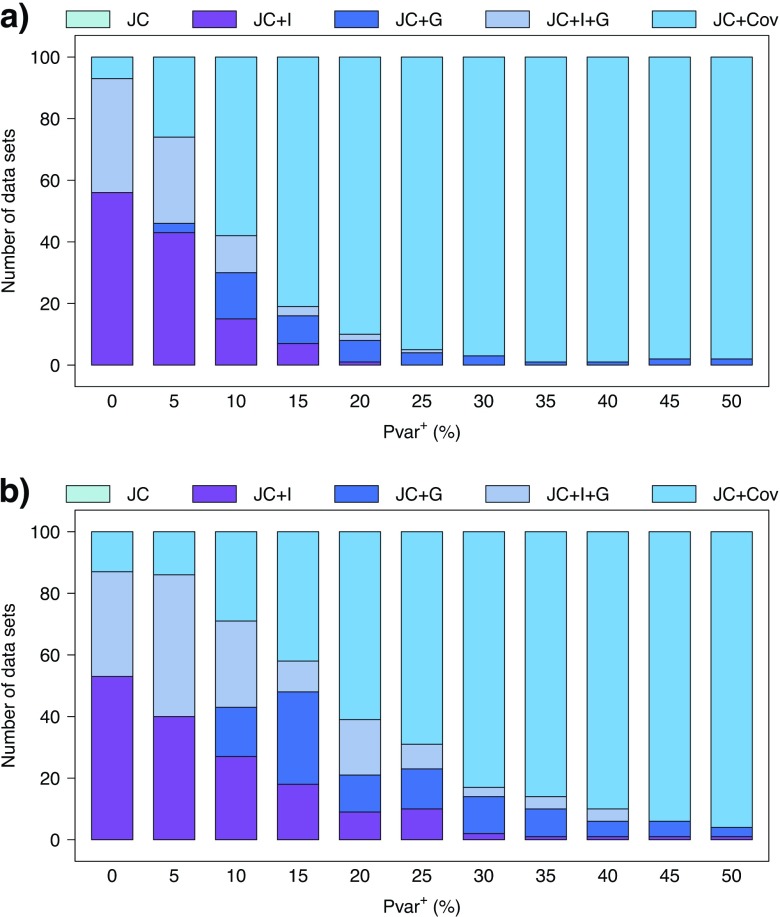
Using the direct comparison of the harmonic means of the estimated marginal likelihoods, for data simulated both with (Fig. 5a) and without (Fig. 5b) the covarion model, when Pvar⁺ (the percentage of invariable sites that become variable in the 2 events) is zero or very small JC + I is chosen most frequently as the best-fit model. Indeed, for Pvar⁺=0 without the covarion model, this is the correct model. However, as Pvar⁺ increases, the JC + Cov model is selected most often (Pvar⁺≥ 10% for data simulated without the covarion model and Pvar⁺≥ 15% for data simulated with the covarion model). The results of AIC and BIC are similar, although some variation occurs (see Supplementary Data).

FIGURE 5.

Best-fit model for the 4-taxon simulations a) without and b) with the covarion model. Comparison of the number of times each of the 5 models (JC, JC + I, JC + G, JC + I + G, and JC + Cov) was found to be the best-fit model using the a direct comparison of the harmonic means of the estimated marginal likelihoods.

The BF in favor of Model 1 over Model 0, $B_{10}$, was calculated for each data set and each pair of models. The resulting BFs were then interpreted according to the Kass and Raftery (1995) version of the guidelines presented by Jeffreys (1961). The number of times a positive (2ln($B_{10})>$ 2) or strong (2ln($B_{10})>$ 6) support for favoring one model over another was summarized (Supplementary Data). Overall, the larger Pvar⁺ was, the higher the number of data sets for which the JC + Cov model was favored. The results for the comparison between the JC + Cov and JC + I are shown in Table 1. When Pvar⁺ is zero or very small, JC + I is selected most frequently. For larger Pvar⁺ (Pvar⁺≥ 15% for data simulated without the covarion model and Pvar⁺≥ 30% for data simulated with the covarion model), JC + Cov is chosen as the best-fit model. These results are congruent with the direct harmonic mean comparisons, AIC, and BIC results.

TABLE 1.

Model-fit comparison between the JC + I and JC + Cov models using BFs

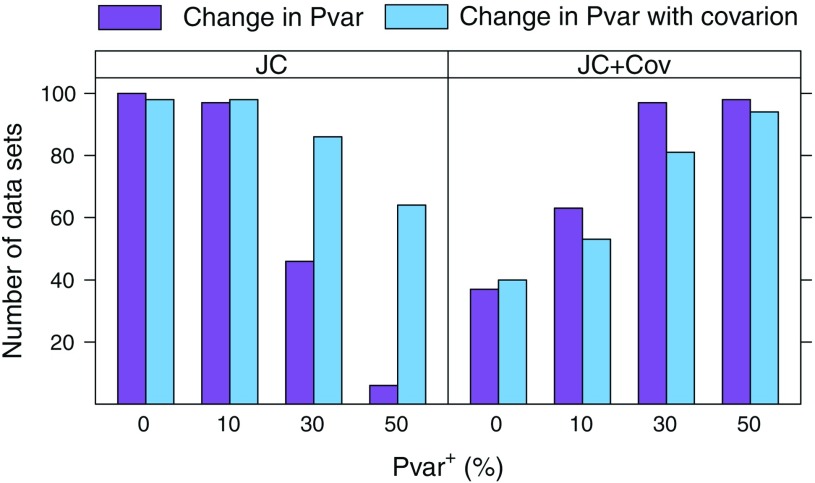
In our simulations, for Pvar⁺≥ 20% with no covarion and Pvar⁺≥ 35% when covarion was incorporated, using the best-fit model (JC + Cov) resulted in erroneous phylogenetic estimates more frequently than correct estimates. We then determined the adequacy of the best-fit model JC + Cov, as well as the other models, using parametric bootstrap based on the posterior predictive distributions (Fig. 6; see Methods section for more detail). As the simulated change in Pvar increases, so does the number of data sets for which the JC + Cov model was rejected. Even when no change in Pvar was simulated (Pvar⁺= 0), this model was rejected for more than 37% of the data sets at the 1% level and 86% at the 5% level (not shown). These results, together with our tree reconstruction results in Figures 3 and 4, suggest that the covarion model used (which assumes a constant number of variable sites) is inadequate at capturing change in proportions of variable sites. This simple covarion model is a priori disadvantaged in the case of our simulated data, as it does not account for the proportion of sites that is invariable throughout the tree. Unfortunately (and although not apparent), the JC + I + Cov model that is expected to fit our data relatively well is not implemented in MrBayes (in fact, any combination of I + Cov is not implemented. Several published papers, including our own, state that the model used was I + Cov [Shavit Grievink et al. 2008] or G + I + Cov [Gittenberger et al. 2004; Hampl et al. 2006], but in practice, the program ignores the I parameter only accounting for invariable sites under the covarion model).

FIGURE 6.

Absolute model-adequacy assessment for data simulated with and without the covarion model for an increasing Pvar⁺=(0, 10, 30, 50). The number of times each model (JC and JC + Cov) was rejected at the 1% level is shown. The JC + I, JC + G, and JC + I + G models were never rejected.

When the covarion model was not used in simulations, the number of data sets for which the JC model was rejected decreased as the change in Pvar increased. When the covarion model was used, this trend was less pronounced. This might be predicted, considering that the JC model does not account for a constant proportion of invariable sites. The increased Pvar effectively decreases the number of invariable sites in the data set. In contrast, the addition of covarion sites effectively increases the number of invariable sites in the data set. Notably, the 3 models that were found adequate for the data also performed well in tree reconstruction, whereas the 2 models that failed the absolute adequacy assessment all displayed lower tree reconstruction accuracy. The simple multinomial statistic used was able to identify model inadequacy, which was probably a result of these models' inability to correctly account for the proportion of invariable sites.

To explore further 1) the poor performance of JC + COV for high values of Pvar⁺ and 2) the fact that it is selected as the best-fit model but fails the absolute tests of model fit, we looked at the parameter values estimated for the case where data were simulated with Pvar⁺= 50% and no covarion. The average switching parameters for JC + Cov are s(off->on)≈1.2 (standard deviation [SD]≈0.16) and s(on->off) ≈4.51 (SD≈0.86). This corresponds to an off frequency of ∼0.8, which is what was simulated but with quite a high switch rate. For JC + I, the average estimated proportion of invariable sites is ≈0.475(SD≈0.018). This is close to the simulated proportion of complete invariable sites (sites that are invariable in all taxa) that was 0.4 in this case. Despite the fact that the parameters of JC + Cov seem to accommodate the proportion of invariable sites, simulating under these parameters (as done for the absolute model-fit test) results in a low proportion of invariable sites compared with the original data (in which at least 0.4 of the sites are invariable) and the model is rejected. From a likelihood perspective, it seems that the probability of an invariant site under the JC + Cov model is larger than the average probability of a variable site under the JC + I model. However, we were unable to investigate this further by looking at site likelihoods as MrBayes does not report these values.

Taxon Sampling

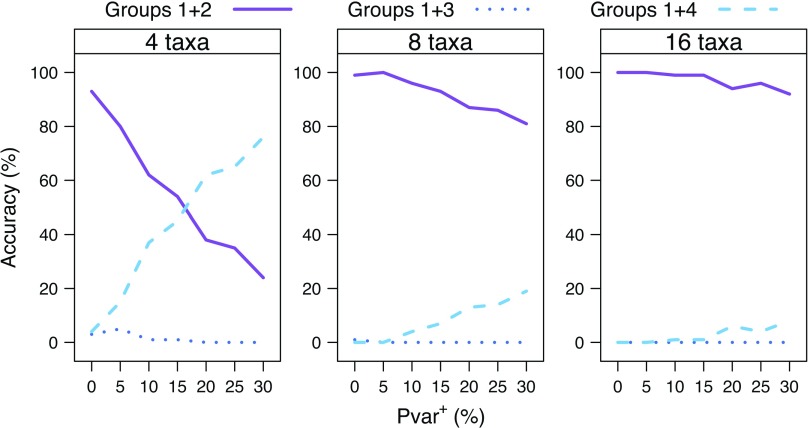
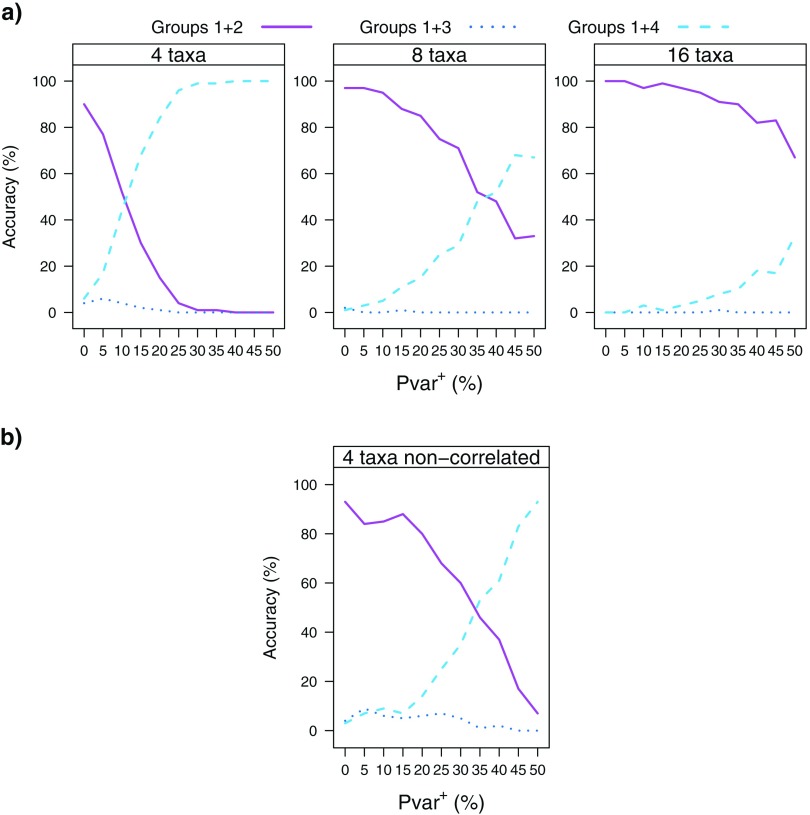
We investigated the effect of taxon sampling on the accuracy of the Bayesian phylogenetic inference by comparing the reconstruction accuracies of the tree T=((Group 1, Group 2),(Group 3, Group 4)) for the 4-, 8-, and 16-taxon simulations. The performance of all 5 models was evaluated for the 4- and 8-taxon simulations. For the 16-taxon simulations, however, only the best-fit model JC + Cov was evaluated. A comparison of the reconstruction accuracies using JC + Cov model is shown in Figure 7. With the addition of taxa, the accuracy with which the correct split (Groups 1 + 2 vs. Groups 3 + 4) is found increases significantly. For the 8-taxon simulations, the correct split is found most often using any of the 5 models (results not shown). These findings are in agreement with earlier observations (Ruano-Rubio and Fares 2007; Shavit et al. 2007; Heath et al. 2008).

FIGURE 7.

The effect of taxon sampling on reconstruction accuracy of the main split of the tree T (Groups 1 + 2 vs. Groups 3 + 4). The reconstruction accuracy for the 4-, 8-, and 16-taxon simulations using the JC + Cov model is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30).

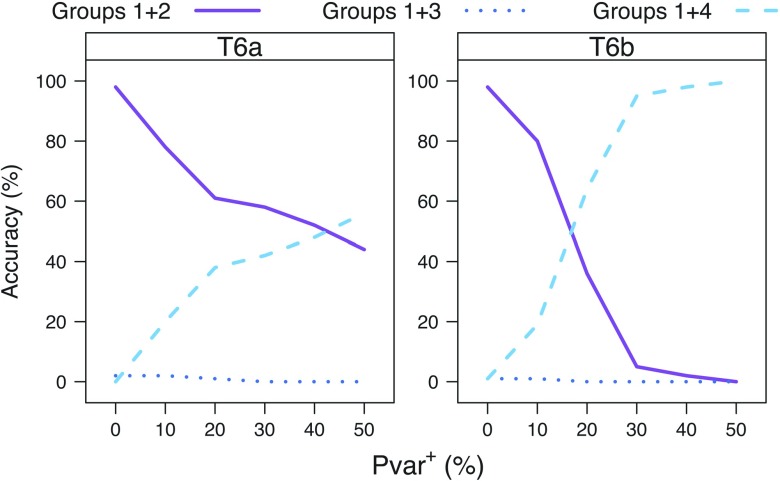
In order to distinguish between improved accuracy due to increased taxon sampling in general versus more extensive sampling of taxa subsequent to the 2 events, we evaluated the accuracy of phylogenetic inference using the JC + Cov model when applied to 2 different 6-taxon trees. Tree $T_{6a}$ contains 2 taxa under each of the 2 events (Groups 2 and 3) and 1 taxon under each of the other 2 lineages (Groups 1 and 4), whereas tree $T_{6b}$ contains only 1 taxon under each of the 2 events and 2 taxa under each of the other 2 lineages (Fig. 1). We found (Fig. 8) that increased taxon sampling in lineages that did not undergo change in Pvar ($T_{6b})$ does not improve the reconstruction accuracy of the main split of the tree T (in comparison to tree reconstruction accuracy for the 4-taxon simulations), whereas increased taxon sampling in the lineages under the 2 events ($T_{6a})$ improves the tree reconstruction accuracy and delays the accuracy hindering effect of change in Pvar.

FIGURE 8.

Comparison of reconstruction accuracy of the main split of the tree T (Groups 1 + 2 vs. Groups 3 + 4) for general increased taxon sampling versus increased taxon sampling under the 2 events. The tree reconstruction accuracy for the data simulated under $T_{6a}=($(A,(E,H)),((I,L),P)) and $T_{6b}=($((A,D),H),(I,(M,P))) using the JC + Cov model is shown for an increasing Pvar⁺=(0, 10, 20, 30, 40, 50).

MP versus Bayesian Analysis

Kolaczkowski and Thornton (2004) reignited a 2-decade long debate when they claimed that MP performs better than ML and Bayesian analysis for a range of parameters. The authors' conclusion was based on a very specific case of heterotachy (convergent change in overall rates in nonsister lineages) with a specific combination of parameters and tree topology. Several contradicting results were later published (Gadagkar and Kumar 2005; Philippe et al. 2005; Spencer et al. 2005) and the biological realism of the original work has been questioned (Steel 2005, but see Thornton and Kolaczkowski 2005). Kolaczkowski and Thornton further declared that MP is unaffected by heterotachy (Kolaczkowski and Thornton 2004; Thornton and Kolaczkowski 2005). However, Philippe et al. (2005) later showed that when the level of rate variation across lineages (level of convergent change in overall rates in nonsister lineages) increases, MP accuracy can either decrease or increase depending on the relative branch lengths. To shed further light on this debate, we present a comparison of the accuracy of MP with that of Bayesian analysis using JC + Cov in reconstructing the correct tree T (see Fig. 1).

Phylogenetic inference using MP was applied to the 4-, 8-, and 16-taxa simulations. The accuracy with which MP reconstructs the correct phylogeny is greatly hindered by the increased Pvar⁺ (Fig. 9a). The increase in taxon sampling does improve MP accuracy; however, the Bayesian analyses (Fig. 7) were found to be more accurate than MP and less affected by the increased Pvar⁺. We also tested the ability of MP to reconstruct the 4-taxon trees ($T_4)$ in the case of uncorrelated events. MP is clearly affected by the increased Pvar⁺ (Fig. 9b), with the wrong tree where the 2 nonsister lineages are grouped together reconstructed most frequently when Pvar⁺> 0.35.

FIGURE 9.

Tree reconstruction accuracy using MP. a) The effect of taxon sampling on reconstruction accuracy of the main split of the tree T (Groups 1 + 2 vs. Groups 3 + 4). b) Tree estimation for the 4-taxon simulations with uncorrelated events (the positions of sites that switch state are independent). The tree reconstruction accuracy is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50).

CONCLUSIONS

Change in the proportions of variable sites causes a model misspecification that can mislead phylogenetic methods. We found that a simple covarion model is inadequate at capturing such changes. A model combining a proportion of sites that are invariable across the tree and covarion evolution is not currently implemented in MrBayes. Although this model does not account for changes in the proportion of variable sites, it is expected to fit such data relatively well. Testing the ability of this model to reconstruct trees from simulated data containing change in the proportion of variable sites is important for our understanding of the effects of model misspecification of this kind.

Our results show that the use of the best-fit model, chosen by a relative criterion, does not guarantee correct tree reconstruction. In fact, the best-fit model for our data performed poorly, whereas other models performed better, and absolute model-fit assessments confirmed that this best-fit model is inadequate for our data. Although none of the tested models accounts for changes in Pvar, some of the models could not be rejected by the absolute model-fit assessment. Importantly, these models were more accurate in tree reconstruction. Further work to test the performances of relative and absolute model-fit tests for a large number of trees and a wide range of parameters is needed before a general conclusion can be drawn. We therefore recommend the use of absolute model-adequacy tests (Goldman 1993; Bollback 2002), along side relative-fit tests, as an integral part of phylogenetic analysis.

We found that taxon sampling has a strong effect on tree reconstruction accuracy. In particular, greater taxon sampling under the events in which a change in Pvar occurred resulted in improved accuracy. Our results imply that more accurate phylogenetic inference can be achieved by inclusion of larger numbers of taxa from lineages for which prior knowledge suggests that a change in the evolutionary process occurred.

In contrast with the reports of Kolaczkowski and Thornton (2004, 2005), we establish that the accuracy of MP can be adversely affected by heterotachy. Increase in taxon sampling did improve the accuracy of MP, yet it was still the least accurate in tree reconstruction.

Currently implemented phylogenetic models do not account for changes in the proportions of variable sites. This model misspecification can result in erroneous tree reconstruction. However, the accuracies of tree estimation using different models vary; and although not accounting for heterotachy, a model can sometimes be adequate for heterotachous data. An absolute goodness-of-fit test is useful in evaluating model adequacy and can help differentiate cases in which tree reconstruction is expected to be accurate from cases in which the model is inadequate, and its use is likely to result in incorrect tree estimation. Branch length mixture models that aim to account for heterotachy (Kolaczkowski and Thornton 2008, Pagel and Meade 2008) exist. Testing the accuracy of such models to the data containing changes in Pvar (such as that simulated here) would be an interesting extension of the present study.

SUPPLEMENTARY MATERIAL

Supplementary material.

FUNDING

This work was financially supported by the New Zealand Marsden fund (05-MAU-033 to B.R.H.).