On Genome-wide Association Studies for Family-Based Designs: An Integrative Analysis Approach Combining Ascertained Family Samples with Unselected Controls

Abstract

Large numbers of control individuals with genome-wide genotype data are now available through various databases. These controls are regularly used in case-control genome-wide association studies (GWAS) to increase the statistical power. Controls are often “unselected” for the disease of interest and are not matched to cases in terms of confounding factors, making the studies more vulnerable to confounding as a result of population stratification. In this communication, we demonstrate that family-based designs can integrate unselected controls from other studies into the analysis without compromising the robustness of family-based designs against genetic confounding. The result is a hybrid case-control family-based analysis that achieves higher power levels than population-based studies with the same number of cases and controls. This strategy is widely applicable and works ideally for all situations in which both family and case-control data are available. The approach consists of three steps. First, we perform a standard family-based association test that does not utilize the between-family component. Second, we use the between-family information in conjunction with the genotypes from unselected controls in a Cochran-Armitage trend test. The p values from this step are then calculated by rank ordering the individual Cochran-Armitage trend test statistics for the genotype markers. Third, we generate a combined p value with the association p values from the first two steps. Simulation studies are used to assess the achievable power levels of this method compared to standard analysis approaches. We illustrate the approach by an application to a GWAS of attention deficit hyperactivity disorder parent-offspring trios and publicly available controls.

Main Text

With the advent of high-throughput genotyping, genome-wide association studies (GWAS) are ubiquitous, and the number of SNPs used in these studies continues to increase. Through this genotyping breakthrough, genetic variants have been identified and reliably replicated for several complex diseases.^1–6 Despite these successes, there are still several factors that limit our current ability to more readily identify disease variants, including insufficient statistical power, population stratification, various forms of between-study heterogeneity, ascertainment schema, environmental influences, and time-varying associations.⁷ There is no doubt that the field of genetic epidemiology as a whole has overestimated the genetic contribution of common genetic variants. Given these drawbacks, it is therefore essential to fully maximize the sample size and the power of the analysis strategy that is used.

Although family-based designs offer the advantage of complete robustness against genetic heterogeneity, this feature comes at the price of reduced statistical power when compared with designs that are based on unrelated subjects. In family-based association designs, the association signal can be orthogonally decomposed into a between-family component and a within-family component. Because the between-family component is biased in the presence of population substructure, family-based association tests (FBATs) have utilized the within-family component for the construction of the association test.^8,9

In this communication, we develop a new overall FBAT for ascertained samples that integrates unselected, genotyped controls from a population-based study into an overall statistical test. This statistical test has broad applications, because it can be applied to any situation in which family data and case-control data are available. The new overall test is more powerful than case-control studies with the same number of cases and unselected controls, while, at the same time, it is still completely robust against population substructures.

As more GWAS data are produced, their control genotypes often become readily available both from publicly available sources (e.g., dbGaP¹⁰) and from commercial companies (e.g., Affymetrix, Illumina, and Perlegen). Because these control genotypes are easily accessible for use at no extra cost and the proposed method can fully utilize these samples in the analysis of family-based GWAS, our method will increase the statistical power of existing studies while not sacrificing any of the robustness properties of the family design. This testing strategy is available for use in the PBAT suite of analysis tools.¹¹

Suppose that n independent parent-offspring trios are sampled and genotyped at s biallelic marker loci with alleles A and B. The genotype of the i^th proband is denoted by X_i. The parental genotypes in the i^th family are also available and are denoted by p_i1 and p_i2. If the parental information is missing, the proposed methodology can be extended by replacing the parental genotype information, p_i1 and p_i2, with the sufficient statistic proposed by Rabinowitz and Laird.⁹ Further, we assume that the trio sample is fully ascertained, i.e., all offspring are affected. The analysis of the family data set is now supplemented by the integration of m controls that have been genotyped at the same s loci as the family sample. These controls may be “selected” or “unselected” for the disease of interest. If the controls are unselected for the disease of interest, then individuals will have the disease at the rate prevalent in the population. In contrast, selected controls are specifically chosen to be free of the disease of interest. For most practical purposes, unselected controls are more likely to be available, because the publicly available databases are not selected to exclude any given disease.

Similar to the approaches by VanSteen,¹² Ionita,¹³ Murphy,¹⁴ and Won,¹⁵ we assessed the evidence of association for each marker locus at a population-based level (i.e., between-family level) and at a within-family level by two statistics that are statistically independent. In order to maintain the original robustness of the family design, we used the transmission disequilibrium test (TDT)⁸/FBAT⁹ to assess the information about the association at a within-family level. Because the TDT/FBAT approach is a conditional test that conditions on the offsprings' phenotype and the parental genotype information, this information, i.e., offsprings' phenotypes and parental genotypes, in addition to the data on the unselected controls, can be used to construct a measure for association at a population-based level that is statistically independent of the TDT/FBAT statistic.¹⁶ Consequently, for each marker, we assessed the evidence for association at the population level by constructing a Cochran-Armitage (C-A) trend test with a 2 × 3 table. In this table, the genotype distribution for the controls is defined by the unselected set of controls that are not part of the family study but are available for the analysis. The genotype distribution for the cases in this table is derived based on the available and/or allowable data from the family study (i.e., offspring phenotypes and the parental genotypes, also known as the between-family information) in addition to the genotype information from any singleton cases that were not used in the TDT/FBAT. As suggested in the conditional mean model approach,¹⁶ we calculated the genotypes of the affected offspring based on Mendelian transmission from the parents, i.e., E(X|pi1, pi2), and derived the genotype distribution for the cases in the 2 × 3 table based on these calculated genotypes in the offspring generation. If the family sample contained additional unaffected siblings, their imputed genotype could be used to enrich the control distribution. Similarly, if there were additional genotypes from individual cases that were not a part of any family, then this genotype information could be included in the C-A trend test. Although we propose a strategy in which the C-A trend test is used in the second stage, this general technique is flexible and can easily be extended to implement other statistical tests in the second stage for case-control data (e.g., a two degree of freedom test). Similarly, any genetic model can be incorporated into the proposed analytic approach.

In this way, we can now construct the population-based component of the overall test for each SNP by computing a C-A trend test statistic for a 2 × 3 table, which is based on the unselected controls and the imputed genotypes for the cases (plus any additional singleton cases). In order to retain the robustness of the original FBAT against population admixture, the p values of the C-A are not obtained on the basis of asymptotic distribution theory but on the basis of the rank of the C-A statistic among the s marker loci. To the i^th ranked SNP based on the C-A statistic, we assign the rank-based p value of $p{T}_i=\left(i-0.5\right)/s$. The value 0.5 is a tuning parameter. The primary purpose of the tuning parameter is to protect against population stratification and maximize the statistical power. Methodological work shows that a tuning parameter of 0.5 will always ensure robustness against population stratification. The normal score statistic that corresponds to the p value pT_i is denoted by Z(T)_i, where Z(T)_i is normally distributed with mean 0 and variance 1.

The within-family component is assessed with the classical TDT statistic⁸ or, if parents are missing and multiple affected and unaffected offspring are available, with the FBAT statistic.⁹ For the i^th marker locus, we denote the p value of the FBAT statistic by p(FBAT_i) and the standardized normal score that reflects the p value by Z(FBAT_i). The overall test integrating the within-family component, the between-family component, and the unselected controls can now be constructed via the weighted Z approach.¹⁷

$$Z_i=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.Z\left(FBA{T}_i\right)+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.Z\left(T_i\right)$$

It is straightforward to see that the overall association tests are normally distributed with mean 0 and variance 1. Via the same arguments as in Won et al.,¹⁵ it is apparent that the rank-based p values in the overall test statistic Z_i will ensure robustness against population admixture and stratification. For the analytical proof of this property, see Won et al.¹⁵ Intuitively, the population robustness is achieved by the fact that the population-based test statistic T uses a rank-based p value. A rank-based p value can never achieve genome-wide significance by itself because it is always greater than the Bonferroni adjusted significance level, i.e., 1/number of markers > 0.05/number of markers. Therefore, because the overall test statistic Z_i can only establish genome-wide significance through the within-family component (FBAT_i), Z_i is inherently robust against population stratification in the same manner that FBATs are robust to population stratification.

Because the unselected controls that are integrated in the overall family-based association statistic will be from a different study than the family sample, the presence of potentially strong population stratification is very likely. Although, as discussed above, the overall test will not be biased in the presence of such substructures, stratification between the unselected controls and the family study poses the danger of reducing the overall statistical power, which would eliminate the benefit of including the unselected controls in the analysis. It is therefore recommended to apply population-based adjustment methods^18,19 to the population-based data, i.e., unselected controls and imputed genotypes, to eliminate such effects and achieve the maximal statistical power.

We performed simulations to evaluate the power of the proposed methodology compared with other methodologies commonly in use. We assumed a 1,000,000 SNP GWAS analysis that was adjusted for multiple comparisons via the standard Bonferroni correction. When comparing the different methodologies, we kept the total number of probands equal to 3000 (i.e., 3000 parent-offspring trios and 3000 case-control pairs) for all analysis methods. We conducted simulations with minor allele frequencies (MAFs) ranging from 10% to 40%. We assumed a genetic effect size, measured as an odds ratio, of 1.3 and assumed a disease prevalence of 5% and 10%. Because of the similar findings, we only present the simulation results for a disease prevalence of 5%. We compared the power of a standard FBAT and a standard case-control analysis to the proposed testing methodology with both unselected and selected control individuals. We also compared the power of the proposed testing strategy via a 1:1 and 1:2 ratio of cases to controls. For each power estimate, we performed 10,000 replicate analyses.

Figure 1 and Figure 2 show the power over a range of MAFs. From these simulations, we see that the power estimates of the new methodology (“New screen”) via a 1:1 ratio of unselected controls to cases is noticeably more powerful than the standard TDT or a standard case-control analysis. Surprisingly, the power for the TDT and the standard case-control analysis is similar, and through additional simulations (data not shown) we found that as the disease prevalence in the population increases (and therefore the number of misclassified individuals in the unselected control sample increases), the power of the new screening method can become even greater than the power for the case-control analysis at specific MAFs. This already happens if the disease prevalence is as small as 10% (data not shown). Figure 1 illustrates the consistent and robust power of our proposed screening method in comparison with either of these default analyses, with increases in power ranging between 10% and 20%.

Figure 1.

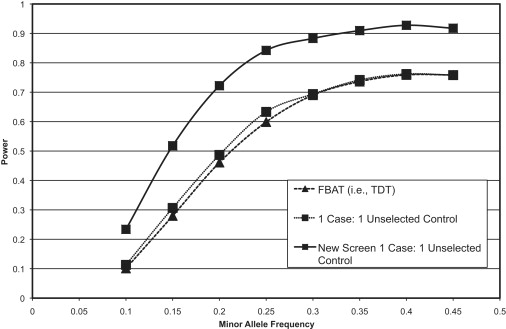
Power Simulations Comparing the Method Proposed Here to the Standard TDT and Case-Control Analyses while Using Unselected Controls

This figure depicts the results of power simulations in which we used 3000 probands and compared the standard TDT and case-control methods to the new screening method we propose in this manuscript. In this example, we assume that the control individuals are unselected for the disease of interest and that there is a 1:1 matching of cases to control individuals. By using unselected controls, we assume that there are cases in the control sample at the rate equal to the prevalence of disease in the population.

Figure 2.

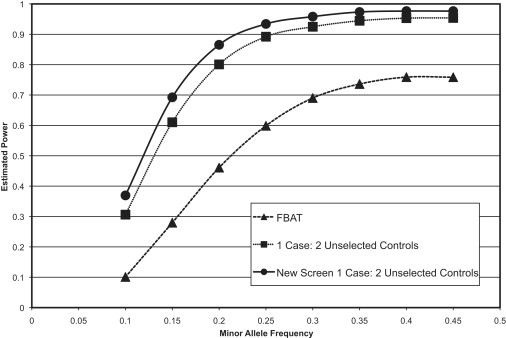
Power Simulations Comparing the Method Proposed Here to Standard TDT and Case-Control Analyses with a 1:2 Ratio of Cases to Unselected Controls

This figure depicts the results of power simulations in which we used 3000 probands and compared the standard TDT and case-control methods to the new screening method we propose in this manuscript. In this example, we assume that the control individuals are unselected for the disease of interest and that there is a 1:2 matching of cases to control individuals. By using unselected controls, we assume that there are cases in the control sample at the rate equal to the prevalence of disease in the population.

If the number of unselected controls is increased to a 1:2 matching ratio, the standard case-control analysis has increased power compared to the TDT, as shown in Figure 2. This figure also illustrates that the proposed methodology consistently remains the highest powered of the three analysis methods.

In some cases, it is possible to obtain a control group that is selected for the disease of interest, meaning that all individuals in the control group are known to not have the disease being studied. Figure 3 shows that, in case of 1:1 case-control matching with selected controls, the new testing strategy substantially outperforms both the TDT and the case-control analysis. Comparable to the situation, as shown in Figure 4, with unselected controls, if the matching is increased to a ratio of two controls for every case, the proposed methodology still outperforms the other two methods but is only marginally better than a standard case-control design. However, one has to bear in mind that this approach still has the additional benefit of being much less susceptible to population stratification, given that a family-based analysis is incorporated into the test statistic.

Figure 3.

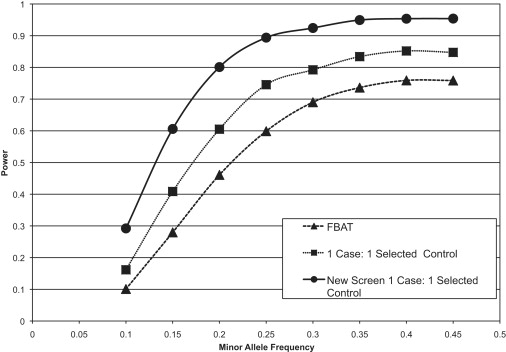
Power Simulations Comparing the Method Proposed Here to the Standard TDT and Case-Control Analyses while Using Selected Controls

This figure depicts the results of power simulations in which we used 3000 probands and compared the standard TDT and case-control methods to the new screening method we propose in this manuscript. In this example, we assume that the control individuals are selected for the disease of interest and that there is a 1:1 matching of cases to control individuals.

Figure 4.

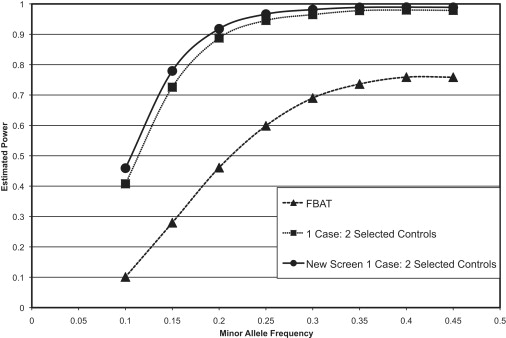
Power Simulations Comparing the Method Proposed Here to Standard TDT and Case-Control Analyses with a 1:2 Ratio of Cases to Selected Controls

This figure depicts the results of power simulations in which we used 3000 probands and compared the standard TDT and case-control methods to the new screening method we propose in this manuscript. In this example, we assume that the control individuals are selected for the disease of interest and that there is a 1:2 matching of cases to control individuals.

We assessed the type I error for our simulations with an overall alpha level of 0.05 and 100,000 replicates. After performing this simulation eight different times, the type 1 error rates ranged from 0.495 to 0.0506, indicating that the type I error rate for the proposed methodology was extremely close to what we would expect.

We applied these data to families that were collected by the International Multicenter ADHD Genetics (IMAGE) project. Families were identified through attention deficit hyperactivity disorder (ADHD) (MIM 143465) probands aged 5 to 17 attending outpatient clinics at the data collection sites in Europe. A total of 958 affected proband-parent trios were initially selected for the GWAS scan (accession number phs000016.v1.p1). Family members were white, of European origin from seven countries around Europe, including Belgium, Germany, Ireland, the Netherlands, Spain, Switzerland, and the United Kingdom, as well as Israel. In this analysis, we excluded all individuals who were of Israeli or Spanish descent because of known differences in ancestral backgrounds for these individuals, making the total number of people that we used in this study 695 parent-offspring trios. More clinical information about the sample can be found elsewhere.²⁰ Genotyping was performed by Perlegen Sciences with the Perlegen platform. The Perlegen array has 600,000 tagging SNPs designed to be in high linkage disequilibrium with untyped SNPs for the three HapMap populations. After the data cleaning and quality control procedures, 429,981 autosomal SNPs were available for analytic use. More details can be found elsewhere.²⁰ All of the procedures to collect the IMAGE data were in accordance with the ethical standards of the responsible committee on human experimentation at each institution.

We obtained 1595 individuals that were a part of the Psoriasis study, including 676 control individuals and 919 psoriasis cases, from the dbGaP database (accession number phs000019.v1.p1).²¹ The institutional review boards at the respective institutions approved these studies. These individuals comprised the control sample that was used in this analysis. In order to minimize problems with population stratification, we used EIGENSTRAT to identify individuals with ancestral backgrounds that are not representative of the ADHD individuals. We identified 35,836 SNPs that had minimal linkage disequilibrium (r² < 0.01) to use in EIGENSTRAT. We used five iterations of subject removal in which individuals were removed if they were greater then six standard deviations from the mean of any of the top ten axes of variation. This resulted in 138 controls and 9 ADHD individuals being removed from the analysis. After we identified a group of ADHD individuals and properly matched control individuals, we used the proposed statistical test to identify genetic associations for ADHD. We also evaluated the quantile-quantile plot to verify that the p values did not deviate significantly from what was expected.

The new method was applied to the IMAGE sample, and the top 20 associated SNPs are listed in Table 1. Two of the associations are in genes that have been linked with ADHD previously. rs2919435 had an uncorrected association p value of 1.85 × 10⁻⁵. This SNP is located in the serotonin receptor 5A (HTR5A [MIM 601305]), which has been studied previously in relation to ADHD with negative findings.²² rs1477941 had an association p value of 5.07 × 10⁻⁵. This SNP is located on the GNAL (MIM 139312) and is also among the top associated SNPs that has been previously studied with regard to ADHD.^23,24 Both animal studies and human studies for ADHD have been performed on GNAL previously. GNAL was significantly altered in both the spontaneously hypertensive rats and the PCB-exposed Sprague Dawley rats that mimic ADHD behaviors.²⁴ Previous genetic associations with ADHD were observed in this gene.²³ Table 1 demonstrates that, although many of the associations identified with the new screening method are also identified with the classical TDT, the SNPs with the strongest genetic associations change. Therefore, if a percentage of SNPs are to be followed up, the lists of SNPs that are carried forward would be different for the two methods. Knowing that the new screening method is more powerful, it is clearly best to select the SNPs with the strongest associations via the new method.

Table 1.

Top Association Findings for ADHD in the IMAGE Population

SNP	Location	Gene	MAF	FBAT P Value	Case-Control P Value	New Screen P Value
rs12972735	19	NA	0.38	0.0010	2.06E-05	1.9E-07
rs925910	2	NA	0.48	0.0004	0.00123	3.03E-06
rs192770	3	NA	0.35	0.0007	0.00066688	3.13E-06
rs9459502	6	NA	0.18	0.0022	0.000527839	7.49E-06
rs829417	1	RAP1GA1 (MIM 600278)	0.30	0.0013	0.001130348	9.30E-06
rs1378945	4	KIAA0746 (MIM 100174136)	0.28	3.22E-05	0.031866027	1.76E-05
rs16889099	4	NA	0.07	3.52E-05	0.03057089	1.78E-05
rs7589522	2	FIGN (MIM 605295)	0.28	4.75E-05	0.026842544	2.16E-05
rs2919435	7	HTR5A (MIM 601305)	0.40	6.98E-05	0.02558088	1.86E-05
rs7743622	6	MOXD1 (MIM 609000)	0.43	0.00092	0.003784992	2.33E-05
rs12686281	9	NA	0.09	5.33E-05	0.036737594	3.10E-05
rs16985637	22	TRIOBP (MIM 609761)	0.06	0.00033	0.012050178	3.11E-05
rs470705	2	NA	0.35	0.01408204	0.000265207	3.14E-05
rs2082412	5	UBLCP1 (MIM 609867)	0.20	0.031522535	7.98E-05	3.38E-05
rs7557548	2	NA	0.22	0.00689115	0.000713226	3.21E-05
rs1585804	17	C17orf54	0.30	0.00928631	0.000566461	3.65E-05
rs1026942	4	NA	0.13	0.001519208	0.004341154	3.88E-05
rs2915806	5	SH3TC2 (MIM 608206)	0.41	0.001822735	0.003700023	3.91E-05
rs1335706	10	NA	0.38	0.00063446	0.009405834	4.07E-05
rs1477941	18	GNAL (MIM 139312)	0.10	0.003568628	0.002502729	5.07E-05

This table lists the top SNPs associated with ADHD that were identified by using ADHD individuals from the IMAGE sample and unselected controls from the freely available psoriasis sample. The association p values are listed from lowest to highest along with relevant information about the SNP, including the chromosomal location, whether it lies within a gene, the minor allele frequency, and the FBAT and case-control p values. NA denotes not available.

After the genetic associations for ADHD were identified from the IMAGE sample, we used an in silico population to replicate the findings. Details about this sample can be found elsewhere (E. Mick, personal communication). Briefly, parent-offspring trios were ascertained at Massachusetts General Hospital, Washington University at St. Louis, and University of California at Los Angeles (UCLA), and this study is called PUWMa (Pfizer-UCLA-Washington University at St. Louis-Massachusetts General Hospital multisite GWAS). Children were 6–17 years of age at initial assessment and met criteria for DSM-IV-TR ADHD. Genomic DNA samples from the Massachusetts General Hospital and Washington University at St. Louis were genotyped with the Illumina Human1M BeadChip, whereas the UCLA samples were genotyped with the Illumina Human1M-Duo array. Genotyping calls were generated and then merged into a single file. After applying all data-cleaning and quality-control filters, there were 835,136 SNPs in 735 ADHD trios from 732 families. All of the procedures to collect this replication population were in accordance with the ethical standards of the responsible committee on human experimentation at each institution.

There were 173,675 common SNPs that were genotyped in both IMAGE and the replication population. We identified the association p values that were less than 0.05 in the IMAGE sample (20,297 SNPs) and merged the association p values at these SNPs with the replication population, resulting in 8,992 genotyped SNPs. Table 2 lists the SNPs with the 20 lowest association p values in the PUWMa sample, among those selected from the IMAGE sample. rs220597 also had a nominal association with ADHD in the IMAGE (p = 0.037) sample and was among the most strongly associated SNPs in the replication population (p = 0.0027). This SNP is in the glutamate receptor subunit gene, has been evaluated previously as a candidate gene, and has been shown to be associated with ADHD.^25,26

Table 2.

Top Replication Association P Values in the PUWMa Replication Sample

SNP	Location	Gene	MAF	IMAGE New Screen P Value	Replication P Value
rs4369599	15	NA	0.245	0.017	0.00033
rs200654	20	TSHZ2 (MIM 128553)	0.432	0.048	0.00082
rs931671	17	NDEL1 (MIM 607538)	0.382	0.034	0.00095
rs4257183	15	NA	0.123	0.015	0.00113
rs7947031	11	NA	0.172	0.025	0.00170
rs4234306	3	NA	0.470	0.009	0.00188
rs16904936	8	ST3GAL1 (MIM 607187)	0.025	0.031	0.00189
rs11706690	3	CHL1 (MIM 607416)	0.356	0.001	0.00204
rs9912168	17	NA	0.335	0.009	0.00209
rs2088108	1	NA	0.140	0.040	0.00239
rs9644708	8	TNKS (MIM 603303)	0.203	0.030	0.00255
rs2255672	18	MRO (MIM 608080)	0.272	0.026	0.00261
rs220597	12	GRIN2B (MIM 138252)	0.348	0.037	0.00269
rs1661281	10	ANKRD22 (MIM 52024)	0.305	0.043	0.00270
rs1504508	18	NA	0.245	0.025	0.00291
rs10109988	8	NA	0.276	0.038	0.00296
rs17829444	14	RAD51L1 (MIM 602948)	0.201	0.029	0.0031
rs210837	17	NA	0.075	0.045	0.0031
rs1895699	2	NA	0.238	0.049	0.0031
rs2149698	13	NA	0.406	0.020	0.0033

This table lists the SNPs with the strongest genetic associations in the PUWMa replication sample. Note that the genotyping platforms for the initial and replication samples were different, and as such there were a substantial number of SNPs that were dropped from this comparison. The replication association p values are listed from lowest to highest along with relevant information about the SNP, including the chromosomal location, whether it lies within a gene, the minor allele frequency, and the initial IMAGE new screen p values. NA denotes not available.

Among the SNPs that were evaluated via the new screening methodology, we were able to identify three SNPs in candidate genes that were identified previously as ADHD candidate genes. Although none of the genetic associations achieved genome-wide significance, the fact that three of these SNPs are in genes that were previously identified for ADHD demonstrate the promise of this new methodology.

In this manuscript, we propose a new testing method for parent-offspring trios in which researchers can take advantage of the readily available control genotypes by performing an analysis that combines both FBAT and case-control analyses. This method is widely applicable because it can be extended to any situation in which both parent-offspring trios and case-control data are available. This method also easily extends to the case in which there are large nuclear families. By continuing to parse the genetic information into the within and between components, a family-based association test and the case-control analysis can be performed separately and then combined, similar to the case of a parent-offspring trio. In such an analysis, the parental information is replaced by the sufficient statistic by Rabinowitz and Laird,⁹ and the correlation among offspring in the same family can be taken into account by conditional logistic regression. Furthermore, a similar approach can be used for quantitative phenotypes as well.

We have found that this analysis strategy has impressive improvements in power compared with an FBAT alone. In addition, this methodology consistently has more power than a case-control analysis of the same sample size. In addition to improvements in power, this methodology is more robust against population stratification because it does not rely on large sample theory. Therefore, the findings are more robust against population stratification when compared with standard methodologies. Despite this, it is still important to make sure that the control individuals are well matched to the cases by using some type of population stratification correction, which can be performed with one of several programs.^18,27 By incorporating additional control individuals, this approach has great promise to identify genetic variants for parent-offspring trios that are not identified with the trios only.

Web resources

The URLS for data presented herein are as follows:

• PBAT Software, http://www.biostat.harvard.edu/∼clange/default.htm

• Online Mendelian Inheritance in Man, http://www.ncbi.nlm.nih.gov/Omim/