Quantitative Determination of Hydrate Content of Theophylline Powder by Chemometric X-ray Powder Diffraction Analysis

Abstract

The purpose of this study was to establish a calibration model to predict the hydrate content in powder materials consisting of anhydrate (theophylline anhydrate (THA)) and theophylline monohydrate (THM) by using various kinds of X-ray powder diffraction (XRPD) analytical methods. XRPD profiles were measured five times each for 11 standard samples containing of THA and THM. THM content in the standard samples was evaluated based on XRPD profiles by the diffraction peak height and area methods, and the Wakelin’s and principal component regression (PCR) methods, respectively. Since THA and THM were cube- and rod-shaped particles, the standard samples consisted of THA and THM showed crystal orientation due to THM crystal shape. THA showed reproducible XRPD profiles, but THM showed fluctuating intensities in some specific peaks in the profiles. The linear calibration models were evaluated based on calibration XRPD datasets of the standard materials by various methods. In the result based on validation XRPD datasets, the order of the mean bias and the mean accuracy were peak height > peak area > Wakelin’s > PCR, indicating that PCR was the best method to correct sample crystal orientation. The effectiveness of the PCR method in construction of calibration models was discussed by a scientific approach based on regression vectors.

INTRODUCTION

The polymorphs and solvates of pharmaceuticals exhibit differing physicochemical properties such as solubility, dissolution rate, stability, and hygroscopicity and differing pharmaceutical properties such as bioavailability, efficacy, degradation, and toxicity (1). Therefore, for bulk drugs which have polymorphism and solvates, pharmaceutical regulations require that an appropriate solid-state of the bulk powders is provided in which only one crystalline modification is included or specified crystalline form contents are controlled (2). X-ray powder diffraction analysis (XRPD) is the most popular and useful evaluation method to identify of crystalline modifications and determine crystalline form content in a bulk powder for pharmaceutical preparations (3). XRPD might be also effective to determine the amounts of crystalline form in medicine as a noncontact, nondestructive inspection technique (4). However, the XRPD method has relatively large errors, around ±5%. This limitation of accuracy is caused by imperfect homogeneity in the crystalline standard samples and crystal orientation when the sample powder is loaded on the glass plate (5). Imperfect homogeneity of the standard sample can be improved by avoiding destruction of the crystalline form during the mixing process (6,7) While crystal orientation is caused by aeolotropic crystal habit of polymorphic forms. In order to obtain accurate XRPD determination, Okumura et al. developed a jet mill micronization and rubber ball mixing method to avoid changes in crystallinity or polymorphic content during mixed of the samples (8). The obtained samples were much better mixing than before but were still far from homogenous.

Meanwhile, since the introduction of guidelines for process analytical technology (PAT) by the Food and Drug Administration, online, real-time analyses as a tool for monitoring and controlling manufacturing processes have become increasingly accepted in the pharmaceutical industry (9,10). Near-infrared spectroscopy (NIR) is currently the most important technique for PAT (11–15), since it can evaluate drug and polymorphic contents in pharmaceutical dosage forms with a quick, noncontact, and nondestructive method. However, it is not easy to measure thick tablet samples by NIR (16), since light does not penetrate deeply into a powder bed. On the other hand, X-ray beam has deep penetration property into a tablet. So, the XRPD is available to evaluate crystalline transformation of bulk powder during pharmaceutical process (17). If the problems of imperfection of the standard sample homogeneity and the crystal orientation are solved, the XRPD will become more robust method for evaluation of crystal content in online pharmaceutical manufacturing processes as one of PAT tools. For this reason, the chemometric XRPD method was investigated as a quantitative method for the prediction of polymorphic content in a previous study (5,7). The results confirmed the importance of standard sample quality and the usefulness of the chemometrics method for accuracy of quantitative XRPD analysis.

In the present study, the chemometrics XRPD method was applied to quantitative evaluation of hydrate and solvate in a solid-dosage form. The determination of theophylline hydrate content as anti-asthma drug is compared with conventional analytical methods, such as the diffraction peak and Wakelin’s methods.

MATERIALS AND METHODS

Materials

Theophylline anhydrate (THA) was obtained from Shizuoka Coffein Co., Ltd. (Shizuoka, Japan), and theophylline monohydrate (THM) was obtained by recrystallization from distilled water as previously reported (18). The XRPD and differential scanning calorimetry (DSC) data for THA and THM identified them as reported anhydrate and monohydrate TH data, respectively (18,19). Standard samples consisting of THA and THM powders were obtained as follows: after both THA and THM sample powders were sieved with a No. 42 mesh screen (350 μm), a total of 5.0 g of powders was mixed at various ratios of THA and THM (0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100% w/w THM) in a swollen plastic bag for 15 min by hand. The actual THM content in 30% and 70% w/w THM standard sample powders were evaluated by measuring of a latent heat of dehydration of THM on differential scanning calorimetry (n = 5) as described below. Since the coefficient of variance of THM content in 30% and 70% w/w THM were within 0.05, it indicated that the THM standard sample powders had sufficient sample homogeneity. In order to evaluate crystal orientation of THA and THM, the standard sample mixed powders were subjected to low pressure and high pressure in a glass sample holder using a glass plate, and then images were taken with a digital microscope.

Microscopic Observation

The THA and THM samples were coated with gold in an ion sputter JFC-1100 (Jeol Datum Co., Japan), and photomicrographs of samples were taken with a scanning electron microscope (SEM) (model JSM-5200LV, Jeol Datum Co., Japan). THA and THM crystals and standard sample mixtures were observed by SEM and digital microscope (Type VH-700, Keyence Co. Ltd., Tokyo, Japan).

Thermal Analysis

DSC was performed with a type 3100 instrument (Mac Science Co., Tokyo, Japan). The operating conditions in the open-pan system were as follows: sample weight, 5 mg; heating rate, 10°C/min; N₂ gas flow rate, 30 ml/min.

X-ray Powder Diffraction Analysis

XRPD profiles were obtained using an X-ray diffractometer (RINT-ULTIMA, Rigaku Co Ltd., Tokyo, Japan). The measurement conditions include: scan mode—step scan, target—Cu, filter—Ni, voltage—40 kV, current—20 mA, scan speed—2.0°/min, receiving slit—0.1 mm, time constant—1 s, scan width—0.1°/step. Eighty milligrams of sample powder was loaded into an X-ray diffraction measurement glass holder with various loading pressure with a glass plate by hands. XRPD measurements were conducted five times each for 11 standard samples.

The peak height and area methods

In the diffraction peak height and area methods, peak height and area were measured by using JADE (Materials Data Inc., CA). Calibration curves for the peak height and area methods were obtained based on the total area of three diffraction peaks at 2θ = 11.50°, 14.72°, and 27.08° attributable to THM, respectively.

Wakelin’s method

Wakelin developed a method for determination of the crystallinity index from XRPD profiles as follows (4,20): The difference of the corrected intensity between THA and THM standard samples and that between THA standard sample and an unknown sample are calculated first over a wide range of diffraction angles, as shown in Eqs. 1 and 2.

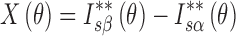1

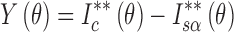2

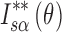: Secondary normalization of diffraction intensity of THA, 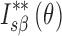: Secondary normalization of diffraction intensity of THM, 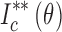: Secondary normalization of diffraction intensity on mixture with THA and THM, 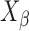: Crystalline content of THM

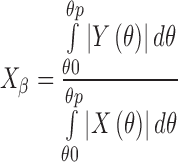3

The integration method considers that 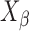corresponds to the ratio of the area enclosed by the curves of 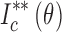and 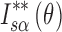to that enclosed by the curves of 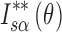and 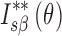over a wide range of Bragg’s angle (θ₀∼θ_p), and 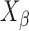can be obtained by Eq. 3.

Principal Component Regression Method (PCR)

To predict value y from a suite of other measurement x_j (where j = 1, 2,..,y = m), we must first establish a relationship between two sets of measurements. If we assume that y, THM content, is linearly related to x, intensity of XRPD, and write:

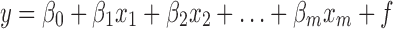4

then, the β specifies the relationship, and f contains the error in describing this relationship. For a set of n samples (i = 1,2,..,n):

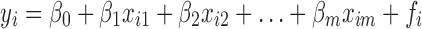5

In matrix format, this becomes

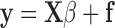6

The error vector, f, is included because it is unlikely that y can be expressed exactly in terms of the X block; f_i is the y residual for the ith sample. The determination of the vector of regression coefficients allows future values to be predicted from future X block measurements. Thus, finding the β vector is described as creating a regression model.

PCR is presented as regression of y on selected principal components of X. Properties of PCR are given together with a discussion on selection of eigenvectors.

A spectrum including n spectral data can be seen as a point in an n-dimensional space. In multivariate data analysis, PCA/PCR of a spectral data matrix X is a basic tool. PCA/PCR decomposes X into three matrices (Eq. 7 (21))

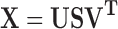7

This decomposition is particularly useful for converting X to a few information plots (score plots and loading plots) and for modeling the systematic structure in X. The U matrix hold the eigenvectors of the row space, the V matrix holds eigenvectors of the column space, S is a diagonal matrix whose diagonal elements are the singular values, T is a scores matrix, and L is a loadings matrix.

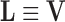8

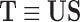9

10

The solution then becomes:

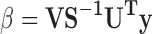11

where this b term is the regression vector. Predicting y from a new x form from:

12

In this study, a XRPD profile consist of the data 1,651 points between 2θ = 6° to 39° was measured for the standard sample mixing with THA and THM. A total of 55 XRPD were measured for 11 standard sample sets with various degree of THM content. Forty-four XRPD were selected for the calibration set and were used to establish a calibration model with which to predict the hydrate content by PCR. The other 11 XRPD were used for prediction of calibration (prediction set). The XRPD for samples were performed a pretreatment to minimize experimental error by using transformations of mean-center method. A chemometric analysis was performed using the PCR program associated with the Pirouette software (InfoMetrix Co., USA). The best conditions were optimized to minimize the standard error of cross-validation (SEV) by the leave-out-one cross-validation method.

RESULTS

Influence of Crystal Orientation on the XRPD Profile of TH Bulk Powder Containing the Hydrate Form

Figure 1 and Table I present the effect of a packing presser on XRPD peak intensity of THA and THM. THA showed reproducible XRPD profiles, but THM had some fluctuating peaks. The intensity of the peaks due to THA was not affected by packing pressure, and the % variance of all of peaks due to THA was less than 13%. In contrast, the peaks at 2θ = 14.7°, 17.8°, and 34.7° in XRPD of THM showed more than 60% variance in peak intensity.

Fig. 1.

Reproducibility of XRPD peak intensity of THA (a) and THM (b)

Table I.

XRPD Diffraction Angle and Intensity of THA and THM

2θ	Average peak (ops)	SD	% Variance
Anhydrate
7.28	2,856	369	12.92
12.78	20,829	1,943	9.33
14.46	2,262	155	6.83
20.22	145	6	4.44
21.06	764	58	7.55
21.76	679	52	7.66
22.28	527	26	4.99
25.78	6,429	322	5.00
27.56	2,896	137	4.73
27.86	2,786	136	4.87
Monohydrate
8.92	7,877	1,995	25.33
11.50	9,659	1,690	17.50
13.42	7,246	961	13.26
14.72	33,519	23,161	69.10
17.84	3,028	1,974	65.17
18.60	4,459	1,508	33.83
23.16	2,351	226	9.59
24.12	2,033	796	39.16
27.08	10,718	3,590	33.49
34.70	1,230	887	72.13

SEM observations of particles and tightly packed THA and THM indicated as follows: the primary particles of THA and THM were observed as cube- and rod-shaped particles. The shapes of THA and THM particles affected on their packing in a glass sample holder. Cube-shaped particles of THA were randomly placed in the holder obtained by low or high pressed. In contrast, Rod-shaped particles of THM were orderly packed in the tightly packed sample by the pressurization. These results showed that rod-shaped particles were oriented by pressurization. Crystal orientation in the sample holder directly affected the peak area intensity of the sample powder, and it reduced accuracy of quantitative determination by XRPD.

Predictability of THM Content by the Peak Height and Area Methods

The calibration curves to evaluate THM content by the peak height and area methods are summarized in Table II: Both of the calibration curves had sufficient linearity and could evaluate THM content.

Table II.

The Calibration Curves to Evaluate THM Content by the Peak Height and Area Method

Method	Slope	Y-intercept	γ
	cps/%	cps
The peak height	405.2	−4,934	0.8686
The peak area	5,381	−34,410	0.9403

Figures 2 and 3 show the relationships between the actual and predicted content of THM by the peak height and area methods. The plots for the peak height and area methods give a straight line with a correlation coefficient constant, γ = 0.7542 and 0.8839, respectively, but the predicted values were not all within the 95% predictive intervals, and all data were dispersed widely. The accuracy of the calibration curve was evaluated based on the validation dataset using the mean bias and mean accuracy ((Bm and Am), Eqs. 13 and 14, respectively) and are summarized in Table III.

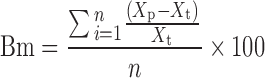13

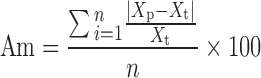14

where Bm is a percentage of the mean bias, Am is a percentage of the mean accuracy, X_p is the predicted value of THM content, X_t is the actual value of THM content, and n is the number of experiments.

Fig. 2.

The relationship between the actual and predicted content of THM by the peak height method. The symbols and error bars present average and standard deviation. The solid line, long dash line, and dotted line represent a regression line, 95% predicted interval, and 95% confidential interval, respectively

Fig. 3.

The relationship between the actual and predicted content of THM by the peak area method. The symbols and error bars present average and standard deviation. The solid line, long dash line, and dotted line represent a regression line, 95% predicted interval, and 95% confidential interval, respectively

Table III.

The γ, Bm, and Am of the Calibration Models Evaluated Based on the Validation Data by Various XRPD Methods

	Peak height	Peak area	Wakelin’s	PCR
γ	0.7545	0.8843	0.9835	0.9843
% Mean bias	−52.33	12.62	13.62	3.231
% Mean accuracy	62.61	31.81	15.31	8.692

Predictability of THM Content by Wakelin’s Method

The calibration plots based on Eq. 3 were obtained from XRPD datasets of the standard samples, and the were evaluated.

Figure 4 shows the relationship between the actual and predicted content of THM by Wakelin`s method. The plot gives a straight line with a correlation coefficient constant, γ = 0.9830. The linearity of the relationship of Wakelin`s method was better than that the peak height and area methods. The Bm and Am of the calibration curve were evaluated based on the validation data, respectively, and are summarized in Table III.

Fig. 4.

The relationship between the actual and predicted content of THM by the Wakelin’s method. The symbols and error bars present average and standard deviation. The solid line, long dash line, and dotted line are the regression line, 95% predicted interval, and 95% confidential interval, respectively

Predictability of THM Content by the PCR Method

In the present study, in order to predict THM content, the calibration models consisting of four principal components (PCs) were established based on XRPD calibration datasets of standard samples consisting of THA and THM by PCR. In Table IV, the SEV value of the calibration model for THM content is 5.670 at PC1, 5.637 at PC2, 4.942 at PC3, and 4.592 at PC4, and the % variance of PC1was 65.65%, the highest.

Table IV.

% Variance and SEV of the Calibration Model by PCR

	% Variance	SEV
PC1	65.65	5.670
PC2	13.85	5.637
PC3	8.45	4.942
PC4	5.83	4.592
PC5	1.75	4.910

Figure 5 shows the relationship between the actual and predicted THM content by PCR. The plot gives a straight line with γ = 0.9846. The obtained calibration model consist of four PCs (4-PC) had good correlation with actual datasets, since the mode had sufficient lower SEV and reasonable percent valiance as show in Table IV. Table III presents correlation parameters of the relationship with the validation approaches. The Bm for the validation of the PCR was calculated to be in the range of 3.231%, and the Am was in the range of 8.692%.

Fig. 5.

The relationship between the actual and predicted THM content by the PCR. The symbols and error bars present average and standard deviation. The solid line, long dash line, and dotted line are the regression line, 95% predicted interval, and 95% confidential interval, respectively

Chemometric Parameters of Calibration Model to Evaluate THM Content by the PCR Method

Figure 6 presents the loading vector of PC1 for the calibration model obtained by PCR. There were positive peaks at 2θ = 8.92°, 11.50°, 14.72°, and 27.08°, and negative peaks at 7.28°, 12.78°, and 25.78° in the loading vector of PC1. This result indicates that the positive peaks were responsible for the positive correlation against increasing THM content and the negative peaks for decreasing content.

Fig. 6.

Loading vector of PC1 for the calibration model obtained by PCR. A and M represent THA and THM

Figure 7 shows the relationship between the score of PC1 and the THM content. The relationship between the score of PC1 and the THM content have a linear (γ = 0.9838), but those for other all PCs did not. The plot of score of PC1 against to THM content had linear relationship except for score of the sample including THM of 100%. This result might indicate that the score of PC1 was closely related to THM content. However, the sample including THM of 100% induced a fluctuation on the PC1 score.

Fig. 7.

The relationship between the score of PC1 and the THM content

Figure 8 presents the regression vector (RV) for the calibration model obtained by PCR. All of the peaks attributable to THM appeared as positive peaks, but the peaks attributable to TMA were as negative. The peak at 2θ = 12.78° was the most responsible for the positive correlation, and the peak at 2θ = 14.72° was the most responsible for the negative correlation against increasing THM. The RV showed almost the same pattern as the loading vector of PC1, since the γ of the relationship between the RV and the loading vector of PCs was calculated to be 0.9480.

Fig. 8.

RV for the calibration model obtained by PCR. A and M represent THA and THM

Figure 9 presents the relationship between the % variance of the diffraction peak intensity of THA and THM against the absolute intensity of the RV. The result suggested that the intensity of the RV attributable to THM decreased with increasing fluctuation of diffraction intensity but that of THA was independent of the fluctuation.

Fig. 9.

The relationship between % variance of the diffraction peak intensity of THA and THM against the intensity of the RV. Arabic numerals in figure indicated 2θ degree of the XRPD peaks of THA and THM

DISCUSSION

Effect of Hydrate Formation on Crystal Orientation and XRPD Profiles of TH

The accuracy of the XRPD determination method is affected by various kinds of errors caused by random and/or systematic problems attributable to instruments and sample quality. Sample homogeneity and crystal orientation of standard samples are related to systematic error. In the present study, the samples were mixed as uniformly as possible without crystalline destruction. However, it is difficult to obtain completely crystal-orientation-free standard samples. Since a quantitative relationship exists between the amount of crystalline solid and diffraction intensity based on randomized particle loading in the sample holder, the diffraction peak intensity of the crystal-oriented sample might be significantly increased or decreased, and accuracy of the XRPD determination method reduced.

Since particles of THA and THM were cube- and rod-shaped particles, the powder bed of THA was packed randomly placed in the holder, but the particles of THM were orderly packed in the holder by pressurization.

In general, the intensity of peaks at a low angle of diffraction fluctuates significantly due to crystal orientation in the holder. Since crystal orientation of THM directly affect on the diffraction peak intensity of the solid, it reduces accuracy of XRPD determination. As shown in Fig. 1 and Table I, the diffraction peaks of THM had more than 60% intensity variance, but those due to THA had small % variance. The results suggested that the standard samples of THA and THM were affected by crystal orientation due to THM content.

Comparative Evaluation of the Hydrate Containing Bulk Powder by Various XRPD Methods

The crystal-oriented standard samples showed the fluctuating diffraction peaks at low angle in XRPD profiles. The effect of the fluctuation of specific diffraction peaks on the accuracy of the determination method was investigated. The plots for the peak height and area methods give straight lines, respectively, but the accuracy of the predicted values was not sufficient as shown in Table III. The result indicated that peak height and area methods had little predictive potential for unstable diffraction datasets.

In order to establish a robust calibration model for crystal-oriented samples, various XRPD methods were applied to TH standard samples. The order of linearity of the calibration models was peak height < peak area < Wakelin’s < PCR, since the γ were 0.7542 and 0.8839, 0.9830 and 0.9846, respectively, as shown results and in Figs. 2, 3, 4, and 5. In the result based on validation data (Table III), the order of both Bm and Am were peak height > peak area > Wakelin’s > PCR; the same as for the calibration model linearity. The result indicated that PCR was the best method to correct sample crystal orientation. This is logical because the peak area method was more accurate than the peak height method, since the peak area method corrected for the particle size effect of XRPD. Wakelin’s method is a conventional statistic method to correct total X-ray diffraction intensity, and the results should be better than the methods based on specific diffraction peaks, such as the peak height and area methods. In contrast, the PCR method corrects for various factors, such as particle size, variability of primary X-ray intensity, crystal orientation, etc., and the results showed the best score of accuracy and reproducibility.

Scientific Background of the Calibration Model to Predict THM Content by the PCR Method

Chemometrics can be used to decompose raw data profiles and help us to understand the significant contributions of specific data groups. In the present study, in order to clarify the scientific background to predict hydrate content of the powder system involving crystal orientation by the PCR method, the calibration models consisting of THA and THM were investigated by analyzing chemometric parameters.

The results of the cross-validation of the calibration model (Table IV) by using SEV indicated the validity of this model with 4-PC. Since the % variance of PC1was 65.65%, it was recognized that the SEV values used to predict the THM content decreased greatly using PC1. The calibration model with 4-PC was showed a linear relationship between the actual and the predicted content of THM (Fig. 5). The γ, Bmm and Am (Table III) of the model based on independent the validation datasets also showed the best scores in the model for linearity and accuracy.

As shown in Figs. 6 and 8, the RV had almost the same pattern as the loading vector of PC1. The γ of the relationship between the RV and the loading vector of PC1 was the best value, 0.9480 as shown in Table V, and the RV was almost governed by the loading vector of PC1. However, the calibration model based on PC1 was not sufficient, since the sample including THM of 100% induced a fluctuation on the PC1 score as shown in Fig. 5. The result indicated that the calibration model with 4-PC was corrected a model to evaluate THM content in the present study.

The result (Fig. 9) of the relationship between the % variance and absolute intensity of RV suggested that analysis accuracy of the PCR method depended on fluctuation of diffraction intensity of THM but that of THA was independent from the fluctuation. This result suggested that the diffraction peak intensity of THM was unstable due to crystal orientation, since the primary particle of THM were rod-shape particle but that of THA was cubic. Accordingly, the RV was calculated quantitatively based on the diffraction intensity of stable diffraction peaks of THM and all of THA by PCR. It was suggested that this selectivity contributed to the improvement in the accuracy of the calibration model, and it was demonstrated experimentally that the PCR efficiently extracted information from the diffraction profiles and cancelled noise.

CONCLUSION

The XRPD method is described in the pharmacopoeia of JP, EU, and USA as an important way to evaluate the crystalline phase of the bulk powder of pharmaceuticals. Since there are some problems with the XRPD method, such as particle orientation in preparing crystalline samples, the degree of precision is relatively low. However, if these problems are solved, the XRPD method can be used for high-quality control of medicine in a nondestructive and noncontact analysis. In the present study, the PCR method could evaluate hydrate content in pharmaceutical powder form without sample destruction to avoid the effect of particle orientation based on statistical theory. The chemometrical-XRPD method was, therefore, demonstrated as potentially effective for the nondestructive and noncontact analysis of PAT.