Kinship between parents reduces offspring fitness in a natural population of Rhododendron brachycarpum

Abstract

Background and Aims

A reduction in offspring fitness resulting from mating between neighbours is interpreted as biparental inbreeding depression. However, little is known about the relationship between the parents' genetic relatedness and biparental inbreeding depression in their progeny in natural populations. This study assesses the effect of kinship between parents on the fitness of their progeny and the extent of spatial genetic structure in a natural population of Rhododendron brachycarpum.

Methods

Kinship coefficients between 11 858 pairs of plants among a natural population of 154 R. brachycarpum plants were estimated a priori using six microsatellite markers. Plants were genotyped, and pairs were selected from among 60 plants to vary the kinship from full-sib to unrelated. After a hand-pollination experiment among the 60 plants, offspring fitness was measured at the stages of seed maturation (i.e. ripening) under natural conditions, and seed germination and seedling survival under greenhouse conditions. In addition, spatial autocorrelation was used to assess the population's genetic structure.

Key Results

Offspring fitness decreased significantly with increasing kinship between parents. However, the magnitude and timing of this effect differed among the life-cycle stages. Measures of inbreeding depression were 0·891 at seed maturation, 0·122 (but not significant) at seed germination and 0·506 at seedling survival. The local population spatial structure was significant, and the physical distance between parents mediated the level of inbreeding between them.

Conclusions

The level of inbreeding between individuals determines offspring fitness in R. brachycarpum, especially during seed maturation. Genetic relatedness between parents caused inbreeding depression in their progeny. Therefore, biparental inbreeding contributes little to reproduction and instead acts as a selection force that promotes outcrossing, as offspring of more distant (less related) parents survive better.

INTRODUCTION

In angiosperms with self-compatible pollination systems, inbreeding can arise as a result of selfing (uniparental inbreeding) or crosses between relatives (biparental inbreeding). Although both modes of inbreeding can reduce the fitness of the resulting offspring (inbreeding depression: Darwin, 1876; Charlesworth and Charlesworth, 1987), most empirical evidence for inbreeding depression in plants comes from uniparental inbreeding in hermaphroditic species (reviewed by Husband and Schemske, 1996). However, biparental inbreeding, and its contribution to inbreeding depression, is likely to be ubiquitous in natural plant populations. In many species, seeds are dispersed over short distances from the maternal plants, and related individuals are thus likely to be neighbours and to cross among each other due to restricted flight distances by pollinators and an increasing probability of pollination with increasing proximity in wind-pollinated species (Levin and Kerster, 1974). Fine-scale genetic structure actually increases biparental inbreeding between plants surrounded by genetically similar neighbours (Williams, 2007; Zhao et al., 2009). In addition, many studies have confirmed that mating between neighbours reduces fitness compared with mating between distant individuals (e.g. Coles and Fowler, 1976; Price and Waser, 1979; Fenster, 1991; Waser and Price, 1991, 1994; Fischer and Matthies, 1997; Byers, 1998; Stacy, 2001; Nuortila et al., 2002; Robertson and Ulappa, 2004). These empirical studies suggest that biparental inbreeding depression occurs frequently in flowering plants. However, little is known about the relationship between the genetic relatedness of the parents and the biparental inbreeding depression that occurs in their progeny in natural populations.

Measuring biparental inbreeding depression is a difficult task if prior information on the relationships among individuals is lacking. For example, evidence of biparental inbreeding depression in crosses between individuals with known parentage was revealed by breeding experiments conducted over 3 years in Raphanus sativus (Nason and Ellstrand, 1995) or over 10 years in Cryptomeria japonica (Kurinobu et al., 1991). As an alternative to breeding over several generations under artificial conditions, molecular markers can be used to estimate natural levels of inbreeding in wild populations, which is especially beneficial in animals and self-incompatible plants, for which crossing experiments are difficult (e.g. Slate et al., 2002; Glémin et al., 2006; Jensen et al., 2007). For example, a ‘mixed-mating model’ has been commonly used to assess the occurrence of biparental inbreeding since the widespread availability of allozyme analysis (Ritland and Jain, 1981; Shaw et al., 1981). In the mixed-mating model, selfing and biparental inbreeding are estimated together as the effective selfing rate, but the negative effect of biparental inbreeding cannot be separated from that of selfing. However, the development of highly polymorphic molecular markers such as microsatellites allows the estimation of genetic relatedness between parents (i.e. can predict the magnitude of biparental inbreeding in their progeny), which can be used to explain the progeny's fitness at an individual level (e.g. Glémin et al., 2006; Teixeira et al., 2009). In addition, progress in statistical methods has allowed the detection of relationships between the degree of genetic relatedness and fitness by more robust methods such as general linear models (Glémin et al., 2006; Armstrong and Cassey, 2007). Therefore, molecular marker-based methods for quantifying biparental inbreeding depression under natural conditions are available.

The magnitude of biparental inbreeding depression can be used to infer patterns of pollen flow in a population. During the past decade, paternity analysis using microsatellite markers in various tree species has shown that a surprising amount of pollen originated from distant sources (e.g. Dow and Ashley, 1998; Streiff et al., 1999; Lian et al., 2001; Latouche-Hallé et al., 2004; Bacles et al., 2005; Cresswell, 2005; Goto et al., 2006). Although the density of pollen grains generally exhibits a leptokurtic distribution, with a rapid decline in density as the distance from the donor increases (e.g. Handle, 1983; Campbell, 1991; Hardy et al., 2004; Robledo-Arnuncio and Gil, 2005), relatively long-distance pollen movement may persist when progeny fertilized by pollen from neighbouring individuals die out because of the effects of biparental inbreeding depression. As supporting evidence, Isagi et al. (2007) demonstrated that long-distance pollen dispersal was made more effective by the local kinship structure in Aesculus turbinata. In this tree population, the survival probability of progeny arising from crosses between neighbours was lower than that of progeny of crosses between less closely related parents during various life stages. Therefore, biparental inbreeding depression can affect both the fitness of the resulting offspring and the effective distance of pollen-mediated gene flow. The tendency for pollen flow to be leptokurtic should lead to the following consequences: (1) the existence of a local kinship spatial structure in plant populations (reviewed by Vekemans & Hardy, 2004), (2) a high likelihood of mating between neighbours (e.g. Handle, 1983; Hardy et al., 2004; Robledo-Arnuncio and Gil, 2005) and (3) selection against offspring that resulted from mating between close relatives (Isagi et al., 2007). Although the first two predictions have been demonstrated in a number of studies, little is known about the selection pressure that acts against mating between related parents through biparental inbreeding depression under natural conditions. One purpose of the present study was therefore to estimate the extent to which biparental inbreeding affects the fitness of the resulting offspring in a natural population.

This study used microsatellite markers to estimate kinship between parents and to infer the magnitude of the inbreeding depression in a natural population of Rhododendron brachycarpum. Like other Rhododendron species, this species has a mixed-mating system (e.g. Kudo, 1993; Escaravage et al., 1997; Kameyama et al., 2000; Ng and Corlett, 2000; Hirao et al., 2006; Ono et al., 2008), in which reproduction occurs both by self-fertilization (selfing) and by mating with other individuals (outcrossing). Thus, the genetic relatedness between individuals varies greatly, from 100 % related (selfing) to completely unrelated. Both uniparental and biparental modes of inbreeding depression can be assessed simultaneously by using a hand-pollination experiment that provides a priori information on the genetic relatedness between individuals.

The primary objective was to determine the effect of parent relatedness on the probability of seed maturation in the field, and the extent of inbreeding depression during seed germination and subsequent seedling survival as measured in a greenhouse. This was accomplished by performing a series of crosses in which a priori information about molecular markers was used to control the crosses to be performed among individuals that varied in their kinship coefficient from 0·5 (self-pollination) to 0 (outcrossing). A second objective was to estimate the natural level of biparental inbreeding in an open-pollinated environment. This was assessed using a mixed-mating model (Ritland, 2002). In addition, the natural levels of inbreeding were estimated at successive stages from mature seeds through germination to reproductively mature adults to verify whether inbreeding is beneficial or detrimental in this species. Finally, population spatial genetic structure was assessed to predict the extent of biparental inbreeding depression.

MATERIALS AND METHODS

Study site and species

This research was conducted in a natural botanical garden at the Mt Hakkoda Botanical Laboratory of Tohoku University in Aomori Prefecture, northern Honshu, Japan (40°38′N, 140°51′E). The altitude of the botanical garden (900 m a.s.l.) corresponds to the transition zone from deciduous broadleaved forest dominated by Fagus crenata to subalpine coniferous forest dominated by Abies mariesii and Betula ermanii. Mean monthly temperatures ranged from −9·3 °C (January) to 20·5°C (August) and mean annual precipitation was 1696 mm between 1997 and 2006.

Rhododendron brachycarpum is an evergreen shrub that reaches heights of up to 3 m. Flowering lasts for 2–4 weeks (between late June and late July) in the botanical garden (Kikuchi, 1976). Adult plants produce axillary inflorescences of 7–20 cream–white flowers. The protandrous flowers have five petals and ten stamens, and attract various types of pollinators, including bumble-bees, honey-bees, small solitary bees, syrphids and other flies, rove beetles, longicorn beetles, and lepidopterans. Fruits mature in October, and include 200–400 tiny seeds that are dispersed by gravity or wind.

Sampling, DNA extraction and genotyping

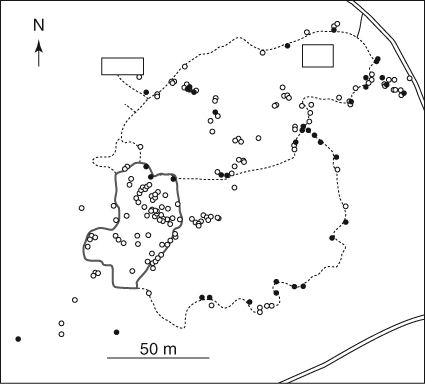
In early June 2006, all flowering adult plants in a part of the botanical garden surrounded by footpaths were mapped (the ‘core area’ in Fig. 1). In addition, about 100 plants from outside the core area were randomly selected and mapped (Fig. 1). The corrected positions of each plant were accurate to less than 1 m as determined with a Pathfinder Pro XR GPS receiver with a real-time differential correction module (Nikon-Trimble, Tokyo, Japan). From these mapped plants (n = 154), leaf samples for genotyping were collected. DNA was isolated using the cetyltrimethyl ammonium bromide extraction procedure (Stewart and Via, 1993). Six loci corresponding to microsatellite markers were used: RM2D2, RM3D1, RM3D2, RM9D6 (Naito et al., 1998), RM2D6 (Kameyama et al., 2001) and RM9D9 (Hirao et al., 2006). The reaction mixture (6 µL) included 10 ng template DNA, 1·2 pmol primers (the forward primers were labelled with fluorescent dye) and 3 µL Multiplex PCR Master Mix (Qiagen, Hilden, Germany). PCR amplification was via a GeneAmp PCR System 9700 (Applied Biosystems, Foster City, CA, USA) under the following conditions: initial denaturation at 94 °C for 15 min; 35 cycles of denaturation at 94 °C for 30 s, annealing at 53 °C for 90 s and extension at 72 °C for 1 min; and a final extension at 60 °C for 30 min. The size of the PCR products was determined using an ABI PRISM 3100 automated sequencer and GENESCAN analysis software (Applied Biosystems).

Fig. 1.

Distribution of sampled individuals of Rhododendron brachycarpum in the study plot. The location of the plants sampled for hand-pollination treatments are shown as closed circles. The area surrounded by the thick grey line represents the ‘core area’ in which all flowering adults of the species were mapped. The open squares represent stations for researchers.

Estimation of kinship coefficients

The following measures of genetic variation were calculated as mean values across the six loci: number of alleles per locus (A), observed heterozygosity (H_o), expected heterozygosity or gene diversity (H_e) and Wright's inbreeding coefficient (f, following the method of Weir and Cockerham, 1984). The significance of f across the loci was determined using the randomized procedures provided in the FSTAT software v. 2·9 (Goudet, 1995). Multilocus kinship coefficients between individuals i and j (F_ij) were estimated according to the method of Loiselle et al. (1995), which is defined as the average across multi-allelic (multilocus) estimates of the kinship coefficient for each allele k:

where p_i and p_j are the frequencies of allele k in individuals i and j, respectively, and 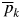is the average frequency of allele k in the population based on a sample size of n individuals. The estimated kinship coefficients were approximated as half of the pedigree-based relatedness: 0·5 for selfed progeny, 0·25 for full-sibs and 0·125 for half-sibs (Loiselle et al., 1995). These calculations were implemented for all pairs of the 154 individuals in the sample (i.e. 11 858 pairs) in SPAGeDi software v. 1·1 (Hardy and Vekemans, 2002).

Pollination experiment

Pairs of plants selected from the total sample of genotyped plants were hand-pollinated to vary the level of the kinship coefficient from self-pollination (assuming F_ij = 0·5) to related plants (full- and half-sibs) to unrelated plants (assuming F_ij = 0·0). In the outcrossed pollinations, pairs were selected to generate a high estimated kinship (F_ij > 0·1) so as to facilitate the detection of biparental inbreeding depression, but they were chosen from among spatially distant (i.e. separated by at least 10 m) individuals to minimize the correlation between spatial genetic structure and inbreeding depression. In late June 2006, 60 plants were selected on this basis, one or two inflorescences per plant were bagged using fine-mesh nets before flower opening. Both hand-selfing and hand-outcrossing pollinations were conducted at least once with each flower with pollen collected from freshly dehisced anthers. Pollinated inflorescences were bagged again until the flowers wilted. In addition, more than 80 flowers of intact plants were marked to estimate mating system parameters (described below) and seed-survival probabilities under open-pollinated treatments. Ripe fruits were collected and counted in October 2006. To assess the success of sexual reproduction, I counted matured and aborted seeds in every fruit under a microscope in the laboratory. Mature seeds were relatively large and plump (≥2·8 ± 0·3 mm long and full), whereas aborted seeds were small and shrunken (Fig. 2). Seed set was calculated as the number of matured seeds divided by the total number of matured and aborted seeds.

Fig. 2.

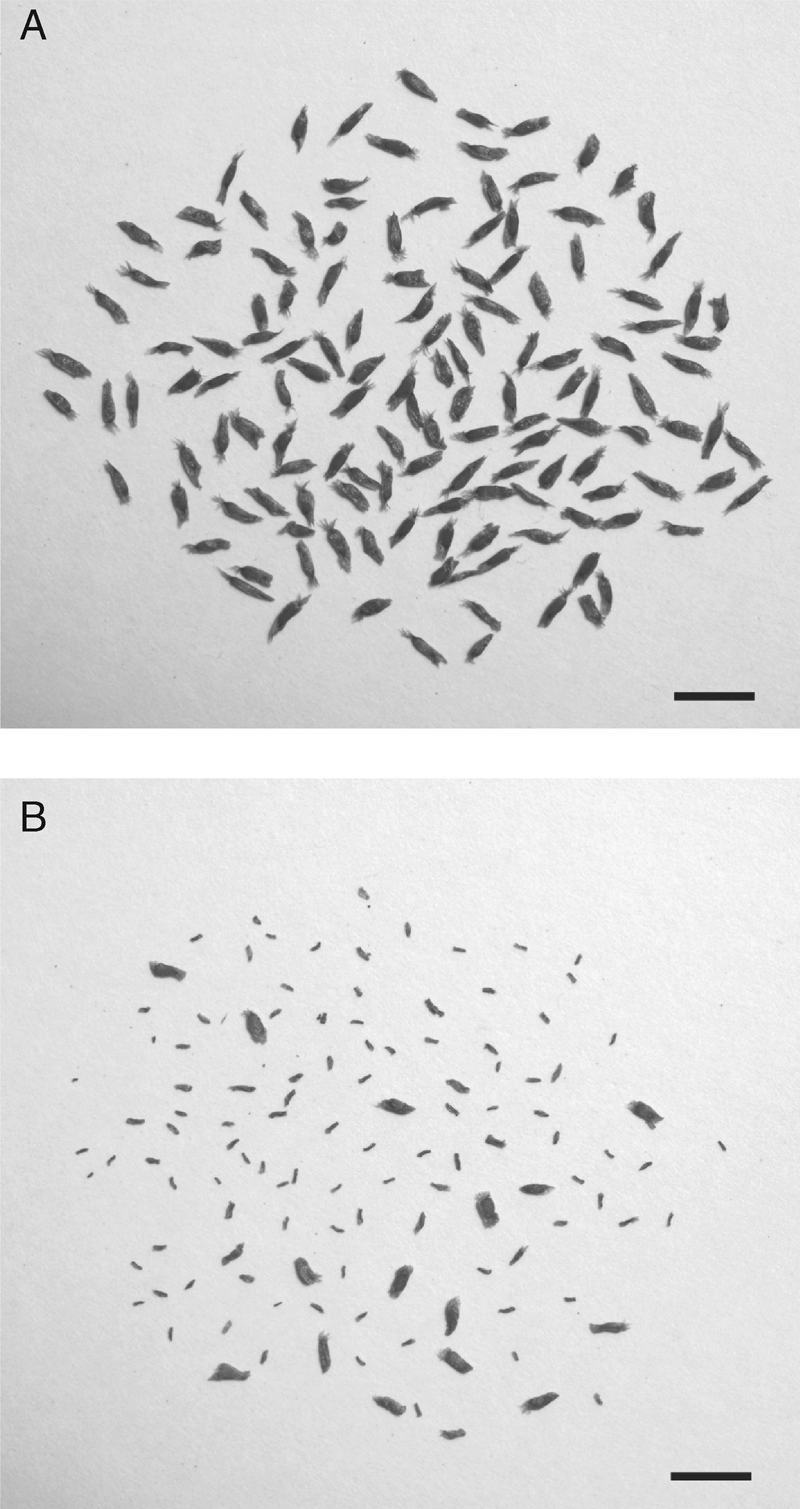
Fully mature seeds from outcross-pollinated fruits (A) and presumed aborted seeds from self-pollinated fruits (B) of Rhododendron brachycarpum. Scale bars = 5 mm.

Seed germination and seedling survival

Offspring fitness was assessed in terms of seed germination and subsequent seedling survival under uniform conditions. In April 2007, 9–60 seeds per fruit were sown on 0·8 % agar medium in 9-cm-diameter Petri dishes and stored them at 4 °C for 2 months as a moist chilling treatment. In total, 544 seeds were sown from 34 hand-selfed fruits, 2056 seeds from 32 hand-outcrossed fruits and 3045 seeds from 56 open-pollinated fruits. After the moist chilling treatment, the dishes were transferred to germination chambers to incubate under a temperature regime of 30/25 °C (12/12 h). I counted germinated seeds after 30 d of incubation to calculate the germination rate (number of germinated seeds divided by number of seeds sowed). At the beginning of July 2007, once true leaves had emerged, more than five germinated seedlings per cross were transferred into peat pots filled with acidic garden compost. In total, 144 seedlings of the hand-selfed seeds were transplanted, 272 seedlings of the hand-outcrossed seeds and 472 seedlings of the open-pollinated seeds. The pots were then placed in a greenhouse under natural sunlight at Hokkaido University, Sapporo (elevation 17 m a.s.l.). Survival rates of the seedlings were recorded at 1-month intervals until November 2007, and seedling survival rate was calculated as the number of surviving seedlings divided by the number of transplanted seedlings on the final observation date.

Mating system

Using 61 seedlings from 26 open-pollinated plants, the proportion of self-fertilized seeds (i.e. the selfing rate) was assessed. Single-locus (s_s) and multilocus (s_m) maximum-likelihood selfing rates were recorded based on Ritland's mixed-mating model (Ritland and Jain, 1981; Ritland 2002). The primary selfing rate (s_p), which represents the selfing rate at the time of pollination, was also estimated by adjusting the observed multilocus estimate (s_m) to account for inbreeding depression using the following formula (Maki, 1993):

where δ is the degree of inbreeding depression during seed maturation (described below).

To estimate the magnitude of biparental inbreeding, two measurements were used: (1) the difference between the single-locus and multilocus estimates of the selfing rate (s_s – s_m), and (2) the correlation of selfing among loci (r_s). The former measurement has been widely used to demonstrate biparental inbreeding, but tends to greatly underestimate its magnitude, especially when the estimates are based on few loci (reviewed by Griffin and Eckert, 2003). In contrast, the estimated r_s corresponds to the proportion of the effective selfing rate that results from true uniparental selfing, with the remainder of the effective selfing rate resulting from biparental inbreeding (Ritland, 2002). These mating system parameters were estimated with MLTR software v. 3·3 (revised May 2008; Ritland, 2002), and the standard errors of these parameters were estimated from 1000 bootstrap replications.

In addition, the selfing rate under open-pollinated conditions was estimated based on the performance of the progeny at three life stages (seed maturation, seed germination and seedling survival) using the following formula (Charlesworth, 1988):

where p_x is the cumulative fitness of the progenies under open pollination, p_w is that of progenies from controlled outcrossing (assuming F_ij = 0) and p_s is that of the selfed progenies (assuming F_ij = 0·5). These fitness values were used to infer the predicted values by means of the logistic analyses described below.

Estimation of inbreeding depression

The degree of inbreeding depression was analysed using generalized linear mixed models (GLMMs), in which the number of surviving offspring at each life-history stage (i.e. matured seeds, germinated seeds and surviving seedlings) over n trials (i.e. aborted seeds plus matured seeds, sown seeds, potted seedlings) follows a binomial distribution with a logit-link function. In the GLMM, the effect of the kinship coefficient between mates (the fixed effect) on offspring survival was assessed using a logistic regression (for details, see Glémin et al., 2006). The y-intercept (β₁) and the coefficient for the kinship (β₂) were tested using the Wald Z-statistic test. The random-effects error structure for survival probability was defined as dependent on the maternal plants. For selfed offspring, the kinship coefficient was adjusted to (1 + F_ii)/2, where F_ii is the inbreeding coefficient of the maternal plants (Glémin et al., 2006). GLMM analysis was conducted using the glmmML function implemented in R software v. 2·7 (R Development Core Team, 2008). To determine whether self-pollinated samples were over-weighted in the results, the GLMM analysis was performed only for hand-outcrossed samples. The relationships were also examined using a general linear model (GLM) to assess the influence of ignoring the dependence on maternal individuals; for this analysis, the glm function provided in R was used. To compare the goodness-of-fit of the above-mentioned models, Akaike's information criterion was calculated (AIC: Akaike, 1974). AIC can be interpreted as the probability that a model is the best one given the observed data and the set of candidate models; that is, the model with the smallest AIC value provides the best fit to the data. The standard measurement of inbreeding depression, 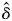, was calculated by comparing the fitness of selfed individuals (assuming F_ij = 0·5) with the fitness of individuals from the controlled outcrosses (assuming F_ij = 0), inferring the predicted values by means of logistic analyses. The magnitude of inbreeding depression was assessed for each life-history stage.

Spatial genetic structure

To assess the spatial genetic structure, spatial autocorrelation analysis was performed on the kinship coefficient. To represent the spatial genetic structure graphically, the average kinship coefficients were calculated for nine distance classes (with the upper limit of these classes at 5, 10, 20, 30, 40, 50, 70, 100 and >100 m). The degree of spatial genetic structure was quantified using the statistic S_p = −b/(1 – F₁), where b is the slope of the linear regression of the kinship coefficient against the natural logarithm of the physical distance, and F₁ is the kinship coefficient for the first distance class (Vekemans and Hardy, 2004). Standard errors for the S_p statistics were estimated using the jackknife procedure across all six loci. I tested for the significance of the genetic structure by comparing b with the values obtained after 9999 permutations of the spatial coordinates for the sampled individuals. In the same way, the 95 % confidence interval for the average kinship coefficient at a given distance was obtained using 9999 permutations. These analyses were conducted in SPAGeDi software v. 1·1 (Hardy and Vekemans, 2002). In addition, the biparental inbreeding depression corresponding to the inferred spatial genetic structure was estimated using the method of Ishihama et al. (2005) but using the following formula:

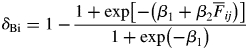where δ_Bi is the degree of biparental inbreeding, 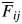is the average kinship coefficient for each distance class that is used to infer the observed value of the spatial genetic structure, and β₁ and β₂ are the y-intercept and parameter estimate for the kinship coefficient, respectively, in the logistic regression used for the estimation of inbreeding depression, as described above. The cumulative amount of biparental inbreeding depression was calculated as the product of the three values from seed maturation to seedling survival.

RESULTS

Genetic variation

In the adult plants, 6–25 alleles per locus were detected, with a mean of 16·7 alleles (Table 1). Expected heterozygosity (H_e) ranged from 0·676 to 0·913, and averaged 0·815 across the six loci. The mean inbreeding coefficient (f) across the loci did not deviate significantly from Hardy–Weinberg expectation (f = −0·013; P > 0·05, randomization test), indicating the existence of a randomly mating population.

Table 1.

Characteristics of the six microsatellite markers used for the genetic analysis based on 154 individual genotypes of Rhododendron brachycarpum

Locus	A	Ho	He	f
RM2D2	16	0·770	0·825	0·067
RM2D6	25	0·914	0·913	−0·001
RM3D1	6	0·733	0·676	−0·085
RM3D2	22	0·892	0·897	0·006
RM9D6	16	0·813	0·783	−0·038
RM9D9	15	0·828	0·794	−0·043
Mean	16·7	0·825	0·815	−0·013

A, number of alleles; H_o, observed heterozygosity; H_e, expected heterozygosity (gene diversity); f, Wright's inbreeding coefficient. The mean f across loci was not significantly different from the expected value under Hardy–Weinberg equilibrium (P < 0·05, randomization test).

Mating

Under open-pollinated conditions, the single-locus and multilocus selfing rates were 0·212 (±0·062 s.e.) and 0·161 (±0·059), respectively. Both s_s – s_m and the correlation of selfing among loci (r_s) indicated that significant biparental inbreeding occurred (s_s – s_m = 0·051 ± 0·040; r_s = 0·675 ± 0·185). The s_s – s_m value indicated that about 25 % (0·051/0·212) of the effective selfing rate was due to biparental inbreeding, whereas the correlation of selfing among loci indicated that biparental inbreeding contributed about 33 % (1 – r_s = 0·325) of the effective selfing. The primary selfing rate (s_p) at the time of pollination, based on the multilocus selfing rate after adjustment for inbreeding depression, was 0·638 ± 0·119.

Magnitude and timing of inbreeding depression

Owing to heavy damage by insects, fruits from only 34 of the 60 pollinated plants could be collected. Almost all of the hand-pollinated flowers, including selfed flowers, developed into fruits if they were not damaged by insects. I collected 34 fruits from the hand-selfed flowers and 52 fruits from the hand-outcrossed flowers.

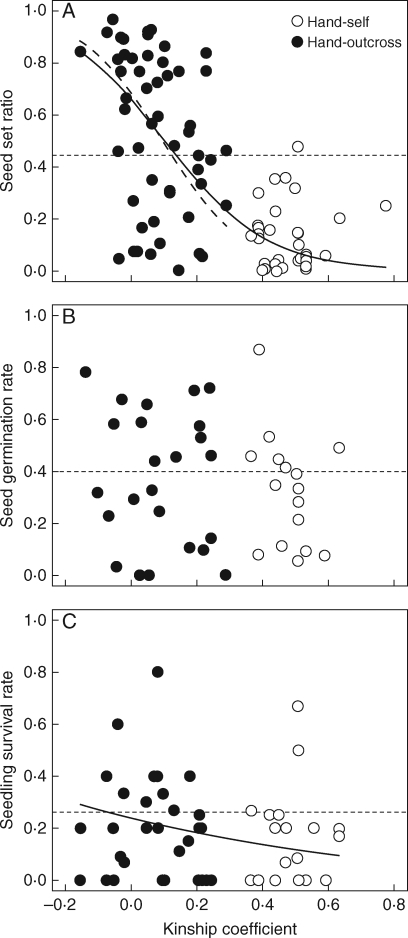
Seed maturation of the hand-pollinated fruit depended significantly on the kinship coefficient (Table 2, Fig. 3A). The GLMM predicted that seed maturation was significantly lower in self-fertilized flowers than in randomly outcrossed flowers (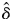 = 0·891, P < 0·05). By contrast, the effect of the kinship coefficient on fitness at the germination stage was not significant ( 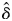= 0·122, P > 0·1; Table 2, Fig. 3B), whereas seedling survival depended significantly on the level of inbreeding ( = 0·506, P < 0·01; Table 2, Fig. 3C). The magnitude of the inbreeding depression was lower during seedling survival than during seed maturation. Cumulative fitness from seed development to seedling survival decreased by 94·6 % in selfed offspring compared with outcrossed offspring. Under the open-pollinated conditions, the survival probabilities of the offspring were 0·436 ± 0·200 (mean ± s.d.) at seed maturation, 0·400 ± 0·239 at seed germination and 0·268 ± 0·196 at seedling survival. The selfing rate of the open-pollinated offspring, as estimated from Charlesworth's (1988) formula, decreased progressively, from 0·404 at seed maturation to 0·151 at seed germination, to 0·023 at seedling survival.

Table 2.

Analysis of the generalized linear mixed model for the relationship between offspring fitness and the kinship coefficient (F_ij) at the three life-cycle stages (seed maturation, seed germination and seedling survival)

	Estimate	s.e.	d.f.	P
Seed maturation
Intercept	0·660	0·282	83	0·0190
	(0·781)	(0·302)	(49)	(0·0098)
Fij	−6·430	0·085	83	<0·0001
	(−8·144)	(0·291)	(49)	(<0·0001)
Seed germination
Intercept	−0·8175	0·354	38	0·0209
	(−0·847)	(0·401)	(22)	(0·0345)
Fij	−0·3665	0·265	38	0·1666
	(−0·097)	1·228	(22)	(0·9371)
Seedling survival
Intercept	−1·171	0·198	53	< 0·0001
	(−1·224)	(0·233)	(30)	(<0·001)
Fij	−1·702	0·655	053	0·0094
	(−1·406)	(1·623)	(30)	(0·3860)

Numbers in parentheses represent the results after excluding the hand-selfed pollinations.

The effect of the kinship coefficient was tested using the Wald Z-statistic test. The data used in this analysis are plotted in Fig. 3.

Fig. 3.

Relationships between kinship coefficient and offspring fitness at three life-cycle stages: (A) seed maturation, (B) germination, and (C) seedling survival. Fitted curves predicted by the generalized linear mixed model are presented when the effect of the kinship coefficient was significant (see Table 2), with hand-self and hand-outcross treatments as indicated. Solid and dashed curves represent the results for all the analysed samples and for the samples after selfing was excluded, respectively. Dashed horizontal lines indicate the level of offspring fitness under open-pollinated conditions.

The GLMMs provided better fits to the data than the GLMs (which ignored random effects), indicating the importance of considering the maternal factor (AIC values for the GLMMs vs. the GLMs: 5391 vs. 10923, respectively, for seed maturation; 239·7 vs. 849·7 for seed germination; and 90·3 vs. 164·9 for seedling survival). Standard deviations of the random effect were 1·56 at seed maturation, 1·42 at seed germination and 0·384 at seedling survival. Even when the GLMM analysis was conducted for only the hand-outcrossed fruit to examine whether self-pollinated samples biased the results, the estimated effect of the kinship coefficient on seed maturation was significant (Table 2, Fig. 3A), supporting the hypothesis that biparental inbreeding depression occurred. However, the effect of the kinship coefficient on seedling survival was not significant when self-pollinated samples were excluded (Table 2, Fig. 3C).

Predicted biparental inbreeding depression based on spatial genetic structure

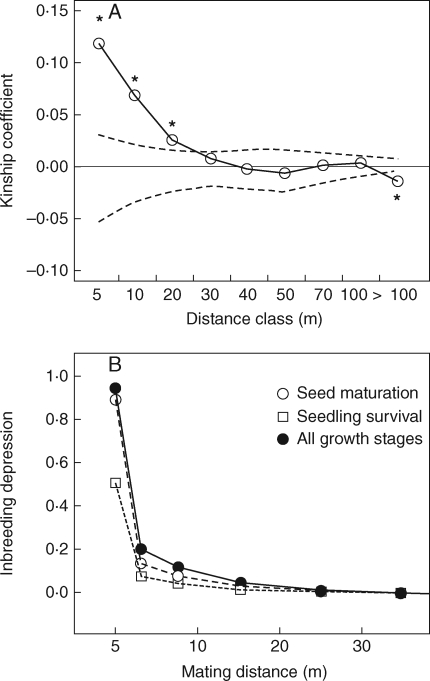
Figure 4A shows the correlogram for the kinship coefficients across pairs of individuals as a function of distance between them. Significantly positive kinship coefficients were detected within a distance of 20 m, and a significantly negative kinship coefficient was detected beyond a distance of 100 m (randomization test, P < 0·05). The kinship coefficients clearly decreased with increasing physical distance, suggesting a significant spatial genetic structure (b = −0·009, S_p = 0·0096; P < 0·001). The estimated inbreeding depression as a function of the spatial genetic structure showed that the cumulative fitness decreased progressively as a function of the distance class: in the distance classes of 0–5, 5–10, 10–20 and 20–30 m, fitness decreased to 20·1, 11·8, 4·5 and 1·4 %, respectively (Fig. 4B).

Fig. 4.

Spatial genetic structure and predicted inbreeding depression. (A) Correlogram for the kinship coefficient among pairs of Rhododendron brachycarpum individuals, expressed for nine distance classes (values on the x-axis represent the upper limit of each distance class). Dashed lines represent the 95 % confidence interval for the null hypothesis that assumes no genetic structure based on 9999 randomizations. Asterisks indicate significance (P < 0·05) for each distance class. (B) Predicted inbreeding depression as a function of the spatial genetic structure for stages.

DISCUSSION

Occurrence of biparental inbreeding depression

The level of inbreeding between mating plants is a key determinant of offspring fitness in Rhododendron brachycarpum, especially during seed maturation. Three additional observations indicate that early-acting inbreeding depression plays the dominant role in reducing self-fertility. First, almost all self-pollinated flowers produced fruits even if no seeds matured. Second, a higher proportion of flattened and shrivelled seeds were present in selfed fruit than in outcrossed fruit (Fig. 2). These observations indicate that self-fertilized ovules were aborted at a post-zygotic stage (i.e. were fertilized but were aborted before maturation). Studies of other Rhododendron species have shown that self-pollen tubes can grow into the style and fertilize ovules as well as pollen tubes produced by cross-pollination (Palser et al., 1989). Third, the aborted seeds showed a ranged of sizes (Fig. 2), suggesting that seeds were aborted at different stages of development after fertilization. If late-acting self-incompatibility had been responsible, embryos would have been aborted at a more uniform stage of development (Seavey and Bawa, 1986). In addition, seed set in the self-pollinated fruits varied from 0·000 to 0·478 among individuals. Variable expression among individuals is considered to be a hallmark of inbreeding depression because of variation in the mutational genetic load (Seavey and Carter, 1994). Thus, I concluded that early-acting inbreeding depression but not late-acting self-incompatibility was responsible for seed abortion in this species. Therefore, biparental inbreeding depression can account for the decrease in seed-set with increasing kinship between parents.

Molecular markers were used to create a range of biparentally inbred progeny and to assess the effect of the degree of inbreeding on progeny fitness under natural conditions. Some previous empirical evidence for biparental inbreeding depression was provided by breeding plants in experimental fields (e.g. Kurinobu et al., 1991; Nason and Ellstrand, 1995; Teixeira et al., 2009), but the present study assessed biparental inbreeding depression during seed maturation in the field. Higher values of genetic relatedness between parents led to higher costs for their offspring's fitness. That is, the magnitude of the biparental inbreeding depression depended on the degree of genetic relatedness between mating partners in a natural population.

Reproductive success decreased through uniparental and biparental inbreeding

Under open-pollinated conditions, self-pollination dominated at the time of pollination (s_p = 0·638). Much of the self-pollen received by stigmata should result from geitonogamy because of the large display of protoandrous flowers and the lack of autogamy in this species (my unpubl. res.). Thus, frequent geitonogamous pollination should lead to a high reproductive cost due to increased severity of inbreeding depression in the selfed progeny. During successive stages, the selfing rate (i.e. the proportion of the survivors produced by selfing) decreased progressively from seed maturation to seed germination to seedling survivals. In addition, the inbreeding coefficient of the adult trees (f = − 0·013; P > 0·05) indicated that inbred progeny were gradually removed from the population over time. Although self-pollination appears to be favoured in terms of reproductive output when the pollen supply from other individuals is limited, this benefit could often be outweighed by severe inbreeding depression and seed discounting (e.g. Herlihy and Eckert, 2002). Therefore, self-pollinations, including geitonogamous pollinations, were not beneficial for the reproduction of R. brachycarpum. The uniparental mode of inbreeding depression thus appears to act as a selection force that promotes outcrossing in this species.

In the natural population of R. brachycarpum, biparental inbreeding was detected; the amount contributed about 25–33 % of the effective selfing observed under open-pollinated conditions. Although the pollen dispersal distances for R. brachycarpum are unknown, investigations in other Rhododendron species have shown a high likelihood of pollination by neighbouring mates (Kameyama et al., 2000, 2001; Escaravage and Wagner, 2004). Here, increasing physical distance between parents decreased the level of inbreeding between mates as a result of a significant spatial genetic structure (Fig. 4). Because the spatial genetic structure was significant within 20 m of a focal plant, this suggested that, on average, pollen arriving from within 20 m will result in some degree of biparental inbreeding. For example, the location of parents within 5 m of each other, for which the average kinship coefficient was similar to that of half-sibs (F_ij = 0·125), would decrease the offspring's fitness by about 80 % (Fig. 4). Biparental inbreeding depression would therefore create a substantial selection pressure against the progeny resulting from mating between neighbouring parents in natural populations that exhibit a distance-dependent genetic structure. Therefore, biparental inbreeding depression would be a selection force that promotes effective pollen movement between unrelated individuals in this species.

Magnitude and timing of biparental inbreeding depression

The magnitude of inbreeding depression in R. brachycarpum was not uniform among the life-cycle stages. It was highest during seed maturation and lower during seed germination and seedling survival. Inbreeding depression is generally expressed more strongly in the harsh environment of a natural habitat than in a regulated environment such as that of a greenhouse (Dudash, 1990). Thus, these estimates of inbreeding depression for germination ability and seedling survival may underestimate the true values because of the artificial conditions. However, the results were consistent with the general pattern of the magnitude and timing of inbreeding depression in angiosperms, in which stronger inbreeding depression typically occurs during seed maturation than during the latter stages of seed germination and seedling survival (Husband and Schemske, 1995; reviewed in Husband and Schemske, 1996; Hufford and Hamrick, 2003; Goodwillie and Knight, 2006). That is, processes that occur before seed dispersal should be directly affected by the intensive selection that results from inbreeding depression, including biparental inbreeding depression. Accordingly, the selection force that is responsible for long-distance pollen movement could be created by more intensive selection before seed dispersal than after. Although Isagi et al. (2007) showed that biparental inbreeding depression promotes effective gene flow over longer distances at the sapling stage than at seedling stage, researchers should verify whether a driving force that promotes long-distance pollen movement also acts before seed dispersal as it does here. Comparisons of the results of paternity analysis of single pollen grains deposited on stigmas (Matsuki et al., 2007; Hasegawa et al., 2009) and of the matured seeds can identify the intensity of selection for the long-distance pollen movement caused by biparental inbreeding depression before seed dispersal.

Accuracy of the marker-based approach

Empirical studies of inbreeding depression suggest that offspring fitness varies greatly among maternal families (Sørensen, 1969; Fowler and Park, 1983; Goodwillie and Knight, 2006). Here, the logistic models that accounted for the random effects of maternal families were strongly supported as a means of evaluating inbreeding depression. The wide variance in progeny fitness among maternal families has often been explained by differences in genetic load (e.g. Sørensen, 1969), but the present study design included non-genetic (environmental) factors, such as soil conditions and the light environment around the maternal plants, which would have had especially significant effects on seed maturation. A more accurate estimate of the variance in genetic load could come from carefully designed experiments such as mutual pollination exchanges between pollen donors and pollen recipients, in which the genetic load of the offspring could be explained by the deleterious alleles provided by the maternal and parental plants.

Estimates of kinship coefficient using six microsatellite markers showed considerable sampling variance, because the precision of estimates increases with increasing number of loci (for details, see Glémin et al., 2006). Although kinship coefficients are expected to range from 0 (assuming full outcrossing) to 0·5 (assuming self-pollination), some estimates here were <0 or >0·5. This wide range of estimates would decrease the slope of the regression curve used to assess the magnitude of inbreeding depression, leading to underestimation of the true value. However, it seems unlikely that this sampling error biased the overall conclusion that the magnitude of inbreeding depression depends on the degree of genetic relatedness between parents and that its expression differs among the three life-cycle stages.

CONCLUSIONS

Genetic relatedness between parental plants of Rhododendron brachycarpum caused biparental inbreeding depression in their progeny. Both uniparental and biparental modes of inbreeding depression decrease the reproductive fitness of the progeny and thus maintain the genetic diversity of this species by favouring the survival of outcrossed individuals. Under a distance-dependent spatial genetic structure, the presence of biparental inbreeding increases the effective movement of pollen, because pollen from more spatially distant (less closely related) paternal plants increases the chances of survival of the progeny. Therefore, the deleterious consequences of inbreeding depression can affect both an offspring's fitness and the magnitude of effective gene flow in plant populations.