Comparison of organ residence time estimation methods for radioimmunotherapy dosimetry and treatment planning—patient studies

Abstract

The estimation of organ residence time is essential for high-dose myeloablative regimens in radioimmunotherapy (RIT). Frequently, this estimation is based on a series of simple planar scans and planar processing. The authors previously performed a simulation study which demonstrated that the accuracy of this methodology is limited compared to a hybrid planar∕SPECT residence time estimation method. In this work the authors applied this hybrid method to data from a clinical trial of high-dose myeloablative yttrium-90 ibritumomab tiuxetan therapy. Image data acquired from 18 patients were comprised of planar scans at five time points ranging from 1 to 144 h postinjection and abdominal and thoracic SPECT∕CT scans obtained at 24 h postinjection. The simple planar processing method used in this work was based on the geometric mean method with energy window based scatter compensation. No explicit background subtraction nor object or source thickness corrections were performed. The SPECT projections were reconstructed using iterative reconstruction with compensations for attenuation, scatter, and full collimator-detector response. Large differences were observed when residence times were estimated using the simple planar method compared to the hybrid method. The differences were not constant but varied in magnitude and sign. For the dose-limiting organ (liver), the average difference was −18% and variation in the difference was 19%, similar to the differences observed in a previously reported simulation study. The authors also looked at the relationship between the weight of the patient and the liver residence time and found that there was no meaningful correlation for either method. This indicates that weight would not be an adequate proxy for an experimental estimate of residence time when choosing the activity to administer for therapy. The authors conclude that methods such as the simple planar method used here are inadequate for RIT treatment planning. More sophisticated methods, such as the hybrid SPECT∕planar method investigated here, are likely to be better predictors of organ dose and, as a result, organ toxicities.

INTRODUCTION

Radioimmunotherapy (RIT) using ⁹⁰Y-Zevalin^® (⁹⁰Y-ibritumomab tiuxetan; IDEC-Y2B8; Cell Therapeutics Inc., Seattle, WA) and ¹³¹I-Bexxar^® (tositumomab and ¹³¹I-tositumomab; GlaxoSmithKline, Philadelphia, PA) has shown great promise in the treatment of non-Hodgkin’s lymphoma (NHL).^{1, 2, 3, 4, 5, 6} In the current FDA-approved therapeutic regimen for ⁹⁰Y-Zevalin, the administered ⁹⁰Y activity is based on the patient weight, platelet levels, and qualitative evaluation of pretherapy ¹¹¹In-Zevalin images. Myelotoxicity has been the dose-limiting side effect in this regimen. Despite the significant response rates, rates of recurrence have also been significant when used at nonmyeloablative doses.

In order to improve response rates and long term prognosis, high-dose myeloablative regimens combined with autologous stem cell transplant are under investigation. A multicenter trial led by Johns Hopkins University and designed to find the maximum tolerated dose (MTD) for high-dose myeloablative ⁹⁰Y-Zevalin therapy has recently ended. Previously, patient-specific pretreatment dosimetry was shown to be a better predictor of toxicity than factors such as patient weight and body surface area.⁷ In this kind of high-dose myeloablative therapy, it was essential to use methods for estimating organ dose that were as accurate and precise as possible.^{8, 9}

As described in a previous simulation study,¹⁰ organ residence times are often estimated using a series of conjugate view whole-body scans. In a typical application of this methodology, a version of the therapeutic agent labeled with a radionuclide suitable for imaging is injected. Planar images are obtained at a series of time points. The activity in each organ is estimated at each time point using planar processing methods. The resulting time activity curve (TAC) for each organ of interest is then fitted with an appropriate function, which is then integrated to give the cumulated activity. The residence times for the organs are then calculated as the cumulated activities divided by the injected activity. The set of residence times for the imaging radionuclide is converted to residence times for the therapeutic radionuclide using the decay constants of each radionuclide. Next, the set of residence times and the MIRD methodology,^{11, 12} e.g., as implemented in the OLINDA software package,¹³ are then used to estimate the specific absorbed dose for each organ. The administered therapeutic activity needed to obtain the target dose for the critical organ is calculated by dividing the target dose by the specific dose for that organ. Thus, errors in estimates of the imaging radionuclide residence time translate directly to errors in the estimates of organ dose and can result in over- or underdosing of the patient.

The ability to obtain quantitatively accurate estimates of organ activity from planar imaging is impeded by several physical effects that degrade the image, as demonstrated in Refs. ^{10, 14, 15, 16}. The degrading factors include overlap of the organ projections with each other and with background activity in the planar projections, scatter and attenuation of photons in the patient, scatter and penetration in the collimator, and partial volume effects.¹⁷

Koral et al. reported a case study comparing a planar with a hybrid planar∕SPECT residence time estimation method (referred to as the hybrid method in the following text) which indicated the importance of SPECT in determining tumor dosimetry using ¹³¹I labeled agents.¹⁸ They also applied these two methods for tumor dosimetry in a phase II study of ten previously untreated patients with lymphoma and concluded that the hybrid method’s estimates of radiation dose for individual tumors provided a stronger correlation with reduction in tumor volume than the dose estimates for composite tumors from their planar method.¹⁹ Although their hybrid method is similar to the one used in this investigation, the focus of our work is on whole organ pretherapy dosimetry for ¹¹¹In-based agents rather than tumor dosimetry for ¹³¹I agents. Since our studies used a SPECT∕CT system while they used separate SPECT and CT systems, registration of SPECT and CT images was less of an issue for us.

Assié et al. compared 2D planar and 3D SPECT dosimetry protocols in ⁹⁰Y-Zevalin RIT of six patients with NHL.²⁰ The 2D planar method used in that work was similar to the simple planar method we used in this study. Their 3D SPECT-based method for quantification of activity used iterative reconstruction-based attenuation, energy window based scatter, and recovery coefficient partial volume compensations. In patient studies, it was demonstrated that there were large differences in dose estimates from the SPECT method compared to a 2D planar method. In addition, a hybrid method had closer agreement with the dose estimates obtained using the SPECT method than the simple planar method. Their partial volume compensation method was based on the assumption that the reconstructed resolution is spatially invariant and it did not include compensation for spill-in of activity from neighboring organs. The SPECT method was validated using a phantom study. The Liqui-Phil phantom modeled the lower torso and did not include the effects of scatter from activity in the heart or the effects of nonuniform attenuation. The SPECT method consistently underestimated the activity in the compartments in the phantom, with the smallest errors obtained for the liver (6%). However, the SPECT method provided better accuracy than the planar method.

In this paper, we applied the simple planar (first planar method described in Ref. 10) and a hybrid planar∕SPECT (first hybrid method in Ref. 10) processing method to 18 sets of patient data in the previously described dose-escalation study. Each set of patient data included five planar scans (obtained at five time points, approximately 1, 5, 24, 72, and 144 h postinjection) and abdominal and thoracic SPECT∕CT scans obtained at approximately 24 h after the injection. The SPECT data were reconstructed using the quantitative SPECT reconstruction (QSPECT) method,¹⁰ and the residence times obtained from the simple planar and hybrid methods were compared. Since there was no independent gold standard available to assess organ activities or residence times, conclusions from these data can only be in terms of differences between the estimates for the two methods.

MATERIALS AND METHODS

Patient population and trial design

Twenty-four patients (14 males, 10 female), with a median age of 55 (range 44–70) and histologically proven NHL or diffuse large B-cell lymphoma, were enrolled in this study between 11∕02 and 11∕07. Six patients (four males, two females) failed to mobilize stem cells and did not receive ⁹⁰Y-Zevalin. Enrollment of patients previously treated with anti-CD20 therapy was limited to those that had achieved partial or complete response. The patients had undergone a range of 1–5 (median of 3) prior chemotherapy regimens for NHL, had less than 35% bone marrow involvement with NHL as measured by bone marrow biopsy or by flow cytometry, and did not have complete replacement of bone marrow with tumor or hypocellular bone marrow (no less than 15% cellularity). All patients met hematopoietic (WBC ≥3000∕mm³, total lymphocyte count ≤5000∕mm³, hemoglobin≥at least 10.0 g∕dl, and platelet count ≥75 000∕mm³), hepatic (bilirubin ≤2 mg∕dl, AST or ALT ≤2 times upper limit of normal), renal (creatinine ≤2 mg∕dl), cardiovascular (LVEF ≥45% by echocardiogram or MUGA), and pulmonary (DLCO ≥50% of predicted) criteria 2 weeks before inclusion in the study.

Patients underwent in vivo purging using Ritixumab and stem cell harvesting using protocols that are standard at our facility. Beginning 4–6 weeks after completion of the last of the four Rituximab infusions, patients received 185 MBq ¹¹¹In-Zevalin IV infused over 10 min on day 1 followed by imaging on days 1, 2, 4, and 7. Based on the results of their dosimetry study, on day 15 the patients received an injection of ⁹⁰Y-Zevalin, which was infused over 10 min. There were large differences among these patients in terms of patient size, disease status, organ size, shape, and distribution of activity.

In this study, the escalation parameter was the dose to critical organ (the liver for all 18 patients). The first three patients received the standard FDA-approved injected activity based on their weights (14.8 MBq∕kg). The fourth patient received a target dose of 14 Gy to the liver. The target dose was then escalated to 18 Gy for patients 5–8, 24 Gy for the patients 9–14, and 28 Gy for the patients 15–18.

Planar and SPECT imaging

All 18 patients had planar scans acquired at 1, 5, 24, 72, and 144 h postinjection of ¹¹¹In-Zevalin. Abdominal and thoracic SPECT∕CT scans were performed immediately after the 24 h planar scan. For both the planar and SPECT∕CT scans, a GE Millenium VG∕Hawkeye SPECT∕CT system with a 1.59 cm thick crystal and a medium energy-general purpose (MEGP) collimator was used.

The same set of energy windows was used for both the planar and SPECT∕CT scans. Due to hardware limitations on the number of possible energy windows, data were acquired using one primary window. The images were obtained by summing photons from 14% wide energy windows centered on both the 171 and the 245 keV photopeaks. Two scatter images with windows spanning the ranges 145.92–158.08 and 184.5–225.5 keV were also acquired and used to perform triple energy window (TEW) scatter compensation.²¹ In the TEW compensation, we assumed that the counts in an energy window above the 245 keV photopeak were zero.¹⁰ The intermediate window (184.5–225.5 keV) served as both the lower window for the 245 keV photopeak and the upper window for the 171 keV photopeak. A detailed description of the scale factors applied to the data in these windows for the TEW scatter compensation method can be found in Ref. 10.

Anterior and posterior planar scans were acquired simultaneously into 256×1024 image matrices with a 2.21 mm pixel size using autocontouring. The scan speeds were 10, 10, 7, 5, and 5 cm∕min for the 1, 5, 24, 72, and 144 h images, respectively. An ¹¹¹In standard source (a syringe with known activity) was placed approximately 10 cm lateral to and below the patient’s feet and imaged in each planar scan. The source was used to calibrate for possible differences in camera sensitivity and scan speed in the different acquisitions.

For the 24 h SPECT acquisitions, the images were acquired into 128×128 projection matrices with a 4.42 mm pixel size at 120 views over 360°. A circular orbit was used. Separate thoracic and abdominal SPECT∕CT scans were obtained. The acquisition time was 30 s per view (total of ∼30 minutes for each SPECT acquisition). Each SPECT acquisition was followed by an x-ray CT scan. This scan was used to provide an attenuation map and a registered volume CT data set that facilitated defining 3D organ volumes of interest (VOIs). The CT images were obtained in 256×256×128 matrices with a 2.21 mm transaxial pixel size and a 4.42 mm slice thickness. The CT images were actually acquired using a 1 cm slice thickness and were interpolated by the software in the GE VH system to the 4.42 mm slice thickness provided in the image files. An additional 1–5 min static image of the same ¹¹¹In standard source used in the planar scans was also obtained for each patient to measure the collimator-detector sensitivity. This measured sensitivity was used to convert the SPECT images to units of activity.

Simple planar processing method

As described in Ref. 10, TEW scatter compensation followed by a voxel-by-voxel geometric mean of the opposing views was first performed for the planar processing method. A conversion factor based on the ratio of the total geometric mean (GM) counts in the body in the 1 h image (which was obtained before the patient had voided) divided by the injected activity was used to convert geometric mean counts to activity.²² No explicit object or source thickness corrections were performed. Transmission data were not acquired because the protocols and equipment needed to perform the transmission scans were not available. The lack of transmission scanning and object thickness corrections has been common in clinical trials using planar imaging for pretherapy treatment planning.^{19, 20} However, the use of the GM counts-to-activity conversion factor provides implicit organ and source thickness corrections that are accurate if the relative activity distribution does not change for subsequent scans. The total ¹¹¹In activity for the ith organ at time t, A_planar(i,t), was calculated using an equation that differs slightly from the one used in the simulation studies [Eq. (2) in Ref. 10]:

$$A_{\text{planar}}\left(i,t\right)=\text{GM}\left(i,t\right)\times \frac{A_{\text{inj}}\times e^{-{\lambda }_{\text{In-}111}\times t_{1\text{h}}}}{\text{GM}\left(wb,1\text{h}\right)}\times \frac{A\left(\text{stdsrc},t\right)\times \text{GM}\left(\text{stdsrc},1\text{h}\right)}{\text{GM}\left(\text{stdsrc},t\right)\times A\left(\text{stdsrc},1\text{h}\right)},$$ (1)

where GM(i,t) is the GM counts in ith organ at time t, A_inj×e^{−λ_In-111×t_{1 h}} is the whole-body activity at the time of the 1 h scan, t_{1 h}, λ_In-111 is the decay constant for ¹¹¹In, A(stdsrc,t) is the standard source activity at time t, and GM(stdsrc,t) is the GM counts in a ROI covering the standard source. Since the standard source was placed on the imaging table away from the body, the standard source geometric mean counts were very close (typically within 1%) to the arithmetic mean of the standard source counts in the anterior and posterior projections. The only difference between Eq. 1 and Eq. (2) in Ref. 10 is the calibration factor

$$\frac{A\left(\text{stdsrc},t\right)\times \text{GM}\left(\text{stdsrc},1\text{h}\right)}{\text{GM}\left(\text{stdsrc},t\right)\times A\left(\text{stdsrc},1\text{h}\right)},$$

which was used to account for the different scan speeds used at the different time points.

The 2D organ ROIs were drawn manually using the projection of manually drawn 3D organ VOIs described in Sec. 2D as a guide. The ROIs were intentionally drawn smaller than the borders of the projections of the 3D VOIs to avoid overlap with other regions and, to some extent, overlap with underlying organs (or background). However, explicit overlap and background corrections were not performed.

QSPECT reconstructions

The SPECT reconstructions were performed using the iterative ordered-subsets expectation-maximization (OS-EM) algorithm²³ with reconstruction-based compensation for attenuation, scatter, and collimator-detector response function (CDRF). We used 30 iterations (24 subsets per iteration) and employed no postsmoothing. The attenuation was modeled using measured CT-based attenuation maps. To account for the different photopeak energies in the summed photopeak energy window, the attenuation map used in the reconstruction was the abundance-weighted average of the maps appropriate for the 171 and 245 keV photons emitted by ¹¹¹In. A detailed description and validation of the QSPECT methods can be found in Refs. ^{10, 24}.

Since the SPECT and CT data provided by the SPECT∕CT system were already well registered (as verified by visual inspection), no further registration step was performed. All the 3D VOIs were created from stacked 2D ROIs manually drawn on transaxial slices using a simultaneous display of the 2D ROI in the QSPECT, CT, and fused QSPECT-CT images in a custom-developed registration∕segmentation program. Images from a diagnostic CT scanner were occasionally used as a visual guide to organ shapes and spatial relationships in drawing the ROIs due to their better axial resolution and reduced motion artifacts.

The organ activities were calculated by multiplying the total counts in each organ VOI by the measured collimator-detector sensitivity and dividing by the acquisition time. The collimator-detector sensitivity was measured by imaging an ¹¹¹In standard source suspended approximately equidistant from the two cameras at a distance approximately equal to the radius of rotation in the patient scans. The standard source counts were computed in regions that were drawn relatively close to the projected boundaries of the source in order to minimize the impact of photons that penetrated the septa or were scattered in the septa or detector. The resulting expression for the activity estimated from the SPECT scan for organ i at time t, A_QSPECT(i,t), is

$$A_{\text{QSPECT}}\left(i,t\right)=C\left(i,t\right)\times \frac{A_{\text{stdsrc}}\times t_{\text{stdsrc}}}{C_{\text{stdsrc}}\times t_{\text{SPECT}}},$$ (2)

where C(i,t) is the sum of the QSPECT image intensity in organ i at time t, A_stdsrc is the ¹¹¹In standard source activity at the time of the collimator-detector sensitivity measurement, C_stdsrc and t_stdsrc are the total recorded counts and acquisition time, respectively, for the collimator-detector sensitivity measurement images, and t_SPECT is the total acquisition time for the SPECT acquisition.

Two methods for estimating residence time

The residence time was estimated using the simple planar and hybrid methods. For the simple planar method, the planar processing methods described above were used to estimate the ¹¹¹In organ activities, A_planar(i,t), at each time point t and for each organ, i. The ¹¹¹In activities were scaled by an appropriate factor to correct for the differences in physical decay constants for ¹¹¹In and ⁹⁰Y. The resulting ⁹⁰Y TAC was then fitted with a mono- or biexponential function. The biexponential function was used when a correlation coefficient for the monoexponential was less than 0.95. The residence time for each organ was estimated by integrating the fitting function and dividing by the injected activity.

For the hybrid method, the activity estimates from the QSPECT method (from a SPECT acquisition acquired 24 h postinjection) were used to rescale the TAC obtained from the planar time series as follows. The planar images were used to compute the decay constant for each organ in the same way as for the simple planar method. The SPECT activity in each organ at the time of the SPECT acquisition was calculated using Eq. 2). The planar TAC for each organ was then rescaled so that it passed through the SPECT activity at the time of the SPECT acquisition.

RESULTS

Table 1 summarizes the percentage difference in organ ⁹⁰Y-Zevalin residence time estimates for the simple planar and hybrid method for the 18 patients studied. The average relative differences and standard deviations of these relative differences are also shown in the bottom row of Table 1.

Table 1.

Percentage difference in organ ⁹⁰Y-Zevalin residence time estimates for the simple planar and hybrid methods. [For each patient, the percentage difference was calculated as (planar-hybrid)∕hybrid∗100%. The mean percentage error and the mean percentage standard deviation were then computed. Negative signs indicate underestimation compared to the hybrid method.]

Patient No.	Heart	Lungs	Liver	Kidneys	Spleen
1	21.73%	15.70%	−29.09%	80.93%	2.37%
2	9.54%	22.84%	−4.77%	31.49%	23.28%
3	403.49%	201.50%	14.61%	68.16%	−15.66%
4	22.59%	24.78%	−16.51%	48.72%	21.86%
5	69.40%	26.92%	−5.71%	58.87%	8.91%
6	68.74%	59.98%	−21.02%	207.02%	50.95%
7	−8.38%	33.65%	−33.15%	79.62%	−35.56%
8	96.49%	17.82%	4.98%	103.31%	15.05%
9	11.51%	−20.91%	−25.80%	89.26%	10.80%
10	33.39%	27.12%	−8.18%	135.21%	22.70%
11	6.91%	16.71%	−7.04%	76.67%	3.60%
12	34.71%	−17.60%	−0.30%	28.48%	38.74%
13	53.59%	37.01%	−14.96%	88.34%	−0.86%
14	1.79%	33.64%	−15.94%	46.20%	3.41%
15	−14.11%	−3.57%	−28.77%	23.41%	6.30%
16	1.63%	−35.32%	−39.46%	−6.06%	282.51%
17	36.20%	−10.81%	−70.08%	90.98%	7.06%
18	8.14%	6.97%	−18.37%	58.74%	17.33%
Mean±standard deviation	(47.63±93.59)%	(24.25±50.21)%	(−17.75±19.06)%	(72.74±47.18)%	(25.71±66.82)%

From Table 1, we see that there were large average differences between the hybrid and simple planar organ residence time estimates. These differences ranged from 73% for the kidneys to −18% for the liver. The standard deviations of these relative differences, a measure of the variability of the estimates from the simple planar method with respect to those from the hybrid method, were also very large, ranging from 94% for the heart to 19% for the liver. Since the actual residence times were not known for the patients, unlike the previous simulation and phantom studies, it is not possible to say definitively which method was better. However, the significance of the average relative differences and standard deviation is discussed in Sec. 4.

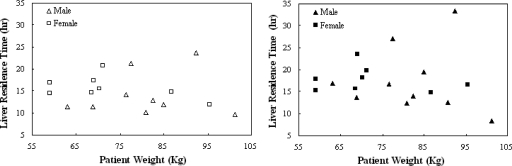
Since treatment planning based on patient weight would be substantially simpler than performing an imaging procedure such as the one in this study, we examined whether patient weight could be used to predict the injected activity. The liver was the dose-limiting organ for all 18 patients, and thus the therapeutic Y-90 injected activity was proportional to its residence time. If there is a relationship between the maximum therapeutic injected activity and patient weight, there should thus be a relationship between liver residence time and patient weight. Figure 1 shows a plot of liver residence time vs patient weight. These data showed no evidence of linear correlation between patient weight and liver residence time for either male or female patients or for either the planar or hybrid method (in all cases the correlation coefficient r² was less than 0.2). This indicates that weight, the basis for the conventional Zevalin regimen, is not sufficient as a predictor for treatment planning in a myeloablative therapy regimen.

Figure 1.

Scatter plots of patient weight vs liver residence time estimated with planar (left) or hybrid (right) method. No linear correlation was found for either method.

DISCUSSION

As mentioned above, for these patient data, the true values of organ residence times were not known. However, both in the single phantom with multiple noise realizations¹⁰ and simulation studies of multiple phantom configurations,²⁵ the accuracy of the hybrid method was very good and substantially better than that of the simple planar method. In the multiple phantom configuration study,²⁵ the residence time estimate from the hybrid method was closer to the true value than the estimate from the simple planar method in 100%, 90%, 94%, 92%, 82%, and 100% of the 49 phantom configurations for the heart, lungs, liver, kidneys, spleen, and marrow, respectively.

Since the TAC used in the hybrid method is the same as the one used in the simple planar method, the relative difference between the residence times for the simple planar and hybrid methods is equal to the relative difference in the estimates of activity at the 24 h time point. The accuracy of QSPECT for estimates of organ activity has been shown to be better than that of the simple planar processing method used in this study.¹⁰ This superiority is not surprising given the rigorous compensations for the degrading effects with the QSPECT methods. Even though the simulation studies modeled uniform distributions of activity inside the organs and assumed perfectly defined and registered organ VOIs, it is reasonable to attribute the majority of the difference between the residence times estimated using the planar and hybrid methods to errors in the planar estimates.

In the following we assume that the differences are reflective of errors for the planar processing method. For most organs (except the liver), the planar method resulted in significant overestimates. For the liver, the planar method underestimated the residence time by an average of 18%. Since the liver was the dose-limiting organ for all patients, giving a therapeutic dose based on the planar estimate would have resulted in the patients receiving a higher-than-expected liver dose.

A full assessment of a measurement method requires consideration of both its accuracy and precision. Since we do not know the truth in these studies, we have compared differences in the estimates of residence times as an analog to accuracy. As an analog to precision, we have computed the standard deviation of the differences in the estimates of residence times of the two methods over the patient population. We will subsequently refer to this as variation in the differences as it characterizes how much the magnitude of the differences in the estimates of the residence time varies over the patient population.

The variations in the sign and magnitudes of the differences of the residence times estimated with the simple planar and hybrid methods are perhaps more significant than the average differences. This is reflected in the percentage standard deviations shown in the % Diff row of Table 1. Since the variation of errors over phantom configurations in the simulation studies were much smaller for QSPECT than for planar processing and recalling that the differences were due to differences in the 24 h image of estimates of organ activity, we again equate the variations in the differences to variations in the errors for the planar method.

Variations in errors in dose, including cases of underestimation and overestimation, are critical for treatment planning. For example, the choice of a therapeutic activity based on the planar estimate of residence time could have resulted in actual liver doses ranging from 37% larger to 1% smaller than the target dose. One possible explanation for the large variation in differences in the dose estimates is that QSPECT methods provide improved compensation for factors, such as attenuation and organ overlap, which vary greatly among patients and are not suitably dealt with when using the simple planar quantification methods.

In planning for RIT treatment, variations in the magnitude and the sign of differences between the estimated and actual organ doses will compound variations in the biological dose response. To the extent that the measurements of the variations are larger than the biological ones, variations in the measurement will result in an underestimation of the maximum tolerated dose in order to avoid organ toxicities. This would then result in reduction of therapeutic efficacy as it would increase the number of patients who received an actual dose below their true maximum tolerated dose.

CONCLUSIONS

In this study, we compared estimated organ residence times using the simple planar and hybrid planar∕QSPECT methods in a clinical trial of myeloablative ¹¹¹In∕⁹⁰Y Zevalin therapy. Large differences were observed between the simple planar and hybrid estimates of residence times. A large variation in the magnitude of the differences was also observed among the 18 subjects. We also examined the relationship between patient weight and liver residence time and found no meaningful correlation for either quantification method. This indicates that weight is not an adequate proxy for residence time in estimating the therapeutically administered activity.

In conclusion, the results of this paper demonstrate that, in planning of therapeutic doses for RIT, the use of simple planar imaging, without background subtraction or object and source thickness corrections, is likely to result in substantial differences compared to a hybrid planar∕SPECT approach. Since previous simulation studies have demonstrated the superiority of the hybrid estimation of residence time over the simple planar approach, these results suggest that the use of the simple planar method for dose estimation in RIT is less quantitatively accurate and precise. The hybrid method may thus be a better choice in future similar trials. The magnitudes of the differences and variation of differences between the simple planar and hybrid approaches suggest that more sophisticated quantification methodologies may have substantial importance in allowing the use of the maximum radiation dose of a RIT agent without producing adverse effects.

DISCLOSURE

The reconstruction code used in this work has been licensed to GE Healthcare for inclusion in a commercial product. Under separate licensing agreements between the GE Healthcare and the Johns Hopkins University and the University of North Carolina at Chapel Hill, Dr. Frey is entitled to a share of royalty received by the universities on sales of products described in this article. The terms of this arrangement are being managed by the Johns Hopkins University in accordance with its conflict of interest policies.

R.L.W. has received speaker fees and research grant support from G.E. Healthcare. R.L.W. has licensed inventions regarding radioimmunotherapy through the University of Michigan to GlaxoSmithKline and Biogen-Idec related to RIT agents Bexxar and Zevalin. He receives royalties from the sale of these agents. These agreements are being managed by the Johns Hopkins University in accordance with its conflict of interest policies.