Model Calcium Sensors for Network Homeostasis: Sensor and Readout Parameter Analysis from a Database of Model Neuronal Networks

Abstract

In activity-dependent homeostatic regulation (ADHR) of neuronal and network properties, the intracellular Ca²⁺ concentration is a good candidate for sensing activity levels because it is correlated with the electrical activity of the cell. Previous ADHR models, developed with abstract activity sensors for model pyloric neurons and networks of the crustacean stomatogastric ganglion, showed that functional activity can be maintained by a regulation mechanism that senses activity levels solely from Ca²⁺. At the same time, several intracellular pathways have been discovered for Ca²⁺-dependent regulation of ion channels. To generate testable predictions for dynamics of these signaling pathways, we undertook a parameter study of model Ca²⁺ sensors across thousands of model pyloric networks. We found that an optimal regulation signal can be generated for 86% of model networks with a sensing mechanism that activates with a time constant of 1 ms and that inactivates within 1 s. The sensor performed robustly around this optimal point and did not need to be specific to the role of the cell. When multiple sensors with different time constants were used, coverage extended to 88% of the networks. Without changing the sensors, it extended to 95% of the networks by letting the sensors affect the readout nonlinearly. Specific to this pyloric network model, the sensor of the follower pyloric constrictor cell was more informative than the pacemaker anterior burster cell for producing a regulatory signal. Conversely, a global signal indicating network activity that was generated by summing the sensors in individual cells was less informative for regulation.

Introduction

Central pattern generating (CPG) neuronal networks produce rhythmic motor activity patterns that are vital for the survival of the organism. Although the constituent cells of CPG networks are faced with changes in environmental conditions and constant molecular turnover, the ability to generate these activity patterns is always maintained (Marder and Calabrese, 1996; Marder and Bucher, 2001). An activity-independent component of this regulation is controlled inherently (MacLean et al., 2003, 2005) or by neuromodulators endogenous to the stomatogastric ganglion (STG) (Thoby-Brisson and Simmers, 1998; Khorkova and Golowasch, 2007). In contrast, in the pyloric CPG network of the crustacean STG that controls the dilation of the pylorus, long-term changes in isolated neurons can result from external stimulation (Turrigiano et al., 1994; Thoby-Brisson and Simmers, 1998; Golowasch et al., 1999a; Zhang et al., 2009). This activity-dependent homeostatic regulation (ADHR) affects ion channel properties (Turrigiano et al., 1994, 1995; Golowasch et al., 1999b; Baines et al., 2001; Nelson et al., 2003) that govern the electrical activity of the neurons (Foster et al., 1993; De Schutter and Bower, 1994; Prinz et al., 2003; Günay et al., 2008). ADHR also affects synapses in CPG networks (Soto-Treviño et al., 2001; Thoby-Brisson and Simmers, 2002) and elsewhere (Turrigiano et al., 1998; Stellwagen and Malenka, 2006; Ibata et al., 2008; Wilhelm and Wenner, 2008). In both isolated and networked cases, ADHR requires an activity sensing mechanism.

The electrical activity of a cell is correlated with the intracellular Ca²⁺ concentration (Ross, 1989), which was found to play a role in ADHR (Turrigiano et al., 1994) by possibly affecting ion channels (Linsdell and Moody, 1995; Golowasch et al., 1999a,b) through Ca²⁺ sensing proteins (Carrión et al., 1999; An et al., 2000; Mellström and Naranjo, 2001; Gomez-Ospina et al., 2006). For instance, the protein frequenin in Xenopus oocytes (Nakamura et al., 2001) and STG cells of the spiny lobster, Panulirus interruptus (Zhang et al., 2003), affects the inactivation gate of the voltage-gated K⁺ transient outward current (I_A). I_A, by modulating the interspike interval, is crucial in regulating activity (Tierney and Harris-Warrick, 1992; Golowasch et al., 1999a).

Such a sensing mechanism was modeled previously (Abbott and LeMasson, 1993; Liu et al., 1998) and succeeded in maintaining a predefined target activity pattern. Also, a model of regulation in the pyloric network showed that stable network states can be reached by modulating ion channels in individual cells (Golowasch et al., 1999b). However, these models only demonstrated regulation with few, fixed sensor parameters. For biological systems, which often exhibit redundant, nonlinear mechanisms, it has proved beneficial to explore the model parameter space (Foster et al., 1993; Golowasch et al., 2002) and store exploration results in databases (Prinz et al., 2003, 2004; Calin-Jageman et al., 2007; Günay et al., 2008). Here, we built a model Ca²⁺ activity sensor database to test the robustness of sensor performance by using an existing database of 20 million pyloric network models (Prinz et al., 2004) as a repository of different network configurations. From these networks, we tested whether the sensors can indicate (1) that a given network is producing functional activity patterns and, if not, (2) the direction into which network parameters need to change to reach a functional state. We achieved this by estimating the network activity from a statistical classifier that is trained as a sensor readout.

Materials and Methods

Model pyloric network database.

This study used a previously described database of 20,250,000 model pyloric networks (Prinz et al., 2004). In the database, each model network consists of three single-compartment conductance-based model neurons, constructed with the Hodgkin–Huxley (Hodgkin and Huxley, 1952) formalism, of a combined anterior burster and pyloric dilator (indicated as AB/PD or just PD throughout this paper) neuron, a lateral pyloric (LP) neuron, and a pyloric constrictor (PY) neuron (Fig. 1). Different network models have model neurons selected from pools of five AB/PD, five LP, and six PY models, whose parameters were described previously (Prinz et al., 2003). The model neurons contain eight currents: a fast sodium current, I_Na; slow and fast transient calcium currents, I_CaS and I_CaT; a transient potassium current, I_A; a calcium-dependent voltage-gated potassium current, I_K(Ca); a delayed rectifier current, I_Kdr; a hyperpolarization-activated mixed-ion inward current, I_h; and a leak current, I_leak. The voltage dependence and kinetics of these currents are based on recordings from STG neurons in the spiny lobster (Turrigiano et al., 1995), except I_h, which is modeled after that found in guinea pig lateral geniculate relay neurons (Huguenard and McCormick, 1992). These conductance parameters are identical in all model neurons (Prinz et al., 2003). The selected maximal conductances for each current and their selection criteria were described in detail previously (Prinz et al., 2004). The synapses between the model neurons are modeled with the dynamics used by Prinz et al. (2004), in which glutamatergic and cholinergic synapses were modeled differently. Each synapse was varied to five or six different maximal synaptic conductance values in different networks. The networks were simulated using a custom C++ program.

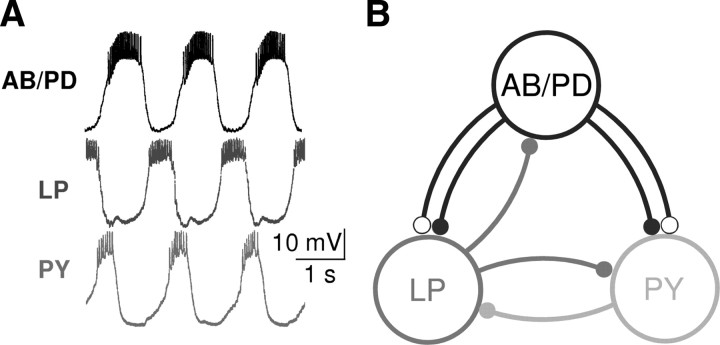
Figure 1.

Biological pyloric rhythmic activity pattern and the model circuit architecture. A, The triphasic rhythm recorded intracellularly from the American lobster (Homarus americanus) pyloric neurons. The figure was reproduced from Prinz et al. (2004) B, Simplified model of the pyloric network. All synapses in the circuit are inhibitory. Open circles represent fast glutamatergic synapses, and filled circles represent slow cholinergic synapses.

Model calcium sensors.

The calcium sensors explored here are inspired by an ADHR model for STG neurons (Abbott and LeMasson, 1993; LeMasson et al., 1993; Siegel et al., 1994; Liu et al., 1998) and measure the electrical activity of the model cell from the Ca²⁺ inflow, I_Ca (Fig. 2). Here, I_Ca = I_CaT + I_CaS and affects the Ca²⁺ dynamics from the same model, which describes the intracellular Ca²⁺ concentration ([Ca²⁺]) by

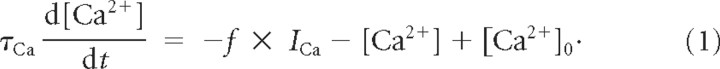In this model, f = 14.96 μm/nA is a factor that relates I_Ca to the derivative of [Ca²⁺], τ_Ca = 200 ms is the time constant for Ca²⁺ removal from the cytosol, and [Ca²⁺]₀ = 0.05 μm is the intracellular equilibrium value of [Ca²⁺]. This model successfully generates Ca²⁺ transients similar to those measured in pattern-generating neurons (Viana di Prisco and Alford, 2004) for different types of electrical activity (Liu et al., 1998), although it assumes that the rate of removing, sequestering, and buffering of Ca²⁺ is proportional to [Ca²⁺].

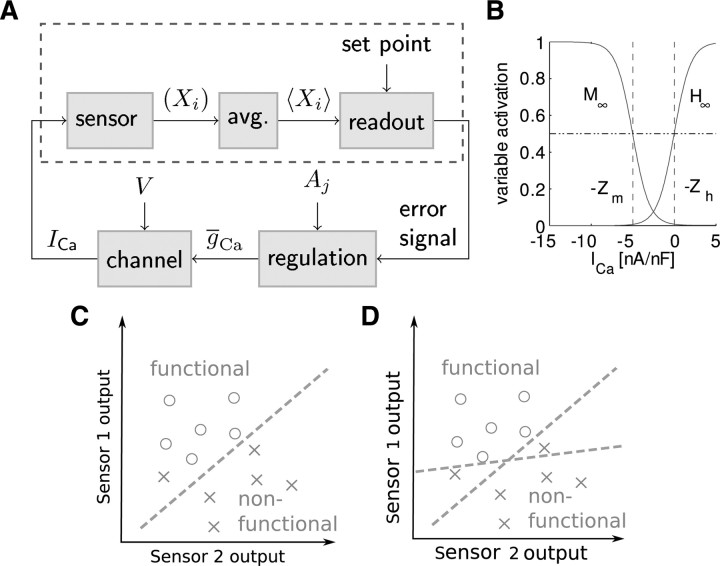
Figure 2.

The sensor and readout components within the context of ADHR. A, Engineering-style schematic illustrating the full feedback loop of ADHR. The scope of this paper is depicted with the dashed rectangle, in which I_Ca is used to generate an error signal. The error is calculated by the readout as the difference between the average of the sensors (average) over the network rhythm period, T, and a set point. Based on this error, a hypothetical regulatory mechanism can use a direction, A_j, to adjust each maximal conductance, such as ḡ_Ca that modulates I_Ca based on voltage, V. B, The sensors are defined with the steady-state curves of their activation (M) and inactivation (H) variables (Eqs. 2–4). C, The readout can be a linear classifier that separates functional networks from nonfunctional networks by drawing a hyperplane in the average sensor parameter space of two example (fast and slow) sensors. D, When the input classes are linearly nonseparable, the readout must use multiple hyperplanes.

Homeostatic regulation, for example through gene transcription, works on timescales much slower (minutes to hours) than the network rhythm period, which is why the readings of these I_Ca-dependent sensors were time averaged (Fig. 2). The sensors were averaged over a network rhythm period to simulate an integrative process with a very long time constant, as opposed to the study by Liu et al. (1998), in which they were averaged over a fixed period of 5 s. The disadvantage of a fixed integration period is that it interacts with the length of the rhythm period, which varies across networks. In either case, averaging loses information about the temporal patterns of I_Ca, which are found to be important for influencing regulatory signal transduction pathways in experiments (Gallin and Greenberg, 1995; Bito et al., 1997). We follow the proposal of Liu et al. (1998) that the temporal information can be retained by averaging with different types of sensors, X, each of which is defined by a product of activation, M, and inactivation, H, variables (Fig. 2B) that depend on I_Ca with different timescales and sensitivities:

For non-inactivating sensors, H is omitted. Both variables, y ϵ {M, H}, obey the formula

where τ_y is the activation or inactivation time constant and the function ȳ(I_Ca) determines the steady-state activation or inactivation, which is defined as

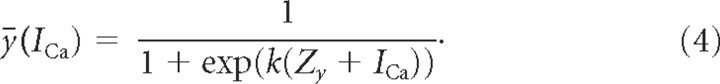Here, k respectively becomes +1 and −1 for defining M̄ and H̄ variables. The Z_y parameters indicate current density thresholds (in nanoamperes per nanofarad). In addition to the temporal averages of sensors, we also investigate the hypothesis that regulation may use the minimal and maximal values of a sensor.

To study the performance of these sensors, we varied their τ_m, τ_h, Z_m, and Z_h parameters according to rules consistent with previous work (Liu et al., 1998): τ_m < τ_h, because activation should be faster than inactivation (Eq. 3), and Z_m > Z_h such that the sensor activates with larger currents (Eq. 4). The time constants are chosen across orders of magnitude from a logarithmic scale of 100 μs, 1 ms, 10 ms, 100 ms, 1 s, and 10 s; and current thresholds were chosen from the values of 0, 5, 10, 15, 20, 30, 40, and 50 nA/nF. This yielded 330 inactivating and 36 non-inactivating sensors. The inactivating sensor parameters were limited by the rules for the fast and slow sensors below.

To detect different types of activity, we also used a case with multiple sensors in each cell (Liu et al., 1998). The fast (F), slow (S), and non-inactivating (D) sensors in this case (see Fig. 5E) were defined by,

where the M and H activation and inactivation variables were defined as above in the single-sensor-per-cell case. The FSD sensors were selected from the available single sensors using rules consistent with Liu et al. (1998):

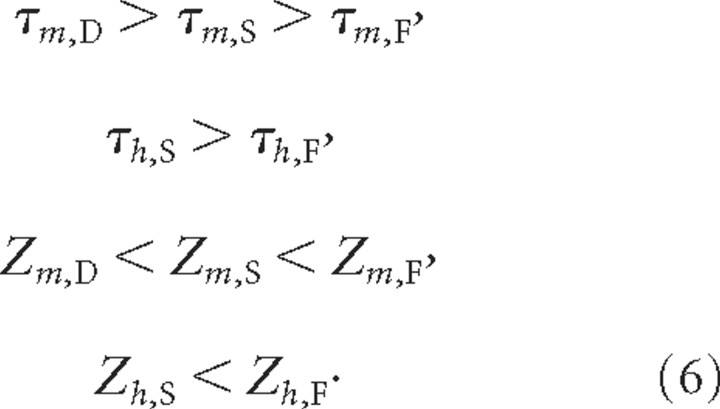These rules reduced the number of possible FSD sensor combinations from 254,803,968 to 85,750.

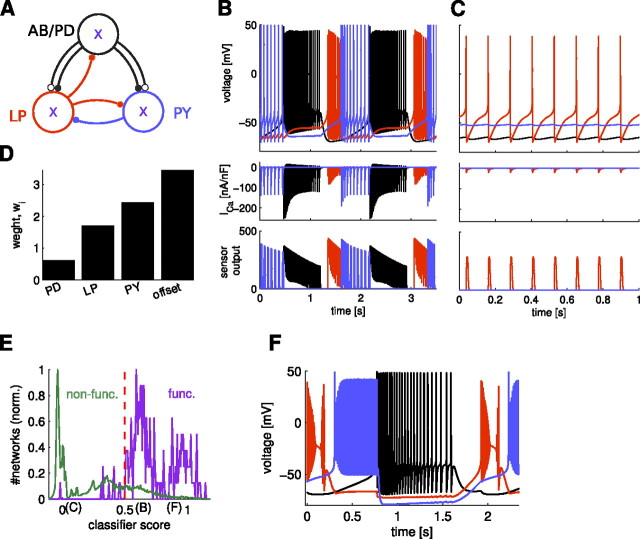
Figure 5.

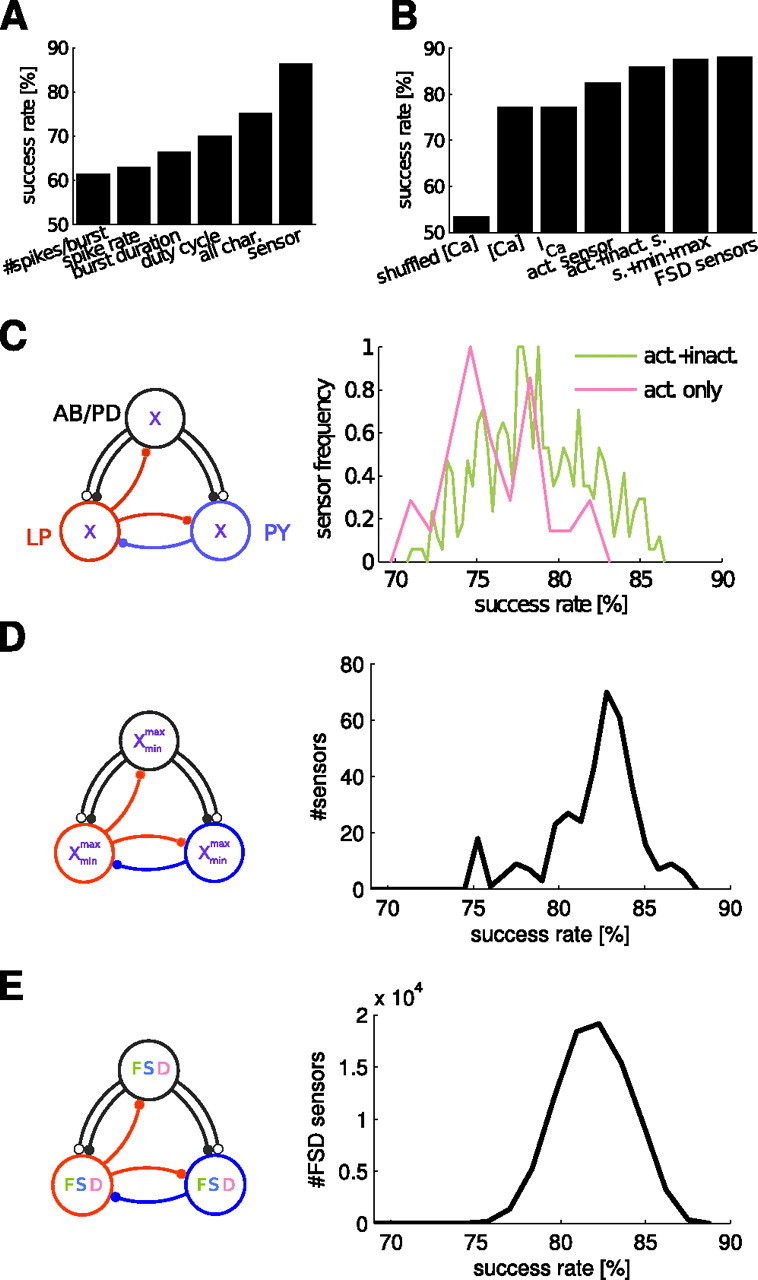
Activity sensors provide more information than activity characteristics such as bursting duty cycle, and activation and inactivation variables improve the estimation from sensors. A, Comparison of estimation success rates obtained from various activity characteristics compared with the success achieved by using activity sensors (#87; for parameters, see supplemental Table S2, available at www.jneurosci.org as supplemental material) in each model cell. all char., Estimation done with all characteristics. 50% success indicates estimation at chance level. B, Comparison of success obtained from Ca²⁺-related quantities and different types of sensors. The best activation-only sensor (#365) is inferior to the best inactivating sensor (#87). C, In the normalized frequency of success obtained from the 366 different calcium sensors tested at the same time in all three model cells, non-inactivating sensors (n = 36) were inferior to inactivating sensors (n = 330). The maximum estimation success reached 86.40%. Success rates were collected in 50 bins for inactivating and in 10 bins for the non-inactivating sensors. D, Using minimum and maximum values of a single (activating and inactivating) sensor in addition to its average increased the estimation success to 87.46%. E, Using the same fast, slow, and DC (FSD) sensors in all model cells (see Materials and Methods) yielded 85,750 combinations of the FSD sensors from which we found a maximum estimation success of 88.17%. Histograms contain 50 bins in last two panels.

During simulation, the time-averaged readings, maxima, and minima of sensors with varying parameters were saved into a file corresponding to the network number. In this manner, a “sensor database” was generated of sensor average and extremum values from each of the three model cell types in the 20,250,000 networks. This sensor database was then read into a relational database management system (Codd, 1970), MySQL (MySQL AB). The database occupied 285 gigabytes (GBs) of space in a table and another 90 GBs for its index structure that enabled optimized access and query to the table for the analysis of the results. The sensor database is available on request from the authors. File management and analysis were performed with scripts in PERL (The PERL Foundation) and Matlab (MathWorks); those scripts are also available on request. The Matlab analysis scripts took advantage of the database analysis functions of the Pandora Toolbox (http://software.incf.org/software/44/view/PANDORA) (Günay et al., 2009). The sensor database was used to separate networks with functional and nonfunctional activity patterns using a classifier algorithm.

Using a classifier.

Of the networks in the database, only 2% were previously categorized as functional because they were within ±2 SDs of recorded data from the lobster in terms of 15 salient features (such as burst period, durations, and phases) of their activity patterns (Prinz et al., 2004). The difference between functional and nonfunctional networks that was reflected in their activity patterns was also captured in their sensors readings (Fig. 3B,C). Based on the average of these sensors, we detected whether a network is functional by training a custom classifier (Fig. 2C).

Figure 3.

Functional versus nonfunctional activity patterns of the model network are reflected in the sensor readings. A, Model network with a single, same activity sensor (X) in each of the three cells. B, Example functional activity pattern produced by the model network (top; see parameters of network #4950096 in supplemental Table S1, available at www.jneurosci.org as supplemental material) and corresponding I_Ca (middle) and sensor readings (bottom traces from sensor #87; for parameters, see supplemental Table S2, available at www.jneurosci.org as supplemental material). Color coding is the same as in A. C, An example nonfunctional network producing tonic and silent firing activity patterns (network #4950003). D, Using the outputs of the best performing sensor, the classifier separated previously labeled functional and nonfunctional networks by assigning different weights to the activity sensor of each cell. The offset value is a constant (see Materials and Methods). E, The classifier score distribution shows the separation between functional and nonfunctional networks with a threshold of 0.5 (dashed vertical line). Scores of networks in other panels are marked on the x-axis line. F, An example nonfunctional model network (#4959071) that lies at the extreme of false-positive classifier estimations with a score of 0.8 (see E).

To find a classification solution that is simple and easily interpretable, we first used a linear classifier. We used the perceptron classifier (Rosenblatt, 1958) using the newff function of Matlab. The perceptron is a single-layered, feedforward artificial neural network (ANN) classifier (Rumelhart and McClelland, 1986) that defines an optimal hyperplane to linearly separate its inputs. Such optimal separating hyperplanes were used previously in similar work to separate neural activity types (Goldman et al., 2001; Taylor et al., 2006).

In the space of multiple sensor readings from the same or different cells, the classifier finds a hyperplane defined by the weight vector w and the offset, b, parameters, w × X_j + b = 0 that best separate functional networks (Fig. 3B) from nonfunctional networks (Fig. 3C) using the sensor vector, Xj, across all networks 1 ≤ j ≤ N (Fig. 2C). It does this by minimizing the sum of squares, S, of the differences between the classifier score, c_j = h(w × s_j + b) and the labels, ĉ_j, which are 0 for nonfunctional or 1 for functional for each network j. To match these labels, we normalized the inputs and output of the function h. The function h is a linear function, which provides a low or high output based on which side of the hyperplane the given sensor values lie. The classifier was initialized with random weights and optimized with the Levenberg–Marquardt training algorithm (Levenberg, 1944; Marquardt, 1963). We judged the success of the classification by the average percentage of correctly and incorrectly classified networks:

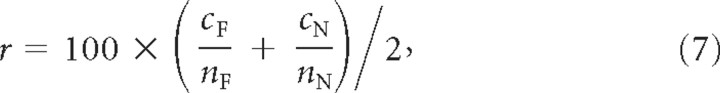where c and n, respectively, denote the correctly classified and total number of networks, and the subscripts F and N, respectively, stand for functional and nonfunctional networks (Taylor et al., 2006).

Training the classifier would suffer from the imbalance in the database between positive and negative samples (2% functional vs 98% nonfunctional networks), which was also preserved in its selected smaller subsets (see Results). To overcome this, we presented each set equally by randomly repeating the fewer functional networks (Lawrence et al., 1998; Günay and Prinz, 2009).

The ANN classifier reached a different suboptimal local minimum for repeated training even with the same sensor inputs because of the random initial conditions, yielding variable success rates. However, the variability was low: the success rate obtained from training a linear classifier 20 times from the readings of the best sensor varied <1% (supplemental Fig. S1, available at www.jneurosci.org as supplemental material). Consistent with our search for an optimal classifier, here we always report the maximum success rate obtained across 10 repeated classifier training runs. We also verified ANN training using a 50% cross-validation set (data not shown).

As a more complex classifier, we used a multilayered perceptron (MLP), or multilayered ANN (Rumelhart et al., 1986). In this classifier, an output layer unit linearly weights the outputs of several single-layer perceptrons, as described above, with e_j = h(Σ_iv_ic_ij + d), where h is a sigmoidal function, c_ij are the outputs of perceptrons, v_i are linear coefficients, and d is another offset. In the multi-hyperplane case, the weights of sensors within each hyperplane, w, as well as the hyperplane weights, v_i, vastly varied across different training runs of the classifier, preventing extraction of consistent rules (supplemental Fig. S5, available at www.jneurosci.org as supplemental material). Two factors contributed to getting different weights every time: (1) sensor weights are multiplied with hyperplane weights, allowing them to switch signs to achieve the same result, and (2) hyperplanes need not be in the same order to achieve the same result. We eliminated these two factors that added to the variation of the resulting weights by: (1) switching all output hyperplane weight signs to positive by inverting their sensor weights if necessary, and (2) sorting hyperplane positions according to the magnitude of their output weights (Guha et al., 2005; Günay and Prinz, 2009).

Training for neither perceptrons nor MLPs required manually specifying any parameters such as learning rate or momentum.

Results

For ADHR, the feedback element should be capable of sensing network activity levels. Here, we show that the proposed calcium sensors perform activity sensing as needed.

Activity sensors are sensitive to firing rate and duty cycle

It was shown previously in individual and networks of model cells (Liu et al., 1998; Golowasch et al., 1999b) that homeostasis can be maintained with activity sensors based on calcium current, I_Ca. When we place sensors of this type in all model cells of our pyloric network (Fig. 3A), firing activity is apparent in sensor readings. In particular, sensor readings look vastly different between example networks with functional (Fig. 3B) and nonfunctional (Fig. 3C) activity patterns.

However, it is not known which features of these activity patterns are important for homeostatic regulation. For instance, the duration of membrane depolarizations in cultured hippocampal neurons affects which gene expression targets are triggered by I_Ca (Mermelstein et al., 2000). Assuming that our I_Ca-based sensors serve a regulatory function also, we asked which activity pattern features are reflected by the sensor outputs. We achieved this by looking for correlations between activity characteristics and sensor averages.

Among all activity characteristics, we found significant correlations between burst duration, number of spikes per period (i.e., firing rate), and bursting duty cycle. It is straightforward to assume that a longer burst duration will increase the sensor average. Traces from example model cells (Fig. 4A) confirm that this relationship is true; however, it is only true when only the burst duration increases and the period is fixed. Without fixing the period, the relation is still true for some model cell types across the networks in the database (regression p < 10⁻⁴ for PY cell) (Fig. 4E) but does not generalize to others (regression p = 0.7 for the AB/PD cell) (Fig. 4C) because the AB/PD cell maintains a fixed duty cycle—the ratio of the burst duration to the cell period (supplemental Fig. S3, available at www.jneurosci.org as supplemental material)—that is consistent with recent experimental evidence from spiny lobsters (Reyes et al., 2008).

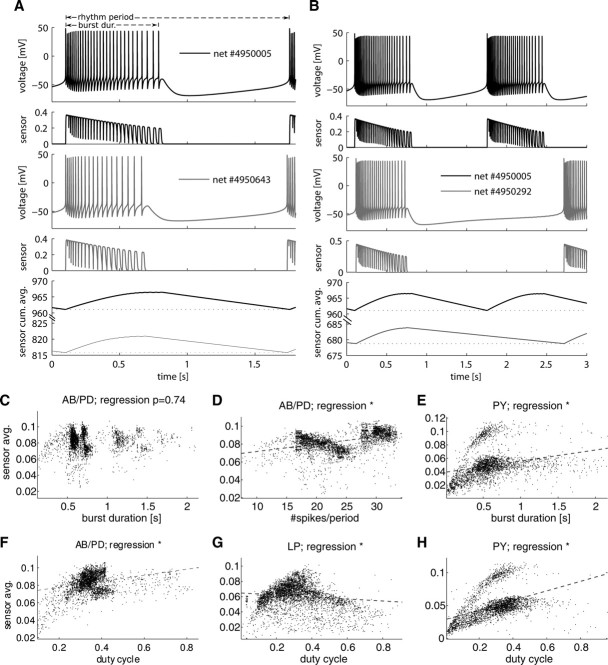
Figure 4.

Activity sensors represented both the bursting activity and the rhythm period of a cell, being a good indicator of the bursting duty cycle. The sensor used is the same as in Figure 3. A, Traces from AB/PD models in two example networks (solid and dashed lines) show that, when the cell rhythm period is invariant (∼1.6 s), an increase in the burst duration (from 0.6 to 0.8 s) increases the sensor cumulative average (sensor cum. avg.; bottom trace) and, therefore, the sensor period average (dotted line). Network model parameters are given in supplemental Table S1 (available at www.jneurosci.org as supplemental material). burst dur., Burst duration. B, Other example AB/PD models show that increasing the rhythm period (from 1.6 to 2.4 s) decreased the sensor period average for cells with similar burst durations (0.7–0.8 s). C, The AB/PD burst duration was not significantly correlated with its sensor average. D, The AB/PD sensor average and number of spikes were significantly correlated (*p < 10⁻⁴). To avoid saturation in the scatter plot, uniform noise between −0.5 and +0.5 was added to the number of spikes after regression. E, The PY sensor average was significantly correlated with its burst duration. F–H, All three model cell sensor averages showed significant correlations to their duty cycle characteristic. The correlation was no longer positive for LP in G for physiologically unrealistic duty cycles larger than 0.5.

A measure of activity that correlates better with the sensor average is the number of spikes in a period (Fig. 4D). However, the number of spikes does not generalize as an activity measure because it does not take into account the effect of the network period on the sensors (Fig. 4B). Duty cycle, which accounts for the period, is consistently and positively correlated with sensor averages from all three model cells (p < 10⁻⁴) (Fig. 4F–H). We next investigated what this means for homeostatic regulation.

An optimal sensor readout can estimate success of homeostatic network regulation

The original networks in the database were categorized as functional if they were producing activity patterns that are within 2 SDs of 15 electrophysiological criteria, including the burst duration, number of spikes in burst, and burst start time (Prinz et al., 2004). Based on this categorization, we trained an optimal classifier to quantify the sensor performance independent of a specific readout or regulatory mechanism (Fig. 2A). If this optimal readout can accurately estimate the functional network state across many network configurations, based alone on the activity sensors, it demonstrates that the sensors provide sufficient information for ADHR. The accuracy of this estimate provides the qualitative measure of goodness for the sensors used, which is calculated as a success rate (see Materials and Methods). Using this readout, we evaluated different parameters of previously proposed sensors (Liu et al., 1998) and their placement in the model networks (Prinz et al., 2004).

Sensors were individually weighted to optimally separate a randomly selected 10,000-network subset of the original network database into functional and nonfunctional networks. Sensor data from all cells were used at the same time, as a global signal, to find the optimal sensor properties. We addressed more realistic cases with sensor data from single cells further below. With a single activity sensor in each model cell (Fig. 3), each sensor weight indicated the importance of the sensor readings of that cell (Fig. 3D). The LP and PY cell sensors were almost twice as influential as AB/PD in determining the functionality of the sensed activity pattern. From the weighted sensors, we calculated a classifier score that successfully distinguished 86.40% of the networks with triphasic bursting activity (Fig. 3E). In the classifier score distribution, most nonfunctional networks are grouped around zero, which also contains tonic-firing networks (Fig. 3C). Some of the nonfunctional networks were estimated to be functional (i.e., classified as false positive), such as ones showing depolarization block during bursts (Fig. 3F). Most functional networks (95%) produced scores above 0.5 (Fig. 3E).

To test whether the results obtained from this random selection of model networks can predict the rest of the model network database, we used the classifier obtained from the selected random subset to classify other sensor subsets from up to 100,000 networks and consistently obtained maximal success rates >85% (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Next, we tested whether this prediction performance is specific to our sensors.

Sensors are more informative than activity characteristics

If the sensor readings are highly correlated with specific activity characteristics, we asked if, in theory, these characteristics can provide sufficient information for homeostatic regulation and replace the sensors completely. To answer this, we compared the estimation power from the optimal readout strategy using the activity characteristics versus the sensors. We found that the duty cycle characteristic has the most estimating power (70%) compared with other activity characteristics, such as spike rate (Fig. 5A). However, although the duty cycle is highly correlated with the sensors, the sensors were +16% better in estimating the network output. Thus, the sensors convey more information than any of these activity characteristics alone or even all combined together (Fig. 5A). To address exactly what features of the sensors are responsible for this added information, we examined the estimation power of the underlying observed quantity, I_Ca.

Activity sensing using I_Ca is as informative as using Ca²⁺

For ADHR, I_Ca may be more informative than the intracellular [Ca²⁺] (Turrigiano et al., 1994) because the mode of Ca²⁺ entry into the cell matters for gene regulation targets (Murphy et al., 1991; Gallin and Greenberg, 1995; Tadross et al., 2008); however, it is not known whether this makes a difference in a model of ADHR. To answer this question, we used a test bed identical to the one used above to make estimations from the three model cells, but instead of sensors, we compared the estimating power of total I_Ca and of [Ca²⁺]. To establish a control case, we shuffled [Ca²⁺] values by assigning them to random networks, which disrupted the classifier and caused it to estimate at close to chance levels (53.37%). Without shuffling, we achieved success rates above the control level and above success obtained from activity characteristics but also found that using either I_Ca or [Ca²⁺] resulted in very similar rates at 77% (Fig. 5B) (supplemental Table S3, available at www.jneurosci.org as supplemental material). This suggests that I_Ca is as informative as [Ca²⁺] for use in homeostatic regulation. However, because the sensors can achieve +9% better success than using I_Ca alone, we investigated the benefits of the activation and inactivation mechanisms in the sensor model.

Sensor inactivation is essential for detecting functional activity

The activation and inactivation of sensors roughly correspond to the production and removal of second-messenger proteins in the cell, and it was shown that inactivation is necessary for detecting different types of activity patterns (Liu et al., 1998). Compared with the 77.14% estimation success obtained with using I_Ca directly, using sensors with only an activation variable increased the success to 82.57% (Fig. 5B) (supplemental Table S3, available at www.jneurosci.org as supplemental material). Adding an inactivation variable further increased the estimation success to 86.40%. To find the optimal sensor from each type of sensor compared, we tested 366 sensors with different activation and inactivation parameters (Fig. 5C). The optimal sensor activated with a time constant of 1 ms and a half-activation threshold of 5 nA/nF of calcium current and inactivated with a time constant of 1 s and a half-inactivation threshold of 0 nA/nF (sensor #87 in supplemental Table S2, available at www.jneurosci.org as supplemental material).

Sensor minimum and maximum are also informative for regulation

In the slow timescale of homeostasis, ADHR may use activity sensor features other than the average. Adding the sensor minimum and maximum to the sensor average in the estimation by using their weighted sum, combined the same way as in FSD sensors (see Materials and Methods), increased the success rate to 87.69% (Fig. 5B,D) (supplemental Table S3, available at www.jneurosci.org as supplemental material). Compared with the optimal sensor, the sensor that had the most information in its minimum and maximum has different parameters (sensor #268 in supplemental Table S2, available at www.jneurosci.org as supplemental material); it is a non-inactivating [direct current (DC)] sensor with Z_m = 0 nA/nF and τ_m = 0.1 s. This suggests that inactivation could be replaced without loss of information by the minimal and maximal values of a slowly activating sensor. Because prediction using multiple values derived from a single sensor improved classification, we also tested using multiple different sensors in each cell.

Using fast, slow, and DC sensors in each cell

For ADHR of conductances in a model neuron, Liu et al. (1998) suggested that a fast, a slow, and a non-inactivating DC sensor (FSD sensors) that correspond to homeostatic regulation pathways operating at different speeds can be combined to detect activity at different timescales. We used these FSD sensors, but they barely improved our success to 88.17% (supplemental Table S3, available at www.jneurosci.org as supplemental material). We generated 85,750 combinations of FSD sensors following previous rules (see Materials and Methods) (Liu et al., 1998). The distribution of classification success obtained these FSD sensor combinations was unimodal (Fig. 5E), similar to the success distribution obtained from networks with a single, same sensor in each cell (Fig. 5C).

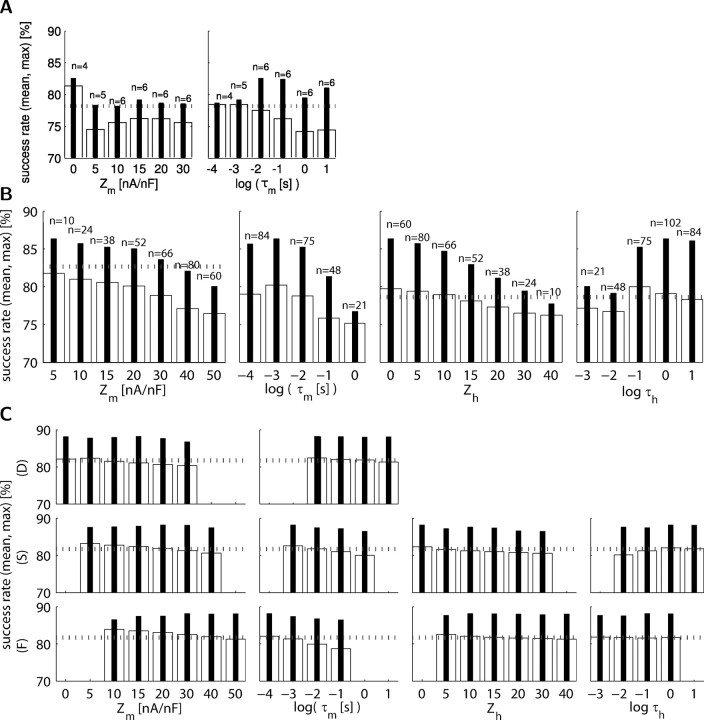
Functional sensor parameters are broadly tuned

It is important to understand the parameters of successful activity sensors to make predictions about possible biological mechanisms that may underlie them. By comparing the maximal success rates obtained for different parameter configurations, we found optimal values for each of these parameters for the non-inactivating (Fig. 6A) and inactivating (Fig. 6B) sensors types separately. The most successful sensor is an inactivating-type sensor with low current threshold values of Z_m = 5 and Z_h = 0 nA/nF and time constant values of τ_m = 1 ms and τ_h = 1 s (same as sensor #87 above in Figs. 2B, 3, 5A). The tendency to select a low activation current threshold implies that the ideal sensor is sensitive to small Ca²⁺ currents, whereas an inactivation threshold of zero indicates that the sensor never inactivates completely, because the calcium current is always negative because of its reversal potential (see Materials and Methods).

Figure 6.

Sensor time constant (τ) and calcium current sensitivity (Z) parameters are broadly tuned. In the bar plots, the inner bars show the maximal success, and open bars show the mean success. The dotted horizontal line shows the mean success from all sensors. A, Success with varying activation variable parameters of the non-inactivating sensors (n = 33; 3 sensors that always produced 0 output were omitted). The n values for each bar vary based on the sensor construction rules (see Materials and Methods). B, Same as A but for inactivating sensors (n = 330). C, Success for parameter values for each of the fast (F), slow (S), and DC (D) sensors.

In general, lower current threshold values yielded higher success, except in the non-inactivating sensors as observed from the success rate distributions. The distributions were unimodal: the success rate diminishes smoothly as parameters vary away from the optimal point, indicating that the sensor is tuned broadly. The parameters have no critical values beyond which the sensors failed, except the DC sensors with Z_m > 0, which are significantly worse. The optimal points found by the mean success value are generally consistent with the points found from maximal success, except for few parameters (e.g., τ_m of inactivating sensors and Z_m on non-inactivating sensors). When assessing optimal values from sensors with multiple varying parameters, the mean and maximal values may be artifacts from dependencies between two or more parameters (Golowasch et al., 2002). However, independently selecting the value of each parameter at the peak of its maximal success corresponds to the parameters of the best sensor (#87) found previously, suggesting that parameters are not interdependent. We completely ruled out the possibility of interdependency by inspecting interactions among all possible parameter pairs for inactivating and non-inactivating sensor types (supplemental Fig. S4, available at www.jneurosci.org as supplemental material).

The parameters of the FSD sensors are also broadly tuned (Fig. 6C). The peaks of the maximal success tuning curves are consistent with the optimal FSD sensor combination (#34,457) we found, whose parameters slightly differ from those used in previous work (Table 1). Although the FSD sensor current thresholds are in decreasing order and time constants are in increasing order (see Materials and Methods), each of the three sensors we found are specialized to different roles (Fig. 6C). Specifically, we observed the following: (1) The activation time constant, τ_m, of the fast and slow sensors tends to be as fast as possible, whereas the DC sensor has no preference. (2) The inactivation time constant, τ_h, of the slow sensor prefers a long value of ∼1 s, which is similar to the case of a single sensor (Fig. 6B), except that the fast sensor produced high success rates irrespective of the selected τ_h. (3) The activation current threshold, Z_m, tends to be higher for fast sensors (20–50), consistent with the idea of DC and slow sensors detecting the bursting envelope and the fast sensor detecting the spike firing activity, which causes larger calcium currents.

Table 1.

Comparison of the parameters of the optimal FSD sensor combination (#34,457) with those of the previously published FSD sensor from the study of Liu et al. (1998)

	Zm,F	τm,F	Zh,F	τh,F	Zm,S	τm,S	Zh,S	τh,S	Zm,D	τm,D
Opt. FSD	50	10−4	30	10−2	40	10−3	10	10−2	10	10−1
Prev. FSD	14.2	5 × 10−4	9.8	1.5 × 10−3	7.2	5 × 10−2	2.8	6 × 10−2	3	5 × 10−1

All Z values are in nanoamperes per nanofarad, and all τ parameters are in seconds. Opt. FSD, Optimal FSD sensor; Prev. FSD, previously published FSD sensor.

Once we found the most effective sensor type and its parameters, we investigated the advantages of local versus global placement of sensors in achieving the best separation between functional and nonfunctional network patterns.

Local sensors can estimate network activity

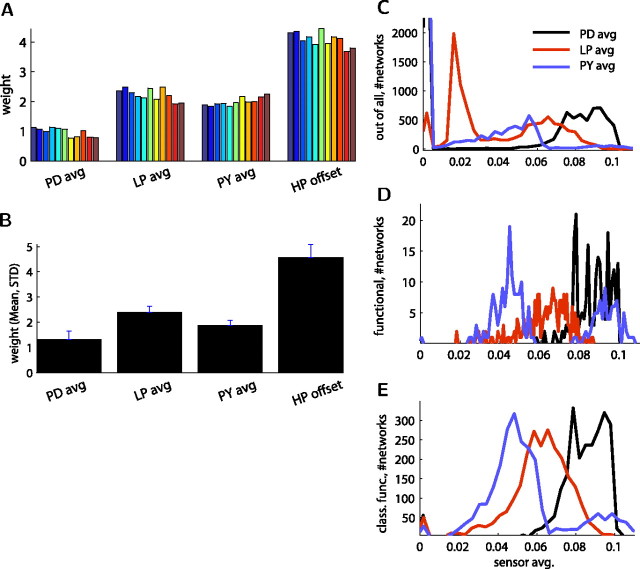
In the above results, we allowed the readout to access sensors from all three cells. However, readouts in living cells are most likely to have access to the local activity sensors only. To test whether local sensors from a model cell can estimate the outcome of the network activity, we measured the estimation power of sensors from each individual model cell (Fig. 7A). From individual cell sensors, we obtained estimation success levels well above chance (Fig. 7A). In particular, different model cells provided different levels of estimation power: the PY cell sensor output is most informative, yielding an 83.34% classification success, whereas the sensors in the LP and AB/PD model cells are less informative, both yielding a success of ∼76%. As opposed to the limited information given by a local sensor, a global sensor may give a more accurate estimation of network activity.

Figure 7.

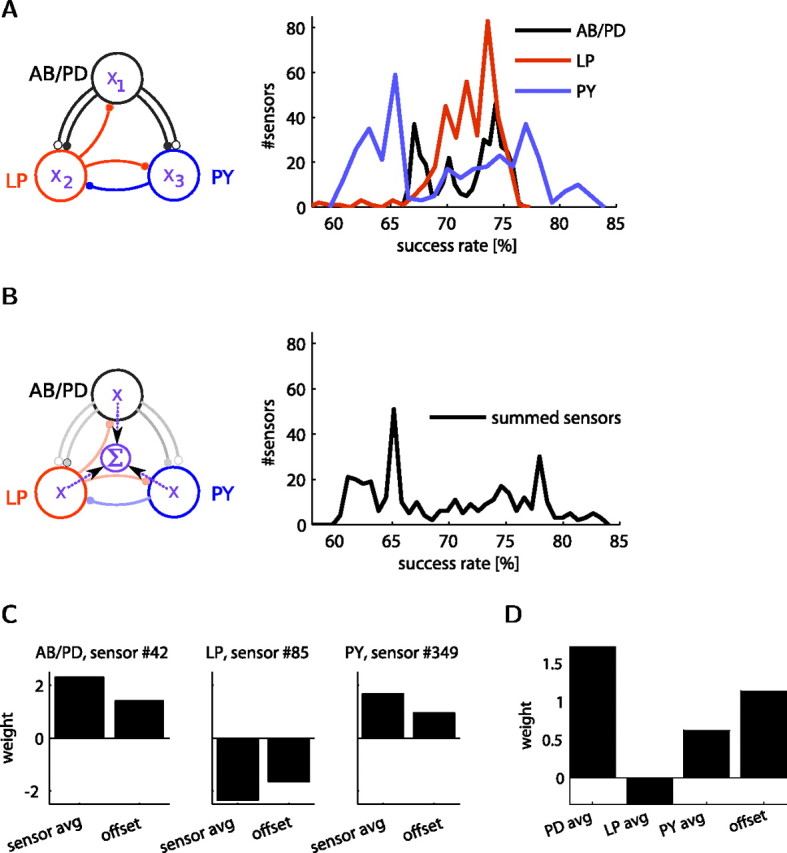
Local sensors can estimate network activity and sensor variety between cells does not yield better estimation success. A, A different activity sensor (X_i, i ϵ 1, 2, 3) in each model cell used individually to estimate the network outcome. The distribution of success rates from 366 sensors (20 bins) in each of the three cells are superimposed for comparison, which showed a different maximal success from each cell sensor. B, Combined sensor readings from three model cells to simulate a global sensor reading (50 bins). C, Classifiers with different weight and offset values were found for each of the different sensor types in each cell (for sensor parameters, see supplemental Table S2, available at www.jneurosci.org as supplemental material) for obtaining the best success rates in A. D, When the outputs of the best sensors from each cell are used together to classify functional networks, the signs of the individual weights found in C are maintained.

A global sensor can estimate network activity

To test whether a global activity sensor can be more informative, we built an abstract model of a global sensor by summing the activity sensors from each model cell into a single value. First, we summed the optimal sensors of each model cell found above, which resulted in a estimation success of 82.46%. Second, we summed the same sensor in all three cells to find the success distribution across all possible sensor parameters, which reached a higher success of 83.66% (Fig. 7B). Considering that the SD of the success rate is 0.15% (supplemental Fig. S1, available at www.jneurosci.org as supplemental material), the global sensor estimations were not better than, but at about the same level with, estimations obtained from individual model cell sensors.

Cells with different roles in the network need not have different activity sensors

The different optimal sensors from each cell estimated the network outcome well independently, but, when they were summed before classification, the estimation success did not increase. Can they generate a better estimation if all of their information is passed to the readout, that is, when their sensors are individually weighted and summed by the classifier? To answer this question, we classified the networks using the optimal sensors from all model cells. If the information given from the PY sensors would add to the information from the other two cells, we would predict reaching a success rate higher than 83.34%. However, this was not the case, and the best three-sensor classifier reached a similar, 83.33%, success rate, almost identical considering an SD of 0.15%. This indicated that (1) the sensors in the three cells contain redundant information that does not add up when combined, and (2) using the optimal sensors for each cell is less informative (83%) than finding one general sensor that maximizes the estimation in the whole network (86%).

Optimal sensors found by independent estimation also gave insights about the sensor readout: the classifier weights for the best sensors for each cell (Fig. 7C) were different from the weights found when the same optimal sensor was used in all cells (Fig. 3D). Specifically, the weight and offset for the LP cell sensor was the reverse of the AB/PD and PY cells. This indicated that the role of the LP cell in affecting the outcome of the network activity is different from the two other cells. This relationship between sensors from the different cells was maintained in the weights obtained from the classifier trained on the combined sensor outputs from the three cells (Fig. 7D) but was inconsistent with weights of the optimal sensor readings (Fig. 3D). The difference between weights may mean that sensors are tuned to best read the activity of a specific neuron based on its function in the network. To address the function of each cell in the network, we looked for a relation with its sensor outputs.

Sensor readings in each cell contribute differently to classifying functional network activity

The classifier weights trained to the best sensor (#87) indicated that the AB/PD activity is approximately half as important as the LP and PY activity (Figs. 3D, 8A). The classifier weights obtained from the next best 10 sensors (Fig. 8A), as well as the statistics of all sensors performing better than a 80% success rate (Fig. 8B) were consistent with this distribution of weights. The weights found were significantly different from cell to cell for the most successful sensors (p < 10⁻⁴ with one-way ANOVA) (Fig. 8B).

Figure 8.

Classifier weights of best performing sensors consistently selected specific proportions of the sensor of each cell for classifying functional network activity. A, Weights found by the top 11 best sensors were consistent (best sensor being the rightmost, brown color). B, Mean and SD of the sensors with success >80% (n = 63) maintained the same proportions between the weights of sensors of different cells and the offset value. The weight of each cell sensor was significantly different from each of the others (p < 10⁻⁴, same for separate one-way ANOVA for each pair and also one for all together). C–E, Distribution of the average optimal sensor readings from the three cells (each into 100 bins) for all networks classified (C; n = 9915, the truncated 0 bins showing no activity were 4208 for AB/PD, 663 for LP, and 5662 for PY), for functional networks (D; n = 221), and for classified functional networks (E; n = 2834).

One explanation for the imbalance between contributions of the activity of the AB/PD cell versus the other cells can be found by inspecting the average sensor readings of the networks: the readings of the AB/PD cell were generally higher than those of the other two cells, PY producing the lowest readings (Fig. 8C). This means that generally the AB/PD cell has a larger duty cycle than the LP cell, and LP has a larger duty cycle than the PY cell. When all networks (n = 9915) are considered (Fig. 8C), activity from nonfunctional networks may confound these results. However, the ranking between the sensed activity of the three cells is preserved for the smaller subsets of networks with functional (n = 221) (Fig. 8D) and networks that were found functional by the classifier (“classified functional,”, n = 2834) (Fig. 8E), with the exception of high activity in the PY cell sensors in the functional networks. From these sensor reading distributions, we were also able to predict types of activity patterns produced by the network (supplemental Fig. S6 and supplemental data, available at www.jneurosci.org as supplemental material).

Linear readout failed to correctly classify specific activity patterns

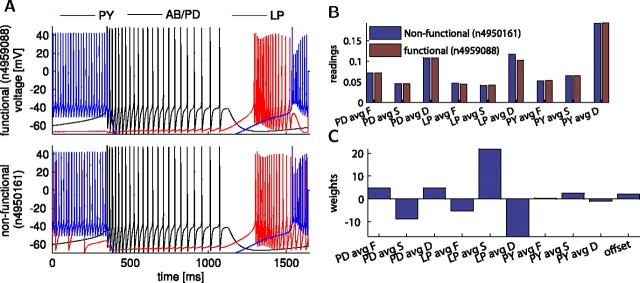
With the linear classifier, although using FSD sensors from each cell improved the estimation of functional network patterns, ∼12% of the networks were still misclassified. This may point to a limitation of either the model calcium sensors or their readout, the linear classifier. To distinguish between these two possibilities, we investigated the types of activity changes that were misclassified. To find hard-to-classify examples, we searched the sensor database subset for examples of similar network activity at the decision threshold of the classifier score: to find two networks that produce activity patterns as similar as possible, while one of them is misclassified. Such an example network pair illustrates that our estimation test bed can confuse two similar types of activity (Fig. 9). In this example, both network activity patterns were estimated as functional, although the activity of one network was categorized previously (Prinz et al., 2004) as nonfunctional (Fig. 9A). The nonfunctional network exhibited an excessive activity in the LP cell that was reflected as an increase in its DC sensor average (Fig. 9B). In turn, this sensor had a negative classifier weight (Fig. 9C), translating the increase in the sensor average into a decrease in the classifier score. This reduced the score of the nonfunctional network down to 0.7 from an initial score of 1.1 in the functional network. However, this decrease was insufficient to cross the decision threshold at 0.5. Therefore, this example demonstrates that the calcium sensors can correctly detect slight changes in activity but the linear classifier used to interpret the sensor readings is too simple to produce the correct output. This suggests that, to improve estimation from sensors, it is necessary to have a better readout mechanism than a classifier that is linear.

Figure 9.

The calcium sensors misclassified ∼12% of the networks. A, Two example network traces, one from a functional (top; network #4950161) and one from a nonfunctional (bottom; network #4950088), producing very similar activity patterns, except when the LP activity overlap with PY activity pushes it outside of the biological range of functional patterns. The two networks have similar parameters (supplemental Table S1, available at www.jneurosci.org as supplemental material). B, The FSD sensor outputs from these two networks were identical, except a larger DC sensor average indicated the longer LP activity in the nonfunctional network. C, Comparison of the classifier weights for each of the nine sensors in the network indicated that the LP sensors were most important in determining the classifier score.

Using a nonlinear readout increased success to 95%

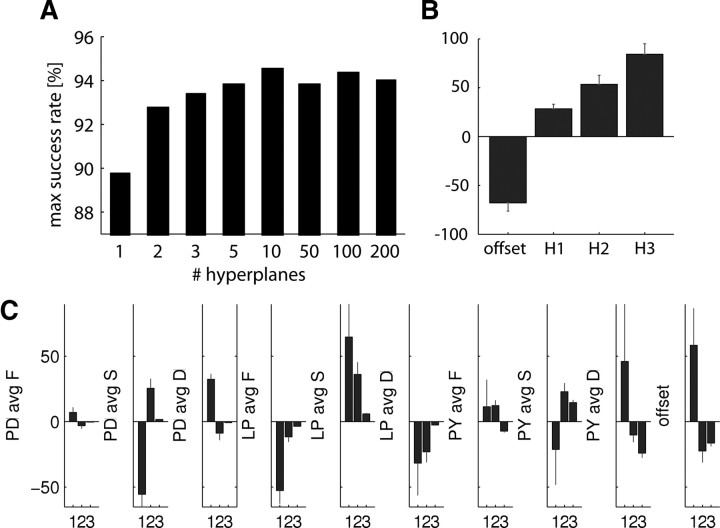
A linear classifier fails when the decision boundary between functional and nonfunctional networks are linearly nonseparable in the sensor space (Fig. 2C). Linearly nonseparable sensor inputs require multiple hyperplanes to correctly separate the two network populations (Fig. 2D). When we increased the number of hyperplanes in classifying from the FSD sensor readings, we reached success rates of 95% correct (Fig. 10A). The success rate saturated after 5–10 hyperplanes, indicating that a small number of decision boundaries is sufficient to make accurate estimations.

Figure 10.

Increasing the number of decision boundaries (hyperplanes) of the classifier allowed to make finer and more accurate estimations of functional network patterns. A, Adding hyperplanes in classifying with the optimal FSD sensor triplet (#34,457; see Table 1) from all cells improved classification success from 88 to 95%. B, Hyperplane weights indicate the importance of each hyperplane in the estimation. C, Mean and SD of sensor weights for hyperplanes 1, 2, and 3.

Solutions provided by the multi-hyperplane classifier contained more weights that were harder to interpret than solutions of the linear classifier. The magnitude of contribution to the classifier estimation by each hyperplane is revealed by sorting hyperplanes by their weights (Fig. 10B). The sensor weights within each sorted hyperplane were similar across training runs (Fig. 10C), which indicated that specific sensor rules carried a specific importance in estimating whether the model network activity pattern is functional. Consistent with the linear classifier results showing that PY and LP sensors contain more information in making estimations (Figs. 3D, 7A, 8), the sensor weights in the most important hyperplane (H3) weighed higher the sensors of PY exclusively. The next important hyperplane (H2) weighed both LP and PY sensors high, and the least important hyperplane (H1) weighed sensors from all cells but used a rule that complements the other two hyperplanes.

Discussion

We generalized and explored an existing, biophysically inspired, abstract Ca²⁺ sensor model (Abbott and LeMasson, 1993; LeMasson et al., 1993; Siegel et al., 1994; Liu et al., 1998) to make predictions about dynamics of Ca²⁺ sensing mechanisms.

A classifier can be used as an optimal readout for regulation

Instead of explicitly defining the readout mechanism as done previously (Golowasch et al., 1999b), we assumed that there is an optimal mechanism by replacing it with a classifier [using a similar approach to that of Poirazi and Mel (2001) and the ideal observer in the study by Felsen and Mainen (2008)]. This classifier generates a single score for each network that indicates on which side of the functional boundary the network lies. It has been shown that such a single error measure can be sufficient, under certain conditions in ADHR modeling studies, to regulate ionic conductances along a line in the parameter space (Liu et al., 1998; Golowasch et al., 1999b; Olypher and Calabrese, 2007; Zhang et al., 2009; Olypher and Prinz, 2010). Linear correlations found between conductances in experimental and modeling studies also support this result (MacLean et al., 2005; Schulz et al., 2006, 2007; Khorkova and Golowasch, 2007) (T. Smolinski, P. Rabbah, C. Soto-Treviño, F. Nadim, and A. A. Prinz, unpublished observation; A. E. Hudson and A. A. Prinz, unpublished observation) (but see Taylor et al., 2009).

Cell activity characteristics correlate with model Ca²⁺

The value of the Ca²⁺ sensors in this study represents the average firing activity and correlates highly with the cell bursting duty cycle (Fig. 4). However, when we used activity characteristics such as duty cycle to make predictions about the network activity, we found that the Ca²⁺ signal and sensors were better predictors (Fig. 5A,B). This indicates a limitation to modeling studies that use spike time-based activity characteristics that disregard the subthreshold voltage dynamics of the cell (Prinz et al., 2003, 2004; Günay et al., 2008; Taylor et al., 2009).

Both Ca²⁺ concentration and current are informative for homeostatic regulation

In general, our methodology is not limited to comparing only one type of sensor, because we showed that the controlling quantity in the sensors is interchangeable between the total Ca²⁺ current (I_Ca) and concentration ([Ca²⁺]) (Fig. 5B); we could as well have chosen to use the membrane voltage as in the study by Rabinowitch and Segev (2006). In this comparison, our [Ca²⁺] dynamics in Equation 1 was limited to only one set of fixed parameters (Prinz et al., 2003). Although varying these parameters would have given a more realistic range of Ca²⁺ dynamics, it would have also increased the parameter space significantly and thus was kept outside the scope of this work. Our use of I_Ca for activity sensing is consistent with experiments showing that ADHR is modulated not by the steady state of the activity level but by its change (Thoby-Brisson and Simmers, 2000). We assume that the change in activity reflects [Ca²⁺] close to the membrane in which it is more likely to affect ion channels (see Materials and Methods). Although this assumption may exclude processes that involve transport and signaling between the nucleus and the cell membrane, it is consistent with the localization of some Ca²⁺ sensing proteins (e.g., frequenin) near the plasma membrane (O'Callaghan et al., 2003).

Despite the experimental evidence connecting Ca²⁺ to regulatory processes (Turrigiano et al., 1994; Linsdell and Moody, 1995; Golowasch et al., 1999a), another modeling study suggested that the Ca²⁺ concentration across different cells may be too variable to be useful for homeostatic regulation (Achard and De Schutter, 2006, 2008). This is inconsistent with our results that correctly predict network regulation targets from readings of [Ca²⁺], I_Ca, and I_Ca-based activity sensors across the vastly different pyloric network models found in our database (Fig. 5A,B). The discrepancy can be explained if the lobster CPG pyloric network uses a very different regulation rule than mouse cerebellar Purkinje cells considered by Achard and De Schutter (2008).

Single, same Ca²⁺ sensor in each cell can indicate whether a network is functional

The use of multiple FSD sensors by Liu et al. (1998) was justified because Ca²⁺ affects ion channel properties through multiple parallel pathways, triggered by proteins such as frequenin, the downstream regulatory element antagonist modulator (Carrión et al., 1999; Mellström and Naranjo, 2001), and a transcription factor encoded by the C terminus of the L-type voltage-gated calcium channel Ca_v1.2 (CCAT) (Gomez-Ospina et al., 2006). Consistent with the specialization of FSD sensors for a division of labor in parallel pathways, our results showed that FSD sensors increased estimation success rates. However, this increase was too small to be important in our simpler task of separating functional from nonfunctional network activity (Fig. 5B) (supplemental Table S3, available at www.jneurosci.org as supplemental material), and rather a single sensing mechanism with activation and inactivation variables in each cell was able to estimate the network activity pattern up to 86% correct (Fig. 5C), which is consistent with other recent pyloric network models (Zhang et al., 2009). Furthermore, this sensor need not be specific for each cell in the network (Fig. 7); thus, it could be one of the possible Ca²⁺ sensing proteins. This prediction can potentially be experimentally tested by blocking these candidate sensor pathways (Carrión et al., 1999; An et al., 2000; Zhang et al., 2003; Gomez-Ospina et al., 2006).

In the search for the optimal sensor, if access to minimal and maximal values of the sensor are also used for the estimation, the success increases to 87% (Fig. 5D). However, this sensor need not have an inactivation variable (supplemental Tables S2, S3, available at www.jneurosci.org as supplemental material), which suggested that inactivation could be replaced without loss of information by the minimal and maximal values of a slowly activating sensor. These peak values were found to be important in the control loops of signaling pathways in the living cell (Pouvreau et al., 2006).

Local activity sensors are capable of network homeostasis

Can global features of network activity be detected by local sensors? Consistent with other models (Golowasch et al., 1999b; Zhang et al., 2009), in this pyloric network model, local sensors in the PY cell were successful estimators across 83% of networks in the database with varying connection topologies (Fig. 7). This follower cell produced higher success rates than the other two cells because of the asymmetric connections specific to the pyloric network (Fig. 1B) (no feedback connection from PY to AB/PD cell), in which observing PY indicates the state of both AB/PD and PY; PY would not burst if AB/PD was not properly bursting. The same asymmetry is confirmed in the weights of the classifier (Fig. 8A) that performs better than local sensors (up to 95% in Fig. 10A) using all global features. This classification paradigm was only used to find optimal sensor configurations for ADHR, because it may be unrealistic for sensors to have global access.

One such global signal appears in mice outside the neurons: in the glial cells. These glial cells were found to regulate the levels of the TNF-α (pro-inflammatory cytokine tumor-necrosis factor-α) to mediate homeostatic synaptic scaling in an activity-dependent manner (Stellwagen and Malenka, 2006). In the pyloric network, although a similar global, activity-dependent homeostatic regulation mechanism is not known, global neuromodulatory inputs to the network modulate ion channel conductances independent of activity (Thoby-Brisson and Simmers, 1998; Khorkova and Golowasch, 2007). However, a single global sensor that we simulated with a simple, instantaneous model by summing individual cell sensors was only as informative as the PY sensors (Fig. 7B). These results together suggest that more complex, network-level communication is necessary between the cells to achieve better ADHR (e.g., through synaptic or intracellular signaling mechanisms).

Optimal sensor parameters are consistent with biological data

The optimal parameters of the calcium sensors that we found predicted suitable ranges of operational parameters for Ca²⁺ sensing proteins that can be tested experimentally by blocking specific proteins and by applying artificial stimulation protocols to drive the regulation. The optimal parameters were consistent with observed biological properties of the pyloric network (Fig. 6), which indicated that homeostatic regulation is insensitive to unphysiologically long bursts but is sensitive to single spike events in the bursts at the millisecond range. This is too fast for many Ca²⁺ sensing proteins that operate a Ca²⁺/myristoyl switch and need to translocate from the cytosol to membranes, except NCS-1/frequenin, whose N-terminal myristoylation targets it at the plasma and trans-Golgi membranes, allowing it to respond quickly to local changes in Ca²⁺ (Burgoyne, 2004).

Similar tuning properties of the parameters were found also for the case of three FSD sensors in each cell (Fig. 6C). For instance, the fast sensor did not prefer an inactivation time constant, because a fast activation variable can follow the I_Ca, making the inactivation unnecessary. This is confirmed by the increasing success of faster non-inactivating sensors (Fig. 6A).

Sensor readout approximates a simple nonlinear boundary

The architecture of the optimal classifier gave us information about the readout mechanism reacting to the calcium sensors. The specific predictions about readout mechanism can be tied to how Ca²⁺ sensing proteins affect their downstream targets, such as ion channel voltage dependence and surface expression (Zhang et al., 2003). Because our results did not improve for more than 5–10 hyperplanes, we can speculate that a nonlinear, biologically feasible decision boundary would be sufficient for the regulatory mechanism to be correct for 95% of the networks (Fig. 10).

Together with the results that a single sensor with a low-dimensional readout decision can perform well for estimation, we can hypothesize that a single optimal sensing pathway (e.g., frequenin) that produces an informative quantity can be used by multiple downstream targets to push the cell toward a functional activity regimen.