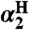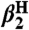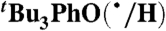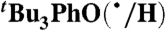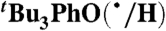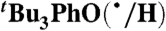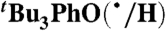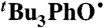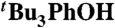Abstract
Chemical reactions that involve net hydrogen atom transfer (HAT) are ubiquitous in chemistry and biology, from the action of antioxidants to industrial and metalloenzyme catalysis. This report develops and validates a procedure to predict rate constants for HAT reactions of oxyl radicals (RO•) in various media. Our procedure uses the Marcus cross relation (CR) and includes adjustments for solvent hydrogen-bonding effects on both the kinetics and thermodynamics of the reactions. Kinetic solvent effects (KSEs) are included by using Ingold’s model, and thermodynamic solvent effects are accounted for by using an empirical model developed by Abraham. These adjustments are shown to be critical to the success of our combined model, referred to as the CR/KSE model. As an initial test of the CR/KSE model we measured self-exchange and cross rate constants in different solvents for reactions of the 2,4,6-tri-tert-butylphenoxyl radical and the hydroxylamine 2,2′-6,6′-tetramethyl-piperidin-1-ol. Excellent agreement is observed between the calculated and directly determined cross rate constants. We then extend the model to over 30 known HAT reactions of oxyl radicals with OH or CH bonds, including biologically relevant reactions of ascorbate, peroxyl radicals, and α-tocopherol. The CR/KSE model shows remarkable predictive power, predicting rate constants to within a factor of 5 for almost all of the surveyed HAT reactions.
Keywords: free radicals, Marcus theory, proton-coupled electron transfer, reactive oxygen species, oxyl radicals
Hydrogen atom transfer (HAT) reactions (Eq. 1) have been a cornerstone of organic and biological chemistry for over a century (1, 2). These reactions are key steps in many important processes, from energy conversion to the chemistry of reactive oxygen species and antioxidants (3). Thus, developing a detailed understanding of the factors that dictate HAT reactivity has long been a goal.
| [1] |
A large number of HAT rate constants have been measured in many laboratories with various techniques (4, 5). Rates of HAT reactions have traditionally been understood by using the Bell–Evans–Polanyi (BEP) relation, which relates the activation energy to the enthalpic driving force (6). Whereas the BEP relation holds well within sets of similar reactions, a comprehensive theoretical understanding of HAT is still emerging (3).
Our group has been exploring the use of the Marcus cross relation (CR) Eq. 2 (7), a corollary of the Marcus theory of electron transfer, as the basis for a general model for HAT rates (8–12). This use of the CR grew out of recognizing HAT as one class of a larger set of reactions in which one electron and one proton are transferred (H• ≡ H+ + e-), termed proton-coupled electron transfer. In this paper, we use “HAT” to refer to any reaction in which H• is transferred from a donor to an acceptor in a single kinetic step (Eq. 1), although other definitions have been used (13).
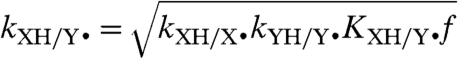 |
[2] |
The CR, with respect to HAT reactions, relates the cross rate constant (kXH/Y•, Eq. 1) to the two degenerate self-exchange rate constants (kXH/X• and kYH/Y•), the equilibrium constant (KXH/Y• = kXH/Y•/kYH/X•), and the frequency factor (f). The variable f is defined as ln(f) = [ln(KXH/Y•)]/4 ln(kXH/X•kYH/Y•Z-2), with the collision frequency Z typically taken as 1011 M-1 s-1 (7). For transition metal complexes, Eq. 2 has been found to predict HAT cross-reaction rate constants within 1–2 orders of magnitude (10). Marcus theory has also been successfully applied to proton transfers (14), hydride transfers (15), and methyl transfers (SN2 reactions) (6, 16), although only within sets of very closely related reactions.
Here we develop a predictive model of HAT rate constants by using the CR explicitly and accounting for both kinetic and thermodynamic solvent effects. The rates of many HAT reactions, particularly those involving O-H bonds, are highly solvent-dependent. Litwinienko and Ingold have described a quantitative kinetic solvent effect (KSE) model for HAT rate constants, on the basis of the strength of the substrate–solvent hydrogen bond (17), which is estimated by using Abraham’s empirical model (18–20). The composite CR/KSE model presented here combines the Marcus CR, Ingold’s KSE model, and Abraham’s H-bonding parameters. The calculated rate constants are compared with directly measured values for a broad range of HAT reactions, including several biologically relevant reactions of vitamin E, vitamin C, peroxyl radicals, and phenoxyl radicals.
Results
Approach.
The Marcus CR in its simplest form (Eq. 2) predicts HAT rate constants kXH/Y• by using three inputs: the equilibrium constant KXH/Y• and the two degenerate self-exchange rate constants kXH/X• and kYH/Y•. Solvent Effects on Equilibrium and Rate Constants provides an overview of how these parameters are obtained, including how adjustments are applied to obtain them in the same solvent. A Test Case: Reactions of Bulky Phenoxyl Radicals with TEMPOH describes measurements of one small set of reactions as a detailed test of the model. Finally, Broader Application of the CR/KSE Model extends this approach to a wide range of HAT reactions. The properties of all of the reactants used in this study are summarized in Table 1; the derivations and citations for these values are given in SI Text.
Table 1.
Properties of reagents: solution BDFEs and self-exchange rate constants (kXH/X•) in selected solvents*
Compound (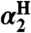 )† )† |
Solvent (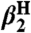 )† )† |
BDFE |
kXH/X• |
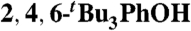 (0.22)‡ (0.22)‡
|
MeCN (0.44) | 77.8 | 20 |
2, 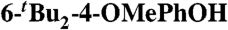 (0.22)‡ (0.22)‡
|
MeCN (0.44) | 74.9 | 20 |
| TEMPOH (0.39) | MeCN (0.44) | 66.5 | 4.7 |
| Phenol (0.60) | DTBP§ (0.35) | 87.8 | 3.2 × 105 |
| 1-naphthol (0.61) | Isopentane (0) | 79.7 | ≤ 9 × 105 |
| 2-naphthol (0.61) | Isopentane (0) | 83.0 | 9 × 105 |
| Tyrosine (0.60) | H2O (0.38) | 88.0 | 1.8 × 106 |
| tBuOOH (0.44) | Isopentane (0) | 80.4 | 500 |
| L-ascorbate (0.27) | MeCN (0.44) | 67.8 | 5 × 105 |
| L-ascorbate (0.27) | H2O (0.38) | 73.6 | 8 × 105 |
| α-tocopherol (0.38) | MeCN (0.44) | 75.1 | 2.2 × 104 |
| Trolox C (0.38)¶ | H2O (0.38) | 78.5 | 3.5 × 105 |
| tBuOH (0.32) | DTBP (0.35) | 104 | 3 × 104 |
| 9,10-dihydroanthracene∥ | DMSO (0.78) | 75 | 5 × 10-11 |
| Toluene∥ | toluene (0.14) | 86.4 | 8 × 10-5 |
*BDFE in kcal mol-1 and kXH/X• in M-1 s-1 at 298 K. Full derivation of BDFEs, self-exchange rate constants and accompanying references are in SI Text.
‡kXH/X• for the 2,6-di-t-butyl-4-R substituted phenols are approximated as equal because of their structural similarity.
§DTBP = tBuOOtBu.
¶Trolox C = ( ± )-6-hydroxy-2,5,7,8-tetramethylchromane-2-carboxylic acid.
∥kXH/X• are not expected to vary with solvent because 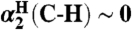 .
.
Solvent Effects on Equilibrium and Rate Constants.
KXH/Y•, bond dissociation free energies (BDFEs), and solvent effects.
Ideally 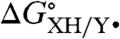 (= -RTlnKXH/Y•) is determined by direct equilibrium measurements in the solvent of interest, which is typically possible only when
(= -RTlnKXH/Y•) is determined by direct equilibrium measurements in the solvent of interest, which is typically possible only when 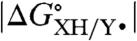 is small. A more general procedure gives
is small. A more general procedure gives 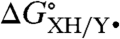 as the difference in the BDFEs of the reactants and products (XH and YH) in the same solvent. Solution-phase BDFEs (Eq. 3) can be calculated from the commonly tabulated gas phase bond dissociation enthalpies (BDEs) by using a two-step procedure. First, BDEs are converted to gas phase BDFEs (Eq. 4) by using S∘(H•) = 27.42 cal K-1 mol-1 and the common assumption that S∘(XH) ∼ S∘(X•) for organic compounds (21–23). Converting these to solution BDFEs (BDFEsolv) requires
as the difference in the BDFEs of the reactants and products (XH and YH) in the same solvent. Solution-phase BDFEs (Eq. 3) can be calculated from the commonly tabulated gas phase bond dissociation enthalpies (BDEs) by using a two-step procedure. First, BDEs are converted to gas phase BDFEs (Eq. 4) by using S∘(H•) = 27.42 cal K-1 mol-1 and the common assumption that S∘(XH) ∼ S∘(X•) for organic compounds (21–23). Converting these to solution BDFEs (BDFEsolv) requires 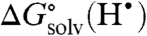 in a given solvent (24) and the difference in the free energy of solvation of XH and X• (Eq. 5).
in a given solvent (24) and the difference in the free energy of solvation of XH and X• (Eq. 5).
| [3] |
| [4] |
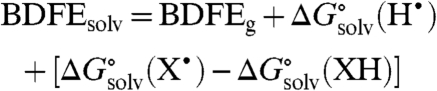 |
[5] |
For the hydroxyl/oxyl radical substrates examined here, the solvation difference 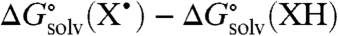 is dominated by the differences in hydrogen bonding between the OH/O• groups and the solvent. Other contributions to solvation essentially cancel because XH and X• have the same charge and are similar in size (25, 26). Abraham et al. have developed an empirical relation to estimate the free energy of formation of 1∶1 complexes X - H⋯Y in CCl4 solvent (18), by using H-bonding acidity (
is dominated by the differences in hydrogen bonding between the OH/O• groups and the solvent. Other contributions to solvation essentially cancel because XH and X• have the same charge and are similar in size (25, 26). Abraham et al. have developed an empirical relation to estimate the free energy of formation of 1∶1 complexes X - H⋯Y in CCl4 solvent (18), by using H-bonding acidity (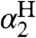 ) and basicity parameters (
) and basicity parameters (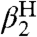 , Eq. 6). We use Eq. 6, following Ingold (17), as a measure of the free energy of solvent-solute hydrogen bonds. The constants
, Eq. 6). We use Eq. 6, following Ingold (17), as a measure of the free energy of solvent-solute hydrogen bonds. The constants 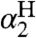 and
and 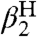 are obtained from ref. 19 and 20, respectively, unless otherwise noted. In aprotic solvents, the
are obtained from ref. 19 and 20, respectively, unless otherwise noted. In aprotic solvents, the 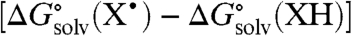 term in Eq. 5 is therefore taken as the energy of the XH-solvent hydrogen bond. In protic solvents, solvent H bonding to X• is included as well. This model gives solution BDFEs of good accuracy, either from gas phase values or by converting BDFEs between solvents (SI Text).
term in Eq. 5 is therefore taken as the energy of the XH-solvent hydrogen bond. In protic solvents, solvent H bonding to X• is included as well. This model gives solution BDFEs of good accuracy, either from gas phase values or by converting BDFEs between solvents (SI Text).
| [6] |
Solution BDFEs can also be derived from redox potentials (E∘) and pKa values [(21, 27); see SI Text]. BDFEs relevant to this study are summarized in Table 1 (and SI Text).
Self-exchange rate constants.
kXH/X• or kYH/Y• are best measured directly, e.g., by NMR line broadening (12, 28), or they can be extracted from “pseudo-self-exchange” reactions between two very similar reagents, as described below. When these values are not available in the solvent of interest, we use Litwinienko and Ingold’s KSE model, which is necessary because HAT rate constants can vary by > 102 between weakly and strongly H-bonding solvents (17). The KSE model gives the rate constant for H-atom abstraction from an O-H or N-H bond in solvent S (kS), in terms of the rate constant for the same reaction in a non-hydrogen-bonding solvent, such as an alkane (k0), and the Abraham H-bonding parameters 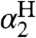 and
and 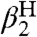 (Eq. 7). Eq. 7 can also be recast to convert k between two H-bonding solvents (SI Text). A key implication of the KSE model is that substrates are unreactive towards HAT when H-bonded to solvent (XH⋯S). Whereas Eq. 7 does not explicitly include solvent effects on KXH/Y•, such effects are included in the CR/KSE treatment developed here (see above).
(Eq. 7). Eq. 7 can also be recast to convert k between two H-bonding solvents (SI Text). A key implication of the KSE model is that substrates are unreactive towards HAT when H-bonded to solvent (XH⋯S). Whereas Eq. 7 does not explicitly include solvent effects on KXH/Y•, such effects are included in the CR/KSE treatment developed here (see above).
| [7] |
A Test Case: Reactions of Bulky Phenoxyl Radicals with 2,2'-6,6'-tetramethyl-piperidin-1-ol (TEMPOH).
Self-exchange and cross-reaction rate constants in various solvents have been measured for bulky phenols/phenoxyl radicals and for the nitroxyl radical/hydroxyl amine TEMPO(•/H) (TEMPO = 2,2′,6,6′-tetramethylpiperidine-1-oxyl radical) (Tables 2 and 3). These reactions all proceed via HAT mechanisms (concerted transfer of H+ and e-; see SI Text), and they therefore provide a detailed test of the CR/KSE model.
Table 2.
Self-exchange rate constants for  and for TEMPO(H) from measured pseudo-self-exchange reactions and from the KSE model (Eq. 7)
and for TEMPO(H) from measured pseudo-self-exchange reactions and from the KSE model (Eq. 7)
Table 3.
Rate constants for 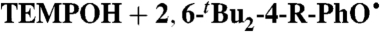 (R = tBu, OMe) [Eq. 9]: measured; predicted from the CR (Eq. 2); and predicted from the CR/KSE model
(R = tBu, OMe) [Eq. 9]: measured; predicted from the CR (Eq. 2); and predicted from the CR/KSE model
Self-exchange reactions.
We have determined the kXH/X• for 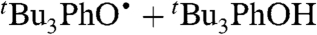 HAT self-exchange in dry CCl4, C6H6, MeCN, and DMSO by studying the reaction of isolated
HAT self-exchange in dry CCl4, C6H6, MeCN, and DMSO by studying the reaction of isolated 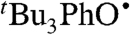 (29) and 2,6-di-tert-butyl-4-methyl-phenol (BHT,
(29) and 2,6-di-tert-butyl-4-methyl-phenol (BHT, 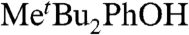 ). The disappearance of
). The disappearance of 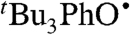 in the presence of excess BHT was monitored by UV-vis stopped-flow spectrophotometry (see Materials and Methods). As described in SI Text, this reaction proceeds by initial HAT from BHT to
in the presence of excess BHT was monitored by UV-vis stopped-flow spectrophotometry (see Materials and Methods). As described in SI Text, this reaction proceeds by initial HAT from BHT to 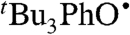 , which is an example of a pseudo-self-exchange reaction, X-H + X′. This is because X and X′ are very similar and because it is essentially isoergic [Keq = 1.45 ± 0.13 in C6H6 (30)]. In such cases (9, 11, 31), kXH/X• is taken as the geometric mean of the forward and reverse rate constants kXH/X′• and kX′H/X• (Eq. 8). Analyzing our rate constants in various solvents, as well as a value in hexane reported by Prokof’ev (32), gives the self-exchange rate constants in Table 2 (SI Text).
, which is an example of a pseudo-self-exchange reaction, X-H + X′. This is because X and X′ are very similar and because it is essentially isoergic [Keq = 1.45 ± 0.13 in C6H6 (30)]. In such cases (9, 11, 31), kXH/X• is taken as the geometric mean of the forward and reverse rate constants kXH/X′• and kX′H/X• (Eq. 8). Analyzing our rate constants in various solvents, as well as a value in hexane reported by Prokof’ev (32), gives the self-exchange rate constants in Table 2 (SI Text).
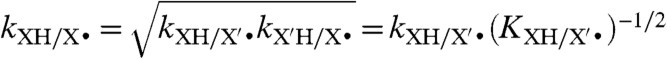 |
[8] |
Self-exchange rate constants for TEMPO(•/H) have been determined from the pseudo-self-exchange reaction of TEMPOH with the stable radical 4-oxo-TEMPO and Eq. 8 (KXH/X′• = 5.5) in benzene and DMSO, complementing prior measurements in MeCN (11) and CCl4 (31) (Table 2).
Testing the KSE model.
The 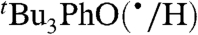 and TEMPO(•/H) self-exchange rate constants provide a test of the KSE model for self-exchange reactions. The needed
and TEMPO(•/H) self-exchange rate constants provide a test of the KSE model for self-exchange reactions. The needed 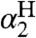 (substrate) and
(substrate) and 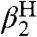 (solvent) values are from ref. 19 and 20, respectively, or from our measurement of
(solvent) values are from ref. 19 and 20, respectively, or from our measurement of 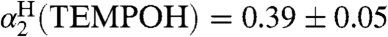 (SI Text), using Abraham’s 1H NMR method (33, 34). To confirm this methodology, we also measured
(SI Text), using Abraham’s 1H NMR method (33, 34). To confirm this methodology, we also measured 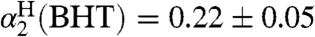 and
and 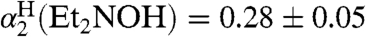 by 1H NMR, which are in excellent agreement with the literature values determined by IR spectroscopy (35, 36).
by 1H NMR, which are in excellent agreement with the literature values determined by IR spectroscopy (35, 36).
The KSE model (Eq. 7) has been used to predict TEMPO(•/H) and 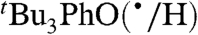 self-exchange rate constants in other solvents by using the rate constant in the least polar solvent as the reference point (the last column of Table 2). The predicted rate constants are within error of the measured values for all but one of the reactions. [The calculated value for
self-exchange rate constants in other solvents by using the rate constant in the least polar solvent as the reference point (the last column of Table 2). The predicted rate constants are within error of the measured values for all but one of the reactions. [The calculated value for 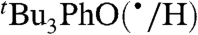 in DMSO deviates by a factor of 2, slightly outside the error limits.] The KSE model thus works well for self-exchange reactions, as expected (17).
in DMSO deviates by a factor of 2, slightly outside the error limits.] The KSE model thus works well for self-exchange reactions, as expected (17).
Cross reactions and application of the CR.
Phenoxyl radicals 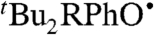 (R = tBu,OMe) rapidly oxidize TEMPOH to give the corresponding phenol and TEMPO (Eq. 9). Rate constants were measured by UV-vis stopped-flow spectrophotometry under pseudo-first-order conditions of excess TEMPOH, monitoring the change from the blue phenoxyl radical to the pale orange TEMPO. As predicted by the KSE model, the reactions are much slower in the more polar solvents (Table 3).
(R = tBu,OMe) rapidly oxidize TEMPOH to give the corresponding phenol and TEMPO (Eq. 9). Rate constants were measured by UV-vis stopped-flow spectrophotometry under pseudo-first-order conditions of excess TEMPOH, monitoring the change from the blue phenoxyl radical to the pale orange TEMPO. As predicted by the KSE model, the reactions are much slower in the more polar solvents (Table 3).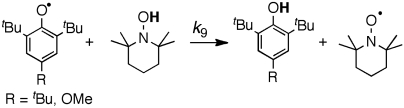 9
9
These cross rate constants provide a test of the CR (Eq. 2), by using the self-exchange rate constants presented above (Table 2) and equilibrium constants from the BDFEs in Table 1 and from the Abraham model (SI Text). The frequency factor (f; see above) has also been included in this analysis (SI Text). The cross rate constants computed from Eq. 2 are in good agreement with those that were directly measured, all within a factor of 6.5. As a test of the CR/KSE model, cross rate constants in polar solvents have also been calculated by using the KSE-derived self-exchange rates from Table 2. The calculated cross-reaction rate constants are again in agreement with those directly measured, within a factor of 4.5. This agreement is expected because the KSE model predicted self-exchange rate constants are close to the measured values. This exercise serves to validate the interchangeable use of KSE-adjusted or directly measured self-exchange rate constants in Eq. 2.
Broader Application of the CR/KSE Model.
To examine the validity of the CR/KSE model over a wider range of reactions, we have culled data from the literature and measured a few more rate constants. In this section we present our new measurements first and then a variety of tests of the model.
Reactions of phenoxyl radicals, ascorbate, and related species.
 abstracts H• from α-tocopherol (TocOH) in MeCN as indicated by disappearance of the UV bands of
abstracts H• from α-tocopherol (TocOH) in MeCN as indicated by disappearance of the UV bands of  and growth of an optical signature characteristic of the α-tocopheroxyl radical (TocO•) (37; SI Text). The measured rate constant kTocOH/tBu3PhO• = 8,100 ± 600 M-1 s-1 is close to that reported for TocOH + 2,6-di-tert-butyl-4-phenyl-phenoxyl (
and growth of an optical signature characteristic of the α-tocopheroxyl radical (TocO•) (37; SI Text). The measured rate constant kTocOH/tBu3PhO• = 8,100 ± 600 M-1 s-1 is close to that reported for TocOH + 2,6-di-tert-butyl-4-phenyl-phenoxyl (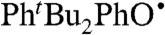 ) in ethanol, kTocOH/PhtBu2PhO• = 8,800 ± 440 M-1 s-1 (38). These reactions have similar driving forces, because the BDFEs of
) in ethanol, kTocOH/PhtBu2PhO• = 8,800 ± 440 M-1 s-1 (38). These reactions have similar driving forces, because the BDFEs of 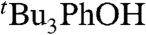 and
and 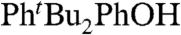 are the same, as measured in benzene (39). The TocOH self-exchange rate constant is best estimated from the CR by using kTocOH/tBu3PhO•, log KTocOH/tBu3PhO• = 2.21 ± 0.18 (30), and
are the same, as measured in benzene (39). The TocOH self-exchange rate constant is best estimated from the CR by using kTocOH/tBu3PhO•, log KTocOH/tBu3PhO• = 2.21 ± 0.18 (30), and 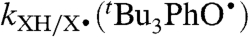 from Table 2, yielding kXH/X•(TocOH) = 2.4 × 104 M-1 s-1 in MeCN (40).
from Table 2, yielding kXH/X•(TocOH) = 2.4 × 104 M-1 s-1 in MeCN (40).
A similar analysis can be done for the reported reaction of TEMPO with 5,6-isopropylidene ascorbate (iAscH-), an organic soluble ascorbate analog (41): The measured kiAscH/TEMPO• = 1,720 ± 150 M-1 s-1 and KiAscH/TEMPO• = 1.2 ± 0.2 in MeCN yield kXH/X•(iAscH-)MeCN = (5.4 ± 1.2) × 105 M-1 s-1. Application of the KSE model with 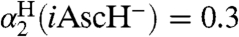 then gives kXH/X•(AscH-) = 3 × 105 M-1 s-1 in water, assuming that ascorbate (AscH-) and iAscH- have similar properties (SI Text).
then gives kXH/X•(AscH-) = 3 × 105 M-1 s-1 in water, assuming that ascorbate (AscH-) and iAscH- have similar properties (SI Text).
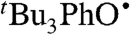 oxidizes 9,10-dihydroanthracene (DHA), to give anthracene and
oxidizes 9,10-dihydroanthracene (DHA), to give anthracene and 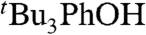 based on UV and 1H NMR spectra. This reaction proceeds by rate limiting HAT, and the rate constant for that step at 298 K in MeCN has been determined (under pseudo-first-order conditions with excess DHA) to be kDHA/tBu3PhO• = (1.1 ± 0.1) × 10-3 M-1 s-1 (SI Text). This reaction is much slower than H-atom abstractions from O-H bonds of comparable strength, as expected (8).
based on UV and 1H NMR spectra. This reaction proceeds by rate limiting HAT, and the rate constant for that step at 298 K in MeCN has been determined (under pseudo-first-order conditions with excess DHA) to be kDHA/tBu3PhO• = (1.1 ± 0.1) × 10-3 M-1 s-1 (SI Text). This reaction is much slower than H-atom abstractions from O-H bonds of comparable strength, as expected (8).
Tests of the CR where kXH/X• and kYH/Y• are known in the same solvent.
By using the experimental results above and literature data (see Tables 1 and 4 and SI Text), there are 17 oxyl radical reactions for which the Marcus CR can be tested by using measured kXH/X• and kYH/Y• values measured in the same solvent. The KXH/Y• values are estimated from the BDFE values in Table 1 and Eq. 6 above. These 17 reactions, indicated in Table 4 by §, include RO• radicals abstracting hydrogen from both O-H and C-H bonds. These reactions span 1012 in cross rate constant (kXH/Y•) and 1018 in equilibrium constant (KXH/Y•). There is very good agreement between experimentally determined rate constants and those predicted by using Eq. 2, as indicated by the average deviation of a factor of 4.4 and as illustrated in Fig. 1 (42). For all but 3 of the 17 reactions, the deviation between kcalc and kobs is less than a factor of 4.
Table 4.
Summary of observed and calculated hydrogen transfer rate constants.
| Entry | Reaction (XH + Y•) | Solvent (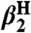 )* )*
|
KXH/Y•† | kobs‡ | kcalc‡ |
| 1§ |
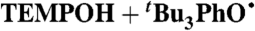 ¶ ¶
|
MeCN (0.44) | 5.0 × 107 | 1.25 × 104 | 2.9 × 104 |
| 2§ |
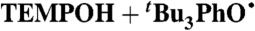 ¶ ¶
|
DMSO (0.78) | 4.7 × 107 | 2.7 × 103 | 7.0 × 103 |
| 3§ |
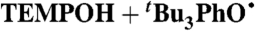 ¶ ¶
|
C6H6 (0.14) | 2.4 × 108 | 9.5 × 104 | 4.0 × 105 |
| 4§ |
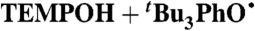 ¶ ¶
|
CCl4 (0.05) | 2.7 × 108 | 9.8 × 104 | 6.2 × 105 |
| 5§ |
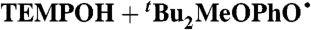 ¶ ¶
|
MeCN (0.44) | 3.2 × 105 | 2.67 × 103 | 3.6 × 103 |
| 6§ |
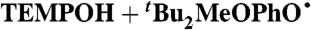 ¶ ¶
|
DMSO (0.78) | 3.4 × 104 | 6.2 × 102 | 8.8 × 102 |
| 7§ |
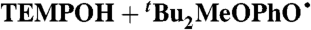 ¶ ¶
|
C6H6 (0.14) | 1.8 × 106 | 1.85 × 104 | 5.6 × 104 |
| 8§ | 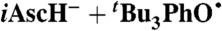 |
MeCN (0.44) | 2.3 × 108 | 3.4 × 106 | 1.3 × 107 |
| 9§ | 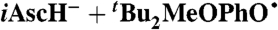 |
MeCN (0.44) | 1.5 × 106 | 5.3 × 105 | 1.9 × 106 |
| 10 |
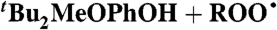 ∥ ∥
|
Styrene (0.18) | 4.5 × 105 | 1.1 × 105 | 3.6 × 104 |
| 11 | BHT + ROO•∥ | Styrene (0.18) | 4.7 × 103 | 1.4 × 104 | 5.0 × 103 |
| 12 | 2,6-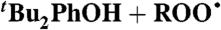 ∥ ∥
|
Styrene (0.18) | 2.3 × 102 | 3.1 × 103 | 1.3 × 103 |
| 13 | TocOH + ROO•∥ | Styrene (0.18) | 4.8 × 105 | 3.2 × 106 | 1.5 × 106 |
| 14§ | 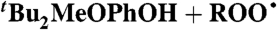 |
Alkane** (0) | 2.4 × 105 | 1.1 × 105 | 8.8 × 104 |
| 15§ | 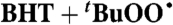 |
Alkane** (0) | 2.5 × 103 | 2.4 × 104 | 1.2 × 104 |
| 16 | 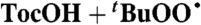 |
Alkane** (0) | 4.0 × 105 | 2.6 × 106 | 3.8 × 106 |
| 17 | tBuOOH + TocO• | EtOH (0.44) | 1.5 × 10-6 | 4.1 × 10-1 | 3.5 × 10-1 |
| 18 | 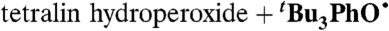 |
PhCl (0.11) | 4.2 × 10-4 | 3.4 × 10-1 | 2.5 |
| 19 | 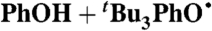 |
Hexane (0) | 3.1 × 10-7 | 5.7 | 17 |
| 20 | 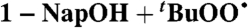 |
Isopentane (0) | 3.5 | 1.5 × 105 | 2.9 × 105 |
| 21 | 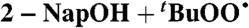 |
Isopentane (0) | 1.4 × 10-2 | 3.1 × 104 | 1.7 × 104 |
| 22 | 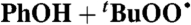 |
Heptane (0) | 5.5 × 10-4 | 3 × 103 | 2.9 × 103 |
| 23§ | 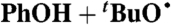 |
DTBP:C6H6 | 1.6 × 1012 | 3.3 × 108 | 5.1 × 109 |
| 24§ | TocOH + PhO• | 2∶1 DTBP:MeCN | 2.6 × 109 | 3.2 × 108 | 1.1 × 109 |
| 25§ | TocOH + PhO• | 3∶1DTBP:C6H6 | 2.6 × 109 | 1.1 × 109 | 1.1 × 109 |
| 26 | Trolox C + PhO• | Water (0.38) | 1.0 × 108 | 4.1 × 108 | 9.7 × 108 |
| 27 | 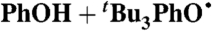 |
PhCl (0.09) | 1.8 × 10-7 | < 8†† | 6.1 |
| 28 | AscH- + Trolox C radical | Water (0.38) | 4.7 × 103 | 1.4 × 107‡‡ | 2.5 × 107 |
| 29 | AscH- + Trolox C radical | Water (0.38) | 4.7 × 103 | 8.3 × 106‡‡ | 2.5 × 107 |
| 30 | AscH- + tyrosyl radical | Water (0.38) | 4.0 × 1010 | 4.4 × 108 | 7.0 × 109 |
| 31 | Trolox C + tyrosyl radical | Water (0.38) | 9.3 × 106 | 3.1 × 108 | 4.5 × 108 |
| 32 | DHA + PhO• | PhCl (0.09) | 1.9 × 108 | < 1.1 × 102†† | 1.8 × 102 |
| 33§ |
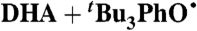 ¶ ¶
|
MeCN (0.44) | 1.2 × 102 | 1.1 × 10-3 | 3.3 × 10-4 |
| 34§ | 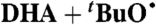 |
DTBP:C6H6 | 4.0 × 1021 | 9.5 × 106 | 6.2 × 105 |
| 35§ | 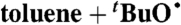 |
DTBP:C6H6 | 8.9 × 1012 | 2 × 105 | 5.0 × 105 |
| 36 | 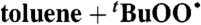 |
Toluene (0.14) | 2.6 × 10-4 | 1 × 10-2 | 1.1 × 10-3 |
*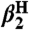 values from ref. 20.
values from ref. 20.
†KXH/Y• in organic solvents from BDFEs and the Abraham model; KXH/Y• in water from thermochemical cycles.
‡k in M-1 s-1 at 298 K unless otherwise noted; full details and citations are given in SI Text.
§Indicates both kXH/X• and kYH/Y• are known in the given solvent.
¶This work.
∥ROO• = polyperoxystyryl.
**Alkane = decane or cyclohexane.
††Rate constant at 333 K.
‡‡Independent determinations of the rate constant for Trolox radical + AscH- give slightly different values (SI Text).
Fig. 1.
Comparison between HAT rate constants measured experimentally (kobs) vs. those determined from the Marcus CR (Eq. 2, kcalc) for reactions where kXH/Y•, kXH/X•, and kYH/Y• have been measured in the same solvent (Table 4). The reactions involve oxyl radicals +O-H bonds (•) or C-H bonds (□).
Tests of the CR/KSE model.
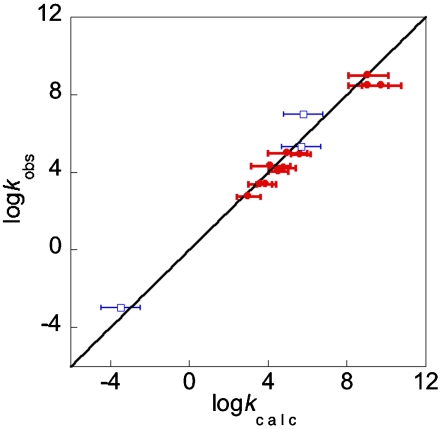
For many HAT reactions, the relevant self-exchange rate constants are known, but not in the solvent of interest. In these cases, we use the KSE model (Eq. 7) to predict self-exchange rate constants in the solvent of the cross-reaction, which expands the set of applicable reactions to 36 (Table 4 and Fig. 2). Some of these HAT reactions are in protic media where, to our knowledge, there have been no reports of HAT self-exchange rate constants. Remarkably, for these 36 reactions the average deviation is 3.8, and the deviation between kcalc and kobs is less than a factor of 5 for all but six of the reactions.
Fig. 2.
Comparison between HAT rate constants measured experimentally (kobs) vs. those from the CR/KSE model (kcalc). The line indicates perfect agreement. The reactions (Table 4) involve oxyl radicals +O-H bonds (•) or C-H bonds (□). The correlation coefficient (R2) for all data is 0.97.
Discussion
Agreement Between Theory and Experiment.
The CR/KSE approach developed here combines the Marcus CR (Eq. 2) and two other well-established empirical models. Ingold’s KSE (Eq. 7) model is used to calculate self-exchange rate constants in one solvent when they have been measured in another, and Abraham’s hydrogen-bonding model allows estimation of KXH/Y• in different solvents. The combined CR/KSE model is a powerful predictor of organic HAT rate constants, on the basis of the close agreement between kcalc and kobs (Table 4 and Fig. 2). By removing the need to have all of the inputs measured in the solvent of interest, the KSE model and Abraham’s H-bonding model dramatically broaden the scope of reactions that can be understood by using the CR. It should be noted, however, that the KSE model is not universally applicable, as noted by Ingold and coworkers (43), and that the Abraham model can be difficult to use in some cases because parameters are not available or because the parameters apply to an entire molecule rather than a particular XH fragment (33). Despite these caveats, the combined CR/KSE model works very well for the diverse set of organic HAT reactions discussed here.
The CR/KSE method is much more powerful than the traditional BEP relation. As noted above, the BEP relation is typically limited to reactions of a series of similar compounds under similar reaction conditions. In contrast, the set of HAT reactions examined here is extensive and diverse, including reactions of phenoxyl, nitroxyl, peroxyl, and alkoxyl radicals with phenols, hydroxylamines, ascorbate, and alkylaromatic compounds. The reaction solvents range from alkanes to water, covering polar, nonpolar, protic, and aprotic media. The reactions have equilibrium constants spanning more than 1020, and the cross rate constants range from 10-3 to 109 M-1 s-1. There are a wide distribution of oxyl radical reactions studied by different physical and spectroscopic techniques and by different research groups over the past 50 years. The broad success of the CR/KSE model is surprising because previous applications of the CR to atom and group transfer reactions (other than electron transfer) have been restricted to limited sets of structurally similar reagents under very similar reaction conditions (6, 14–16).
Implications and Limitations of the Model.
The success of the CR/KSE model provides fundamental understanding of HAT reactions. First, it indicates that HAT reactions should be described by using free energies rather than the enthalpies commonly used in free-radical chemistry (including the BEP relation). All of the components of the CR/KSE model use free energies, and this is an essential feature of Marcus theory. Furthermore, recent work from our group on a specific transition metal HAT reaction shows directly that free energies are more appropriate than enthalpies (27).
It should be emphasized that the model developed here is not simply an extended linear free energy relation (44). Linear free energy relations, such as Hammett analyses and the Brønsted relation, are valuable but are typically limited to a set of closely related compounds or reactions, and the parameters are derived from the analysis (like Hammett ρ values). In the CR/KSE model, all of the parameters—kXH/X•, kYH/Y•, KXH/Y•, 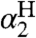 , and
, and 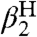 —are measured from independent experiments and have independent meaning. The rates of HAT cross reactions are directly related to the rates of the corresponding self-exchange reactions and the hydrogen-bonding properties of the reagents with the solvent.
—are measured from independent experiments and have independent meaning. The rates of HAT cross reactions are directly related to the rates of the corresponding self-exchange reactions and the hydrogen-bonding properties of the reagents with the solvent.
For a particular reaction, the success of the CR/KSE treatment indicates that it proceeds by a HAT mechanism (concerted H• transfer) because all of the inputs (kXH/X•, kYH/Y•, and KXH/Y•) are for HAT mechanisms. In addition, Ingold has emphasized that Eq. 7 does not hold for reactions that do not proceed by HAT, for instance, when the mechanism is sequential proton loss and then electron transfer (17). Thus, all of the reactions discussed here appear to follow a HAT mechanism, on the basis of the agreement between experiment and theory (as well as other evidence; cf. SI Text).
The success of the CR/KSE model is remarkable given that it ignores or simplifies various aspects of HAT reactions. The CR, and the Marcus theory of electron transfer (ET) from which it is derived, applies to unimolecular reactions of weakly bound precursor and successor complexes (7). In ET reactions, these complexes are typically weakly associated, and their energies are often estimated with a simple electrostatic calculation. In HAT, the electrostatic term is usually not needed because no net charge is transferred and because typically at least one of the reactants is neutral (as is the case for all of the reactions here). However, H-transfer occurs over very short distances (3) so HAT precursor complexes have distinct configurations, often with a hydrogen bond. A more complete analysis of HAT reactions, including these precursor and successor complexes, and estimating their energies using the Abraham model, is given in SI Text. As described there, the more complex treatment may be preferred in special cases, when there is a large variation in 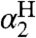 values and in protic solvents. Still, the CR/KSE model described here gives excellent agreement in most cases.
values and in protic solvents. Still, the CR/KSE model described here gives excellent agreement in most cases.
A more fundamental concern with the CR/KSE treatment is the use of the CR at all. It was derived for ET reactions of weakly interacting reagents, and there is little theoretical basis for its application to HAT reactions. Hydrogen tunneling, nonadiabatic effects, vibrational excited states, and donor-acceptor motions are all included in the current theoretical models of HAT (45) but are not in the Marcus treatment. The TEMPO(•/H) self-exchange reaction proceeds predominantly by hydrogen tunneling (31), making the success of the CR for this reagent even more remarkable.
In our view, the striking success of the CR/KSE model in predicting rate constants is largely because it captures the most important aspects of a HAT reaction: the driving force (KXH/Y•); the intrinsic barriers (kXH/X•); and the interaction of the reactants with solvent. In terms of predicting a HAT rate constant to within a factor of 5, one can usually ignore other effects such as hydrogen tunneling, nonadiabatic behavior, and precursor complex formation. The success of the CR, in this and other applications, may partially be a result of its inherent averaging, as pointed out by Sutin (7).
Conclusions
A kinetic model has been developed for hydrogen atom transfer reactions by using the Marcus CR. We use Ingold’s KSE analysis and Abraham’s hydrogen-bonding parameters to account for solvent effects on the parameters for the CR (kXH/X•, kYH/Y•, and KXH/Y•). This combined CR/KSE model is shown to be very successful at predicting rate constants for oxyl radicals abstracting H• from O-H bonds in phenols, hydroxyl amines, and ascorbate and from C-H bonds in alkylaromatic compounds. Of the 36 hydrogen atom transfer reactions that have been examined, the model predicts kXH/Y• with an average deviation from the measured value of a factor of 3.8 and is within a factor of 5 for all but six cases. The reactions span 28 orders of magnitude in KXH/Y• and 12 orders of magnitude in kXH/Y• and occur in solvents ranging from alkanes to water. The success of this approach over a broad set of reactions and solvents indicates that the model captures the three primary determinants of the rate of a HAT reaction: the driving force KXH/Y• (ΔGXH/Y•); the intrinsic barriers (from self-exchange rate constants, kXH/X• and kYH/Y•); and solvent-solute H bonding. Taken together, the data show that the CR/KSE model is a conceptual and predictive tool that can be used to understand a wide range of organic HAT reactions in solution, including biologically important hydrogen atom transfer reactions involving tocopherol, ascorbate, and hydroperoxides.
Materials and Methods
Physical Techniques and Instrumentation.
UV-vis stopped-flow measurements used an OLIS RSM-1000. 1H NMR spectra were recorded on Bruker Avance spectrometers at 300 or 500 MHz. All reactions were performed anaerobically by using standard glovebox and high vacuum techniques.
Materials.
Reagent grade solvents were purchased from Fischer Scientific, unless otherwise noted. Anhydrous MeCN (Honeywell Burdick and Jackson) was sparged with Ar. C6H6 and DMSO were dried by using a Seca solvent system. CCl4 (99.9%; Aldrich) was used as received in a Sure/Seal bottle. Deuterated solvents were obtained from Cambridge Isotope Laboratories. CDCl3 was stored over CaH2 and freshly distilled before use. TEMPOH (27) and 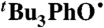 (29) were prepared according to the literature. 4-oxo-TEMPO was sublimed under static vacuum onto a -78 °C cold finger. BHT and DHA were recrystallized 3 times from absolute EtOH and dried in vacuo.
(29) were prepared according to the literature. 4-oxo-TEMPO was sublimed under static vacuum onto a -78 °C cold finger. BHT and DHA were recrystallized 3 times from absolute EtOH and dried in vacuo.
Stopped-Flow Kinetic Experiments.
In a typical procedure, solutions of 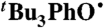 (1.1 mM) and BHT (5.5–78 mM) were prepared in anhydrous MeCN in an N2-filled glovebox and loaded into syringes. The two syringes were removed from the glovebox and placed immediately into the stopped-flow apparatus. The mixing chamber of the stopped-flow apparatus was flushed with reagents before collecting kinetic data. A minimum of five kinetic runs were collected at each concentration. The data were well fit over four half-lives in using an A → B kinetic model with SPECFIT software. Plots of the pseudo-first-order kobs as a function of [BHT] were linear with a zero intercept, the slope giving the bimolecular rate constant.
(1.1 mM) and BHT (5.5–78 mM) were prepared in anhydrous MeCN in an N2-filled glovebox and loaded into syringes. The two syringes were removed from the glovebox and placed immediately into the stopped-flow apparatus. The mixing chamber of the stopped-flow apparatus was flushed with reagents before collecting kinetic data. A minimum of five kinetic runs were collected at each concentration. The data were well fit over four half-lives in using an A → B kinetic model with SPECFIT software. Plots of the pseudo-first-order kobs as a function of [BHT] were linear with a zero intercept, the slope giving the bimolecular rate constant.
Supplementary Material
Acknowledgments.
Professor Michael Abraham is acknowledged for helpful discussions concerning the H-bonding properties of tBuOOtBu. We gratefully acknowledge support from the National Institutes of Health (GM50422) and the University of Washington, Department of Chemistry.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0910347107/DCSupplemental.
References
- 1.Fossey J, Lefort D, Sorba J. Free Radicals in Organic Chemistry. New York: Wiley; 1995. [Google Scholar]
- 2.Halliwell B, Gutteridge JMC. Free Radicals in Biology and Medicine. 3rd Ed. New York: Oxford Univ Press; 1999. [Google Scholar]
- 3.Hynes JT, Klinman JP, Limback HH, Schowen RL, editors. Hydrogen Transfer Reactions. Vol 1–4. Weinheim: Wiley-VCH; 2007. [Google Scholar]
- 4.Fischer H, editor. Radical Reaction Rates in Liquids. Vol 18, Subvols A–E2. Berlin: Springer; 1994. (Landolt-Börnstein New Series). (Supplement to Vol 13) [Google Scholar]
- 5.Neta P, Grodkowski J. Rate constants for reactions of phenoxyl radicals in solution. J Phys Chem Ref Data. 2005;34:109–199. [Google Scholar]
- 6.Shaik SS, Schlegel HB, Wolfe S. Theoretical Aspects of Physical Organic Chemistry: The SN2 Mechanism. New York: Wiley; 1992. pp. 11–23. [Google Scholar]
- 7.Sutin N. Theory of electron transfer reactions: Insights and hindsights. Prog Inorg Chem. 1983;30:441–499. [Google Scholar]
- 8.Mayer JM. Proton-coupled electron transfer. Annu Rev Phys Chem. 2004;55:363–390. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- 9.Waidmann CR, et al. Slow hydrogen transfer reactions of oxo- and hydroxo-vanadium compounds: The importance of intrinsic barriers. J Am Chem Soc. 2009;131:4729–4743. doi: 10.1021/ja808698x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roth JP, Yoder JC, Won TJ, Mayer JM. Application of the Marcus cross relation to hydrogen atom transfer reactions. Science. 2001;294:2524–2526. doi: 10.1126/science.1066130. [DOI] [PubMed] [Google Scholar]
- 11.Mader EA, Larsen AS, Mayer JM. Hydrogen atom transfer from iron(II)-Tris[2,2′-bi(tetrahydropyrimidine)] to TEMPO: A negative enthalpy of activation predicted by the Marcus equation. J Am Chem Soc. 2004;126:8066–8067. doi: 10.1021/ja049246k. [DOI] [PubMed] [Google Scholar]
- 12.Wu A, Mayer JM. Hydrogen atom transfer reactions of a ruthenium imidazole complex: Hydrogen tunneling and the applicability of the Marcus cross relation. J Am Chem Soc. 2008;130:14745–14754. doi: 10.1021/ja805067h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. HAT vs. proton-coupled electron transfer nomenclature is discussed in ref. 9.
- 14.Albery WJ. The application of the Marcus cross relation to reactions in solution. Annu Rev Phys Chem. 1980;31:227–263. [Google Scholar]
- 15.Lee I-SH, Jeoung EH, Kreevoy MM. Marcus theory of a parallel effect on a α for hydride transfer reaction between NAD+ analogues. J Am Chem Soc. 1997;119:2722–2728. [Google Scholar]
- 16.Marcus RA. Theory of rate of SN2 reactions and relation to those of outer sphere bond rupture electron transfers. J Phys Chem A. 1997;101:4072–4087. [Google Scholar]
- 17.Litwinienko G, Ingold KU. Solvent effects on the rates and mechanisms of reaction of phenols with free radicals. Acc Chem Res. 2007;40:222–230. doi: 10.1021/ar0682029. [DOI] [PubMed] [Google Scholar]
- 18.Abraham MH, et al. A general treatment of hydrogen bond complexation constants in tetrachloromethane. J Am Chem Soc. 1988;110:8534–8536. [Google Scholar]
- 19.Abraham MH, et al. Hydrogen bonding part 7. A scale of solute hydrogen-bond acidity based on log K values for complexation in tetrachloromethane. J Chem Soc Perk T. 1989;2:699–711. [Google Scholar]
- 20.Abraham MH, Grellier PL, Prior DV, Morris JJ, Taylor PJ. Hydrogen bonding part 10. A scale of solute hydrogen-bond basicity using log K values for complexation in tetrachloromethane. J Chem Soc Perk T. 1990;2:521–529. [Google Scholar]
- 21.Mader EA, et al. Trends in ground-state entropies for transition metal based hydrogen atom transfer reactions. J Am Chem Soc. 2009;131:4335–4345. doi: 10.1021/ja8081846. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
22. For example, in the case for phenol,
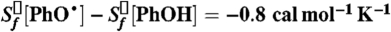 . See Burcat A, Ruscic B (2005) TAE Report No. 960; Technical Report ( ftp://ftp.technion.ac.il/pub/supported/aetdd/thermodynamics)
. See Burcat A, Ruscic B (2005) TAE Report No. 960; Technical Report ( ftp://ftp.technion.ac.il/pub/supported/aetdd/thermodynamics)
- 23.Afeefy HY, Liebman JF, Stein SE. Neutral thermochemical data. In: Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. Gaithersburg, MD: National Institute of Standards and Technology; [Retrieved May 21, 2009]. Available at http://webbook.nist.gov. [Google Scholar]
-
24.Roduner E. Hydrophobic solvation, quantum nature, and diffusion of atomic hydrogen in liquid water. Radiat Phys Chem. 2005;72:201–206. shows that
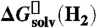 is a good approximation to
is a good approximation to 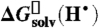 (see SI Text). [Google Scholar]
(see SI Text). [Google Scholar] - 25.Mulder P, et al. Critical re-evaluation of the O—H bond dissociation enthalpy in phenol. J Phys Chem A. 2005;109:2647–2655. doi: 10.1021/jp047148f. [DOI] [PubMed] [Google Scholar]
- 26.Borges dos Santos RM, Costa Cabral BJ, Martinho Simões JA. Bond-dissociation enthalpies in the gas phase and in organic solvents: Making ends meet. Pure Appl Chem. 2007;79:1369–1382. . Martinho Simões and co-workers have criticized this model when applied to solution bond dissociation enthalpies. Since Abraham’s model is based upon free energies it is expected be more appropriate for solution BDFEs. [Google Scholar]
- 27.Mader EA, Davidson ER, Mayer JM. Large ground-state entropy changes for hydrogen atom transfer reactions of iron complexes. J Am Chem Soc. 2007;129:5153–5166. doi: 10.1021/ja0686918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yoder JC, Roth JP, Gussenhoven EM, Larsen AS, Mayer JM. Electron and hydrogen-atom self-exchange reactions of iron and cobalt coordination complexes. J Am Chem Soc. 2003;125:2629–2640. doi: 10.1021/ja0273905. [DOI] [PubMed] [Google Scholar]
- 29.Manner VW, Markle TF, Freudenthal JH, Roth JP, Mayer JM. The first crystal structure of a monomeric phenoxyl radical: 2,4,6-tri-tert-butylphenoxyl radical. Chem Commun. 2008;2008:256–258. doi: 10.1039/b712872j. [DOI] [PubMed] [Google Scholar]
- 30.Lucarini M, Pedrielli P, Pedulli GF, Cabiddu S, Fattuoni C. Bond dissociation energies of O-H bonds in substituted phenols from equilibration studies. J Org Chem. 1996;61:9259–9263. [Google Scholar]
- 31.Wu A, et al. Nitroxyl radical plus hydroxylamine pseudo self-exchange reactions: Tunneling in hydrogen atom transfer. J Am Chem Soc. 2009;131:11985–11997. doi: 10.1021/ja904400d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Prokof’ev AI, Malysheva NA, Bubnov NN, Solodovnikov SP, Kabachnik MI. Investigation of fast reactions of sterically hindered aroxyl radicals. B Acad Sci USSR Ch+ 1976;25:494–497. [Google Scholar]
- 33.Abraham MH, Abraham RJ, Byrne J, Griffiths L. NMR method for the determination of solute hydrogen bond acidity. J Org Chem. 2006;71:3389–3394. doi: 10.1021/jo052631n. [DOI] [PubMed] [Google Scholar]
-
34. Abraham’s 1H NMR method in dry CDCl3 or DMSO gives
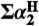 , which, for a solute with only one H-bonding R-OH group, is essentially equal to
, which, for a solute with only one H-bonding R-OH group, is essentially equal to 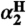 (33) [Google Scholar]
(33) [Google Scholar] - 35.Litwinienko G, Ingold KU. Abnormal solvent effects on hydrogen atom abstractions 1. The reactions of phenols with 2,2-diphenyl-1-picrylhydrazyl (dpph•) in alcohols. J Org Chem. 2003;68:3433–3438. doi: 10.1021/jo026917t. [DOI] [PubMed] [Google Scholar]
-
36.Astolfi P, Greci L, Paul T, Ingold KU. Revision of the
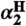 value for N,N-dialkylhydroxylamines based on kinetic and spectroscopic measurements. J Chem Soc Perk T. 2001;2:1631–1633. [Google Scholar]
value for N,N-dialkylhydroxylamines based on kinetic and spectroscopic measurements. J Chem Soc Perk T. 2001;2:1631–1633. [Google Scholar] - 37.Gregor W, Grabner G, Adelwöhrer C, Rosenau T, Gille L. Antioxidant properties of natural and synthetic chromanol derivatives: Study by fast kinetics and electron spin resonance spectroscopy. J Org Chem. 2005;70:3472–3483. doi: 10.1021/jo047927s. [DOI] [PubMed] [Google Scholar]
- 38.Shin-ichi N, Kuranaka A, Tsuboi H, Nagashima U, Mukai K. Mechanism of antioxidant reaction of vitamin E. Charge transfer and tunneling effect in proton transfer reaction. J Phys Chem. 1992;96:2754–2761. [Google Scholar]
- 39.Brigati G, Lucarini M, Mugnaini V, Pedulli GF. Determination of the substituent effect on the O-H bond dissociation enthalpies of phenolic antioxidants by the EPR radical equilibration technique. J Org Chem. 2002;67:4828–4832. doi: 10.1021/jo025755y. [DOI] [PubMed] [Google Scholar]
- 40. f is taken to be 1 for this calculation of kXH/X•(TocOH). By using the derived value of kXH/X•(TocOH), f = 0.85, indicating that taking f = 1 introduces only a small error.
- 41.Warren JJ, Mayer JM. Surprisingly long-lived ascorbyl radicals in acetonitrile: Hydrogen atom transfer reactions and thermochemistry. J Am Chem Soc. 2008;130:2774–2776. doi: 10.1021/ja802055t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. The deviation is defined as kobs/kcalc or kcalc/kobs, whichever is greater than 1.
- 43.Snelgrove DW, Lusztyk J, Banks JT, Mulder P, Ingold KU. Kinetic solvent effects of hydrogen-atom abstractions: Reliable, quantitative predictions via a single empirical equation. J Am Chem Soc. 2001;123:469–477. [Google Scholar]
- 44.Lowry TH, Richardson KS. Mechanism and Theory in Organic Chemistry. 3rd Ed. New York: Harper & Row; 1987. pp. 143–159. [Google Scholar]
- 45. Hammes-Schiffer S, Proton-Coupled Electron Transfer: Theoretical Formulation and Applications, ref. 3, Vol. 2, pp. 479–502.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.