DNA as a universal substrate for chemical kinetics

Abstract

Molecular programming aims to systematically engineer molecular and chemical systems of autonomous function and ever-increasing complexity. A key goal is to develop embedded control circuitry within a chemical system to direct molecular events. Here we show that systems of DNA molecules can be constructed that closely approximate the dynamic behavior of arbitrary systems of coupled chemical reactions. By using strand displacement reactions as a primitive, we construct reaction cascades with effectively unimolecular and bimolecular kinetics. Our construction allows individual reactions to be coupled in arbitrary ways such that reactants can participate in multiple reactions simultaneously, reproducing the desired dynamical properties. Thus arbitrary systems of chemical equations can be compiled into real chemical systems. We illustrate our method on the Lotka–Volterra oscillator, a limit-cycle oscillator, a chaotic system, and systems implementing feedback digital logic and algorithmic behavior.

Chemical reaction equations and mass-action kinetics provide a powerful mathematical language to describe and analyze chemical systems. For well over a century, mass-action kinetics has been used to model chemical experiments and to predict and explain their dynamical properties. Both biological and nonbiological chemical systems can exhibit complex behaviors such as oscillations, memory, logic and feedback control, chaos, and pattern formation—all of which can be explained by the corresponding systems of coupled chemical reactions (1–4). Whereas the use of mass-action kinetics to describe existing chemical systems is well established, the inverse problem of experimentally implementing a given set of chemical reactions has not been considered in full generality. Here, we ask: Given a set of formal chemical reaction equations, involving formal species X₁,X₂,…,X_n, can we find a set of actual molecules M₁,M₂,…,M_m that interact in an appropriate buffer to approximate the formal system’s mass-action kinetics? If this were possible, the formalism of chemical reaction networks (CRNs) could be treated as an effective programming language for the design of complex network behavior (5–9).

Unfortunately, a formally expressed system of coupled chemical equations may not have an obvious realization in known chemistry. In a formal system of chemical reactions, a species may participate in multiple reactions, both as a reactant and/or as a product, and these reactions progress at relative rates determined by the corresponding rate constants, all of which imposes formidable constraints on the chemical properties of the species participating in the reactions. For example, it is likely hard to find a physical implementation of arbitrary chemical reaction equations using small molecules, because small molecules have a limited set of reactivities.

Thus, formal CRNs may appear to be an unforgiving target for general implementation strategies. Indeed, most experimental work in chemical and biological engineering has started with particular molecular systems—genetic regulatory networks (10), RNA folding and processing (11), metabolic pathways (12), signal transduction pathways (13), cell-free enzyme systems (14, 15), and small molecules (16, 17)—and found ways to modify or rewire the components to achieve particular functions. Attempts to systematically understand what functional behaviors can be obtained by using such components have targeted connections to analog and digital electronic circuits (10, 18, 19), neural networks (20–22), and computing machines (15, 20, 23, 24); in each case, complex systems are theoretically constructed by composing modular chemical subsystems that carry out key functions, such as boolean logic gates, binary memories, or neural computing units. Despite its apparent difficulty, we directly targeted CRNs for three reasons. First, shoehorning the design of synthetic chemical circuits into familiar but possibly inappropriate computing models may not capture the natural potential and limitations of the chemical substrate. Second, there is a vast literature on the theory of CRNs (25, 26) and even on general methods to implement arbitrary polynomial ordinary differential equations as CRNs (27, 28). Third, as a fundamental model that captures the essential formal structure of chemistry, implementation of CRNs could provide a useful programming paradigm for molecular systems.

Here we propose a method for compiling an arbitrary CRN into nucleic-acid-based chemistry. Given a formal specification of coupled chemical kinetics, we systematically design DNA molecules implementing an approximation of the system scaled to an appropriate temporal and concentration regime. Formal species are identified with certain DNA strands, whose interactions are mediated by a set of auxiliary DNA complexes. Nonconserving CRNs can be implemented because the auxiliary species implicitly supply energy and mass.

Conveniently, the base sequence of nucleic acids can determine reactivity not only through direct hybridization of single-stranded species (29) but also through branch migration and strand displacement reaction pathways (30–32). These powerful reaction primitives have been used previously for designing nucleic-acid-based molecular machines with complex behaviors, such as motors, logic gates, and amplifiers (33–37). Here we use these reaction mechanisms as the basis for the implementation of arbitrary CRNs. Our work advances a systematic approach that aims to provide a general mechanism for implementing a well-specified class of behaviors.

Molecular Primitive: Strand Displacement Cascades

Because simple hybridization reactions cannot be cascaded, we use the more flexible strand displacement reaction as a molecular primitive. [We use “strand displacement” as a shorthand for toehold-mediated branch migration and strand displacement reactions (33, 38), combined with the principles of toehold sequestering (34) and toehold exchange (35).]

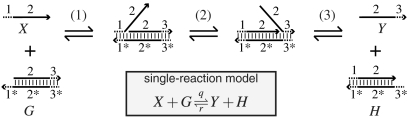
Intuitively, in a strand displacement reaction (Fig. 1) a strand (X) displaces another strand (Y) from a complex (G). In our diagrams, each subsequence that acts as a single functional unit (a domain) is labeled with a unique number (e.g., the two functionally distinct domains of strand X are 1 and 2). We assume strong sequence design such that domain x^∗ is complementary to domain x and interacts with no other, allowing us to analyze DNA systems entirely at the domain level. Short (dashed) domains are called toeholds. A strand displacement reaction starts when two single-stranded toehold domains (e.g., 1 and 1^∗) bind each other. Then, a random walk process (branch migration) follows, where two domains with identical sequences compete for the same complementary domain. Domain 2 of strand 2–3 competes with and is partially displaced by domain 2 of strand 1–2. Finally, the initially bound strand 2–3 is released when toeholds 3 and 3^∗ separate. To obtain a fast and reliable reaction, the toehold domains must be short (e.g., 6 nt) whereas the branch migration domains must be long (e.g., 20 nt). Despite the complex mechanism, a strand displacement reaction is well modeled by a single reversible reaction (38, 39) under a large range of experimental conditions where toehold binding is rate limiting (Fig. 1, Inset). Removing toehold 3 slows the reverse reaction enough that we can consider the forward reaction effectively irreversible (38, 40).

Fig. 1.

Strand displacement molecular primitive. Domains are labeled by numbers, with * denoting Watson–Crick complementarity. Multiple elementary steps are indicated: (1) binding of toeholds 1 and 1^∗; (2) branch migration, a random walk process where domain 2 of strand 2–3 is partially displaced by domain 2 of strand 1–2; (3) the separation of toeholds 3 and 3^∗. (Inset) The single-reaction model of strand displacement.

Strand displacement reactions are programmable by the design of sequences. A single base mismatch significantly impedes branch migration (32, 41). By varying the binding strength of the initiating toeholds, the reaction rate constant can be controlled over 6 orders of magnitude (38, 39). In turn, the length and sequence composition of the toeholds controls their binding strength. The forward and reverse rate constants q and r increase with the hybridization energy of their respective toehold domains (1 to 1^∗ and 3 to 3^∗). The same strand (X) can react at different rates to different complexes, e.g., G and G^′. To attain smaller q^′ < q for G^′, we can use a toehold domain 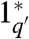that is not a full complement of 1. For example, 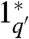can be a truncation of 1^∗ (39) (Fig. S1).

In the following, we construct systems of molecules whose interactions are mediated by strand displacement reactions. To ensure desired reactions and exclude undesired reactions, we use modular components that incorporate three key design principles. First, we design the system so that all long domains are always double-stranded, thus ensuring that toeholds and their complements are the only single-stranded domains capable of hybridizing together. Second, we require that toeholds are short enough that this interaction is fleeting unless it triggers strand displacement. Thus we need to consider only strand displacement, and not hybridization, of long domains. Third, only the desired target must have the correct combination of toehold and displacement regions, preventing any undesired strand displacement reactions. Satisfying these three design principles, which can be verified by inspection of the modules, guarantees that arbitrarily complex systems will function as intended for ideal strand displacement reactions.

Implementing Networks

We implement CRNs in DNA by using three types of modules, which specify the DNA molecules to create for each target reaction (either unimolecular or bimolecular) and for each target species. Initially, we suppose that our target CRN uses rate constants and concentrations that are realistic for aqueous-phase nucleic-acid strand displacement reactions. Additionally, the signal species must always be at much lower concentrations than the auxiliary species. Thus, the feasibility of a CRN depends upon its behavior; for example, we can implement explosive reactions like X₁ → X₁ + X₁ for only a limited time. If the target CRN operates outside of a physically realistic regime, we will need to relax the goal of implementing the exact target system and instead allow a uniform scaling down of concentrations and/or slowing down of the kinetics. We will show that such scaling can also arbitrarily increase the accuracy of our construction.

Unimolecular Reactions

DNA Implementation.

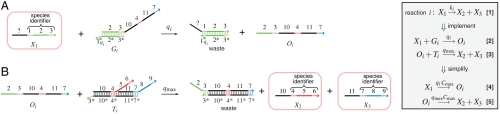
Standardizing the molecular equivalents of the formal species facilitates their assignment to roles as reactants or products in multiple reactions. We implement a formal species as a single-stranded DNA molecule (signal strand) consisting of an inert history domain and a unique species identifier (a long domain flanked by two toehold domains; Fig. 2, orange boxes) that regulates its interactions with other molecules. The history domain depends on the formal reaction producing the species: If X_j is a product of multiple reactions, signal strands with differing history domains but the same species identifier would represent the same formal species X_j. In our scheme, the signal strand is active when fully single-stranded and inactive when bound to another DNA molecule. Signal strands react exclusively by strand displacement reactions initiated at the left toehold of their species identifier; thus, sequestering the left toehold into a double helix is sufficient to inactivate them. The sum of the concentrations of the active signal strands for X_j gives [X_j], and the changes in [X_j] are effected either by the inactivation of a signal strand when it binds to a complementary DNA molecule or by the release of a previously bound strand.

Fig. 2.

Unimolecular module: DNA implementation of the formal unimolecular reaction X₁ → X₂ + X₃ with reaction index i. Orange boxes highlight the DNA species that correspond to the formal species X₁ (species identifier 1-2-3), X₂ (4-5-6), and X₃ (7-8-9). Domains identical or complementary to species identifiers for X₁, X₂, and X₃ are colored red, green, and blue, respectively. Black domains (10 and 11) are unique to this formal reaction. To reduce rate constant q_i, toehold domain 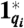may not be a full complement of domain 1. (A) Complex G_i undergoes a strand displacement reaction with strand X₁, with X₁ displacing strand O_i. (B) O_i displaces X₂ and X₃ from complex T_i. Without buffer cancellation, 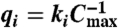; with buffer cancellation, 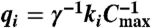. Reaction equations of type 2–3 are used in simulations (Figs. 5 and 6); simplified reaction equations 4–5 are useful for analysis.

Being composed of entirely distinct domains, DNA signal strands do not interact with each other directly, but rather a set of auxiliary DNA complexes present at large concentrations mediates exactly the desired reactions. Suppose the ith formal reaction is unimolecular, as in Fig. 2. We implement reaction equation 1 as inactivation of a signal strand with species identifier X₁ coupled with activation of strands with identifiers X₂ and X₃. These chemical steps are done through two strand displacement reactions involving two auxiliary complexes G_i and T_i (for “gate” and “translater,” respectively) as shown in Fig. 2. A two-step cascade ensures that arbitrary species identifiers can be connected in this reaction because there is no sequence dependence between X₁, X₂, and X₃. To implement other effective net reactions—even catalytic or autocatalytic reactions such as X₁ → X₁ + X₂ or X₁ → X₁ + X₁—only the auxiliary complexes need to be modified. A system of multiple coupled unimolecular reactions is implemented simply by starting with the auxiliary complexes for all the desired reactions, along with appropriate initial concentrations of the signal strands. Implementing unimolecular reactions with differing numbers of products requires extending or shrinking the intermediate output O_i. Removing auxiliary complex T_i altogether results in unimolecular decay reactions like X₁ → ∅, where ∅ indicates the absence of products.

Kinetic Analysis.

To approximate ideal unimolecular mass-action kinetics, we require the dynamics of the target reaction network to be slow relative to the fastest strand displacement steps and the concentration of auxiliary DNA species to be much larger than the signal concentrations. Here and in the next section, we present an informal argument that the desired kinetics will be attained under these conditions. In SI Text we prove the convergence to the desired kinetics in the limit of high concentration of appropriate auxiliary species relative to the concentrations of the signal species.

For simplicity, we assume all full toehold domains have equal binding strength yielding a maximum strand displacement rate constant q_max. Let C_max be the starting concentration of auxiliary complexes G_i and T_i. The strand displacement cascade of Fig. 2 follows reaction equations 2 and 3, where q_i ≤ q_max is a partial-toehold strand displacement rate constant controlled by the binding energy of domains 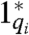and 1, and 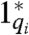is chosen to obtain the desired rate constant for formal reaction i. Letting τ be the experiment’s duration, we assume a regime where τk_i max([X₁]) ≪ C_max, and k_i ≪ q_maxC_max, and set the partial-toehold strand displacement rate constant q_i = k_i/C_max. Then over a sufficiently short duration τ, [G_i] and [T_i] remain effectively constant at their initial concentration C_max, and the cascade becomes equivalent to a pair of unimolecular reactions (Fig. 2, Eqs. 4 and 5, where q_iC_max = k_i). Further, reaction 4 is the rate-limiting step, and we obtain the desired unimolecular kinetics for formal reaction 1: The instantaneous rate of the consumption of X₁ and the production of X₂ and X₃ in this module is k_i[X₁].

Adding Bimolecular Reactions

DNA Implementation.

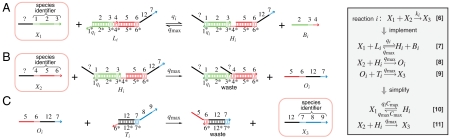
We now extend the construction to realize bimolecular in addition to unimolecular reactions. Suppose the ith formal reaction is bimolecular, as in Fig. 3. Implementing reaction equation 6, X₁ must not be consumed in the absence of X₂ and vice versa, which seems difficult because X₁ and X₂ cannot react directly, and therefore one of them (say, X₁) must react with an auxiliary complex first without knowing whether the other is present. The challenge here is to minimize the X₂-independent “drain” on X₁; later we will show how we can exactly compensate for it by rescaling rate constants.

Fig. 3.

Bimolecular module: DNA implementation of the formal bimolecular reaction X₁ + X₂ → X₃ with reaction index i. The black domain (12) is unique to this formal reaction. (A) X₁ reversibly displaces B_i from complex L_i producing complex H_i. (B) X₂ displaces O_i from complex H_i. Occurrence of reaction B precludes the backward reaction of A. (C) O_i displaces X₃ from complex T_i. Without buffer cancellation, q_i = k_i; with buffer cancellation, q_i = γ^-1k_i. Reaction equations of type 7–9 are used in simulations (Figs. 5 and 6); simplified reaction equations 10–11 are useful for analysis.

Our construction (Fig. 3) solves this problem by introducing a reversible first step. Strand X₁ reversibly displaces B_i (the “backward” strand) from auxiliary complex L_i, producing activated intermediate H_i. If no X₂ is present, B_i can reverse the reaction and release X₁ back into solution. But if X₂ is present, it can react with intermediate H_i to release intermediate output O_i. As in the unimolecular module, this in turn releases the final output X₃ and makes the overall reaction irreversible. The species identifiers of the reactants and all products can be arbitrarily specified as in the unimolecular modules. Not all B_i are necessarily unique DNA species: If reactions i and i^′ have the same reactants, then B_i would have the same sequence as B_i^′.

Kinetic Analysis.

The kinetics of the module of Fig. 3 is modeled using reaction equations 7–9. Set the initial concentration of L_i, B_i, and T_i to C_max and partial-toehold rate constant q_i = k_i. By assuming τk_i max([X₁]) max([X₂]) ≪ C_max and max([X₁]) ≪ C_max, the concentrations [L_i], [B_i], and [T_i] remain effectively constant throughout the duration of the experiment, and reaction 8 is the rate-limiting step of the pair 8–9. This system of reactions can then be approximated by reaction equations 10 and 11. Further, (informally) if in the target reaction network [X₁] varies on a slower time scale than that of the equilibration of reaction 10, we can assume that X₁ and H_i attain instant equilibrium through reaction 10 with [X₁]/[H_i] = q_max/k_i. Then the instantaneous rate of reaction 11 is q_max[X₂][H_i] = k_i[X₁][X₂]. At first glance this appears to give the correct kinetics for the production of X₃; however, X₃ is buffered: Some fraction of it will quickly equilibrate with H_i^′ of other reactions in which X₃ is the first reactant, resulting in a lower effective rate of production of X₃. X₁ and X₂ are likewise buffered. Let fr(X₁) be the set of bimolecular reactions in which X₁ is the first reactant. Reactions 10 in the different reaction modules create instant equilibrium between all species in the equilibrium set of X₁, es(X₁), consisting of X₁ and every H_i, i∈fr(X₁). Producing or consuming a unit of any species in the equilibrium set of X₁ results in the fraction γ₁ ≡ [X₁]/[es(X₁)] of a unit change in [X₁]. Thus the effective instantaneous rates of the consumption of X₁, consumption of X₂, and production of X₃ because of reaction 11 in the above module are γ₁k_i[X₁][X₂], γ₂k_i[X₁][X₂], and γ₃k_i[X₁][X₂], respectively.

Making the additional assumption k_i ≪ q_max shifts equilibria of reactions 10 to the left such that γ_j approaches 1. Then the instantaneous rates of variation in X₁, X₂, and X₃ because of this reaction module approach the desired bimolecular kinetics value of k_i[X₁][X₂].

Canceling out the Buffering Effect.

We can exactly cancel out the buffering effect, thereby easing the requirement k_i ≪ q_max for bimolecular reactions and allowing the implementation of much larger rate constants. Intuitively, because the buffering effect systematically counteracts desired concentration changes of X_j when γ_j < 1, we should be able to compensate by increasing the rate constants of all reactions involving X_j. Because a reaction between species with different γ_j will behave as if it has incorrect stoichiometry, we want all γ_j to be equal. However, even with equal γ_j, we cannot simply multiply all k_i by 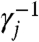because that would in turn change γ_j.

Let σ_j = Σ_i∈fr(Xj)k_i be the sum of formal rate constants of bimolecular reactions with X_j as the first reactant, and let 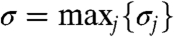. We ensure that the fraction γ_j is equal for all X_j by using a new buffering module (Fig. 4) for each X_j for which σ_j < σ. Each buffering module is modeled as reaction equation 12. Initially [LS_j] = [BS_j] = C_max, and as for the bimolecular module we can reduce 12 to 13. The equilibrium set of X_j now includes HS_j. It is not hard to show that with the buffering-scaling factor 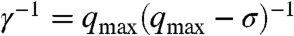, setting qs_j = γ^-1(σ - σ_j), and replacing k_i by 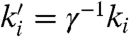for the formal rate constants when setting q_i in reactions 2 and 7, we obtain a common buffer fraction γ_j = γ, which is exactly compensated for by the γ^-1 scaling of formal rate constants. For initial concentrations c_j of formal species X_j, we start with initial concentrations γ^-1c_j of DNA strands X_j. Then all species in es(X_j) quickly equilibrate yielding [X_j] = c_j.

Fig. 4.

Buffering module: DNA implementation of the buffering module used to cancel out the buffering effect. A buffering module is needed for each formal species X_j for which σ_j < σ. The buffering module for species X₂ is shown. X₂ reversibly displaces BS₂ from complex LS₂ to produce complex HS₂ similarly to the first reaction of the bimolecular module. The black domain (13) is unique to this buffering module for species X₂. Set qs_j = γ^-1(σ - σ_j). Reaction equations 12 are used in simulations (Figs. 5 and 6); simplified reaction equations 13 are useful for analysis.

See SI Text for a summary of our algorithm for compiling an arbitrary CRN into DNA-based chemistry.

Rescaling for Feasibility and Accuracy

The above procedure will not yield a functional DNA system if the original formal CRN has infeasibly high reaction rates or concentrations. In that case, we scale the system to use lower rate constants and concentrations while maintaining the same, albeit scaled, behavior. If [X_j](t) are solutions to differential equations arising from a set of unimolecular and bimolecular reactions, then β·[X_j](t/α) are solutions to the same set of reactions but in which we multiply all unimolecular rate constants by 1/α and all bimolecular rate constants by 1/(α·β). We introduce a mixed concentration-time-scaling parameter δ with α = δ and β = 1/δ, which scales down the concentration and slows down the dynamics by a factor of δ without increasing the largest rate constant.

We justified the accuracy of our construction by assuming the target system operates in a regime with concentrations sufficiently smaller than C_max, a physically determined parameter. This may not hold without rescaling, but thankfully, arbitrarily high accuracy for arbitrarily large duration of interest τ can still be attained in a regime of smaller concentrations of formal species and slowed down dynamics. We prove the convergence of the DNA-based kinetics with buffer cancellation to the target CRN in the limit C_max → ∞ by using singular perturbation theory (27, 42) (see SI Text). Whereas taking the limit C_max → ∞ is more mathematically convenient, increasing C_max by a factor of δ is equivalent, up to scaling in concentration of the experimental implementation, to decreasing all [X_j] by a factor of δ, decreasing all formal unimolecular rate constants by a factor of δ, and increasing τ by a factor of δ to simulate the same behavior.

Examples

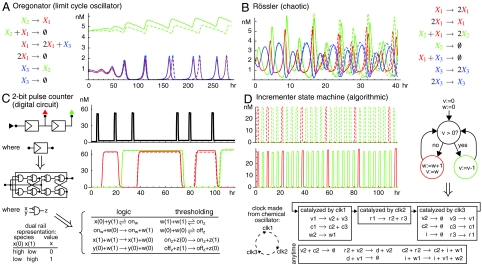
We illustrate our method on the Lotka–Volterra chemical oscillator shown in Fig. 5A. The concentration oscillations are in the range of about 0–2. Under typical nucleic-acid experimental conditions, maximal second-order rate constants for strand displacement reactions are about 10⁶/M/s, and maximum concentrations are on the order of 10^-5 M. To fit into this regime with reasonable simulation accuracy and time span, we scale the original system by a time-scaling factor of α = 300, and a concentration-scaling factor β = 10^-8 employing units of seconds and molar, and use C_max = 10^-5 M and q_max = 10⁶/M/s. The DNA species for our implementation, including buffering modules, are shown in Fig. S2 and the possible strand displacement reactions in Fig. S3. The equations governing our DNA implementation as derived by using the transforms described in Figs. 2–4 are shown in Fig. 5B. Simulations shown in Fig. 5C confirm that the DNA implementation nicely approximates the ideal formal chemical system. Because C_max < ∞, deviations between the DNA implementation and the target system gradually develop, as the depletion of complexes L₁, G₁, and G₂ and the buildup of strands B₁ alter the effective rate constants.

Fig. 5.

Lotka–Volterra chemical oscillator example. (A) The formal chemical reaction system to be implemented with original (unscaled) and scaled rate constants. Desired initial concentrations of X₁ and X₂ are 2 and 1 unscaled and 20 and 10 nM scaled. (B) Reactions modeling our DNA implementation. Each formal reaction corresponds to a set of DNA reactions as indicated. Species X₂ requires a buffering module because σ₂ < σ (σ = σ₁ = k₁ and σ₂ = 0). Maximum strand displacement rate constant q_max = 10⁶ M^-1 s^-1 and initial concentration of auxiliary species G_i, T_i, L_i, B_i, LS_j, and BS_j is C_max = 10 μM. Buffering-scaling factor γ^-1 = q_max(q_max - σ)^-1 = 2. The initial concentrations of strands X₁ and X₂ introduced into the system is γ^-120 nM = 40 nM and γ^-110 nM = 20 nM. (C) Plot of the concentrations of X₁ (Red curve) and X₂ (Green curve) for the ideal system (Dashed line) and the corresponding DNA species (Solid line).

We next apply our construction to more complex systems (Fig. 6). For fastest behavior, all systems are scaled so that the largest q_i or qs_j is q_max = 10⁶/M/s, and C_max = 10^-5 M, leaving only one free scaling parameter δ, which determines both implementation accuracy and the speed of the dynamics. The Oregonator limit-cycle oscillator (Fig. 6A) is a simplified model of the Belousov–Zhabotinsky reaction (43). The DNA implementation of this system is relatively slow because of the wide range of rate constants. The chaotic system due to Willamowski and Rössler (44) exhibits complex concentration fluctuations and is particularly sensitive to perturbations at long time scales (Fig. 6B). The DNA implementation follows the ideal system relatively well for a few revolutions around the strange attractor. Fig. 6C demonstrates the efficacy of our construction for implementing a chemical logic circuit responding to an external input signal (black trace). The 2-bit counter is a classic example of a digital circuit with feedback (45); the high or low values of the red and green output species give the binary count of the number of input pulses, 0–3. This feedback circuit contrasts with the use-once circuits of ref. 34. Fig. 6D shows a different style of algorithmic behavior: a state machine (5, 6). This state machine increments the number of green spikes between consecutive red spikes by 1 every time.

Fig. 6.

Examples showing more complex behavior. In all the maximum strand displacement rate constant q_max = 10⁶ M^-1 s^-1 and the initial concentration of auxiliary species C_max = 10 μM. See Figs. S4 and S5 and SI Text for the rate constants used in A–D, as well as the details of C and D. Plots show the ideal CRN (Dashed lines) and the DNA reactions (Solid lines).

Experimental Considerations

The correctness of our systematic construction was predicated on several idealizations of DNA behavior, and it is worth considering the deviations that we would expect in practice. A good approximation to strong sequence design (domain x binds exclusively to x^∗) should be possible for several thousand long domains by using existing techniques developed for strand displacement systems (46). There are a limited number of short toehold domain sequences available, but it is straightforward to modify our construction to reuse toehold sequences without introducing errors. This limit also constrains choices for reaction rate constants but can be countered by adjustment of auxiliary complex concentrations. More serious issues are presented by leak reactions in which an output is produced even if no input is present. Although experimentally characterized strand displacement systems exhibit leak rate constants up to a million times slower than the fastest desired reactions (35, 39), a leak could pose a problem for some target CRNs. One way to ameliorate a leak, while also allowing for unbounded running times, would be to provide auxiliary complexes at low concentrations in a continuous-flow stirred-tank reactor (1). These issues are discussed further in SI Text.

Conclusions

With a rich history and extensive theoretical and software tools, formal CRNs are a powerful descriptive language for modeling chemical reaction kinetics. By providing a systematic method for compiling formal CRNs into DNA molecules, our work suggests that CRNs can also be regarded as an effective programming language and used prescriptively for the synthesis of unique molecular systems. This view is bolstered by the fact that CRNs can implement arbitrary ordinary differential equations, analog and digital circuits, Turing-universal behavior, and—in the limit of small signal species concentrations and finite reaction volume—stochastic CRNs (47, 48). It is perhaps surprising that a simple primitive such as sequence-specific strand displacement proves sufficient for the implementation of arbitrarily complex chemical reaction kinetics, somewhat akin to how a few basic electronic elements such as transistors and wires are sufficient for the construction of arbitrarily complex logic circuits.

Our construction has several notable features for future molecular programming efforts. First, the signal species, entirely unreactive by themselves, react only when immersed in a complex buffer of auxiliary complexes. Thus, when implementing a system, one focusses on designing the buffer rather than the signal species, which stay the same regardless of the system. Our construction also highlights the rich dynamical behavior possible in multistranded nucleic-acid systems even without enzymes and covalent bond modification. Furthermore, established techniques for interfacing DNA to other chemistries (e.g., ref. 49) can enable programmable DNA reaction networks to respond to or control non-nucleic-acid systems, such as complex chemical synthesis pathways, biomedical diagnostics in vitro, or cellular functions in vivo. Finally, our construction and variants thereof (48) rely exclusively on a very simple molecular primitive, sequence-specific strand displacement reactions, suggesting that it could be adapted for other molecular substrates, such as RNA (11) or even peptides (17).

Many important chemical behaviors, such as pattern formation and self-assembly, involve geometric aspects that are beyond the scope of well-stirred reactions considered here. However, with a slight extension of our approach—controlling the relative diffusion rates of signal species—it would be possible to implement arbitrary reaction-diffusion systems (1). Though more challenging, regulating molecular assembly and disassembly steps with DNA signal species would allow for qualitatively more powerful computational systems (50) and systems capable of movement and construction of molecular-scale objects. We hope that the methods presented here provide a framework for successfully generalizing and unifying the existing experimental achievements in this direction (36, 37, 51).