Hydrophobically stabilized open state for the lateral gate of the Sec translocon

Abstract

The Sec translocon is a central component of cellular pathways for protein translocation and membrane integration. Using both atomistic and coarse-grained molecular simulations, we investigate the conformational landscape of the translocon and explore the role of peptide substrates in the regulation of the translocation and integration pathways. Inclusion of a hydrophobic peptide substrate in the translocon stabilizes the opening of the lateral gate for membrane integration, whereas a hydrophilic peptide substrate favors the closed lateral gate conformation. The relative orientation of the plug moiety and a peptide substrate within the translocon channel is similarly dependent on whether the substrate is hydrophobic or hydrophilic in character, and the energetics of the translocon lateral gate opening in the presence of a peptide substrate is governed by the energetics of the peptide interface with the membrane. Implications of these results for the regulation of Sec-mediated pathways for protein translocation vs. membrane integration are discussed.

A critical step in the biosynthesis of many proteins involves either translocation of the protein across a cellular membrane or integration into the membrane (1, 2). Both proceed via the Sec translocon—a ubiquitous and highly conserved transmembrane channel (3–5). Using atomistic and coarse-grained (CG) simulations and free-energy calculations, it is demonstrated that hydrophobic peptide substrates stabilize large-scale conformational changes in the translocon. The energetics of this conformational gating is dominated by the substrate–membrane interface, suggesting a regulatory mechanism for the Sec-facilitated protein translocation and integration pathways in which the translocon acts as a conformational switch under the control of the peptide substrate.

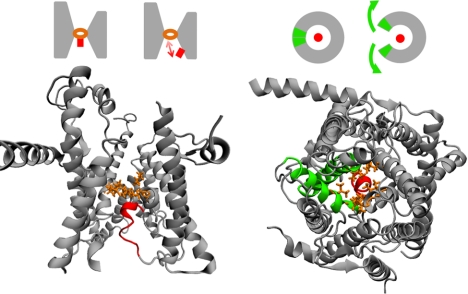
The Sec translocon is a heterotrimeric complex of membrane-bound proteins that forms a passive channel for posttranslational and cotranslational protein translocation, as well as the cotranslational integration of proteins into the phospholipid bilayer (6). Structural (7–11), biochemical (12, 13), and genetic (14) studies indicate that the translocon undergoes large-scale conformational changes during both the translocation and integration pathways. The translocon channel exhibits a ring, or pore, of hydrophobic amino acid residues, as well as an α-helical plug moiety that rests against the pore to occlude the channel; secretion of protein domains via the translocation pathway requires displacement of the plug with respect to the pore (Fig. 1, Left) (8, 12, 14). A pair of transmembrane helices in the translocon forms a lateral gate (LG) that opens to expose the interior of the channel to the membrane bilayer (Fig. 1, Right) and facilitates membrane integration (13, 15, 16).

Fig. 1.

Structural features of the Sec translocon. (Left) The translocon is viewed from within the plane of the membrane, with the pore residues shown in orange and the plug moiety shown in red. The schematic illustrates the pore-plug displacement that is needed to allow for protein translocation via the channel. (Right) The translocon is viewed from outside the membrane on the cytosolic side, with the pore and plug colored as before and with the TM2b and TM7 helices that form the lateral gate shown in green. The schematic illustrates the lateral gate motion that opens the interior of the translocon to the membrane.

The interaction between the peptide and the membrane lipid is recognized to play an important role in directing the integration of transmembrane helices (TMs) (16–18). This view has been supported by the measurement of striking correlations between a “biological hydrophobicity scale” for peptides and the relative fraction of peptides that undergo Sec-mediated integration vs. translocation (19–21), and it has been justified in terms of an effective thermodynamic partitioning for peptide substrates between the largely hydrophilic interior of the channel and the hydrophobic interior of the membrane (16, 19). However, the detailed mechanism for membrane integration via the LG and the role of translocon conformational changes in gating between the protein translocation and membrane integration pathways remain unclear.

In this paper, the conformational landscape for the Sec translocon is investigated using atomistic and CG molecular simulations. We find that inclusion of a hydrophobic peptide substrate in the translocon stabilizes an open conformation of the LG that is necessary for membrane integration, whereas inclusion of a hydrophilic peptide substrate favors only the closed LG conformation. We demonstrate that the translocon plug moiety adopts markedly different conformations in the channel, depending on whether the substrate peptide is hydrophobic or hydrophilic in character. Finally, we show that the energetics of the translocon LG opening in the presence of the substrate peptides can be modeled in terms of the energetics of the peptide interface with the membrane. These results are consistent with an alternative interpretation of the biological hydrophobicity scale in terms of the free-energy cost for opening the LG of the translocon, which suggests a refinement of the hydrophobic partitioning model in which substrate-controlled conformational gating of the translocon LG leads to regulation of the protein translocation and integration pathways.

Conformational Landscape of the Sec Translocon

To investigate the conformational flexibility of the translocon in the absence of peptide substrates, we calculate its 2D free-energy surface in the LG and pore-plug (PP) motions using both atomistic and CG molecular dynamics (MD) simulations.

Atomistic Simulations.

The archaeal Sec translocon (7) was studied using MD simulations with over 115,000 atoms. The channel is modeled in a membrane composed of 254 palmitoyloleoylphosphatidylcholine lipid molecules and with 24,296 explicit water molecules. Atomistic interactions were described using the CHARMM27 force field with the TIP3P water model (22). Counterions were included to achieve electroneutrality at a salt concentration of approximately 50 mM. MD trajectories were performed at constant temperature and pressure using orthorhombic periodic boundary conditions. Long-range electrostatics were calculated using the particle mesh Ewald technique (23). Details of the atomistic simulations and initialization protocol are described in Atomistic Simulations in SI Appendix.

Coarse-Grained Simulations.

Simulations were also performed using a residue-based CG representation for the system. Each amino acid in the channel was represented with one particle to describe the backbone group containing the α-carbon and, for residues other than glycine, a second particle to describe the side-chain group (24); the lipid molecules, counterions, and solvent are similarly coarsened using the MARTINI potential (25). Following the atomistic simulations, the CG simulations were performed at constant temperature and pressure using orthorhombic periodic boundary conditions, as is detailed in Coarse-Grained Simulations in SI Appendix.

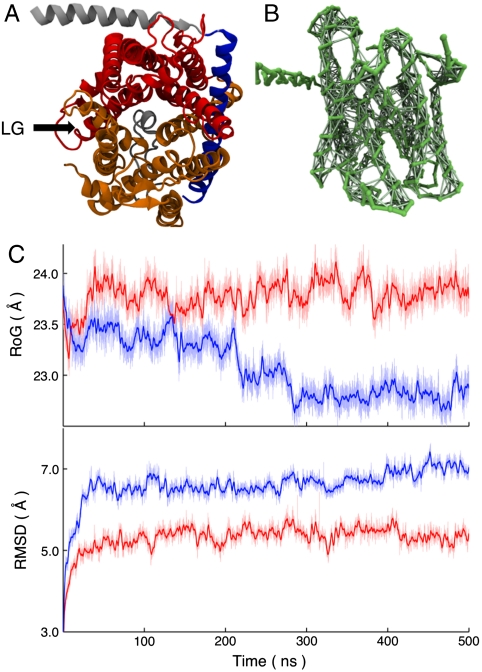
Although the CG potential is parameterized to reproduce pairwise interactions for amino acid side-chain and backbone groups, it has been found to poorly preserve protein tertiary structure for long MD simulations (26, 27). As shown in the blue curves in Fig. 2C, this issue also arises in our simulations for the Sec translocon. The radius of gyration of the channel, defined as the rms distance between CG particles in the translocon and its center of mass, drifts downward as the channel deforms with increasing simulation time. Similarly, the rms displacement of the translocon backbone CG particles following best-fit rigid-body alignment (28) drifts upward. To stabilize the CG simulations, we thus introduce scaffolding for sections of the translocon by adding weak interactions between pairs of the CG particles. Pairs of CG particles that are included in the scaffolding share an auxiliary harmonic bond with an optimal distance equal to the separation of the particles in the crystal structure and with a force constant equal to 0.2 kcal mol^-1 Å^-2. Scaffolding interactions are included for a pair of CG particles if both are contained in one of the following subsets of the translocon: (i) residues Lys²-Val⁴⁵ and Ile⁷¹-Pro²⁰⁵ in the α-subunit, and the entire β-subunit (Fig. 2A, Gold); (ii) residues Trp²⁹-Arg⁶⁶ in the γ-subunit, which include the domain that forms the hinge for the translocon (Fig. 2A, Blue); and (iii) residues Pro²⁰⁵-Leu⁴³³ in the α-subunit, which include the TM6-10 (Fig. 2A, Red). Scaffolding interactions are also included between particles in subsets i and ii and between particles in subsets ii and iii. However, they are not included between particles in subsets i and iii, and all scaffolding interactions are restricted to pairs of CG particles that are within 7 Å in the original mapping from the crystal structure (7). The translocon scaffolding is designed to stabilize the CG simulations without biasing or hindering the LG or PP motions. The red curves of Fig. 2C demonstrate that the scaffolding succeeds in stabilizing the structure of the translocon in long timescale CG simulations, and the results presented in Scaffolding Contribution to the FE Profile and Trajectories Without Scaffolding in SI Appendix indicate that the scaffolding does not significantly alter the conformational landscape of the translocon.

Fig. 2.

Stabilizing the CG model. (A) Subsets of the translocon, viewed from top, are used in the CG scaffolding protocol described in the text. (B) The auxiliary scaffolding interactions among CG particles for the translocon backbone, viewed from the side, are shown explicitly. (C) Without scaffolding, the CG model does not preserve the structural integrity of the translocon in long simulations, as is demonstrated for the translocon radius of gyration (RoG) along an MD trajectory (Blue). Inclusion of the pairwise scaffolding interactions stabilizes CG MD simulations of the translocon (Red). The rms displacements for the translocon backbone CG particles are also included. The heavier lines indicate the 1 ns rolling averages.

Collective Variables and Free-Energy Calculations.

The free-energy surface for the translocon is calculated as a function of collective variables that quantify opening of the LG, d_LG, and the displacement of the plug moiety from the channel pore, d_PP,

[1]

where k_B is Boltzmann’s constant and P(d_LG,d_PP) is the equilibrium probability distribution for the collective variables at temperature T. The LG distance d_LG is defined as the distance of minimum approach between the line of least-squares fitting for the α-carbons of the residues in the TM2b helix and the corresponding line for the TM7 helix. The PP distance collective variable d_PP is defined as the distance between the center of mass of the α-carbons for the residues that comprise the isoleucine ring of the channel and the center of mass of the α-carbons for the residues of the plug domain. Full details and illustrations of the collective variables are provided in Collective Variables in SI Appendix. The crystal structure reported in ref. 7 exhibits collective variable values of (d_LG,d_PP) = (5.99 Å,10.64 Å) in the atomistic representation.

The weighted histogram analysis method (WHAM) (29) in two dimensions was used to construct the free-energy surface from over 80 independent MD trajectories that were restrained to different reference values for the collective variables. These trajectories included the auxiliary restraining potential 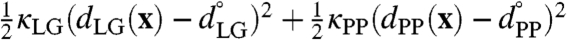, where x is the set of Cartesian positions for the atoms, and where κ_LG = 15.0 kcal mol^-1 Å^-2 and k_PP = 10.0 kcal mol^-1 Å^-2. The restraint values for the collective variables formed a uniform 8 × 10 grid spanning 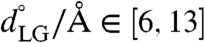and 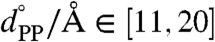. To achieve adequate sampling in the atomistic simulations, additional trajectories were performed with restraints of 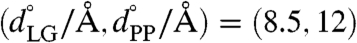, (8.5, 13), (8.5, 14), (8.5, 15), (8.5, 17), (8.5, 18), and (8.5, 19). Each restrained MD trajectory was run for a length of 2 ns in the atomistic model and 20 ns in the CG model. To minimize the equilibration time, which includes the first 0.8 ns in the atomistic trajectories and 8 ns in the CG trajectories, the restrained trajectories were initialized from trajectories performed with neighboring values of the restraint. A modified ridge estimator was used to smooth the calculated free-energy surfaces. Error estimates for the atomistic and CG free-energy profiles are provided in Scaffolding Contribution to the Free-Energy Profile in SI Appendix.

Atomistic and CG Free-Energy Surfaces.

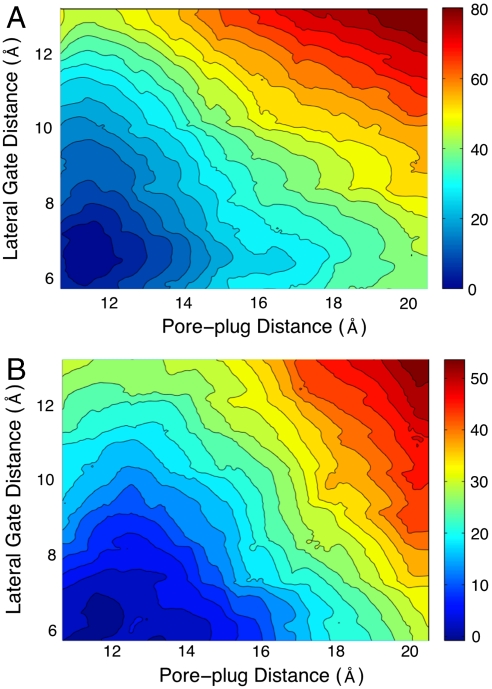
Fig. 3A presents the free-energy surface calculated from the atomistic simulations of the Sec translocon. It reveals a simple conformational landscape with a single minimum located around the values for the collective variables corresponding to the experimental crystal structure. No metastable open conformations for the channel are found with regard to displacements in either the LG or PP distances. The free-energy surface supports the conclusion that the crystal structure captures the relevant conformation for the membrane-bound translocon, in agreement with previous MD simulations (30–33). However, it also indicates that structural fluctuations in the translocon that are large enough to allow for either protein translocation or membrane integration are thermodynamically unfavorable. Given that an α-helical peptide is approximately 10–12 Å in diameter, Fig. 3A suggests that a free-energy penalty in excess of 20 kcal mol^-1 must be incurred for either the protein translocation or the membrane integration pathways in the absence of other facilitating interactions. Below, we consider the role of the substrate in altering this free-energy landscape.

Fig. 3.

Free-energy profiles for the Sec translocon from atomistic (A) and CG (B) simulations. Energies in kcal mol^-1.

Fig. 3A also reveals very little correlation between the opening of the LG and the displacement of the plug moiety. Indeed, as is shown in Free-Energy Surface Cross-Sections in SI Appendix, the LG free-energy profile at different fixed values of the PP distance is essentially unchanged. This suggests that the stabilization of the LG does not explicitly depend on the displacement, or perhaps even mutation, of the plug moiety (8, 12, 34), at least according to this measure.

Fig. 3B presents the corresponding free-energy surface for the translocon from our CG simulations. Although the thermodynamic penalty for displacing the LG and the PP is reduced in the CG model, the results in Fig. 3B compare well with those in Fig. 3A, suggesting that the CG model and the scaffolding protocol reproduce the conformational landscape from the atomistic simulations. The effect of the scaffolding interactions on this calculation are discussed in Scaffolding Contribution to the FE Profile in SI Appendix. Given the agreement between the atomistic and CG models, as well as the fact that the CG simulations increase the computational speed of the simulations by more than an order of magnitude, we employ the CG model for the remainder of the study.

Substrate Peptides Alter Translocon Conformation

Hydrophobic Vs. Hydrophilic Peptide Insertion.

To investigate the influence of substrate peptides on the conformational landscape of the translocon, we consider the 1D free-energy profile along the LG distance for the translocon containing either a hydrophobic polyleucine (Leu₃₀) peptide substrate or a hydrophilic polyglutamine (Gln₃₀) peptide substrate. The side chains for the leucine and glutamine residues occupy similar steric volumes (24), allowing the simulations to isolate the role of peptide hydrophobicity. The entire system, including the inserted peptides, are simulated using the CG protocol described previously. To prevent the diffusion of the peptides into the membrane, and thus to ensure a well-defined free-energy profile for the translocon containing the substrate peptide, a weak restraint potential was used to tether the center of mass of the peptide to the center of mass of the channel pore residues. The details of the initialization protocol and simulations for the translocon–substrate system are provided in Initializing the Peptide Substrate in SI Appendix. The WHAM algorithm was again employed to construct the free-energy profile from nine independent trajectories for the translocon–substrate system that are harmonically restrained to different values for the LG distance on a uniform grid in the range 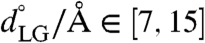using κ_LG = 5.0 kcal mol^-1 Å^-2; to achieve adequate sampling, an additional trajectory was performed with the hydrophobic substrate at 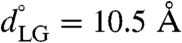and two additional trajectories were performed with the hydrophilic substrate at 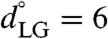and 9.5 Å. Each of the 21 sampling trajectories was run for a simulation time of 1.5–1.6 μs, where all but the last 800 ns was discarded as equilibration.

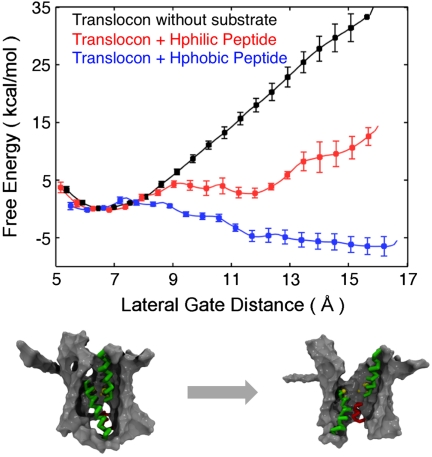
Fig. 4 presents free-energy profiles calculated for the translocon peptide substrate. The black curve, for reference, presents the result for the translocon without peptide substrate and is consistent with the data presented in Fig. 3B. These results demonstrate that the hydrophilic peptide shares the same basin of stability as the translocon in the absence of substrate, whereas an open conformation for the LG motion is stabilized for the translocon containing the hydrophobic substrate. The robustness of the calculated free-energy profiles with respect to the definition of the LG collective variables is explored in Alternative Collective Variable Definitions in SI Appendix.

Fig. 4.

Free-energy profiles along the lateral gate distance for the translocon, with and without peptide substrates. (Bottom) Snapshots showing the translocon in closed versus open configurations of the lateral gate distance.

Recent structural studies have considered the role that translocon-docking macromolecules play in stabilizing the open LG; crystal structures with the Sec translocon in complex with SecA (9) or a Fab fragment (10) exhibit partial opening of the LG, whereas a recent, subnanometer-resolution microscopy study finds no such opening of the LG for the translocon docked with the ribosome (11). The results in Fig. 4 predict the hydrophobic substrate to stabilize the open LG, even in the absence of such complexation events.

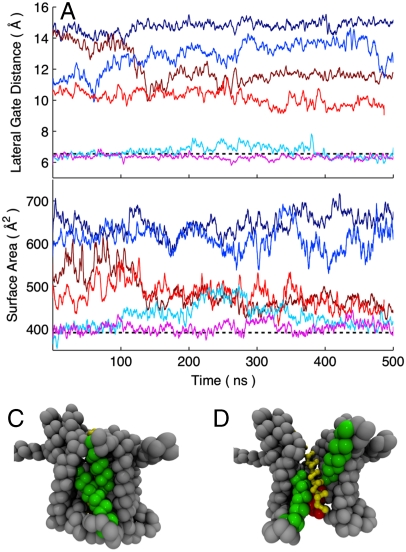
To investigate the metastability of the LG conformations for the translocon containing the substrate peptides, long CG MD trajectories were initialized from open (d_LG = 15 Å), partially open (d_LG = 11 Å), and closed (d_LG = 6 Å) configurations for the LG. The time evolution of these trajectories was unrestrained with respect to the LG distance and the center of mass of the peptide substrate. The trajectories are plotted in terms of the LG distance in Fig. 5A. For the trajectories initialized from the closed LG with either the hydrophobic and hydrophilic peptide substrate, the LG remains closed on the timescale of the simulations. However, for the trajectories initialized from the open LG, the simulation with the hydrophobic substrate remains open, whereas the simulation with the hydrophilic substrate relaxes toward smaller values of d_LG on the timescale of hundreds of nanoseconds. Similarly, for the trajectories initialized from the partially open LG, the simulation with the hydrophobic substrate relaxes toward larger values of d_LG, whereas the simulation with the hydrophilic substrate exhibits gradual closure of the LG over the course of the trajectory. Additional trajectories performed without scaffolding interactions are reported in Trajectories Without Scaffolding in SI Appendix.

Fig. 5.

CG MD trajectories for the translocon containing either the hydrophobic (Blue-shaded) or hydrophilic (Red-shaded) substrate are initialized from open, partially open, and closed configurations of the lateral gate. (A) The lateral gate distance d_LG for the trajectories is plotted as a function of simulation time. (B) The lateral gate surface area for the trajectories is plotted as a function of simulation time. Heavy lines indicate 1 ns rolling averages. Also shown are snapshots of the translocon at the end of the initially closed trajectory with hydrophilic substrate (C) and the initially open trajectory with hydrophobic substrate (D).

The trajectories in Fig. 5A for the initially open and partially open LG with the hydrophilic peptide relax toward the closed configurations, but they do not fully close the LG distance within the 500 ns of simulation time. This slow timescale for relaxation is related to the conformation of the plug moiety for the translocon. As is illustrated in Fig. 5B, the translocon in these simulations has in fact eliminated the open surface area of the LG (defined in Collective Variables in SI Appendix), but this is not captured by the LG distance collective variable that is plotted in Fig. 5A. It is not clear whether the ability of the plug to partially prop open the region between TM2b and TM7 at the bottom of the translocon channel is functionally relevant, although it is thought that a peptide signal sequence performs this function at the top of the channel (7, 35).

The results in Fig. 5B indicate that a metastable closed state for the LG of the translocon is supported by both the hydrophilic and hydrophobic substrate with a surface area of approximately 400–450 Å², whereas a metastable open state for the LG is supported only by the hydrophobic substrate with a surface area of 600–650 Å². The closed state allows for little contact of the peptide substrate with the hydrophobic membrane interior and exhibits values for the LG surface area and distance values that are typical of the translocon without substrate, whereas the open state allows for extensive exposure of the substrate to the membrane and provides space for the exit of the substrate from the channel (Fig. 5C and D). Although the fact that the closed state is metastable for both the strongly hydrophobic and strongly hydrophilic substrates suggests that the closed state would also be metastable for substrates of intermediate hydrophobicity, additional trajectories provided in Trajectories with Substrate of Intermediate Hydrophobicity in SI Appendix show this explicitly.

Orientation of the Substrate Peptide and the Translocon Plug.

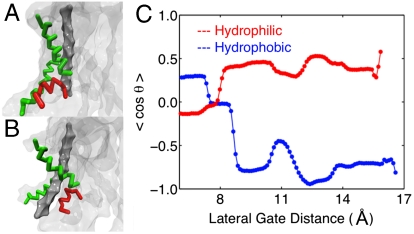
The reason that long (> 1.5 μs) sampling trajectories were needed to equilibrate the free-energy profiles in Fig. 4 is due to the slow reorientation of the channel plug moiety with respect to the peptide substrate (Initializing the Peptide Substrate in SI Appendix). Fig. 6A illustrates that, for the hydrophilic substrate, the plug is preferentially positioned between the peptide substrate and the LG, whereas for the hydrophobic substrate, the orientation is reversed such that the plug is behind the substrate with respect to the LG opening.

Fig. 6.

Relative orientation of the peptide substrate (Dark Gray), the plug moiety (Red), and the LG helices (Green). (A and B) Snapshots illustrating that the hydrophilic peptide (A) is behind the plug residue with respect to the LG, whereas the hydrophobic peptide (B) is in front of the plug residue and closer to the interior of the membrane. (C) The ensemble average for the order parameter describing the relative orientation of the substrate and plug.

To quantify this effect, we introduce an order parameter for the relative orientation of the pore and the plug residue. We define θ to be the angle between a vector υ₁ that points from the peptide substrate to the plug moiety and a vector υ₂ that points outward from the opening of the LG. If cos(θ) > 0, then the plug is between peptide and the LG, as is shown for the snapshot of the hydrophilic peptide in Fig. 6A. For cos(θ) < 0, the reverse orientation is observed. A detailed and illustrated definition of θ is provided in Collective Variables in SI Appendix.

Fig. 6C presents the equilibrium expectation value for the orientational order parameter cos(θ) as a function of the LG distance, again obtained using the WHAM algorithm and the simulation data corresponding to Fig. 4. Indeed, this plot reveals that for open configurations of the LG, the relative orientation of the plug moiety and the peptide substrate is strongly dependent on the nature of the peptide. The trend observed in Fig. 6C indicates that the hydrophobic substrate assumes an orientation that achieves greater exposure to the hydrophobic lipids of the membrane interior, whereas the hydrophilic substrate favors the orientation in which it remains more fully in the channel and shielded from the membrane by the plug. This result may suggest that the plug [or its replacement moiety in a plug-deletion mutant of the translocon (8, 36)] plays a role in guiding the substrate toward either the translocation or membrane integration pathways.

Hydrophobicity and the Energetics of the Lateral Gate.

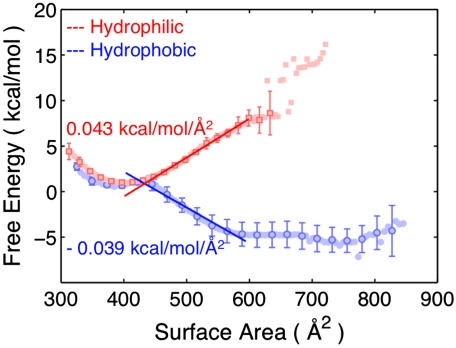
To analyze the energetics of the LG motion for the translocon including peptide substrates, we calculate the free-energy profile for these systems as a function of the LG surface area. This calculation again employs the WHAM algorithm and the simulation data corresponding to Fig. 4. A detailed definition of the LG surface area collective variable, which quantifies the area between the TM2b and TM7 helices that comprise the LG, is provided in Collective Variables in SI Appendix. The free-energy profiles calculated as a function of the LG surface area are presented in Fig. 7. Closed configurations for the LG correspond to a surface area of approximately 400–450 Å² (Fig. 5B). As the LG opens, the linear behavior for the free-energy profiles is consistent with a model, F = σA, in which the free-energy of opening the LG, F, is equal to the product of the LG surface area, A, and a constant marginal free-energy, σ. Linear fits to the free-energy profiles in the range of 450–600 Å² and the resulting estimates for σ are also included in the figure; the fitting range is chosen based on the characteristic values for the LG surface area for the closed and open states of the LG observed in Fig. 5B.

Fig. 7.

Free-energy profiles for the translocon with peptide substrates as a function of the LG surface area. The slopes for the linear fits of the data are shown.

Fig. 7 suggests that the energetics of the LG conformation is governed by a simple balance between hydrophobic and hydrophilic contacts in the system. For the case of the hydrophilic substrate, the opening of the translocon LG corresponds to the formation of an interface between the hydrophobic interior of the membrane and the hydrophilic substrate in the channel. It is thus reasonable that the calculated value of σ = 0.04 kcal mol^-1Ų for this case is similar to the range of values (0.025–0.035 kcal mol^-1Ų) that have been estimated for the surface tension between hydrophilic residues and the lipid bilayer (37, 38). On the other hand, the opening of the LG for the case of the hydrophobic substrate thus corresponds to the removal of a hydrophobic/hydrophilic interface from the system. The interior of the channel for the Sec translocon is a largely hydrophilic environment (7, 39, 40), such that opening the LG replaces an area of hydrophobic–hydrophilic contacts between the substrate and the channel interior with more favorable hydrophobic–hydrophobic contacts between the substrate and the membrane.

For larger values of the LG surface area, the free-energy profile for the hydrophobic substrate deviates from the linear fit as expected. Once the surface area is sufficiently large to allow for full contact between the hydrophobic substrate and the membrane (600–650 Å², Fig. 5B), further opening of the LG does not allow for any additional favorable hydrophobic contacts; it instead introduces contacts between the membrane and the hydrophilic interior of the channel, leading to a change in the marginal free-energy and the calculated turnover in the free-energy profile. The agreement of the simulation data in Fig. 7 with the expression F = σA suggests that the relative free energy between the metastable LG closed state (approximately 400 Å²) and the open configurations that allow for membrane integration (approximately 600 Å²) is governed by the interfacial energy between the peptide substrate and the membrane interior. This free-energy relationship depends linearly on both the LG surface area and the hydrophobicity of the peptide substrate, such that if it is assumed that the sequential ordering of the substrate residues can be ignored (21), then the relative free energy between the closed and open states depends simply on the number of hydrophobic and hydrophilic peptides in the substrate. Given that the simulation data indicate that changing from a completely hydrophobic 30-residue peptide to one that is completely hydrophilic alters the relative free energy of LG opening by approximately 12 kcal mol^-1, this analysis suggests that replacing a single hydrophobic residue in the substrate with a hydrophilic residue will lead to a change in the free energy of LG opening of approximately 0.6 k_BT. It follows that for substrates of intermediate hydrophobicity, the thermodynamic balance between open and closed LG states can be significantly shifted by changing only a small number of substrate residues. Naturally, the simplicity of the CG model employed should discourage overinterpretation of the quantitative details of the simulation results, and a more extended discussion of the accuracy of the CG model is provided in Side-Chain Transfer Free Energies for the CG Residues in SI Appendix. However, the energy scales obtained from the simulations reported here and the linear dependence of the calculated free-energy profiles on the LG surface area support a simple and intuitive analysis of the energetics of the translocon LG in the presence of a peptide substrate. Mutations in the Translocon Pore Residues in SI Appendix further discusses how the free energy of LG opening depends on the hydrophobicity and bulkiness of the translocon pore residues.

Implications for Translocon Regulatory Function

Efforts to understand the regulatory function of the Sec translocon have focused on the strong correlation between the water/octanol transfer free energy for a transmembrane peptide domain and the relative fraction of substrate peptides that undergo membrane integration vs. translocation (19–21). This correlation has been interpreted in terms of a two-state model in which the peptide equilibrates between the hydrophobic membrane environment and the hydrophilic channel environment (16, 19). Assuming that this equilibrium is genuinely realized (and assuming that the solvation free energy for the peptide in the channel does not change with the predominant LG conformation), then the partitioning of the peptide substrate between the translocon and membrane environments would be independent of the LG conformation. That is, switching of the predominant LG conformation between open and closed states under the control of the substrate hydrophobicity (Fig. 7) would not affect the regulation of the substrate peptides between the Sec-mediated membrane insertion and translocation pathways.

However, if instead of being completely reversible, the exit of the peptide substrate from the translocon is irreversible, then the results presented here suggest an alternative interpretation of the data of Hessa et al. (20, 21). Assuming that only the open LG allows for membrane integration, and utilizing the separation between the timescale upon which substrates are driven into the channel by either the ribosome or another molecular motor (∼milliseconds) and the timescale upon which the LG undergoes conformational rearrangements (∼100 ns), then the rate at which the integration product is formed is proportional to the population of the open LG conformation, k_integ ∝ P_open. Similarly, the rate for the translocation is proportional to the population of the closed LG conformation, k_trans ∝ P_closed. The balance of this conformational partitioning of the LG, as we have argued in connection with Fig. 7, depends primarily on the effective hydrophobicity of the substrate peptide.

This model describes a regulation between the translocation and integration pathways that is controlled by substrate sensitive conformational gating of the translocon. It is consistent with the experimental observation of a two-state balance between translocation and integration, and it predicts the experimentally observed correlation of that balance with peptide hydrophobicity. The model is based on a nonequilibrium description of the slow substrate insertion dynamics and an equilibrium description of the faster conformational motions of the translocon; because both open and closed states have finite equilibrium populations, all substrates will experience at least fleeting exposure to the interior of the membrane (16). Direct, nonequilibrium simulations of protein translocation and membrane integration will yield further insights into this possible mechanism of regulation.