Hydrophobicity – Shake Flasks, Protein Folding and Drug Discovery

Abstract

Hydrophobic interactions are some of the most important interactions in nature. They are the primary driving force in a number of phenomena. This is mostly an entropic effect and can account for a number of biophysical events such as protein-protein or protein-ligand binding that are of immense importance in drug design. The earliest studies on this phenomenon can be dated back to the end of the 19^th century when Meyer and Overton independently correlated the hydrophobic nature of gases to their anesthetic potency. Since then, significant progress has been made in this realm of science. This review briefly traces the history of hydrophobicity research along with the theoretical estimation of partition coefficients. Finally, the application of hydrophobicity estimation methods in the field of drug design and protein folding is discussed.

INTRODUCTION

Hydrophobicity (or lipophilicity) is a well-known and extensively studied phenomenon. It is commonly understood to be the tendency of non-polar molecules to form aggregates in order to reduce their surface of contact with polar molecules such as water [1]. Its manifestations include simple observable macroscopic phenomena such as the immiscibility of oil and water or modern techniques such as chromatographic separation. The importance of hydrophobic interactions on atomic or molecular scale has long been recognized in various facets of science [1]. While the concepts have changed and the applications have expanded, the fact remains that hydrophobic interactions are often the driving force in a variety of physical and biological phenomena. In this review, we introduce the concept of hydrophobic interactions, present a very short history and discussion of theoretical and experimental studies on the phenomenon. A key theme of this review is that the same set of forces and interactions that partitions a molecule between polar and hydrophobic solvent phases, i.e., determines its hydrophobicity, is pervasive in all biological interactions including small molecule binding and protein folding. Finally, we present an in-depth perspective on computational studies involving hydrophobic interactions. These studies include methods for estimation of the hydrophobic nature of small and large biological molecules and applications of this in drug discovery or design. Another aim is to suggest future directions in hydrophobicity research, with the hope of stimulating interest in the field.

A brief historical overview of hydrophobicity

Even before the turn of the 20^th century, the importance of hydrophobic interactions in biological phenomena, particularly drug activity, was recognized by the work of Meyer and Overton [2,3,4]. In 1937, Butler showed a linear relationship between heat of hydration and entropy of hydration [5]. He estimated the energies of interaction of different functional groups with water and showed that the heats of hydration are additive in nature. He also explained that the heats of hydration do not determine the free energy of interactions, but that there is a direct proportionality between them. The origins of this phenomena were unclear at this point, but it was hypothesized that entropy might be dependent on the size of the “cavity” that contains the molecule. The importance of H-bonds was also briefly discussed as formation of H-bonds between polar parts of the molecule causes an increase in entropy, which favors dissolution of an otherwise non-polar molecule.

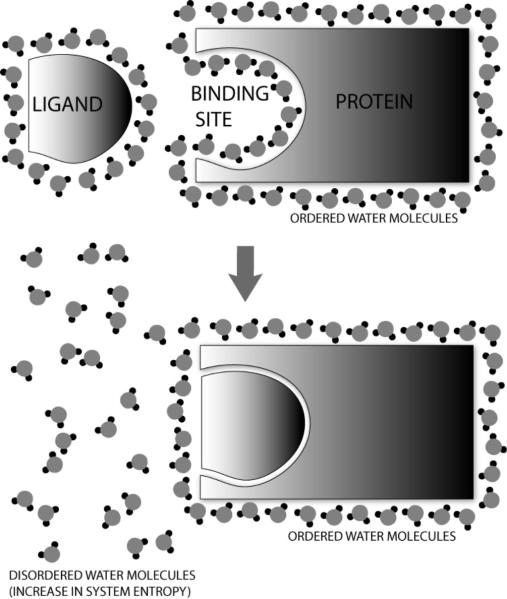
Frank and Evans, in the middle of the 20^th century, described the formation of “icebergs” of water around non-polar parts of molecules [6]. Their findings were based on the deviation of entropy of vaporization for certain substances when dissolved in aqueous and non-aqueous solutions. The formation of a regularized lattice-like structure of water molecules surrounding non-polar moieties has been experimentally validated with crystallography [7] and is now more or less taken for granted. This theory was extended to proteins by Klotz, who explained the variation in pK_a, molecular volume, denaturation and the masking of expected behavior of protein functional groups in terms of this “iceberg” formation [8]. In fact, the association of two molecules can become energetically favorable due to the increase in entropy when these ordered water molecules are scattered or disordered (see Figure 1).

Figure 1. The Hydrophobic Effect.

Hydrophobic molecules are surrounded by an ordered cage of water molecules. When two such molecules come together, they aggregate in order to reduce their surface area in contact with the polar water molecules. This causes a number of water molecules to be removed from their ordered formation, thus increasing disorder (increased entropy) and potentially making the process energetically favorable.

Kauzmann first coined the term “hydrophobic bond” in 1959, which caught the attention of many scientists at the time; this notion was supported by a number of research investigations of that era [9]. The work of Némethy, Scheraga and Steinberg also supported the use of this term [10]. Perhaps it was the tendency of the non-polar substances to form aggregates that caused scientists to draw parallelisms with the definition of a bond – “the tendency of two atoms to stay together in space”. Hydrophobic bonds have been described as endothermic, i.e., as temperature increases their strength increases until a maximum value is reached at approximately 60°C [10]. However, the stability of proteins depends on not only these hydrophobic “bonds,” but also hydrogen bonds. These have an inverse behavior, i.e., they become weaker with increasing temperature. Thus, as temperature increases, hydrophobic interactions would decrease in strength and hydrogen bonds would be predominant in maintaining protein structure. Hence, at higher temperatures proteins would unfold.

In the 1970s, Robert Hermann published a series of three papers on “the theory of hydrophobic bonding” [11-13] where the large negative entropy of partitioning a hydrophobic molecule into a non-polar solvent was explained by the loss of order in water molecules in direct contact with the hydrophobic surface. The ordered arrangement of water molecules on the surface of a molecule is due to dipole-dipole interactions with the immediate next layer of waters. In effect, this phenomenon is similar to surface-tension where the first layer arranges itself in order to reduce contact with the hydrophobic air, while less order exists in the second and succeeding layers. Order continues to decrease in layers away from the hydrophobic surface and there is a linear, but inverse, correlation between hydrophobic surface area and its solubility in water [11]. Hermann also determined that the free energy for hydration of a hydrophobic molecule is linearly related to the number of water molecules that can be packed around it. This first study did not take into account cavity curvature and was restricted to small molecules. Later work [12] described a correlation between a molecule's hydrophobic surface area and its solubility in water. Hermann also introduced a simple mathematical treatment of hydrophobic interactions [13] that addresses hydrophobic interactions at a distance taking into account not only solubility, but also the distances between hydrophobic entities with the Lennard-Jones potential as has also been suggested by Reynolds et al [14]. Leo, Hansch and Jow established a relationship between hydrophobicity and two other factors – the nature of the solute surface and the molecular (CPK) volume [15]. The major innovation of this study is that they used the partition coefficient for 1-octanol/water (LogP_o/w) as a measure of hydrophobicity rather than solubility. This parameter has been used almost ubiquitously in studies thereafter. Most importantly, these observations could not be explained by the simple concept of a “hydrophobic bond”, but rather as a complex phenomenon involving the interplay of flexible molecules and solvent under particular conditions.

The argument on semantics over the use of the term “hydrophobic bond” has continued ever since, but the fact that hydrophobic phenomena can explain a multitude of observations in science cannot be ignored. In this review, we attempt to explain how naming and characterizing this effect has changed the realms of computational chemistry and drug design. The preceding paragraphs provide an outline of the sequence of events and were not intended to serve as a comprehensive guide to the principles behind hydrophobic phenomena. However, a comprehensive review of the research on hydrophobicity is available elsewhere [1].

CALCULATIONS OF HYDROPHOBICITY AND THE HYDROPHOBIC EFFECT

Estimation of LogP_o/w

Hansch and Leo published their seminal paper on the determination and uses of partition coefficients in 1971 [16]. This paper was, and perhaps continues to be, the most comprehensive article on the subject. It explains the fundamentals of partition phenomena and provides detailed descriptions of the history and theory of the same. It also contains a very comprehensive tabulation of LogP values for various substances. However, most interesting to theoreticians is the discussion on additive-constitutive properties wherein the utilization of the Hammett equation in calculations of partitioning free energy and the effects of various stereoelectronic effects on the partition coefficient are described. Also, various uses of partition coefficients for such diverse research topics as countercurrent distribution, measurement of equilibria, hydrophile-lipophile balance, drug dissolution and “hydrophobic bonding ability” are outlined. Of note, the partitioning of alcohols between water and red cells was compared to their partitioning between water and 1-octanol. The energy of partitioning per methylene group was the same for both cases, i.e., approximately −690 cal mol⁻¹. The repercussions of this quantification of hydrophobic interaction energies have been key to drug design projects as well as computational chemistry. The Hansch and Leo method for theoretical estimation of molecular LogP values, which is the basis of the C-LOGP method (vide infra), is also described in great detail.

A loose categorization of different methodologies for estimation of LogP is provided in Table 1, complete with a few typical examples of each. Here, the discussion on these methods will be limited to a general overview highlighting the application of these methods in drug design and the relevance of accuracy for these prediction methods in that context. Several comprehensive reviews on the computational estimation of octanol-water partition coefficients are available [17-21]. These articles are highly recommended for those who intend to learn about the estimation methods in detail or to understand the nuances of their relative accuracies for particular applications.

Table 1.

Various types of methods for LogP calculations This table shows a rough classification of methods used for theoretical prediction of LogP for compounds. Examples of all the different types are included.

Approach	Methodology	Example(s)
Substructure approaches	Fragment-based methods	Rekker's method [22], Leo's C-LOGP method [23-27], ACD/LogP method [28]
	Atom-based methods	XLOGP method [33-35], Ghose-Crippen method [29-32]
Whole molecule approaches	Molecular Lipophilicity Potential and related approaches	MLP [107-108]
	Topology descriptions	MS-WHIP [40]
	Molecular Property descriptions	Toulmin's ΔLogP method [41]

To commence, it is a monumental understatement to say that a lot of good research has been done in this field. Many diverse empirical methods exist today that predict LogP of various molecules with different degrees of context-dependent certainty [17, 20]. Some of the major types are discussed below.

Fragment-based methods

Rekker's fragment based system was the first fragment-based computational method to estimate LogP [22]. Fragment-based methods implement and statistically deconvolve empirical data from experimental LogP values of compounds. See Appendix 1 for a short explanation of this approach. In order to explain the effect of inter-fragmental interactions, certain additive correction factors are introduced. Several other algorithms of this type exist including the C-LOGP [23-27] and ACD/LogP [28] methods. The criticism most often applied to this methodology is that the fragmentation of the target molecule is “arbitrary”. This is not actually true for C-LOGP as there are a complete and unambiguous set of rules. However, they can be difficult to visualize, and fragments can be much more complex than organic functional groups. Thus, fragments observed in new molecules can be missing from the C-LOGP database library, yielding poor predictions of LogP [17,20]. However, there are also advantages to these methods: significant and complex electronic interactions are automatically taken into account when they exist within a library fragment [20]; when the fragments coincide with real organic functional groups their interpretation is intuitive; the correction factors can be used to understand the relationship between functional groups or the effect of the observed feature on solubility, e.g., factors representing aliphatic chain branching explain the increased water solubility of branched hydrocarbons; and since fragment methods are based on empirical data, their associated algorithms are very fast and practical to implement in software.

Atom-based methods

These are similar to the fragment-based methods, but assume the hydrophobicity of a molecule to be the sum of the individual atomic contributions. Appendix 2 provides an overview of the principle behind atom-based additive methodologies. Again, several methodologies of this type exist, including the well known Ghose-Crippen [29-32] and XLOGP [33-35] methods. Mostly these algorithms avoid correction factors by taking into account these sorts of contributions with a large set of atom types according to the individual environment it exists in within the molecule [20]. In order to somewhat reduce the atom type set the XLOGP algorithm implements a small number of correction factors. The reduced dependence on corrections is the major advantage of these methods. As described by Buchwald and Bodor, the major disadvantage of this method is that often, the molecule is “more than a sum of its parts” [17]. Furthermore, human interpretability is reduced as the size of the atom database set grows and the correspondence with organic and medicinal chemistry principles is lost.

Molecular methods

Over the last two decades quantum mechanical calculations have been increasingly used in applied research including drug discovery, particularly with respect to estimations of interactions between solute and solvent molecules. A number of studies have used quantum chemical principles for estimation of molecular hydrophobicity [17]. Early work includes that of Rogers and Cammarata [36,37] and also that of Hopfinger and Battershell [38]. Klopman and Iroff used charge densities to calculate partition coefficients [39]. More recently, Bravi and Wikel described a method to predict LogP using a technology called Molecular Surface – Weighted Holistic Invariant Parameters (MS-WHIP) [40]. Unfortunately, a relatively large standard deviation between predicted and actual LogP was observed [18]. Toulmin et al. described another prediction method for octanol/water partition coefficients [41] that correlated minimized molecular electrostatic potentials with the H-bonding capability of molecules. In this method ΔLogP is defined as the difference between LogP_oct (logarithm of the 1-octanol/water partition coefficient) and their predicted LogP_hxd (logarithm of the hexadecane/water partition coefficient). H-bonding capability has a profound effect on partition coefficients with a strong correlation between ΔLogP and V_min (minimized molecular electrostatic potential). A strong correlation was also reported between ΔLogP or LogP_hxd and CNS penetration of compounds, i.e., through the blood-brain barrier. This highlights the importance of H-bond donors and acceptors in normal partitioning phenomena.

Livingstone et al. described a method that uses neural networks (NN) to predict LogP values from a training set of electrotopological descriptors [42] of 900 drug and pesticide-like compounds [43]. Other studies involving artificial-intelligence utlilize parameters calculated by various methods in unsupervised-learning processes to develop predictive models [44,45]. Taskinen and Yliruuski provide an in-depth analysis of such models in their review on NN modeling [46]. They note that while NN methods are accurate in predicting LogP values of molecules within the size, functional group, etc. confines of the training set, they are less accurate in predictions for molecules outside the training set. However, this is the case for all LogP estimation methods.

Hydrophobicity of amino acids and proteins

Understanding the hydrophobic behavior of amino acids, peptides and proteins has implications far beyond the seemingly simple task of calculating LogP for twenty or so small molecules (the amino acids). Abraham and Leo extended the Hansch and Leo fragment-based method of LogP calculation to amino acid zwitterions and side-chains [47]. Excellent agreement was reported for 19 out of the 20 natural amino acids. Proline, however, was calculated to be more hydrophilic than in reality, probably due to poor fragment parameterization for its secondary cyclic amine. With this method, hydrophobicity values for amino acid side chains were best predicted if a field effect was applied to the alpha-carbon. The field effect is the sum total of polar proximity effects of both the backbone amidic (peptide) bonds surrounding the alpha-carbon atom of any given residue. This field effect parameter accounts for the charge distribution on side-chain atoms and hence directly affects the hydrophobic/hydrophilic nature of the residue. Application of this effect allowed a higher correlation between predicted and calculated values of hydrophobicity for side-chains. In additional studies, Buchwald and Bodor reported a correlation between the van der Waal's volume of peptides with their LogP values [48]. Another approach was adopted by Steinmetz, where 3-D QSAR Comparative Molecular Field Analysis (CoMFA) studies were applied in a similar manner [49]. Experimentally determined LogP values of free and blocked di- and tripeptides were analyzed statistically to produce another set of parameters [50]. Akamatsu's work on the solvent partitioning of peptides using regression analysis of the experimental data to abstract the hydrophobic parameters [51-54] is commonly regarded as the most convincing and accurate [55]. A comparison between software programs in predicting peptide LogPs was published recently [56]. In general, fragment-based methods are sensitive to composition but not to peptide sequence, which can be considered to be a major flaw of these programs. Also, it is important to note that most current programs are inefficient and ineffective in calculating LogP values for long peptides.

Summary of LogP estimation methods

A lot of effort has gone into devising methods for high prediction accuracy for LogP. However, most methods are accurate for members or close relatives of their own training sets but continue to be less accurate outside their training sets. It should also be pointed out that a considerable portion of the predictive inaccuracy may, in fact, lie with the data itself. Such data has often been obtained with experimental procedures whose accuracy varies with the method used [57]. One example brings this into focus: as many drugs and drug-like molecules contain ionizable functional groups, the conditions of measurement, particularly pH, are extremely relevant to measured LogP. Thus, if a user attempts to estimate LogP for a molecule, e.g., by specifying a carboxylic acid-containing species, what LogP value should be reported? The molecule in its acid form? The molecule in its ionized (nominally pH 7) form? Or the weighted average representing the equilibrium between the two forms? (This is what the experiment, as performed on the molecules in the training set, measured.) As other functional groups on the molecule can shift that equilibrium, how does this affect the contribution of the carboxylic acid/carboxylate fragment (or constituent atoms) to the predicted LogP?

While whole-molecule approaches are designed to estimate LogP values with great accuracy without extensive piecemeal (atom- or fragment-wise) empirical parameterization, their predictive nature in the end must also be compared to experimental data, limiting our ability to really judge the accuracy of predictions. This begs the question: do we need to emphasize accuracy of predictions so much? We suggest that when it comes to drug design, it is largely the ΔLogP changes between analogues that will drive the evolution in design with respect to physicochemical properties of the molecule. Virtually all methods of estimating LogP can accurately describe the replacement of a proton by a hydroxyl, the halogenation of an aromatic ring, substitution of an amine for a methyl, or nearly any of the chemical modifications that would be performed in fine-tuning a lead compound. The prediction of LogP for random organic compounds is probably not an important real world exercise. Also, representing such an important physicochemical property as a simple scalar value underutilizes the information content of the molecule's 3-D topology and, particularly, its hydropathic structure. The combination of topology and hydropathy provides us with structural details of immense importance, which play a direct role in intermolecular interactions, e.g., ligand binding, protein-protein associations, etc. However, we do recognize the importance of LogP in QSAR studies, and also in assessing the drug likeness of a compound, both of which will be discussed below.

Can predictive methods for estimating the LogP of a peptide translate into a meaningful number for protein hydrophobicity? The idea that an additive atom-based or fragment-based algorithm (or even a whole molecule approach) could describe the dissolution of a protein into water and/or 1-octanol is probably preposterous. To start, it is likely that a severe conformational change would occur if macromolecules pass from aqueous to organic solvents, e.g., hydrophobic residues would rearrange to the surface while the hydrophilic ones attempt to optimize hydrogen bonding and/or electrostatic interactions at the core. In other words, a protein would be an entirely different chemical species when interacting with solvents of different polarity – if it could actually be solubilized. However, the atomic, fragment or residue-level components of such a total LogP should be useful descriptors for understanding the forces and energetics of protein secondary, tertiary and quaternary structure, and have been used in various schemes of describing and predicting protein folding for more than 20 years.

HYDROPHOBICITY SCALES AND PROTEIN FOLDING

There has long been evidence that protein secondary structure is dependent on the hydrophobic properties of the amino acid residue side chains. There is, in fact, a reproducible pattern of these properties in well-defined secondary structural elements such as α helices and β sheets. Thus, considerable effort has been expended in developing hydrophobicity scales that can aid in predictions of protein folding patterns. Some of these scales are based on water-ethanol transfer free energies [58,59], while others are based on partitioning between the bulk aqueous phase and the air-water interface [60], or on water-vapor partition free energies [61]. Kyte and Doolittle discussed the weaknesses of all three of these in a paper that also introduced their own hydrophobicity scale [62]. In their view, water-ethanol transfer free energy-based methods suffer because some amino acids are known to be insoluble in both water and ethanol and the latter may not be a truly inert solvent. Using partition data from transfer between the aqueous phase and air-water interfaces was also problematical because the hydrogen bonds that must be broken and the charges that must be neutralized to remove a residue from the aqueous phase during the formation of the native structure probably remain unchanged at an air-water interface. Thus, they would not be a factor in the overall reaction.

The “hydropathy” parameter of Kyte and Doolittle [62] is an amalgam of water-vapor transfer free energies and the interior-exterior distribution of amino acid side-chains determined by Chothia [63]. A moving-segment approach that continuously determines the average hydropathy while it advances through a sequence is used to obtain a plot of hydropathy as a function of sequence. On this plot, any parts of the sequence that are above the average hydropathy for the sequence are termed hydrophobic and correspond well with experimentally determined “internal” regions of proteins. Conversely, sequence elements with hydropathy below the average are termed hydrophilic and correspond well with areas of the protein that are “exterior” and likely to be in contact with the polar solvent. The motivation is that analysis of these data may indicate the “folding” pattern of the sequence. To further exploit this, Wimley and White reported a new forcefield derived from partitioning two series of model peptides into the interface of neutral (zwitterionic) phospholipid membranes [64]. An alternative approach was introduced in 1986 by Eisenberg and McLachlan [65] for calculating the stability of protein structures in water based on atomic coordinates. The contribution of each protein atom to the solvation free energy is estimated as the product of the solvent accessibility of the atom and an atomic solvation parameter.

Li and Deber [66] used circular dichroism (CD) data to rank order helical propensity of proteins within membranes. Residues such as Ile, Val and Thr, which usually exist as β-sheets in an aqueous environment, prefer an α-helical conformation in lipid membranes. Thus, the helical propensity of amino acid residues correlates with the hydrophobic nature of the side chain. More recently, Dyson, Wright and Scheraga have explained [67] how strict classification of side chains as polar or non-polar has obscured certain facts about protein folding. For example, methylene groups present in large polar or charged amino acid side chains like the four methylenes in the lysine side chain can be considered non-polar. Interestingly, this fact was imbedded as one of the factors in the Hansch and Leo system for estimating LogP [68] nearly 30 years earlier! These methylenes can aggregate with other non-polar groups and assist in hydrophobic collapse of the sequence.

Felitsky et al. introduced the use of a new parameter called “average area buried upon folding” (AABUF) [69] that explains both local contacts and long-range interactions. AABUF was used to study folding of apomyoglobin and provided additional insight into hydrophobic collapse and early folding events. Studies on polyalanine and polyleucine helices in water by MacCallum et al. [70] confirmed that in folding many unfavorable enthalpic events are counterbalanced by favorable entropic contributions by the solvent. This indicates a very small free energy barrier for folding. Thus, folding is mainly a desolvation phenomenon. Similarly, the Mardia and Nyirongo procedure for generating virtual protein C_α traces simulates the hydrophobic effect during folding [71] and produces models that are globular and compact.

Another related application of hydrophobicity is in the development of algorithms to simulate folding of hydrophobic-polar (HP) models in 2 and 3 dimensions [72]. The concept is to simplify the complex problem of folding by reducing it to representing residues by spheres with H (hydrophobic) and P (polar) character. The ensuing simulations are based on the observation that hydrophobic forces are the major forces determining native conformation of small globular proteins. These model simulations have been used to develop mathematical strategies for solving the combinatorial explosion problem, rather than actually simulating the hydrophobic effect [73-74].

As these studies have progressed over the past 20 years or so, the understanding of the hydrophobic effect and its impact on protein structure has matured. The early emphasis of using hydrophobicity scales to define folding patterns has shifted to algorithms that define protein folding in terms of mathematical approaches to reduce the calculational combinatorial explosion caused by exhaustive sampling of conformational space. However, it must be repeated that the same forces and energetics that drive solvent partitioning in the shake flask are at the core of protein folding. The difficulty is to unravel them and define algorithms that can simulate folding in these terms.

LogP IN DRUG DESIGN

Small molecule hydrophobicity has long been a consideration in drug discovery and design. The relationship between anesthetic effect of certain gases and their hydrophobicity has been extremely well established [4,75,76]. As described by Meyer in 1937 [3], chemically inert substances accumulate in “lipoids” and at a certain concentration, produce narcosis. The concentration itself is dependent on the animal, but independent of the narcotic itself. Hansch et al. also confirmed the Meyer-Overton hypothesis about a direct relation between hydrophobic nature of a compound and its anesthetic capabilities [75] through statistical correlations. However, Hansch suggested the additional involvement of a polar factor because molecules with polar hydrogens showed greater anesthetic action. Hansch et al. also introduced a similar theory for the hypnotic effect of barbiturates [76]. Other studies also have shown the important correlation of partition coefficients with binding affinities of drugs to receptors [77,78]. McFarland used a very simple probabilistic treatment of drug diffusion from the site of administration to the site of action via a collection of hydrophobic and hydrophilic barriers [79]. Inclusion of the Hammett equation into this study gave an intuitively satisfying parabolic relationship between drug potency and hydrophobicity (Appendix 3): higher doses of drugs with unfavorable partition coefficients (either too high or else too low) are required for them to reach the site of action. Recently, Kier has proposed a general theory of inhaled anesthetics [80].

The Lipinski “Rule of 5”

Hydrophobicity, of course, has also been a key factor in Lipinski's “rule of 5” [81,82]. In simple terms, Lipinski's rule can be stated as such: Poor absorption or permeation is more likely for a chemical entity when: a) there are more than 5 H-bond donors (sum of OHs and NHs); b) the molecular weight is over 500; c) the LogP is over 5; or d) there are more than 10 H-bond acceptors (sum of Ns and Os). The only exceptions to these rules were said to be substrates for biological transporters and natural products, which have a tendency to be highly complex molecules with multiple stereogenic centers and rarely contain nitrogen [83,84]. In 2000 Lipinski introduced changes to address terms such as ‘drug-like’ because it was predicted that ADME (Absorption, Distribution, Metabolism and Excretion) screening of molecules (into drug-like or non-drug-like) would precede screening for activity at biological receptors [82]. The rule of 5 was further extended [85] to define a number of useful parameters: a) the presence of greater than 10 rotatable bonds reduces oral bioavailability; b) 0 < LogD < 3 enhances the probability of good intestinal permeability (LogD is logarithm of the distribution coefficient D, which is in turn defined as the ratio of the sum of concentrations of all forms of a substance distributed between two mutually immiscible phases); c) a polar surface area (PSA) of less than 60-70 describes CNS active compounds; d) an N+O count of less than or equal to 5 enhances the probability of passing the blood-brain barrier; e) if LogP – (N + O) > 0, the molecule tends to be CNS active; f) orally-active drugs have lower molecular weight and fewer H-bond donors, acceptors and rotatable bonds; g) pulmonary drugs tend to have a larger PSA; and h) if the molecular weight < 300, LogP < 3, H-bond donors and acceptors < 3 and rotatable bonds < 3, the compound can be called “lead-like”.

This revolutionary work, which brilliantly summarized over 100 years of Medicinal Chemistry trial and error, made possible a number of rational filters and screens that, in principle, would improve the likelihood that a compound with promising “activity” could produce a “lead” and eventually yield a “drug”. Muegge described various methods for classification of drug-like compounds in his 2003 publication [86]. Similar publications addressing the terms ‘drug-like’ and ‘tool-like’ were also made [87,88]. Oprea et al. reported the presence of a “medicinal chemistry lead-like space” and urged careful use of Lipinski's rules [89]. A very interesting discussion [82] on how the properties of drug candidates from two pharmaceutical companies have varied across time pointed out that stress on rational methods of drug design in Merck laboratories caused no significant change in MLogP (Moriguchi LogP [90]) values across time. In contrast, there was a measurable increase in MLogP values for candidates from Pfizer since almost 50% of their hits were discovered with high-throughput screening (HTS) methods. Because the easiest method to increase in-vitro potency is to appropriately position a hydrophobic moiety onto a lead compound, HTS methods almost invariably select more hydrophobic candidates. Similar trends were observed [91] in that more than half of the molecules reported to have high-activity towards the end of the last century had a high LogP (> 4.25), high molecular weight (>425) and log of solubility in its neutral state (estimated from its molecular weight and LogP values), i.e., LogS_w (< −4.25), only about 35% of the true lead compounds had these properties. It was also noted that as these molecules go through clinical trials, there is a distinct decrease in LogP values for compounds that make it to the market. One thing is clear from these studies and an analysis by Proudfoot of drugs currently on the market [92]: the lipophilicity of molecules that make it all the way to commercialization has remained in the same range for a number of years. In other words, there is a delicate balance between the hydrophobic and hydrophilic nature of a molecule that is absolutely essential for it to be transported to the site of action by diffusion across membranes.

Hydrophobicity in QSAR

Similarity between molecules is often perceived by chemists both qualitatively and quantitatively. A synthetic chemist would describe two molecules as similar if they have similar topologies, bond connectivities, functional groups or maybe synthetic strategies. Structure-Activity Relationships (SARs) are based on such comparisons in the context of physiological function, but are mostly limited to qualitative or semi-quantitative treatments of biological phenomena or activities. However, more stringent definitions of similarity have been formulated and can be used with chemical computing software to perceive (and even predict) chemical equivalence provided the likeness is scrutinized critically. Thus, a more mathematical and quantitative approach called the Quantitative Structure-Activity Relationship (QSAR), wherein affinities of ligands for their binding sites, inhibition constants, rate constants and other biological activities are correlated to molecular properties such as lipophilicity, polarizability, electronic and steric properties, was developed. Comprehensive reviews have been published on the subject in the past [93,94], which should be referred to by those wishing to learn about the QSAR concept in depth. Here, we will focus on the key role of hydrophobicity in these studies.

There are many different approaches used in classical QSAR studies, including establishment of relationships between activity and physicochemical properties such as steric properties (Hansch analysis, extrathermodynamic approach), structural features (Free Wilson analysis) [94], or topological descriptors (Kier-Hall indices) [42]. 3D QSAR methods, especially those such as CoMFA, consider three-dimensional ligand structures and use those to propose the binding modes of those ligands at a common protein active site [94]. Data is often analyzed by statistical methods such as Multiple Linear Regression (MLR), Partial Least Squares (PLS) or by use of artificial intelligence (AI) methods such as Neural Networks (NN) or Support Vector Machines (SVM) [95] in order to detect correlations between a target activity and various descriptors (like LogP).

Hansch and Fujita first introduced their method, and coined the term QSAR, for correlation of biological activity to chemical structure in the 1960s [78,96-98]. The method correlated, with the use of regression analysis, ligand structural variations to the biological activities of those ligands. In time, these studies would become a distinct scientific field and a mainstay of drug discovery and design research. Many applications have been reported across the past five decades. A review by Kubinyi has described, in great detail, the various subtleties of the science [99]. Indeed, in the absence of a detailed target or receptor structure, this ligand-based drug design method gives invaluable quantitative information to drug designers. It is important to note that the first publication on QSAR in 1962 [78] showed the importance of hydrophobicity through LogP. Appendix 4 explains the general concept behind the Hansch Analysis technique where the free energy-based substituent constant π is based on the Hammett function σ. π is dependent on the substituent's chemical nature and, since molecules must repeatedly partition between lipid membranes to be effective drugs, the constituting fragments of π should be such that their additive effect would allow easy partitioning into either membranous or aqueous phases.

It must be noted, however, that hydrophobicity is not always the principal parameter determining activity [100]. For example, when DNA is the drug target, e.g., in binding to the major or minor groove, QSAR analyses often shows negligible hydrophobic terms because the negatively charged phosphate groups of DNA are hydrophilic. On the other hand, DNA intercalation would likely be a hydrophobic effect. Radical reactions also typically lack hydrophobic terms in QSAR analyses, although these studies are mostly on small datasets and more thorough studies would be desirable. Finally, it has been suggested from QSAR studies on Multiple Drug Resistance that this process might be accomplished without hydrophobic assistance, although this conflicts with the fact that efficiency of efflux pumps is often correlated with the hydrophobicity of their substrates [101].

3D QSAR methods like Comparative Molecular Field Analysis (CoMFA) [102] generate 3D field maps around aligned molecules to display zones of steric, electronic and lipophilic tolerance or intolerance. This gives a visual understanding of biological activity that contrasts well with the often messy collection of molecular descriptors in classical QSAR studies, thereby allowing easier interpretation of results. This, in turn, may lead to a better basis for designing novel scaffolds and/or chemical substituents to the existing scaffold. The basic idea behind this method is explained in Figure 2. Kellogg et al. introduced a method for hydrophobic field calculation for CoMFA [103] using an empirical force field (Hydropathic INTeractions or HINT, discussed in detail below). This was one of the first attempts in 3D QSAR to modify the purely enthalpic treatment of ligand-receptor binding by inclusion of an implicit entropic term. References to the use of HINT-CoMFA in drug design are available [103-106]. Another attempt to include hydrophobicity into CoMFA was made by Gaillard, Testa and coworkers in their papers [107,108] describing the use Molecular Lipophilicity Potential (MLP) in 3D QSAR along with its applications. This alternative method of using hydrophobicity in CoMFA studies has found a number of applications in molecular modeling and drug design work [109-111].

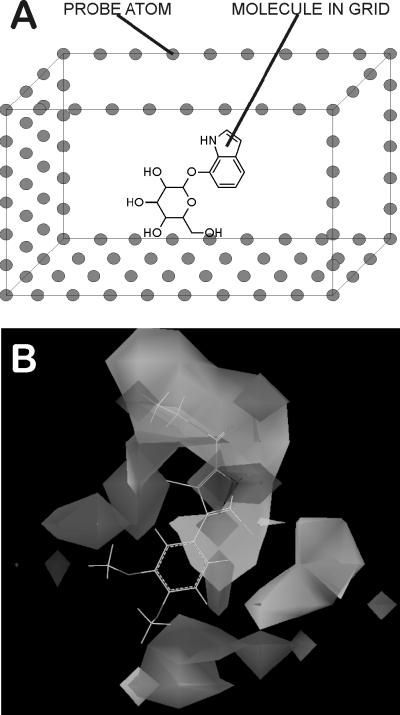
Figure 2. 3D QSAR.

3-Dimensional Quantitative Structure Activity Relationships (3D QSAR) are models generated by taking into account the 3-dimensional positions of various physicochemical characteristics of a set of overlapped molecules and the effect they have on drug potency [94,99]. A) Molecules are overlapped and placed in a superimposed grid with extents of several Angstroms in all directions. Each grid point is treated as a probe; neutral carbon atoms probe for Van der Waal's interactions, while charged atoms probe Coulombic interactions. Fragments can also be used as probes for elucidating H-bond donors or acceptors. Simple physics equations calculate the energy (data value) at each grid point. These data are examined for trends using PLS, MLR or AI algorithms fit to the biological properties of the molecules. B) The resultant map indicates regions where certain physicochemical parameters, e.g., charge or steric bulk, are tolerated (or not tolerated), which serves as an aid to chemists designing analogs with improved properties.

QUANTIFICATION OF HYDROPHOBIC INTERACTIONS

Equations calculating energy from structure, a.k.a. force fields, have been in use for many years in computational chemistry and molecular modeling [112]. Generally, force fields have been restricted to enthalpic terms that are simple to correlate with bond formation or bond breaking and simple Newtonian physical phenomena like bond stretches and bends, electrostatics and dispersion. The hydrophobic effect is, in some measure, an entropic phenomenon, and is not easily derivable from these first principles. Nevertheless, a few examples of quantifying lipophilicity and its effect on biomolecular energetics have been reported [12,113-119]. Hermann and Chothia [12,113], among others, proposed that hydrophobicity can be quantified by the calculation of hydrophobic surface area. Oobatake and Ooi present an excellent review of this approach [114]. Cramer and Truhlar introduced a solvation model [115] that included charge distributions on solute molecules, the energetic effects of cavity formation and restructuring of water around such cavities, and even subtle variations in charge distribution due to interactions between solute particles and surrounding solvent molecules. Sharp and coworkers introduced a new solvation model illustrating the dependence of the hydrophobic effect on curvature of the site [116]. This was an attempt to explain the difference between the calculated energy for hydration of hydrocarbons (about 25 cal mol⁻¹ Å⁻²) and the surface tension at the water-hydrocarbon interface (about 75 cal mol⁻¹ Å⁻²). This altered surface area measurement suggested that the “macroscopic” hydration energy is 47 cal mol⁻¹ Å⁻². Indeed, the assumption that the energy of hydrophobic interactions is dependent on the area of the hydrophobic-water interface is the mainstay of much research in the area. However, alternative approaches have had some success. Cesari et al. presented a model describing the hydrophobic interactions within globular proteins based on analysis of X-ray data [117] where fold definitions were clearly shown to be a function of hydrophobicity. Hummer described the development of a hydrophobic force field as an alternative to surface-area models [118]. The best developed model for quantitating hydrophobic interactions has been the HINT (Hydropathic INTeractions) system that is discussed below.

The HINT paradigm

A notably different approach was taken by Kellogg and Abraham [119,120] in designing the “natural” force field HINT (see Appendix 5). This non-covalent interaction force field is derived from partition coefficients based on the Hansch and Leo LogP estimation method. It is very empirical in nature and approximates all components of biomolecular interactions, including hydrogen bonding, Coulombic interactions along with entropy and solvation/desolvation effects in addition to hydrophobic interactions because all of these effects are inherent in the experiments that measure LogP [68]. Interestingly, the Hansch and Leo method encodes many interaction effects within the “correction” factors. For example, intramolecular hydrogen bonding within a small molecule, which would make the molecule less polar (and seemingly more hydrophobic) because the involved polar hydrogen and its partner acceptor are less able to interact with water solvent, is encoded with a factor that gives an internally calibrated indication of the energetics of hydrogen bonding (0.6 – 1.0 LogP units, i.e., 0.8 – 1.4 kcal mol⁻¹).

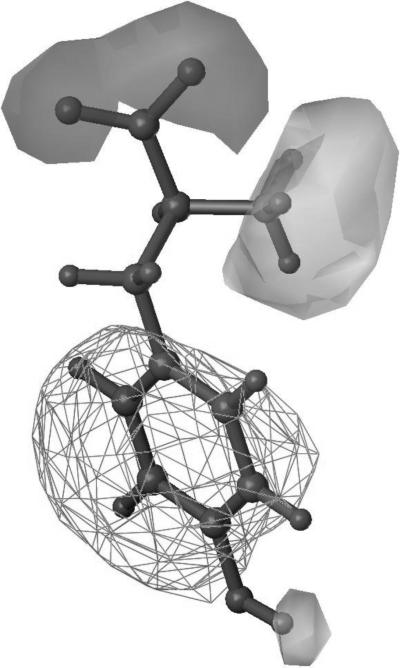
A key principle behind HINT is that significant understanding of biological phenomena, particularly interactions, can be revealed by representing hydrophobicity as a 3D “field” property rather than as a simple scalar (number) [121]. For example, consider the Tyrosine molecule shown in figure 3. Hydropathic properties of the molecule are mapped in three dimensions around the structure of Tyrosine, creating a HINT map. The use of these maps creates a visual representation of properties that are often mentioned casually, such as hydrophobic or polar nature of functional groups. Not only does this methodology allow a chemist to form a qualitative understanding of the molecular topology, but also forms the basis for quantitative estimation of physicochemical properties by using the HINT force field. This may further be used in the depiction of molecular interactions, which has a direct repercussion in drug design.

Figure 3. HINT map for the molecule of Tyrosine.

This map shows a hydrophobic area on the molecule represented as a cage around the benzene ring. The polar areas on the map are further depicted: acidic (light grey lobes) and basic (dark grey lobe).

Intermolecular Interaction Analysis

Perhaps the most important application of HINT is in the assessment of intermolecular interactions. HINT calculations derive an interaction score that in numerous studies [122-125] has been shown to correlate with free energy of interaction. Although it is data set dependent, i.e., for specific protein-ligand or polynucleotide-ligand systems, it is estimated that, on average, 515 HINT score units correspond to 1 kcal mol⁻¹ free energy of binding [119]. A recent report indicated the value of the HINT score in ligand docking studies by a comparison to the scoring functions within FlexX, AutoDock and GOLD [123]. The most important advantage of the HINT methodology is that it inherently estimates enthalpic as well as entropic contributions to binding (Appendix 5). It has been shown [122,126] that errors in prediction for very diverse sets of protein-ligand complexes are approximately ± 2.6 kcal mol⁻¹, although within a family of ligands binding to the same protein this error can approach ± 1 kcal mol⁻¹. There often is an order of magnitude difference between values of K_i measured by different laboratories on the same protein-ligand complex, which corresponds to a possible 1.0-1.5 kcal mol⁻¹ experimental uncertainty. Thus, the error value reported above between experimental results and HINT scores indicates that HINT is a robust method for binding affinity predictions. Further sources of error include uncertainties in positions of atoms in models, incorrectly assigned atom types, or (often) missing solvent molecules in the source crystallographic structure data. The HINT method has been used successfully in quite a number of projects [122,126-129]. In a recent example, Tripathi et al. generated a model capable of predicting antiproliferative activity of pyrrole derivatives against cancer cell lines. In this study, experimentally determined IC₅₀s of a number of compounds were correlated with HINT scores from docking these ligands to αβ-tubulin to generate molecular models that could be scored, and yielded a significant correlation. This correlation could distinguish active molecules from inactive ones by the HINT score value and, thus, provides a basis for design of novel molecules with anticancer activity. In another interesting application the sequence specificity of anthracycline groove-binding intercalators was evaluated and predicted by HINT score [130]. This work illustrated that the HINT score could be parsed into relevant free energy subsets that can be ranked and compared for particular intercalator functional groups and/or nucleotide bases in DNA double helix strands.

Computational Titration

An extension of the HINT force field known as Computational Titration [124] is used to evaluate the ionization states of functional groups on ligands or residues at the binding site. It is well known that these variations can have a strong influence on binding affinities. The method models, in parallel, multiple ionization states for both ligand and protein creating a collection of ionization state ensembles. Each distinct protonation state ensemble is optimized for hydrogen bonding, including water positions, and analyzed by HINT score. The best scoring complex indicates the optimum state for binding and suggests the corresponding pH for that optimum binding. However, the pH at which crystals are grown and analyzed can be different from this optimum pH. The resulting model can help reconcile the differences between in silico models and data. However, at room temperature, where binding data is measured, there are likely to be many protonation models of similar, accessible energy. Computational Titration analysis helps develop an understanding of the relationship between these states. There is now a computational titration server for public use at http://hinttools.isbdd.vcu.edu/CT [131].

Analysis of Bridging Waters

Another factor relating to the stability of biomolecular complexes is the contribution of water molecules within the binding site and bridging between the ligand and biomolecule [125,132]. The presence of these bridging water molecules can be a very important factor in binding of molecules, but water molecules can play a variety of roles as they facilitate biomolecular interactions and stabilize structure. Often, due to a variety of experimental reasons, positions of water molecules in crystal structures are not well defined, even after x-ray crystallographic analysis. This mischaracterization and non-detection of water positions can be correlated with x-ray crystallographic resolution, with better resolution both locating a larger number of water molecules and placing their positions more accurately. Thus, to thoroughly evaluate structure, it is often necessary to verify water molecules systematically with tools such as the GRID program of Goodford [133]. Concomitantly, it is desirable to know which of these waters are subject to displacement by ligands and which are conserved. Using HINT score combined with a metric based on geometry, Amadasi et al. developed a robust method to calculate the relevance of binding site waters; those with particularly high relevance score would be expected to yield extra entropy if a ligand was designed to displace it, i.e., similar to the cyclic HIV-1 protease inhibitors [134]. In another study, the contribution of bridging water molecules to overall free energy of binding has been derived and quantitated [132].

3D QSAR with HINT

A very early application of the HINT force field was the introduction of field hydrophobicity parameters into 3D QSAR technology, to complement the original steric and electronic fields in CoMFA [103]. The steroid data set originally reported by Cramer et al. [102] was reexamined with the addition of a HINT-derived field. While this study provided little advantage in terms of statistical improvement due to a variety of reasons described previously [119], it provided a distinct advantage in chemical interpretability for chemists aiming to design new molecules based on such a QSAR study. Quite a few reports of studies based on the HINT-CoMFA methodology have been reported since then [104-106,135-140] and some, particularly where the ligands or active sites are particularly non-polar, do show significant statistical improvement when hydrophobic fields are included. Fields in 3D QSAR are another class of descriptor that often needs to be optimized for the data set [141] in that each data set has forces and structures that may be best represented hydrophobically, sterically, electrostatically, or with other types of fields.

CONCLUSIONS AND FUTURE DIRECTIONS

Hydrophobicity impacts every aspect of drug design and even delivery, as has been repeatedly pointed out over the past century. Studies of this phenomenon have resulted in multiple theories, algorithms and tools for applying the concept. A large amount of effort has been put forth into studying the partition coefficient both experimentally, especially in terms of its prediction because of its importance in “druggability” of compounds. Many theoretical methods are robust in estimating LogP for molecules similar to their training set, but large errors are fairly common for compounds with large chemical and structural differences from that set.

Since Hansch and Fujita introduced the QSAR method, drug design projects have repeatedly found use for hydrophobic parameters. This dependence of drug design on lipophilicity is intuitive arising from drugs and proteins coming together, or proteins folding, in order to reduce the surface area in contact with polar water molecules. Quantification of this phenomenon has taken many forms, such as calculating of hydrophobic surface contact area to represent hydrophobic interactions, supplementing 3D QSAR with hydrophobic fields (HINT and MLP) [103,107-109], and with direct quantification of intermolecular interactions with HINT [123,126-129]. While there are numerous force fields available, most are Newtonian in origin and concentrate on H-bonding, Coulombic interactions, van der Waal's interactions and London forces for estimating the strength of molecular interactions, all of which are mostly if not entirely enthalpic. HINT is different in that it accounts for both hydrophobic and hydrophilic interactions, and is derived from a free energy experiment. The availability of the HINT toolkit [142,143] makes it possible to develop application programs for computer-aided drug discovery and design.

The complex phenomena of hydrophobicity and hydrophobic interactions are still only poorly understood and remain quite difficult to simulate. Considerable resources and effort will continue towards development of accurate experimental and theoretical methods to determine/predict the partition coefficient. However, understanding and exploiting the hydrophobic effect in drug design, e.g., docking, target structure prediction, etc., will undoubtedly be increasingly important in the future. It is generally accepted that proteins fold in such a way that hydrophobic groups are largely shielded from water by hydrophilic groups. While evaluating the factors that affect prediction of protein folds, Park et al. noted that hydrophobicity of residues is the largest force defining protein structure, but that other factors were involved as well [144]. Accurate hydrophobicity measurements and estimation of hydrophobic interactions could have a tremendous impact on the modeling of protein folding and side chain orientation. Better modeling and representation of hydrophobic interactions will also contribute to the understanding of biological processes implicating hydrophobicity such as drug resistance caused by efflux. There is no doubt in our mind as to the applications of this phenomenon in computational life sciences and computer-aided drug design. Hydrophobicity may not be the “Holy Grail” of biomolecular phenomena, but it is definitely the one of the “Commandments”.

Appendix 1. Fragmental methods for determination of LogP values.

Rekker's method is highlighted with an example adapted from Mannhold and van de Waterbeemd [18].

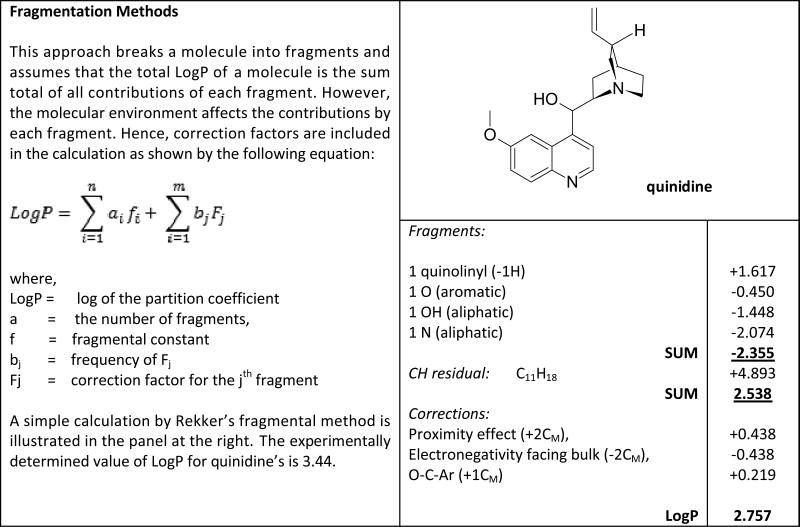Appendix 2. Atom contribution methods.

the calculation of LogP for quinidine by atom contributions is shown (adapted from Mannhold and van de Waterbeemd [18]).

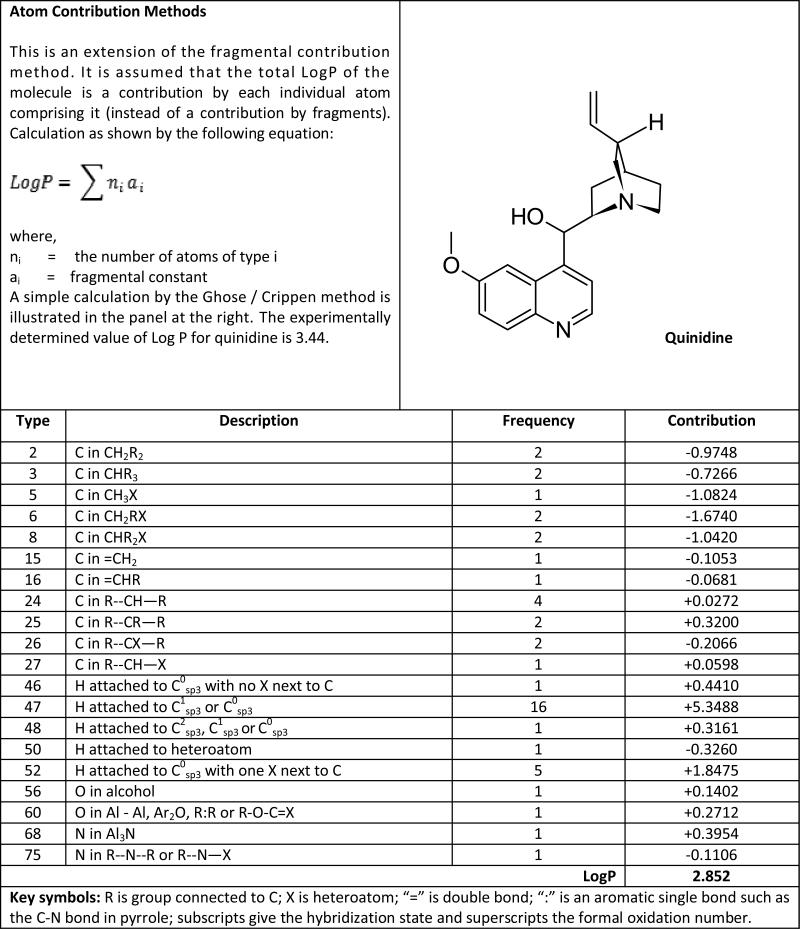Appendix 3. A parabolic relationship exists between drug potency and hydrophobicity.

An equation relating probability and partition coefficient was derived by McFarland [79].

Appendix 4. Hansch Analysis.

a method to relate physicochemical parameters to drug potency. For details, refer to Hansch and Fujita [95].

Appendix 5. The HINT Paradigm.

A “natural” free energy force field based on LogP. It is available as a toolkit, allowing flexibility in development of applications. Refer to Kellogg and Abraham [118] for details.