Out-of-equilibrium conformational cycling of GroEL under saturating ATP concentrations

Abstract

The molecular chaperone GroEL exists in at least two allosteric states, T and R, that interconvert in an ATP-controlled manner. Thermodynamic analysis suggests that the T-state population becomes negligible with increasing ATP concentrations, in conflict with the requirement for conformational cycling, which is essential for the operation of molecular machines. To solve this conundrum, we performed fluorescence correlation spectroscopy on the single-ring version of GroEL, using a fluorescent switch recently built into its structure, which turns “on,” i.e., increases its fluorescence dramatically, when ATP is added. A series of correlation functions was measured as a function of ATP concentration and analyzed using singular-value decomposition. The analysis assigned the signal to two states whose dynamics clearly differ. Surprisingly, even at ATP saturation, ∼50% of the molecules still populate the T state at any instance of time, indicating constant out-of-equilibrium cycling between T and R. Only upon addition of the cochaperonin GroES does the T-state population vanish. Our results suggest a model in which the T/R ratio is controlled by the rate of ADP release after hydrolysis, which can be determined accordingly.

ATP-driven protein machines are abundant and contribute to multiple essential biological processes (1). Such protein machines undergo motor-like rotational motion (like F₁-ATPase), carry cargos (like kinesin), or fold proteins (like GroEL, the subject of this paper). An important feature of all ATP-driven molecular machines is a functional cycle that involves sequential transitions between several conformational states (2). Understanding the dynamics of conformational cycling is, therefore, essential for the full elucidation of the mechanism of action of a protein machine.

The Escherichia coli molecular chaperone GroEL is a machine that assists protein folding by undergoing a series of allosteric transitions that facilitate protein substrate binding and release (3, 4). GroEL is made up of two homoheptameric rings, stacked back-to-back, with a cavity at each end (5), in which protein folding can take place. The allosteric transitions of GroEL are induced by ATP binding that occurs with positive cooperativity within rings and negative cooperativity between rings (6). It has been suggested that the intraring positive cooperativity is an outcome of a concerted switch between two conformations, T and R, with low and high affinities for ATP, respectively. GroEL functions in conjunction with a heptameric ring-shaped cochaperonin, GroES. Binding of GroES to the so-called cis ring induces an additional conformational change that leads to the R’ conformation and triggers dissociation of bound protein substrate into the cavity (7). The structures of the three relatively stable conformations, T, R, and R’, have been determined using x-ray crystallography and electron microscopy (8, 9). It is not known whether additional intermediate conformations are populated as the protein interconverts between these states. In particular, it is not clear whether the ADP-bound state is in a T-like conformation, R-like conformation, or an additional, distinct conformation (for a review see ref. 10).

Common wisdom, backed by standard thermodynamic models of allostery (11) as well as by a recent determination of ATP affinities for the T and R states (12), maintains that saturating ATP concentrations should fully shift the equilibrium of GroEL molecules to the R conformation (or the R’ conformation in the presence of GroES). However, because a protein substrate can only bind to the T form, this picture suggests that ATP saturation will stall the folding activity of the chaperonin. A different way to phrase this is that ATP puts GroEL under “allosteric pressure,” forcing it to convert to the R state and, thus, potentially preventing it from fulfilling its role as a molecular chaperone. This is a general problem for ATP-driven protein machines—saturating concentrations of the nucleotide push them into one conformation, and a resetting mechanism is required. In the case of the F₁-ATPase, this problem is solved by timing the rotation through sequential hydrolysis of ATP and release of ADP and P_i from three separate sites (13). In kinesin, ADP release is again the trigger that resets the kinetic cycle, causing it to be ultraslow in the absence of microtubules and much faster when microtubules are available (14). The slow release of ADP from the trans ring of GroEL (i.e., the ring without bound GroES) is known from kinetic studies to time the cycle of the chaperone by effectively modulating the interaction between the two rings (15, 16). Such slow ADP dissociation has the effects that (i) folding in the cis cavity can continue for a longer period of time and that (ii) the trans ring has ample time to bind a protein substrate and, thus, initiate a new reaction cycle. However, the impact of slow ADP dissociation on the relative populations of T and R states has not been determined.

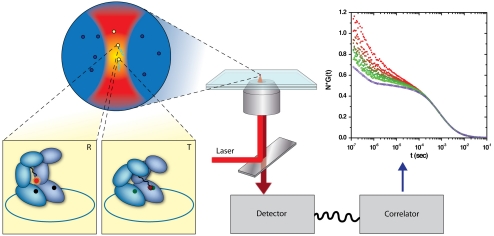
In this paper, we present direct evidence for conformational cycling between the T and R states, which continues even at high ATP concentrations. We arrive at this observation from the analysis of fluorescence correlation spectroscopy (FCS) (17) curves of a single-ring version of GroEL termed SR1 (18), using a fluorescent switch that we have recently built into the structure of the molecule (Fig. 1) (19). Steady-state (20) and transient kinetic analysis (21, 22) have shown that intraring allostery in SR1 is similar to that of the double-ring GroEL. Our fluorescent switch is “off” (i.e., weakly fluorescent) in the T state and “on” (highly fluorescent) in the R (or R’) state. Singular-value decomposition (SVD) of ATP-dependent FCS curves shows that they can all be described as linear combinations of the same two states. Unexpectedly, even at ATP saturation, only ∼50% of the molecules are in the R-like state, pointing to steady-state (out-of-equilibrium) cycling between the two states. This observation allows us to estimate the rate of release of ADP, which is found to be similar to the rate of ATP hydrolysis.

Fig. 1.

FCS measurements of a fluorescent switch built into the structure of SR1 molecules. SR1 molecules diffuse in and out of a focused laser beam. In the T conformation, the fluorescent dye (Atto655), which labels a cysteine at position 327, is close enough to a tryptophan residue at position 44 (W44) to form a ground-state complex that quenches it. In the R conformation, the dye is too far from the tryptophan for quenching to occur, and it fluoresces more strongly. Fluorescence is collected by a microscope, and registered by a single-photon detector. Correlation functions of the fluorescence are generated by a hardware correlator.

Results and Discussion

FCS Experiments on SR1.

FCS measures the fluctuations of the fluorescent signal of molecules diffusing through a focused laser beam (23). The method, therefore, facilitates sampling molecular dynamics on a time scale faster than diffusion. In the case of SR1, the diffusion time is ∼1 millisecond. Since the time scale for interconversion between conformational states of SR1 is expected to be longer than a millisecond (21), FCS curves should be linear combinations of contributions of the individual states of the molecule. Therefore, FCS should allow us to enumerate the number of states at each ATP concentration and obtain their relative populations. This was achieved as described below through SVD analysis.

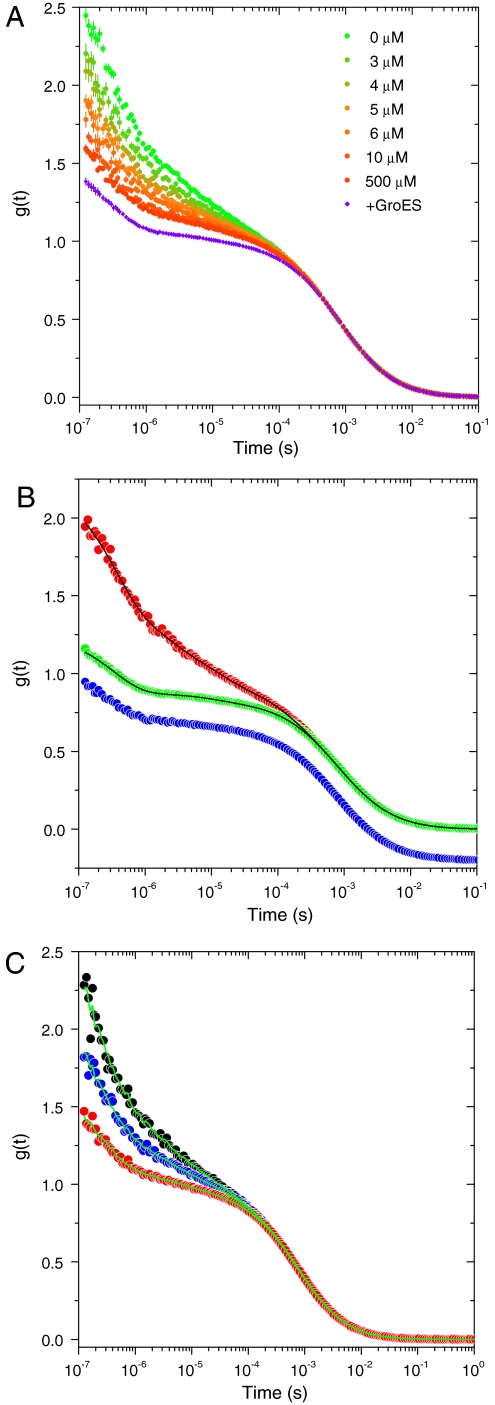
We previously generated SR1 molecules with the replacements F44W and K327C (SR1WC), and labeled Cys327 with the fluorescent dye Atto655 (19). In the absence of ATP, the dye is quenched by the tryptophan at position 44. Quenching is alleviated when ATP is added, due to the ATP-induced conformational change, whereas addition of ADP has no effect. We performed FCS experiments on SR1WC at varying concentrations of ATP (Fig. 2A). Clearly, while the long-time part of the curves, which is due to diffusion of protein molecules in solution, does not depend on ATP, the curves demonstrate a major change in their short-time part as ATP is added. To understand the origin of this change, we collected FCS curves of a labeled tryptophanless version of the protein (SR1C). We found that these curves are essentially the same under all ATP concentrations and very much resemble the FCS curve of SR1WC taken in the presence of 500 μM ATP and 250 nM GroES (Fig. 2B), a combination that is known to lock SR1 in the R’ conformation (18). We therefore conclude that the curves shown in Fig. 2A reflect a gradual conversion of the population of GroEL molecules from the T to the R conformation.

Fig. 2.

FCS measurements of SR1 molecules and their reconstruction by SVD analysis. (A) A series of FCS curves of SR1WC measured at increasing concentrations of ATP (as indicated in the panel), and normalized by their diffusion part (SI Discussion). The Violet curve was measured in the presence of 500 μM ATP and 250 nM GroES. (B) FCS curve of SR1WC in the absence of ATP (Red) compared to FCS curves of SR1WC in the presence of 500 μM ATP and 250 nM GroES (Green) and of SR1C in the absence of ATP (Blue, shifted downward for clarity). The latter curves are very similar, as they both reflect the absence of quenching by W44. The Black Lines on two of the curves are from their global nonlinear fit, as described in the text. (C) Reconstruction (Green Lines) of three FCS curves measured at different ATP concentrations (Black, 0 μM ATP; Blue, 4 μM ATP; and Red, 500 μM ATP) using the first two singular vectors obtained from the SVD analysis.

Singular-Value Decomposition of FCS Curves.

SVD enables the representation of complex datasets as a linear combination of the smallest required number of “singular vectors” (24). The analysis also provides the weights of these vectors in terms of “singular values.” We performed SVD on the dataset of ATP-dependent FCS curves, including the curve of the protein in the R’ state. It was found that the first two singular values are almost 10 times larger than the remaining singular values, which implies that the whole dataset can be spanned by the first two singular vectors. We verified that this is the case by reconstructing each FCS curve using these two vectors. Three of these reconstructions are shown in Fig. 2C. Because a successful reconstruction of all FCS curves was achieved in this manner, it is clear that they can indeed all be represented as a linear combination of two basis curves. It can, therefore, be concluded that the conformational space of SR1 molecules comprises only two states with respect to our observable. This leads, of course, to the classical view of the chaperone ring populating either of two stable states, T and R, without intermediates. The SVD analysis thus affirms that intermediate states between T and R either do not exist or are not probed by the fluorescent switch.

In principle, it is possible to choose any two vectors that are linear combinations of the singular vectors and then represent the dataset in terms of these. It is natural to select two vectors that correspond to two stable states of GroEL, namely T and R. Clearly, the FCS curve measured without ATP can stand for the T state, but it is not obvious which curve corresponds to the R state. Because the whole dataset, including the FCS curve taken in the presence of GroES, is spanned by the same two vectors, it is obvious that our measurements do not distinguish between the R and R’ states. We can, therefore, use the FCS curve taken in the presence of saturating ATP concentrations and GroES, in which SR1 is locked in the R’ state, to represent also the R state.

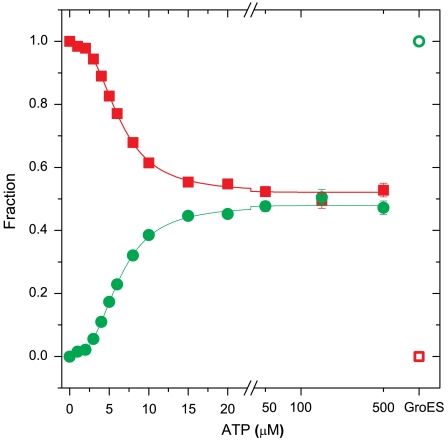
It is simple to calculate the weights of the linear combination of T and R’ curves that reproduce each FCS curve in the set from the respective weights of the singular vectors. The weights of the components in a linear combination of correlation functions are functions of the population fractions of the species involved and the ratio of their quantum efficiencies (SI Discussion). Given a known ratio of quantum efficiencies, the calculation leads to two sets of ATP-dependent population fractions, one for the T state and one for the R state. From our previous work (19) it can be estimated that the ratio of the quantum efficiencies of the R and T states is between 2 and 3. In Fig. 3, we show the population fractions calculated using a quantum efficiencies ratio of 2.5. By definition, at 0 M ATP the whole population is in the T state (the fraction of the T state is 1 and the fraction of the R state is 0) whereas in the presence of saturating ATP concentrations and GroES, the whole population is in the R (R’) state (the fraction of the T state is 0 and the fraction of the R state is 1). In between these two extremes, the fraction of the T state decreases while the fraction of the R state increases. Surprisingly, at ATP saturation (and in the absence of GroES) the fraction of the T state does not reach 0, and the fraction of the R state does not reach 1. The functional dependence of the two fractions on ATP concentration suggests a cooperative process. Indeed, it was possible to fit the two sets of fractions to a Hill-type function with a Hill coefficient of 2.7 ± 0.1, which is similar to values obtained by other very different methods (14–16). Most importantly, even at the highest concentration of ATP the fraction of molecules in the T state is not 0 but 0.53 ± 0.02. Thus, under these conditions, only about half of the molecules populate the R state, while the other half reside in the T state. This result, which is the key finding of our study, implies constant cycling between the T and R states at all ATP concentrations. It solves the conundrum posed in the introduction regarding the ability of the GroEL machine to function at ATP saturation. The above conclusion does not depend on the exact value of the quantum efficiencies ratio: The calculated R-state population at ATP saturation varies from 60% to 40% when the quantum efficiencies ratio is varied from 2 and 3.

Fig. 3.

The fractions of the T and R states (in Red Squares and Green Circles, respectively), as obtained from SVD analysis of curves measured at varying ATP concentrations, using a quantum efficiencies ratio of 2.5. At ATP saturation, the fraction of the R state is not more than 50%. The empty symbols designate the fractions in the presence of GroES. The full lines are the results of a fit to a Hill-like function with a Hill coefficient of 2.7 ± 0.1.

Nonlinear Fit of FCS Curves.

To obtain further insight about the dynamic processes responsible for the differences between the FCS curves, we undertook a global nonlinear least-squares analysis of the SR1WC curves measured in the absence of ATP and in the presence of 500 μM ATP and 250 nM GroES. This analysis and its results are described more fully in SI Discussion, and the fitted curves are shown in Fig. 2B. Briefly, in the absence of ATP, four exponential functions are required to fit the short-time part of the FCS curve. On the other hand, the FCS curve of SR1WC taken in the presence of saturating ATP concentrations and GroES requires only two of these exponentials to fit its short-time part, thus indicating a significant change in internal dynamics. Two dynamic processes active in the T conformation, having time constants of 2.4 ± 0.6 μs and 130 ± 20 μs, seem to disappear upon transition to R. The faster process might be due to local motion of the fluorescent dye with respect to the tryptophan side chain that quenches it, but the slower process is likely to be due to internal dynamics of the protein. It will be interesting to investigate in future work whether this dynamic process is related to motions that promote the allosteric transition.

A Model for Conformational Cycling Under Allosteric Pressure.

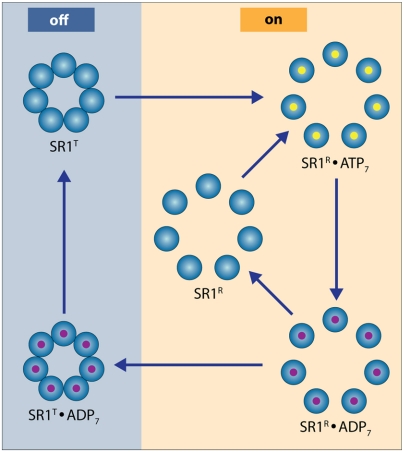
Our findings can be rationalized through the following model. Consider the cycle shown in Fig. 4. The binding of ATP transforms SR1 from a T-like to an R-like conformation. In the absence of GroES, the hydrolysis of ATP leads to an ADP-bound form of SR1. If the release time of ADP following hydrolysis is very short (compared to the ATP hydrolysis time, as well as to the time for conversion back from R to T), then the ring will rebind ATP before it converts back to a T-like form. This will prevent cycling between the T and R states. However, if ADP release is relatively slow and the R-to-T conversion time is relatively fast, the ADP-bound form of the ring has enough time to revert to a T-like form, and ADP release then completes the cycle. However, in order for the cycle to be functional, the chaperone should remain in the T-state enough time for rebinding a protein substrate. This can be achieved by modulating the ADP release time. By including the ADP release step in a standard kinetic model for the allosteric transitions of SR1 (SI Discussion), it can be shown that the fraction of molecules in the R state at saturating ATP concentrations is given by:

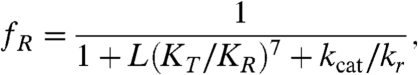[1]

where L is the T to R equilibrium constant in the absence of ATP, K_T and K_R are the binding constants of ATP to the T and R states, respectively, and k_cat and k_r are the rates of formation of ADP from ATP and of its release from GroEL, respectively. Because L(K_T/K_R)⁷ is much smaller than 1 (see ref. 12), the fraction of molecules in the R state at ATP saturation is determined by the ratio of k_cat to k_r. If the dissociation of ADP is much faster than ATP hydrolysis by the protein (k_r≫k_cat), then f_R approaches 1, and cycling is effectively prevented as discussed above. However, if the release time of ADP is long, becoming comparable to the hydrolysis time, then the fraction of molecules in the R state is smaller than 1. Thus, it is possible to tune f_R by modulating the dwell time of ADP on the protein. Even more tunability can be obtained when the reaction involves the release of two products (such as ADP and P_i) upon ATP hydrolysis (although, in the case of GroEL, P_i release is fast (25), and therefore only ADP release is rate limiting). In this case, as shown in SI Discussion, the fraction of the R state may depend on the values of two rates of release. Based on Eq. 1 and the f_R value of ∼0.5 obtained from our measurements, we find that k_r is ∼k_cat. The value of k_cat of SR1 molecules measured in our lab is ∼0.05 sec^-1, and it is therefore also our estimate for k_r. A slightly larger value is estimated from the data of Inobe et al. (20), who measured k_cat ∼ 0.09 sec^-1. Slow release of ADP has been inferred in the past based on bulk kinetic experiments (12, 26).

Fig. 4.

The SR1 cycle. The blue-colored side of the cycle depicts the molecule in a T-like state, while the orange-colored side of the cycle represents the molecule in an R-like state. If ADP release is very fast, then ATP binds before the chaperone reconverts from R to T. This may preclude the binding of substrates, which is preferentially done by the T state. Slower release of ADP alleviates this problem. Indeed, we find that even at ATP saturation ∼50% of the molecules are in the T state.

In summary, our measurements allow us to estimate the fraction of molecules in each of the two allosteric states of GroEL; we find that even under saturating ATP concentrations only ∼50% of the molecules are in the R state. We suggest that ADP release is used to kinetically tune conformational cycling, so as to prevent stalling in the R state and allow ample time for substrate binding in the T state even at high ATP concentrations. This result indicates that GroEL employs the same universal strategy for conformational resetting used by many other protein machines. More generally, our results also indicate that some reformulation of the classical models of allostery (10) is needed (SI Discussion) in order to apply them for analyzing nucleotide-dependent molecular machines operating out of equilibrium.

Methods

Protein Purification and Labeling.

The preparation, purification and labeling of the SR1C and SR1WC mutants were achieved as described (19), and full details are given in SI Methods. Briefly, E. coli BL21 cells bearing a plasmid containing the gene for SR1 modified with His₅-tag at the C terminus and the desired mutations (i.e., F44W or F44W/K327C) were grown in 500 ml of 2 × TY medium containing 100 μg/ml ampicillin. Protein expression was induced by addition of isopropyl-β-D-thiogalactopyranoside. Six hours after the induction, cells were collected by centrifugation and disrupted by sonication. The clear lysate obtained after centrifugation was loaded on a Ni-chelating agarose column and eluted with imidazole. The eluted protein was concentrated using a centrifugal concentration device and transferred into 50 mM Tris⋅HCl buffer (pH 7.5) containing 10 mM KCl and 10 mM MgCl₂.

Protein modification with Atto 655 maleimide was carried out for 2 h at room temperature, in the dark. The unreacted fluorophore was removed by a desalting column and repeated concentration and dilution within a centrifugal concentration device. The labeled protein was snap-frozen and stored at -80 °C.

Fluorescence Correlation Spectroscopy.

A homemade confocal microscopy setup was used for FCS measurements, and is fully described in SI Methods. Briefly, excitation light emitted from a 641 nm diode laser was focused by a water-immersion objective into a flow cell loaded with the sample (preparation of flow cells is described in SI Methods). Emission was collected by the same objective and transmitted through a dichroic mirror and a set of emission filters. The fluorescent signal was passed through a pinhole and split equally between two avalanche photodiodes using a nonpolarizing beam splitter. The signals from the two detectors were cross-correlated using a hardware digital correlator.

All FCS measurements were conducted at 25 °C. At least 30 curves of 60 sec were collected and averaged for each ATP concentration and this procedure was repeated four times. Errors were estimated by comparing results from separate analyses of the four datasets. A small number of curves in each dataset was found to be aberrant and filtered out before averaging.