Multi-muscle synergies in a dual postural task: evidence for the principle of superposition

Abstract

We used the framework of the uncontrolled manifold hypothesis to quantify multi-muscle synergies stabilizing the moment of force about the frontal axis (M_Y) and the shear force in the anterior–posterior direction (F_X) during voluntary body sway performed by standing subjects. We tested a hypothesis whether the controller could stabilize both M_Y and F_X at the same time when the task and the visual feedback was provided only on one of the variables (M_Y). Healthy young subjects performed voluntary body sway in the anterior–posterior direction while different loads were attached at the ankle level producing horizontal forces acting forward or backwards. Principal component analysis was used to identify three M-modes within the space of integrated indices of muscle activation. Variance in the M-mode space across sway cycles was partitioned into two components, one that did not affect a selected performance variable (M_Y or F_X) and the other that did. Under all loading conditions and for each performance variable, a higher value for the former variance component was found. We interpret these results as reflections of two multi-M-mode synergies stabilizing both F_X and M_Y. The indices of synergies were modulated within the sway cycle; both performance variables were better stabilized when the body moved forward than when it moved backward. The results show that the controller can use a set of three elemental variables (M-modes) to stabilize two performance variables at the same time. No negative interference was seen between the synergy indices computed for the two performance variables supporting the principle of superposition with respect to multi-muscle postural control.

Introduction

A central problem in human motor control is the degrees-of-freedom (DOF) problem, also called the problem of motor redundancy (Bernstein 1935, 1967). This problem refers to the fact that at any level of analysis, the system for movement production has fewer constraints than it has elements. As a result, typically, an infinite number of solutions exist for any motor task. A typical problem of motor redundancy is: How are particular muscle activations selected from an infinite set able to solve the problem? A key approach to this problem is the idea of synergies. Bernstein suggested that the controller united muscles into groups (synergies) to decrease the number of variables to manipulate.

Recently, this idea has received support in a series of studies of muscle coordination during postural and locomotion tasks (Saltiel et al. 2001; Krishnamoorthy et al. 2003a, b, 2004; d’Avella et al. 2003; Ivanenko et al. 2005, 2006; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2007). These studies used matrix factorization techniques to define sets of muscle groups within which the muscles showed parallel scaling of their activation levels. Such groups have been addressed as “muscle synergies” or “muscle modes”. Note, however, that a smaller set of such muscle groups may still be redundant with respect to typical tasks (Krishnamoorthy et al. 2003a, b; Robert et al. 2008). This has led to a hypothesis that the control system is hierarchical and redundant at both levels of the hierarchy (reviewed in Latash et al. 2007; Latash 2008). At the lower level, the muscles are united into groups (to avoid confusion, we will address these as muscle modes or M-modes) that can be identified with the mentioned computational methods. At the upper level, a redundant set of gains at M-modes is manipulated to ensure stability of important performance variables.

This development of the concept of synergies follows traditions set by Gelfand and Tsetlin (1966) and is based on the principle of abundance (Gelfand and Latash 1998). This principle assumes that families of goal-equivalent solutions are facilitated during natural actions. Synergies can be quantitatively studied using the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2002b). In a simplified form, the idea of the UCM-hypothesis is that the neural controller defines a sub-space (a UCM) in the space of elemental variables corresponding to a desired value of a performance variable and then confines variability of the elemental variables to the UCM. Hence, for any given value of a performance variable, the elemental variables may be viewed as forming two subspaces. Variability of the elemental variables within the UCM leaves the selected performance variable unaffected (“good” variability), whereas variability of the elemental variables orthogonal to this subspace does affect the performance variable (“bad” variability). Operationally, when “good” variance is larger than the “bad” one (quantified per DOF of each of the subspaces), the hypothesis that a synergy stabilizes that performance variable is accepted (Scholz and Schöner 1999). An index of synergy (ΔV) has been used in several of the cited studies to quantify synergies (reviewed in Latash et al. 2007); this index reflects the normalized difference between the amounts of “good” and “bad” variance.

A number of studies used the mentioned idea of a two-level hierarchy to explore synergies among M-modes (viewed as elemental variables) stabilizing such performance variables as the coordinate of the center of pressure (COP, the point of application of the resultant force acting on the body from the support surface) and the shear force (Krishnamoorthy et al. 2003b; Danna-dos-Santos et al. 2007; Robert et al. 2008). Most of the mentioned studies explored stabilization of only one variable by a redundant set of M-modes. Note, however, that typical sets consisted of 3–4 M-modes. Such a set is redundant even if the task requires specification of two performance variables. Only one earlier study explored both COP coordinate and shear force stabilization during a rather unusual task of quick shear force pulse production performed by standing persons (Robert et al. 2008). That study reported that M-mode synergies stabilizing both variables could co-exist although they showed a degree of competition. In the current study, we used a much more simple and natural task of cyclic voluntary sway to explore the limits to which the central nervous system (CNS) is able to stabilize both moment of force around the frontal axis and shear force time patterns simultaneously.

Based on the results of the mentioned study by Robert and colleagues (2008), we formulated two hypotheses. Since the task in the current study was more simple and natural than the task in the study of Robert et al. (2008), we hypothesized that subjects would be able to stabilize both moment of force and shear force time patterns simultaneously. Since the moment of force, as measured by a force platform, has a component dependent on the shear force, we used a task within which variations of the moment of force were larger than the expected contributions from variations in the shear force by more than an order of magnitude. We also expected the time profiles of the index of the two synergies to show reciprocal (out-of-phase) patterns. This prediction is based on the mentioned study by Robert et al. (2008) that reported a degree of competition between the synergy indices computed with respect to these two variables. Besides, if a small set of elemental variables (M-modes) shows a high index of co-variation with respect to a common performance variable, M-mode variation is mostly limited to a sub-space compatible with a certain value of this variable. If another performance variable is stabilized at the same time, M-mode variation has also to be mostly aligned with a sub-space compatible with a value of that variable. Only the intersection of the two sub-spaces allows to stabilize both variables at the same time. So, there are fewer solutions available for stabilization of a performance variable if another one is stabilized at the same time.

Several studies have shown a drop in synergy indices with an increase in the rate of change of the salient performance variable, possibly related to the variance in the timing of involvement of elemental variables (Latash et al. 2002a; Goodman et al. 2005; Shim et al. 2005a). During cyclic sway, we expected to see a natural modulation of the rate of both performance variables over the cycle. This leads to our secondary hypothesis that indices of synergies stabilizing the two variables will show modulation within the cycle with lower values corresponding to higher rates of change of the variables.

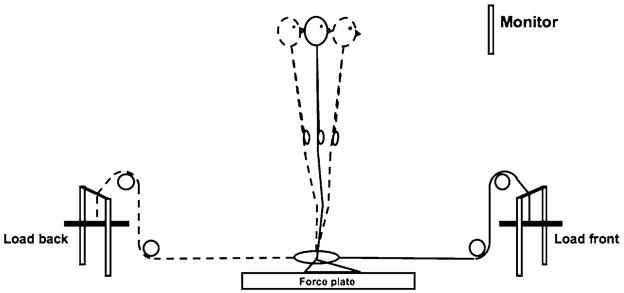
To explore the specific hypotheses, we used a voluntary sway task, which allows to collect many sway cycles within a reasonable time to be able to perform across-cycles analysis of variance. Our earlier experience with such tasks has shown that they allow to identify and quantify muscle modes and multi-M-mode synergies (Danna-dos-Santos et al. 2007, 2008). The task involved visual feedback on one of the main performance variables, namely moment of force about the frontal axis. To explore possible interactions between synergies stabilizing this variable and those stabilizing shear force, we used different loads attached at the level of the ankle joint. The loads created horizontal bias forces that could act forward or backwards. Postural sway at the frequency chosen in our experiment is primarily associated with swaying about the ankle joint. Hence, we selected the site of load attachment to minimize interference between the bias force and the modulation of the moment of force in the ankle joint.

Methods

Subjects

Eleven subjects (7 males and 4 females) with the mean age 28.9 years (±7.5 SD), mean weight 72.0 kg (±11.4 SD) and mean height 1.77 m (±0.076 SD) participated in the experiment. All subjects were healthy, without any known neurological or muscular disorder. All subjects gave their written informed consent based on the procedures approved by the Office for Research Protection of The Pennsylvania State University.

Apparatus

The horizontal component of the reaction force in the anterior–posterior direction (F_X) and the moment of force around the frontal axis (M_y) was recorded using a force platform (AMTI, OR-6). Disposable self-adhesive electrodes (3 M Corporation) were used to record the surface muscle activity (EMG) of the following muscles of the right leg and trunk: gastrocnemius lateralis (GL), gastroc-nemius medialis (GM), tibialis anterior (TA), biceps femoris (BF), semitendinosus (ST), rectus femoris (RF), vastus lateralis (VL), vastus medialis (VM), lumbar erector spinae (ES), and rectus abdominis (RA). The electrodes were placed over the muscle bellies on the right side of the subject’s body. The distance between the two electrodes of each pair was 3 cm. The signals from the electrodes were pre-amplified (×3,000) and band pass filtered (60–500 Hz). All signals were sampled at 1,000 Hz with a 12-bit resolution. A desktop computer (Dell 2.40 GHz) was used to control the experiment and to collect the data using customized Labview-based software (Labview 8.2—National Instruments, Austin, TX, USA).

Procedures

In the initial position, subjects were standing on the force plate with their feet in parallel at hip width (the inside of the feet 15 cm apart). This foot position was marked on the top of the platform and reproduced across trials. Arms were kept straight downwards along the sides of the body.

At the start of the experiment, two control trials were performed that were used in the data processing for normalization of the EMG signals. A detailed description of the procedure is given in Danna-dos-Santos et al. (2007). In summary, subjects were standing quietly and holding a standard load (5 kg) in front of their body with their arms fully extended for 10 s. The subjects held the load by holding the circular panels at each side of a handle bar. The load was either suspended from the middle of the bar producing a downward force, or it was attached through a pulley system such that it produced upward acting force on the bar. Two trials were performed for each subject. The time interval between the two trials was 30 s. In a third control trial, the subject was asked to sway as much forward and backward as possible, to determine the maximum amplitude of swaying without any additional load. The target amplitude of sway for the main task was set at 60% of the maximum amplitude when swaying backwards.

The main task involved continuous voluntary sway in the anterior–posterior direction at 0.5 Hz paced by a metronome. Swaying at this frequency is associated primarily with motion in the ankle joint (see Danna-dos-Santos et al. 2007). Three different loads (1.8, 3.2, and 6.1 kg) were attached at the ankle level via a pulley system such that they produced a horizontal force acting forward or backward (Fig. 1). The loads were attached at the level of the medial and lateral malleoli using a strap that was 0.5 cm thick and 2 cm wide. The average height of the attached load from the force plate surface was 11.4 cm (SD 0.8 cm). Note that attaching the loads at the ankle level causes minimal effects of their force on the moment of force in the ankle joint. There was also a no-load condition. During the trials, continuous visual feedback was provided on the moment of force about the medio-lateral axis (M_Y) by the monitor placed 2.0 m in front of the subject at the eye level. To define zero M_Y level for the feedback, M_Y was determined during quiet stance for each condition by asking the subjects to stand quietly on the force plate for 30 s. Prior to data collection, a period of familiarization with the task was given to each subject. During the familiarization period, subjects performed the sway in the no-load condition for as long as necessary to be able to sway consistently while matching the M_Y amplitude specified on the monitor. The amplitude of the sway was set at 60% of the maximum backward sway amplitude.

Fig. 1.

A schematic representation of the subject and the experimental setup during the main trials. A load was attached at the ankle level; it could be placed at the front or at the back of the subject

Each condition started with a quiet-stance trial. Then, the metronome was turned on, and the subject started swaying. Data collection started after the subject had completed at least two complete sway cycles. Four trials of 30 s each were performed for each condition. Each load direction was performed in a block. The order of the two directions was randomized across subjects. The order of the loads within each direction was randomized. Between conditions, a resting period of 60 s was given. During the change of the load direction, subjects were allowed to sit and relax. The average duration of the experiment was 45 min, and none of the subjects complained of fatigue.

Data processing

All signals were processed off-line using Matlab 7.6 software package. For each condition, on average, 50 sways (±1) were used for analysis. The duration of each cycle was time normalized to 100%. The initiation (t₀) and end (t₁) of each cycle were defined by two consecutives extreme anterior positions of M_y.

The variables F_X and M_Y were filtered with a 20 Hz low-pass, 2th order, zero-lag Butterworth filter. The displacement of M_Y was computed by subtracting the average M_Y coordinate over the trial duration from the average M_Y coordinate computed over each 1% window of the cycle. An identical procedure was carried out for F_X. These procedures resulted in time profiles of deviations of M_Y and F_X from their averages, ΔM_Y(t) and ΔF_X(t).

EMG signals were rectified and filtered with a 50 Hz low-pass, second-order, zero-lag Butterworth filter. The rectified EMG signals were integrated over 1% time windows of the cycles (IEMG). IEMG data were normalized (IEMG_norm) using the method described by Krishnamoorthy et al. (2003a, b); Wang et al. 2005) to compare IEMG indices across muscles and subjects:

$${\text{IEMG}}_{\text{norm}}=\frac{\text{IEMG}-{\text{IEMG}}_{\text{qs}}}{{\text{IEMG}}_{\text{ref}}}$$

where IEMG_qs, average rectified EMG obtained during a quiet stance trial integrated over a time window of the same duration as IEMG; IEMG_ref, average rectified EMG in the middle of the trial obtained during the two control trials when holding a 5 kg load in front or behind the body integrated over a time window of the same duration as for IEMG. For the dorsal muscles (GL, GM, BF, ST, ES) IEMG indices were divided by the EMG integrals when the load was held in front of the body. For the ventral muscles (TA, VM, VL, RF, RA), IEMG indices were divided by the EMG integrals when the load was suspended behind the body.

Defining M-modes with principal component analysis

The objective of this step of analysis is to define groups of muscles (muscle modes or M-modes) that show co-varied levels of activation (IEMG_norm) across tasks with different load magnitudes. M-modes were used as the elemental variables for further analysis of M-mode synergies (see later). This step reduces the ten-dimensional muscle activation space to a three-dimensional M-mode space.

For each subject and each load condition the IEMG_norm data formed a matrix with ten columns representing the ten muscles and the number of rows corresponding to 1% time windows of the cycles analyzed (i.e., 50 sway cycles give 5,000 rows). A five-point moving average was applied to smooth the IEMG_norm data. The correlation matrix between the IEMG_norm was subject to PCA, using Matlab 7.6 software. Within each task and subject, the first three PCs contained at least one muscle with a significantly high loading each (over ±0.5; Hair et al. 1995). Visual inspection of the scree plots confirmed the validity of this criterion. The first three PCs explained on average 79.0% of the variance in the data. They were subjected to Varimax rotation with factor extraction. The factors will be addressed as M-modes. The M-mode magnitudes were obtained by multiplying the IEMG_norm matrix with the loadings of the PCs after the Varimax rotation.

Defining the Jacobian (J matrix) using multiple regression

Linear relations were assumed between small changes in the magnitude of the M-modes (ΔM) and the change (ΔPV) in each of the two performance variables (M_Y and F_X). Multiple linear regression over all cycles within a condition was used to define the relations between ΔM and ΔPV for each subject and each condition separately. Both ΔM and ΔPV were filtered with a 10 Hz low-pass, second-order, zero-lag Butterworth filter before applying multiple linear regression. For each subject, ΔM and ΔPV values were computed over all cycles for each 1% of the cycle duration. The analysis was run over full cycles:

$$\mathrm{\Delta }\text{PV}=k_1^{\ast }\mathrm{\Delta }{\text{M}}_1+k_2^{\ast }\mathrm{\Delta }{\text{M}}_2+k_3^{\ast }\mathrm{\Delta }{\text{M}}_3$$ (1)

The coefficients of the regression equations were arranged in a matrix reduced to a vector that is a Jacobian matrix (J):

$$J={[\begin{array}{ccc}{k}_1& k_2& k_3\end{array}]}^T$$ (2)

Uncontrolled manifold analysis: index of synergy

The UCM hypothesis assumes that the controller manipulates a set of elemental variables and tries to limit their variance to a sub-space corresponding to a desired value of a performance variable. Within the UCM analysis, the trial-to-trial variance in the elemental variables is divided into two components. The first component lies within a subspace (the UCM) where the selected performance variable does not change. The second component of the variance lies within the orthogonal complement to the UCM. Comparing the two components of the variance, normalized by the dimensionality of their respective sub-spaces, produces an index of variance that is compatible with stabilization of the selected performance variable.

In the current study, M-modes (calculated in step 1) are the elemental variables, while changes in F_X and M_Y represent the performance variables. The ΔM space has dimensionality n = 3. The hypothesis that ΔPV is stabilized, accounts for one degree of freedom (d = 1). Thus the system is redundant with respect to the task of stabilizing each of the two performance variables, F_X and M_Y. For each time window, the mean magnitude over the number of cycles of each of the M-modes was calculated ( $\overline{\mathrm{\Delta }M}$) and was subtracted from the vectors of the individual changes in the magnitudes of the M-mode (ΔM) for each cycle, for each time window:

$$\mathrm{\Delta }{M}_{\text{demeaned}}=\mathrm{\Delta }M-\overline{\mathrm{\Delta }M}$$

The residual mean-free vectors ΔM_demeaned were calculated for each condition and for each of the subjects.

The UCM sub-space was approximated with the null-space of the corresponding Jacobian matrix J, see Eq. (2). The null-space of J is a set of all vector solutions x of a system of equations Jx = 0. The null-space is spanned by basis vectors, ε_i. The vector ΔM_demeaned was resolved into its projection onto the UCM (f_UCM) and the orthogonal subspace (f_ORT):

$$\begin{array}{l}{f}_{\text{UCM}}=\sum _{i=1}^{n-d}{\left({\epsilon }_i^T·\mathrm{\Delta }{M}_{\text{demeaned}}\right)}^T·{\epsilon }_i^T\\ f_{\text{ORT}}=\mathrm{\Delta }{M}_{\text{demeaned}}-{(f_{\text{UCM}})}^T\end{array}$$

The trial-to-trial variance in each of the two subspaces (V_UCM and V_ORT) as well as the total variance (V_TOT) normalized by the number of DOF of the respective spaces was calculated as:

$$\begin{array}{l}{V}_{\text{UCM}}={\sigma }_{\text{UCM}}^2=\frac{1}{(n-d)N_{\text{trials}}}\sum _{i=1}^N{f}_{\text{UCM}}^2\\ V_{\text{ORT}}={\sigma }_{\text{ORT}}^2=\frac{1}{\text{d}{N}_{\text{trials}}}\sum _{i=1}^N{f}_{\text{ORT}}^2\\ V_{\text{TOT}}={\sigma }_{\text{TOT}}^2=\frac{1}{(d+n)N_{\text{trials}}}\sum _{i=1}^N{(\mathrm{\Delta }{M}_{\text{demeaned}})}^2\end{array}$$

To quantify the relative amount of variance that is compatible with stabilization of the selected performance variable, an index of synergy ΔV was calculated. The normalization of the index by the total amount of variance is carried out as described in earlier studies (Krishnamoorthy et al. 2003b; Danna-Dos-Santos et al. 2007; Robert et al. 2008) to facilitate comparison across subjects and conditions:

$$\mathrm{\Delta }V=\frac{V_{\text{UCM}}-V_{\text{ORT}}}{V_{\text{TOT}}}$$ (3)

where all variance indices are computed per degree of freedom.

Statistics

Average peak-to-peak values were calculated for both performance variables F_X and M_Y for each condition and each subject. Two-way ANOVA with factors Loading (4 levels) and Direction (2 levels) was performed to investigate peak-to-peak changes for each performance variable.

Since V_UCM, V_ORT, and V_TOT are computed per DOF, the index of synergy ΔV ranges between 1.5 (all variance is within the UCM) and −3 (all variance is in the orthogonal sub-space). For further statistical analysis, the ΔV values were transformed using a Fisher’s z-transformation (ΔV_z) adapted to the boundaries of ΔV:

$$\mathrm{\Delta }{V}_z=\frac{1}{2}·log\left[\frac{3+\mathrm{\Delta }V}{(1.5-\mathrm{\Delta }V)}\right]$$

Furthermore, ΔV_z was analyzed within the following four intervals of 11 data points each: (1) 95–100% and 1–5% taken together, (2) 20–30%, (3) 45–55%, and (4) 70–80%. Average values for each of these intervals were calculated for each subject and each condition and used for further statistical data analysis.

To quantify if a synergy is stabilizing the selected performance variable one sample Student’s t tests were performed to check whether ΔV_z was significantly different from 0.5 * log(2) (i.e., ΔV is significantly different from zero).

A three-way ANOVA was performed on ΔV_z computed for each of the two performance variables with the factors Loading (4 levels), Direction (2 levels) and Interval (4 levels) to determine: (1) If the selected performance variable was better stabilized at different phases of the cycle; (2) The influence of the amount of weight attached to the ankles on ΔV_z; and (3) If the synergy stabilizing the selected performance variable was influenced by the direction of the horizontal force.

To verify if one performance variable was better stabilized than the other one, a three-way ANOVA was performed on ΔV_z with factors Loading, Performance-variable (F_X and M_Y) and Interval for each of the directions separately. Tukey’s pairwise contrasts were used to explore significant effects; Bonferroni corrections were used to reflect the multiple comparisons.

Data are presented in the text and figures as means and standard errors.

Results

Patterns of shear force, moment around the frontal axis and general EMG

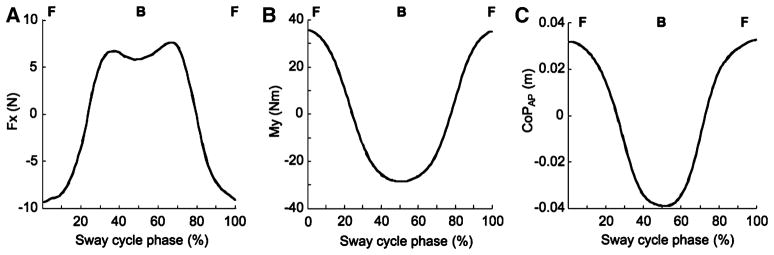
All eleven subjects were able to show qualitatively similar ‘sine-like’ time profiles of the moment of force about the frontal axis (M_Y) across the seven load conditions. The panel in the middle of Fig. 2 shows a typical example of M_Y averaged across 51 cycles when the 1.8 kg load was attached at the ankle level and produced horizontal force (F_X) acting backwards. The left panel shows the time profile of F_X for the same condition. The right panel shows the time profile of the center of pressure in the anterior–posterior direction (COP_AP). At 0% and 100% of the time cycle, the subject was in the most forward position (F). At 50% the subject was in the most backward position (B). A positive moment of force is a dorsiflexion moment in the ankle joint. Note that the M_Y and COP_AP patterns are nearly identical (except for the scales) and both differ from the F_X pattern. We observed very similar records in all subjects; based on these records, we selected M_Y and F_X as the two performance variables analyzed in the study.

Fig. 2.

Time profiles of the shear force F_X (left), the moment of force about the frontal axis M_Y (middle), and the center of pressure in anterior–posterior direction (COP_AP, right) averaged across 51 cycles for a typical subject who performed the task with the 1.8 kg load attached at the ankle level pulling backward. At 0 and 100% of the sway cycle the subject was in the most forward position (F) (dorsiflexion at the ankle joint). At 50% of the sway cycle, the subject was in the most backward position (B) (plantarflexion at the ankle joint). Note that time patterns of the COP_AP and M_Y are nearly identical. For further analysis, F_X and M_Y were defined as the two performance variables

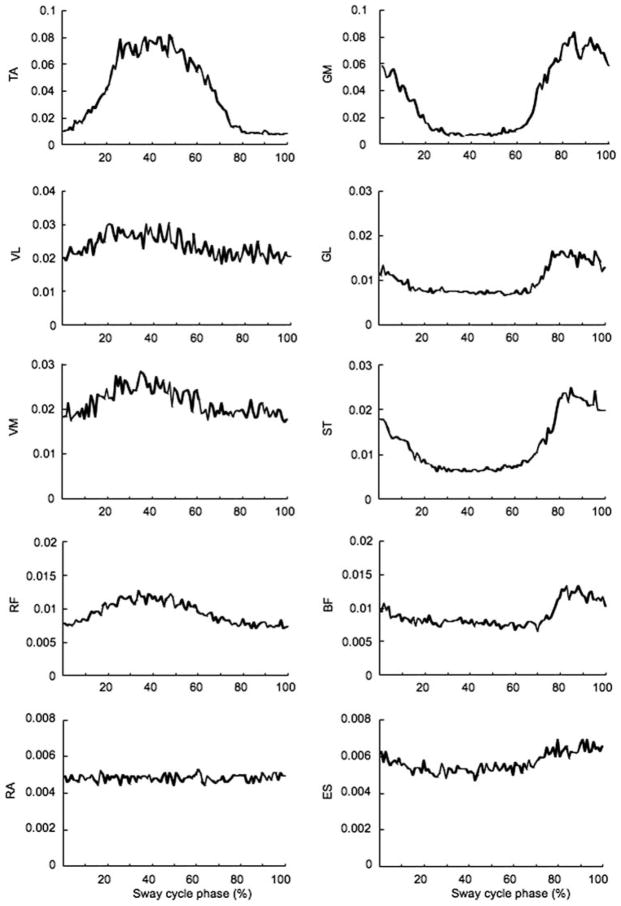
The activation profiles (EMGs) of the ten muscles showed substantial modulation within the M_Y cycle in most subjects. The activation patterns were highly variable across subjects and also across trials performed by the same subject. Some of the muscles could show little modulation over the cycle in some subjects. Figure 3 shows averaged across cycles filtered and rectified EMG patterns for one of the subjects. In that particular subject, EMGs of RA and ES showed little modulation within the cycle period. Figure 3 does not present indices of EMG variability; such indices for a similar task can be found in a previous publication (Fig. 3 in Danna-dos-Santos et al. 2007).

Fig. 3.

EMG activity in the ten muscles averaged across 50 cycles for a typical subject when the 1.8 kg load was attached at the ankle level pulling backward. The EMG was normalized to the muscle activation levels seen in the control trials (see “Methods”). TA tibialis anterior, VL vastus lateralis, VM vastus medialis, RF rectus femoris, RA rectus abdominis, GM gastrocnemius medialis, GL gastrocnemius lateralis, ST semitendinosus, ES erector spinae

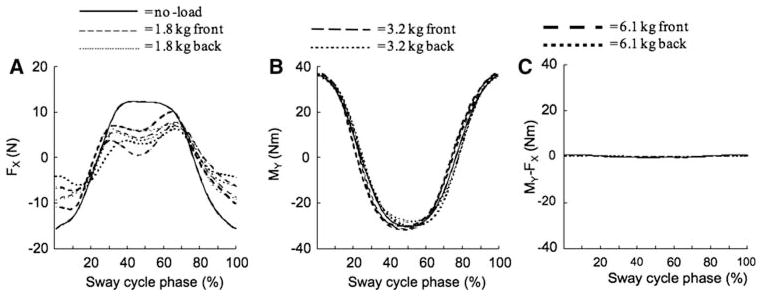
The M_Y time profiles were similar across all the loading conditions (Fig. 4, middle). This was expected since the subjects received visual feedback on M_Y and were instructed to produce similar M_Y time profiles. The F_X time profiles were more condition dependent (Fig. 4, left). In particular, the largest peak-to-peak F_X variations were seen under the zero load condition (the thick gray line in Fig. 4). When the external load was not zero, F_X time profiles showed two peaks at about 30 and 70% of the cycle (halfway between the most forward and most backward positions) and a valley close to the most backward position. In contrast, the M_Y time profiles were smooth with extrema at the most forward and most backward position.

Fig. 4.

Time profiles of the shear force F_X (left), moment of force around the frontal axis M_Y (middle), and moment of force around the frontal axis produced by F_X (M_Y–F_X, right) averaged across cycles for a typical subject for each of the loading conditions. Note the very small values of M_Y–F_X, and the different time profiles of F_X and M_Y. Also note the similar M_Y profiles across the conditions and the largest F_X peak-to-peak excursion in the no-load condition

Since F_X variation was expected to contribute to the M_Y variation as measured by the force plate, we estimated these contributions quantitatively. The right panel of Fig. 4 shows the component of M_Y calculated from the F_X data (M_Y–F_X). Note that F_X variation contributed less than 2% to the total M_Y variation (compare panels B and C). This was true across subjects and conditions.

Two two-way ANOVAs were run on peak-to-peak M_Y and F_X with the factors Loading (0, 1.8, 3.2, and 6.1 kg) and Direction (front and back). The ANOVA showed no significant effects for M_Y. There was a significant effect of Loading for F_X [F_(3,70) = 60.627, p < 0.001]. Tukey’s pair-wise comparison revealed a significant difference for the no-load condition compared to the three other load conditions. There was also a significant Direction × Loading interaction for F_X [F_(3,70) = 2.786, p < 0.05]; differences in peak-to-peak values for different loadings were smaller when the load was acting in forward direction than in backward direction. Furthermore, there seem to be a directional correspondence related to the amount of load applied when the load was acting in backward direction; peak-to-peak values were smaller with a high load than with a small load. When the load was acting in forward direction, no directional correspondence was found.

Identification of M-modes and Jacobians: results of PCA and multiple regression

The normalized integrated EMG indices (IEMG_norm) for all sways and all muscles for each load condition and each subject were subjected to principal component analysis (PCA) with factor extraction to identify groups of muscles (M-modes) whose activity was modulated in parallel during body sway (see ‘Methods’ for details). As a result, the ten-dimensional muscle activation space was reduced to a three-dimensional M-mode space. The four PCs accounted on average for 79.0% (SE 0.7%) of the total variance across all subjects and load conditions. The average amount of variance explained by the first three factors was 43.4% (SE 0.9%), 21.7% (SE 0.7%), and 13.9% (SE 0.6%), respectively. Table 1 shows an example of the loadings for all the muscles on the three factors for a representative subject when a load of 1.8 kg was acting forwards. The significant loadings (with the magnitude over 0.5; see Hair et al. 1995) are in bold.

Table 1.

Representative results of PCA

Muscle	M1-mode	M2-mode	M3-mode
TA	0.7206	0.4257	0.0974
VL	0.9122	−0.0809	0.0087
VM	0.9118	−0.1082	−0.0356
RF	0.6321	0.3887	−0.1536
RA	0.1230	0.0517	0.8289
GM	−0.4220	−0.6732	−0.0889
GL	0.0523	−0.7670	0.0159
ST	−0.2067	−0.7847	0.1413
BF	0.0745	−0.7268	0.1459
ES	−0.1940	−0.2661	0.7794

Loading factors for a typical subject are presented for the condition when the 1.8 kg load was applied acting in the backward direction (TA tibialis anterior, VL vastus lateralis, VM vastus medialis, RF rectus femoris, RA rectus abdominis, GM gastrocnemius medialis, GL gastrocnemius lateralis, BF biceps femoris, ST semitendinosus, ES erector spinae). Significant loadings (higher in magnitude than 0.5) are shown in bold

We defined co-contraction patterns as those when activation indices for muscles on the opposite sides of the body entered the same M-mode, their loading coefficients were high (over 0.5 in magnitude), and the coefficients had the same signs. In the current study 67 co-contraction patterns were found out of 231 across all subjects. Most of the co-contractions were found in the proximal muscles, 47 in the thigh, 17 around the hip, and 3 at the calf. Co-contractions seem not to be related to loading or direction of load.

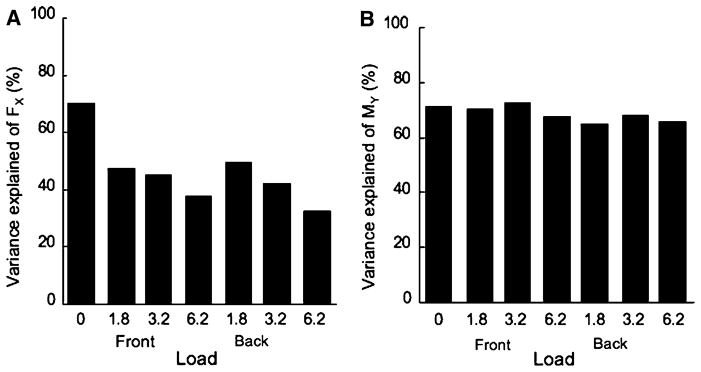
Linear relations between small changes in the magnitude of the muscle modes (ΔM) and small changes in each of the two performance variables (ΔF_X and ΔM_Y) were assumed and expressed using the Jacobian matrix (see ‘Methods’ for details). The coefficients of multiple linear regression analysis were calculated for each subject and each performance variable (F_X and M_Y) for each of the seven loading condition. For each regression analysis, the data were pooled over the 1% time intervals within a cycle across all the accepted cycles. Figure 5 shows the average amount of variance explained across subjects for each loading condition and each of the performance variables. The changes in the M-mode magnitudes explained, on average across subjects and loading conditions, 49.6% of the F_X variance and 69.4% of the M_Y variance.

Fig. 5.

The amount of variance explained by linear regression of ΔF_X (left) and ΔM_Y (right) against the changes in the three M-mode magnitudes for each of the loading conditions (F load in front, B load in the back) averaged over subjects. Note the relatively low values for F_X and the higher values for M_Y

A similar amount of variance was explained in the zero load condition for both F_X and M_Y (approximately 71%). A two-way ANOVA was performed on the z-transformed values of the explained variances with the factors Loading, and Direction. A significant effect was found for the amount of explained variance for Loading for both. F_X [F_(3,70) > 34.57, p < 0.001] and M_Y [F_(3,70) > 3.18, p < 0.05]. However, Tukey post-hoc contrasts only showed significant differences in F_X for the no-load condition compared to each of the other loading conditions, the amount of variance dropped with the load magnitude. A significant effect was also found in Direction for M_Y [F_(1,70) > 5.53, p < 0.05]. The amount of variance explained was large for both, but larger when load was acting in forward direction than in backward direction.

Uncontrolled manifold analysis: index of synergy

Data from 50 (SD 1) sway cycles under the seven loading conditions were used to carry out the UCM analysis for each subject. The UCM analysis was used to estimate two components of variance in the M-mode space, one that did not affect the averaged across cycles value of a selected mechanical variable F_X or M_Y (V_UCM) and the other that did (V_ORT). An index (ΔV) reflects the difference between V_UCM and V_ORT both quantified per DOF within each sub-space. Positive values of ΔV are interpreted as reflecting a multi-M-mode synergy stabilizing the selected performance variable.

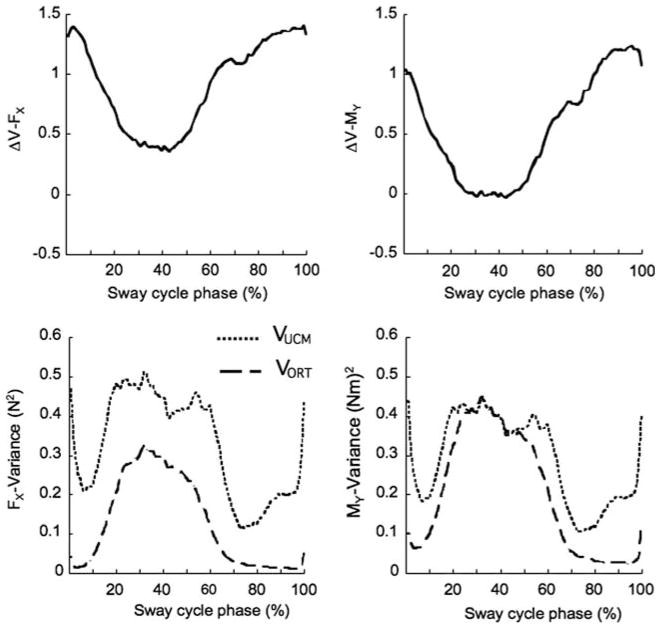
Figure 6 illustrates a typical example of the time profiles of ΔV for both performance variables F_X (left) and M_Y (right) when a load of 1.8 kg was applied in the backward direction.

Fig. 6.

Time profile of the ΔV synergy index for the shear force F_X (top left) and the moment of force M_Y (top right). The components of variance, V_UCM (solid line) and V_ORT (dashed line), are shown for F_X (bottom left) and M_Y (bottom right). The data are for a typical subject when the 1.8 kg load was producing horizontal force in the backward direction

Note the similar ΔV time profiles for F_X and M_Y in the top panels. Both show larger values at the beginning and end of the sway cycle and a drop between approximately 20 and 70% of the sway cycle. M_Y shows smaller ΔV values as compared to F_X, although ΔV > 0 in both panels corresponding to multi-M-mode synergies stabilizing both F_X and M_Y over the whole cycle. Student’s t tests was performed on the z-transformed values of ΔV_FX and ΔV_MY. The test confirmed that both ΔV_FX and ΔV_MY were significantly larger than zero (p < 0.05).

That ΔV > 0 can also be explained with the bottom figures. The variance within the UCM (V_UCM) show higher values than the variance orthogonal to the UCM (V_ORT). When V_UCM and V_ORT are similar, ΔV = 0. The decrease in ΔV is caused by an increase in both V_UCM and V_ORT. For F_X the change in V_UCM was slightly larger, for M_Y the change in V_ORT was slightly larger.

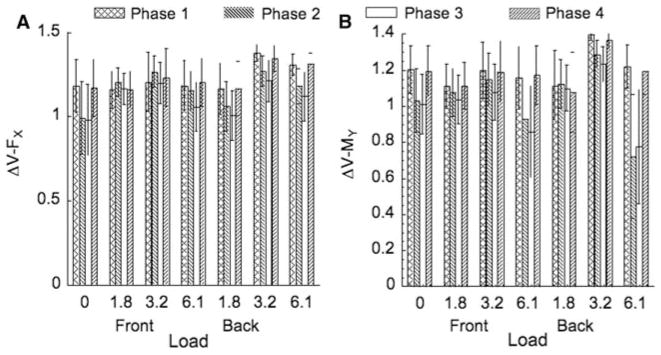
For further analysis, four phases were selected within the sway cycle: Phase 1 (95–100 and 1–5% of the cycle), Phase 2 (20–30% of the cycle), Phase 3 (45–55% of the cycle), and Phase 4 (70–80% of the cycle). Figure 7 shows the ΔV indices for each loading condition (F front, B Back), for each of the four phases, and for each performance variable, averaged across subjects.

Fig. 7.

Synergy index ΔV for F_X (left) and M_Y (right) for the seven loading conditions (F front, B back) averaged over subjects with standard error bars. The four columns for each condition refer to four phase intervals within the sway cycle: Phase 1 (0–5 and 95–100%), Phase 2 (20–30%), Phase 3 (45–55%), and Phase 4 (70–80%)

A three-way ANOVA on the z-transformed values of ΔV_FX and ΔV_MY with the factors Loading, Direction, and Phase was performed to determine the effect of Direction; no significant effects were found.

Note in Fig. 7 that ΔV values are in general higher in Phases 1 and 4, and they show a drop in Phases 2 and 3. This was confirmed with a three-way ANOVA performed on the z-transformed values of ΔV with the factors Loading, Variable, and Phase. Significant effects of Phase were found for ΔV [F_(3,662) > 13.30, p < 0.001]. Tukey post hoc contrasts revealed that in Phase 1 and 4, ΔV was higher than in the phases 2 and 3. The same ANOVA revealed significant effects of Loading [F_(3,662) > 11.20, p < 0.001]. Tukey’s pairwise comparisons revealed that ΔV was higher (by approximately 20%) for the 3.2 kg load as compared to the no-load condition and the 1.6 kg load condition. As mentioned before, both performance variables were stabilized by multi-mode synergies. However, the ANOVA showed significant effects of Variable [F_(1,662) > 7.42, p < 0.05]; higher ΔV indices were found for the performance variable F_X than for the performance variable M_Y.

Discussion

In the Introduction, three hypotheses were formulated. Two of them have been falsified, and one has been confirmed. The first hypothesis was related to the possibility of simultaneous stabilization of the shear force in the anterior–posterior direction (F_X) and the moment of force around the frontal axis (M_Y) by a single set of muscle modes. The results showed two synergies that were stabilizing both performance variables at the same time. The second hypothesis suggested that the time profiles of the synergy indices related to stabilization of F_X and M_Y would be out of phase. The results were exactly opposite showing similar time profiles for both synergy indices. Note that the synergy index related to F_X stabilization was higher, although the explicit instruction and visual feedback were related to M_Y time profiles. The third hypothesis suggested that the indices of synergies would show lower values in sway phases corresponding to higher rates of change of the corresponding performance variables. This hypothesis was also refuted: synergy indices were related not to the time derivative of the variables (F_X and M_Y), but to the direction of movement. Both performance variables were better stabilized when the body moved forward than when it moved backward.

In the following sections we discuss the implications of the results for such issues as hierarchical control of multi-muscle systems, the control of postural tasks, the purpose of multi-muscle synergies, and the principle of superposition in motor control.

Hierarchical control of posture

Bernstein (1935, 1967) suggested that the CNS solves the famous problem of motor redundancy by uniting elements into groups (synergies) and thereby decreases the number of variables to be manipulated by the controller. Later work by Gelfand and Tsetlin (1966) refined the idea of synergies by suggesting a neural organization of many elements in a hierarchical way: a synergy receives an input from a hierarchically higher synergy and produces an output, which serves as an input for a hierarchically lower synergy. At any level of a control hierarchy, synergies ensure low variability (high stability) of a particular overall output variable of that level.

The notion of muscle synergies has been used with respect to the control of movements in a variety of species (Bradley and Bekoff 1990; Johnson and Bekoff 1996; Saltiel et al. 2001; Holdefer and Miller 2002; Lemay and Grill 2004). Using muscle synergies has been viewed as a solution to the problem of motor redundancy (Bernstein 1967; Turvey 1990) by decreasing the number of DOF at the control level. In several recent studies (d’Avella et al. 2003; Krishnamoorthy et al. 2003a, b; Ivanenko et al. 2004, 2006; Ting and Macpherson 2005; Tresch et al. 2006; Danna-dos-Santos et al. 2007; Robert et al. 2008; reviewed in Latash et al. 2007; Latash 2008) it has been suggested that multi-muscle control of vertical posture is based on a hypothetical hierarchical scheme. At the lower level, muscles are organized into groups (M-modes; addressed as “synergies” in some papers). At the upper level, the gains at muscle modes are manipulated to produce required actions.

Synergies at the upper level of the hierarchy are based on elemental variables (M-modes) that are recruited with gains that show co-variation across repetitive trials (cycles) to stabilize performance variables such as coordinate of the center of pressure and shear force magnitude. Several recent studies have supported the existence of flexible synergies at the lower level suggesting that muscle mode composition may change under challenging conditions and with practice (Danna-dos-Santos et al. 2008; Asaka et al. 2008).

A number of studies investigated synergies at the lower hierarchical level using matrix factorization methods applied to integrated indices of muscle activation (Henry et al. 1998; Ivanenko et al. 2004, 2006; Weiss and Flanders 2004; Torres-Oviedo et al. 2006; Ting and McKay 2007). In those studies, the identified vectors in the muscle activation space (synergies) were linked to the production of specific time patterns of potentially important mechanical variables. In our study, we focused on two such variables, F_X and M_Y. The choice of these particular variables was based on the following considerations. First, we wanted to make sure that the number of performance variables was two (smaller than the number of modes we expected to accept in the analyses—3, and larger than one), that the variables were important for postural control, and that they were relatively independent. F_X and M_Y are two variables that are important for balance. Besides, our assessment of the contribution of F_X modulation to M_Y changes showed that this contribution was small (under 2%).

In contrast to the cited studies, we focused not on time patterns of the two selected variables but on their stability (reflected in across-trials variability). In this analysis, we quantified synergy indices stabilizing each of these two variables at the upper level of the hierarchy. These indices reflected the amount of “good variance” (compatible with a certain magnitude of the selected variable, F_X or M_Y) in the total amount of variance within the space of elemental variables, M-modes. The highly positive values of the synergy index observed in the study imply that most of the across-cycles variance in the M-mode space was within the UCM, i.e., it was compatible with the average across cycles values of M_Y and F_X. We interpret these results as reflections of neural synergies stabilizing both these variables across cycles. It is possible that biomechanical factors had effects on the measured indices. At this time, we cannot estimate such effects quantitatively. However, relatively quick changes in such indices with practice (Asaka et al. 2008) suggest that they are predominantly defined by neural factors.

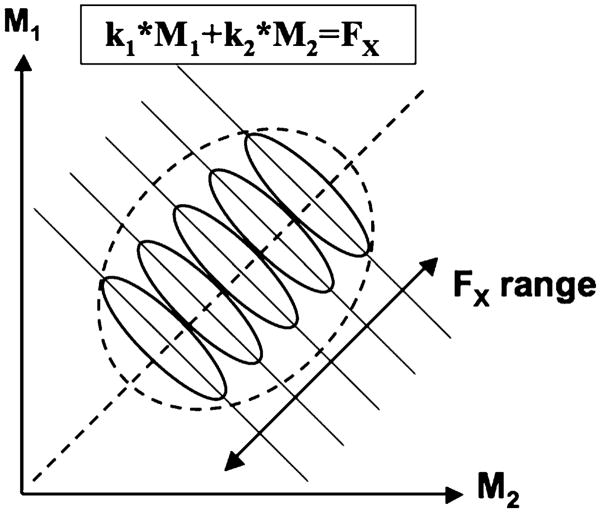
The total amount of variance accounted for by three M-modes, identified using PCA applied to integrated indices of muscle activation, was similar to the values observed in earlier studies (Krishnamoorthy et al. 2003a, b; Danna-Dos-Santos et al. 2007, 2008; Robert et al. 2008). At the next step, when the Jacobian of the system was applied, a rather small amount of variance (just under 50%) was accounted for by the multiple linear regression of changes in F_X against small changes in the M-mode magnitudes. This result may be explained given the relatively small range of F_X changes within the cycle and the large indices of synergies stabilizing F_X. Figure 8 uses a simplified illustration (with only two M-modes) of hypothetical distributions of M-mode magnitudes for each F_X value. The large synergy index implies that “good variance” (along the lines k₁ * M₁ + k₂ * M₂ = F_X, solid slanted lines in Fig. 8) was much larger than “bad variance” (along the orthogonal, dashed line corresponding to a change in F_X). Data distributions at specific phases of the sway cycle are shown as ellipses elongated along the solid lines. Different solid lines reflect different F_X values in different phases of the sway cycle. Since the range of F_X change was relatively small (see Fig. 2 in “Results”), the overall data distribution (shown by the dashed, large oval) might have been expected to be only slightly elongated along the “bad variance” direction. But this is exactly the direction of change in F_X, and variance along that direction is expected to benefit the amount of variance explained at the step of multiple linear regression. Note that the relatively large range of changes in the other performance variable, M_Y, was associated with substantially higher amount of variance accounted for by the linear regression analysis (about 75%, comparable to the results in Danna-Dos-Santos et al. 2007; Robert et al. 2008). These results emphasize the necessity to have a large range of changes in a performance variable to identify the Jacobian of the system with high confidence.

Fig. 8.

A schematic illustration of a performance variable stabilized by a two-M-mode synergy. A linear relation is assumed: F_X = k₁ * M₁ + k₂ * M₂. The solid slanted lines illustrate UCMs for different values of the performance variable. The ellipses illustrate possible data point distributions across cycles assuming that F_X is stabilized by a multi-M-mode synergy. The dashed slanted line corresponds to the orthogonal complement to the UCM. Note that linear regression analysis is only able to account for much of the F_X variance if F_X range is large

Principle of superposition

The idea that biological processes obey some kind of a superposition principle has been debated for many years. This principle implies that total output of a set of elements with several inputs equals the sum of the outputs produced by each of the inputs applied separately. Violations of this principle in neurophysiology are common, and a number of recent studies questioned applicability of the principle of superposition in studies of such diverse objects as motor unit firing patterns and maintenance of vertical posture (Demieville and Partridge 1980; Latt et al. 2003). Several research teams tried to find regularities of behaviors of large populations of such elements that would behave in a nearly linear fashion and obey the principle of superposition. Ruegg and Bongioanni (1989) reported nearly linear input–output properties of motoneuronal pools in tasks that involved a superposition of steady-state and ballistic contractions. Studies of neuronal populations in different areas of the brain have also supported applicability of the principle of superposition (Kowalski et al. 1996; Glazer and Gauzelman 1997). In a recent study, Fingelkurts and Filngelkurts (2006) have come up with a conclusion that integrative brain functions can be manifested in the superposition of distributed multiple oscillations according to the principle of superposition (see also Karakas et al. 2000).

One of the major findings of the current study is the demonstrated possibility of stabilizing two performance variables at the same time based on a single set of three elemental variables. Indeed, both M_Y and F_X showed highly positive synergy indices over the sway cycle. The set of three M-modes is redundant with respect to two constraints (associated with the two variables). So, having two synergies is theoretically possible (cf. Zhang et al. 2008). However, a priori, one could have expected that imposing a novel constraint (the necessity to produce a certain F_X value) might interfere with co-variation among the M-modes stabilizing M_Y that was the instructed variable. The lack of such an interference exemplifies a major advantage of using synergic control: possibility to perform a secondary task or to adapt to a new constraint without disruptive effects on the primary task (see Shapkova et al. 2008; Zhang et al. 2008; Gera et al. 2009).

The two variables, F_X and M_Y, are not perfectly independent. In fact, M_Y, as measured by the force platform, involves a component produced by F_X because of the non-zero moment arm of F_X. However, in our task of swaying over a relatively large range at a relatively low frequency, the two variables were nearly perfectly decoupled. Indeed, their typical time profiles differed (see Fig. 2) and the estimated contribution of the within-the-cycle modulation of F_X to M_Y changes was under 2%. Hence, we assumed that the performed analysis of the M-mode variance with respect to the two variables was not a priori expected to produce similar results. Indeed, in an earlier study (Robert et al. 2008), we saw signs of a competition between the two synergies related to these two variables. Hence, we consider the lack of negative interference between the two synergies stabilizing F_X and M_Y time profiles (see Figs. 6, 7 in “Results”) as a non-trivial finding.

This finding resembles earlier results in prehension studies supporting the principle of superposition (Shim et al. 2003, 2005b; Zatsiorsky et al. 2004; Shim and Park 2007; Zhang et al. 2008). The principle of superposition for grasping, originally introduced in robotics (Arimoto et al. 2001), suggests that skilled actions can be decomposed into several elemental actions that are controlled independently by separate controllers. The outputs of such sub-controllers are summed up at the level of output elements. Our find-ings generalize this principle to multi-muscle actions in postural tasks.

Time modulation of the synergy index

Several earlier studies of both discrete and cyclic actions showed consistent modulation of the synergy index (computed similarly to the δV index in this study) over the movement time or cycle phase (Latash et al. 2002a; Goodman et al. 2005; Friedman et al. 2009). Typically, the synergy index showed a drop when the performance variable, with respect to which the index was computed, changed quickly. This drop was largely produced by an increase in the “bad” component of variance, possibly due to timing errors across different realizations of the task (trials or cycles). We expected to observe a similar behavior of the δV index in this study. Note also that a transient drop in δV computed for the anterior–posterior center of pressure coordinate was observed in a task with a quick, discrete COP shift by standing subjects (Wang et al. 2006).

Our results did not confirm the prediction. Indeed, no visible modulation of δV computed for both variables (F_X and M_Y) was observed at the times of peak rate of change of those variables. These results are similar to those described in the study of cyclic sway by standing subjects where multi-M-mode synergies were quantified with respect to the COP coordinate in the anterior–posterior direction (Danna-Dos-Santos et al. 2007). Taken together, these results suggest a major difference in the structure of variance between discrete and cyclic tasks. This conclusion fits well recent studies suggesting a basic difference in the neural mechanisms of control of discrete and cyclic actions (Schaal et al. 2004; Hogan and Sternad 2007).

In our study, there was consistent modulation of the δV indices within the sway cycle. However, lower δV values were observed not at phases corresponding to the peak rates of change of the performance variables, but during a half-cycle corresponding to the body sway backwards. This result may not look particularly surprising given an overall higher difficulty of the backward sway as compared to the forward sway (e.g., Krishnamoorthy and Latash 2005); however, it is not trivial either given the data mentioned in “Introduction” on a drop in synergy indices with an increase in the rate of change of the salient performance variable (Latash et al. 2002a; Goodman et al. 2005; Shim et al. 2005a). Note also that postural tasks performed in more challenging conditions have been shown to lead to lower indices of multi-M-mode synergies (Krishnamoorthy et al. 2004; Asaka et al. 2008).

What is the purpose of ‘good’ variance?

As described earlier, our analysis of synergies is based on estimating two components of variance at the level of elemental variables. “Good” variance, by definition, has no effect on the performance variable with respect to which it is computed. Why would the controller facilitate large amounts of this, seemingly irrelevant “good” variance? A higher amount of “good” variance implies having a larger family of possible solutions that lead to the same value (time profile) of a potentially important performance variable. So, synergies do not necessarily reduce variability (Shapkova et al. 2008; Gorniak et al. 2008) of performance, but they allow performing secondary tasks, handling new constraints, and dealing with perturbations (Zhang et al. 2008; Gera et al. 2009; Gorniak et al. 2009). For example, a multi-joint synergy stabilizing vertical orientation of a hand-held glass of wine may allow clicking glasses, opening a door by pressing on the handle with the elbow of the same arm, and drinking from both sturdy and fragile glasses.

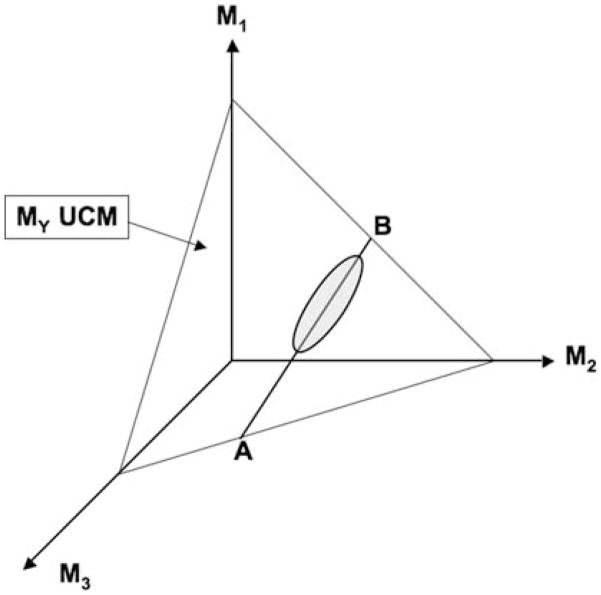
In the current study, high indices of synergies were found for both F_X and M_Y in the same phases of the sway cycle without any signs of competition between the two synergies (in contrast to Robert et al. 2008). A strong synergy stabilizing M_Y implies that most variance in the three-dimensional M-mode space is confined to a two-dimensional sub-space, that is, it represents “good” variance for M_Y. Figure 9 illustrates a three-dimensional M-mode space and a hypothetical two-dimensional subspace, the UCM for a certain M_Y value. To have a strong synergy for another performance variable (F_X) requires “good” variance for that variable to be significantly larger than the “bad” variance, i.e. variance leading to F_X changes. Barring an unlikely coincidence, that “good” variance sub-spaces for the two mechanical variables happen to be parallel to each other, the two UCMs (for M_Y and F_X) intersect, and create a uni-dimensional space in the M-mode space corresponding to stabilization of both performance variables (line AB in Fig. 9, the ellipse illustrates a possible data distribution within the UCM for M_Y). Note that having large amounts of variance within the UCM for M_Y increases chances of having substantial amounts of variance along its sub-space, such as the AB line in Fig. 9. This allows the controller to stabilize both M_Y and F_X at the same time. Altogether, the finding of very high indices of synergy for both variables support the idea that facilitating large amounts of “good” variance is a purposeful strategy that allows the CNS to stabilize two or more performance variables at the same time.

Fig. 9.

A thee M-mode space is illustrated. The plane crossing all three axes corresponds to the UCM for the moment of force (M_Y). The line AB shows the intersection between this UCM and another UCM corresponding to stabilization of the other variable, F_X. The gray ellipse illustrates a data point distribution corresponding to stabilization of both M_Y and F_X