Bayesian rule learning for biomedical data mining

Abstract

Motivation: Disease state prediction from biomarker profiling studies is an important problem because more accurate classification models will potentially lead to the discovery of better, more discriminative markers. Data mining methods are routinely applied to such analyses of biomedical datasets generated from high-throughput ‘omic’ technologies applied to clinical samples from tissues or bodily fluids. Past work has demonstrated that rule models can be successfully applied to this problem, since they can produce understandable models that facilitate review of discriminative biomarkers by biomedical scientists. While many rule-based methods produce rules that make predictions under uncertainty, they typically do not quantify the uncertainty in the validity of the rule itself. This article describes an approach that uses a Bayesian score to evaluate rule models.

Results: We have combined the expressiveness of rules with the mathematical rigor of Bayesian networks (BNs) to develop and evaluate a Bayesian rule learning (BRL) system. This system utilizes a novel variant of the K2 algorithm for building BNs from the training data to provide probabilistic scores for IF-antecedent-THEN-consequent rules using heuristic best-first search. We then apply rule-based inference to evaluate the learned models during 10-fold cross-validation performed two times. The BRL system is evaluated on 24 published ‘omic’ datasets, and on average it performs on par or better than other readily available rule learning methods. Moreover, BRL produces models that contain on average 70% fewer variables, which means that the biomarker panels for disease prediction contain fewer markers for further verification and validation by bench scientists.

Contact: vanathi@pitt.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

High-throughput ‘omic’ data that measure biomarkers in bodily fluids or tissues are accumulating at a rapid pace, and such data have the potential for the discovery of biomarkers for early diagnosis, monitoring and treatment of diseases such as cancer. Data mining methods that learn models from high-dimensional data are being increasingly used for the multivariate analyses of such biomedical datasets. Together with statistical univariate analyses, some insights into predictive biomarkers of disease states can be gleaned, though the results may not generalize due to the small sizes of available training data, typically less than 200 samples.

Due to the large imbalance between variable dimensionality (several thousand) and the sample size (a few hundred), there is a need for data mining methods that can discover significant and robust biomarkers from high-dimensional data. Rule learning is a useful data mining technique for the discovery of biomarkers from high-dimensional biomedical data. We have previously developed and applied rule learning methods to analyze ‘omic’ data successfully (Gopalakrishnan et al., 2004, 2006; Ranganathan et al., 2005). Rules have several advantages, including that they are easy for humans to interpret, represent knowledge modularly and can be applied using tractable inference procedures.

In this article, we develop and evaluate a novel probabilistic method for learning rules called the Bayesian rule learning (BRL) algorithm. This algorithm learns a particular form of a Bayesian network (BN) from data that optimizes a Bayesian score, and then translates the BN into a set of probabilistic rules. The use of the Bayesian approach allows prior knowledge (as probabilities) to be incorporated into the learning process in a mathematically coherent fashion. The possibility of over-fitting is attenuated by the incorporation of prior probabilities into the rule-discovery process. BRL outputs the predictive rule model with the best Bayesian score, which represents the probability that the model is valid given the data.

The remainder of the article is organized as follows. Section 2 presents the BRL algorithm and briefly reviews other popular rule learning methods. Section 3 describes the datasets and the experimental setup to evaluate BRL. Section 4 presents the results of applying BRL to 24 published ‘omic’ datasets, and compares its performance with multiple rule-learning algorithms. Section 5 presents our conclusions.

2 METHODS

In biomedical data mining, a typical task entails the learning of a mathematical model from gene expression or protein expression data that predicts an individual phenotype, such as disease or health. Such a task is called classification and the model that is learned is termed as a classifier. In data mining, the variable that is predicted is called the target variable (or simply the target), and the features used in the prediction are called the predictor variables (or simply the predictors). Rule learning is a useful technique for knowledge discovery from data that is discrete.

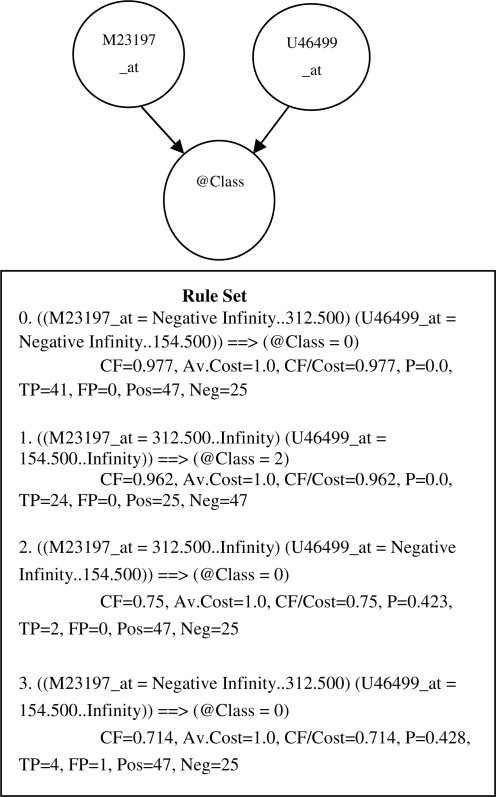
In this article, we present a Bayesian method for learning BNs and translating it into rules as shown in Figure 1. A rule model is a set of rules that together comprise a classifier that can be applied to new data to predict the target. The main contribution of this BRL method is its ability to quantify uncertainty about the validity of a rule model using a Bayesian score. This score is used for model selection. We now discuss in detail the BRL method. This algorithm learns BN models from the data and the model is then translated into a set of rules with associated statistics.¹ These rules are mutually exclusive and exhaustive over the values of the predictor variables, and hence inference using these set of rules becomes trivial. Given a new test case, the rule that matches its values for the predictor variables is used to infer the value of the target variable.

Fig. 1.

ABN structure learned by BRL on the acute lymphoblastic leukemia (ALL) versus acute myeloid leukemia (AML) dataset (Golub et al., 1999) and its equivalent set of rules. @Class refers to the target variable that can take on values of either 0 (ALL) or 2 (AML) in this example. Each rule is associated with statistics from the training data (see note 1).

2.1 Bayesian networks

A BN is a probabilistic model that consists of two components: a graphical structure and a set of probability parameters. The graphical structure consists of a directed acyclic graph, in which nodes represent variables and variables are related to each other by directed arcs that do not form any directed cycles. Associated with each node (let us call it a child node) is a probability distribution on that node given the state of its parent nodes, and all the probability distributions for all the nodes taken together provide a factored (and often concise) representation of the joint probability distribution over all the variables (Pearl, 1988). Learning a BN is a two-step process corresponding to learning the structure and the parameters of the model, and several methods have been developed to automatically learn BNs from data (Neapolitan, 2004). Here, we use the Bayesian method called K2 (both the K2 scoring measure and the K2 forward stepping search heuristic) for learning BNs (Cooper and Herkovits, 1992).

The K2 scoring measure (Cooper and Herskovits, 1992) assumes that the variables are discrete, the cases (training examples) occur independently, there are number of cases that have variables with missing values² and there is a uniform prior probability distribution over the space of all possible network structures. The K2 measure also assumes that every possible probability distribution over the values of a node given a state of its parents is equally likely (uniform). Under these assumptions, a closed form solution for the Bayesian score is given by the following equation (Cooper and Herskovits, 1992):

(1)

where M is the BN structure under consideration, D the data used to learn M, n the number of variables in M, q_i the number of parent states of child variable i, r_i the cardinality (number of values or states) of variable i and N_ijk the number of instances in the training database D for which variable i has the value k and the parents of i have the value state denoted by index j. Also, N_ij is the sum over k of N_ijk.

Since it is usually computationally intractable to search over all possible BN structures to locate the one with the highest score, a greedy search in the space of BNs is employed. The greedy search method used by K2 (Cooper and Herskovits, 1992), requires an ordering on the variables and a user-specified parameter for the maximum number of parents any variable in the network can have.

2.2 Bayesian rule learning

The BRL algorithm uses the score given by Equation (1) to learn simple BNs. In particular, (i) BRL considers constrained BNs where the BN consists of one child variable, which is the target to be predicted, and other variables are parents of it; (ii) only the target node is evaluated with the Bayesian score; and (iii) models are searched by utilizing a beam (memory of particular size) to store high-scoring BNs. The beam refers to a restricted memory size for storing BN structures and is implemented as a priority queue of fixed width (beam size), where BNs are stored according to their score. This reduces the memory requirement for heuristic, best-first search, by exploring only those BN structures that are high scoring, while at the same time providing the ability to improve upon greedy search with a beam size of 1.

Using the constrained structure of the algorithm in Figure 2, as illustrated by the model shown in Figure 1, Equation (1) simplifies further to the following equation:

(2)

where q is the number of joint parent states of the target variable, r the cardinality (number of values or states) of the target variable and N_jk the number of instances in the training database D for which the target variable has the value k and its parents have the joint value state denoted by index j. Also, N_j is the sum over k of N_jk.

Fig. 2.

The BRL algorithm.

Figure 1 depicts an example of BN structure M learned by BRL, where @Class represents a target variable and two genes M23197_at and U46499_at are its parents. The values or expression of these genes influence the target class. Figure 1 depicts M and the set of rules derived from M. A rule set is defined as the conditional probability, such as the conditional probability P(@Class | M23197_at, U46499_at) for all values of M23197_at and U46499_at. In the example, each of the two genes can take on two discrete ranges of values. Hence, the total number of possible combinations of the values for the predictor variables is four (Rules 0–3).

The Bayesian score [Equation (2)] represents the joint probability of the model and the data under the assumption of uniform structure priors. Since P(M|D) ∝ P(D|M), given the assumption that all models are equally likely a priori, the Bayesian score can be directly utilized as a measure of model uncertainty and used to prioritize and select models. Breadth-first marker propagation (Aronis and Provost, 1997) is utilized to record the matching statistics (or counts) and greatly speeds up the calculations by requiring just one pass through the training data to record the counts. BRL is thus very efficient and runs in O(n²m) time given n + 1 variables and m training examples, using the default constant values for beam size b and the maximum conjunct parameter MAX_CONJS, which are both user-specified.

The BRL algorithm is shown in Figure 2. It takes as input a set of input variables X, a target variable T, an upper bound on the number of parents that T can have and training data containing vectors of values for X's and the corresponding value for T. The user can also provide a beam width b that restricts the number of BNs that are in the priority queue. The default beam width is 1000.

In Step 1, a BN containing just the target node with zero parents is created, and it is scored using Equation (2). Step 2 initializes the list of variables X that appear in models that have good scores and cannot have a better score by the addition of any single parent of T. The loop condition in Step 3 checks to see whether there are still models on the beam that can be expanded further by the addition of a parent variable such that the score would improve. Steps 4–8 perform one-step forward search by adding one more allowed variable as an additional parent of the target T to the structure. Specialization refers to the addition of a parent variable (not already present) to the structure of current model, such that the total number of parent variables in the model does not exceed the upper bound MAX_CONJS. The default value we use for MAX_CONJS is 5.

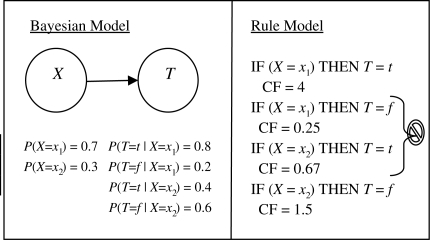
In Step 9, a check is made to see whether the score of the model removed from the beam improved after all one-step specializations. If not, that model is placed on a priority queue containing final model structures ordered according to their Bayesian scores. Even though we store many final models on the final priority queue, only the best scoring model is presented to the user in the form of a rule model in Step 10. For each value of target variable T, its probability given each state of possible values of its parent variables is calculated from the training data. The certainty factor is calculated as shown in Figure 3.

Fig. 3.

Example of a BN (left) to a set of rules (right), where the CF is expressed as the likelihood ratio of the conditional probability of the target value given the value of its parent variable. As seen in Rule 1, the CF is the likelihood ratio 0.8/0.2 = 4. The two rules in the middle are automatically pruned by BRL and only the higher CF rule for each unique rule antecedent is retained in the rule model.

We perform a simple pruning in Step 10, wherein we output only the rule with the target value that has the highest probability given the particular state of its parent variables (Fig. 3). There are many other methods that could be used to perform pruning of the rules generated in Step 10, such as the number of training examples covered by the rule (Han and Kamber, 2006).

Also, we perform an optimization to increase search efficiency of the BRL algorithm. As can be seen in Step 9, the algorithm keeps track of those sets of variables that cannot be specialized further by addition of single variables as parents of the target such that the Bayesian score improves. The assumption is that if a predictor is in some final rule, then it is unlikely to be a strong predictor in another rule. While empirically, we observe that this assumption works well for most datasets that we have analyzed, it is certainly possible that there are datasets for which the assumption will not work well. Thus, extensions to this basic BRL algorithm can be explored along several directions to overcome some of the assumptions and limitations.

2.3 Rule learning methods

For our experiments we used three readily available rule learning methods: Conjunctive Rule Learner, RIPPER and C4.5. Conjunctive Rule Learner is a simple rule learner that learns a set of simple conjunctive rules that optimizes the coverage and predictive accuracy. It uses a technique called Reduced Error Pruning (Furnkranz and Widmer, 1994) to trim an initial set of rules to the smallest and simplest subset of rules that provide highest discrimination. Repeated Incremental Pruning to Produce Error Reduction (RIPPER) was developed by Cohen (1995) and uses the REP technique in Conjunctive Rule Learner, but performs multiple runs (Cohen, 1996). C4.5 is a decision tree learner developed by Quinlan (1994) that extends the basic decision tree learner ID3 (Quinlan, 1986) to improve classification. These improvements include parameterization of the depth of the decision tree, rule post-pruning, ability to handle continuous-valued attributes, ability to choose the best attribute to use in growing the decision tree and an increase in computational efficiency (Gabrilovich and Markovitch, 2004; Xing et al., 2007).

2.4 Discretization

The rule learners described above require variables with discrete values. We used a new discretization method called heuristic efficient Bayesian discretization (EBD; Lustgarten, 2009), which we developed for transforming continuous data to discrete. EBD uses a Bayesian score to discover the appropriate discretization for a continuous-valued variable and runs efficiently on high-dimensional biomedical datasets. Compared with Fayyad and Irani's (FI) discretization method (Fayyad and Irani, 1993), which is an efficient method commonly used for discretization, EBD had statistically significantly better performance in the evaluation report in Lustgarten et al. (2008).

3 EXPERIMENTAL SETUP

3.1 Biomedical datasets

The performance of BRL and the three comparison rule learning methods were evaluated on 24 biomedical datasets [21 publicly available genomic datasets, two publicly available proteomic datasets from the Surface Enhanced Laser/Desorption Ionization Time of Flight (SELDI–TOF; Wright et al., 1999) mass spectrometry platform and one University of Pittsburgh proteomic dataset, which is a diagnostic dataset from a Amyotrophic Lateral Sclerosis study obtained using the SELDI–TOF platform]. The datasets, along with their type (prognostic/diagnostic), number of instances, number of variables and the majority target-value proportions are given in Table 1.

Table 1.

Biomedical datasets used for the comparison experiments

#	T	#C	#A	#S	M	Reference
1	D	2	6584	61	0.651	Alon et al. (1999)
2	D	3	12 582	72	0.387	Armstrong et al. (2002)
3	P	2	5372	86	0.795	Beer et al. (2002)
4	D	5	12 600	203	0.657	Bhattacharjee et al. (2001)
5	P	2	5372	69	0.746	Bhattacharjee et al. (2001)
6	D	2	7129	72	0.650	Golub et al., 1999
7	D	2	7464	36	0.500	Hedenfalk et al. (2001)
8	P	2	7129	60	0.661	Iizuka et al. (2003)
9	D	4	2308	83	0.345	Khan et al. (2001)
10	D	4	12 625	50	0.296	Nutt et al. (2003)
11	D	5	7129	90	0.642	Pomeroy et al. (2002)
12	P	2	7129	60	0.645	Pomeroy et al. (2002)
13	D	26	16 063	280	0.574	Ramaswamy et al. (2001)
14	P	2	7399	240	0.145	Rosenwald et al. (2002)
15	D	9	7129	60	0.506	Staunton et al. (2001)
16	D	2	7129	77	0.746	Shipp et al. (2002)
17	D	2	10 510	102	0.150	Singh et al. (2002)
18	D	11	12 533	174	0.150	Su et al. (2001)
19	P	2	24 481	78	0.562	van't Veer et al. (2002)
20	D	2	7039	39	0.878	Welsh et al. (2001)
21	P	2	12 625	249	0.805	Yeoh et al. (2002)
22	D	2	11 003	322	0.784	Petricoin et al. (2002)
23	D	3	11 170	159	0.364	Pusztai et al. (2004)
24	D	2	36 778	52	0.556	Ranganathan (2005)

In the type (T) column, P signifies prognostic and D signifies diagnostic. #C represents the number of classes, #A the number of attributes within the dataset, #S the number of samples and M is the fraction of the data covered by the most frequent target value. The first 21 datasets contain genomic data, whereas the last three datasets contain proteomic data.

3.2 Data mining techniques and statistical analysis

As mentioned, for comparison, we used three rule learners, namely, Conjunctive Rule Learner, RIPPER and C4.5 as implemented in WEKA version 3.5.6 (Witten and Frank, 2005). We used two versions of BRL, namely, BRL₁ (beam size set to 1) and BRL₁₀₀₀ (beam size set to 1000). We used heuristic EBD for discretization; the discretization cutpoints were learned from the training set and then applied to both the training and test sets. We implemented EBD in Java, so that it can be used in conjunction with WEKA.

We evaluated the rule learning methods using 10-fold cross-validation performed two times. The methods were evaluated using two measures: balanced accuracy (BACC), which is the average of sensitivity and specificity over all one-versus-rest comparisons for every target value, and relative classifier information (RCI; Sindhwani et al., 2001). These measures are described below.

The BACC differs from accuracy in that it compensates for skewed distribution of classes in a dataset. BACC is defined as follows:

where C is the set of the target variable values, and Sensitivity(c) [Specificity(c)] refers to the sensitivity (specificity) of the target value c versus all other values of the target. TP_(c|c) is the number of samples predicted to have the value c for the target variable given that the observed value is c, FN_(¬c|c) is the number of samples predicted to have a value other than c for the target variable given that the observed value is c, TN_(¬c|¬c) is the number of samples predicted to have a value other than c for the target variable given that the observed value is not c and FP_(c|¬c) is the number of samples predicted to have the value c for the target variable given that the observed value is not c.

RCI is an entropy-based performance measure that quantifies how much the uncertainty of a decision problem is reduced by a classifier relative to classifying using only the prior probability distribution of the values of the target variable uninformed by any predictor variables (Sindhwani et al., 2001). The minimum value for RCI is 0%, which is achieved by a classifier that always predicts the majority target-value, and the maximum value is 100%, which is achieved by a classifier with perfect discrimination. RCI is sensitive to the distribution of the target values in the dataset, and thus compensates for the observation that it is easier to obtain high accuracies on highly skewed datasets. Like the area under the receiver operating characteristic curve (AUC), RCI measures the discriminative ability of classifiers. We did not use AUC since there are several interpretations and methods to compute the AUC when the target has more than two values.

4 RESULTS

The average BACCs obtained from 10-fold cross-validation performed two times for each of the 24 datasets are shown in Table 2. As can be seen from the average BACCs for the 24 datasets, both BRL₁ and BRL₁₀₀₀ clearly perform better than the other rule learning methods. This holds for both the genomic datasets (1–21) and the proteomic datasets (22–24).

Table 2.

BACC from 10-fold cross-validation performed two times on the 24 datasets depicted along with the overall averages (AVG) and their SD

#	Conj_ RL	Ripper	C4.5	BRL1	BRL1000
1	98.34	98.65	100.00	100.00	100.00
2	29.83	44.20	66.91	86.22	100.00
3	47.29	54.39	60.41	50.71	54.88
4	47.46	43.92	43.47	59.29	69.15
5	30.24	32.45	37.68	41.17	47.17
6	87.42	81.83	84.50	83.75	82.75
7	81.70	81.70	81.70	97.50	100.00
8	20.70	25.54	38.56	45.00	63.75
9	41.89	47.36	42.56	61.41	74.71
10	37.19	59.83	58.96	59.92	61.24
11	26.04	29.62	38.81	45.62	48.90
12	51.76	53.40	55.53	57.08	47.50
13	51.73	62.48	70.28	65.00	68.46
14	40.81	44.81	42.93	43.31	49.63
15	43.55	46.64	46.39	54.56	57.78
16	47.13	59.48	71.69	80.50	83.17
17	40.93	47.59	40.73	82.17	74.67
18	23.91	29.88	33.80	26.95	55.78
19	40.52	55.57	48.71	76.83	77.50
20	50.22	71.30	83.81	60.00	73.75
21	40.98	43.09	42.52	49.29	51.27
22	53.54	48.19	54.92	61.59	65.07
23	44.60	57.38	50.05	64.34	53.20
24	61.99	50.79	64.47	75.83	63.33
AVG	47.57	52.80	56.64	63.66	67.65
(SD)	(19.03)	(17.44)	(17.91)	(18.45)	(16.57)
GA	46.74	52.89	56.66	63.16	68.67
(SD)	(20.08)	(18.64)	(19.06)	(19.58)	(17.39)
PA	53.38	52.12	56.48	67.25	60.53
(SD)	(8.70)	(4.74)	(7.34)	(7.55)	(6.41)

Averages over the genomic datasets 1–21 (GA) and their SDs, as well as averages over the proteomic datasets 22–24 (PA) and their SDs. Bold numbers indicate highest performance on a dataset.

We see that BRL₁₀₀₀ has the highest BACC on 15 datasets, while BRL₁ has the highest BACC on 4 datasets. On the remaining five datasets, C4.5 has the highest BACC on three, ties with BRL on one and Conjunctive Rule Learner has the highest on one. Only the first dataset is very easy to classify by all rule learners. As seen in Table 3, the performance of both BRL₁ and BRL₁₀₀₀ are statistically significantly better than C4.5, its nearest competitor in terms of BACC. When compared with each other, BRL₁₀₀₀ outperforms BRL₁.

Table 3.

Statistical comparisons between C4.5 and the two BRL algorithms using BACC

Comparison	Average	Diff.	t-test	Wilcoxon
			(t-score)	(Z-score)
BRL1versus	63.66 versus	7.02	0.015	0.011
C4.5	56.64		(2.624)	(2.555)
BRL1000 versus	67.65 versus	11.01	0.001	0.001
C4.5	56.64		(3.988)	(3.254)
BRL1000 versus	67.65 versus	3.99	0.050	0.029
BRL1	63.66		(2.071)	(2.190)

We do not compare Ripper and Conjunctive Rule Learner because C4.5 and the two BRL algorithms completely dominate on both performance measures. BRL₁ stands for BRL with beam size 1 and BRL₁₀₀₀ represents BRL with beam size 1000. We use both two-sided t-test and two-sided Wilcoxon signed rank test. Those P-values that are significant (≤0.05) are in bold and scores with a positive value favor the first method in the comparison.

The average RCIs obtained by the various rule learning methods are shown in Table 4. BRL₁₀₀₀ has the highest RCI on 19 datasets, whereas BRL₁ has the highest RCI on 3 datasets. There was one tie among the two BRL methods and C4.5. In addition, C4.5 has the highest RCI on one dataset. In Table 5, we compare the difference in performance using the RCI measure between C4.5 with BRL₁ and BRL₁₀₀₀ and both BRL methods are statistically significantly better than C4.5; the difference in performance using the RCI measure between BRL₁₀₀₀ and BRL₁ is statistically significant in favor of BRL₁₀₀₀.

Table 4.

RCI results on the 24 datasets (from 2 × 10-fold)

#	Conj_RL	Ripper	C4.5	BRL1	BRL1000
1	93.70	93.83	100.00	100.00	100.00
2	31.58	46.79	70.83	91.27	100.00
3	0.09	4.35	6.81	4.3	20.04
4	18.35	46.16	45.69	62.31	64.1
5	0.38	0.71	1.07	65.44	75.71
6	42.64	43.64	35.37	44.28	43.02
7	71.59	71.59	71.59	85.44	100.00
8	0.56	1.22	0.45	35.56	66.77
9	16.28	64.87	58.30	84.12	85.6
10	23.63	38.02	37.47	38.07	38.25
11	4.32	21.15	27.71	32.58	43.66
12	3.13	1.85	3.01	31.07	39.7
13	13.55	50.01	61.84	51.34	62.36
14	0.17	1.01	0.61	11.14	23.57
15	5.30	24.85	24.47	36.67	42.59
16	16.12	20.34	24.52	27.53	54.65
17	33.54	39.00	33.38	67.33	36.37
18	7.25	55.32	62.59	49.89	64.21
19	19.56	26.83	23.51	37.09	41.79
20	15.39	24.92	28.75	18.39	20.83
21	0.23	0.73	0.59	12.75	7.2
22	1.02	13.94	7.21	17.82	19.02
23	9.18	17.22	12.60	40.45	57.5
24	13.61	8.84	14.66	32.26	38.39
AVG	18.38	29.88	31.38	44.88	51.89
(SD)	(23.16)	(25.42)	(27.46)	(26.38)	(26.60)
GA	19.87	32.25	34.22	46.98	53.83
(SD)	(24.38)	(26.36)	(28.24)	(27.39)	(27.29)
PA	7.9	13.3	11.5	30.2	38.3
(SD)	(6.4)	(4.2)	(3.8)	(11.5)	(19.2)

Table 5.

The statistical comparisons between C4.5 and the two BRL implementations using RCI

Comparison	Average	Diff.	t-test	Wilcoxon
			(t-score)	(Z-score)
BRL1 versus	44.88 versus	13.50	0.001	0.001
C4.5	31.38		(3.853)	(3.376)
BRL1000 versus	51.89 versus	20.51	<0.001	<0.001
C4.5	31.38		(4.975)	(3.984)
BRL1000 versus	51.89 versus	7.01	0.008	0.001
BRL1	44.88		(2.894)	(3.194)

Table 6 depicts a comparison of the average number of variables (markers) appearing in the rule models for C4.5, BRL₁ and BRL₁₀₀₀, when run with default parameter settings. The average was calculated over the models generated from 20 folds (obtained from stratified 10-fold cross-validation repeated two times) on the 24 datasets. As shown, the BRL models have ∼70% less variables on average in their models than C4.5.

Table 6.

Comparison of the average number of variables in the models produced by C4.5 and BRL over all folds

#	C4.5	BRL1	BRL1000
1	1.00	1.00	1.00
2	3.00	3.00	3.00
3	5.00	4.00	5.00
4	7.00	5.00	5.00
5	6.00	5.00	5.00
6	6.00	2.00	2.00
7	5.00	4.00	4.00
8	7.00	5.00	5.00
9	5.00	3.00	4.00
10	5.00	4.00	4.00
11	12.00	5.00	5.00
12	4.00	3.00	3.00
13	8.00	4.00	4.00
14	1.00	1.00	1.00
15	7.00	5.00	5.00
16	30.00	5.00	5.00
17	4.00	4.00	4.00
18	26.00	5.00	5.00
19	18.00	5.00	5.00
20	15.00	5.00	5.00
21	88.50	5.00	5.00
22	32.00	5.00	5.00
23	27.00	5.00	5.00
24	7.00	3.00	3.00
Average	13.72	4.00	4.08

If each predictor variable has only two discretized ranges of values, then BRL with default parameters would generate between 2³ and 2⁵ rules on average. However, discretization could yield a larger number of value ranges for a variable, thereby increasing the number of rules generated by BRL. To reduce the number of rules, we can prune rules with zero coverage, that is, those rules whose left-hand side does not match any of the samples in the training data. We notice that pruning does not harm BRL's performance. However, rule pruning could cause problems during testing, since rules that do not match training data could still match test data. We include an example of pruned rules and also C4.5 rules in the Supplementary Material. The variables chosen in BRL's predictive models are often different from those chosen by C4.5.

4.1 Discussion

There are several advantages that accrue from BRL that are not available in current rule learning algorithms. BRL allows for the evaluation of the entire rule set using a Bayesian score. Using such a score results in a whole model evaluation instead of a per rule (or local) evaluation, which often occurs with Ripper and C4.5. The Bayesian score allows us to capture the uncertainty about the validity of a rule set. BRL currently uses this score only for model selection. However, the score could be utilized in extensions to BRL for performing inference when rule sets can be weighted by this score, which would be a form of Bayesian model averaging.

A Bayesian approach allows incorporation of both structure and parameter priors. When training data are scarce, such as in ‘omic’ data analysis, it is useful to incorporate prior knowledge to improve the accuracy of learned models. For example, a scientist could define all of the variable relationships using either a knowledge base or restrict the possible variables with which to build the model (Frey et al., 2005; Miriam et al., 2005). In a Bayesian approach, a scientist might provide prior knowledge specifying conditional independencies among variables, constraining or even fully specifying the network structure of the BN. In addition to providing such structure priors, the scientist might also specify knowledge in the form of prior distributions over the parameter values of the model. Structure priors are arguably the most useful, however, because in our experience scientists are often more confident about structural relationships than about parameter values.

We have not explored informative priors in this article. We used uniform parameter and uniform structure priors. Exploring informative structure priors in this domain is a direction for future research.

There are different ways of representing non-informativeness of parameters using the Dirichlet priors. We have explored one approach, it would be useful to explore other approaches as well.

An interesting open problem is to investigate methods for BRL rule ordering and pruning within a set of rules. For example, pruning a set of BRL rules based on using local structure and scores (Chickering et al., 1997; Friedman and Goldszmidt, 1996; Visweswaran and Cooper, 2005) would be worth investigating.

A major advantage of BRL is that it can find models with fewer variables (markers) that have equivalent or greater classification performance than those obtained from several other rule learning methods. Fewer variables mean fewer markers for biological verification and subsequent validation. This is important in biomarker discovery and validation studies that have to be designed carefully and under tight resource constraints.

5 CONCLUSIONS

We have shown that using a BN approach to generate rule models not only allows a more parsimonious model (in terms of the number of variables), but also produces results that are statistically significantly superior to common rule learning methods. It also allows the creation of probabilistic rules that are optimized on the rule model level as opposed to the current method of evaluation per rule. Using BN as a generating model also provides a coherent method for incorporating different types of prior information and updating the rule model.

The basic BRL algorithm presented here can be extended in many ways, which include experimenting with different priors, pruning and rule ordering methods. The use of multiple data mining methods to analyze biomedical ‘omic’ datasets has become important as these techniques often complement one another in terms of discoveries. In this article, we present and evaluate a novel approach that can complement existing methods for biomedical data mining. We hope that researchers will find this approach useful for efficient knowledge discovery from biomedical datasets and that future extensions will yield additional improvements.