Power to detect selective allelic amplification in genome-wide scans of tumor data

Abstract

Motivation: Somatic amplification of particular genomic regions and selection of cellular lineages with such amplifications drives tumor development. However, pinpointing genes under such selection has been difficult due to the large span of these regions. Our recently-developed method, the amplification distortion test (ADT), identifies specific nucleotide alleles and haplotypes that confer better survival for tumor cells when somatically amplified. In this work, we focus on evaluating ADT's power to detect such causal variants across a variety of tumor dataset scenarios.

Results: Towards this end, we generated multiple parameter-based, synthetic datasets—derived from real data—that contain somatic copy number aberrations (CNAs) of various lengths and frequencies over germline single nucleotide polymorphisms (SNPs) genome-wide. Gold-standard causal sub-regions were assigned within these CNAs, followed by an assessment of ADT's ability to detect these sub-regions. Results indicate that ADT possesses high sensitivity and specificity in large sample sizes across most parameter cases, including those that more closely reflect existing SNP and CNA cancer data.

Availability: ADT is implemented in the Java software HADiT and can be downloaded through the SVN repository (via Develop→ Code→SVN Browse) at: http://sourceforge.net/projects/hadit/.

Contact: ninad.dewal@dbmi.columbia.edu

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The characterization of genes and variants that cause cells to proliferate out of control has been an activity long at the forefront of cancer research. Such variants are thought to confer selective advantage to progenitor cancer cells from the perspective of the disease and therefore would be observed with greater probability within a progressing tumor (Nowell, 1976). According to the commonly accepted Two-Hit Hypothesis, at least two such variants, or ‘hits’, are required for cells to become cancerous (Knudson, 1971). We adopt this concept to focus on integrating variation that can be transmitted through the germline with somatically occurring changes. We consider a method to localize specific variants that are selected for by the disease.

Germline variants due to point mutations serve as the first variant type. Well-known examples include mutations in BRCA1 (Miki et al., 1994) and BRCA2 (Wooster et al., 1995) that lead to breast cancer. Common germline variants in the form of single nucleotide polymorphisms (SNPs) have also been detected by genome-wide association studies (GWAS) as contributing to risk of developing cancer. Recently demonstrated examples of such associations include loci implicated in colorectal and prostate cancer susceptibility on chromosome 8q24 (Amundadottir et al., 2006; Freedman et al., 2006; Gudmundsson et al., 2007; Tomlinson et al., 2007; Zanke et al., 2007), as well as loci associated with lung (Amos et al., 2008; Hung et al., 2008; Thorgeirsson et al., 2008), breast (Ahmed et al., 2009; Easton et al., 2007; Fletcher et al., 2008) and ovarian cancers (Song et al., 2009). However, examining SNPs alone has limitations. For example, disease markers, especially those with small effects, necessitate large sample sizes—often in the thousands—to generate sufficient power. Furthermore, population stratification within a cohort may either corrupt results or, if taken into account, reduce the effective sample size. Lastly, SNPs by themselves are unlikely to adequately explain the complexity of cancer, a disease with a genetic component that is inherently somatic.

A hallmark of tumor genomics is the existence of copy number aberrations (CNAs)—the second type of variant we consider—in somatic DNA. Long regions of amplification, recurrent over multiple tumor samples, have been observed in studies over the last two decades (Cher et al., 1996; Joos et al., 1995; Kallioniemi et al., 1992; Korn et al., 1999; Paris et al., 2004; Sun et al., 2007; Zhao et al., 2005) and can be visualized in Figure 1. These regions encompass extra copies of contained genes and may result in overexpression, as seen for example with HER2 in breast cancer (Slamon et al., 1987). Yet, the span of these recurrent CNA regions as detected by comparative genomic hybridization (CGH) experiments is often greater than 1 Mb, much broader than a single gene, thus making it difficult to pinpoint specific genes in such regions (Bentz et al., 1998; Solinas-Toldo et al., 1997).

Fig. 1.

Amplified regions within a chromosome. The figure displays an example of amplification status of calls across a chromosome as observed in real data. Recurrent stretches (or regions) of amplification are denoted by lines that span across many of the samples, highlighted by the translucent rectangle, with the driver SNP located at the midpoint, as indicated by the dotted line. Non-recurrent (or sample-specific) amplified regions are represented as stray stretches. During the evaluation experiments that simulate such data, four parameters are defined and tested: (i) the mean length of recurrently amplified regions in base pairs, (ii) the number of recurrently amplified regions across the genome, (iii) the mean length of non-recurrently (or sample specific) amplified regions in base pairs, and (iv) the number of non-recurrently (or sample specific) amplified regions per sample.

We discuss a new method for examining germline SNPs within somatically amplified CNA stretches to help target particular locations, putative disease genes, within these lengthy regions. The typing of both of these types of variants can be obtained from SNP array platforms using algorithms for genotype calling and copy number inference (Komura et al., 2006; Korn et al., 2008; Laframboise et al., 2007; Nannya et al., 2005). At a high level, our approach—called the amplification distortion test (ADT)—utilizes SNP and CNA information to perform a genome-wide scan for SNP alleles and haplotypes that are selected for somatic amplification across tumor samples. Hits that pass genome-wide significance thresholds (GWST) can eventually undergo fine mapping, which will reveal existing and novel oncogenes. A basic flavor of this method uses only information from heterozygote tumor calls, in a manner analogous to the transmission disequilibrium test (TDT) in germline genetics. We further present and discuss variants of our method that tally additional information from homozygous tumor calls.

This manuscript provides a formal description of ADT, generalizes the method to haplotypes, and focuses on assessing the method's power to detect such causal variants. This is done via analyzing ADT's performance across a variety of synthetic datasets that represent hypothetical tumor data. Results emphasize the dependence of sensitivity of ADT on practical parameters; and confirm this test to be powerful for large sample sizes.

The remainder of the article is partitioned into the following sections. Section 2 delineates the ADT method itself, significance testing, and algorithmic optimizations. Section 3 describes the evaluation of ADT's power. The final section summarizes our work and discusses future avenues.

2 METHODS

Amplification distortion builds on allele calls from all copies of a locus within a region of somatic amplification. While two of these calls make up the original germline genotype, additional calls indicate a copy-gain aberration and specify the amplified allele. We hypothesize that, on occasion, amplification of a particular allele may be causing tumor development and therefore will be selected over the other allele across many tumor samples. This selection implies that by ascertaining cases with tumors that had been subjected to selective pressure, we should expect to find such samples with this allele amplified and referred over its alternative allele more often than the converse. It is in heterozygote samples that such competition between alleles will be most directly observable, allowing determination of imbalanced amplification in ascertained tumors. Homozygote samples offer complementary information towards this end, as described later. This persistent selective imbalance has been reported in targeted somatic regions in mouse and human tumor DNA (Ewart-Toland and Balmain, 2004; Ewart-Toland et al., 2003; Nagase et al., 2003).

Towards quantifying this distortion, we were inspired by the TDT, formulated to perform association analysis on genetic germline data across parent–offspring duos (Spielman et al., 1993). TDT builds on Mendel's First Law—transmission of either allele at a marker from a heterozygous parent to an offspring with equal probability. TDT posits that this equality holds for affected offspring over many duos, a null hypothesis that is violated when a particular allele at the marker is associated with the disease trait. TDT therefore measures imbalance from 0.5/0.5 transmission across duos via the binomial test. Exclusive examination of transmission within families makes TDT immune to population stratification effects.

We use this idea of a distorted passing down of an allele to formulate our method, the ADT, to analyze tumor data for selective imbalance of allelic amplification. The null hypothesis states that during tumor formation across samples, either allele at a heterozygous marker is amplified with equal chance, and this amplified allele is clonally passed down along with the original germline allele pair to future somatic generations. Thus, according to this hypothesis, the amplified allele in a heterozygous tumor may be any of the two germline alleles with equal probability. The alternative hypothesis proposes that one of the alleles instead is amplified with significantly greater chance (distortion), and amplification of this particular allele has passed down the lineage (along with the original germline allele pair) because it confers selective advantage to the progression of the tumor. ADT calculates distortion using a binomial test on amplified instances of an allele as well as on amplified instances of haplotypes, as described in detail below. The focus on somatic tumor tissue within an individual—namely the clonal transmission of allelic amplification down a cellular lineage during the tumor's growth—grants the binomial test within ADT the benefit of being robust against population stratification. This allows identification of selected alleles across individuals of varying ethnic background.

As selection of a particular allele implies advantage of that allele towards tumor growth, it may be informative to analyze homozygous calls at a marker across samples as well. Comparing the ratio of amplified and non-amplified instances of homozygous genotypes may lend support towards selective amplification of an allele. This will be addressed following the focus on heterozygote analysis.

The formal definition of ADT is as follows. The input comprises of SNP and CNA call data for m markers and n tumor samples as two m × n matrices: D⁰ and D¹, where the former matrix contains copy number information for the SNP Array designated A allele and the latter matrix for the B allele. For example, the call for a copy-neutral heterozygous sample j at SNP i would be represented by D⁰[i, j] = 1, D¹[i, j] = 1, with 0 ≤ i < m and 0 ≤ j < n. However, a heterozygous sample j with an extra copy (amplification) of the A allele would be represented as: D⁰[i, j] = 2, D¹[i, j] = 1. These matrices can be referenced by D^x, where allele x ∈ {0, 1}.

We first define an m × n matrix Z, which indicates the number of distinct alleles somatically amplified at a call:

Zero values of Z represent copy-neutral or copy-loss regions. Those calls containing amplification of one allele, indicated by Z = 1, are of interest to us. Amplification of both homologous chromosomes, indicated by Z = 2, is a rare event that we discount.

We next define an m × n matrix G that contains the germline genotype information for the calls. We limit ourselves to diploid, autosomal loci due to our dependence on heterozygous calls. In addition, we only consider calls that are copy neutral at the germ line level. Such information can be obtained via calls on matched normal samples or through previously published copy number variation regions available online, such as the database of genomic variants (Iafrate et al., 2004).

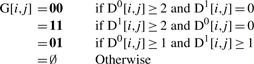We also define an m × n matrix A over {0, 1, ∅} that registers the identity of the amplified alleles:

Note that amplification of both homologous chromosomes is very rare and is discounted as ∅.

2.1 Distortions at individual SNPs

We first proceed with identifying the single SNPs within the A matrix at particular positions; we will explore haplotypes later. We define an m × 2 matrix C = [c_i,x], which stores the number of amplified instances of allele x participating strictly in heterozygous calls at a SNP i.

(1)

In other words, for single SNP analysis, an amplified instance of x equates to a heterozygous call that contains amplification of x exclusively. Thus, ‘amplified instances of x’, or c_i,x, signifies the number of heterozygous calls across samples at a SNP i possessing amplification strictly for x. For each allele x, we define the complement operator such that 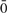=1 and =0. We also define a vector h = [h(0),…, h(m − 1)] of size m, which stores the total number of amplified instances of x and at a SNP i:

(2)

We can now define our hypotheses mathematically. Let Xⁱ₀, Xⁱ₁,…, Xⁱ_h(i)−1 be random indicator variables corresponding to the heterozygous, amplified samples at SNP i, specifying which allele would be amplified. Xⁱ_j are therefore independent, identically distributed Bernoulli variables. The random variable of their sum Sⁱ₁ = ΣXⁱ should match c_i,1. Symmetrically, we define the random variable Sⁱ₀ = h(i) − Sⁱ₁, observed to match c_i,0.

The null hypothesis states that neither allele at i is selected for amplification over the other across many samples. Formally, we hypothesize that:

(3)

We set a significance threshold α according to the binomial distribution, reporting c_i,x as significant if:

(4)

Traditionally α is 0.05; however, we assign a GWST to α to address multiple hypotheses, as described later in Section 2.3.

Significance of x and is clearly mutually exclusive. To test the hypotheses, we utilize the binomial test to calculate the probability of observing at least the number of amplified instances of x. In our case, the binomial test assumes 0.5 for its probability of success, which is appropriate under the null hypothesis:

(5)

Each p-value_i(x) is then converted to a logarithm-of-odds (LOD) score via performing: −log₁₀[p-value_i(x)]. The LOD score is a direct quantification of amplification distortion for an allele at a SNP.

2.2 Haplotype distortions

As amplicons span long regions of the genome, SNPs neighboring a distorted SNP are amplified as well. Linkage disequilibrium (LD) would thus produce amplified haplotypes. ADT can be generalized to detect those haplotypes selected for amplification.

It is first necessary to define an m × n matrix U over {0, 1, ∅} that registers the identity of the unamplified (non-amplified) alleles that correspond to the amplified alleles present in the A matrix via residing on the respective homologous chromosomes:

Note that we have used amplification status to implicitly phase the data into the A and U matrices, and as such, ADT does not require the input data to be previously phased. Somatic amplification is a rare event that typically occurs along only one of the two homologous chromosomes; as such, amplified calls are likely to lie along the same chromosome and thus comprise an amplified haplotype instance. The corresponding non-amplified haplotype instance is the haplotype formed from non-amplified calls residing on the other homologous chromosome. ADT quantifies distortion for a particular haplotype by comparing the number of amplified instances to the sum total of amplified instances and corresponding non-amplified instances of that haplotype across samples. Justification for such a comparison will be covered shortly. Note that since we discount calls that possess no amplification or calls with both alleles amplified, we avoid ambiguity in assigning phase.

In addition, note that the definition of U allows for homozygous calls. In the single SNP case, we considered exclusively amplified heterozygous calls. Heterozygosity at the haplotype level for a sample, however, requires only one heterozygous call at minimum to exist in the spans of the homologous haplotype pair; this allows for homozygous calls to be included in haplotypes. Haplotypes consisting of exclusively homozygous calls result in no distortion, as there will be an equal number of amplified and corresponding non-amplified instances of each haplotype across samples.

We now proceed with details of ADT's haplotype distortion detection:

Let w represent the window size, or haplotype length, where (1 ≤ w ≤ m). For single SNP analysis again, w = 1. This variable is user-defined and is used consistently across the genome in an overlapping sliding window fashion.

Let i represent an index of a marker, where (0 ≤ i < m − w + 1)

A^w[i, j] is the amplified haplotype string from matrix A starting at index i for a sample j with window size w, such that it is the concatenation of characters (A[i, j], A[i + 1, j],…, A[i + w − 1, j]).

A_i^w is the set of unique strings from all A^w[i, j] (0 ≤ j < n), excluding those A^w[i, j] strings that contain ∅ characters.

U^w[i, j] is the corresponding non-amplified haplotype string from matrix U starting at index i for a sample j with window size w, such that it is the concatenation of characters (U[i, j], U[i + 1, j],…, U[i + w − 1, j]).

U_i^w is the set of unique strings from all U^w[i, j] (0 ≤ j < n), excluding those U^w[i, j] strings that contain ∅ characters.

ALL_i^w is the set of unique strings from (A_i^w∪ U_i^w). Set elements can be accessed using index k (0 ≤ k <|ALL_i^w|).

Now we have a set of unique haplotype strings per genome position and window size. For haplotypes starting at SNP i with length w, we define vectors C^A = [c_k^A], C^U = [c_k^U] and C^Total = [c_k^Total], each of size |ALL_i^w|. These vectors store the respective amplified, corresponding non-amplified, and sum total counts of the unique haplotype strings:

(6)

(7)

(8)

It was mentioned above that ADT calculates distortion by comparing c_k^A with c_k^Total; the rationale for this is provided here. In the single SNP case, we compared the amplified counts of allele x with 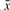via testing allele count c_i,x against the sum total count h(i). This translates similarly to the haplotype case, with the major difference that |ALL_i^w| can be as large as 2^w.

Let h_k represent the haplotype ALL_i^w[k]. The haplotypes across the n samples can then be depicted in (amplified / corresponding non-amplified) pairs for each amplified sample as, for instance: (h₀/h₁), (h₀/h₂), (h₀/h₃), (h₁/h₂), (h₁/h₃), (h₂/h₀),…, (h₀/h₂). To accurately calculate distortion for h_k, we must examine only those pairs that include h_k. c_k^A is the number of pairs in which h_k is amplified. c_k^U is the number of pairs in which h_k remains non-amplified while the other haplotype in the pair is amplified. Comparing c_k^A with c_k^U via c_k^Total translates to comparing h_k with the other haplotypes (with which it pairs) starting at i, thus revealing the level of selection for amplification of h_k. A high c_k^U over c_k^A suggests against such selection.

We can now revisit our hypotheses mathematically. Let ωⁱ_k represent all the haplotype pairs across the n samples starting at marker i such that each pair: possesses h_k and another haplotype, and either h_k or the other haplotype are amplified. Note that c_k^Total = |ωⁱ_k|. Let Tⁱ_k be a random variable representing the number of amplified instances of h_k in ωⁱ_k. In the haplotype case, the null hypothesis states that h_k is not selected for amplification over the other haplotypes with which h_k forms pairs across samples. We formally hypothesize:

(9)

We set a significance threshold α according to the binomial distribution, reporting c_k^A as significant if:

(10)

In other words, the alternative hypothesis states that h_k is selected for amplification over the other haplotypes with which h_k forms pairs across samples. Traditionally α is 0.05; however, we assign a GWST to α to address multiple hypotheses, as described later in Section 2.3.

To test the hypotheses, we utilize the binomial test to calculate the probability of observing at least the number of amplified instances of h_k. In our case, the binomial test assumes 0.5 for its probability of success, which is appropriate under the null hypothesis:

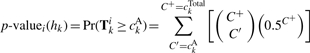(11)

Each p-value_i(h_k) is then converted to a logarithm-of-odds (LOD) score via performing: –log₁₀[p-value_i(h_k)]. The LOD score is a direct quantification of amplification distortion for a haplotype h_k at SNP i.

2.3 Significance testing

Running ADT over thousands of SNPs introduces a high risk of spurious results. To alleviate effects from multiple hypotheses, permutation testing is performed for single SNP or haplotype analysis to determine a respective genome-wide threshold of significance for LOD scores. In both cases, our approach requires permuting the dataset over t = 10⁴ iterations. During each iteration k of the t iterations, the amplification status of alleles for a sample j is uniformly flipped in heterozygous calls genome-wide with 50% probability. To model this, we define a k × j matrix F = [f_k,j], which represents whether the call values for sample j are flipped during an iteration k:

We now define new D_k^x matrices, each of size m × n, to reflect the changes made during an iteration k:

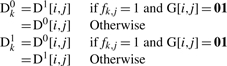The respective A and U matrices, as well as the single SNPs or haplotypes, can be subsequently determined from the D_k^x matrices during an iteration k. We define a list L that retains the top t LOD scores over all iterations. The GWST is set to the LOD score s that has at most 0.05 probability of appearing on average over the t iterations:

(12)

The LOD scores that ADT calculated from analyzing the original D^x matrices are compared with GWST. Only those scores that are greater than or equal to GWST are deemed to be significant genome-wide and are unlikely to be an effect of noise. This is equivalent to comparing the binomial test p-values with α, where α = 10^(−GWST).

Alternatively, we can set a chromosome-wide significance threshold (CWST), defined similarly to the GWST but restricted to a chromosome-by-chromosome basis. We define a list L_c that retains the top t LOD scores over all iterations from chromosome c. The threshold for c, CWST_c, is set to the LOD score s_c that has at most 0.05 probability of appearing on average over the t iterations:

(13)

CWST is designed to offer a targeted option within ADT. This alleviates the situation in which moderately amplified regions containing distortion on one chromosome are discounted due to falling below a GWST that is influenced by highly amplified regions on another chromosome. A consequence of this addition is an increase in the power of the method, as discussed later.

Lastly, ADT and the permutation testing procedure examine only those SNPs with six or more amplified heterozygous calls as a means to explicitly reduce testing burden. However, by the nature of the calculation of the GWST and CWST, SNPs with fewer calls would be automatically eliminated from consideration anyway, as they would reside at the bottom of lists L and L_c, thereby unable to affect determination of the thresholds.

2.4 Algorithmic optimizations

The hefty computation requirements of permutation testing necessitated optimizations in memory use and execution time. Towards this end, ADT uses object pools and sliding windows in an optimal fashion, keeping track of amplified haplotype windows and counts by using bounded buffers and bit vectors. ADT is implemented in the Java software Haplotype Amplification Distortion in Tumors (HADiT); location of the source code with these optimizations is given in Supplementary Material (Section Software).

ADT is also highly parallelizable. With the requirement that data files be partitioned by chromosome, ADT can multi-thread chromosome processing to take advantage of multi-core machines. ADT can be further parallelized to run over a computing cluster, letting each machine process a chromosome or specified set of chromosomes. These optimizations allow ADT to scale robustly to larger dataset sizes, such as the magnitude of sequencing data.

2.5 Analysis of homozygous calls

Up until this point, ADT utilizes only heterozygous calls, analysis that is unique to this application. However, this ignores potentially useful information from homozygous calls, whose analysis can rely on existing techniques from GWAS studies. Briefly, skewed ratios of somatically amplified to non-amplified homozygous counts at a marker may imply selection of an allele being amplified, thereby complementing or adding to the information provided by the binomial test alone. Similar to the germline tests of case-control association versus TDT, the additional information from homozygotes comes at a price of sensitivity to population structure here as well.

Towards this end, we adapted two commonly used chi-square based tests that utilize homozygote information and incorporated them under the ADT ‘umbrella’ to work alongside the binomial test. Each test is applied on one SNP marker i at a time but is not applied towards haplotypes.

The first of these is the Cochran–Mantel–Haenszel (CMH) test, which examines a series of 2 × 2 × k tables to compare two groups in a binary response. For each of the k tables, the binary response is either ‘amplified’ or ‘non-amplified’. The k (where k = 3) group pairs are, respectively: AA/BB; AA/AB (with the A allele amplified); and BB/AB (with the B allele amplified). These tables are depicted in Supplementary Figure 28. Each table cell contains the appropriate counts for the SNP in question. Because the first table is not independent of the latter two, it is analyzed separately. The CMH test is first applied to this table exclusively to produce a p-value and LOD score. The CMH test is then applied to the latter two tables together to produce another LOD score. The maximum LOD score is taken to represent SNP i. A GWST is generated for the LOD scores and is discussed below.

The second of these tests is the Cochran–Armitage (CA) Trend test, applied widely in GWAS to determine associations between germline alleles (via genotypes) and phenotypes. In our case, we adapted the CA test via assigning amplification status as the phenotype. As such, for a SNP i, we generate a 3 × 2 table, with each column representing the genotypes AA/AB/BB and the rows representing the phenotype (‘amplified’ / ‘non-amplified’) (see Supplementary Fig. 29). Each table cell contains the appropriate counts for SNP i. We also construct two more 3 × 2 tables, identical to the original with the exception of the amplified heterozygous cell. In the first new table, this cell contains counts of the heterozygous calls with the A allele amplified. In the second new table, this cell contains counts of the heterozygous calls with the B allele amplified. These two tables are created to test for allele specificity in the amplified heterozygous calls. The CA test is applied to each of the three tables at SNP i, and the minimum p-value of the three is retained.

The permutation procedure for obtaining a GWST is common to both of these tests. For each SNP i, the number of amplified calls z_i is known from the tables generated above. For each permutation iteration j of t = 10³ iterations, we randomly assign z_i genotypes at SNP i to be amplified, thus keeping the number of amplified calls across iterations constant. The respective test is then run on the amplified and non-amplified genotype counts. The LOD scores are stored and sorted, and the score with 0.05 significance genome-wide is set as the respective threshold. Performance of these tests is given in Section 3.

As mentioned above, population stratification may confound results. For example, if a dataset consists of two groups, in which a region tends to be somatically amplified in the first group but not in the second, the prevalent alleles in the region in the first group may appear to be selectively amplified despite no biological phenomenon occurring in reality. As such, precautions should be taken to ensure that the dataset consists of individuals within the same population.

Lastly, our CMH and CA tests allow for homozygous calls in which both copies of the allele are amplified. This contrasts with our discarding of double amplifications in heterozygous calls, as they would imply ambiguous phase during ADT binomial test analysis. Phase is not an issue for homozygous calls, especially when performing single SNP analysis. Furthermore, since homozygous calls contain two or more copies of the same allele, we are only concerned with whether the call is amplified or not, versus knowing which allele is exclusively amplified as is the case with heterozygous calls. For these reasons, we retain homozygous calls with double amplifications during CMH and CA analysis.

3 EVALUATION AND RESULTS

It is imperative to measure ADT's power across a variety of tumor dataset scenarios. To this effect, we generated numerous synthetic datasets containing causal regions and assessed ADT's ability to detect those regions. These simulations revealed that ADT possesses sensitivity proportional to the dataset size, while specificity remains consistently high. This analysis provided critical insight into ADT's ability to accurately analyze real cancer data.

In further detail, simulation of a particular dataset first requires an existing phased dataset containing only genotype information for n samples. Recurrent stretches of amplification are assigned to several regions in the genome. Each stretch contains a causal driver SNP at its mid-point, and the driver may or may not be allele-specific, as suggested by our alternate and null hypotheses, respectively. In other words, for a heterozygous sample j, either the phase containing the driver allele is amplified with a certain probability, or the other phase is amplified. For a homozygous sample j, either phase can be chosen for amplification. LD with the driver allele allows neighboring SNPs to partake in amplification distortion and result in distorted haplotypes. We thus define truth positive regions as 390 kb regions centered at the driver SNP; 390 kb represents the mean length of recurrent amplification stretches as observed in real cancer data, a detail utilized and described in Table 1.

Table 1.

Parameter definitions

Parameter name	Default	Description
Mean length of a recurrently amplified stretch	390 kb	This parameter represents the mean of an exponential distribution, which upon sampling determines the length of a recurrently amplified region across samples. By default, the distribution possesses a mean of 390 kb. This exponential distribution can produce recurrent stretches of over 1 or even 2 Mb.
Number of recurrently amplified stretches	5	This parameter determines the number of recurrently amplified stretches in the genome, all of which contain causal (driver) SNPs. A value of five represents a realistic number of truth positive regions.
Mean length of a non-recurrently amplified stretch	2.5 Mb	This parameter represents the mean of an exponential distribution, which upon sampling determines the length of a non-recurrent (sample specific) amplified stretch for an individual sample. By default, the distribution possesses a mean of 2.5 Mb.
Number of non-recurrently amplified stretches	5	This parameter determines the number of non-recurrently amplified stretches for a particular sample. No such stretch contains causal (driver) SNPs.
Probability of amplifying the driver allele	0.90	At a driver SNP within a recurrently amplified stretch, a driver allele is pre-selected to be the factor driving tumor development. For a sample j heterozygous at the SNP, this parameter is the probability for: amplifying the phased haplotype within the stretch containing the driver allele. Otherwise, the other phased haplotype is amplified instead.
Probability of amplifying a sample within a recurrently amplified stretch	0.20	The mean probability that: a sample j (and therefore all its calls) is amplified within a recurrently amplified region. The true probability of such amplification for a sample j is determined via sampling from a normal distribution with μ = the parameter value and σ = 0.03. The default and σ values reflect what is observed in recurrently amplified regions in the real Illumina 550K data.
Bias to amplify driver allele homozygous calls	0.70	Either the major or minor allele at a driver SNP can be selected to be the driver allele. This parameter determines the ‘proportion’ of homozygous calls (corresponding to the driver allele) that are to be amplified at the driver SNP. The complement of this parameter (subtracted from 1.0) determines the ‘proportion’ of homozygous calls that are to be amplified for the complementary allele at the driver SNP. The ratio of this parameter value to its complement can be viewed as the relative risk (risk of amplification relative to the homozygous genotype). In other words, the ratio of this parameter value to its complement (the relative risk) is equal to the ratio of the proportion of homozygous calls that are amplified for the driver allele to the proportion of homozygous calls amplified for the other allele.

The parameters used in the simulations are described above. The default values were obtained by observing parameter-specific properties in a real Illumina 550K dataset obtained from The Cancer Genome Atlas (TCGA). The derivation of the default parameter values is discussed in Supplementary Material (Determination of simulation default parameters section).

Non-recurrent stretches of amplification are also sprinkled over individual samples. Such stretches are not causal and thus possess no driver alleles. Along with non-amplified regions, they represent the dataset's truth negative regions, which are then partitioned into segments of up to 390 kb in length; 390 kb was chosen in order to maintain consistency with truth positive region lengths.

A visual example of a dataset is depicted in Figure 1. Each simulated dataset is analyzed by ADT, which returns LOD scores for each SNP. We test whether ADT returns genome-wide significant LOD values—as determined by permutation testing—within truth positive regions as well as a lack of genome-wide significant hits in truth negative regions.

Note that ADT itself does not require input data to be phased; phasing is used only during this evaluation procedure to assign CNA stretches along haplotypes when generating simulated data. ADT treats all input data as if it was unphased and uses amplification status to implicitly phase the data.

The variability across the synthetic datasets is implemented via a set of seven parameters, described in Table 1 and Figure 1. We performed 100 trials for each parameter value combination when iterating over the parameters' value space, generating a dataset per trial and calculating a GWST for each dataset via permutation testing. To prevent exponential growth of the value space, we iterated over only one parameter at a time while maintaining the other parameters at their default values. This allowed us to restrict ourselves to ∼72 000 synthetic datasets instead of a prohibitive 250 × 10⁹. The parameter default values were modeled from observations made in a real glioblastoma cancer dataset, described in the next section.

3.1 Evaluation results

As stated above, an existing phased dataset is required for the simulation procedure. We had obtained three such SNP datasets. The first consists of 204 glioblastoma samples from The Cancer Genome Atlas (TCGA) that were run on the Illumina 550K platform (designated as Dataset A). Genotype and CNA information were determined using log R ratio and B-allele frequency information. In addition, we had obtained another dataset (Dataset B) comprised of 698 lung tumor samples run on the Affymetrix 500K platform, Sty component (250K SNPs) by the Broad Institute. Genotype and CNA information were determined via the PLASQ procedure (Laframboise et al., 2007). The caveat with this dataset is that only roughly half of the samples are published online. Because of the importance of demonstrating ADT's power on a large publicly available dataset, we delineated a third dataset (Dataset C) that is a subset of Dataset B, consisting of 345 lung tumor samples whose raw data are available online (see Supplementary Material Introduction section).

The genotype component of each dataset was extracted and then phased computationally using Beagle 3.0 (Browning and Browning, 2007). These phased genotypes were used as master templates (Template A, B and C, respectively). Recurrent and non-recurrent amplified stretches were assigned to the templates independently during each simulation trial when iterating over the parameters. Default parameter values were modeled from observations made only in Dataset A due to the reliability of copy number calls in this dataset versus the other datasets. As such, CNA properties learned from Dataset A were used to assign CNA stretches to all three templates. Datasets B and C were used strictly for the large sample sizes they offered.

3.1.1 Results from the binomial test component of ADT

We observed that the GWST typically increases as the number or length of amplified stretches increases, encoded via four parameters and depicted in Supplementary Figures 1–12. The underlying reason is that the overall number of amplified heterozygous calls—targeted in permutation testing and contained in such stretches—grows, thereby elevating the threshold. This in turn reduces sensitivity, as driver regions have difficulty meeting such high thresholds due to insufficient amplified heterozygous calls (inadequate power) at the driver SNPs. These sensitivity plots in Supplementary Figures 1–12 reflect performance of all driver regions—those that are sufficiently well-powered to meet the threshold as well as those that are not. The plots reveal that sensitivity is greater in larger sample sizes (∼0.84), moderate in moderate sample sizes (∼0.62), but reduced in smaller sample sizes (∼0.35). Specificity remains at 0.99 across cases and is not displayed.

The final two simulation parameters (probability of amplifying the driver allele, probability of amplifying a sample within a recurrently amplified stretch) represent the parameters of the binomial distribution that underlies ADT. In fact, the latter parameter dictates the number of samples amplified within a recurrent stretch. This translates to the number of amplified heterozygous calls at a driver SNP and therefore has a direct impact on power. Low values for this parameter signifies that sample size is effectively reduced.

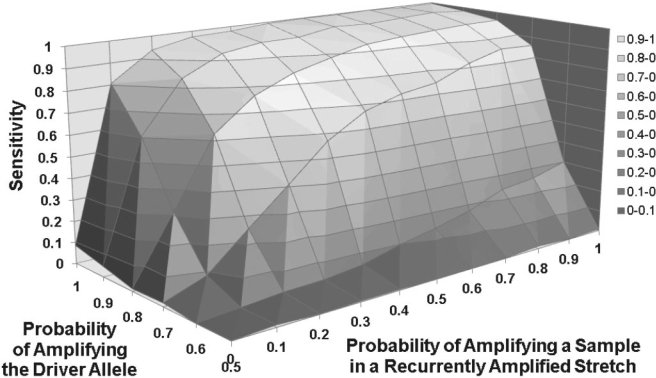
We calculated the GWST for each of these two parameters jointly (Supplementary Figs 13 and 14). The joint performance for Dataset B is displayed in Figure 2, while the joint performances for Datasets A and C are displayed in Supplementary Figures 15 and 16. We observe that ADT's sensitivity increases as the parameters' values grow. It stands at 0.84 in Dataset B at the default values, in which the probability of the driver allele being amplified in an amplified heterozygous call averages 0.90 and the proportion of amplified samples in a recurrent stretch averages 0.20.

Fig. 2.

Sensitivity across value combinations of two parameters. Dataset B: 698 Samples. The two parameters are denoted on the z- and x-axes and have the ability to significantly affect sensitivity of ADT. This graph is produced from performing simulations on the 698 sample Affymetrix 250K dataset. Sensitivity jumps when the sample amplification parameter reaches 0.1 but tapers afterwards. Sensitivity also increases when the driver allele amplification parameter reaches 0.7. Sensitivity at the default parameter values (0.2 for sample amplification and 0.9 for driver allele amplification) reaches 0.84. Considering the default parameter values represent properties seen in real data, this indicates that ADT will perform well on real datasets with large sample sizes.

In Datasets A and C, the sensitivity stands at 0.35 and 0.62 at the default values, respectively. Sensitivity will either rise or reduce on real datasets whose parameter values either, respectively, exceed or fall below these default values. One must use ADT with caution on datasets whose SNPs contain low proportions of amplified heterozygous calls across samples. These results support that increasing sample size boosts sensitivity due to increase in power. Note that the number of samples remains well below the thousands typically required in GWAS studies. Again, specificity is not shown because it resides consistently at 0.99 across cases.

As mentioned above, sensitivity suffers in Dataset A because many driver regions do not possess enough power—the amplified heterozygous calls necessary at a driver SNP—to meet the GWST levels. When the number of such calls (Sⁱ₀ + Sⁱ₁ at SNP i) is too low, the threshold cannot be crossed even if maximum distortion (Sⁱ₀ = 0 or Sⁱ₁ = 0 exclusively) is observed. If the same occurs with SNPs neighboring a driver SNP, the driver region as a whole will remain insufficiently powered. The simulations reveal that this is often the case with small sample sizes, leading to the reported sensitivities.

To alleviate the concerns between power at driver SNPs and the GWST, we measured performance using CWSTs instead. The results on Dataset A are presented in Supplementary Figures 17–21. Results indicate an increase in sensitivity to between 0.5 and 0.55. This potentially comes at a cost of specificity, but any decreases in specificity appeared to be negligible. ADT could thus alternatively be used in a more targeted manner to identify significant distortions.

Lastly, ADT can report peaks in driver regions that lie below the GWST, thus providing the researcher the option of fine mapping such regions. The simulation experiments reveal that ADT performs well with larger datasets but does not perform as optimally with smaller dataset sizes. Furthermore, the parameter default values represent properties observed in real data, thereby providing support of ADT's strong performance—an overall sensitivity of 0.84 and 0.62 with practical parameter values—on large and moderate datasets, respectively.

3.1.2 Results from the chi-square test components of ADT

As noted in the Methods section, the binomial test component of ADT utilizes only heterozygous calls, potentially reducing power as heterozygous calls comprise only a subset of genotypes at a driver marker. Information from homozygous calls can also be used to implicate alleles selected for amplification.

Towards this end, we adapted and incorporated the CMH and CA test under the ADT umbrella as alternative or complementary methods to the binomial test. These tests depend on ratios of amplified homozygous calls at a marker, determined by the parameter bias to amplify driver allele homozygous calls.

Performance was measured in Dataset A. Results from CMH are displayed in Supplementary Figures 22 and 24, while results from CA are provided in Supplementary Figures 23 and 25. The first two figures from CMH and CA involve the minor allele being selected as the driver allele, while the latter two figures involve the major allele being selected as the driver allele. The graphs show joint performance of the parameters: bias to amplify driver allele homozygous calls, probability of amplifying a sample within a recurrently amplified stretch.

For both CMH and CA, when the minor allele is selected, sensitivity generally rises to a peak (for a given value of bias to amplify driver allele homozygous calls), after which it begins to decline as the number of samples amplified increases. This occurs because: as the proportion of samples to be amplified increases (starting from zero), the homozygous calls of the minor allele are preferred to be amplified. The rise to the peak signifies that the fraction of minor allele homozygous calls being amplified is becoming larger than that of the major allele (and large enough to cross GWST). However, as the proportion of samples amplified increases further, the minor allele homozygous calls eventually saturate with amplification, and so the major allele homozygous calls are increasingly chosen to be amplified instead (in order to maintain the total proportion of samples amplified). Thus, the fraction difference reduces, leading to a decline in sensitivity.

When the major allele is selected, sensitivity builds more slowly towards the peak for both CMH and CA. The reason is that many more amplified samples are needed to achieve an amplified homozygous fraction difference between the major and minor allele that would cross genome-wide significance levels (when the major allele homozygous calls are being selected for amplification). However, sensitivity begins to first decline and then plummet when more than 80% of samples are amplified. The cause is that both minor and major allele homozygous calls are saturating with amplification, resulting in a shrinking amplified homozygous fraction difference.

Given this preliminary view of performance of CMH and CA, a potential question is: how do they compare to the ADT binomial test? More specifically, in which parameter scenarios do CMH or CA perform better than ADT, and vice versa? Before proceeding, one caveat to keep in mind is that ADT analyzes information different from that of CMH or CA. For example, as mentioned earlier, ADT examines only heterozygote calls while the first table in CMH utilizes only homozygous calls. Furthermore, CA utilizes both homozygous and heterozygous calls. Thus, the tests may not be directly comparable due to differing input data. However, it is still important to ascertain which test performs best in which scenario, as defined by the parameters in Table 1.

The binomial test's performance for Dataset A is displayed in Supplementary Figure 15; we focus mainly on the trend line for which probability of amplifying the driver allele is 0.90, as this parameter was retained at its default value for CMH and CA. Recall that this parameter applies only to heterozygous calls. For CMH and CA, we focus for now on the trend line for which bias to amplify driver allele homozygous calls is defaulted to 0.70. In this manner, we can compare CMH and CA with ADT on a common parameter: probability of amplifying a sample within a recurrently amplified stretch.

Comparisons of the graphs reveal that ADT binomial test performs stronger while varying this common parameter (refer to Table 2). At the default values of all parameters, CMH and CA possess a sensitivity of ∼0 regardless of the allele selected to be the driver. ADT binomial test, on the other hand, possesses a sensitivity of 0.35. Furthermore, ADT binomial test outperforms CMH or CA when the proportion of amplified samples drops below the 0.20 default value. For such small amplified sample counts, ADT binomial test LOD scores are better able to pass their significance thresholds than can the CMH or CA LOD scores. On the other hand, when the proportion of amplified samples rises to 0.30 or 0.40, ADT still performs better, reaching sensitivities of 0.57 and 0.70. With the minor allele selected to be the driver, CMH, respectively, performs at 0.02 and 0.22, and CA performs at 0.12 and 0.24. With the major allele selected, CMH, respectively, performs at ∼0 and 0.04, and CA performs at 0.18 and 0.24.

Table 2.

Comparison of ADT binomial test, CMH and CA across two parameters

The following is a comparison table between the three tests incorporated under the ADT umbrella across two parameter value ranges as indicated in the table. Each cell contains the color shading code of the test that possesses the greatest sensitivity for that row and column value. If multiple tests have sensitivities close in value, they are depicted in rank order within the cell from greatest (left) to least (right). The color shading codes are: ADT-Binomial Test (light grey), CMH with the minor allele selected to be the driver allele (vertical stripes), CMH with the major allele selected to be the driver allele (diagonal stripes), CA with the minor allele selected to be the driver allele (horizontal stripes), and CA with the major allele selected to be the driver allele (black). The cell containing ‘Default’ corresponds to the default parameter values.

When the minor allele is selected, CMH and CA sensitivities peak with 50% of samples being amplified, but their sensitivities still fall below ADT binomial test's 0.74 sensitivity. Afterwards, the CMH and CA sensitivities fall while the binomial test's sensitivities continue to rise; the reasoning for this decline was provided earlier. When the major allele is selected instead, the CMH and CA sensitivities continue to rise but never quite reach the ADT binomial test sensitivities (∼0.90) when many samples are amplified; afterwards, the CMH and CA sensitivities drop. These results indicate that ADT binomial test performs stronger than CMH or CA across the range of proportion of samples to be amplified (while other parameters remain at their default values).

However, if we vary the parameter bias to amplify driver allele homozygous calls, we observe cases in which CMH and CA perform equivalently or better than ADT binomial test (for which bias to amplify driver allele homozygous calls always possesses its default 0.70 value). Such cases are depicted in Table 2. Although ADT binomial test consistently performs better when the bias parameter is ≤0.70 (due to similar fractions of amplified homozygous calls for the two alleles at a driver SNP), CMH or CA often gain the upper hand when this parameter exceeds 0.70. For example, when the sample amplification parameter is low and the bias parameter is high, both CA and CMH possess higher sensitivities (when the driver allele is the minor allele). As the sample amplification parameter increases while the bias parameter remains high, CA (with the driver allele being the major allele) climbs to the top. ADT binomial test returns to possessing the greatest sensitivity when the sample amplification parameter reaches 0.90 or above.

These results reveal that ADT binomial test performs well in many cases, including practical ones defined by default parameter values, while CMH and CA perform well in others. As such, if real tumor data possesses properties for which CMH or CA are known to perform better, those tests should be used to achieve greater sensitivity for detecting selectively amplified alleles. Conversely, if real tumor data possesses properties for which ADT binomial test is known to perform better, then that test should be utilized.

To relieve the user from making such a choice, the HADiT software package can conduct all three tests on an input tumor dataset, generating three corresponding LOD scores per SNP. Respective permutation tests can then be performed to determine the GWST for each test type. A SNP is reported as significant if at least one of its three LOD scores crosses the respective threshold. The benefit of this ‘OR operation’ is that SNPs that are significant via different tests can be reported at once. For example, if SNP i is significant according to the ADT binomial test but is not significant via CMH or CA, it would still be reported. Likewise, if SNP j is significant according to CMH or CA but not according to ADT binomial test, it would also be reported. Moreover, SNPs that are deemed significant by more than one test make stronger candidates for drivers. Performance of utilizing all three tests in this fashion is provided in Supplementary Figures 26 and 27.

The ‘OR operation’ was performed versus combining the three p-values because the tests possess differing null distributions and utilize input data that are dependent, thus violating assumptions of standard p-value combination methods (e.g. Fischer's method) and highly complicating permutation testing procedures.

A consequence of the ‘OR operation’ is that none of the three tests affects the sensitivity of the other; rather, they represent options under the ADT umbrella. Results from CMH or CA may serve to support the significance of driver alleles discovered by ADT binomial test, or vice versa. HADiT thus offers the user the functionality of these tests in a complementary fashion.

3.2 Biological results

We analyzed Dataset A using the binomial test portion of ADT and present the results in Figure 3 and Table 3. Only two SNPs (rs1997375, rs10250847) cross the GWST of 3.61. As a quality control measure, we filtered out SNPs that had more than 10% missed calls. In addition, we imputed the genotypes at the top genome-wide significant SNPs using Beagle 3.0 (Browning and Browning, 2007). The rationale behind this is that regions with amplification are problematic for genotype calling algorithms and may lead to erroneous calls. We thus checked the original genotype calls and imputed calls for genotype concordance for each top SNP. Although the best hit rs1997375 displays much discordance and thus is deemed unreliable, the next hit rs10250847 displays strong concordance, lending support towards its potential validity (see Table 3).

Fig. 3.

ADT binomial test results. Dataset A: 204 samples. This displays a Manhattan plot of amplification distortion p-values (y-axis in a −log₁₀ scale) along the genome (x-axis). Signals on chromosome 7 exceed the 3.61 genome-wide significance threshold, indicated by the horizontal line. Only two SNPs cross this threshold (rs1997375, rs10250847). The SNP rs10250847 passes certain quality control criteria and may motivate further biological investigation. The distribution of the ADT binomial test statistic is provided in a quantile–quantile (QQ) plot in Supplementary Figure 30.

Table 3.

Genotype discordances between original genotypes and imputed genotypes (Dataset A: 204 samples)

SNP	rs1997375	rs10250847
No. of calls	204	204
No. of AB calls imputed to be AA or BB	41	0
No. of AA or BB calls imputed to be AB	4	0
No. of AA or BB calls imputed to be BB or AA	3	0
No. of total genotype discordances	48	0

The table contains a summary of genotype comparisons between the original genotype calls and the Beagle 3.0-imputed genotype calls for the top two genome-wide significant SNPs. The top SNP (rs1997375) displays many (48) discordances in total. However, the second SNP (rs10250847) does not, lending evidence towards it being a stronger hit.

Furthermore, this latter SNP resides within the epidermal growth factor receptor (EGFR) region (∼434 kb telomeric to the transcriptional start site of the EGFR locus), which is well-known to be involved in various cancers (Olayioye et al., 2000). Intriguing connections between the germline and somatic genomes are starting to appear in the literature. For example, in lung cancer patients, it has long been recognized that individuals of Asian ancestry have a higher prevalence of somatically acquired EGFR mutations than individuals of European ancestry (Nomura et al., 2007; Shigematsu et al., 2005). These mutations are strongly correlated with response rate to EGFR tyrosine kinase inhibitors (Huang et al., 2004; Lynch et al., 2004; Paez et al., 2004; Pao et al., 2004; Shigematsu and Gazdar, 2006; Tam et al., 2009; Zhang et al., 2005). While the mechanism underlying the prevalence difference is unknown, it is conceivable that there is an inherited predisposition to developing the somatic mutation. More recently, a trio of studies demonstrated a strong association between a germline haplotype and a somatically acquired mutation in JAK2 in myeloproliferative neoplasms (Jones et al., 2009; Kilpivaara et al., 2009; Olcaydu et al., 2009). It is clear that complex interactions can occur between the germline and tumor genomes; how prevalent this phenomenon is, however, will require further investigation. Our results suggest that rs10250847 is a preliminary candidate motivating further examination into this genetic region in glioblastomas.

4 DISCUSSION AND CONCLUSIONS

Previous studies had observed anecdotal evidence of particular nucleotide alleles being preferred in amplified regions in tumors. We formalized this notion via hypothesizing amplification distortion, in which a certain tumor-driving allele is selected to reside in amplified regions versus the other allele over many tumor samples. LD allows this distortion to extend to haplotypes centered at the driver. To test this hypothesis, we devised the ADT. ADT accepts genome-wide SNP and CNA data from SNP arrays and returns LOD distortion scores for each allele or haplotype starting at each SNP. ADT can also permute the data to determine a genome-wide threshold of significance for these scores. Alleles with significant LOD values are either potential causal variants or are associated with causal variants. Techniques such as fine mapping can then be used to identify cancer genes proximal to such alleles.

We evaluated the power that ADT possesses to detect distorted alleles. We generated synthetic datasets that represent the hypothetical variety of cancer data consisting of SNP and CNA information. The results on such datasets indicate that ADT performs well with large sample sizes, especially if the simulated data reflects properties of true cancer data. One limitation may be that such large SNP array tumor datasets are not currently available publicly. However, in the coming years, it may be possible to obtain or aggregate sufficient quantities of tumor SNP array data, akin to the datasets that have been available for GWAS studies. Alternatively, labs may privately possess hundreds of tumor samples that are not yet published. Such groups could use ADT to identify potential causal variants with strong power.

Since the purpose of ADT is to localize causal variants—putative genes—within amplicons, a natural extension is to incorporate gene expression data towards the distortions. In other words, are there associations between enriched expression levels of proximal or perhaps distal genes with alleles that are selected for amplification? The interesting methodological challenges would stem from the complexities of examining associations with distal genes specifically. Another direction for future study is the adaptation of ADT towards sequencing data. Although we expect ADT to scale well to the size of such datasets, the method will need to handle the inherent differences between sequence and SNP array data. For instance, sequence data will include all nucleotides, not just SNPs, which will have an impact on amplified haplotype detection. Furthermore, somatic mutations can be detected and incorporated into the algorithm. Such enhancements in the near future will further empower ADT.

In the pursuit of detecting causal variants, it aids the cancer community to integrate multiple sources of information. We present a method that aims to do this. The strong evaluation of ADT provides us confidence to offer the community this powerful genome-wide scanning method. We hope that cancer researchers will benefit from its use towards helping lay the groundwork for discovering variants and possibly oncogenes.