Abstract
Purpose: To find and verify the optimum sliding characteristics and material compressibility that provide the minimum error in deformable image registration of the lungs.
Methods: A deformable image registration study has been conducted on a total of 16 lung cancer patients. Patient specific three dimensional finite element models have been developed to model left and right lungs, chest (body), and tumor based on 4D CT images. Contact surfaces have been applied to lung-chest cavity interfaces. Experimental test data are used to model nonlinear material properties of lungs. A parametric study is carried out on seven patients, 20 conditions for each, to investigate the sliding behavior and the tissue compressibility of lungs. Three values of coefficient of friction of 0, 0.1, and 0.2 are investigated to model lubrication and sliding restriction on the lung-chest cavity interface. The effect of material compressibility of lungs is studied using Poisson’s ratios of 0.35, 0.4, 0.45, and 0.499. The model accuracy is examined by calculating the difference between the image-based displacement of bronchial bifurcation points identified in the lung images and the calculated corresponding model-based displacement. Furthermore, additional bifurcation points around the tumor and its center of mass are used to examine the effect of the mentioned parameters on the tumor localization.
Results: The frictionless contact model with 0.4 Poisson’s ratio provides the smallest residual errors of 1.1±0.9, 1.5±1.3, and 2.1±1.6 mm in the LR, AP, and SI directions, respectively. Similarly, this optimum model provides the most accurate location of the tumor with residual errors of 1.0±0.6, 0.9±0.7, and 1.4±1.0 mm in all three directions. The accuracy of this model is verified on an additional nine patients with average errors of 0.8±0.7, 1.3±1.1, and 1.7±1.6 mm in the LR, AP, and SI directions, respectively.
Conclusions: The optimum biomechanical model with the smallest registration error is when frictionless contact model and 0.4 Poisson’s ratio are applied. The overall accuracies of all bifurcation points in all 16 patients including tumor points are 1.0±0.7, 1.2±1.0, and 1.7±1.4 mm in the LR, AP, and SI directions, respectively.
Keywords: contact surfaces, deformable image registration, finite elements, friction, lungs, hyperelastic, Poisson’s ratio
INTRODUCTION
The high demand to improve the quality of radiation delivery while sparing healthy tissues has intensified the need for accurate knowledge on the position and shape of the target. Intensity-modulated radiation therapy requires the exact location and 3D shape of the target to be identified. Stereotactic body radiation therapy, where a single or a few high-dose fractions are delivered, involves a high degree of precision in identifying the target. The development of imaging modalities such as CT, MRI, and PET has enabled improvements in target definition at treatment planning. Further advancement is also attributed to the emergence of image-guided radiotherapy, where patient alignment is performed in each treatment. Image registration is the common requirement in these techniques.
Image registration is used for diagnosis, planning, delivery, and post-treatment response evaluation.1 It also adds value to images by combining anatomical (CT, MR, and ultrasound) and functional (PET, SPECT, and fMRI) image modalities in one coordinate system.2 Rigid image registration has been commonly used in clinical applications3 where the segmentation task is performed with low computational complexity. Rigid registration is suitable in sites with a little change in geometry and position. However, most human tissues experience a large deformation and movement, making them unsuitable for rigid registration.2 Therefore, deformable image registration is required to account for tissue deformation.
A number of techniques have been used for deformable image registration4 including biomechanical modeling which is based on the continuum mechanics theory. As a part of biomechanical modeling, finite element modeling is proven to be “a promising approach”5 that has been used in deformable image registration of different anatomical sites.6, 7, 8, 9, 10 The lung is one of the challenging organs that requires deformable image registration due to its large respiration movement.
The potential benefits of understanding the biomechanical behavior of the lung and its interplay with the surrounding tissues are increasing as image guidance techniques at the time of radiation treatment provide information about the complex and changing environment of the lung. Although several deformable image registration techniques are capable of deforming the lung from exhale to inhale including thin plate spline,11 B-spline,12 and Demons,13, 14 and potentially accommodating the sliding interface, the understanding of the biomechanics of the lung may aid in understanding and modeling the tumor response or progression and normal tissue changes in the lung. Prior to investigating the changes in the biomechanical models of the lungs as a result of therapeutic intervention, a comprehensive and accurate understanding of the biomechanics of the lung must be obtained. Once this is achieved, investigations into the effect of tumor response, increasing fibrosis, and pneumonitis can be explored. Initial investigations have indicated the potential benefits of biomechanical based deformable modeling of the lungs.
Great attention has been paid to the investigation of the solid mechanics of the lung15, 16, 17, 18, 19, 20, 21, 22, 23 including finite element models.24, 25, 26, 27, 28, 29 Realistic simulation of the interaction between the lungs and the surrounding tissues and the material properties can play a major role in the accuracy of the model.
Since lungs and chest cavities are surrounded by a pleural membrane lubricated by a thin layer of pleural liquid,30 sliding of the lungs is important for their functionality.31, 32 An experimental investigation found that the average coefficients of friction on the lung surface are 0.045 and 0.078 at high and low sliding speed, respectively.32 This aspect has been often ignored in lung models by segmenting out the lung prior to deformable registration or accepting errors at the boundary, such as unrealistic motion of the ribs. Recent investigations have pursued methods to modify geometric, intensity based deformable image registration algorithms, such as B-splines and Demons, to handle the sliding between the lungs and the ribs. Wu et al.33 demonstrated the feasibility of segmenting the lungs from the surrounding anatomy and performing a two-step registration that is then matched at the boundary on using Demons and B-splines. Contact surfaces in lungs were used by Zhang et al.27 to find the projection of the inhale and exhale position where only the lung is considered in the model.
Realistic mechanical material properties are required for an accurate simulation of the lung using finite element modeling. One of these properties is Poisson’s ratio representing the degree of compressibility of the tissue. Different values of Poisson’s ratio have been reported in literature. Lia-Fook and Hyatt34 found that Poisson’s ratio was between 0.41 and 0.45, depending on age and transpulmonary pressure with a tendency of the lung to become incompressible with a Poisson’s ratio of 0.5 as the age increased. This variation in the Poisson’s ratio has been reflected on its value used in the finite element modeling of the lung ranging from 0.2 to 0.4,24 0.35,27 0.45,9, 25 0.25, 0.3, and 0.35 values.26
Recently, the authors of this study investigated the effect of the sliding of the lungs inside chest cavities on the accuracy of modeling lung’s motion due to respiration for seven patients. A preliminary report of the investigation was provided elsewhere.29 Inhale and exhale images from 4D CT scans were used to determine the optimal material parameters and coefficient of friction between the lung and the pleural surface. The optimization was based on minimizing the residual error of the predicted superior-inferior (SI) motion of bronchial bifurcations identified on the images. The accuracy of the model was improved by including the contact model with a frictionless surface.
In this study, these results are expanded by including the residual errors in the left-right (LR) and anterior-posterior (AP) of the bronchial bifurcations as well as the residual errors in predicting the motion of the tumor in all directions. In addition, the optimal parameters are validated on additional nine patients.
METHODS AND MATERIALS
Patient data and model configuration
Patient specific finite element models have been developed using the image data of a total of 16 nonsmall cell lung cancer patients, 10 female and 6 male, with an average age of 74 yr (range from 58 to 89 yr). The average size of the tumor is 13.73 cm3 (range from 0.08 to 78.03 cm3). In one case (P6) the tumor is in the mediastinal region. Patient’s data including comorbidity are listed in Table 1.
Table 1.
Patient’s data.
| Patients | Gender | Tumor location | Tumor size (cm3) | Comorbid illnessa |
|---|---|---|---|---|
| P1 | F | RML | 21.51 | CHF, MI, colon cancer |
| P2 | F | LLL | 1.57 | COPD, psoriasis |
| P3 | F | RLL | 4.63 | N∕A |
| P4 | M | RUL | 10.82 | COPD, HTN |
| P5 | M | LLL | 25.24 | N∕A |
| P6 | M | Mediastinum | 78.03 | N∕A |
| P7 | M | LUL | 0.14 | COPD, CHF, MI, HTN |
| P8 | F | LLL | 2.63 | AtrialFib, PMR, hyperthyroidism |
| P9 | M | RML | 4.14 | Asthma, tonsillar cancer, H∕N cancer |
| P10 | F | RUL | 0.67 | Breast cancer, colon cancer |
| P11 | M | LUL | 0.08 | CHF, MI, COPD, HTN, PVD |
| P12 | F | RUL | 2.83 | COPD |
| P13 | F | RUL | 59.33 | None |
| P14 | F | LUL | 2.05 | COPD, CHF, MI, PMR |
| P15 | F | LLL | 5.3 | HTN |
| P16 | F | LUL | 0.76 | Rectal∕colon cancer |
CHF: Congestive heart failure, COPD: Chronic obstructive pulmonary disease, HTN: hypertension, MI: Myocardial infarction (heart attack), PMR: Polymyalgia rheumatica, PVD: Peripheral vascular disease.
Respiration correlated 4D CT images were collected using a Varian RPM system on a GE Medical Systems CT scanner (GE Medical Systems, Milwaukee, WI). The 3D images are reconstructed to a matrix of 512×512×(between 112 and 160 slices) with a voxel size of 0.98×0.98×2.5 mm3. The inhale (0%) and exhale (50%) breathing phases are imported into a treatment planning system (PINNACLE version 7.6, Philips Medical Systems, Madison, WI). The contours of the body, left and right lungs, and tumor are constructed using the treatment system and exported as a binary mask image.
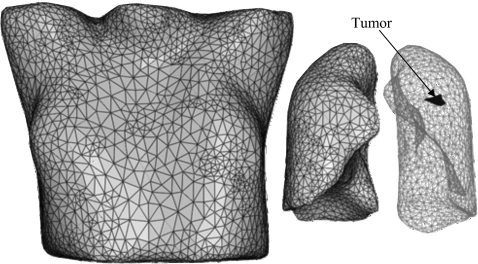
Triangulated surfaces of the manually contoured body, lungs, and tumor are created for inhale and exhale breathing phases. Using the triangulated surfaces of the inhale representation of the body, left and right lungs, and tumor, a volumetric mesh is created using a finite element preprocessor (HYPERMESH, version 8.0, Altair Engineering, Troy, MI), as shown in Fig. 1. Four-node tetrahedral elements are used for all components. The contact surfaces are added using ABAQUS∕CAE (ABAQUS version 6.7, ABAQUS, Inc., Pawtucket, RI). The model is analyzed using ABAQUS finite element package. More details of the development of image-based models have been described elsewhere.9
Figure 1.
Model components including body, lungs, and tumor.
Surface interaction and boundary conditions
Sliding of lungs inside the chest cavities is simulated using a contact model. A surface based contact model is applied on the surface of each lung and its corresponding cavity. Since each lung is surrounded by a pleural sac made of two layers with a gap filled with a pleural liquid,30 viscosity of the liquid in addition to surface asperties may restrict the lung from sliding. This can be modeled as a friction. An experimental investigation found different values of friction on this interface.32 During normal breathing, the value of friction on the pleural surface is independent of the sliding velocity, making it similar to Coulomb friction.35 Therefore, three values of coefficient of Coulomb friction of 0, 0.1, and 0.2 are applied in this study to investigate its effect on the accuracy of the models.
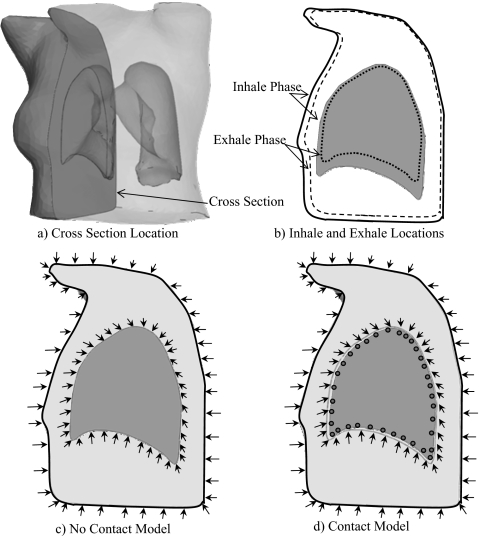
The application of boundary conditions is illustrated in Fig. 2 using a cross section of the model that passes through the right lung and body [Fig. 2a]. The difference in geometry between the inhale and the exhale phases, as shown in Fig. 2b, can be characterized by a set of displacements. These displacements are applied to the surface of the expanded body and lung to deform them to exhale configurations. This process is conducted by projecting the triangulated surface nodes of the inhale lungs and body onto the surfaces of the exhale phase. A surface projection program HYPERMORPH (Hypermesh, Altair Engineering) is used. These boundary conditions are applied directly to the surface nodes of the body and the chest cavities. The lung nodes are attached to the cavity nodes in the models without contact surface, as shown in Fig. 2c. However, in the contact models, the nodes of the lungs are separated from those of the chest cavities [Fig. 2d], allowing them to slide inside the chest cavity in the same way that they move inside the body during breathing.
Figure 2.
Boundary conditions on (a) a model cross section where (b) the geometry differences between inhale and exhale phases are applied in a form of displacements to the body and chest cavity. In the model without the contact surface (c) these displacements are applied to the lung’s nodes directly since they are attached to those of the chest cavities. However, in the contact model (d) the boundary conditions are applied to the chest cavity nodes, not to the lungs, allowing sliding of lungs inside chest cavities. Note: The gap between the lung and chest cavity in (d) is magnified for the sake of clarity.
Material properties
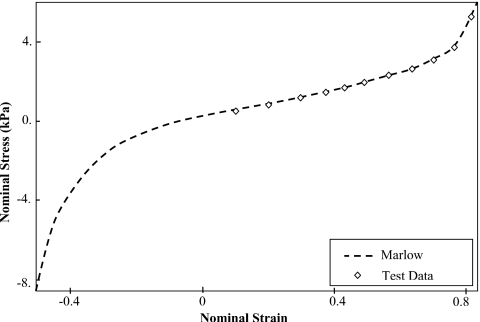
Nonlinear hyperelastic material properties are used for the lungs where the stress-strain plot is based on the experimental investigation on human lung tissues conducted by Zeng et al.36 This stress-strain relationship is evaluated using ABAQUS∕CAE to find the best strain energy form fitting the test data. Although both van der Waals and Marlow models match the test data,28 the Marlow model is used in this study, as shown in Fig. 3. Poisson’s ratios of 0.35, 0.4, 0.45, and 0.499 are used for lungs. For a comparison purpose, an elastic model without contact surface is investigated using elastic material properties of the lungs with a modulus of elasticity of 3.74 kPa. This value represents the tangent of the linear segment of the stress-strain relationship. The tumor is modeled as an elastic material with modulus of elasticity of 7.8 kPa and Poisson’s ratio similar to that used with the lung. Elastic material properties are used for the body material with an elastic modulus of 6.0 kPa and Poison’s ratio of 0.4. Early study shows that it has a little effect on the lung’s performance since the boundary conditions are applied by the adjacent nodes of the body around the lung.24
Figure 3.
Experimental test data of human lung tissue represented by a nominal stess-strain relationship. The data are verified using the Marlow model for hyperelastic material properties.
Model accuracy
Bifurcations of vessels and bronchi are identifiable in the images and used as landmarks to evaluate the accuracy of the model. The average distance of all bifurcation points and the number of the points at 5, 10, 15, and 20 mm distances from the chest wall are listed in Table 2. These bifurcation points are located in the primary image of the lung (inhale) and tracked in the secondary image (exhale). The number of these points varies from 53 to 113, depending on the bronchial structure in the lung. Our experience has shown that the bronchial structures visible on CT images are different among patients. This variation is likely due to the lung damage caused by diseases.
Table 2.
The distribution of bifurcation points relative to their distance to the chest wall.
| Patient | Average distance (mm) | Number of point at different distances | |||
|---|---|---|---|---|---|
| <5 mm | <10 mm | <15 mm | <20 mm | ||
| P1 | 15.4 | 2 | 14 | 28 | 40 |
| P2 | 15.9 | 0 | 15 | 36 | 39 |
| P3 | 13.5 | 12 | 18 | 26 | 30 |
| P4 | 17.4 | 2 | 4 | 22 | 35 |
| P5 | 20.7 | 1 | 10 | 31 | 58 |
| P6 | 17.4 | 3 | 12 | 29 | 48 |
| P7 | 15.5 | 0 | 10 | 28 | 49 |
| Average | 17.0 | 3 | 12 | 29 | 43 |
The difference in coordinates between inhale and exhale location of each point represents the image-based displacement of that point. This displacement is compared to the calculated value using the finite element model. The difference between two displacements represents the error. The average of the absolute errors and the standard deviation are found in the LR, AP, and SI directions.
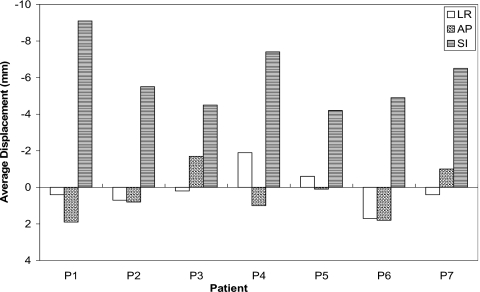
Although displacements vary between patients as a result of physiological differences, the average maximum vector displacement of all lungs’ nodes among patients is 21.1±3.6 mm. Figure 4 shows the average bifurcation displacement of points in the seven patients of the parametric study in the LR, AP, and SI directions. The largest displacement generally occurs in the SI direction, making it a critical factor in the analysis.
Figure 4.
Average bifurcation displacement in the seven patients of the parametric study.
RESULTS
Parametric study
Table 3 illustrates the model matrix that includes the type of material, Poisson’s ratio, and contact surface condition investigated in each model. Only Poisson’s ratio is considered in the elastic and hyperelastic models where no contact surface is applied. In the subsequent models, the contact surface is applied (ContFr=0, ContFr=0.1, ContFr=0.2) using hyperelastic material with all values of Poisson’s ratio (ν) in addition to coefficients of friction (0.0, 0.1, and 0.2).
Table 3.
Model matrix of the parametric study.
| Model | Material | Poisson’s ratio (ν) | Contact model conditions |
|---|---|---|---|
| Elastic | Elastic | 0.35,0.4, 0.45, 0.499 | No contact surface |
| Hyperelastic | Hyperelastic | 0.35,0.4, 0.45, 0.499 | No contact surface |
| ContFr=0 | Hyperelastic | 0.35,0.4, 0.45, 0.499 | Contact with 0.0 friction |
| ContFr=0.1 | Hyperelastic | 0.35,0.4, 0.45, 0.499 | Contact with 0.1 friction |
| ContFr=0.2 | Hyperelastic | 0.35,0.4, 0.45, 0.499 | Contact with 0.2 friction |
Table 4 shows the average absolute error and the average standard deviation in the LR, AP, and SI directions in the seven patients using the five models. The smallest errors of 1.1±0.9, 1.5±1.3, and 2.1±1.6 mm are found in the LR, AP, and SI directions, respectively, when applying a frictionless contact surface model with a Poisson’s ratio of 0.4. Although, the errors increase slightly as the Poisson’s ratio and coefficient of friction increase, only models with Poisson’s ratios of 0.35 and 0.4 and frictionless contact surface have an average absolute error of less than 2.5 mm in the SI axis in all seven patients (100% success rate). Of a particular interest is the case of P6 where the tumor is attached to the pleura. The performance of the contact model is similar to the rest of the patients where the errors are 1.1±0.9, 1.8±1.3, and 1.9±1.6 mm in the LR, AP, and SI directions, respectively.
Table 4.
Average absolute error in the LR, AP, and SI directions of the seven patients in the parametric study.
| Model | Average absolute error (±SD) (mm) | |||
|---|---|---|---|---|
| ν=0.35 | ν=0.4 | ν=0.45 | ν=0.499 | |
| LR direction | ||||
| Elastic | 1.3±1.0 | 1.3±1.0 | 1.2±1.0 | 1.2±1.0 |
| Hyperelastic | 1.3±1.0 | 1.2±1.0 | 1.2±1.0 | 1.2±1.0 |
| ContFr=0 | 1.2±0.9 | 1.1±0.9 | 1.1±0.9 | 1.3±1.0 |
| ContFr=0.1 | 1.1±0.9 | 1.1±0.9 | 1.2±0.9 | 1.3±1.0 |
| ContFr=0.2 | 1.2±1.0 | 1.2±1.0 | 1.2±1.0 | 1.3±1.0 |
| AP direction | ||||
| Elastic | 1.9±1.5 | 1.8±1.5 | 1.8±1.4 | 1.7±1.4 |
| Hyperelastic | 1.9±1.4 | 1.7±1.4 | 1.7±1.4 | 1.8±1.4 |
| ContFr=0 | 1.5±1.3 | 1.5±1.3 | 1.5±1.3 | 1.8±1.4 |
| ContFr=0.1 | 1.6±1.4 | 1.6±1.3 | 1.6±1.3 | 1.8±1.5 |
| ContFr=0.2 | 1.7±1.4 | 1.6±1.3 | 1.7±1.4 | 1.9±1.5 |
| SI direction | ||||
| Elastic | 3.4±2.7 | 3.2±2.6 | 2.9±2.3 | 2.6±2.0 |
| Hyperelastic | 3.0±2.5 | 2.6±2.1 | 2.5±1.9 | 2.5±1.9 |
| ContFr=0 | 2.1±1.7 | 2.1±1.6 | 2.2±1.7 | 2.5±1.9 |
| ContFr=0.1 | 2.2±1.8 | 2.2±1.8 | 2.4±1.8 | 2.8±2.1 |
| ContFr=0.2 | 2.4±2.0 | 2.4±1.9 | 2.5±1.9 | 2.8±2.2 |
t-test has been conducted to investigate the statistical difference between the average absolute error using optimum model (frictionless surface with 0.4 Poisson’s ratio) and other models. It is shown that the average absolute error of optimum parameters is statistically significantly different in comparison to that of the elastic and hyperelastic models (using a Poisson’s ratio of 0.4) in the AP and SI directions but not in the LR direction. The p values in the SI direction are 0.01 and 0.03 when it is compared to the elastic and hyperelastic models, respectively, while it is not significantly different in comparison to the average of the model with frictions of 0.1 (p=0.31) and 0.2 (p=0.12). Similarly in the AP direction, the p values of the optimum model in comparison with the elastic and hyperelastic models are 0.05 and 0.02, respectively, while it is higher in friction models of 0.1 (p=0.15) and 0.2 (p=0.08). In the LR direction, there is no statistically significant difference between elastic, hyperelastic, 0.1 and 0.2 frictions models with p values of 0.12, 0.16, 0.70, and 0.35, respectively.
In addition, the accuracy of the model has been validated using additional points around the tumor and its center of mass. Using frictionless contact model with Poisson’s ratio of 0.4, the residual errors in the LR, AP, and SI direction are reduced to 1.0±0.6, 0.9±0.7, and 1.4±1.0 mm, respectively (Table 5). Although the error decreases in all three directions using the optimum parameters, the reduction is noticeable in the SI direction where the largest deformation is expected.
Table 5.
Average absolute error of the points surrounding the tumor in the LR, AP, and SI directions of the seven patients in the parametric study.
| Model | Average absolute error (±SD) (mm) | |||
|---|---|---|---|---|
| ν=0.35 | ν=0.4 | ν=0.45 | ν=0.499 | |
| LR direction | ||||
| Elastic | 1.3±0.7 | 1.3±0.7 | 1.2±0.7 | 1.0±0.7 |
| Hyperelastic | 1.3±0.7 | 1.3±0.7 | 1.1±0.7 | 1.1±0.8 |
| ContFr=0 | 1.0±0.6 | 1.0±0.6 | 1.0±0.6 | 1.1±0.8 |
| ContFr=0.1 | 1.1±0.6 | 1.1±0.6 | 1.0±0.6 | 1.0±0.8 |
| ContFr=0.2 | 1.2±0.7 | 1.0±0.6 | 1.0±0.7 | 1.1±0.8 |
| AP direction | ||||
| Elastic | 1.2±0.9 | 1.1±0.9 | 1.1±0.8 | 1.3±1.0 |
| Hyperelastic | 1.2±0.9 | 1.1±0.8 | 1.2±0.9 | 1.4±1.2 |
| ContFr=0 | 0.9±0.7 | 0.9±0.7 | 1.0±0.8 | 1.4±0.9 |
| ContFr=0.1 | 0.9±0.7 | 1.0±0.7 | 1.2±0.9 | 1.6±1.0 |
| ContFr=0.2 | 1.0±0.8 | 1.0±0.7 | 1.3±1.1 | 1.7±1.1 |
| SI direction | ||||
| Elastic | 2.6±1.8 | 2.4±1.7 | 2.1±1.7 | 1.8±1.4 |
| Hyperelastic | 2.4±1.7 | 1.9±1.6 | 1.6±1.3 | 1.8±1.3 |
| ContFr=0 | 1.4±1.1 | 1.4±1.0 | 1.5±1.2 | 1.8±1.4 |
| ContFr=0.1 | 1.4±1.2 | 1.4±1.1 | 1.6±1.1 | 1.7±1.3 |
| ContFr=0.2 | 1.7±1.4 | 1.6±1.3 | 1.6±1.2 | 1.8±1.4 |
Model verification
The optimum parameters (Poisson’s ratio of 0.4 and frictionless surface) found in the study are tested using an additional nine lung cancer patients. Hyperelastic material properties and contact surface models are applied. Similar to the parametric study, bifurcation points are used to check the accuracy of the analytical results. The average absolute errors in the LR, AP, and SI directions in addition to the standard deviation (±SD) in all patients are listed in Table 6. The average errors of all nine patients are 0.8±0.7, 1.3±1.1, and 1.7±1.6 mm in the LR, AP, and SI directions, respectively. As a result, the frictionless contact surface model with a Poisson’s ratio of 0.4 provides the least displacement error.
Table 6.
Average absolute error of bifurcation points in lungs in the LR, AP, and SI directions.
| Patient | Average absolute error (±SD) (mm) | ||
|---|---|---|---|
| LR | AP | SI | |
| P8 | 0.8±0.7 | 1.1±0.9 | 2.2±2.9 |
| P9 | 0.5±0.4 | 0.7±0.8 | 0.9±0.8 |
| P10 | 0.9±0.9 | 1.8±1.8 | 2.1±1.7 |
| P11 | 0.9±0.6 | 1.9±1.6 | 2.2±1.9 |
| P12 | 0.7±0.6 | 1.2±0.9 | 1.3±0.9 |
| P13 | 0.9±0.7 | 0.8±0.8 | 2.0±2.0 |
| P14 | 0.8±0.6 | 1.0±0.6 | 1.0±0.7 |
| P15 | 1.0±0.7 | 1.6±1.3 | 1.3±1.1 |
| P16 | 1.1±1.4 | 1.4±1.4 | 2.5±2.2 |
| Average | 0.8±0.7 | 1.3±1.1 | 1.7±1.6 |
DISCUSSION
Effect of material compressibility
As shown in Table 4, the effect of Poisson’s ratio is more pronounced in the elastic and hyperelastic models without contact surfaces. In the elastic model, the average error in the SI axis ranges between 3.4 and 2.6 mm with Poisson’s ratios of 0.35 and 0.499, respectively. Similarly, the average error decreases from 3.0 to 2.5 mm in the hyperelastic model. On the contrary, the error increases as the Poisson’s ratio increases in the contact models. This is mainly related to the sliding of the lungs inside the chest cavities, which makes the lungs move with relative independence to the applied displacement by the surrounding body. On the other hand, the lungs are attached to the chest cavity in the elastic and hyperelastic models without contact surfaces.
The vector displacement of the tumor surface is shown in Table 7 using Poisson’s ratios of 0.35 and 0.499 in the elastic model. This displacement, which includes rigid movement (translation and rotation) and deformation, is compared to the original position, shown as a gray shadow in the table. In most cases, the tumor moves more with the higher Poisson’s ratio of 0.499. However, in patient P6, where the tumor is on the surface of the lung, the tumor moves a little more with a Poisson’s ratio of 0.35. The vector displacement error of using bifurcation points around the tumor is calculated for each patient. In general, the error decreases as the Poisson’s ratio increases. However, the error slightly increases in the case of patients P1 and P7 which may be related to the tumor size and location.
Table 7.
The surface deformation of the tumor (U), as well as the vector displacement error using elastic model with Poisson’s ratios of 0.35 and 0.499 without contact surfaces (all dimensions in mm).
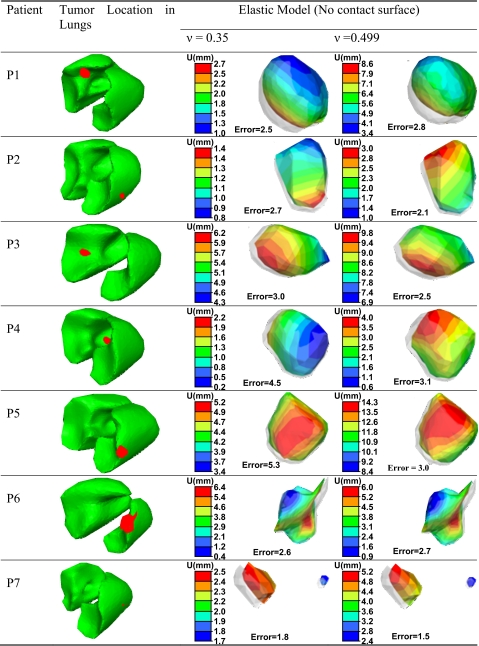 |
|||
Effect of coefficient of friction
The average error increases slightly as the coefficient of friction increases (Table 4). The largest error increase is 0.3 mm when the coefficient of friction increases from 0.0 to 0.2. This indicates that within the investigated range of coefficient of friction, it has little effect on the lung’s behavior. The results also show that the actual coefficient of friction is very low demonstrating the lubricating effect of the pleural fluid. This agrees with the experimental findings of 0.045 and 0.078.32
Table 8 illustrates the effect of increasing the coefficient of friction from 0.0 to 0.2 on the tumor displacement in the contact models with a Poisson’s ratio of 0.35. As expected, the tumor moves more in the frictionless surface as a result of low sliding restriction. In addition, similar movement pattern of the tumor is observed with both coefficients of friction in most patients, as shown by the displacement distribution on the surface of the tumor. This is mostly related to the small effect of friction on the movement of the lungs within the range of friction investigated in this study (Table 4).
Table 8.
The surface deformation of the tumor (U), as well as the vector displacement error using Poisson’s ratio of 0.35 and coefficients of friction of 0 and 0.2 (all dimensions in mm).
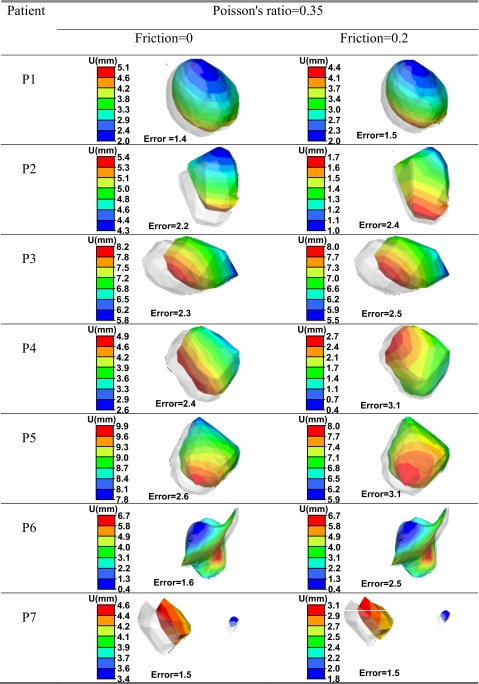 |
||
The vector displacement error included in the table using the absolute average error in all three directions of the surrounding points of the tumor and its center of mass increases slightly as the coefficient of friction increases from 0.0 to 0.2. The largest error increase is in the case of P6 where the tumor is attached to the surface of the lung.
CONCLUSIONS
Parametric and verification studies are conducted to find the accuracy of deformable image registration of the lungs using three dimensional finite element models. Hyperelastic material properties of human lungs based on experimental data are applied with different Poisson’s ratios of 0.35, 0.40, 0.45, and 0.499. Sliding of the lungs inside the chest cavities is modeled using contact surfaces with different friction coefficients of 0.0, 0.1, and 0.2. Bronchial bifurcations are used to check the accuracy of the model.
Frictionless contact surface with a Poisson’s ratio of 0.4 is found to be the optimum model with minimum absolute errors of 1.1±0.9, 1.5±1.3, and 2.1±1.6 cm in the LR, AP, and SI directions, respectively. Similarly, minimum residual errors of the tumor points are also attained using the optimum model. All of the seven patients of the parametric study have a residual error of less than 2.5 mm (slice thickness) in the SI direction using this optimum model. These results are verified using nine additional patients where the average absolute errors are 0.8±0.7, 1.3±1.1, and 1.7±1.6 cm in the LR, AP, and SI directions, respectively.
It is interesting to note that the error slightly increases as the Poisson’s ratio and coefficient of friction increase in the models with contact surfaces. However, the error decreases as the Poisson’s ratio increases in models without contact surfaces where the lungs are attached to the chest cavity.
The parameters investigated have shown improvement in the registration. Future work will evaluate additional improvements in registration using heterogeneous materials for different lung structures (i.e., bronchial tree) and the effect of the pluera in the biomechanical model.
ACKNOWLEDGMENTS
The authors would like to thank Andrea Bezjak, the Addie MacNaughton Chair in Thoracic Radiation Oncology, and Kevin Franks for their assistance in obtaining the patient data. This work was supported by the National Cancer Institute of Canada—Terry Fox Foundation and NIH 5RO1CA124714-02.
References
- Kessler M. L., “Image registration and data fusion in radiation therapy,” Br. J. Radiol. 79, S99–S108 (2006). 10.1259/bjr/70617164 [DOI] [PubMed] [Google Scholar]
- Crum W. R., Hartkens T., and Hill D. L. G., “Non-rigid image registration: Theory and practice,” Br. J. Radiol. 77, S140–S153 (2004). 10.1259/bjr/25329214 [DOI] [PubMed] [Google Scholar]
- Maintz J. B. A. and Viergever M. A., “A survey of medical image registration,” Med. Image Anal. 2, 1–36 (1998). 10.1016/S1361-8415(01)80026-8 [DOI] [PubMed] [Google Scholar]
- Holden K., “A review of geometric transformations for nonrigid body registration,” IEEE Trans. Med. Imaging 27, 111–128 (2008). 10.1109/TMI.2007.904691 [DOI] [PubMed] [Google Scholar]
- Carter T. J., Sermesant M., Cash D. M., Barratt D. C., Tanner C., and Hawkes D. J., “Application of soft tissue modelling to image-guided surgery,” Med. Eng. Phys. 27, 893–909 (2005). 10.1016/j.medengphy.2005.10.005 [DOI] [PubMed] [Google Scholar]
- Yan D., Jaffray D. A., and Wang J. W., “A model to accumulate fractionated dose in a deforming organ,” Int. J. Radiat. Oncol., Biol., Phys. 44, 665–675 (1999). 10.1016/S0360-3016(99)00007-3 [DOI] [PubMed] [Google Scholar]
- Bharatha A., Hirose M., Hata N., Warfield S. K., Ferrant M., Zou K. H., Suarez-Santana E., Ruis-Alzola J., Kikinis R., Jolesz F. A., and Tempany C. M. C., “Evaluation of three-dimensional finite element-based deformable registration of pre- and intraoperative prostate imaging,” Med. Phys. 28, 2551–2560 (2001). 10.1118/1.1414009 [DOI] [PubMed] [Google Scholar]
- Brock K. K., Hollister S. J., Dawson L. A., and Balter J. M., “Technical note: Creating a four-dimensional model of the liver using finite element analysis,” Med. Phys. 29, 1403–1405 (2002). 10.1118/1.1485055 [DOI] [PubMed] [Google Scholar]
- Brock K. K., Sharpe M. B., Dawson L. A., Kim S. M., and Jaffray D. A., “Accuracy of finite element model-based multi-organ deformable image registration,” Med. Phys. 32, 1647–1659 (2005). 10.1118/1.1915012 [DOI] [PubMed] [Google Scholar]
- Brock K. K., Dawson L. A., Sharpe M. B., Moseley D. J., and Jaffray D. A., “Feasibility of a novel deformable image registration technique to facilitate classification, targeting, and monitoring of tumor and normal tissue,” Int. J. Radiat. Oncol., Biol., Phys. 64, 1245–1254 (2006). 10.1016/j.ijrobp.2005.10.027 [DOI] [PubMed] [Google Scholar]
- Coselmon M. M., Balter J. M., McShan D. L., and Kessler M. L., “Mutual information based CT registration of the lung at exhale and inhale breathing states using thin-plate splines,” Med. Phys. 31, 2942–48 (2004). 10.1118/1.1803671 [DOI] [PubMed] [Google Scholar]
- McClelland J. R., Blackall J. M., Tarte S., Chandler A., Hughes S., Ahmad S., Landau D. B., and Hawkes D. J., “A continuous 4D motion model from multiple respiratory cycles for use in lung radiotherapy,” Med. Phys. 33, 3348–3358 (2006). 10.1118/1.2222079 [DOI] [PubMed] [Google Scholar]
- Samant S. S., Xia J., Muyan-Ozcelik P., and Owens J. D., “High performance computing for deformable image registration: Towards a new paradigm in adaptive radiotherapy,” Med. Phys. 35, 3546–3553 (2008). 10.1118/1.2948318 [DOI] [PubMed] [Google Scholar]
- Steina D., Tetzlaff R., Wolf I., and Hans-Peter M., “Accuracy of non-rigid registration for local analysis of elasticity restrictions of the lungs,” Proc. SPIE 7261, 72611P–72619P (2009). [Google Scholar]
- Mead J., Takishima T., and Leith D., “Stress distribution in lungs: A model of pulmonary elasticity,” J. Appl. Physiol. 28, 596–608 (1970). [DOI] [PubMed] [Google Scholar]
- Fung Y. C., “A theory of elasticity of the lung,” ASME J. Appl. Mech. 41, 8–14 (1974). [Google Scholar]
- Lee G. C., “Solid mechanics of lungs,” J. Engrg. Mech. Div. 104, 177–199 (1978). [Google Scholar]
- Liu J. T. and Lee G. C., “Static finite deformation analysis of the lung,” J. Engrg. Mech. Div. 104, 225–239 (1978). [Google Scholar]
- Fung Y. C., Tong P., and Patitucci P., “Stress and strain in the lung,” J. Engrg. Mech. Div. 104, 201–223 (1978). [Google Scholar]
- Vawter D. L., Fung Y. C., and West J. B., “Constitutive equation of lung tissue elasticity,” J. Biomech. Eng. 101, 38–45 (1979). [Google Scholar]
- De Wilde R., Clement J., Hellemans J. M., Decramer M., Demedts M., Boving R., and Van DeWoestijne K. P., “Model of elasticity of the human lung,” J. Appl. Physiol. 51, 254–261 (1981). [DOI] [PubMed] [Google Scholar]
- Maksym G. N. and Bates J. H., “A distributed nonlinear model of lung elasticity,” J. Appl. Physiol. 82, 32–41 (1997). [DOI] [PubMed] [Google Scholar]
- Denny E. and Schroter R. C., “A model of non-uniform lung parenchyma distortion,” J. Biomech. 39, 652–663 (2006). 10.1016/j.jbiomech.2005.01.010 [DOI] [PubMed] [Google Scholar]
- Matthews F. L. and West J. B., “Finite element displacement analysis of a lung,” J. Biomech. 5, 591–600 (1972). 10.1016/0021-9290(72)90031-0 [DOI] [PubMed] [Google Scholar]
- Sundaram S. H. and Feng C. C., “Finite element analysis of the human thorax,” J. Biomech. 10, 505–516 (1977). 10.1016/0021-9290(77)90104-X [DOI] [PubMed] [Google Scholar]
- Villard P., Beuve M., Shariat B., Baudet V., and Jaillet F., “Simulation of lung behaviour with finite elements: Influence of bio-mechanical parameters,” Proceedings of the Third International Conference on Medical Information Visualisation—BioMedical Visualisation, MediVi,V2005, London, UK (July 5–7, 2005), IEEE Computer Society, pp. 9–14.
- Zhang T., Orton N. P., Mackie T. R., and Paliwal B. R., “Technical note: A novel boundary condition using contact elements for finite element based deformable image registration,” Med. Phys. 31, 2412–2415 (2004). 10.1118/1.1774131 [DOI] [PubMed] [Google Scholar]
- Al-Mayah A., Moseley J., and Brock K. K., “Contact surface and material nonlinearity modeling of human lungs,” Phys. Med. Biol. 53, 305–317 (2008). 10.1088/0031-9155/53/1/022 [DOI] [PubMed] [Google Scholar]
- Al-Mayah A., Moseley J., Velec M., and Brock K. K., “Effect of friction and material compressibility on deformable modeling of human lung,” International Symposium on Computational Models for Biomedical Simulation - ISBMS ’08, London, UK (July 7–8, 2008), LNCS 5104, Lecture Notes in Computer Science (Springer-Verlag, Heidelberg, Germany: ), pp. 98–106.
- Widmaier E. P., Raff H., and Strang K. T., Vander’s Human Physiology: The Mechanisms of Human Body Function, 10th ed. (McGraw-Hill, New York, 2006). [Google Scholar]
- D’Angelo E., Loring S. H., Gioia M. E., Pecchiari M., and Moscheni C., “Friction and lubrication of pleural tissues,” Respir. Physiol. Neurobiol. 142, 55–68 (2004). 10.1016/j.resp.2004.05.006 [DOI] [PubMed] [Google Scholar]
- Loring S. E., Brown R. E., Gouldstone A., and Butler J. P., “Lubrication regimes in mesothelial sliding,” J. Biomech. 38, 2390–2396 (2005). 10.1016/j.jbiomech.2004.10.012 [DOI] [PubMed] [Google Scholar]
- Wu Z., Rietzel E., Boldea V., Sarrut D., and Sharp G. C., “Evaluation of deformable registration of patient lung 4DCT with subanatomical region segmentations,” Med. Phys. 35, 775–781 (2008). 10.1118/1.2828378 [DOI] [PubMed] [Google Scholar]
- Lai-Fook S. J. and Hyatt R. E., “Effect of age on elastic moduli of human lungs,” J. Appl. Physiol. 89, 163–168 (2000). [DOI] [PubMed] [Google Scholar]
- Butler J. P. and Loring S. H., “A potential elastohydrodynamic origin of load-support and Coulomb-like friction in lung/chest wall lubrication,” J. Tribol. 130, 041201-1–7 (2008). 10.1115/1.2958076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Y. J., Yager D., and Fung Y. C., “Measurement of the mechanical properties of the human lung tissue,” J. Biomech. Eng. 109, 169–174 (1987). 10.1115/1.3138661 [DOI] [PubMed] [Google Scholar]