Mechanism of C–F Reductive Elimination from Palladium(IV) Fluorides

Abstract

The first systematic mechanism study of C–F reductive elimination from a transition metal complex is described. C–F bond formation from three different Pd(IV) fluoride complexes was mechanistically evaluated. The experimental data suggest that reductive elimination occurs from cationic Pd(IV) fluoride complexes via a dissociative mechanism. The ancillary pyridyl-sulfonamide ligand plays a crucial role for C–F reductive elimination, likely due to a κ³ coordination mode, in which an oxygen atom of the sulfonyl group coordinates to Pd. The pyridyl-sulfonamide can support Pd(IV) and has the appropriate geometry and electronic structure to induce reductive elimination.

Introduction

Aryl fluorides are valuable compounds as pharmaceuticals,¹ agrochemicals,² and tracers for positron-emission tomography.³ Electrophilic⁴ and nucleophilic⁵ fluorination, as well as the pyrolysis of diazonium tetrafluoroborates,⁶ are established methods for the synthesis of fluoroarenes. However, conventional fluorination reactions exhibit a limited substrate scope with respect to the electronic structure of the arene and the functional groups tolerated, and are therefore typically not applicable to late-stage introduction of fluorine into complex functionalized molecules.⁷

Transition metal-catalyzed carbon–heteroatom bond formation for C–N⁸, C–O⁹ and C–S¹⁰ bonds has become increasingly efficient over the past decade, with palladium being one of the most common transition metals for catalysis. By contrast, the development of transition metal-mediated C–F bond formation has been slower.¹¹ Two general approaches have been employed for Pd-mediated C–F bond formation: 1) Pd(0)/Pd(II)-mediated nucleophilic fluorination as studied by Grushin,¹² Yandulov,¹³ and Buchwald,¹⁴ and 2) Pd-mediated electrophilic fluorination as demonstrated by Sanford,¹⁵ Yu,¹⁶ Vigalok,¹⁷ and us.¹⁸ The two distinct approaches differ by the source of fluorine: either nucleophilic or electrophilic fluorinating reagents are employed. Nucleophilic fluorination using fluoride anion is complicated by the high basicity of fluoride. Protic functional groups such as alcohols, primary or secondary amines, and N–H-containing amides that attenuate the nucleophilicity of fluoride can be problematic¹⁹ due to the strong H–F hydrogen bonding²⁰ and resulting bifluoride formation.²¹ Protic functional groups are generally tolerated by electrophilic fluorinating reagents, but electrophilic fluorination can be problematic with basic functional groups such as amines and sulfides due to unproductive reactions with the electrophilic fluorinating reagent. As such, the two approaches are complementary.

Aryl fluoride synthesis by confirmed C–F reductive elimination from any transition metal complex was not established until our original report in 2008.^18b Previously, independent efforts by Grushin and Yandulov had focused on C–F reductive elimination from aryl Pd(II) fluorides.^12,13 Yandulov observed the formation of 10% arylfluoride from a phosphine-stabilized Pd(II) complex. Although the reaction mechanism has not been elucidated, the mechanistic investigations by Grushin and Yandulov significantly contributed to recognizing the challenges associated with C–F reductive elimination. In 2009, Buchwald reported a Pd(0)/Pd(II) catalyzed aromatic fluorination reaction of functionalized aryl triflates and bromides in 57–85% yield.¹³ Buchwald also demonstrated C–F reductive elimination from a discrete phosphine Pd(II) fluoride complex in up to 55% yield. The development of bulky, monodentate phosphine ligands that facilitate C–X reductive elimination from Pd(II) successfully led to the first highly sought-after Pd(0)-catalyzed fluorination reaction. Pd(II)-catalyzed, electrophilic fluorination reactions are less well understood. While high-valent Pd(III) or Pd(IV) fluoride intermediates seem reasonable, their relevance to catalysis has not yet been mechanistically substantiated. Aside from our initial report in 2008, mechanistic investigations of C–F bond formation by confirmed reductive elimination from high-valent Pd complexes have not yet been disclosed.

A Pd(IV) trifluoride complex was reported by the Sanford group in 2009 and afforded aryl fluoride in trace amounts upon thermolysis. However, upon addition of various oxidants such as XeF₂, (PhSO₂)₂NF, and N-bromosuccinimide to the Pd(IV) trifluoride complex, high-yielding C–F bond formation was observed. The C–F bond formation may proceed by reductive elimination from Pd(IV) and studies to gain further mechanistic insides into the oxidant-promoted C–F coupling process are ongoing in the Sanford lab.²²

Currently, only two transition metal complex classes—Buchwald’s phosphine Pd(II) fluoride and our pyridylsulfonamide Pd(IV) fluoride— have been identified to afford C–F bond formation via reductive elimination.^{11a, 22} Here we report the first systematic mechanism investigation of C–F bond formation via well-defined reductive elimination from a transition metal complex. C–F bond formation is a challenge in both nucleophilic and electrophilic transition metal-catalyzed fluorination reactions and, hence, mechanistic understanding of C–F reductive elimination may support the rational development of more efficient transition metal catalysts suitable for C–F bond formation.

Mechanisms of C–C and C–heteroatom reductive elimination have been studied from Pd(II),²³ Pd(III),²⁴ and Pd(IV)²⁵ complexes and have contributed to a better understanding and rational reaction improvement. Mechanistic insight into C–F bond reductive elimination has been elusive because no well-defined reaction was available for systematic investigation.

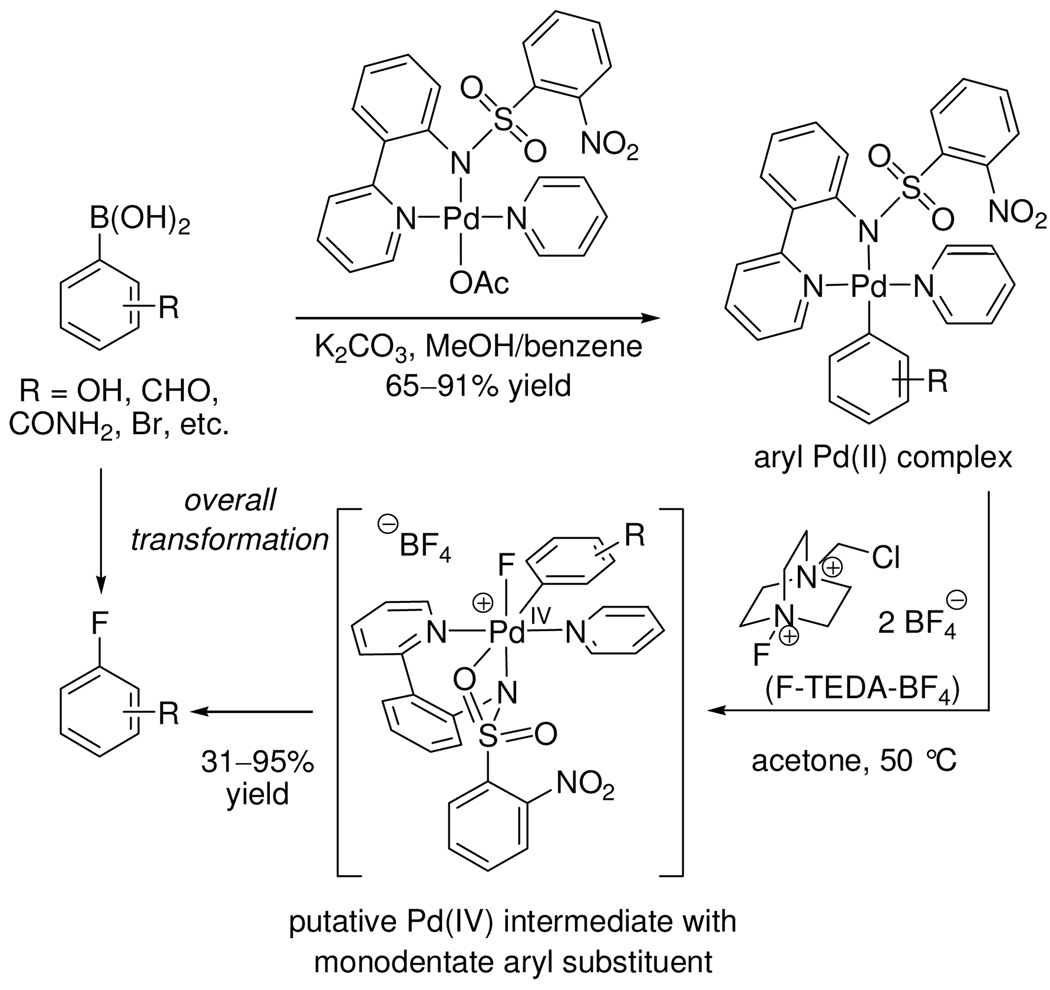
We identified that a variety of functionalized arylboronic acids can be converted to the corresponding aryl fluorides via pyridylsulfonamide-stabilized Pd complexes (Scheme 1). Addition of the electrophilic fluorinating reagent F-TEDA-BF₄ to the arylpalladium complexes in acetone at 50 °C afforded aryl fluorides, typically in 70 to 90% yield.^18a

Scheme 1.

Fluorination of functionalized arylboronic acids via arylpalladium(II) complexes by the electrophilic fluorination reagent F-TEDA-BF₄

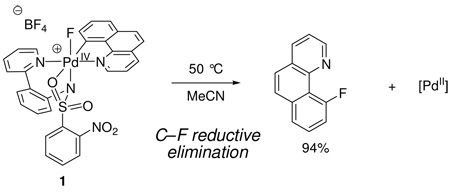
We hypothesized the intermediacy of Pd(IV) fluoride complexes but could not spectroscopically observe them due to fast C–F bond formation to afford the aryl fluoride products. To study the mechanism of C–F bond formation, our strategy entailed rigidifying the ligand environment on palladium to retard reductive elimination from a putative Pd(IV) fluoride intermediate. The strategy was executed by substitution of the aryl and pyridine ligand of the aryl Pd(II) complex shown in Scheme 1 with the bidentate benzo[h]quinolyl ligand. The more rigid benzo[h]quinolyl ligand, when compared to independent phenyl and pyridine ligands, allowed the synthesis of spectroscopically observable Pd(IV) fluoride complexes such as 1 (eq 1).^18b The modular structure of the pyridyl-sulfonamide-stabilized Pd(IV) fluoride 1 and its well-defined, high-yielding reductive elimination to form a C–F bond permitted us to address key questions that influence C–F bond formation. Is the pyridyl-sulfonamide ligand special? What is the nature of the transition state for C–F reductive elimination? What factors accelerate C–F reductive elimination? Herein, we provide experimental and computational evidence that supports reductive elimination via a concerted pathway from a cationic, pentacoordinate Pd(IV) fluoride. The pyridyl-sulfonamide ligand can stabilize the high-valent, octahedral Pd(IV) fluoride by tricoordinate facial coordination and support the electronic requirements for reductive elimination.

(1)

Results

Structure assignment of Pd(IV) fluorides

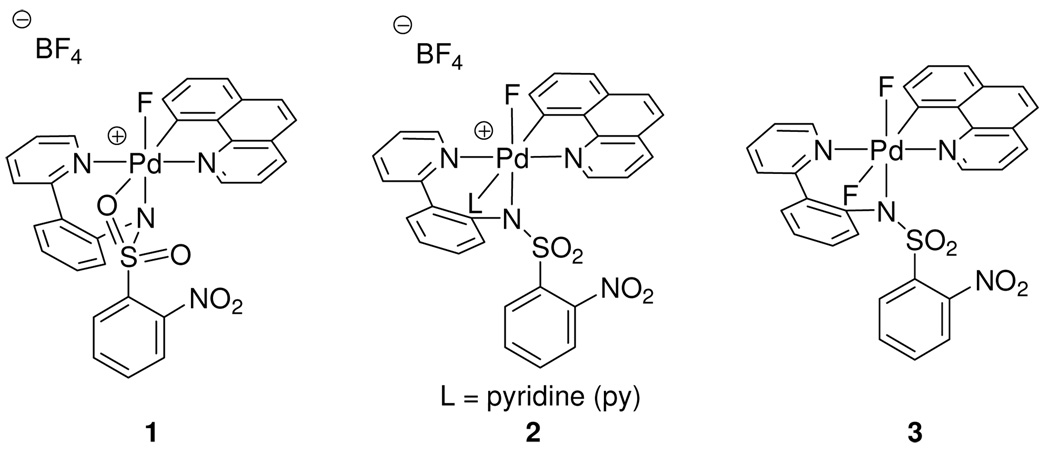
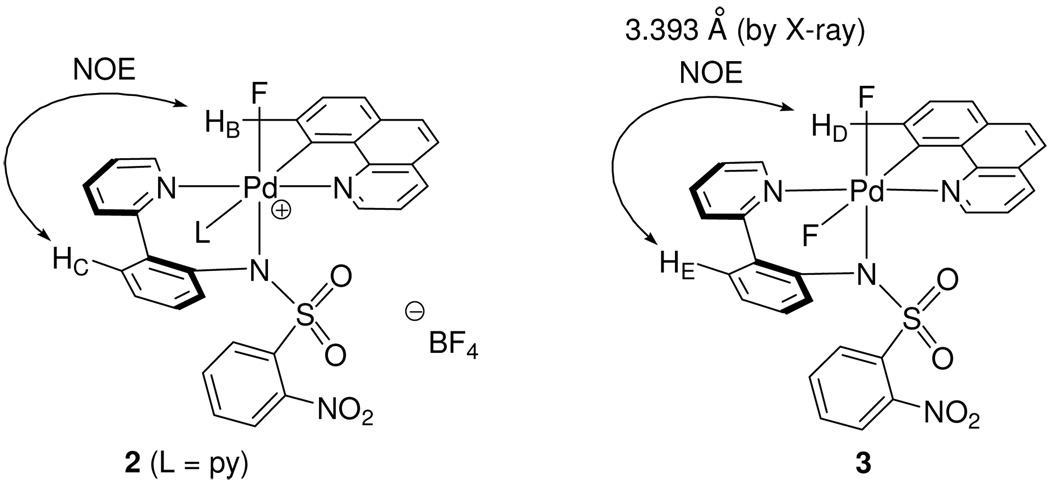
Three Pd(IV) fluoride complexes were investigated: the pyridyl-sulfonamide-stabilized cationic Pd fluoride 1, complex 2, in which a pyridine ligand occupies the coordination site trans to the carbon ligand, and the neutral Pd difluoride complex 3 (Figure 1, for the synthesis of 1–3, see Supporting Information). Complexes 1–3 feature the benzo[h]quinolyl ligand that was introduced to obtain higher stability of the Pd(IV) fluoride complexes for mechanistic analysis. For a meaningful discussion of the mechanism of C–F reductive elimination, an unambiguous assignment of the solution ground state structures of the Pd(IV) fluoride complexes was essential. The complexes 1–3 have C₁ symmetry, and six coordination sites are occupied by six different ligands with the exception of 3, which features two fluoride ligands. The low symmetry of the complexes provides the opportunity to investigate the effect of each ligand independently and gain insight into the transition state for reductive elimination.

Figure 1.

Pd(IV) fluoride complexes 1–3 analyzed in this study.

Solid state structure of 3

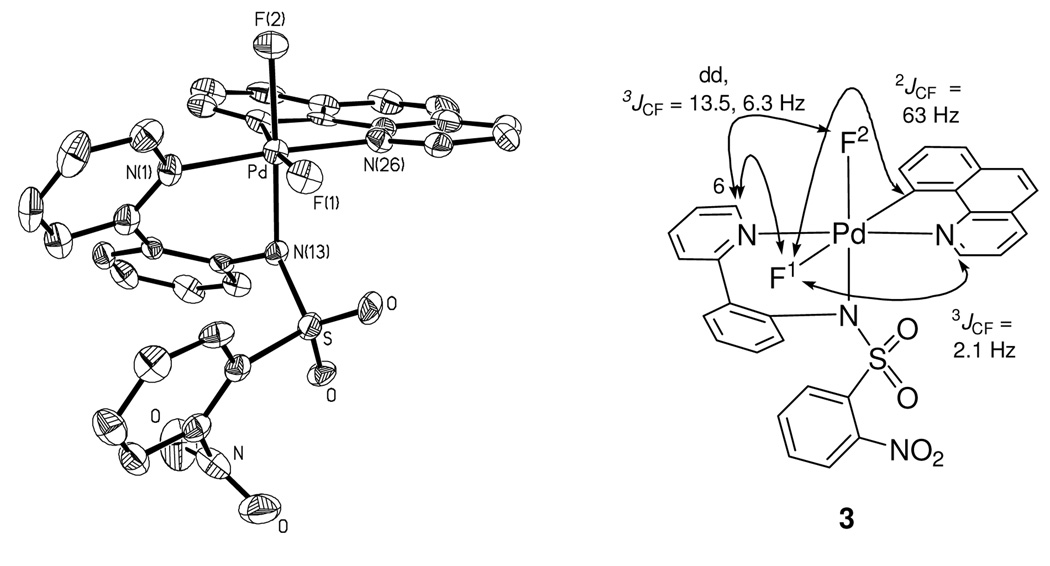
Attempts to obtain X-ray quality crystals for cationic complexes 1 and 2 were unsuccessful. Complexes 1 and 2 could be observed in acetonitrile but decomposed upon precipitation by addition of excess Et₂O at −20 °C. The difluoro Pd(IV) complex 3 was more stable than cationic complexes 1 and 2, and its X-ray crystal structure was obtained.^18b Unlike many reported Pd(II) fluoride complexes,^12,13,26 complex 3 is stable to moisture; it was synthesized from 1 and tetramethylammonium fluoride tetrahydrate. Isolation and purification of 3 were carried out under ambient atmosphere. Difluoro Pd(IV) complex 3 showed resistance to decomposition by water; less than 10 % of decomposition was observed when a DMSO solution of 3 was kept at 23 °C for 1 day in the presence of 10 equivalents of water. The crystal structure of 3 is shown in Figure 2. The two Pd(IV)–F bond lengths are 1.955 Å and 2.040 Å, respectively. The Pd–F(1) bond trans to the carbon ligand is longer by 0.085 Å, which is consistent with the strong trans-influence²⁷ of the carbon ligand. The Pd–F bond lengths in 3 are 0.13 Å and 0.05 Å shorter than the average of Pd(II)–F bond length of 2.09 Å, respectively²⁸ and similar in length to Pd(IV)–F bond lengths in a Pd(IV) trifluoride reported by Sanford in 2009 (1.923 Å, 1.931 Å).^22,29

Figure 2.

ORTEP diagram of the Pd(IV) difluoride 3 (left) and characteristic ¹³C–¹⁹F coupling constants (right). Selected bond lengths [Å] and angles [°]: Pd–F(1) 2.040(3), Pd–F(2) 1.955(3), Pd–C(35) 2.008(5), Pd–N(13) 2.019(4), Pd–N(1) 2.027(5), Pd–N(26) 2.012(5), F(1)–Pd–F(2) 88.27(13)°, F(2)–Pd–N(13) 173.48(15)°.

Solution state structure of 3

Solution state structures of the three Pd(IV) fluoride complexes 1–3 were assigned by NMR spectroscopy. The resonances in the ¹H and ¹³C NMR spectra of 1–3 were well resolved and, after ¹H–¹H COSY, ¹H–¹³C HSQC, ¹H–¹³C HMBC, and ¹H–¹H NOESY analysis, could be assigned (see Supporting Information). The observation of ¹H–¹⁹F and ¹³C–¹⁹F coupling constants provided information for the assignment of the configuration and solution conformation of the Pd(IV) fluoride complexes. As shown in Figure 2, the vicinal trans C–Pd–F coupling constant (²J_CF = 63 Hz),³⁰ and the C–F coupling constant (³J_CF = 2.1 Hz)³¹ indicate that the benzo[h]quinolyl and the fluorine (F¹) ligand are located in the same plane. Coupling constants of the pyridyl 6-carbon of the pyridyl-sulfonamide ligand were observed to both fluoride ligands (³J_CF = 13.5 and 6.3 Hz), consistent with structure 3.

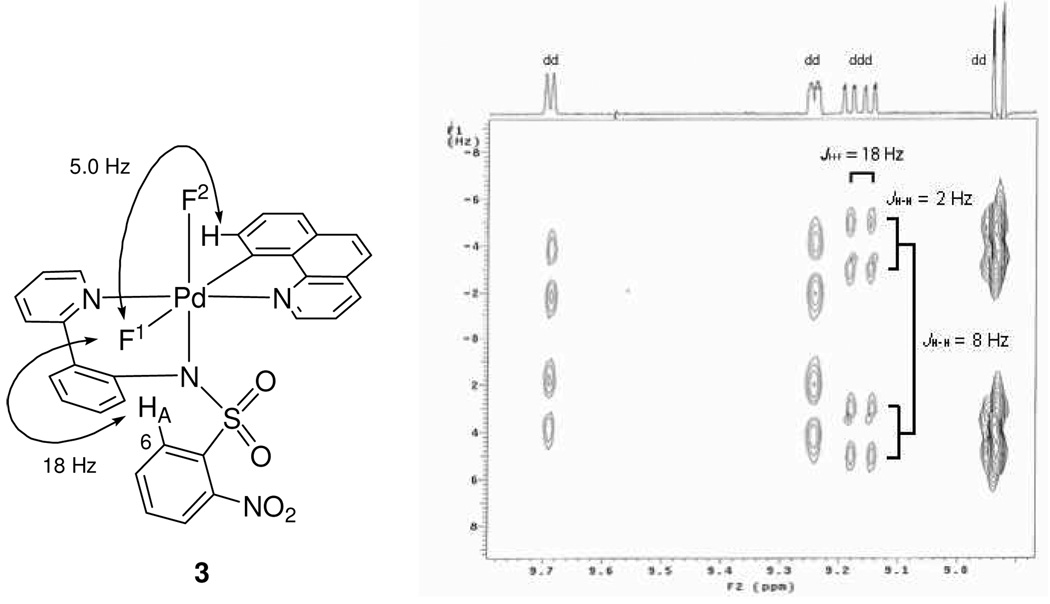
¹H–¹⁹F coupling constants can provide further structural information. ¹H–¹H coupling constants can often be similar in size as ¹H–¹⁹F coupling constants.³² Therefore, a HOM2DJ spectrum³³ was obtained to differentiate ¹H–¹⁹F coupling constants from ¹H–¹H coupling constants as shown in Figure 3. In a one dimensional ¹H NMR spectrum, chemical shift and coupling constants, ¹H–¹H and ¹H–¹⁹F, are observed along the same axis. A HOM2DJ experiment separates ¹H–¹H from ¹H–¹⁹F coupling constants along two different axes. As can be seen in Figure 3, ¹H–¹H coupling constants are resolved in the Y-axis, whereas ¹H–¹⁹F coupling constants are resolved in the X-axis. Two long-range ¹H–¹⁹F couplings were identified from the HOM2DJ spectrum. A ¹H–¹⁹F through-space coupling was observed between F¹ and H_A, which is located in the 6-position of the ortho-nitrobenzenesulfonamide moiety. Observation of the F¹–H_A coupling constant confirmed that the conformation of the ortho-nitrobenzenesulfonamide is similar in solution to the conformation observed in the solid state (Figure 2) where H_A and F¹ are 2.212 Å apart. Based on the combined structural information, we assigned the solution structure of 3 to be similar to the structure of 3 in the solid state. The assignment of the solution structure of 3 was instructive for the elucidation of the solution structures of 1 and 2 that lack crystallographic characterization.

Figure 3.

HOM2DJ spectrum and ¹H–¹⁹F couplings. The ¹H NMR is shown in the X axis and the ¹H–¹H coupling constants are shown in the Y axis. The doublet of doublets resulting from ¹H–¹H scalar coupling constants are resolved in the Y axis. Two coupling constants (2 Hz, 8 Hz) out of three shown in the Figure for the doublet of doublets of doublets are resolved in the Y axis. The one remaining coupling constant (18 Hz) is resolved only in the X-axis and, hence, corresponds to a ¹H–¹⁹F coupling.

Solution state structure of 1 and 2

The solution state structures of the monofluoro Pd(IV) complex 1 and pyridine complex 2 were assigned by NMR analysis in comparison to the analysis performed on 3. All ¹H and ¹³C NMR signals of 1 and 2 were assigned based on ¹H–¹H COSY, ¹H–¹³C HSQC, ¹H–¹³C HMBC, and ¹H–¹H NOESY spectra. The analysis of the 2D NMR spectra of the pyridine complex 2 was complicated compared to the analysis of 1 due to signal overlap and required an additional ¹H–¹H TOCSY spectrum for unambiguous assignment. In a TOCSY experiment, each ¹H spin system can be identified separately. A ¹H spin system includes all ¹H resonances that are mutually connected by an uninterrupted ensemble of scalar couplings.³⁴ Hence, the pyridine ¹H spin system in 2 could be identified because none of the ¹H nuclei of the pyridyl ligand has a scalar coupling to any ¹H nucleus outside the pyridine ¹H spin system in 2. Assignments of the configuration of complexes 1 and 2 were supported by two key observations: 1) an NOE signal between H_B and H_C and 2) the lack of a characteristic trans C–Pd–F coupling.

The observed NOE signal between H_B and H_C is consistent with the configuration shown in Figure 4 (left). A similar NOE signal was observed for the difluoride complex 3, in which H_D and H_E are 3.393 Å apart in the solid state (Figure 4, right). The observation of the H_B–H_C NOE signal in 1 and 2 leaves two possibilities for the configuration of complexes 1 and 2: the fluoride and carbon ligands oriented cis or trans to one another. Because no characteristic trans C–Pd–F coupling constant was observed in the ¹³C NMR spectra of 1 and 2, respectively, the fluoride ligand was assigned to be oriented cis to the carbon ligand as shown for 2 in Figure 4. For the hexacoordinate cationic complex 2, only one coordination site remains for pyridine coordination, trans to the carbon ligand.

Figure 4.

Characteristic NOE signals for configuration determination.

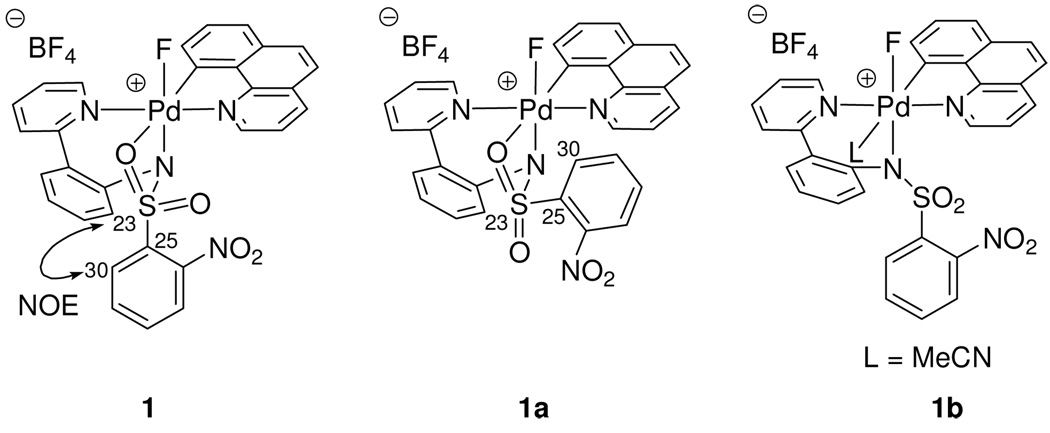
Complex 1 was prepared in MeCN and we originally assigned structure 1b (Figure 5) to the cationic Pd(IV) fluoride, in which an MeCN ligand occupies the sixth coordination site, analogous to the pyridine ligand in 2. However, no evidence for MeCN coordination could be obtained, even upon cooling to −30 °C. While the lack of evidence for MeCN coordination in MeCN cannot rule out structure 1b, significant evidence in favor of structure 1 was obtained, in which the pro-S oxygen atom of the sulfonyl group occupies the sixth coordination site trans to the carbon ligand. While oxygen coordination in sulfonamide complexes has been established crystallographically,³⁵ the tridentate κ³ coordination geometry of the pyridyl-sulfonamide is not well known, possibly due to the scarcity of pyridyl-sulfonamide ligands in transition metal chemistry.

Figure 5.

Considered structures for the cationic Pd(IV) fluoride complex. The data are consistent with structure 1.

The observation of an NOE signal between hydrogen atoms H²³ and H³⁰ is consistent with κ³ coordination of the pyridyl-sulfonamide ligand and also rules out the diastereomer 1a as a potential structure for the Pd(IV) fluoride. An analogous NOE signal in the pyridine complex 2 was not observed. To further bolster our assignment, we compared the ¹³C resonances of all carbon atoms in 1 with the corresponding carbon atom resonances in 2 and identified that the largest difference in shift (6.9 ppm) was observed for the arenesulfonyl ipso carbon C²⁵, while the average difference in shift was only 1.1 ppm (see Supporting Information for detail).

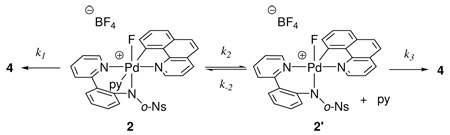
More evidence for the structure of 1 was obtained by dynamic NMR experiments. The pyridine complex 2 can be prepared by addition of pyridine to 1 in MeCN. The equillibrium constants K_eq between 1 and 2 were calculated from data obtained by comparing the integrations of NMR resonances in the ¹H NMR spectra acquired at temperatures between −35 °C and 25 °C. The free enthalpy, free entropy, and Gibbs free energy of the reaction 1→2 (eq 2) were determined as follows: ΔH° = −4.46 ± 0.28 kcal·mol⁻¹, ΔS° = −13.1 ± 1.1 eu, ΔG°₂₉₈ = −0.57 ± 0.03 kcal·mol⁻¹. The measured Gibbs free energy of ΔG°₂₉₈ = −0.57 further supports the κ³coordination structural assignment of 1 over the MeCN coordinated structure assignment 1b because a larger ΔG°₂₉₈ would be expected if an MeCN ligand from a hypothetical complex 1b was displaced by a pyridine ligand to afford 2.³⁶ Pyridine coordination is significantly stronger than acetonitrile coordination and a larger K_eq and, hence, a more negative ΔG°₂₉₈ would be expected. For example, the Pd(II) complex 5 (vide infra) features a pyridine ligand that is not replaced to any observable extent by MeCN, even in MeCN as solvent.

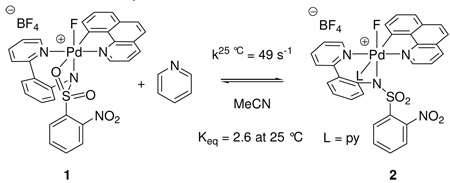(2)

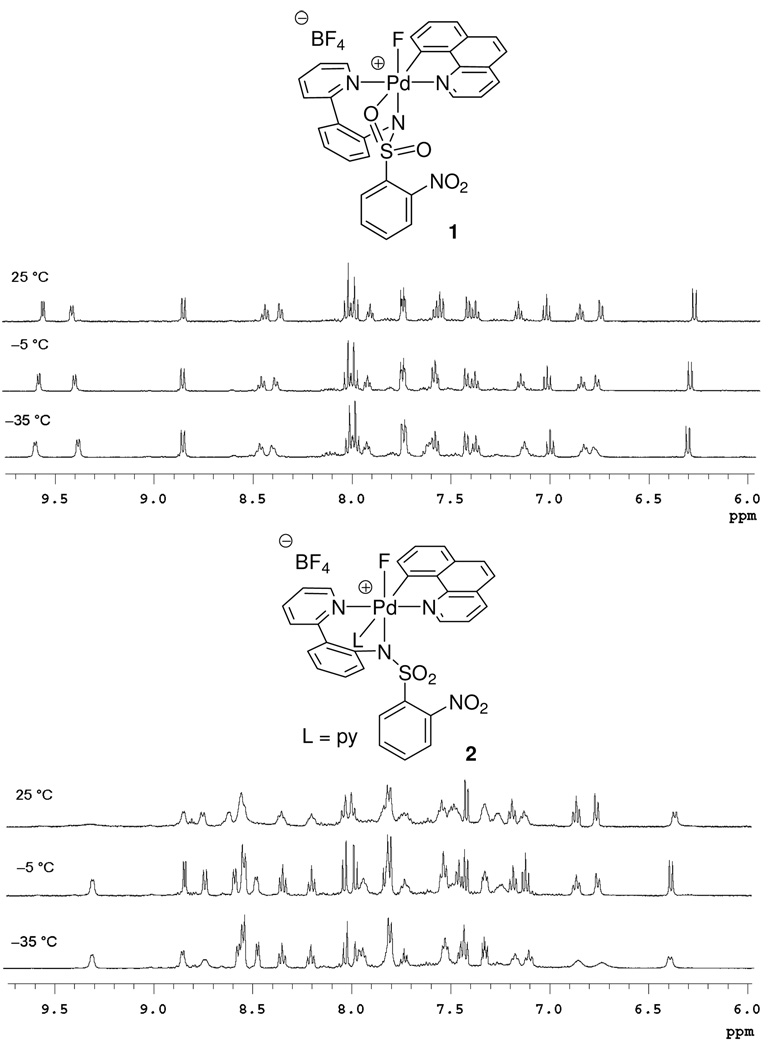
The comparison of temperature-dependent ¹H NMR spectra of 1 and 2 provided additional circumstantial evidence for structure 1. As shown in Figure 6, the ¹H NMR resonances for 1 were sharp from −30 °C to 25 °C; no dynamic behavior that could be attributed to MeCN exchange was observed on the NMR timescale. On the other hand, the ¹H NMR resonances for 2 were broad at 25 °C and became sharper when the temperature was decreased to −5 °C, consistent with slow pyridine exchange at −5 °C. To substantiate that the observed dynamic behavior can be attributed to pyridine dissociation from 2, we determined the rate constant at equilibrium as well as the activation parameters for the reaction from 1 to 2 shown in eq 2. The temperature-dependent rates were calculated from a ¹H NMR line-shape analysis experiment³⁷ executed between −24 °C and 11 °C. The activation parameters were: ΔH^‡ = 14.0 ± 1.3 kcal·mol⁻¹, ΔS^‡ = −3.99 ± 4.79 eu, ΔG^‡₂₉₈ = 15.1 ± 0.2 kcal·mol⁻¹. As discussed later, the rate of exchange between 1 and 2 is about 10⁶ times faster than the rate of C–F reductive elimination. No pentacoordinate cationic complex was identified by NMR spectroscopy at any temperature between −35 °C and 25 °C. Line-broadening around −35 °C for both 1 and 2 is consistent with slowed rotation around single bonds such as the sulfonamide C–S bond. Acquisition of NMR spectra at lower temperatures was complicated by the melting point of MeCN (−45 °C).

Figure 6.

Comparison of the temperature-dependent ¹H NMR spectra of 1 and 2.

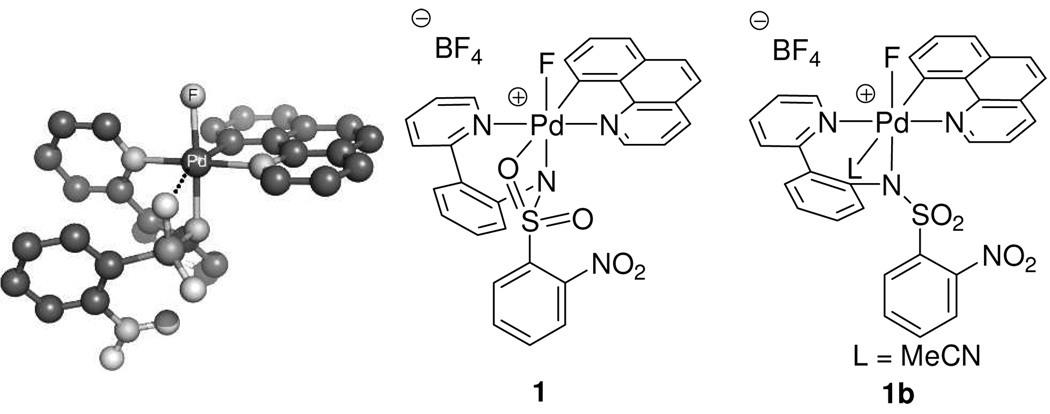
Quantum mechanical calculations using the M06 flavor³⁸ of density functional theory (DFT) (see Supporting Information for computational details) also predicted structure 1 in favor of structure 1b. Acetonitrile coordination to 1 to form 1b was predicted to be endothermic by 2.2 kcal·mol⁻¹. In addition, the computed Pd–N (MeCN) distance of 2.40 Å, compared to 2.27 Å for the Pd–N (pyridine) distance in 2 supports the lability of the MeCN ligand in 1b. Figure 7 shows the energy minimized structure of 1.

Figure 7.

Energy minimized structure of 1. The computed energy difference (ΔH₂₉₈) between 1 and 1b is 2.2 kcal·mol⁻¹ favoring 1.

Reductive elimination from the monofluoro Pd(IV) complexes 1 and 2

With established solution ground state structures for the Pd(IV) fluoride complexes 1–3, we evaluated the kinetic profile for C–F bond formation by reductive elimination. Complexes 1 and 2 underwent C–F reductive elimination following a first order rate law and afforded 10-fluoro-benzo[h]quinoline (4) coordinated to Pd as the only observable organic product (eq 3). The Pd complex after reductive elimination is likely the cationic Pd(II) complex A. While isolation and purification of A was not achieved, presumably due to the weak coordination of 4 to Pd, ¹H and ¹⁹F NMR spectroscopy is consistent with a structure in which 4 is bound to Pd. The ¹H and ¹⁹F NMR resonances that correspond to the 10-fluoro-benzo[h]quinoline ligand in A differed from the resonances of isolated and purified 10-fluoro-benzo[h]quinoline (4). In addition, computation predicted structure A as the product of reductive elimination from 1 with a Pd–F bond length of 2.22 Å. Addition of 4.0 equiv of pyridine after complete consumption of the starting material 1 provided Pd(II) complex 5, whose identity was confirmed by independent synthesis from the corresponding acetato Pd(II) complex, AgBF₄, and pyridine.

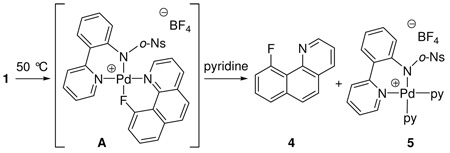(3)

In the following section we will systematically evaluate the rate of reductive elimination from derivatives of 1 as a function of temperature, polarity of the reaction medium, and electronic structure of the ligands to collect data relevant to elucidating the mechanism of reductive elimination (Figure 8).

Figure 8.

Methods employed in this mechanistic study.

Determination of activation parameters

We obtained activation parameters of C–F reductive elimination from both complex 1 and pyridine complex 2 by measuring the rate of C–F reductive elimination in the temperature range of 23–61 °C and 28–65 °C by ¹H NMR spectroscopy, respectively. Reductive elimination from 1 proceeded with ΔH^‡ = 26.5 ± 0.4 kcal·mol⁻¹, ΔS^‡ = 12.4 ± 1.3 eu, and ΔG^‡₂₉₈ = 22.8 ± 0.02 kcal·mol⁻¹, while reductive elimination from 2 proceeded with ΔH^‡ = 32.8 ± 2.5 kcal·mol⁻¹, ΔS^‡ = 30.7 ± 7.8 eu, and ΔG^‡₂₉₈ = 23.7 ± 0.2 kcal·mol⁻¹. The yield of 4 was only slightly affected by the reaction temperature; 4 was obtained in 92–95% and in 79–85% from complexes 1 and 2, respectively.

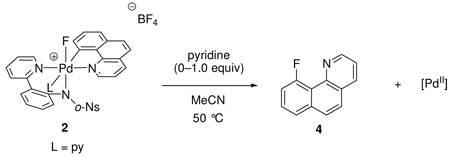
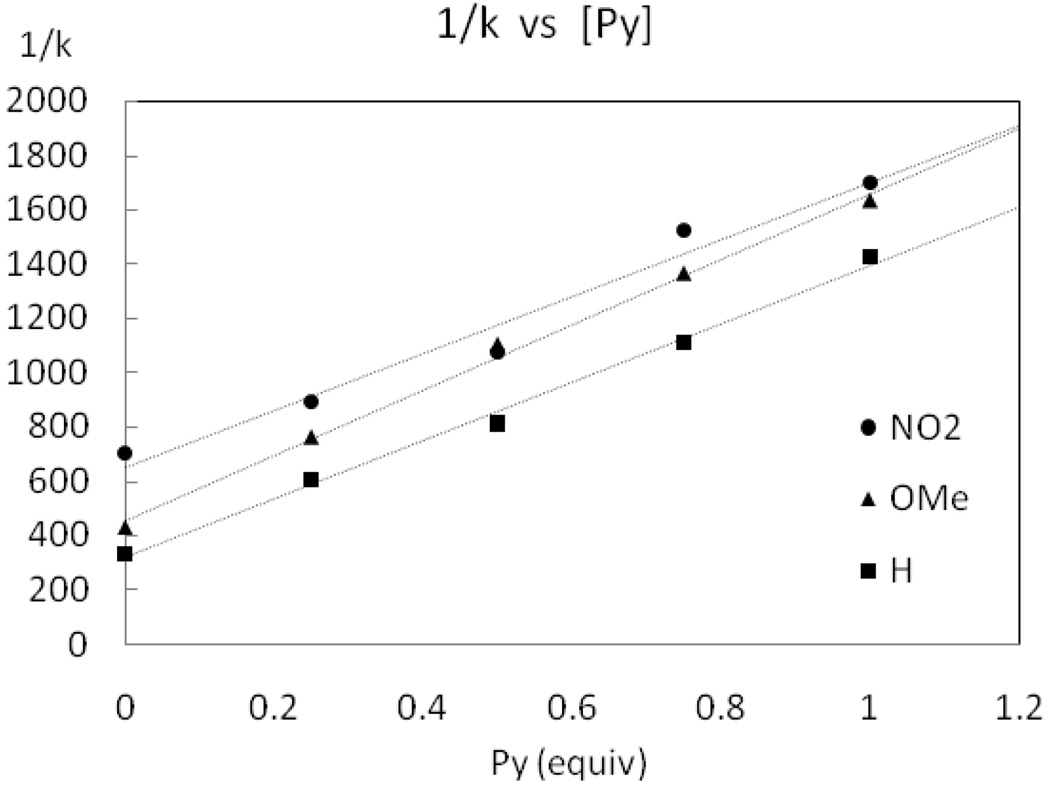
Rate dependence for reductive elimination from complex 2 with excess pyridine

Complex 2 was heated at 50 °C in the presence of varying concentrations of pyridine and the rate of C–F reductive elimination was measured by ¹H NMR spectroscopy as a function of pyridine concentration. The inverse rate as a function of pyridine concentration is shown in Figure 9. A positive, linear dependence of the reciprocal of the rate of C–F reductive elimination from 2 (1/k) vs pyridine equivalent was observed as well as a non-zero intercept. The positive linear dependence shows that pyridine slows the rate of reductive elimination. The yield of fluorination was 90% for 2 without additional pyridine and decreased to 74% with 1.0 equivalent of added pyridine. The yield further decreased with addition of more than one equivalent of pyridine. For example, addition of two equivalents of pyridine afforded 4 in only 43% yield. Therefore, the data with more than one equivalent of added pyridine are not included in the analysis shown in Figure 9.

Figure 9.

Rate dependence on pyridine concentration.

The rate of reductive elimination from 1 was independent of MeCN concentration at high MeCN concentrations. While no rate change was observed, the experiment could only be executed in the presence of a large excess of MeCN (460–2298 equiv compared to complex 1) because 1 was prepared in MeCN and not stable in the absence of MeCN. Therefore, saturation kinetics cannot be excluded.

Rate dependence for reductive elimination from complex 1 on the polarity of the reaction medium

The rate of a reaction can depend on the polarity of the reaction medium.³⁹ Polar transition states are stabilized relative to the corresponding ground states by polar solvents, and measurement of the reaction rate as a function of solvent can give important information about the mechanism. The monofluoro Pd(IV) complexes 1 and 2, however, were always prepared in acetonitrile because the use of other solvents did not result in clean formation of the Pd(IV) complexes. Thus, the polarity of the reaction medium was modified by addition of tetra(n-butyl)ammonium tetraflluoroborate (n-Bu₄NBF₄).⁴⁰ Complex 1 was thermally decomposed at 53 °C in the presence of various amounts of n-Bu₄NBF₄. The rate of reductive elimination reaction was independent of the concentration of n-Bu₄NBF₄ from 0–2.0 M. The yield of fluorination was not significantly influenced by the addition of n-Bu₄NBF₄ and remained between 90 and 96%.

Rate dependence on electronic perturbation of each ancillary ligand (Hammett plots⁴¹)

A Hammett plot is helpful for obtaining information on the magnitude and sign of charge buildup in the transition state.⁴¹ A Hammett study of C–F reductive elimination from 1 is particularly informative due to the low symmetry of the complex and the resulting opportunity to sequentially modify several ligands independently. We studied the influence of three different ligand substitutions on the rate of C–F reductive elimination from a total of 21 analogs of the monofluoro Pd(IV) complex 1: 1) sulfonamide substitution R¹, 2) pyridine (pyridyl-sulfonamide) substitution R², and 3) benzo[h]quinolyl substitution R³ (Figure 10). The synthesis and characterization of the functionalized monofluoro Pd(IV) complexes is described in the Supporting Information.

Figure 10.

Hammett study by independent modification of the sulfonamide, benzo[h]quinolyl, and pyridine ligand substitution.

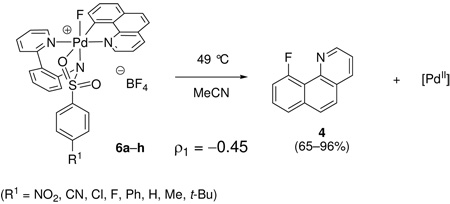
Effect of sulfonamide substitution on the rate of C–F reductive elimination from 1

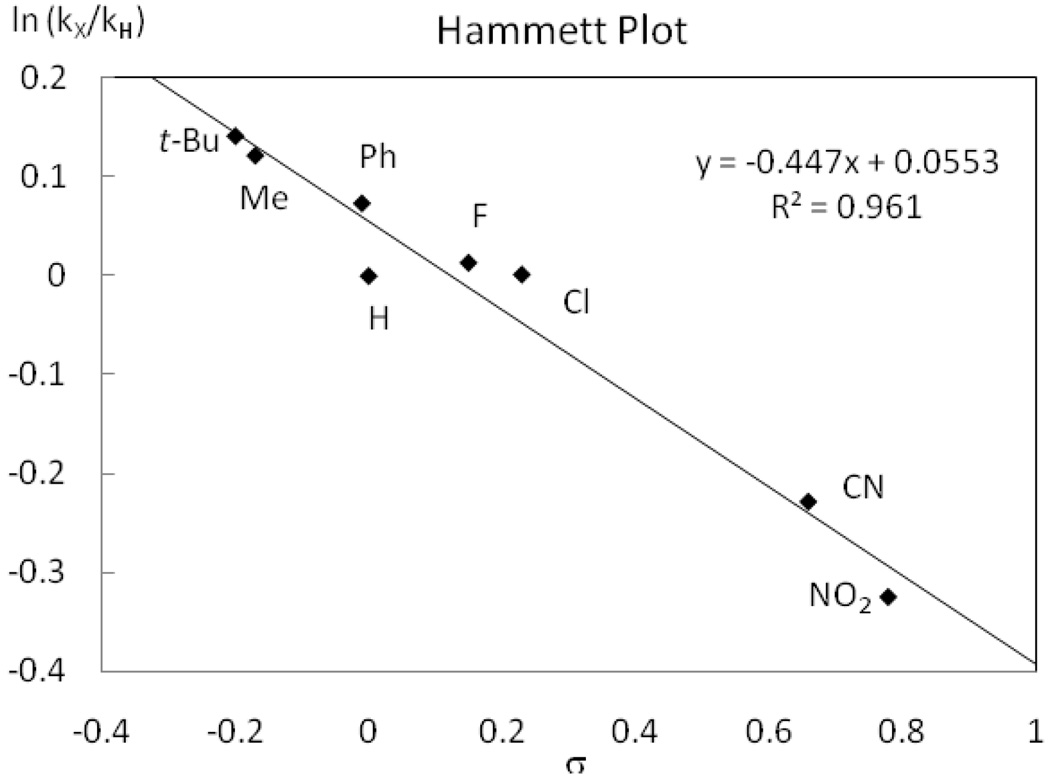
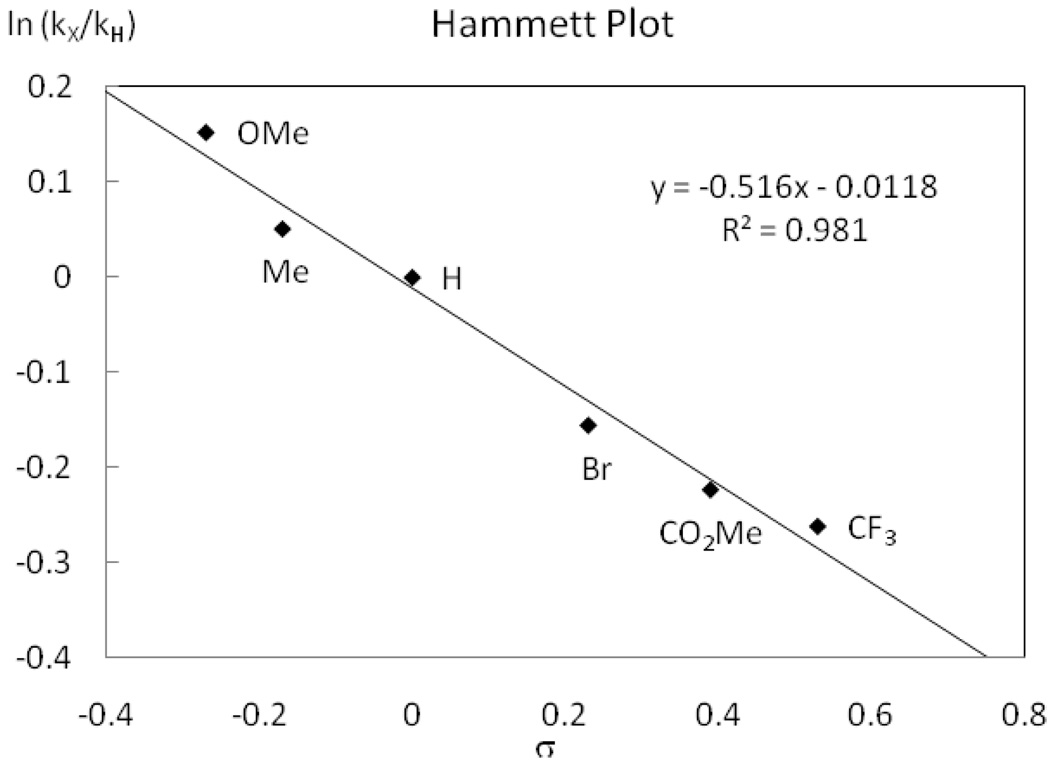
Eight monofluoro Pd(IV) complexes 6a–h with different sulfonamide substituents (R¹ = NO₂, CN, Cl, F, Ph, H, Me, t-Bu) were synthesized. Complexes 6a–h were subsequently decomposed thermally at 49 °C in MeCN and the rate of C–F reductive elimination was measured by ¹H NMR spectroscopy. The yield of fluorination was higher for complexes featuring electron-withdrawing sulfonamides (96%, when R = NO₂) than for complexes with electron-donating sulfonamides (65%, when R = t-Bu), but in all cases both product formation and starting material consumption followed first order rate laws. As shown in the Hammett plot in Figure 11, a ρ value of −0.45 was obtained, which demonstrates that electron-donating substituents at the para position of the sulfonamide have an accelerating effect on the rate of C–F reductive elimination.

Figure 11.

Hammett plot for sulfonamide substitution.

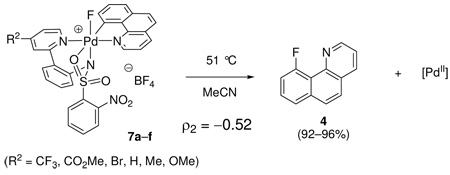
Effect of pyridine (pyridyl-sulfonamide) substitution on the rate of C–F reductive elimination from 1

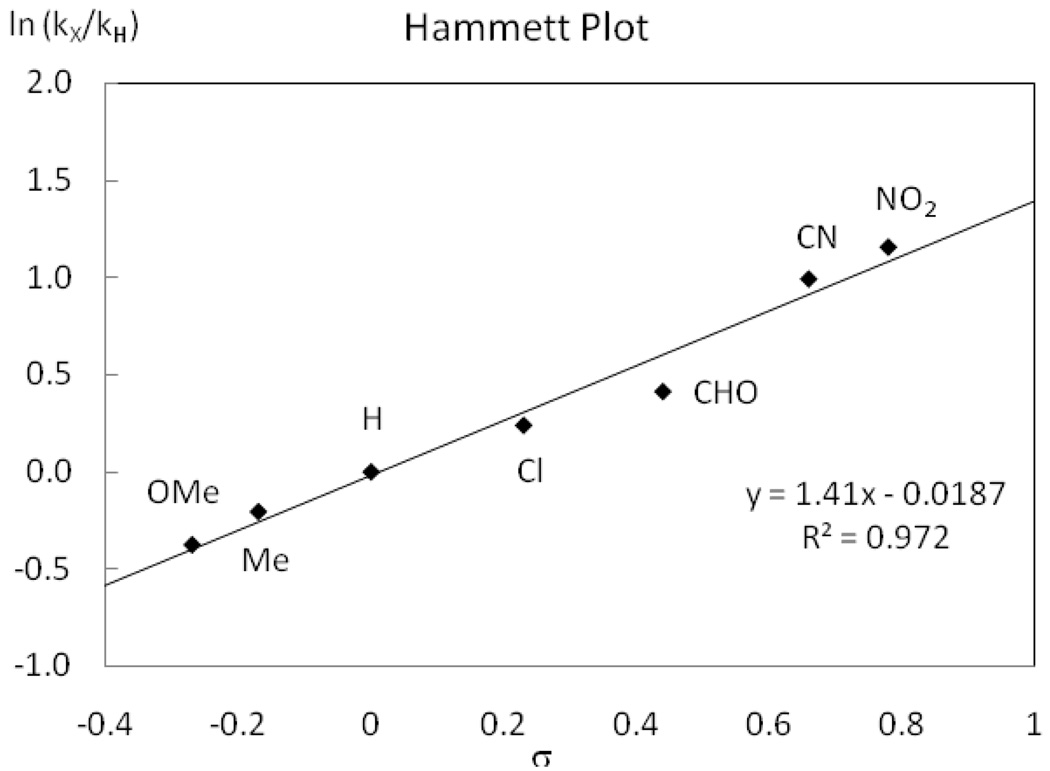
The monofluoro Pd(IV) complexes 7a–f were prepared from commercially available 4-substituted 2-halopyridines (R² = CF₃, CO₂Me, Br, H, Me, OMe). Complexes 7a–f were thermally decomposed at 51 °C in MeCN and the rate of C–F reductive elimination was measured by ¹H NMR spectroscopy. The yield of fluorination did not correlate with substitution of the pyridine ligand of the pyridyl-sulfonamide and was uniform between 92 and 96%. The Hammett plot shown in Figure 12 afforded a ρ₂ value of −0.52, which illustrates that electron-donating groups at the para position of the pyridine of the pyridyl-sulfonamide ligand accelerate the rate of C–F reductive elimination. Our results show that the sulfonamide aryl group substitution (R¹) has a stronger influence on the rate of C–F reductive elimination than the pyridine substituent (R²). Similar ρ values for the two Hammett plots for sulfonamide substitution (R¹, ρ₁) and pyridine substitution (R², ρ₂) are observed but the aromatic bearing the R¹ substituent is separated from Pd by two additional bonds compared to the aromatic bearing the R² substituent.^41b

Figure 12.

Hammett Plot for pyridine (pyridyl-sulfonamide) substitution.

Effect of benzo[h]quinoline substitution on the rate of C–F reductive elimination from 1

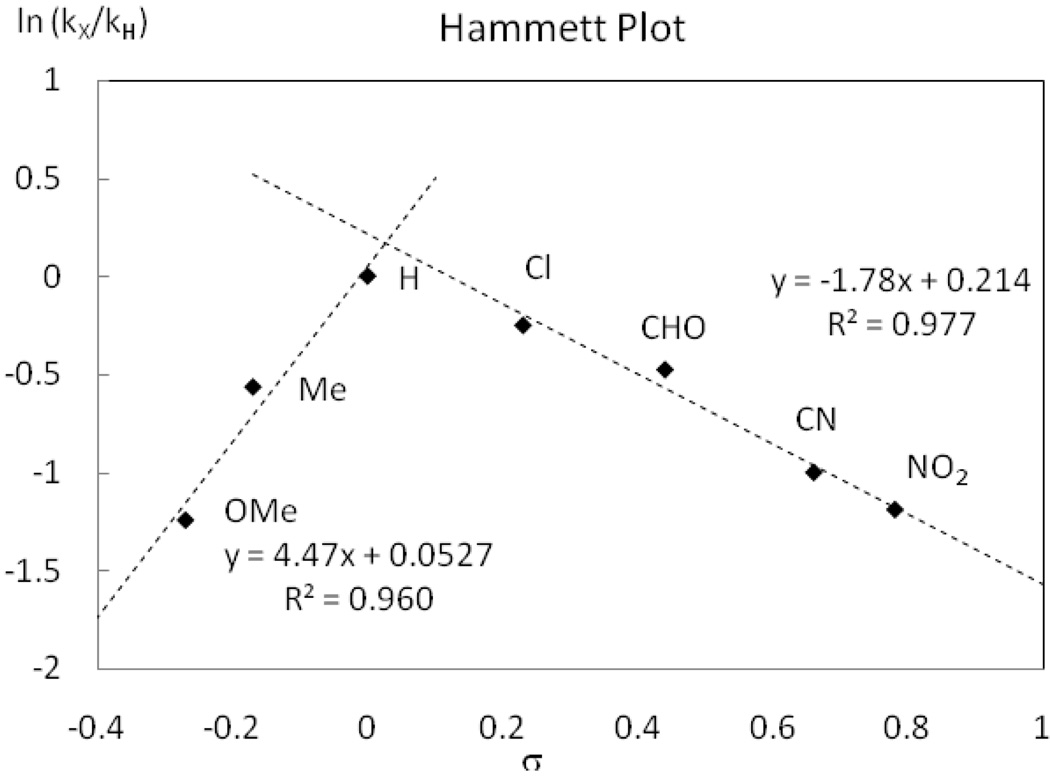
A series of 7-substituted benzo[h]quinolines was synthesized from 7-nitrobenzo[h]quinoline.⁴² After cyclopalladation, pyridyl-sulfonamide ligand complexation, and oxidation, the monofluoro Pd(IV) complexes 8a–g (R³ = NO₂, CN, CHO, Cl, H, Me, OMe) were obtained. Complexes 8a–g were subsequently thermally decomposed at 50 °C and the rate of C–F reductive elimination was monitored by ¹H NMR spectroscopy. The yield of the fluorination products 9a–g varied (70–94%) but did not correlate with the σ values of the substituents. The Hammett plot shown in Figure 13 shows a ρ value of +1.41, which shows that, unlike for the sulfonamide and pyridine substituents, electron-withdrawing substituents on the benzo[h]quinolyl substituent accelerate C–F reductive elimination.

Figure 13.

Hammett plot for benzo[h]quinoline substitution for complexes 8a–g.

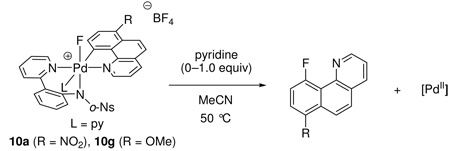
Effect of benzo[h]quinoline substitution on the rate of C–F reductive elimination from 2

The Hammett plot for reductive elimination from 1 with respect to benzo[h]quinolyl substitution is linear as shown in Figure 13. In contrast, a non-linear Hammett plot was observed for the identical experiment with the pyridine complex 2. The pyridine complexes 10a–g were thermally decomposed at 50 °C in MeCN and the rate of C–F reductive elimination was monitored by ¹H NMR spectroscopy. The yield of fluorination products 9a–g varied (69–85%) but the kinetic data followed first order rate laws. As shown in Figure 14, the Hammett plot shows two segments; one for electron-withdrawing substituents (NO₂, CN, CHO, Cl) and one for electron-donating to -neutral substituents (OMe, Me, H). The two ρ values for the two segments are −1.78 and +4.47, respectively. In contrast to the rate of reductive elimination from 1, both electron-withdrawing and electron-donating substituents slow the rate of reductive elimination from the pyridine complexes 10.

Figure 14.

Hammett Plots of benzo[h]quinoline substitution for pyridine complexes 10a–g.

Rate dependence of reductive elimination from derivatives of complex 2 with excess pyridine

The rate of reductive elimination from complex 2 as a function of pyridine concentration is shown in Figure 9. The rate of reductive elimination as a function of pyridine concentration was also determined for the two derivatives of complex 2, in which the benzo[h]quinolyl substituent in 2 was substituted with a 7-NO₂ (10a) and a 7-OMe (10g) substituent, respectively (Figure 15). A positive, linear dependence of the reciprocal of the rate of C–F reductive elimination (1/k) vs pyridine concentration was observed for all three complexes, as well as a non-zero intercept. The positive linear dependence shows that pyridine slows the rate of reductive elimination for all investigated complexes.

Figure 15.

Rate dependence on pyridine concentration for the three 7-substituted benzo[h]quinolyl Pd(IV) pyridine complexes 2, 10a, and 10g.

Reductive elimination from difluoro Pd(IV) complex 3

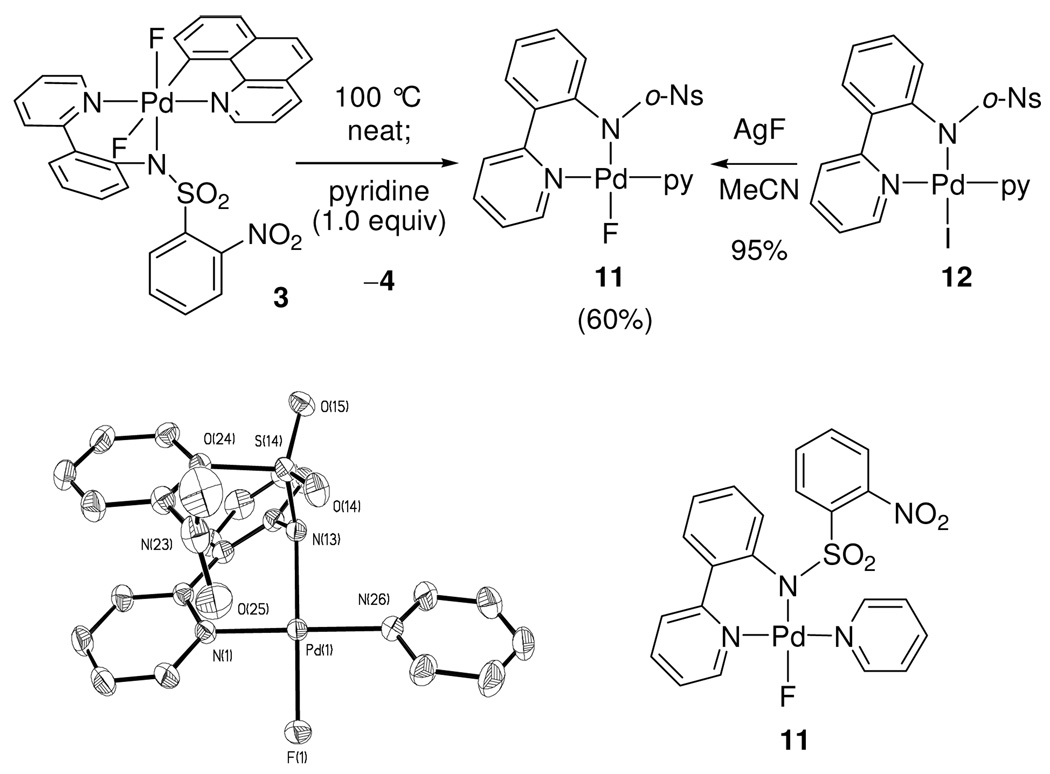
Complex 3 afforded C–F bond formation product 4 in 97% yield upon heating in DMSO at 150 °C for 10 min. Pd(IV) complex 3 could also be pyrolyzed as a solid, without solvent, and afforded product 4 at 100 °C in 4 hr in 98% yield. After addition of 1.0 equivalents of pyridine after complete consumption of 3, the Pd(II) fluoride complex 11 was isolated in 60% yield from the reaction mixture and characterized by ¹H, ¹³C, ¹⁹F NMR spectroscopy, and X-ray crystallography. Complex 11 was also independently synthesized from the corresponding iodo Pd(II) complex 12 (Scheme 2).

Scheme 2.

Pd(II) product 11 after reductive elimination; ORTEP representation of Pd(II) fluoride complex 11 with ellipsoids drawn at 50% probability (hydrogen atoms omitted for clarity). Pd-F: 1.981 Å.

Temperature and solvent dependency of C–F reductive elimination from 3

When the difluoro Pd(IV) complex 3 was thermally decomposed in DMSO at 50 °C, reductive elimination to 4 was observed in only 38% yield. The major product was the Pd(II) aryl complex 13 that is formally derived from reduction of 3 by F₂ elimination (eq 4). The fate of the fluorine could not be determined; no ¹⁹F NMR resonances other than those corresponding to 4 and 11 were observed. From a synthetic standpoint, the formation of 13 is not desirable because the yield of 4 is reduced by formation of 13. The ratio of 4 : 13 was dependent on the solvent and the temperature (Table 1). Higher temperatures favored the formation of 4 over the formation of 13. No correlation between the ratio of 4 : 13 and solvent polarity was observed. When 3 was heated as a solid in the absence of solvent, 4 was formed exclusively, independent of temperature; no 13 was detected by ¹H NMR.

Table 1.

Dependence of fluorination yield on reaction conditions

entry	solvent	temperature	yield [%] 4 : 13a)
1	pyridine	50 ºC	<1:50
2		75 ºC	<1:57
3		100 ºC	<1:72
4	DMSO	50 ºC	38:60
5		75 ºC	48:50
6		100 ºC	66:32
7		150 ºC	97:1
8	chloroform	50 ºC	54:44
9		75 ºC	64:33
10		100 ºC	70:27
11	neat	75 ºC	95:<1
12		100 ºC	97:<1
13		150 ºC	98:<1

^a)Yield determined by ¹H and ¹⁹F NMR using an internal standard.

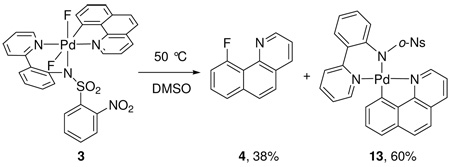(4)

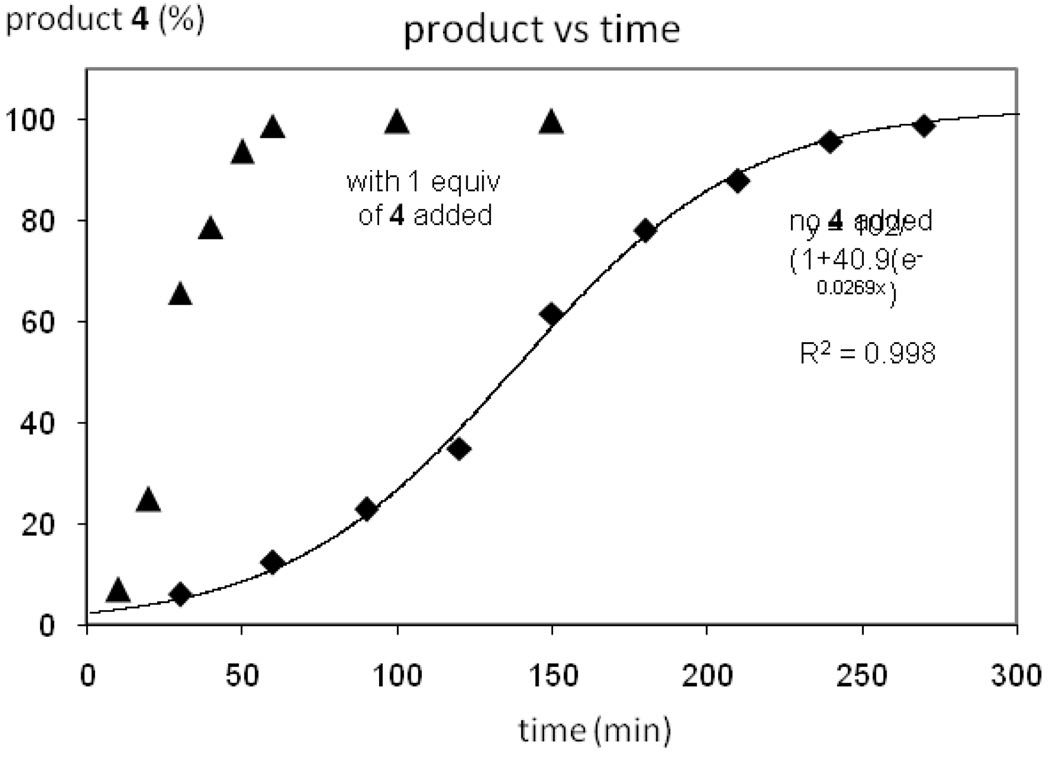
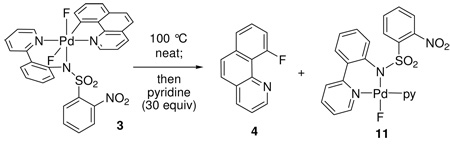
Kinetic profile of C–F reductive elimination from 3

Rate measurements of reductive elimination from 3 to form 4 in solution were complicated by the fact that the yield of 4 was temperature dependent. Therefore, the Pd(IV) difluoride 3 was decomposed at 100 °C without the use of solvent. The reaction was stopped after different reaction times by cooling the reaction mixture to 23 °C. The reaction mixtures were subsequently dissolved in CDCl₃ and 30 equivalents of pyridine-d5 with respect to 3 were added to form 4 and 11. Product formation and starting material disappearance were monitored by ¹⁹F NMR spectroscopy. The rate of C–F reductive elimination from 3 was slower than the rates of reductive elimination from the cationic complexes 1 and 2, respectively. The kinetic profile for the reaction from 3 to 4 is shown in Figure 16 (shown with squares). The rate of product formation was fitted to a logistic curve of the general form y = A/(1+B×exp(−Cx) with an R² value of over 0.99. Kinetic profiles of reactions that are accelerated by autocatalysis follow sigmoid curves such as the one shown in Figure 16.⁴³ When 1.0 equiv of 4 (m.p. 50 °C) were added before heating solid 3, significant rate acceleration was observed (Figure 16, shown with triangles). However, the sigmoidal curve shown in Figure 16 is likely not due to molecular autocatalysis of products 4 or 11 because rate acceleration was also observed when naphthalene (m.p. 77 °C) was added prior to heating to 100 °C. For more detail, see Discussion Section and Supporting Information.

Figure 16.

Kinetic data of C–F reductive elimination from 3.

Computational studies

Density functional theory calculations were performed using the M06 functional,³⁸ which has been shown to be appropriate for the description of transition metal complexes.⁴⁴ The calculation of the structure of 3 was employed to determine the level of theory necessary to accurately describe palladium in the +IV oxidation state and the Pd–F bond because a crystal structure of 3 was available for comparison (for a comparison of relevant metrical parameters, see Supporting Information). Based on the structural method validation, we determined that geometry optimization with a triple-ζ basis set was required for Pd and F. Energies computed at the M06/LACV3P++**(2f) level of theory predicted the tridentate coordination of the pyridyl-sulfonamide with N,O- κ³ coordination of the sulfonamide in 1. Binding of MeCN to 1 to afford 1b was calculated to be endothermic by 2.2 kcal·mol⁻¹. The predicted result is supported experimentally as described in the first section of this manuscript.

The calculated values for the enthalpies of activation for reductive elimination from 1 and 2 are in good agreement with the experimentally determined values (Table 2). The trends of the rate changes of reductive elimination as a function of ligand substitution (Hammett plots Figure 11–Figure 13) are correctly predicted by computation (see Supporting Information for detail). The free energy of activation for the reductive elimination from 1 was underestimated computationally by 7.7 kcal·mol⁻¹ (ΔG^‡_298(exp) = 22.8 ± 0.02 kcal·mol⁻¹ , ΔG^‡_298(pred) = 15.1 kcal·mol⁻¹) as a result of a deviation in the calculated entropy of activation (ΔS^‡_(exp) = 12.4 ± 1.3 eu, ΔS^‡_(pred) = 30.9 eu).⁴⁵ This calculated entropy of activation was determined in the absence of MeCN. The computationally determined entropy of activation for the MeCN complex 1b was estimated at 1.7 eu. The calculated entropies of activation for 1 and 1b suggest the involvement of a solvent molecule in the transition state of reductive elimination from 1 in MeCN solution, in which MeCN competes with O-coordination of the sulfonamide. The calculated activation parameters for reductive elimination from 2 (ΔH^‡ = 33.3 kcal·mol⁻¹, ΔS^‡ = 26.5 eu, and ΔG^‡₂₉₈ = 25.4 kcal·mol⁻¹) are in agreement with the experimentally determined parameters (ΔH^‡ = 32.8 ± 2.5 kcal·mol⁻¹, ΔS^‡ = 30.7 ± 7.8 eu, and ΔG^‡₂₉₈ = 23.7 ± 0.2 kcal·mol⁻¹).

Table 2.

Enthalpy of activation for reductive elimination from 1 and 2 determined experimentally (exp) and predicted computationally (pred).

	ΔH‡ [kcal·mol−1]
	exp.	pred.
1	26.5 ± 0.4	24.3
2	32.8 ± 2.5	33.3

Discussion

Structure of Pd(IV) fluoride complexes 1–3

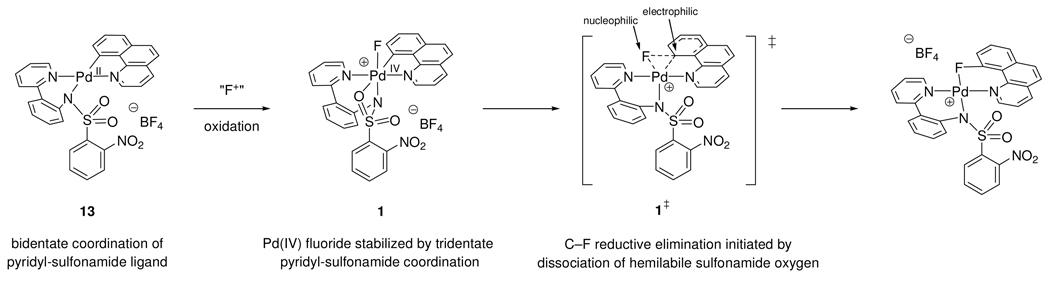
Originally, we proposed the structure 1b for the cationic Pd(IV) fluoride complex, in which an MeCN ligand is coordinated to Pd. Based on temperature-dependent line shape analysis of the ¹H NMR spectra of 1 and 2, the small equilibrium constant of K_eq = 2.61 for the equilibrium between 1 and 2 with added pyridine, the ¹³C resonance shift of the sulfonamide ipso carbon atom C²⁵, and computational support (Figure 5–Figure 7), we revised our assignment to structure 1, in which the pyridyl-sulfonamide ligand is tricoordinate facially with κ³-coordination to Pd of the pro-S oxygen atom and the nitrogen atom of the sulfonyl group. Pyridyl-sulfonamide ligands are not prevalent in transition metal chemistry but we propose that they provide a suitable ligand geometry to facilitate oxidation from Pd(II) to Pd(IV) and C–X bond forming reactions through κ³-coordination.

The pyridyl-sulfonamide-stabilized aryl Pd(IV) fluoride complexes are so far the only high-valent Pd complexes that have been observed to undergo C–F bond reductive elimination. While we do not suggest that pyridyl-sulfonamide ligands are uniquely suited to promote C–F bond formation from Pd(IV), we propose that the κ³-coordination mode, together with their electronic properties, vide infra, may be responsible for facile and efficient C–F bond formation. The pyridyl-sulfonamide ligand in 1 may stabilize the high-valent oxidation state of Pd because facial κ³-coordination can stabilize hexacoordinate Pd(IV) complexes.⁴⁶ Upon dissociation of the hemilabile oxygen donor atom of the sulfonyl group, a pentacoordinate Pd center is generated, from which C–F reductive elimination can occur. We propose that the geometry of the ancillary ligand and the capability to adopt bidentate coordination in the square planar and tridentate coordination in the octahedral complex with a hemilabile oxygen ligand is the reason for the utility of the pyridyl-sulfonamide ligand in C–F reductive elimination from Pd(IV).

In the Pd(IV) fluoride complexes 1–3 the weakly σ-donating ligands—κ³-sulfonamide oxygen, pyridine, and fluoride for 1, 2, and 3, respectively—are placed trans to the strongly σ-donating aryl ligand. In all cases, fluoride and sulfonamide are coordinated trans to each other. The trans orientation of the fluoride ligand and the sulfonamide ligand can be rationalized by ionic contributions to both Pd–ligand bonds. The fluoride and sulfonamide ligands could strengthen the Pd–F and the Pd–N bonds by mutually enhancing their ionic contribution to the bonding.^28,47,48

Potential reaction mechanisms of C–F reductive elimination from 1 and 2

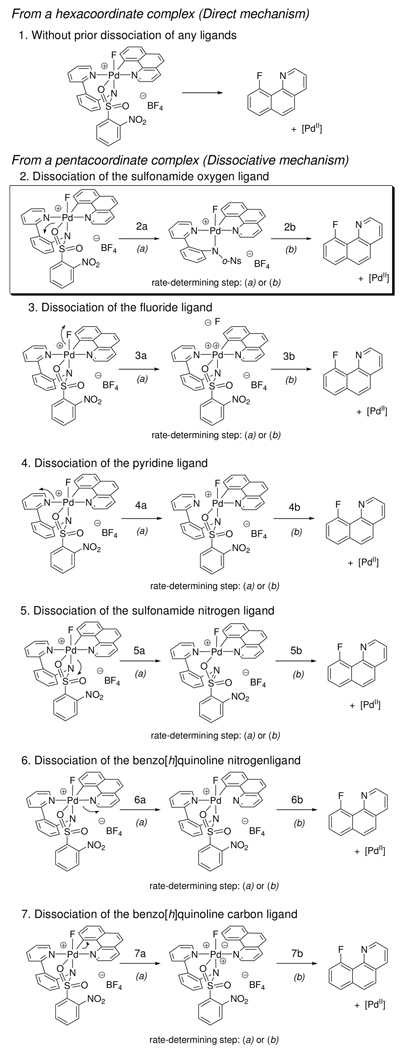
As shown in Figure 17, we classified 15 potential reaction mechanisms of C–F reductive elimination from 1 into two categories: 1) reductive elimination from a hexacoordinate complex (direct mechanism), and 2) reductive elimination from a pentacoordinate complex (dissociative mechanism). The dissociative mechanism class was further divided into six sub-classes, depending on the ligand that dissociates prior to reductive elimination. In all six sub-classes, there are at least two distinct mechanisms depending on the rate-determining step; (a) dissociation of the ligand to form a pentacoordinate complex and (b) C–F bond formation from the pentacoordinate complex.

Figure 17.

Considered mechanisms for reductive elimination from 1. The data are consistent with mechanism (2b).

In our analysis, we disregarded the possibility of dissociation of the benzo[h]quinolyl carbon ligand to form an aryl anion (mechanisms (7a) and (7b)). Carbon ligand dissociation was excluded due to the high pK_a (ca. 43) of the hydrocarbon. We also disregarded the possibility of the dissociation of two or more ligands from the hexacoordinate Pd atom prior to reductive elimination because formation of tetra or lower-coordinate complexes for a Pd(IV) d⁶ would be energetically disfavored.⁴⁹

Mechanism of C–F reductive elimination from 1

Through analysis of the experimental and computational results, we concluded that of the mechanisms shown in Figure 17, only mechanism (2b) is consistent with our data for C–F reductive elimination from 1. Our rationale for proposing mechanism (2b) is described below.

First, the activation parameters obtained for the C–F reductive elimination from 1 do not support mechanisms (1) and (2a). A process, in which reductive elimination proceeds from a hexacoordinate complex (mechanism 1) should have an activation entropy close to zero.⁵⁰ For example, in 2003, Goldberg reported an activation entropy of ΔS^‡ = 3 ± 3 eu for C–H reductive elimination from a Pt^IV complex via a direct mechanism.^50a We measured an activation entropy of ΔS^‡ = 12.4 ± 1.3 eu for reductive elimination from 1, which would be large for direct mechanism (1). Additionally, reductive elimination from hexacoordinate metal complexes typically require that all ligands be tightly bound to the metal, as are alkyl, hydrido, and bidentate phosphine ligands.⁵⁰ In complex 1, however, the sulfonamide oxygen ligand is not tightly bound as established by the rate of the equilibrium between complex 1 and 2, which is as fast as 49 s⁻¹ at 25 °C (ΔG^‡₂₉₈ = 15.1 ± 0.2 kcal/mol) compared to the rate of C–F reductive elimination from 1 (8.2 × 10⁻⁵ s⁻¹ at 23 °C). The fast dissociation of the sulfonamide oxygen atom in 1 also excludes oxygen dissociation as the rate-determining step (mechanism (2a)).

Second, the rate of reductive elimination was independent of the concentration of added n-Bu₄NBF₄ (0–2.0 M). Addition of salts such as n-Bu₄NBF₄ increases the dielectric constant of the reaction medium. The indifference of the rate on the concentration of n-Bu₄NBF₄ suggests that the transition state is not more ionic than the ground state and, hence, disfavors mechanisms (3a) and (3b).

Third, the ρ₂ value of −0.52 for the rate dependence as a function of pyridine substitution of the pyridyl-sulfonamide as determined from the Hammett plot in Figure 12 renders mechanism (4b) unlikely. If pyridine dissociation preceded rate-determining reductive elimination (mechanism (4b)) a ρ₂ value smaller in size (closer to zero) would be expected because a dissociated pyridyl ligand would only have a small influence on the rate of C–F bond formation without being covalently bound to Pd.

Fourth, the ρ₃ value of +1.41, determined from the Hammett plot in Figure 13, in which the rate was plotted as a function of substitution on the benzo[h]quinolyl ligand, disfavors mechanisms (4a), (5a), and (6a). A negative ρ₃ value would be expected for mechanisms (4a), (5a), and (6a) because electron-donating substituents should increase the rate of dissociation of the pyridyl (4a), sulfonamide (5a), or benzoquinoline nitrogen (6a) ligands, respectively, by increasing the electron density at Pd.

Fifth, the ρ₁ value of −0.45 determined in the Hammett plot shown in Figure 11, in which the rate is depicted as a function of sulfonamide substitution, is inconsistent with sulfonamide dissociation because sulfonamide substitution could not have a significant influence on the rate if the sulfonamide were not ligated to Pd during the rate-determining step. However, dissociation of the sulfonamide nitrogen to afford the eight-membered O-bound Pd sulfonamide shown in mechanism (5b) cannot be excluded by our experimental data. Computationally, a local minimum with an O-bound, but not N-bound sulfonamide could not be located. In addition, calculations predicted a shortening of ∼0.05 Å of the Pd–N(sulfonamide) bond in the transition state structure compared to the structure of 1 (vide infra). Therefore, we characterize mechanism (5b) as unlikely.

Sixth, mechanism (6b) cannot be excluded by our experimental results. We were not able to synthesize the Pd(IV) complexes with 4-substituted benzoquinolyl ligands. In addition, an attempt to utilize analogs of 1, in which the benzo[h]quinolyl ligand of 1 was replaced by 2-phenylpyridyl substituents, for kinetic analysis was not successful because the Pd(IV) complexes resulting from the 2-phenylpyridine complexes could not be prepared as cleanly as the corresponding benzo[h]quinolyl-derived complexes. Therefore, the kinetic data would not be accurate. Hence, we investigated mechanism (6b) computationally and did not identify a local minimum or a transition structure where the Pd and the benzo[h]quinolyl nitrogen atom are not involved in covalent bonding. Computationally, a bond lengthening of the Pd–N (benzo[h]quinolyl) bond distance by only 0.05 Å at the transition structure was predicted.

All experimental and theoretical results are consistent with reductive elimination from a cationic, pentacoordinate Pd(IV) upon dissociation of the oxygen atom of the sulfonamide as shown in mechanism (2b).

Proposed transition state structure for C–F reductive elimination from 1

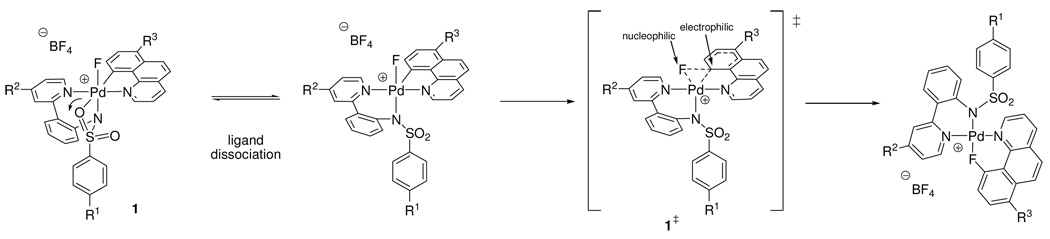
The Hammett studies not only provide information about the operative mechanism for reductive elimination but also about the structure of the transition state for the C–F reductive elimination from complex 1. Based on the data obtained, we propose a reaction mechanism via the transition state 1^‡ as shown in Scheme 3.

Scheme 3.

Proposed mechanism for C–F reductive elimination from 1.

The three ρ values, ρ₁–ρ₃, obtained from the Hammett studies (Figure 11–Figure 13) indicate charge build-up in the transition state. The benzo[h]quinolyl carbon ligand is electrophilic at carbon in the transition state, whereas the fluoride ligand is nucleophilic. The positive ρ value of ρ₃ = 1.41 for benzo[h]quinolyl 7-substitution is consistent with an electrophilic carbon ligand in the transition state; electron-withdrawing substituents accelerate reductive elimination. Electron-donating ancillary ligands on Pd accelerate reductive elimination. The negative values for both ρ₁ (sulfonamide substitution) and ρ₂ (pyridine (pyridyl-sulfonamide) substitution) are consistent with the ancillary ligand supporting the Pd as it is being reduced to Pd(II). The Pd–F bond is broken with nucleophilic fluoride participating in C–F bond formation. The computed natural charges for the transition state (see Supporting Information) are in agreement with the proposed charge distribution based on experimentally determined values. The proposed mechanism of C–F bond formation from 1 has similar electronic requirements as a nucleophilic aromatic substitution reaction.^41,52

Upon O-sulfonamide dissociation of the hexacoordinate Pd(IV) complex 1 to form a cationic, pentacoordinate complex, ligand rearrangement may take place for C–F reductive elimination. Previously reported experimental and theoretical data support that reductive elimination from pentacoordinate transition metal complexes likely proceeds from distorted trigonal bipyramidal structures, in which the three equatorial ligands are in a Y-shaped arrangement. The two ligands to be reductively eliminated are in equatorial positions.⁴⁹ The Y-shaped, distorted trigonal bipyramidal transition state positions the two ligands to be reductively eliminated in close proximity and, therefore, facilitates reductive elimination.

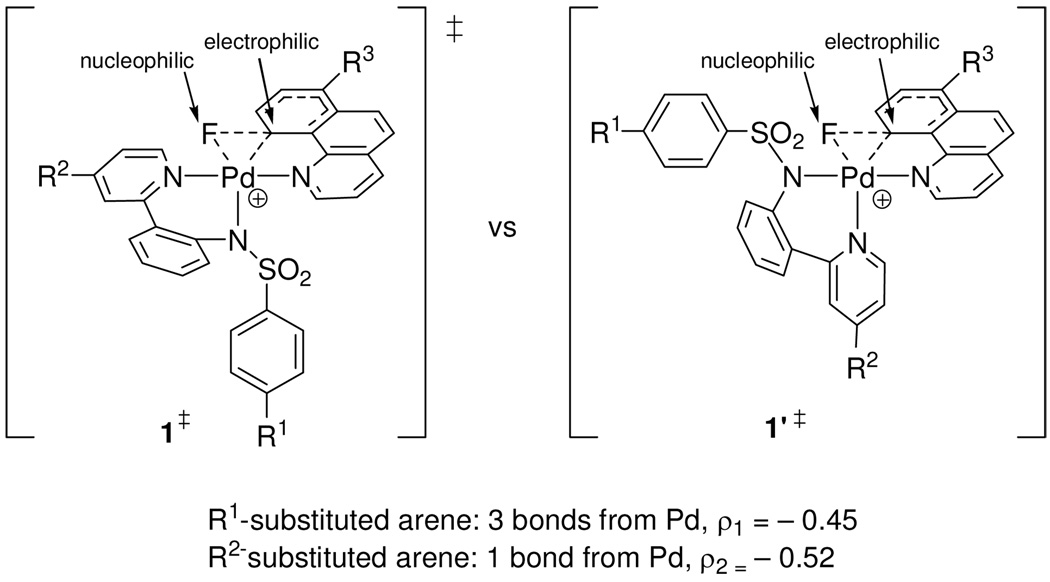
Only two Y-shaped distorted trigonal bipyramidal transition state structures are conceivable for reductive elimination from 1, under the assumption that the benzo[h]quinolyl ligand cannot occupy two equatorial positions due to the large bond angle in a Y-shaped arrangement (Figure 18): In one transition state, the equatorial sulfonamide nitrogen ligand is coordinated in the basal position of the Y-shaped transition state (1^‡) and in the other transition state, the pyridine of the pyridyl-sulfonamide ligand is coordinated in the basal position of the Y (1’^‡).

Figure 18.

Two potential Y-shaped Pd(IV) transition states for C–F reductive elimination.

Previously, it has been argued that the ligand in the basal position of a Y-shaped complex can have a strong influence on the rate of reductive elimination due to π-donation.⁵³ The negative ρ₁ value of −0.45 for p-sulfonamide substitution (Figure 11) illustrates that more electron-rich sulfonamide ligands accelerate reductive elimination. Potential π-donation of the nitrogen atom of the sulfonamide to Pd in the transition state 1^‡ will be attenuated by the π-accepting sulfonyl group. In the hypothetical transition state 1’^‡, the pyridine of the pyridyl-sulfonamide ligand is positioned in the basal position of the Y. The ρ₂ value for pyridine (pyridyl-sulfonamide) substitution was determined to be ρ₂ = −0.52. While the values for ρ₁ and ρ₂ are similar in size (ρ₁ = −0.45, ρ₂ = −0.52), sulfonamide substitution has a larger electronic influence on the rate of reductive elimination because the arene substituent of the sulfonamide (R¹) is remote from the Pd atom by two additional bonds compared to the arene substituent of the pyridine (R²). Therefore, increased electron-donation of the sulfonamide substituent has a larger influence on the rate of reductive elimination than increased electron-donation of the pyridine substituent. The ligand in the basal position of the Y (sulfonamide in 1^‡) will have a larger effect on the rate of reductive elimination than ligands in the apical positions (pyridines in 1^‡), because the ligand–Pd orbitals of the ligand in the Y-base are trans to the Pd–ligand orbitals of the two substituents to be reductively eliminated. The analysis of the ρ values is consistent with transition state 1^‡.

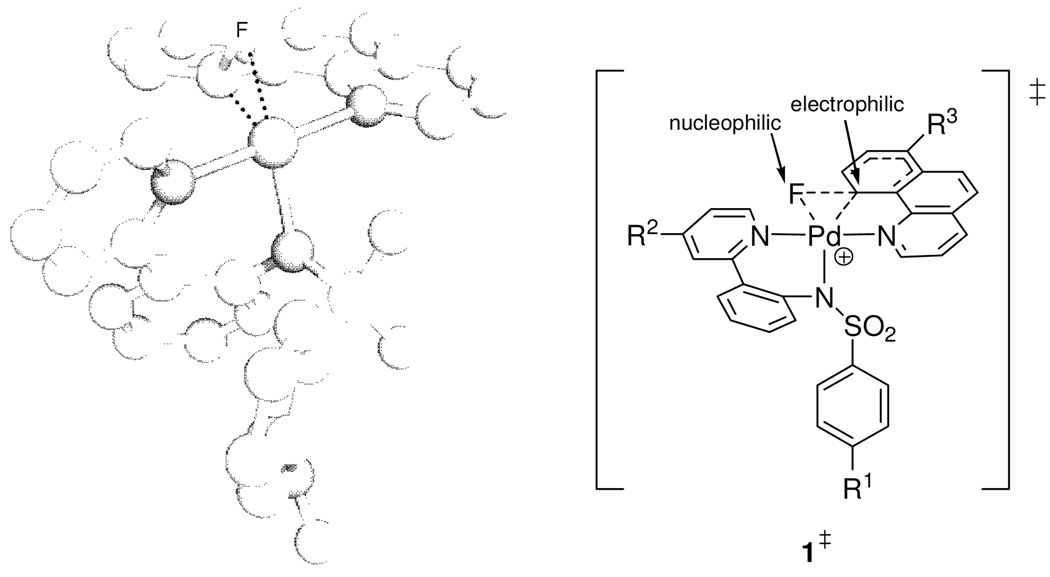
Computational analysis supported the proposed transition state structure based on Hammett analysis shown in Figure 18 with the two pyridine substituents in the apical positions of the distorted trigonal bipyramidal structure and the nitrogen atom of the sulfonamide in the basal position of the Y. The computed transition state geometry is shown in Figure 19 (left) next to the structure for the proposed transition state from experiment (right). The computed bond length of the Pd–N (sulfonamide) bond is about 0.05 Å shorter in the computed transition state 1^‡ than in 1, consistent with a stronger bond of the sulfonamide nitrogen to Pd in the transition state. No significant N–Pd π-donation could be observed in the computed transition state (for molecular orbital analysis, see Supporting Information).

Figure 19.

Computed transition state 1^‡ for reductive elimination from 1 and predicted transition state based on Hammett analysis.

Mechanism of C–F reductive elimination from 2.⁵⁴

Reductive elimination from 2 could proceed by a dissociative pathway beginning with fast, reversible pyridine dissociation. A competing pathway could be a direct mechanism from hexacoordinate 2. Reductive elimination by both competing pathways with the corresponding two-term rate law is shown in eq 5.

$$\begin{array}{cc}rate=k_{obs}[2];& k_{obs}=k_1+\frac{k_2{k}_3}{k_{-2}[py]+k_3}\end{array}$$ (5)

The linear dependence of the reciprocal of the rate of C–F reductive elimination from 2 (1/k) vs pyridine concentration (Figure 9) established that the rate constant for the direct mechanism (k₁) is significantly smaller than the rate constants k₂ and k₃. If k₁ is negligibly small compared to k₂ and k₃, k_obs simplifies to eq 6, which correctly describes the positive, linear dependence (see Supporting Information for detail). The positive, linear dependence of the reciprocal of the rate of C–F reductive elimination from 2 (1/k) vs pyridine concentration was only measured for small pyridine concentrations because the yield for C–F bond formation significantly decreased upon addition of more than one equivalent of additional pyridine to 2. Therefore, our results cannot exclude mechanisms competing with the dissociative mechanism via k₂ and k₃, such as the direct mechanism from hexacoordinate 2.

$$\begin{array}{cc}{k}_{obs}=\frac{k_2{k}_3}{k_{-2}[py]+k_3};& \frac{1}{k_{obs}}=\frac{1}{k_2}+\frac{k_{-2}}{k_2{k}_3}[py]\end{array}$$ (6)

The activation parameters for the reductive elimination from 2 were determined: ΔH^‡ = 32.8 ± 2.5 kcal·mol⁻¹ , ΔS^‡ = 30.7 ± 7.8 eu, and ΔG^‡₂₉₈ = 23.7 ± 0.2 kcal·mol⁻¹ . The activation entropy for C–F reductive elimination from 2 was 30.7 ± 7.8 eu, which is about 20 eu higher than for the reductive elimination from 1. The large activation entropy is consistent with a dissociative mechanism, with pre-equilibrium pyridine dissociation before C– F bond formation. We have established that the rate of pyridine dissociation is at least 10 times faster at 23 °C than C–F bond formation by measurement of the rate of the equilibrium between 1 and 2 (eq 2). A more thorough kinetic analysis for the reductive elimination from 2 is complicated by several pathways from 2 that are relevant on the timescale of reductive elimination. For example, we have established that the equilibrium between 2 and 1 is significantly faster than reductive elimination from 2 (eq 2, free energy of activation for equilibrium between 1 and 2: ΔG^‡₂₉₈ = 15.1 ± 0.2 kcal·mol⁻¹).

As shown in the Hammett plot in Figure 14, two different segments are observed for the dependence of the rate of reductive elimination from 2 as a function of 7-benzo[h]quinolyl substitution. Non-linear Hammett plots can be observed due to a change in mechanism, in the rate-determining step, or in the geometry of the transition state; Hammett plots with a large change in ρ value such as observed for 2, +4.47 for electron-donating substituents to −1.78 for electron-accepting substituents, are rare.⁵⁵

The analysis of the mechanism of reductive elimination from pyridine complexes such as 2 is complicated by the fact that the equilibrium constant between 1 and 2 changes with substitution of the benzo[h]quinolyl substituent. For example, the equilibrium constant for the reaction of 1 + py → 2 at 25 °C is K_eq = 2.6, whereas the equilibrium constant for the reaction of the p-nitro-substituted Pd(IV) complex 8a + py → 10a at 25 °C is K_eq = 3.1. Moreover, the Hammett plot analysis for reductive elimination from complex 2 is convoluted because the change in 7-benzo[h]quinolyl substitution not only effects the electronic structure of the carbon ligand but also influences the palladium– pyridine bond trans to the carbon ligand.

Experimentally, we found that addition of pyridine inhibits reductive elimination from 2 and also from its p-NO₂ and p-OMe-substituted derivatives 10a and 10g (Figure 15). Pyridine dependence for reductive elimination was observed at the apex and both extremes of the Hammett plot shown in Figure 14. Because our experimental results could not explain the unusual Hammett plot,⁵⁵ we calculated the transition state energies and geometries for 2^‡, 10a^‡, and 10g^‡. Determination of the solvation-corrected electronic energies of the three transition states without thermodynamic corrections revealed that 10a^‡ and 10g^‡ are higher in energy than 2^‡ by 2.7 and 3.1 kcal·mol⁻¹, respectively, in qualitative agreement with experiment. All of the calculated transition states contained the pyridine ligand as part of the transition state structure with increased Pd–N bond lengths compared to 2, consistent with the possibility of a competing direct mechanism (k₁, eq 5) Analysis of the transition state geometries revealed that the Pd–N(pyridine) bond length in 2^‡ was longer by 0.2 Å than the Pd–N(pyridine) bond length in 2, which was the most significant change in bond length from 2 to 2^‡. For both 10a^‡ and 10g^‡ transition state geometries similar to the geometry of 2^‡ were found, respectively (see Supporting Information for details). Both our current experimental and computational results cannot rationalize the non-linear Hammett plot shown in Figure 14, and additional studies are required to elucidate the origin of the non-linearity.

Mechanism of C–F reductive elimination from 3

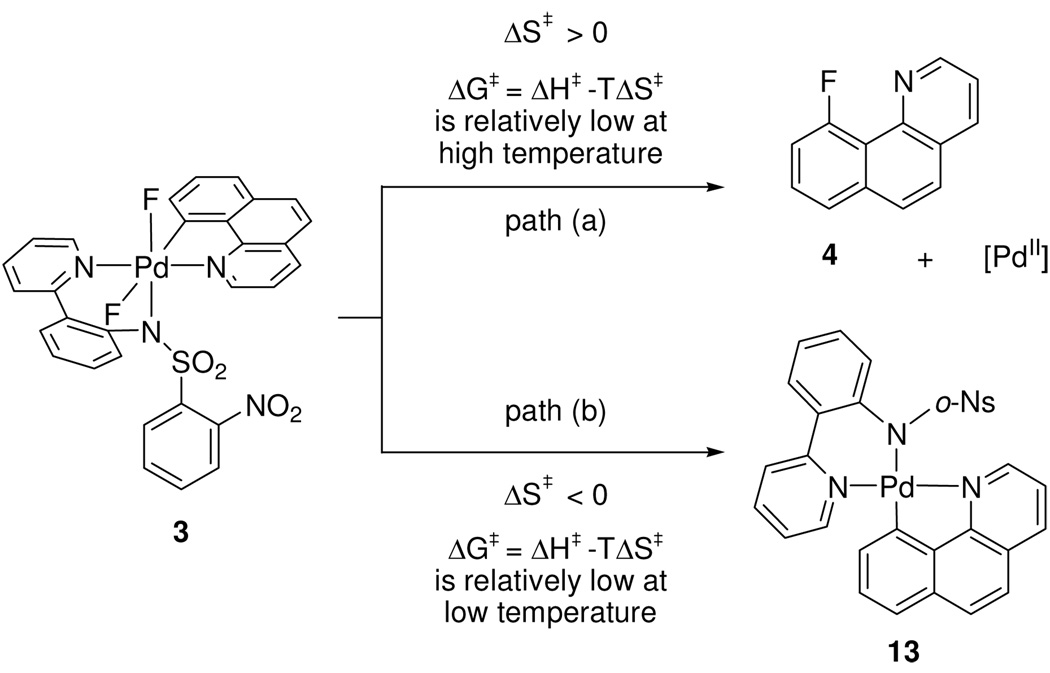
The difluoride complex 3 is thermally more stable than 1 and 2. Although C–F bond formation is significantly more efficient for cationic monofluoro complexes such as 1 than it is for 3, we briefly comment on C–F reductive elimination from 3. Formation of the aryl Pd(II) product 13 decreases the yield of product formation resulting from C–F reductive elimination. The yield for reductive elimination from 3 is dependent on solvent and temperature as shown in Table 1. At higher reaction temperatures, the predominant formation of the desired product 4 is observed (Scheme 4). The temperature dependence of the yield of C–F bond formation compared to formal reduction (4 versus 13) may be due to a large difference in activation entropies between the two competing pathways. The mechanism of C–F reductive elimination could take place by fluoride dissociation via a similar or analogous cationic intermediate as proposed for reductive elimination from 1. A dissociative pathway, in which Pd–F ionization is concerted with C–F bond formation, similar to the mechanism predicted for 2, is also consistent with our results. The higher required temperature for reductive elimination from 3 is consistent with a slower dissociation of a fluoride ligand from a neutral Pd(IV) as supposed to the dissociation of a neutral oxygen atom of the sulfonamide in 1 or a pyridine ligand from 2. The preference for the formation of 4 over the formation of 13 at high temperatures indicates that the mechanistic pathway for the formation of 4 has a large, positive activation entropy because the Gibbs free energy of activation will be lower at high temperatures for reactions with large entropies of activation.

Scheme 4.

Proposed rationale for the dependence of fluorination on solvent and reaction temperature.

As shown in Figure 16, the difluoro Pd(IV) complex 3 did not undergo C–F reductive elimination following a first order rate law. An induction period was observed and product formation could be fitted to a logistic curve, which is typical for reactions accelerated by autocatalysis.⁴³ To obtain high yields, the reaction had to be performed by heating solid 3 without solvent. The product 4, 10-fluorobenzo[h]quinoline, has a melting point of 50 °C. At temperatures below 50 °C, the Pd(IV) difluoride is stable in the solid state. At the reaction temperature of 100 °C, 10-fluorobenzo[h]quinoline (4) melted. The observation of reaction kinetics typically observed for autocatalytic reactions may be explained by formation and subsequent presence of 4 as a liquid. Addition of 1.0 equivalents of 10-fluorobenzo[h]quinoline (4), accelerated the reaction of reductive elimination from 3 and complete conversion of starting material was observed at 100 °C within one hour, whereas only 12% of conversion of 3 was observed without additional 10-fluorobenzo[h]quinoline (4) at 100 °C in one hour. A similar rate acceleration was observed upon the addition of naphthalene, which has a melting point of 77 °C. While the sigmoidal shape of product formation as a function of time (Figure 16) is intriguing and can be fitted to a logistic curve as is common for autocatalytic reactions, the experimental results suggest that a medium effect is responsible for rate acceleration.

Conclusion

We report a mechanism study of C–F reductive elimination from Pd(IV) fluorides. A better understanding of aryl fluoride formation by reductive elimination has previously been elusive due to the absence of any transition metal fluoride complexes that allowed the systematic investigation of high-yielding C–F bond formation. To date, only two transition metal complex classes have been identified that can provide aryl fluorides by C–F reductive elimination. We identified that C–F reductive elimination proceeds efficiently from aryl Pd(IV) fluoride complexes, stabilized by pyridyl-sulfonamide ancillary ligands. We propose that the pyridyl-sulfonamide ligand plays a crucial role for facile and efficient C–F bond formation. The ability of the pyridyl-sulfonamide ligand to function as a bidentate-tridentate-bidentate coordinating ligand during oxidation and reductive elimination, combined with the appropriate electronic requirements of the sulfonamide to position the aryl substituent trans to the sulfonamide ligand in the Pd(II) complex and the fluoride ligand trans to the sulfonamide ligand in the Pd(IV) complex, may be the reason for facile C–F bond formation (Scheme 5). The pyridyl-sulfonamide ligand is, therefore, a promising ancillary ligand for redox processes beyond C–F bond formation, in which a transition metal changes its coordination geometry and oxidation state.

Scheme 5.

Oxidation and reductive elimination supported by the pyridyl-sulfonamide ligand.

Intuitively, it could be expected that electron-withdrawing substituents on the ancillary ligands of the Pd(IV) fluoride complexes accelerate reductive elimination. Electron-withdrawing substituents could increase the tendency of the resulting electron-deficient, high-valent Pd to undergo a reductive elimination to attain the Pd(II) oxidation state. Instead, we found that electron-donating ancillary ligands accelerated C–F bond formation, presumably due to stabilization of the Pd as it is being reduced to Pd(II) and increasing nucleophilic character of fluoride as it attacks the electrophilic carbon substituent. On the carbon ligand that participates in reductive elimination, electron-withdrawing substituents accelerate reductive elimination. The electronic requirements for C–F bond reductive elimination from the pyridyl-sulfonamide-stabilized Pd(IV) fluoride complexes studied in this manuscript are comparable to the electronic requirements of a nucleophilic aromatic substitution reaction. The functional group tolerance, however, of the Pd(IV)–F-mediated fluorination is larger than the functional group tolerance of nucleophilic aromatic substitution reactions.^18a The identification of the influencing factors for C–F reductive elimination and the identification of the pyridyl-sulfonamide as an important ancillary ligand have potential to support the successful future design of transition metal catalysts for functional group-tolerant fluorination reactions.