Diffusion‐limited binding explains binary dose response for local arterial and tumour drug delivery

Abstract

Background:  Local drug delivery has transformed medicine, yet it remains unclear how drug efficacy depends on physicochemical properties and delivery kinetics. Most therapies seek to prolong release, yet recent studies demonstrate sustained clinical benefit following local bolus endovascular delivery.

Objectives:  The purpose of the current study was to examine interplay between drug dose, diffusion and binding in determining tissue penetration and effect.

Methods:  We introduce a quantitative framework that balances dose, saturable binding and diffusion, and measured the specific binding parameters of drugs to target tissues.

Results:  Model reduction techniques augmented by numerical simulations revealed that impact of saturable binding on drug transport and retention is determined by the magnitude of a binding potential, B_p, ratio of binding capacity to product of equilibrium dissociation constant and accessible tissue volume fraction. At low B_p (< 1), drugs are predominantly free and transport scales linearly with concentration. At high B_p (> 40), drug transport exhibits threshold dependence on applied surface concentration.

Conclusions:  In this paradigm, drugs and antibodies with large B_p penetrate faster and deeper into tissues when presented at high concentrations. Threshold dependence of tissue transport on applied surface concentration of paclitaxel and rapamycin may explain threshold dose dependence of in vivo biological efficacy of these drugs.

Introduction

Pharmacological treatments of solid tumours and vascular pathologies, such as intimal hyperplasia, must overcome a twofold challenge: one of pharmacology and the other of pharmacokinetics. That is, not only must the drug possess appropriate pharmacological parameters, but it must also penetrate tissue at adequate concentrations and reside in the vicinity of its target cells for a sufficient duration. Drug pharmacokinetics depend not only on physicochemical properties of the drug, but also on the mode of its delivery as this determines delivered dose, its kinetics and the impact of metabolism. Indeed, local drug delivery has transformed vascular medicine and oncology. Release of paclitaxel and rapamycin from endovascular stents in amounts that would not have an effect if administered systemically, virtually eliminates intimal hyperplasia and clinical restenosis (1, 2). Local infusion of antineoplastic drugs has similarly significant effects (3). Yet, in both applications efficacy is binary, toxicity is dose related and local delivery is not efficacious for all drugs. There appears to be a threshold that must be exceeded to induce effect, below which no response is observed and after which toxicity alone, rises (4). Clinical effect has been postulated to require relative drug insolubility to enable sustained release and enhance tissue retention through hydrophobic interaction (5, 6, 7). Toxicity is presumed to occur as amount of retained drug mounts and induces nonspecific effects on tissue.

As evolution of controlled release technology allows for a range of kinetic profiles, concentrations, and drug properties (5, 8, 9, 10), the question arises whether sustained release or tissue loading is more critical, and whether these are independent elements. The resurgent use of balloon catheters (11) and intra‐arterial injection (12) to deliver large boluses of drugs is an example of progression of such thought. Early evidence supports a clinical effect for bolus delivery of paclitaxel in treating arterial restenosis (13). We now ask whether the change in concentration that accompanies more rapid delivery modalities simply scales tissue loading and penetration, or whether more complex tissue kinetics are observed.

Here, we show that equilibrium interaction of locally administered drugs and arterial tissue is concentration dependent and consistent with saturable bimolecular binding. But we also demonstrate that the arterial equilibrium dissociation constant (K_d) that defines molecular interaction cannot alone define tissue–drug interaction. Heparin, paclitaxel and rapamycin all share a similar K_d, and yet they demonstrate significantly different tissue distribution after local delivery (6, 7, 14). To examine issues related to concentration gradients that local delivery can induce and the spectrum of binding properties for different drugs, we created an integrated mathematical construct with consideration of binding site density and drug diffusion within arteries. Previous model systems have introduced elements that described binding for high‐affinity receptors or low ligand concentrations (15, 16, 17). We now address cases of low‐affinity compounds and high local concentrations. By balancing constitutive affinity properties of a receptor for its ligand with ligand diffusivity and receptor and ligand concentrations, we can begin to consider how tissue loading and penetration scale with dose and delivery kinetics. All of these elements can be included in a single dimensionless parameter, B_p, the ratio of the maximum binding capacity B_M to the product of K_d and fraction of accessible tissue volume. This equilibrium constant (18) is also known as the binding potential (19) and has previously only been used to characterize binding at low concentrations. We show that magnitude of B_p critically determines concentration dependence of the dynamics of drug penetration into tissue and correspondingly, of the spatio‐temporal propagation of biological effects.

Combination of modelling and empirical data provides mechanistic underpinning for the unusual dose–responses seen in local therapies (4, 10, 20) and a rational framework by which to choose drugs, release platforms and release kinetics for specific tissue effects. It may be possible now to formally evaluate emerging therapies like drug release from endovascular balloons, apparent divergence in dose–response for toxicity and efficacy for endovascular stent‐eluted rapamycin and paclitaxel, or impact of lesion complexity and tissue state on drug effect (21). Classic diffusion alone cannot provide this insight nor do empirical models explain these findings. Use of a combined parameter like B_p can indeed explain threshold dependence on applied dose and delivery kinetics. Optimal dose need no longer be considered as solely determined by pharmacological considerations, but by minimal concentration that ensures adequate tissue penetration as well. Such a paradigm can then readily incorporate alterations in tissue with disease and/or concomitant systemic pharmacotherapy wherein binding sites are disrupted or their affinity altered.

Materials and methods

Modelling and simulations

Arterial drug uptake from a well‐mixed solution of luminal drug is modelled as a one‐dimensional transport problem with constant concentration boundary and initial conditions

C = ɛC_bulk, x = 0, t ≥ 0  (1a)

(1b)

C = 0, B = 0, t = 0, 0 < x < L  (2)

Here B and C, are, respectively, local concentrations of bound and free drug in the tissue; C_bulk is the concentration of bulk drug in the uptake medium; ɛ is the fraction of accessible tissue volume; t is time after initial exposure to drug; x is the distance from the lumen; and L is thickness of the artery wall. Local concentration of arterial drug is determined by the balance between saturable binding (16, 22)

(3)

and diffusion (with diffusion coefficient D) (15, 16, 22)

(4)

Here, k_f is the association rate constant, k_r is the dissociation rate constant, and B_M is the concentration of tissue binding sites. (1a), (1b), (2), (3), (4) were solved numerically using the chemical engineering module in the finite element package COMSOL with parameter values that correspond to drug transport in arteries (Table S1, Supporting Information, L = 1000 µm). The computational domain was meshed using 240 Lagrange quadratic elements. The resulting system of algebraic equations was integrated using a fifth order backward differencing scheme with variable time stepping and tight tolerances (relative tolerance of 10⁻¹⁰ and absolute tolerance of 10⁻¹²). Drug loading per unit area was evaluated as the spatial integral of B+ C.

Model reduction

The degree to which diffusion limits ligand‐receptor binding can be assessed by defining a Damköhler number Da, as the ratio of rates of binding and diffusion

(5)

A small Damköhler number implies that diffusion is the faster process so that ligand‐receptor binding is the (slow) rate limiting process that determines tissue loading kinetics. Small Damköhler numbers typically arise in highly porous gels (23) or when the diffusive path in tissue is very small. On the contrary, arterial dynamics of heparin, paclitaxel and rapamycin are all characterized by large Damköhler numbers (Fig. 1), implying that binding is diffusion limited (15, 22) and that concentrations of bound and free drug coexist in a quasi‐equilibrium so that

Figure 1.

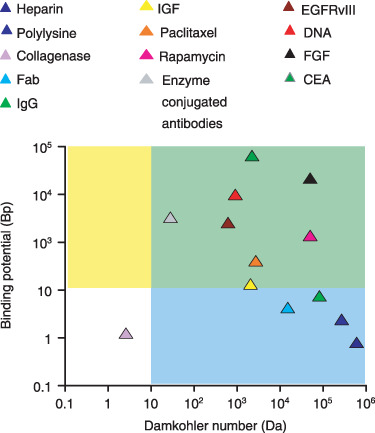
Classification of drug‐tissue pairs (Table S1) according to the magnitudes of the Damköhler number and the binding potential. Our analysis of equilibrium drug retention will focus on large binding potentials (B_p > 10, yellow and green regions). Analysis of drug transport will further presume that transport is diffusion limited (Da > 10, green regions). These assumptions will be validated for paclitaxel and rapamycin and can be seen to include a range of antibodies and growth factors.

(6)

where equilibrium dissociation constant is determined by ratio of dissociation and association rate constants, K_d = k_r/k_f. Total local concentration of drug in the tissue, T, is then a function of local concentration of free drug

(7)

and satisfies a diffusion equation

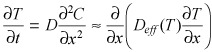(8)

with concentration dependent effective diffusion coefficient of the form

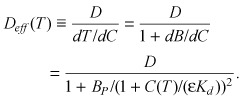(9)

Here C(T) is the concentration of free drug in the tissue as determined by eqn (7)

(10)

and B_p signifies the dimensionless ratio of equilibrium binding parameters

B_P ≡ k_fɛ⁻¹ B_M/k_r = B_M/(ɛK_d).  (11)

While the Damköhler number is large for many ligand transport scenarios (Fig. 1), the magnitude of B_p varies significantly with drug and tissue type (Fig. 1). In particular, arterial B_p of paclitaxel and rapamycin is much larger than that of heparin – the impact of such variations is at the focus of the current study.

Experimental

Unlabelled and radiolabelled rapamycin were generously donated by Johnson & Johnson/Cordis (Miami, FL, USA), radiolabelled paclitaxel was obtained from ViTrax (Placentia, CA, USA) and unlabelled paclitaxel was from LC Laboratories (Woburn, MA, USA). Fresh calf internal carotid arteries were cleaned of excess fascia, opened longitudinally, cut into segments (40–60 mg), and placed in centrifuge tubes with 1.0 ml of drug solution at room temperature. To assay for binding specificity, concentration of unlabelled drug was varied over 3‐log orders while holding concentration of radiolabelled drug constant (10 nm[³H]paclitaxel or 10 µm[¹⁴C]rapamycin). Segments were allowed to equilibrate for 60 h and were then processed for liquid scintillation counting. The drug count of each tissue sample was normalized by tissue mass to determine concentration of radiolabelled drug in the tissue (T). Tissue partition coefficient (κ) was defined as tissue concentration of labelled drug (T) at equilibrium normalized by total bulk concentration at equilibrium (C_bulk):

κ = T/C_bulk.

Net tissue binding capacity (B_M) and equilibrium dissociation constant (K_d) were then estimated by varying bulk concentration of drug and fitting experimental partition coefficient values to relationship implied by bimolecular binding of small hydrophobic drugs that have access to the entire tissue volume (e.g. eqn 7 with ɛ = 1)

κ = 1 + B_M/(K_d+C_bulk).

Curve fitting was performed using GraphPad Prism 3.0. Note that eqn (7) cannot be used directly for estimating equilibrium binding parameters in an experimental protocol such as ours that correlates between tissue‐associated labelled drug and total bulk drug, rather than labelled bulk drug as is standard.

Results

Bolus endovascular drug delivery can saturate arterial binding sites

Concerns over long‐term complications with drug‐eluting stents have spurned development of novel bolus endovascular delivery modalities that deliver large dose over short times (11, 12). In particular, clinical studies have shown that short (1 min) endovascular exposures to paclitaxel‐coated balloon catheters can inhibit stent restenosis in a range of arterial beds, for more than 6 months (13, 24). Although promising, in the absence of clear mechanistic underpinning these results remain intriguing and are difficult to translate to other drugs. Such delivery is best approximated as a bolus infusion. Previously, we have measured equilibrium loading of paclitaxel (6) in calf carotid arteries and concluded that it was proportional to equilibrium bulk concentrations. Those experiments employed 100% radiolabelled paclitaxel and were limited to concentrations up to 0.23 µm, falling short of typical concentrations employed in bolus endovascular delivery (12). To circumvent safety limitations set by intensity of the radioactive label, we now measured equilibrium arterial loading of paclitaxel and rapamycin using mixtures of labelled and unlabelled drug (Fig. 2). Equilibrium partition coefficient of both drugs decreased as total bulk concentration increased, consistent with saturable binding. Analysis of equilibrium partitioning curves yielded estimates of net arterial dissociation constant and binding capacities (Fig. 2). Notably, net dissociation constants of both drugs are in the micromolar range, similar to heparin (25). By contrast, net arterial binding capacities for paclitaxel and rapamycin (Fig. 2) are more than 10‐fold higher than for heparin (25). When these estimates are used to simulate bolus endovascular delivery, significant differences emerge between heparin and paclitaxel with regard to impact of binding on dynamics of drug distribution (Fig. 3). Whereas a model of nonsaturable binding, which assumes proportionality between local concentrations of free and total drug (26), adequately predicts distribution of heparin (Fig. 3a,b), this is not the case for paclitaxel or rapamycin. The full model ((1a), (1b), (2), (3), (4)), which correctly accounts for saturable binding, predicts deeper and more uniform penetration of paclitaxel (Fig. 3c) and rapamycin (Fig. 3e) and, therefore, lower net arterial loads (Fig. 3d,f).

Figure 2.

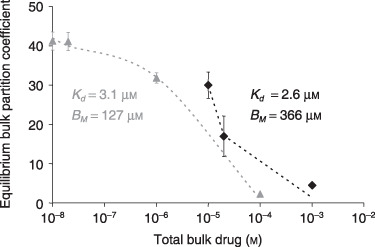
Experimental validation of saturable binding to arteries. The equilibrium net arterial partition coefficient of paclitaxel (grey triangles) or rapamycin (black diamonds) was measured as described in the Materials and methods. Bimolecular binding fit the experimental results (dashes) and provided estimates of the equilibrium binding parameters of paclitaxel (R ² = 0.997) and rapamycin (R ² = 0.970).

Figure 3.

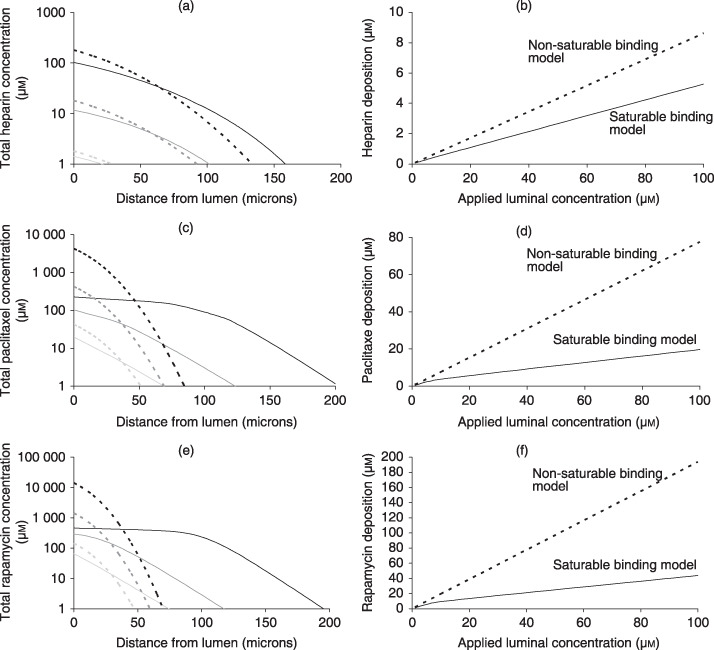
Concentration dependence of bolus endovascular delivery. Simulated transmural drug concentrations (a,c,e) and average arterial deposition (b,d,f) at the end of 3‐min bolus endovascular delivery of heparin (a,b), paclitaxel (c,d) or rapamycin (e,f). Predictions of the saturable binding model (lines) and nonsaturable binding model (dashes) were contrasted over three decades of luminal concentration: 1 µm (light grey), 10 µm (grey) or 100 µm (black). Deviations between the two models scale with the applied luminal concentration and are particularly pronounced for paclitaxel and rapamycin. Interestingly, the nonsaturable binding model significantly underestimates the depth of paclitaxel (c) and rapamycin (e) penetration into the artery while overestimating their total arterial deposition (d, f).

Typically, differences in drug penetration due to binding interactions have been attributed to differences in binding dissociation constants (27, 28). Yet, net arterial dissociation constants of heparin, paclitaxel and rapamycin are all in the micromolar range (Table S1). Rather, our finding that net arterial binding capacities for paclitaxel and rapamycin are more than 10‐fold higher than that for heparin (Table S1) suggests that binding capacity may also significantly impact drug distribution. Subsequent analysis corroborates this hypothesis and elucidates the prediction of marked concentration dependence of arterial paclitaxel distribution upon bolus delivery.

Fractional drug retention

The success of endovascular drug delivery appears to be predicated upon arterial residence time of the drug (29). Since free drug diffuses and washes away upon removal of the drug source, we first asked what determines fraction of tissue‐bound drug?

To examine this, we plotted fraction of bound drug (B/T) for a range of drugs and tissues (Fig. 1) as a function of total concentration of drug in the tissue (T). Evaluating the fraction of bound drug as 1 – C/T, with C provided by eqn (10), and scaling total concentration of drug to maximal potential concentration of retained drug, B_M, we found that the magnitude of B_p dictates a hierarchy of fractional drug retention curves (Fig. 4a). Drugs with low B_p (such as heparin) are predominantly free, regardless of applied concentration and duration. At larger B_p drug is predominantly bound at states of excess binding sites and fraction of bound drug decreases appreciably only as total concentration exceeds binding capacity. The degree of drug retention and sharpness of transition between states of excess binding site and excess drug, both scale with B_p. Detailed analysis of eqn (10) (Appendix A) illustrates that an appreciable pool of free drug exists in the tissue only above threshold bulk concentration:

Figure 4.

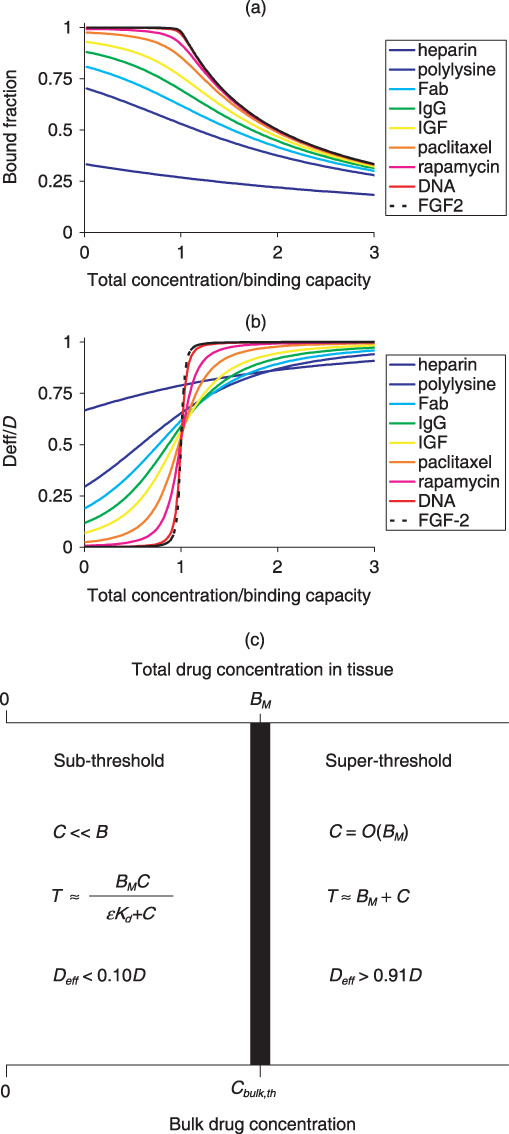
Drug retention and mobility are determined by the magnitude of B_p. The fraction of bound drug (a) and the effective mobility (b) are plotted as a function of the total local drug content relative to the number of binding sites for a range of drugs and tissues (Table S1). Drugs are colour coded according to their B_p with cold colours (e.g. blue) designating small B_p values. Scaling analysis of the equilibrium concentration of free drug and the effective diffusivity (Appendix A) provides an estimate of the threshold bulk concentration for binding saturation and drug diffusion (c).

(12)

Such a well‐defined threshold exists only at large B_p (Fig. 4a), so that C_bulk,th is at once much larger than binding dissociation K_d and much smaller than binding capacity B_M.

Effective drug diffusivity

As only free drug is mobile, the magnitude of B_p also dictates a hierarchy of effective diffusivity curves (Fig. 4b). At one extreme are molecules like FGF‐2 and antibody fragments with huge binding potentials (> 1000; Table S1) whose mobility at the excess‐ligand regime (C > B_M) is three orders of magnitude larger than their mobility in the unsaturated binding regime (C < K_d). At the other extreme, of weakly retained drugs (B_p < 1) we find heparin (B_p = 0.8; Table S1) whose effective arterial diffusivity increases by no more than 30% with total concentration. Paclitaxel and rapamycin, and certain growth factors and antibodies, display an intermediate concentration dependence that becomes more pronounced with increasing B_p (Fig. 4b). Rigorous analysis of these trends (Appendix A) reveals that diffusivity is essentially unhindered (D _eff > 0.9D) at supersaturating concentrations, drops by 50% at parity between total drug concentration and binding capacity, and is less than 10% of free diffusivity and strongly concentration dependent at subsaturating concentrations (Fig. 4c). These predictions are borne out by paclitaxel (B_p = 40.7), but not by compounds with lower B_p such as heparin (Fig. 4b).

Results of the last two sections illustrate the profound effects of B_p on drug retention and transport and begin to explain differential retention and distribution of heparin, paclitaxel and rapamycin. Based on their B_p, paclitaxel and rapamycin are classified as strongly retained drugs with markedly concentration‐dependent arterial transport. In contrast, heparin is classified as a weakly retained drug whose arterial transport is insensitive to applied luminal concentration.

Arterial penetration of strongly retained drugs

To further elucidate concentration dependence of endovascular drug delivery, we analysed effective diffusion equation (eqn 8) subject to uniform initial conditions:

T = 0, x > 0, t = 0,  (13)

and applied luminal concentration

(14)

At short times, before an appreciable amount of drug reaches the far surface of the tissue, it is valid to approximate the artery as a semi‐infinite medium (30) for which it is possible to derive insightful analytical solutions in limits of large B_p.

Sub‐threshold bulk concentrations (receptor excess)

At total surface concentrations below binding capacity, effective diffusion coefficient is nonlinear and approximated by D_eff(T)/D ≈ B_p ⁻¹(1 – T/B_M)⁻²(Appendix A).

Kinetics of tissue loading per unit area are then (Appendix B)

(15)

where the parameter β is evaluated numerically as root of the following equation

(16)

Numerical simulations (Fig. 5) illustrate that eqn (15) closely approximates arterial loading kinetics of paclitaxel (B_p = 40.7, C_bulk,th = 0.16B_M) and rapamycin (B_p = 139, C_bulk,th = 0.08B_M) but underestimates uptake of heparin (B_p = 0.8, C _bulk,th = 1.4B_M). At 5 h super‐threshold, bulk concentrations of paclitaxel and rapamycin fully penetrate the artery, and the sub‐threshold approximation (eqn 15) underestimates drug loading.

Figure 5.

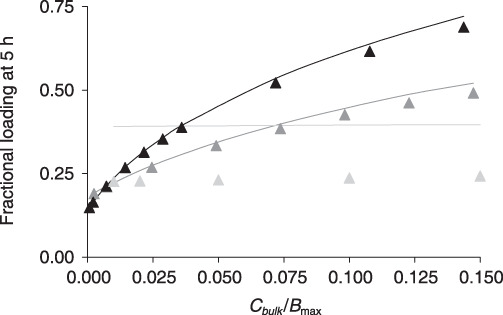
Tissue loading in the unsaturated binding regime. Tissue associated rapamycin (black), paclitaxel (dark grey) or heparin (light grey) at 5 h is normalized to the equilibrium drug content and plotted versus the normalized concentration of bulk drug. Numerical results (lines) are contrasted with the sub‐threshold approximation (eqn 15, solid triangles).

Dependence of tissue loading on bulk concentration can be rendered explicit in boundary cases of the sub‐threshold regime. Low bulk concentrations compared to equilibrium dissociation constant (C_bulk < K_d/3) provide for (Appendix B)

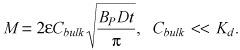(17)

The latter result is specialization of celebrated nonsaturable binding result (30) in the limit of strong retention (B_p >> 1)

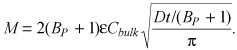(18)

The nonsaturable binding result approximates the uptake of heparin in the concentration range C_bulk ≤ 0.15B_M, but not of strongly retained drugs such as paclitaxel and rapamycin wherein condition K_d << B_M restricts validity of the nonsaturable regime to very low apparent concentrations (not shown).

Near threshold bulk concentrations 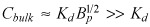(eqn 12), provide for (Appendix B)

(19)

The latter result consistently overestimates numerical predictions for paclitaxel and rapamycin at low bulk concentrations but becomes quantitative as the bulk concentration approaches C_bulk,th (not shown).

Super‐threshold bulk concentrations (drug excess)

The effective diffusion coefficient of strongly retained drugs approaches free diffusivity D at saturating concentrations and drops to negligible values for nonsaturating concentrations (Fig. 4b,c). This can be idealized as a step discontinuity

(20)

Correspondingly, the luminal boundary condition (eqn 14) simplifies to

T = T₀ = ɛC_bulk + B_M, x ≤ 0, T > 0.  (21)

Limit of a discontinuous diffusion coefficient (eqn 20) can be solved analytically for short times, prior to full penetration of the matrix as (30)

T = T₀ – (T₀ – B_M) erf[kx/(2S)]/erf(k/2), 0 < x S(t),  (22)

where

(23)

is the location of the discontinuity front and k is the root of the transcendental equation

(24)

The cumulative amount of drug in the tissue (per unit area) is then

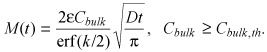(25)

Numerical simulations (Fig. 6) illustrate that (23), (24) accurately predict the location of the binding saturation front for paclitaxel (B_p = 40.7) and rapamycin (B_p = 139.2) at super‐threshold bulk concentrations, but overpredict penetration at lower bulk concentrations. Correspondingly, eqn (25) accurately predicts the loading kinetics of paclitaxel and rapamycin at super‐threshold bulk concentrations, but overpredicts tissue loading at sub‐threshold concentrations (Fig. 7). These trends become even more apparent for heparin, as its threshold concentration C _bulk,th falls in the middle of the concentration range examined in Fig. 7 (C_bulk,th = 1.4B_M). Adequate approximation of super‐threshold heparin loading by eqn (25) reflects the latter's correct asymptotic convergence to loading kinetics of freely diffusible drugs: 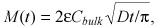 C_bulk >> C_bulk,th (30).

Figure 6.

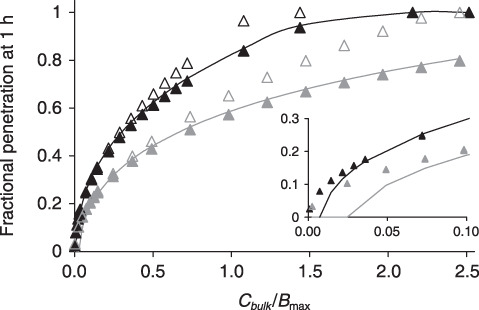
Concentration dependence of drug penetration and effect. The depth at which arterial binding sites become half saturated at the end of 1 h of incubation in paclitaxel (dark grey) or rapamycin (black) is plotted versus normalized bulk concentration. Numerical solutions (lines) are contrasted with S/L (solid triangles, (23), (24)) or 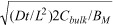(empty triangles, (23), (26)). (23), (24) predict the location of the binding penetration front in all but subsaturating bulk concentrations (insert).

Figure 7.

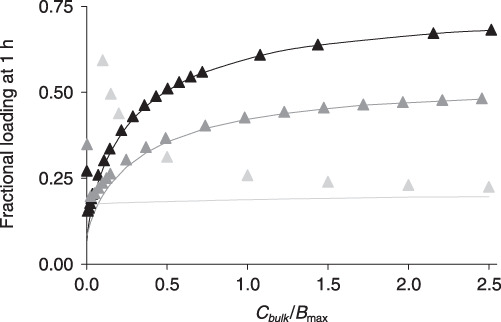
Tissue loading in the saturable binding regime. The predicted concentration dependence of drug uptake from bulk solutions of rapamycin (black), paclitaxel (dark grey) or heparin (light grey). Tissue associated drug at 1 h is normalized to the corresponding equilibrium uptake and plotted versus the normalized concentration of bulk drug. Numerically simulated loadings (lines) are contrasted with the super‐threshold approximations (eqn 25, solid triangles).

At near threshold bulk concentrations,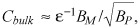

(26)

and eqn (19) is recovered (31), implying seamless overlap of sub‐ and super‐threshold approximations. Together, the sub‐ and super‐ threshold approximations describe loading kinetics of strongly retained drugs at any bulk concentration. Numerical examples illustrate that eqn (26) accurately predicts location of the binding saturation front for intermediate bulk concentrations, C_bulk,th < C_bulk < 0.5B_M, but increasingly overestimates penetration as bulk concentrations increases (Fig. 6). Similarly, eqn (19) accurately predicts mass uptake for intermediate bulk concentrations, C_bulk,th < C_bulk < 0.5B_M, but underestimates drug loading at super‐threshold bulk concentrations (not shown).

Discussion

As binding affinity is synonymous with binding strength, it is widely held that affinity also provides a measure of impact of binding on a compound's transport and equilibrium properties. However, differences in binding affinity cannot alone explain significant differences in the vascular retention and transport of, for example, heparin compared to paclitaxel and rapamycin. Similarly, immunoglobulin G and the EGFRvIII‐specific single‐chain antibody fragment bind to solid tumours with similar binding affinities (Table S1); yet transport of the former is only slightly affected by such binding (18), whereas the latter is dominated by it (16, 32). In estimating the impact of binding on drug transport and retention, molecular affinity must be scaled with binding capacity. Such scaling is inherent to B_p, which is the product of binding capacity and apparent affinity constant (eqn 11). The larger B_p, the sharper the transition between states of receptor excess and ligand excess (Fig. 4a). Correspondingly, strongly retained drugs are characterized by large B_p (> 10) and effective diffusion coefficients that exhibit switch‐like dependence on total drug concentration (Fig. 4b).

In the extreme of large B_p (> 40) concentration dependence of effective diffusivity facilitates derivation of approximate analytical solutions that provide complete description of uptake of strongly retained drugs across the range of possible bulk concentrations (4, 5, 6). This is noteworthy, as B_p > 40 for paclitaxel and rapamycin and a range of important cytokines and antibodies (Fig. 1 and Table S1). Above and beyond these detailed quantitative predictions, our analysis elucidates the dependence of ligand transport on constitutive binding properties of the tissue for the ligand, and the degree to which ligand concentration can modulate shape of ligand gradients in tissue (Fig. 3). In particular, our analysis predicts that saturation of specific binding sites by strongly retained compounds can be accelerated significantly by ramping up bulk concentration well beyond K_d, but that this effect plateaus above threshold concentration for drug mobility 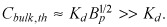Drug distribution and effect can then be modulated by altering applied drug load or conversely by manipulating threshold concentration. For example, threshold concentration would be lower for drug analogues with larger binding affinities (1/K_d) as these saturate tissue binding sites more readily. Alternatively, threshold concentration at which drug mobility is significantly impeded by binding should rise for drugs that access a larger tissue volume fraction (larger ɛ). This is particularly relevant for hydrophilic antibodies as these are restricted to interstitial spaces and progressively access smaller volume fractions as their molecular weight increases (33, 34).

Optimization of binding specificity

Directing therapy to potentially overexpressed receptors is a popular means of selective molecular targeting to specific cells and tissues (35). Affinity maturation, wherein K_d is minimized, maximizes target selectivity. Previous analyses only described diffusion and binding for high‐affinity receptors or low ligand concentrations (15, 16, 17) and, thus, it remains unclear how minimization of dissociation constant affects molecular penetration into tissues (16, 28, 32). By elucidating dependence of penetration depth on the magnitudes of the B_p across the gamut of bulk drug concentration (Fig. 6), our analysis clarifies this issue. In the binding regime where K_d >> C_bulk, drug transport is governed by constant effective diffusion coefficient D/(1 + B_P) (eqn 23). Thus, drug profiles decay over a typical diffusion length scale that varies inversely
with the 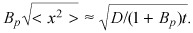 B_p is inversely related to K_d and as the latter is reduced, not only is target selectivity increased, but penetration depth also drops proportionately. Behaviour in the saturated binding regime (C_bulk >> K_d) is more intricate and less dependent upon K_d. In this domain drug penetration is less sensitive to variations in magnitude of equilibrium dissociation constant (Fig. 6), and only dependent on binding capacity for drugs with large B_p.

Thus, drug penetration drops with the dissociation constant (Fig. 6 inset) only for low bulk drug concentrations and not for high. However, concentration levels are relative. Bulk concentration at which effective diffusion coefficient is equal to half its maxima; C_bulk,th is itself a function of equilibrium dissociation constant and decreases as the latter is minimized, 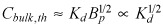(eqn 12). These findings provide notes of caution and opportunity. As there is finite resolution to detection of radio and fluorescently labelled drugs, these compounds are often used at the highest concentration levels. Drug penetration under these conditions is least sensitive to the dissociation constant and apparent results may be biased to overestimate penetration and underestimate change in penetration with time and modulation of the physicochemical properties, such as the dissociation constant. The opportunity arises in manipulation of drug binding in molecular analogues. Minor modifications in chemical structure of sirolimus, for example, create analogues with retained biological activity but markedly altered interaction with mTOR and FK506 binding protein (36, 37). It may be possible to affect penetration and binding of analogues of the parent compound in a directed and predicted fashion.

Local delivery can optimize the efficacy of strongly retained drugs

Our prediction that penetration of strongly retained drugs is markedly dependent on prescribed surface concentration implies that biological effect may become dominated by drug gradients in target tissue. In particular, threshold concentration dependence of effective diffusivities of paclitaxel and rapamycin (Fig. 4b) and the resulting concentration dependence of binding site occupancy inside the tissue (Fig. 6) may explain threshold dose–response of paclitaxel in local endovascular delivery (10, 20) and with systemic chemotherapy of solid tumours (4), although the latter may be more problematic than the former. Advantages of dose‐dependent penetration may be largely counterbalanced by dose‐dependent toxicity, especially with lack of targeting specificity in systemic delivery. It may be that the full benefits of dose‐dependent penetration can only be achieved with targeted local drug delivery. Indeed, marked concentration dependence of paclitaxel penetration into arteries (Fig. 3c) may explain successful inhibition of restenosis up to 12 days after short exposures (3 min) of injured arteries to extremely high doses of paclitaxel (100–220 µm) that significantly exceed its predicted threshold concentration (C _bulk,th = 20 µm) (12). Even higher B_p of rapamycin and larger threshold concentration (C _bulk,th = 31 µm) make it a good candidate for this mode of bolus delivery (Fig. 3e).

In contradistinction to balloon catheters that deliver high drug loads over short durations, stents provide a platform for local delivery long after initial intervention and implantation. First‐generation drug‐eluting stents were designed to deliver their loads in a sustained fashion, with the aim of prolonging drug residence time and providing drug throughout various stages of restenotic response (38). Yet clinical efficacy of drug‐eluting stents is not solely predicated on elution rates from the stent (39), and bolus delivery of paclitaxel from coated balloons also provides sustained inhibition of restenosis (13, 24). Thus, the question arises as to whether other elements such as tissue absorption and retention could contribute to prolonging exposure regardless of release. Our results shed light on these issues as they demonstrate that rate of absorption and ultimate retention of drugs such as paclitaxel and rapamycin can exhibit a threshold dependence on the delivered dose. Our analysis is of particular significance to second‐generation drug‐eluting stents that can deliver higher drug doses with minimal washout (36). Such devices typically deliver drugs by a diffusion‐controlled mechanism wherein cumulative drug release can be parameterized as M =M _rel(t/t_rel)^1/2 (5, 8, 10). Our analysis predicts that arterial penetration kinetics of strongly retained drugs (B_p > 40) following diffusion‐controlled release will exhibit threshold dependence on the dose intensity parameter 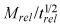(Appendix B). Penetration increases dramatically as dose intensity is increased up to a threshold that is set by arterial transport parameters of the drug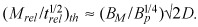

Thus, in absence of significant washout effects, there exists a balance between absorbed dose and duration of elution. Drug accumulation is determined by tissue binding capacity, binding potential and drug diffusivity, and until a threshold is reached increasing the eluted dose leads to increasing drug absorption, penetration and occupancy of tissue binding sites. When this threshold is exceeded, for example, with large bolus delivery, enhancement of penetration and occupancy is lost. Luminal washout further complicates analysis as it introduces a distinction between eluted and delivered doses. In the absence of arterial binding, fractional drug absorption following elution is solely determined by the balance between the rates of elution and arterial diffusion (40). Our results now imply that arterial binding should also be factored into this balance and that fraction of absorbed dose can exhibit threshold dependence on the eluted dose. Thus, stent elution of sub‐threshold doses of paclitaxel or rapamycin will result in absorption of a significant fraction of the eluted drug as tissue‐absorbed drug is predominantly bound and therefore retained. Increasing eluted dose above absorption threshold will only result in transient enhancement of arterial load; as such, enhancement establishes a pool of free drug near the lumen that quickly washes away. Our estimates (Table S1) imply that dose intensity thresholds of paclitaxel and rapamycin are both in the order of 3 µg/cm²/h^1/2. It is therefore noteworthy that dose intensity provided by the Taxus stent can reach as much as 20.3 µg/cm²/h^1/2 (8), significantly exceeding threshold absorption dose intensity of this drug and implying significant washout.

Generalizations and limitations

Our mathematical model of arterial drug distribution makes certain simplifying assumptions that are not generally true. Although perivascular permeability is low (26), our assumption that the far end is impermeable (eqn 1b) is not generally valid. Nevertheless, steepness of spatial drug gradients prior to tissue breakthrough (30, 41) ensures that during this phase drug transport is insensitive to perivascular boundary conditions. At longer times, drug clearance at the far end may invalidate our quantitative predictions.

Our model of drug binding to fixed saturable sites is adequate for modelling arterial distribution of small hydrophobic drugs, such as paclitaxel and rapamycin, but does not account for two processes that arise in antibody and cytokine transport in tissues, receptor endocytosis and binding to (low affinity) nonsaturable sites in the tissue. When the assumption of purely saturable binding is relaxed, effects of nonspecific binding can be read from our results by simply redefining binding capacity and total concentration as B_M → B_M/(1 + ɛ⁻¹ K_ns) and T_M → T/(1 + ɛ⁻¹ K_ns), where 1 + K_ns is partition coefficient of nonspecific binding (see Appendix C). Whereas paclitaxel and rapamycin both bind to intracellular pharmacological targets, many antibodies and cytokines bind to specific receptors on the cell surface and are endocytosed, as these receptors internalize by nonspecific or ligand‐induced mechanisms. While beyond the scope of the current work, the same methodology of model reduction and analytical approximations can elucidate transport of strongly retained drugs that undergo endocytosis. A detailed analysis is forthcoming, but it is already clear that nonspecific endocytosis (with rate constant k_t) results in addition of a sink term in the effective diffusion equation (eqn 7). Definition of effective diffusion coefficient (eqn 9) remains essentially the same in the face of endocytosis, with the simple proviso that equilibrium dissociation constant is replaced by an apparent dissociation constant that depends on the endocytosis rate constant as K _d,app = (k_r + k_t)/k_f (42). Thus, our analysis of concentration dependence of the effective diffusion coefficient remains valid for endocytosing compounds, as does our prediction that retention scales as the ratio of binding capacity to apparent dissociation constant K _d,app = (k_r + k_t)/k_f (42), and that local delivery of strongly retained compounds (B_M >> K _d,app) should significantly enhance their penetration.

Appendix A 
Equilibrium drug retention

Drug retention is an equilibrium property of a drug–tissue pair and is directly related to fraction of free equilibrium drug. The stronger the retention, the smaller the pool of equilibrium free drug. To analyse potential binding scenarios, it is informative to rewrite the equilibrium free concentration (eqn 10) as

(A1)

where we defined the auxiliary variable

(A2)

Equation (A2) diverges for saturating drug concentrations such that T = B_M + K_d, reducing eqn (10) to 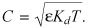In fact, it can be shown that this result remains valid near the singularity in r

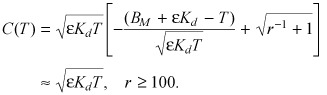(A3)

On the contrary, when r is small, the fraction of free drug is determined by the ratio of the drug load to the sum of the equilibrium binding parameters

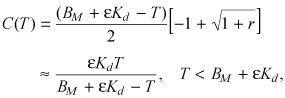(A4)

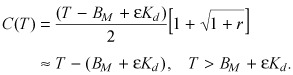(A5)

The error associated with results (A4) and (A5) is less than 10% for r < 0.40.

Strongly retained drugs

Results (A4) and (A5) are both invalid for drug concentrations close to the singularity of r(T), in which case eqn (A3) should be used. Noting that

we can estimate the half width of the singularity zone relative to the binding capacity as

(A6)

Thus, the larger the binding potential B_P is, the sharper the transition between the nonsaturated and supersaturated binding regimes. At non‐saturating drug concentrations T < (1 – δ)B_M the drug is predominantly bound (eqn A4)

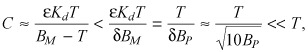(A7)

B = T – C ≈ T.  (A8)

In contrast, at supersaturating total drug concentrations, T > (1 + δ)B_M, a significant fraction of the drug is free (eqn A5)

(  (A9))

B ≈ B_M.  (A10)

At the threshold region itself, (1 – δ)B_M < T < (1 + δ)B_M, the concentration of free drug is only a function of the equilibrium binding parameters (eqn A3) and

(A11)

Noting the proportionality of equilibrium concentrations of free drug in the tissue and the bulk medium (eqn 1a), we infer the existence of a threshold bulk concentration

(A12)

When the bulk concentration is below this threshold value, drug is predominantly bound (retained). At bulk concentrations above this threshold, a significant fraction of drug is free, representing a significant potential for drug washout in vivo. Importantly, the threshold bulk concentration for drug washout is large compared to the binding dissociation constant.

Effective drug diffusivity

The dependence of the effective diffusivity upon B_p can be rigorously quantified by substituting appropriate approximations of the free fraction into the definition of the effective diffusivity (eqn 9). At parity between total drug concentration and binding capacity (eqn A12) the effective diffusivity is equal to half its maximal value

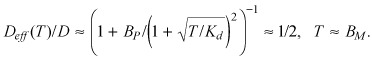( (A13a))

At lower tissue concentrations (eqn A7), drug mobility is less than 10% of the free mobility and strongly concentration dependent

( (A13b))

At supersaturating tissue concentrations (eqn A9), diffusivity is almost unimpeded by binding

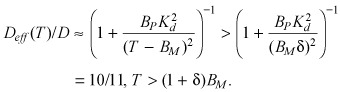(  (A13c))

Taken together, the analysis in this appendix implies that drug transport and retention are strongly concentration dependent and inversely correlated. Drug transport is most significantly retarded at low concentrations so that retention is maximal, and increases dramatically above a well‐defined threshold concentration. Substituting ( (A13b)), (  (A13c)) into the effective diffusion equation, we were able to derive analytical approximations for early loading kinetics of strongly retained drugs across the gamut of bulk drug concentrations, below and above the threshold.

Appendix B 
Transport of strongly retained drugs

I. Prescribed sub‐threshold surface concentrations

Spatial distribution.  Fujita (43) modelled solvent transport into a polymer matrix as a diffusion process with a concentration‐dependent diffusion coefficient of the form

(B1)

Here T is the concentration of the solute in the polymer, T ₀ is the bulk solute concentration in the uptake medium, D(0) is the asymptotic value of solute diffusivity in the limit of low concentrations, and α is an empirical parameter that scales the concentration dependence of D (0 < α < 1). Fujita's similarity solution for solute uptake into a semi‐infinite polymer slab can be cast as (43)

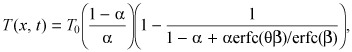( (B2))

where β and θ are determined by transcendental equations and can be evaluated sequentially. First, β is evaluated from

(B3)

Subsequently, θ is evaluated by solving the transcendental equation

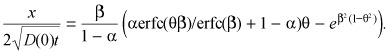( (B4))

Thus, whereas a one‐to‐one correspondence exists between α and β, each α value is associated with a family of θ(x/t ^1/2). Fujita used his similarity solution to simulate spatio‐temporal solvent profiles in the semi‐infinite medium and also to show that the classical diffusion solution is recovered on the limit that α → 0. Adaptation of Fujita's results to the problem of effective diffusivity at sub‐threshold bulk concentrations is achieved by setting

D(0) = D/B_p, α = T₀/B_M.  (B5)

Mass uptake  Since θ is an implicit function of the spatial coordinate, it is not possible to evaluate mass uptake kinetics directly from the concentration profile (eqn B2). This limitation can be overcome by using the flux balance relationship at the bath/tissue interface

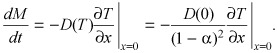(B6)

As Fujita's solution is a function of the similarity variable

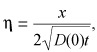it is informative to use the chain rule to rewrite the right‐hand side of eqn (B6) as

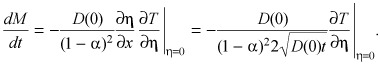(  (B7))

Using Fujita's results (43) we evaluated ∂T/∂η |_η=0 without recourse to eqn (B2) as

∂T/∂η|_η=0= –T₀(1 – α)² 2β/α.  (B8)

Combining (  (B7)), (B8) we find

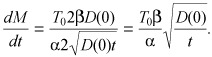(B9)

and

(B10)

Equation (15) in the main text is then obtained by invoking the correspondence α = T ₀/B_M (eqn B5).

The dependence of mass uptake on bulk concentration can be rendered explicit in the boundary cases of the sub‐threshold regime. Low bulk concentrations compared to the equilibrium dissociation constant (C_bulk < K_d/3) provide for (43)

(B11)

and

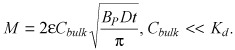(B12)

As the bulk concentration increases beyond the linear binding regime and approaches the threshold concentration 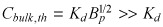(eqn A12)

(B13)

and

(B14)

II. Prescribed surface flux

Problem statement  Our detailed analysis of drug transport under prescribed surface concentrations is very informative, and allowed us to consider idealized in vitro and in vivo scenarios wherein the bulk or luminal concentration is prescribed over some time interval. Here we illustrate the relevance of these detailed results for the case wherein the prescribed quantity is the surface flux, rather than the surface concentration. For concreteness, we focus our discussion to diffusion controlled processes wherein the applied flux is of the form

F(t) = Q/t^1/2.  (B15)

These idealized fluxes model relevant local delivery modalities and are amenable to analytical study.

Correspondence  Our analysis of diffusion controlled uptake under prescribed surface concentration illustrated that mass uptake per unit area increases as the square root of time

M = 2Q · t^1/2.  (B16)

The effects of specific binding were manifest as a concentration dependence of the prefactor Q. Using the results and nomenclature of the main text ((15), (19), (25))

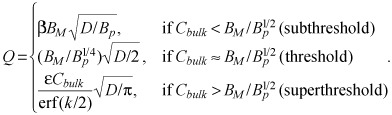( (B17))

For one‐sided uptake from a bulk solution at x = 0, the following mass balance relationship holds between bulk tissue uptake per unit area (eqn B16) and the surface flux

–D(∂C/∂x)_x=0 = dM/dt = Q/t^1/2.  (B18)

The latter result provides a direct and unique correspondence between the kinetics of mass uptake and distribution under prescribed surface concentration and prescribed surface flux (44). Given a prescribed surface concentration C_bulk, an equivalent surface flux F(t = Q/t^1/2) can be identified using eqn (B17). This correspondence is unique and invertible as eqn (B17) implies a monotonic relationship between Q and C_bulk.

Appendix C
Inclusion of nonspecific binding

To include the effects of nonspecific binding, we introduce a rate law for nonsaturable binding

(C1)

(1a), (1b), (2), (3) remain unaltered but eqn (4) now includes a nonspecific binding sink term

(C2)

and the total concentration of drug generalizes to

T = C + B + B_ns.  (C3)

Equilibrium binding fraction

Mass balance at equilibrium now implies that

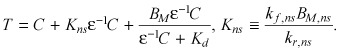(C4)

Dividing (C4) through by the nonspecific partition coefficient, 1 + K_ns, and solving for the concentration of free drug in the tissue, we find

( (C5))

where we introduced the simplifying notations

(C6a)

(C6b)

Thus, the sole effect of nonspecific binding is a renormalization of the specific binding capacity and the total drug concentration as in (C6a), (C6b). When K_ns > 1, a significant fraction of drug is bound nonspecifically, reducing the fraction of specifically bound drug. The relative importance of specific binding is then determined by the renormalized binding potential β_M/(ɛK_d) = B_P/(1 + ɛ⁻¹ K_ns), which may be significantly smaller than B_P. For systems such that β_M/(ɛK_d) >> 1, the fraction of free drug changes rapidly for total drug concentrations in the vicinity of B_M(T/B_M = Θ/β_M ≈ 1). The normalized width of the region of rapid transition scales as (compare to eqn A6)

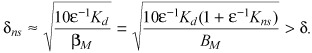(C7)

If the bulk drug concentration is not very high, T < (1 – δ_ns)B_M, then a negligible fraction of the drug inside the tissue is free

(C8)

and most of it is specifically bound

B ≈ T – (1 + ɛ⁻¹K_ns)C = (1 + ɛ⁻¹K_ns)(Θ – C) ≈ (1 + ɛ⁻¹K_ns)Θ = T. (C9)

Otherwise, if the bulk drug concentration is higher than the binding capacity, T > (1 + δ)B_M, then the concentration of free drug is in great excess of the specific dissociation constant

(C10)

such that all the specific binding sites are occupied

(C11)

In fact, the specific binding sites are already saturated at intermediate drug loads (1 – δ_ns)B_M < T(1 + δ_ns)B_M, as such loads imply that

(C12)

Kinetic implications at high Damköhler numbers

When the pools of free, nonspecifically bound and specifically bound drug are all in a state of dynamic equilibrium; the total concentration of drug can be related to the free concentration of drug as in eqn (C4). We can then define an effective diffusion coefficient as

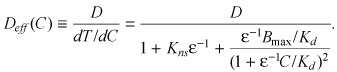(C13)

At sub‐threshold bulk concentrations

and

( (C14))

At supra‐threshold concentrations

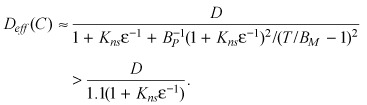( (C15))

Once again, these results are analogous to the case of purely saturable binding and can therefore be readily appreciated. When K_ns << 1, only a small fraction of the drug is bound nonspecifically and the model analysed in the main text provides a good approximation. When K_ns > 1, a significant fraction of drug may be bound nonspecifically. The relative importance of saturable binding versus nonspecific binding is then determined by the renormalized binding potential β_M/(ɛK_d) = B_P/1(1 + ɛ⁻¹ K_ns). In particular, large B_P/1(1 + ɛ⁻¹ K_ns) values imply that binding is predominantly saturable and the effects of nonspecific binding are quantitative, rather than qualitative, and correspond to a rescaling of the effective diffusivity as in (C13), ( (C14)), ( (C15)).

Supporting information

Table S1 Transport parameters of representative molecules and tissues.

Please note: Wiley‐Blackwell are not responsible for the content or functionality of any supporting information supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

Supporting info item