On the Mechanisms of α-Amino-3-hydroxy-5-methylisoxazole-4-propionic Acid (AMPA) Receptor Binding to Glutamate and Kainate

Abstract

The α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid (AMPA) subtype of ionotropic glutamate receptors mediates much of the fast excitatory neurotransmission in the central nervous system. The ability of these receptors to shape such responses appears to be due in part to dynamic processes induced by agonists in the ligand-binding domain. Previous studies employing fluorescence spectroscopy and whole cell recording suggest that agonist binding is followed by sequential transitions to one or more distinct conformational states. Here, we used hydrogen-deuterium exchange to determine the mechanisms of binding of glutamate and kainate (full and partial agonists, respectively) to a soluble ligand-binding domain of GluR2. Our results provide a structural basis for sequential state models of agonist binding and the free energy changes of the associated state-to-state transitions. For glutamate, a multi-equilibrium binding reaction was discerned involving distinct ligand docking, domain isomerization, and lobe-locking steps. In contrast, kainate binding involves a simpler dock-isomerization process in which the isomerization equilibrium is shifted dramatically toward open domain conformations. In light of increasing evidence that the stability, in addition to the extent, of domain closure is a critical component of the channel activation mechanism, the differences in domain opening and closing equilibria detected for glutamate and kainate should be useful structural measures for interpreting the markedly different current responses evoked by these agonists.

Introduction

As a consequence of glutamate binding, AMPA² receptors produce a rapid flux of cations into post-synaptic neurons that is vital for information transfer in the central nervous system. In addition, these receptors undergo fast deactivation and desensitization along with slower recovery kinetics, which together shape the time course of current decay and restoration (1–6). Structurally, AMPA receptors are tetrameric membrane-bound proteins composed of modular subunits having two large extracellular domains, a membrane-spanning ion channel, and a C-terminal intracellular region (4, 7–12). One of the extracellular domains, S1S2, is a bilobed structure that binds agonists in a cleft between its lobes (13). Domain closure of S1S2 around the agonist leads to channel opening, and maximum currents have been attributed to complete lobe closure upon complex formation with full agonists (13–17). However, among the full agonists examined, those like glutamate, which are less potent and which bind to S1S2 with lower affinity, produce higher rates of channel deactivation and resensitization (18), despite inducing the same degree of cleft closure in S1S2. This suggests that AMPA receptor function is dependent not only on the extent of lobe closure caused by the agonist but also on the lobe closing and opening dynamics associated with agonist binding and dissociation (19).

A prevailing model for the binding reaction is

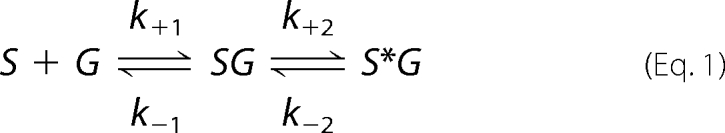where SG represents a state in which glutamate (G) has rapidly docked to sites in lobe 1 of S1S2 (S) (20). The species S*G establishes key contacts between glutamate and lobe 2, which brings about domain closure and triggers the opening of a gate in the ion channel. This has been referred to as the dock-isomerization model and is consistent with data from stopped flow (20) and time-resolved Fourier transform infrared spectroscopy experiments (21). However, the following model, which was recently proposed based on whole cell recordings of GluR2 channels, implies a related but more complicated binding reaction (18),

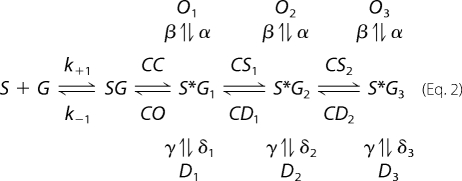where O_i and D_i (where i = 1, 2, or 3) denote open and desensitized channel states, respectively. Although this model accounts for structural changes occurring throughout a subunit of the tetrameric receptor, SG, S*G₁, S*G₂, and S*G₃ were suggested to represent unique conformational states in the binding cleft of S1S2, with S*G₃ possessing the highest degree of cleft closure stability (18, 19). The sequential nature of this mechanism was found to be critical to reproduce current responses for full agonists of varying potency and binding affinity for S1S2. For glutamate, receptors primarily occupy S*G₁, whereas higher potency full agonists show increased occupation of S*G₂ and S*G₃. Importantly, though, longer application of glutamate followed by its sudden removal under nondesensitizing conditions leads to slower current decays corresponding to increased sampling of S*G₂ and S*G₃. According to Equation 2, these deactivation rates are dependent on agonist binding affinity and application time because increases in either of these variables increase the probability that the binding cleft of S1S2 is closed and populating S*G₂ or S*G₃ (18). However, solution studies of S1S2 have yet to answer the more fundamental question of whether lobe opening and closure occur by way of a single domain isomerization event, according to Equation 1, or whether there are indeed additional conformational equilibria in the binding cleft distinct from lobe isomerization that have measurable free energies, as suggested by Equation 2.

In the present study, this question was addressed by performing hydrogen-deuterium (HD) exchange experiments on complexes of glutamate and kainate with S1S2J, a 30-kDa agonist-binding domain excised from a full-length GluR2 subunit (14) (Fig. 1A). To evaluate binding mechanisms, we determined free energy changes, ΔG_E = −RT ln K_E, associated with the solvent exposure of backbone NH protons (H^Ns) in S1S2J that are protected, in most cases by H-bonds, as a consequence of agonist binding and cleft closure. Assuming EX2-type Linderstrøm-Lang kinetics (22, 23), equilibrium constants, K_E, were estimated from K_E = k_HDX/k̃_HDX, where k_HDX is the measured HD exchange rate, and k̃_HDX is the exchange rate in solvent-exposed states (see “Experimental Procedures”). Importantly, K_E, in addition to providing a thermodynamic measure of structural stability, supplies mechanistic detail, because the OD⁻-catalyzed exchange reaction requires complete disruption of pre-existing H-bonds, including ones made to water molecules (24, 25). Previous studies have argued that small thermal fluctuations are not expected to lead to successful reactions but rather that separations of at least a few angstroms are required (25, 26). Based on this view, domain opening and agonist dissociation events were inferred from the detection of hydrogen exchange at key sites protected through ligand binding and lobe closure.

FIGURE 1.

Key backbone H^Ns and selected H-bonds involved in glutamate binding and lobe closure of GluR2-S1S2J; adapted from Protein Data Bank entry 1FTJ (14). A, S1S2J (ribbons) shown bound to glutamate in a closed cleft conformation. B, section of the glutamate binding site of protomer C of 1FTJ, in which the backbone of Asp⁶⁵¹–Gly⁶⁵³ adopts a conformation that makes interlobe H-bonds with H_Y450^N and H_G451^N. Additional crystal structures (27) and solution NMR data (28) suggest that this is the dominant conformation. The yellow spheres are oxygen atoms of crystallographic water molecules. C, alternate backbone conformations of Asp⁶⁵¹–Gly⁶⁵³ in 1FTJ.

The key sites considered were H_Y450^N, H_G451^N, H_T480^N, H_S654^N, and H_T655^N (Fig. 1B). H_T480^N in lobe 1 and H_S654^N and H_T655^N in lobe 2 are solvent-protected as a result of H-bonding to glutamate. In contrast, H_Y450^N and H_G451^N are protected via interlobe H-bonds with the backbone COs of Asp⁶⁵¹ and Ser⁶⁵², respectively, where the former interaction is mediated by a water molecule. However, these interlobe H-bonds are not made in all of the glutamate-bound S1S2J crystal structures because of the ability of Asp⁶⁵¹–Gly⁶⁵³ to adopt distinct backbone conformations (14) (Fig. 1C). Notably, for full agonists that have higher binding affinity than glutamate, the Asp⁶⁵¹–Gly⁶⁵³ peptide tends to favor more the conformer that enables interlobe H-bond formation (14–16), and this apparent shift in equilibrium may be related to the increase in occupation probabilities of S*G₂ and S*G₃ for such agonists over glutamate (18).

Understanding the relative conformational free energies associated with the interlobe H-bonds and the interactions between glutamate and sites on lobe 2 is central to determining the binding mechanism. Assuming that glutamate docking to lobe 1 is rapid, similar free energy changes for these equilibria would provide strong evidence for a single-step mechanism of domain opening and closure, such as that implied in Equation 1. On the other hand, distinct free energy changes for these equilibria would be more consistent with Equation 2. Below, we provide evidence for the latter view, namely, that the mechanism of cleft closure for glutamate binding comprises multiple equilibria. However, our results for kainate binding, in which the interlobe H-bonds are absent (13, 14, 28), are consistent with Equation 1 and hence with previous results reported for kainate binding to GluR4-S1S2 (20).

EXPERIMENTAL PROCEDURES

All experiments were performed on the 263-residue protein S1S2J (14) derived from the rat GluR2-flop subunit (4). S1S2J was expressed in BL-21(DE3) Escherichia coli grown in fully deuterated minimal medium, and perdeuterated samples of the native protein were prepared via refolding from inclusion bodies and extensive purification (29, 30). NMR spectroscopic measurements were made using a Varian 500 MHz spectrometer fitted with a cryoprobe. The spectra were processed using Lorentzian-to-Gaussian window functions and modeled using Gaussian line shapes for the estimation of peak volumes (V) (31). ¹H-¹⁵N peaks were identified based on assignments made previously (30, 32).

HD Exchange Measurements

The HD exchange rates, k_HDX, for ∼70 binding cleft H^Ns were determined by fitting V(t) = V₀ exp(−k_HDXt) to measured V(t) results. The measured peak intensity profiles were obtained from series of ¹H-¹⁵N heteronuclear single quantum coherence-transverse relaxation optimized (33) spectra acquired after purified samples were transferred into deuterated buffers. Uncertainties in V were estimated based on the spectral noise, and errors in the fitted parameters were calculated from Monte Carlo simulations (31). For each spectrum, 192 × 2048 total (real plus imaginary) points were recorded with 32 scans performed per increment, which corresponded to ∼2 h. HD exchange measurements were carried out with solutions of 0.3 mm S1S2J, 25 mm sodium acetate, 25 mm NaCl, 3 mm sodium azide, and either glutamate (0.45, 1, 4, or 10 mm) or kainate (4 or 10 mm).

In most experiments, single protein samples were used to collect multiple series of spectra at progressively increasing temperatures (T). This procedure helped identify conditions yielding appreciable intensity decays for accurately computing k_HDX. Furthermore, for sites experiencing modest peak intensity loss at lower temperatures, it enabled k_HDX determination for additional temperatures. Estimates for higher temperatures benefited from increased line sharpening. Specifically, the data in Figs. 2 (A–C), 2 (D and E), 3 (A–C), 3 (D–F), 3G, 3H, 5 (C and D), and 5E were taken from eight experimental runs carried out at {10, 14, 18, 21, 25 °C}_{10 mm,5.1,F}, {10, 18 °C}_{1 mm,5.1,S}, {14, 20, 25 °C}_{10 mm,6.65,F}, {14, 20, 25 °C}_{1 mm,6.4,F}, {25 °C}_{4 mm,6.68,S}, {25 °C}_{0.45 mm,6.68,S}, {10, 14 °C}_{10 mm,5.1,F}, and {25 °C}_{4 mm,6.63,S}, respectively. The subscripts specify the agonist concentration, pD (34), and whether freeze-drying (F) or solution exchange (S) was used to bring the sample into a deuterated buffer immediately prior to recording NMR spectra. Freeze-dried samples of agonist-bound S1S2J were resuspended in pure D₂O buffered by deuterated acetic acid, whereas solution exchanges were carried out to >99% via two or three 15-min dilution-concentration cycles using Millipore Amicon Ultra-4 concentrators at 2 °C.

FIGURE 2.

A–E, ¹H-¹⁵N peak intensity versus time curves from two HD exchange experiments conducted at pD 5. 1 with 0.3 mm GluR2-S1S2J and either 10 mm (A–C) or 1 mm (D and E) glutamate. In each experiment, runs at different temperatures were performed consecutively without removing the sample from the magnet (see “Experimental Procedures”). Fitted τ_HDX are shown in parentheses. The increasing peak intensity profiles presumably arise from reduced magnetic relaxation due to more rapid HD substitution at nearby sites, such as in the Arg⁴⁸⁵ side chain for H_T480^N (see Fig. 1B). F, ¹H-¹⁵N magnetization build-up curves resulting from CLEANEX-PM exchange experiments (37). Intensity ratios (V/V_ref) are plotted as a function of the mixing time τ_m. τ_HHX estimated from initial slope analysis are given in parentheses.

FIGURE 3.

¹H-¹⁵N peak intensity-time profiles from four HD exchange experiments involving 0. 3 mm GluR2-S1S2J. A–C, 10 mm glutamate, pD 6.65, and 14, 20, or 25 °C. D–F, 1 mm glutamate, pD 6.4, and 14, 20, or 25 °C. G, 4 mm glutamate, pD 6.68, and 25 °C. H, 0.45 mm glutamate, pD 6.68, and 25 °C. The dashed lines in H derive from fits that excluded the first six data points or approximately 12 h, over which time small intensity losses occurred for strongly protected sites. For sites that exchange substantially at these conditions (e.g. H_Y450^N, H_T480^N, and H_D651^N), such losses do not alter τ_HDX significantly.

FIGURE 5.

A and B, ligand-binding cleft of GluR2-S1S2J bound to either glutamate (A) or kainate (B). Glutamate induces full cleft closure with interlobe H-bonds formed by H_Y450^N and H_G451^N, and several side chain-side chain interactions (Protein Data Bank entry 1FTJ, protomer C) (14). In contrast, kainate prevents full cleft closure and formation of most of these interlobe interactions (Protein Data Bank entry 1FW0) (13, 14). C–E, ¹H-¹⁵N peak intensity-time profiles from two HD exchange experiments. C and D, 10 mm kainate, pD 5.1, and 10 or 14 °C. E, 4 mm kainate, pD 6.63, and 25 °C. The dashed lines in E derive from fits that excluded the first six data points (see caption to Fig. 3H).

Sequential Binding Reaction Mechanism with HD Exchange

Expressions were considered for relating measured k_HDX to equilibrium constants in sequential reactions. Our aim was to formulate a general scheme that reduces to Equations 1 or 2 for two or four agonist-bound states of S1S2J, respectively. However, we note that whereas Equations 1 and 2 describe forward reactions for agonist binding followed by domain closure, we considered the reverse reaction in our HD exchange analysis. This view was taken because it is conventional and convenient to consider transitions from solvent-protected to solvent-exposed states.

In particular, the general reaction

was employed, which progresses from a native complex (P₀) through a series of conformational transition states (P_i) ultimately to a state where the ligand (L) dissociates (P_M). M is equal to both the number of transition states and the number of agonist-bound states. The X_i states denote that the H^N being monitored has undergone HD exchange, which was assumed to occur irreversibly in solutions containing nearly 100% D₂O. Structurally, P₀ contains the maximum number of protective H-bonds (or other interactions), and movement in the direction of P₀ to P_M corresponds to the successive disruption of H-bonds.

HD exchange rates are typically used (26, 35) to determine equilibrium constants for simpler structural opening events as described by Equation 4 (22, 23),

whose general solution is as follows.

In this case, K₁ = k_E1/k_P1, where k_E1 and k_P1 are transition rates into solvent-exposed and protected states, respectively. k̃_HDX is the HD exchange rate in the solvent accessible state. In the EX2 limit (k_P1 ≫ k_E1, k̃_HDX) (23), Equation 5 reduces to K₁ = k_HDX/k̃_HDX. This ratio of HD exchange rates can be computed directly from experimental data and is defined here as K_E = k_HDX (T, pD)/k̃_HDX (T, pD). K_E was calculated for several H^Ns in S1S2J and related to the conformational equilibrium constants (K_i) of Equation 3.

By extension, for any M in Equation 3,

and the overall binding dissociation constant is

where [L] is the free ligand concentration. Equations 6 and 7 assume that k̃_HDX ≡ k̃_HDX,1 = k̃_HDX,2 = … = k̃_HDX,M, exchange is slow relative to the conformational transition rates, and ΔG_E ≫ RT (or K_E ≪ 1), which implies that the H^N is well protected from solvent exposure (see supplemental materials).

For the determination of K_E, k̃_HDX was estimated using the random coil approximation, i.e. k̃_HDX = k̃_D[D⁺] + k̃_OD[OD⁻] + k̃_D2O[D₂O], where k̃_D, k̃_OD, and k̃_D2O are tabulated, sequence-specific HD exchange rates for H^Ns in model peptides (36). For particular H^Ns in S1S2J, this approximation was found to be inaccurate, and corrected values were estimated as described under “Results.”

HH Exchange Measurements

Although this study focused primarily on HD exchange, we also conducted several HH exchange experiments to obtain an independent assessment of H-bond stability. For example, a CLEANEX-PM pulse sequence (37) was used to test whether ¹H-¹⁵N magnetization could be built up over millisecond time scale windows by HH transfer from water (for which coherent ¹H magnetization was maintained) to S1S2J H^N sites. Such experiments were applied to solutions of 0.3 mm S1S2J, 25 mm NaCl, 3 mm sodium azide, 10 mm sodium glutamate, and 25 mm of either sodium acetate (pH 5.1, 6.0, 6.9, 7.5, and 8.7), EPPS (pH 8.0), CHES (pH 9.5), or CAPS (pH 10.3). In general, as the buffer pH is increased typically to above 10, the EX1 limit (k̃_HHX ≫ k_P1, k_E1) (23) is approached for protected H^Ns, and Equation 5 becomes k_HHX = k_E1. However, at such pHs, S1S2J was observed to be unstable. Thus, k_HHX measurements using CLEANEX at pHs nearer to 9 were made to obtain lower bounds for structural opening rates. Although k_HHX could be measured for H_G451^N and H_G653^N using this approach, these pHs were too low to detect HH transfer for the more stable key binding site H^Ns. The particular ¹H-¹⁵N magnetization build-up curves shown in Fig. 2F were acquired from experiments involving 256 × 1024 total points and 64 scans/increment. Peak intensities, V(τ_m), were obtained for seven mixing times, τ_m, involving 30, 40, 60, 80, 100, 120, or 150 mixing cycles of ∼350 μs. These V(τ_m), along with intensities from reference heteronuclear single quantum coherence spectra, V_ref, were used to estimate k_HHX according to established procedures (37). Uncertainties in V(τ_m) and V_ref were estimated from the spectral noise and were propagated to obtain the uncertainties in V/V_ref.

RESULTS

Key Binding Site H^Ns in Glutamate-bound S1S2J Undergo HD Exchange over a Wide Range of Time Scales

HD exchange lifetimes, τ_HDX = 1/k_HDX, for S1S2J backbone H^Ns were measured over 10–25 °C, pD 5.1–6.68, and several glutamate concentrations. Under these conditions, exchange is base catalyzed (k̃_HDX = k̃_OD [OD⁻]), and in the EX2 limit where k_HDX is proportional to k̃_HDX, k_HDX changes by a factor of 10^ΔpD for a change ΔpD at a given T. At the slowest exchange conditions considered (pD 5.1, 10 °C), all of the key H^Ns involved directly in binding and lobe closure were found to be sufficiently protected for HD exchange analysis.

Figs. 2 and 3 demonstrate that these sites exchange over distinct time scales. In particular, H_G653^N and H_G451^N undergo rapid exchange with τ_HDX of 3.4 and 9.3 h, respectively, at pD 5.1 and 10 °C (Fig. 2A). As shown in Fig. 2F, exchange at these sites is fast enough to be detected from HH transfer experiments (37) performed under alkaline conditions at which ¹H-¹⁵N magnetization was built up over 50 ms via proton exchange from water. The k_HHX reported for pH 9.5 may be considered as lower bounds for the structural transition rates that expose H_G653^N and H_G451^N to solvent. In contrast, H_Y450^N and H_T480^N do not experience significant HD exchange for any T explored at pD 5.1. For these H^Ns, higher pDs of ∼6.5, where the driving force for exchange is 25 (10^1.4) times greater, were required to obtain quantifiable τ_HDX (Fig. 3). Finally, H_S654^N and H_T655^N exchange on intermediate time scales with τ_HDX comparatively long at pD 5.1 (Fig. 2, A–E) and short at pDs near 6.5 (Fig. 3, A, D, and G).

τ_HDX for H^Ns That Make H-bonds with Glutamate Depends Strongly on Ligand Concentration, whereas τ_HDX for H^Ns That Form Interlobe H-bonds Shows an Apparent Independence

When glutamate is bound to both lobes of S1S2J through H-bonding as shown in Fig. 1B, H_T480^N, H_S654^N, and H_T655^N are protected from undergoing HD exchange. Hence, the τ_HDX of these H^Ns should decrease significantly for decreasing concentrations of glutamate because, after dissociation, τ_HDX is determined largely by a competition between ligand rebinding and HD exchange. We tested for such a dependence first through HD exchange measurements at pD 6.4 and 1 mm glutamate. Compared with pD 6.65 and 10 mm glutamate, τ_HDX for sites insensitive to the ligand on-rate should increase by a factor of ∼1.8 (10^0.25), whereas τ_HDX for sensitive sites should increase less or show appreciable decreases. The results in Fig. 3 (A–F) demonstrate that such a distinction is observed for several H^Ns. Specifically, the τ_HDX of H_T480^N, H_S654^N, and H_T655^N are reduced by a factor of 2 (or 4 when the difference caused by changes in pD is corrected) at 1 mm glutamate, indicating a sensitivity to glutamate concentration. This dependence is also seen in Fig. 3 (G and H), which plot intensity decays for pD 6.68, 25 °C, and either 4 or 0.45 mm glutamate, respectively. At 0.45 mm glutamate, τ_HDX for H_T480^N is reduced by a factor of 7, and H_S654^N and H_T655^N exchange too rapidly to yield detectable peaks. Finally, Fig. 2 (A, B, D, and E) present results for pD 5.1 and either 1 or 10 mm glutamate, which show 3–7-fold smaller τ_HDX for H_S654^N and H_T655^N at 1 mm glutamate.

In striking contrast to what is observed for H_T480^N, H_S654^N, and H_T655^N, the τ_HDX of H_Y450^N and H_G451^N, as well as H_D651^N and H_G653^N located directly across the cleft, exhibit essentially no dependence on glutamate concentration (Figs. 2 and 3).

Estimated K_E Indicate That the Binding Reaction Involves Multiple Equilibria

Fig. 4A presents K_E and ΔG_E results for the key binding site H^Ns based on the τ_HDX given in Figs. 2 and 3 and k̃_HDX set to random coil values (36). Notably, particular pairs of H^Ns that occupy similar regions of the binding site have similar K_E, which suggests that their solvent exposure arises from related conformational opening events. For example, the K_E of H_G451^N (1.9 × 10⁻³) and H_G653^N (2.9 × 10⁻³) are relatively large and comparable in magnitude. Structurally, H_G653^N resides directly across the cleft from H_G451^N and shares a peptide bond with the CO of Ser⁶⁵²; this CO in turn forms an interlobe H-bond with H_G451^N (Fig. 1, B and C). The K_E results imply that this H-bond is relatively unstable and that its breakage is associated with backbone flexibility in lobe 2 near Gly⁶⁵³, a view consistent with previous interpretations (14).

FIGURE 4.

K_E and ΔG_E for key binding site H^Ns in S1S2J. The arrows point in the direction of increasing glutamate concentration. A, results for glutamate binding, where k̃_HDX was assigned to the HD exchange rates of model random coil peptides (36). B, corrected results for glutamate and kainate binding. For H_Y450^N in glutamate-bound S1S2J, k̃_HDX was determined from experiments with kainate (see text). For H_T480^N, K_E was back-predicted from K_Ds. For H_G451^N, H_G653^N, H_S654^N, and H_T655^N, k̃_HDX was based on random coil rates as in A.

In addition, at several conditions tested, H_S654^N exchanges approximately two times faster than H_T655^N (Figs. 2 and 3), and such rates lead to similar K_E because random coil predictions for H_S654^N are two times greater than those for H_T655^N (36). As these H^Ns form the only direct interactions between glutamate and the backbone of lobe 2 (Fig. 1B), the results suggest that the HD transfer events emanate from a structural equilibrium involving detachment of glutamate from lobe 2. That the K_E of H_S654^N and H_T655^N are larger than those of H_T480^N is suggestive of unique ligand docking and lobe isomerization equilibria (Fig. 4A). However, as discussed in the next subsection, the high degree of protection of H_T480^N appears to be due in part to departure of solvent-exposed states from random coil behavior.

Although the random coil approximation is commonly applied to solvent-exposed states of H^Ns in proteins, it must be used carefully because departure from random coil behavior can clearly lead to erroneous k̃_HDX and hence ΔG_E. Furthermore, it may be difficult to identify and correct for such discrepancies when ΔG_E corresponds to local backbone unfolding events. However, because the key H^Ns considered in the present study presumably become solvent-exposed upon ligand detachment or domain opening, it is possible in principle to estimate their k̃_HDX from experiments employing either the Apo protein or agonists that stabilize the H^Ns in solvent-exposed states. As discussed below, the latter approach was found to be useful for evaluating the exchange behavior of H_Y450^N.

Surprisingly, the K_E of H_Y450^N (based on random coil values for k̃_HDX) suggest a high degree of protection (Fig. 4A). The increased stability relative to H_S654^N and H_T655^N is particularly interesting given that the latter two H^Ns make H-bonds to glutamate that are buried beneath where H_Y450^N forms an interlobe H-bond (Figs. 1B and 5A). In addition, the K_E of H_Y450^N are independent of glutamate concentration, unlike those of H_S654^N and H_T655^N. There are seemingly only two explanations for these results: either (i) the lobes of Apo S1S2J adopt closed conformations that protect H_Y450^N in a way that leads to the observed glutamate concentration independence or (ii) H_Y450^N can become solvent accessible in closed cleft conformations with glutamate bound but residual structure slows k̃_HDX well below random coil estimates. Although solution x-ray scattering studies suggest that Apo S1S2J adopts a mixture of open and closed domain states (38), the rapid docking of agonist to the protein (20, 21) argues against explanation (i). Similar arguments against extended closed states in the Apo protein can be made from free energy calculations as a function of the degree of lobe closure (39, 40).

Further support for explanation (ii) was obtained from additional HD exchange experiments with kainate as the agonist. Relative to glutamate, the lobes of S1S2J are substantially more open in the presence of kainate, and formation of the interlobe H-bonds involving H_Y450^N and H_G451^N is prevented (Fig. 5, A and B) (13, 14, 28). As a first approximation, we assigned k_HDX for H_Y450^N measured with kainate to k̃_HDX for H_Y450^N in glutamate-bound S1S2J. Fig. 5 (C and D) shows that H_Y450^N exchanges with τ_HDX,kai of 33 and 17 h for pD 5.1, 10 mm kainate, and 10 or 14 °C, respectively. The τ_HDX,kai for 14 °C, in combination with the τ_HDX,glu in Fig. 3 (A and D), provides an estimate of K_E,glu ≈ τ_HDX,kai (T, pD)/τ_HDX,glu(T, pD) for H_Y450^N of 0.0033 ± 0.0004 (the estimates in Fig. 4B for 20 and 25 °C assume τ_HDX,kai increases with T by similar factors as those observed for τ_HDX,glu, namely 3.2 and 6.6, respectively; see Fig. 3). Remarkably, this K_E is comparable in magnitude with the K_E obtained for H_G451^N and H_G653^N (Fig. 4B). Thus, these results imply that, like the interlobe H-bond formed by H_G451^N, the interactions protecting H_Y450^N have similar stability.

Although the random coil approximation appears to be poor for H_Y450^N, several points suggest that it is realistic for H_G451^N, H_G653^N, H_S654^N, and H_T655^N. First, as discussed earlier in this section, the similarity in the K_E of H_G451^N and H_G653^N on the one hand and H_S654^N and H_T655^N on the other agrees with our expectation that conformational openings expose both H^Ns in these pairs approximately equally. Second, the K_E for H_S654^N and H_T655^N predict realistic dissociation constants (K_D) (see below). Finally, the values of τ_HDX for these four H^Ns measured using kainate seem to be consistent with random coil approximations, which predict τ̃_HDX of ∼1 min for pD 5.1 and 10 °C (36). For example, at these conditions (Fig. 5C), we found no detectable peak intensity for H_G451^N and H_G653^N in the first spectrum in the series. We also did not detect peaks for these H^Ns in similar experiments with shorter NMR acquisition times of 30 min. These observations suggest an upper bound for τ_HDX on the order of minutes consistent with the random coil values. H_S654^N and H_T655^N also exchange very rapidly at pD 5.1 and 10 °C despite being protected by kainate.

Based on the corrected K_E results in Fig. 4B, we next sought to determine the mechanisms of binding of glutamate and kainate to S1S2J. This was achieved by using Equations 6 and 7 to relate K_E to conformational equilibria and agonist binding constants for different numbers of agonist-bound states (M).

M = 2; Distinct Dock-isomerization Equilibria Detected for Glutamate- and Kainate-bound S1S2J

We first applied the K_E results to the dock-isomerization model given by Equation 1. In this case, M = 2 in Equation 3, and Equations 6 and 7 simplify to Equations 8 and 9.

K₁ and K₂ are the equilibrium constants for domain opening and ligand dissociation from lobe 1, respectively. In the next section, it is argued utilizing the K_E of H_Y450^N and H_G451^N that M > 2 for glutamate binding because of the presence of significant interlobe interactions. Here, these interactions are ignored, and the relative lobe closure stabilities of glutamate- and kainate-bound S1S2J are analyzed based solely on the K_E of H_T480^N, H_S654^N, and H_T655^N.

Application of K_E for H_S654^N and H_T655^N to Equation 8, which assumes exchange from both P₁ and P₂, results in K₁ = 8.1 × 10⁻⁵ ± 4.1 × 10⁻⁵ and K₂ = 4.0 ± 0.6 mm for glutamate binding. This calculation was based on five pairs of K_E in Fig. 4B corresponding to two glutamate concentrations, identical temperatures, and similar pDs. By Equation 9, K_D = 320 ± 120 nm, which is consistent with competition binding results for this protein (K_D 450 nm) (14) and for two related GluR2-S1S2 proteins that differ only in the regions where the domains are excised from the full subunit (120 and 250 nm) (41, 42).

It was also possible to estimate K_D from the K_E of H_T480^N. However, calculations assuming either exchange from both P₁ and P₂, or from P₂ only, lead to values of ∼4 nm, which are too small. Thus, as with H_Y450^N, random coil HD exchange rates (36) seemingly overestimate k̃_HDX for H_T480^N. This is not surprising though because, unlike H_S654^N and H_T655^N, H_T480^N resides more deeply in the binding cleft and in a more stable section of the protein (29, 43, 44).

Despite the apparent error in the random coil values of H_T480^N, its measured τ_HDX was used to correctly estimate the K_D for kainate (based on the K_D for glutamate determined above) via Equation 10.

In accordance with a dock-isomerization mechanism, this expression assumes that H_T480^N exchanges only from P₂ in Equation 3 with M = 2, i.e. K_E = K_D/[L] (τ̃_HDX does not appear in Equation 10 by τ̃_HDX,glu = τ̃_HDX,kai). Application of the τ_HDX in Figs. 3 (C and F–H) and 5E to Equation 10 leads to K_D,kai = 4.1 ± 2.3 μm, which agrees well with the competition binding results of 8.0, 1.3, and 2.3 μm (41, 42, 14).

This value of K_D,kai was used to estimate K_1,kai and K_2,kai for comparison with K₁ and K₂ determined for glutamate. Figs. 2A and 5C show that H_S654^N and H_T655^N exchange 60–80 times faster for kainate relative to glutamate at pD 5.1, 10 °C, and 1 mm agonist. Equation 10 assumes that exchange occurs from P₂ only and requires that τ_HDX,glu/τ_HDX,kai = K_D,kai/K_D,glu for equal concentrations of glutamate and kainate. However, for H_S654^N and H_T655^N, τ_HDX,glu/τ_HDX,kai ≫ K_D,kai/K_D,glu, suggesting that exchange occurs from P₁, i.e. from domain opening, more readily for kainate than glutamate. By applying the K_E for H_S654^N and H_T655^N to Equation 8, we estimated that K_1,kai = 0.0050 ± 0.0005 and K_2,kai = 0.8 ± 0.08 mm. Thus, relative to kainate, these results suggest that glutamate binds to the open domain state of S1S2J with roughly five times lower affinity but shifts the domain isomerization equilibrium 60-fold toward cleft closure.

M > 2; Ligand Concentration Independence of K_E for H_Y450^N and H_G451^N Suggests Lobe Locking Equilibria Distinct from Domain Isomerization in Glutamate-bound S1S2J

We showed above that the K_E for H_Y450^N and H_G451^N are relatively large and essentially independent of glutamate concentration. Clearly, it is impossible to fit these K_E to the dock-isomerization scheme (M = 2) with K₁ = 8.1 × 10⁻⁵ and K₂ = 4 mm obtained in the preceding section. This implies that the binding reaction for glutamate consists of M > 2 states and that the domain-isomerization step must be decomposed into subequilibria. Thus, we considered the next simplest model, M = 3, shown in Equations 11 and 12.

Here, K₁, K₂, and K₃ characterize lobe unlocking, domain opening, and agonist dissociation equilibria, respectively.

In accordance with our calculations for M = 2, we assumed that H_T480^N exchanges only from P₃ (K_E = K_D/[L]), H_S654^N and H_T655^N exchange from P₂ and P₃ (K_E = K₁K₂ + K_D/[L]), and H_Y450^N and H_G451^N exchange from P₁, P₂, and P₃ (Equation 11). In this way, K₁, K₂, and K₃ could be determined using the K_E given in Fig. 4B. In particular, application of H_G451^N K_E leads to 0.0019 ± 0.0002, 0.043 ± 0.004, and 4.0 ± 0.6 mm, respectively; H_Y450^N K_E yield 0.0031 ± 0.0002, 0.026 ± 0.002, and 4.0 ± 0.6 mm. These results imply that the K_E of H_Y450^N and H_G451^N are essentially ligand concentration-independent because K₁ is much greater than K₁K₂ and K₁K₂K₃/[L]. This is a direct consequence of the sequential mechanism and the distinctness of the lobe-locking and domain isomerization steps.

The K₁ correspond to ΔG of roughly 6 RT, which suggests that lobe locking is a significant step in the binding reaction for glutamate. In this analysis, we calculated K₁ separately for H_Y450^N and H_G451^N based on a parsimonious choice of M = 3. Of course, differences in the K_E for these two H^Ns could plausibly support M = 4, but we cannot discriminate such differences because of the experimental errors involved. Other stabilizing interlobe interactions, such as those operating through interactions of the side chains of Tyr⁴⁵⁰ and Leu⁶⁵⁰, Lys⁴⁴⁹ and Ser⁶⁵², and Thr⁶⁸⁶ and Glu⁴⁰² (Fig. 5A), could also conceivably constitute additional equilibria because they are present in crystal structure protomers lacking the H-bonds mediated by H_Y450^N and H_G451^N (14). Moreover, a number of mutagenic studies have shown that alteration of these side chain interactions impacts domain closure stability and receptor function (19, 20, 45–49).

DISCUSSION

The lobe dynamics occurring in S1S2 of AMPA receptors appear to be tailored for the efficacious binding and fast release of glutamate to produce large activating currents in combination with efficient channel deactivation and resensitization (14, 19, 18). Models based on channel recordings suggest a sequential multi-state binding mechanism comprising rapidly and slowly equilibrating components (18). Here, using hydrogen-deuterium exchange, we have provided evidence for such a mechanism for glutamate binding and have estimated the thermodynamic stabilities of the detected states. Furthermore, for kainate binding, which lacks the interlobe interactions constituting distinct states in the complex with glutamate, we have confirmed the two-state dock-isomerization mechanism first proposed from stopped flow experiments (20) and have shown that this reaction has a higher proclivity for sampling agonist-bound open domain conformations.

The HD exchange rates presented in this study have uncertainties typically much less than 10%. Yet the associated K_E were evaluated carefully due to the use of random coil exchange rates for estimating k̃_HDX. Although random coil rates have been validated for H^Ns in denatured proteins (36, 50, 51) and appear to be realistic measures for many solvent-exposed H^Ns in native proteins (52), examples of poor predictions have been reported (53, 54). Thus, for the key binding site H^Ns in S1S2J, we either justified the use of the random coil approximation or provided corrections through experiments. It is important to note, however, that our main conclusions can also be justified without invoking this approximation. First, the significance of the lobe-locking equilibrium in the binding reaction for glutamate is evident by the much higher degree of protection of H_Y450^N and H_G451^N in complexes with glutamate compared with kainate. Second, the uniqueness of the lobe-unlocking and domain opening equilibria is established by the insensitivity of the HD exchange rates of H_Y450^N and H_G451^N to changes in glutamate concentration. For if these equilibria were not unique, then these H^Ns would become solvent-exposed only upon domain opening and a strong glutamate concentration dependence similar to that exhibited by H_S654^N and H_T655^N would have been observed. Finally, the higher tendency for glutamate binding to induce closed cleft states in S1S2J relative to kainate is apparent in the 60–80-fold smaller exchange rates of H_S654^N and H_T655^N measured for glutamate.

We have demonstrated that the binding reaction for glutamate is composed of multiple states, but the question arises as to how this relates to the functional model in Equation 2 (18). One might speculate that, for the HD exchange model of Equation 3 with M = 3, P₃ is the state S, and P₂ is the state SG, i.e. glutamate docked to lobe 1 without H-bonding to H_S654^N and H_T655^N in lobe 2. P₁ would then correspond to the state S*G₁, for which glutamate interacts with lobe 2 in the absence of the interlobe H-bonds mediated by H_Y450^N and H_G451^N. Whether the side chain interactions shown in Fig. 5A are made in this state or in S*G₂ or S*G₃ is unclear (all of the crystal structure protomers of glutamate-bound S1S2J contain these side chain interactions, whereas only some of the protomers show the interlobe main chain H-bonds) (14, 27). Finally, P₀ would be associated with S*G₂ and/or S*G₃ in some way and include the H-bonds formed by H_Y450^N and H_G451^N. In the present study, we could only detect the breakage of H-bonds made to backbone H^Ns, but clearly the side chain interactions are an essential component of the binding mechanism and may be energetically and kinetically separable from the main chain interactions.

In the whole cell experiments for measuring deactivation upon which Equation 2 is partially based, glutamate was applied to GluR2 restrained in the nondesensitizing state by cyclothiazide (18). Seemingly, for this reason S*G₁ was primarily populated with lower percentages observed for S*G₂ and S*G₃. In contrast, our HD exchange measurements were performed on S1S2J, which lacks structural restraints present in the nondesensitizing state. Because the ΔG_E of H_Y450^N and H_G451^N are significant, free S1S2J appears to favor transitions to states with stronger interactions across the cleft, which may be active in the desensitized state. This is consistent with the finding that the EC₅₀ for glutamate activation of GluR2 (in cyclothiazide) is 300 μm (18) but that the binding affinity for the desensitized state is much higher (1 μm) (55). Likewise, glutamate binds to GluR2 S1S2J with a K_D of roughly 300 nm (41, 42, 14), suggesting that this complex represents the desensitized state, as proposed previously (14).

Thus, the process of successive H-bond disruption measured via HD exchange may account for structural changes in S1S2 that occur during recovery from desensitization. On the other hand, the responses of nondesensitizing (or resting) GluR2 to brief glutamate applications would seemingly be dominated by agonist docking and domain isomerization events (consistent with occupation of S*G₁) (18) with less lobe locking than that observed in S1S2J. This would account for the ability of AMPA receptors to activate and deactivate rapidly. The lobe-locking equilibria presumably become more functionally active during extended glutamate applications (consistent with increased occupation of S*G₂ and S*G₃) (18) and aid in the stabilization of glutamate binding in desensitized states geared to abolish macroscopic currents.

Because full and partial agonists sample similar unitary conductance levels in single channels (17) and the extent of channel activation can be correlated with the degree of cleft closure in S1S2J (17, 28, 56), a more significantly closed cleft apparently acts to increase the probability that a channel gate opens rather than promote a gradually more open gate. Such a mechanism would also seemingly depend on the probability that the cleft is closed when agonist is bound, and this is consistent with recent studies showing that domain closure stability also influences activation (18, 19, 48). However, this form of structural stability is difficult to characterize energetically from crystal structures and ps–μs dynamics because domain opening in S1S2J occurs on slower time scales. Thus, the methods established in the present study, which probe ms and longer time scale motions and yield equilibrium constants for lobe opening in agonist-bound S1S2J, should be useful for such characterizations.

As a case in point, kainate binding to nondesensitizing GluR2 generates currents that are 50 times smaller than those evoked by glutamate (45), and this has been attributed to the smaller degree of cleft closure in S1S2 induced by kainate (13, 14). However, a broader view that includes domain closure stability measures is obtained from the K₁ of our two-state binding model (Equation 3; M = 2), which indicates that S1S2J adopts agonist-bound, open cleft states (identified by the HD exchange of H_S654^N and H_T655^N) much more often for kainate than glutamate. Although it is difficult to assess the relative importance of cleft closure extent and stability on channel activation for kainate, these results support a dynamic view of agonism consistent with an activation mechanism that depends not only on the extent of cleft closure but also on the probability that the cleft is closed when agonist is bound.