Encoding of tangential torque in responses of tactile afferent fibres innervating the fingerpad of the monkey

Abstract

Torsional loads are ubiquitous during everyday dextrous manipulations. We examined how information about torque is provided to the sensorimotor control system by populations of tactile afferents. Torsional loads of different magnitudes were applied in clockwise and anticlockwise directions to a standard central site on the fingertip. Three different background levels of contact (grip) force were used. The median nerve was exposed in anaesthetized monkeys and single unit responses recorded from 66 slowly adapting type-I (SA-I) and 31 fast adapting type-I (FA-I) afferents innervating the distal segments of the fingertips. Most afferents were excited by torque but some were suppressed. Responses of the majority of both afferent types were scaled by torque magnitude applied in one or other direction, with the majority of FA-I afferent responses and about half of SA-I afferent responses scaled in both directions. Torque direction affected responses in both afferent types, but more so for the SA-I afferents. Latencies of the first spike in FA-I afferent responses depended on the parameters of the torque. We used a Parzen window classifier to assess the capacity of the SA-I and FA-I afferent populations to discriminate, concurrently and in real-time, the three stimulus parameters, namely background normal force, torque magnitude and direction. Despite the potentially confounding interactions between stimulus parameters, both the SA-I and the FA-I populations could extract torque magnitude accurately. The FA-I afferents signalled torque magnitude earlier than did the SA-I afferents, but torque direction was extracted more rapidly and more accurately by the SA-I afferent population.

Introduction

Torques, tangential to the fingertips, are common in the majority of natural manipulations. Most dexterous tasks, such as writing with a pen or using a knife, are impossible without controlling for the effects of tangential torques. When grasping a book by its spine and rotating it to a vertical orientation, to place the book on a shelf, torsional load is substantial and increases as the book is rotated. Even simple grasp and lift manoeuvres, such as lifting a coffee cup, result in torques on the digits because the grip axis rarely passes through the centre of mass of the object. Control mechanisms for torsional loads have been investigated in human experiments employing two-digit opposition grip (Goodwin et al. 1998; Wing & Lederman, 1998; Johansson et al. 1999) and in tasks where objects are held in a multi-digit grasp (Burstedt et al. 1999; Flanagan et al. 1999; Latash et al. 2004; Shim et al. 2005, 2006; Aoki et al. 2006).

When objects are handled, tangential forces and torques on the digits will result in slip unless the grip force has an appropriate magnitude (Johansson & Westling, 1984; Kinoshita et al. 1997). Kinoshita et al. (1997) showed that when an object exerts simultaneous tangential torque and force on a fingertip, the minimum grip force required to maintain a stable grasp increases approximately linearly with both torque and tangential force. Most aspects of object manipulation, including the coordination of loads and grip forces, rely on predictive strategies based on internal representations (Wolpert & Miall, 1996). However, it has also been shown that optimal utilization of internal models requires either continuous tonic input from cutaneous receptors or some intermittent reiteration (Monzée et al. 2003; Duque et al. 2005). Comparison of predicted sensory events with actual sensory events is vital for updating these representations and, if errors occur, for modifying subsequent movements (Flanagan et al. 2006). Cutaneous mechanoreceptors play a critical role in providing this sensory information which is relayed from the periphery to the central nervous system (Nowak et al. 2003).

In experiments designed to investigate how humans deal with torque during manipulations (Goodwin et al. 1998) subjects grasped and tilted an instrumented test object. Throughout the task, the motor control system automatically coordinated and adjusted the grip forces according to the changes in torque. The required grip force depended on parameters such as the shape and frictional properties at the grasp sites.

Despite the ubiquitous nature of torque in everyday manipulations, virtually nothing is known about how, and with what accuracy, torques tangential to the grasp surfaces are encoded by tactile mechanoreceptors. Engineering studies of elastic robot ‘fingers’ subjected to torsional loads provide some clues about possible mechanical events at the fingertips (Howe et al. 1988; Zee et al. 1997), but there are no studies showing how mechanoreceptive afferents respond.

In the present study we quantified low-threshold cutaneous mechanoreceptive afferent responses to torques equivalent to those occurring during everyday manipulations. Torques of different magnitudes and direction were applied to a central site on the monkey fingertip on a background of different levels of grip (normal) force. We recorded from afferents innervating glabrous skin covering the entire distal segment of the finger in order to obtain a representative picture of the whole population response (Johnson, 1974; Khalsa et al. 1998; Birznieks et al. 2001).

Population responses were modelled from single afferent responses to assess the ability of the populations to discriminate, concurrently, the three stimulus parameters, namely torque magnitude, torque direction and background normal force. A Parzen window classifier model was used enabling us to quantify discrimination as a function of time during the task, which is equivalent to real-time discrimination during a manipulation.

Methods

Neural recordings

Experiments were performed on three anaesthetized Macaca nemestrina monkeys weighing from 4.5 to 7.6 kg. All procedures were approved by the University of Melbourne Ethics Committee and conformed to the National Health and Medical Research Council of Australia's Code of Practice for non-human primate research. Our experiments comply with the policies and regulations of The Journal of Physiology (Drummond, 2009).

At the beginning of each of the 11 experimental sessions, a dose of ketamine hydrochloride (15 mg kg⁻¹, i.m.) plus atropine sulphate (60 mg kg⁻¹, i.m.) was given, followed by anaesthetisation of the upper airway with lignocaine hydrochloride spray (4%). An endotracheal tube and intraperitoneal catheter were inserted. Surgical anaesthesia was induced by administration of sodium pentabarbitone (15–20 mg kg⁻¹, i.v.) and was maintained throughout the experiment by sodium pentabarbitone diluted in saline (15 mg ml⁻¹, i.p.) administered hourly through the catheter (dose as required). The catheter was also used for fluid replacement. Body temperature was monitored by a rectal thermometer and was maintained at 37°C by a heating blanket and insulating blankets. Respiration rate, end-tidal carbon dioxide level, blood pressure, heart rate and oxygen saturation levels were monitored throughout the experiment. Depth of anaesthesia was assessed by reflexes, blood pressure, heart rate and respiration rate. Antibiotic cover was provided by amoxycillin (18 mg kg⁻¹, i.m.) every 6 h. Standard procedures were used to isolate and record from single cutaneous mechanoreceptive afferents in the median nerve (Goodwin et al. 1995). A maximum of four experiments (upper and lower, left and right arms) were performed in each monkey with a separation of at least 2 weeks between experiments. At the end of each experiment, the incision was sutured in layers and a single dose of procaine penicillin (60 mg kg⁻¹, i.m.) was given. Animals were returned to a heated padded cage to recover and were monitored several times a day until the conclusion of experiments. The monkeys used were captive bred obtained from the National Health and Medical Research primate colony. Following the final experiment on each monkey, it was returned to the colony for breeding.

Single fibres were classified as slowly adapting type I (SA-I), fast-adapting type I (FA-I), or fast-adapting type II (FA-II) afferents by the established criteria of responses to static stimuli, responses to rapidly changing stimuli, and receptive field size (Vallbo & Johansson, 1984). In order to obtain a representative picture of the entire afferent population response, all responding SA-I and FA-I afferents innervating the glabrous skin of the distal phalanx of digits 2, 3 and 4 were included in our study. We did not focus on FA-II (Pacinian) afferents, because our stimuli did not excite them reliably. Receptive field locations were estimated using calibrated von Frey hairs. The digits were splayed and the dorsal aspect of the hand was embedded in plasticine up to the mid-level of the middle phalanges of the digits. To stabilize the distal phalanges, the fingernails were glued to small metal plates, each of which was firmly fixed to a post embedded in the plasticine. The glabrous skin of the distal phalanges of digits 2, 3 and 4 did not contact the plasticine, thereby allowing the fingertip to deform as it might if it was actively pressed against a surface (see Methods in Birznieks et al. 2001).

Sample of afferents

We recorded from 97 low-threshold mechanoreceptive afferents with receptive field centres (RFCs) located on the glabrous skin of the terminal phalanx of digits 2, 3 and 4. Sixty-six afferents were classified as SA-I and 31 as FA-I. For three afferents (two SA-I and one FA-I) the effects of torque were tested only at one normal force, 2.5 N, and they were excluded from analyses assessing normal force effects.

Stimulation procedure

Stimulator

A custom-built stimulator, computer controlled using Labview 5 software (National Instruments, Austin, TX, USA), allowed concurrent application of normal forces and torques to the fingerpad. Two torque motors drove the stimulator. One motor generated the torque. This motor was mounted on a balanced beam, which was attached to a second motor. The second motor generated a normal force on the finger and was coupled to an adjustable damper mechanism. A six-axis force–torque transducer (Nano FT; ATI Industrial Automation, Apex, NC, USA) measured the three-dimensional forces and torques applied to the fingerpad with a resolution of 0.0125 N and 0.0625 mN m, respectively. The stimulus was a flat circular surface (diameter 24 mm) covered with fine grain sandpaper (500 grade); the sandpaper was renewed for each afferent recorded from.

Application of torsional loads

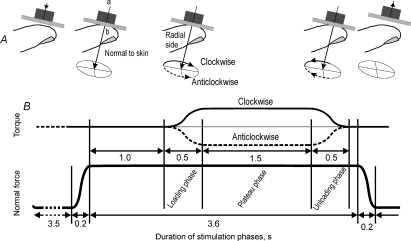
The stimulus was applied to a standard test site on the relevant fingertip referred to for convenience as the initial contact point (Fig. 1A). For each finger the initial contact point was located at the centre of the flat portion of the volar surface of the fingertip. The stimulator was positioned so that the rotational axis of torque was aligned with that predefined location and was at right angles to the skin surface.

Figure 1. Temporal sequence of forces and torques.

A, position of the stimulus surface. The surface was oriented parallel to the flat portion of skin on the fingertip and was positioned just above the skin surface. The rotational axis of the torque load (a) was aligned with the centre point of the flat portion of the fingertip's volar surface termed the initial contact point (b). At the beginning of each trial the stimulus was advanced, normal to the skin, compressing the fingertip until the target normal force level was reached. Torques of different magnitudes were then applied. B, force and torque profiles showing the various phases; torques were applied in clockwise (continuous line) and anticlockwise (dashed line) directions.

Torques of different magnitude were applied in clockwise and anticlockwise directions with a range of contact forces normal to the contact area; the normal forces corresponded to the grip forces generated during object manipulation (Johansson & Westling, 1988; Goodwin et al. 1998). Before the commencement of an experimental protocol, the surface was lowered to just above the skin, and the damper setting was adjusted such that contact with the skin was smooth (at a velocity of about 20 mm s⁻¹) and critically damped. Our aim was to use force and torque parameters that were comparable to those used in human manipulations, scaled appropriately to account for the differences in mechanical properties of human and monkey fingers. Each protocol included three contact forces, 1.8, 2.2 and 2.5 N, in combination with three torques. Torque magnitudes of 2 and 3.5 mN m were applied at all three normal forces. An additional, greater, torque load was applied at each normal force, with a magnitude of 4, 4.5 or 5.5 mN m at a normal force of 1.8, 2.2 and 2.5 N, respectively. Torques were delivered in both the clockwise and anticlockwise directions.

Each trial consisted of a phase of increasing normal force lasting 0.2 s, a constant normal force phase lasting 3.6 s, and a phase of normal force retraction lasting 0.2 s (Fig. 1B). Torques were superimposed on the constant normal force and commenced 1 s after commencement of the normal force plateau. The torque loading phase was 0.5 s in duration, followed by a phase of constant torque lasting 1.5 s, and then a torque unloading phase lasting 0.5 s. Normal force unloading commenced 0.1 s after the end of the torque unloading phase. For each afferent the entire experimental protocol was comprised of 12 runs. Each run commenced with two normal force-only trials at 1.8 N followed by trials with torques in ascending order of magnitude superimposed on the 1.8 N force. The ascending order of magnitude minimized interaction from preceding stimuli. Then an equivalent sequence of stimuli was applied at the 2.2 N normal force level and finally at the 2.5 N level. Thus, during each run, lasting about 3 min, all combinations of normal force and torque were tested in one torque direction (clockwise or anticlockwise). The same sequence of forces and torques was repeated 5 times (n= 6). The stimulator was then reconfigured to apply torques in the opposite direction and the next six identical runs were completed with torque applied in that direction. Force and torque traces were examined off-line to verify that there were no overt slips between the stimulus and the finger and also to confirm that there were no irregularities in force and torque delivery.

Standardised finger

To combine data from different digits and different animals, receptive field centres and torque directions were referenced to a standardised fingertip. The standardised finger was on the right hand. For afferents innervating the left hand, an anatomical match was obtained by mirror imaging the location of the receptive field centre and the torque direction before plotting on the standardised fingertip. Thus, clockwise was defined as rotation of the stimulus along a path from ulnar to distal to radial aspects of the fingertip regardless of which hand torque was applied to.

Statistical analysis of single afferent data

Recorded neural activity, forces and torques were analysed and displayed graphically using custom-written programs in Igor Pro 5 (Wavemetrics, Portland, OR, USA) and MATLAB (The Mathworks, Natick, MA, USA). For each stimulus, we calculated four response measures to torque. Three measures were calculated as the number of nerve impulses evoked (1) during the torque loading phase, (2) during the plateau phase, and (3) during the unloading phase (Fig. 1B). A fourth measure was calculated as the latency of occurrence of the first spike after commencement of the torque loading phase.

Non-parametric statistics were used because the data may not have been normally distributed and some datasets had relatively small sample sizes (Siegel & Castellan, 1988). Correlations between torque magnitude and afferent response measures were calculated by the Spearman's rank correlation coefficient (rs); responses to the normal force-only condition (zero torque) were not included in these correlation analyses. Afferents that did not show graded responses to torque magnitude within the tested torque range were further subjected to a Mann–Whitney U test for two independent samples in order to determine whether their responses were influenced by the presence of superimposed torque per se, regardless of magnitude, compared to the normal force-only condition. Afferents showing a significant effect of torque magnitude, as assessed by Spearman's rank correlation, are referred to as torque-scaled afferents, while the subset of remaining afferents responding to torque as determined by the Mann–Whitney test is referred to as afferents with non-graded responses to torque.

In order to compare torque effects between afferents and between different stimulus conditions, we calculated a torque sensitivity index I_T using responses to the two torque magnitudes (2 and 3.5 mN m) tested at all three normal forces. This torque sensitivity index was calculated as the difference in spike count divided by the sum of the counts at those two torques: I_T= (R_3.5−R₂)/(R_3.5+R₂) where R_Z is the response at torque magnitude Z. For the first spike latency I_T was calculated as the difference between response latencies at torques of 3.5 and 2 mN m.

To assess differences between afferents assigned to different groups, Kruskal–Wallis one-way analysis of variance by ranks (for 3 and more groups) was used as indicated in Results. Bonferroni correction was applied for multiple comparisons.

In all tests, the level of probability selected as significant was P < 0.05.

Discrimination by populations of afferents

The capacity of the SA-I and FA-I populations to extract information about the three stimulus parameters during a manipulation were determined using a Parzen window classifier model (Duda et al. 2000).

A Parzen window classifier is a pattern-matching tool which attempts to match an unknown test pattern to one of a discrete number of known pattern types, or classes. A template for each of the known classes is constructed using a series of labelled example training patterns. The expected noise, or variation, in each class pattern is also characterised using these same training samples. Given a test pattern, its similarity (probabilistically quantified) to each of the candidate classes is evaluated, and the test pattern is assigned to the most similar class.

The notion of a ‘pattern’, in the majority of applications, may be simplified by considering that all patterns can be transformed into a single vector of features. The application described here considers a feature vector to consist of a list of afferent spike counts, as described in the following sections.

Feature vector ensemble

The model was based on data from afferents for which all combinations of stimuli were used. For each afferent there were 18 stimulus combinations comprising: three normal forces (1.8, 2.2 and 2.5 N), three torque magnitudes (0, 2 and 3.5 mN m) and two directions (clockwise and anticlockwise). Each combination was applied 6 times leading to 108 stimulus events. Torques above 3.5 mN m were not used in the model because they were not tested at each normal force magnitude.

For any stimulus event, i⊂{1, …, 108}, the responses from each of the k afferents in a population are considered as a simultaneously acquired ensemble, and hence constitute a k element feature vector, x_i=[x_i1, x_i2, …, x_ik]. Combining the feature vectors for the 58 SA-I afferents generated a 108 × 58 feature matrix and similarly a 108 × 23 feature matrix for the 23 FA-I afferents.

Classifier model

A Parzen window classifier model was employed to assign the multi-dimensional feature vector, x_i, to a particular class, ω (Duda et al. 2000; see also Löw et al. 2003; Gepshtein et al. 2005); for example, there are three classes for normal force, 1.8, 2.2 and 2.5 N. The classifier was trained using 107 vectors and the remaining vector was used to test discrimination. Since each vector represents a point in the feature space, training was achieved by approximating the density of points in this space associated with each class. Discrimination was performed by assigning the test vector to the class with the greatest density at the location represented by that test vector in the feature space. The density was estimated using a non-parametric Parzen window technique, with a radial basis function window. The density for class ω at point x is given by:

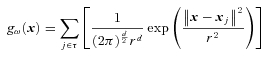(1)

The variable r serves to adjust the smoothness of the non-parametric density estimation by changing the width of the radial basis function. A value r= 1 was used, after each afferent response had been standardised across the 107 training values, by removing the mean and dividing by the standard deviation. d is the dimension of the feature space. τ={1, …, 108} is the set of instances in the training set, which excludes the test vector, x_i.

A discrimination task outcome result ω_x is found as:

that is, the classification algorithm decision process selects that stimulus class ω, which maximises eqn (1). A leave-one-out cross-fold validation procedure was used to obtain an unbiased estimate of classification performance (Duda et al. 2000), as described above, using 107 vectors for training, and introducing the remaining vector at a later stage for test classification.

To evaluate the temporal course of the discrimination accuracy during manipulation, the classification procedure was performed with the analysis windows expanding in 10 ms steps starting at the beginning of the torque loading phase. The response of each afferent was measured by the total number of spikes evoked during the chosen analysis window.

Results

First, we examine the effect of torque at a background normal force level of 2.5 N, analysing how the magnitude and direction of torque influenced afferent responses during the different phases of stimulation. Second, we address the question of how the level of background normal force influenced the torque sensitivity of afferents. Finally, at a background normal force of 2.5 N, we investigate whether the first spike latencies depends on torque and thus whether codes such as recruitment order might be the fastest source of tactile information available to signal the parameters of torque at the fingertips (Johansson & Birznieks, 2004).

Effect of torque on discharge rate of SA-I afferents

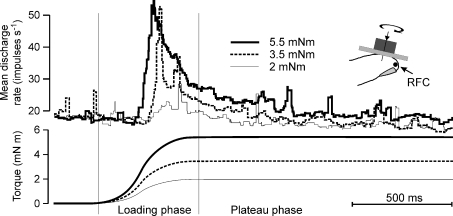
To avoid rotational slips, torques must be applied on an adequate level of background normal force. Therefore, each torque stimulus was preceded by a normal force ramp-step designed to reach the desired level of background normal force. Typically, SA-I afferents were excited by the normal force showing an initial brisk increase in discharge rate, which declined during the plateau phase to a steady level before the onset of the torque loading phase. The most frequently observed response during the torque loading phase was excitatory, but suppression of responses was also observed. Responses of a single SA-I afferent to the three magnitudes of torque applied in a clockwise direction are illustrated in Fig. 2. Note the pronounced scaling of this afferent's discharge rate during the loading phase as torque magnitude increased. SA-I responses to torque had a dynamic response component characterized by a sudden increase in discharge frequency, which declined to a steady level during the torque plateau phase. The overall effect of torque magnitude was similar during the loading and plateau phases (see also Fig. 3A and B). Inspection of single trials in SA-I afferents indicated that the early part of the plateau phase contributed most to the response differences (Fig. 2). Afferents tended to adapt during the course of the plateau phase (which lasted 1.5 s) to a point where the differences became smaller.

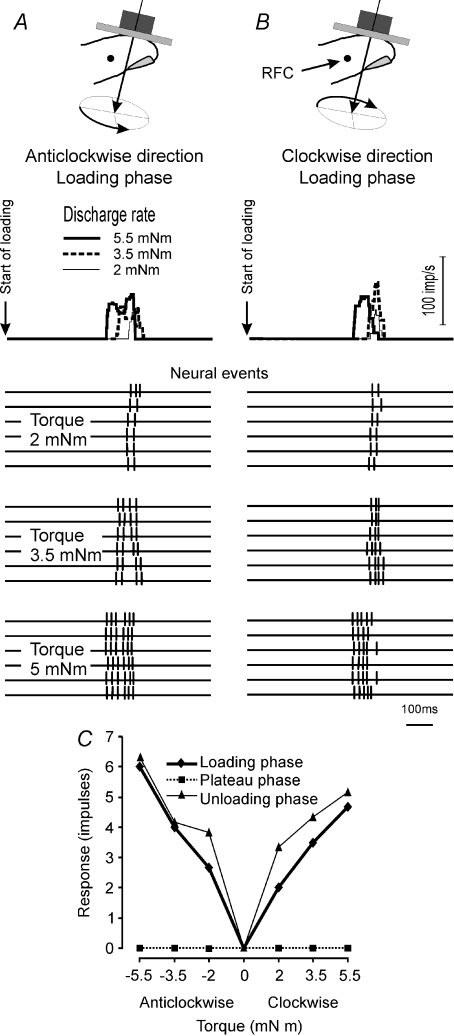
Figure 2. Responses of a single SA-I afferent to torque applied in a clockwise direction.

Top panel shows the instantaneous discharge rate (averaged over 6 trials) when torques of three different magnitudes (2, 3.5 and 5.5 mNm) were superimposed on the steady level of background normal force (2.5 N). Location of the afferent's receptive field centre (RFC) is shown in the inset at top right. Thin vertical lines indicate separate phases of stimulation.

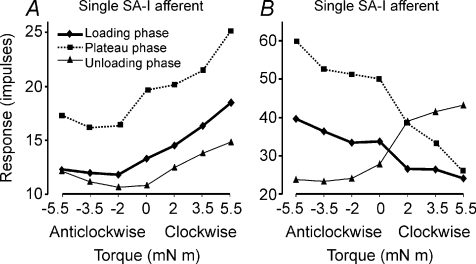
Figure 3. Responses of two single SA-I afferents to torques during the three phases of stimulation.

A, typical response pattern of SA-I afferents. This afferent showed a scaling effect for torque magnitude in the clockwise direction but showed little effect in the anticlockwise direction, thus exemplifying the rotational direction selectivity of SA-I afferents. The pattern was similar during all three phases of stimulation. B, response pattern of a SA-I afferent showing positive or negative response scaling depending on the direction and phase of the torque. During the loading and plateau phases, the afferent's response was positively scaled by torque in the anticlockwise direction and negatively scaled (suppressed) in the clockwise direction. The reverse effect was observed during the unloading phase; the afferent was excited in the clockwise direction and suppressed in the anticlockwise direction. Afferent responses were measured as spike counts during the respective phases of stimulation and were averaged over six trials.

Comparison of the loading and unloading phases revealed two distinct patterns. For those afferents that were excited by torque during the loading phase, the unloading phase merely represented a return towards the background discharge levels (Fig. 3A). In contrast, afferents suppressed by torque during the loading phase showed an excitatory dynamic response during the unloading phase (Fig. 3B). The magnitude of the excitatory unloading response was proportional to the amount of suppression during the loading phase, thus showing scaling with an inverse sign. Statistical analysis showed that for the afferent in Fig. 3A, responses were scaled significantly with changes in torque magnitude applied in the clockwise direction while changes in torque magnitude in the anticlockwise direction had no statistically significant effect. For the afferent in Fig. 3B, response scaling was significant for both the clockwise and anticlockwise directions.

Loading phase

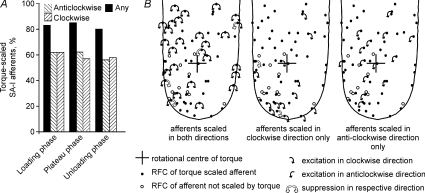
As seen in Fig. 2, the effect of torque was most dramatic during the loading phase. Using the number of spikes during the loading phase as the response measure, the majority of SA-I afferent responses were scaled by the torque magnitude. In total 62% (41/66) of SA-I afferents were scaled in the clockwise direction (Fig. 4A). The same proportion of afferents (62%; 41/66), but not necessarily the same afferents, were scaled in the anticlockwise direction. All together 83% (55/66) of SA-I afferents were scaled by torque magnitude in at least one direction, i.e. either in the clockwise, anticlockwise or both directions. Twenty-seven afferents were scaled by torque in both directions while 28 afferents were scaled by torque in one of two directions.

Figure 4. Effect of torque on the population of SA-I afferents.

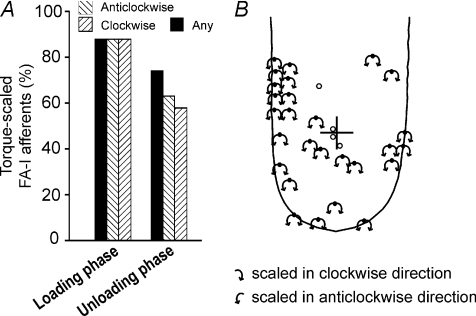
A, the proportion of SA-I afferents scaled by torque magnitude during the three phases of stimulation. Two patterns of hatched bars correspond to afferents scaled by torque in the clockwise or anticlockwise directions, respectively. Black bars represent afferents that were scaled by torque in any direction, i.e. either clockwise, anticlockwise or both directions. B, torque effect in SA-I afferents during the loading phase shown in relation to the location of their receptive field centres. The three standardised fingers depict afferents scaled by torque in both directions, afferents scaled only in the clockwise and only in the anticlockwise directions, respectively. RFCs of afferents not scaled by torque are represented by open circles. Black arrows originating from the receptive field centres indicate the torque direction in which excitatory scaling of the afferent's response was significant as assessed by Spearman's rank correlation. White arrows indicate a significant suppressive effect (negative scaling) of torque on the afferent's response. The rotational centre of the applied torque (initial contact point) is indicated by the cross. Torque was applied on a 2.5 N background normal force.

Afferents with receptive fields all over the distal phalanx had responses that were scaled by torque magnitude (Fig. 4B). Directional preferences were not related to the ulnar or radial location of their receptive field centres, measured relative to a longitudinal line drawn through the centre of the finger. For afferents with RFCs located on the radial side, an equal number were scaled in the clockwise and anticlockwise directions (23 vs. 23) as was the case for afferents with RFCs located on the ulnar aspect of the finger (18 vs. 18).

In six afferents, the background response was suppressed by torque in one of the directions (Fig. 4B). Five of those afferents were excited by torque in the opposite direction, thus showing an overall trend similar to the single afferent depicted in Fig. 3B.

Some afferents responded to torque, but failed to show any reliable scaling by torque magnitude within the range tested in the current study. The responses of those afferents were further analysed for a non-graded torque effect, in which responses to the normal force-only trials were different from responses to the trials where torque was applied, regardless of its magnitude. As assessed by the Mann–Whitney test, 16 afferents scaled by torque in only one direction showed non-graded responses to torque in the opposite direction. In eight afferents for which scaling by torque could not be demonstrated in any direction, a non-graded response to torque could still be detected in either one or both directions.

To assess the effect of torque quantitatively, we calculated the torque sensitivity index I_T (see Methods). During the loading phase I_T, averaged over the torque-scaled SA-I afferents, was 0.16 (s.d.= 0.24) in the clockwise direction and 0.23 (s.d.= 0.31) in the anticlockwise direction. The relationship between I_T and the position of the afferent's RFC was assessed firstly within the contact area, corresponding to a radius of 5 mm from the torque rotational centre, and secondly across the whole finger. Within the contact area, I_T did not depend on the distance of the RFC from the torque rotational centre, either in the clockwise or the anticlockwise direction (P > 0.05; Spearman's rank correlation). The only obvious spatial relationship we could discern was that I_T tended to be larger for afferents with RFCs located outside the contact area in comparison to afferents with receptive field centres in contact with stimulus, but this effect was significant only for the anticlockwise direction (P < 0.05; Mann–Whitney test).

Plateau and unloading phases

We investigated whether the torque effect measured during the loading phase extended to the other phases of stimulation as well. In terms of the number of SA-I afferents with responses scaled by torque there was little difference between phases (Fig. 4A). In total 83% (55/66) of afferents were scaled during the loading phase, 85% (56/66) during the plateau phase, and 80% (53/66) during the unloading phase in at least one torque direction.

The average torque sensitivity index, both directions pooled, was compared for a matched sample of SA-I afferents scaled by torque during all three phases. The index was similar during the loading (I_T= 0.18) and plateau (I_T= 0.18) phases and lower (I_T= 0.15) during the unloading phase (n= 43; both directions pooled).

Direct assessment of spatial relationships

In a few experiments we shifted the rotational centre of torque (initial contact point) relative to the afferent's RFC in order to analyse, more systematically, the effect of this distance on torque sensitivity. The aim of this approach was to separate the distance effect from the effect of the location of the afferent's RFC on the finger. Tests were performed in three suitable SA-I afferents located close to the centre of the fingerpad. Afferent no. 8 was tested with the initial contact point at distances of 0, 1.5 and 5.5 mm from the RFC; the RFC remained within the contact area at all three distances. In the clockwise direction, the torque sensitivity index (I_T) was similar at distances of 0 and 1.5 mm while at 5.5 mm the afferent became insensitive to torque. In the anticlockwise direction the largest torque effect occurred when the rotational axis passed through the RFC. Sensitivity decreased at 1.5 mm and remained at the same low level at 5.5 mm. Afferent no. 9 was tested at distances of 1 and 3 mm. In the clockwise direction torque had no effect on discharge rate regardless of distance. In the anticlockwise direction the torque effect was significant only at a distance of 3 mm. Afferent no. 10 was tested at distances of 4 and 7 mm. At 4 mm the afferent's RFC remained within the contact area, but at 7 mm the RFC was outside the contact area. In the clockwise direction the afferent was insensitive to torque at both locations while in the anticlockwise direction I_T at 7 mm was double the value at 4 mm.

Thus, we conclude that observations using the receptive field anchored approach are consistent with the results from the constant initial contact point approach. The effects of distance between the RFC and the rotational axis of torque are not uniform and exhibit complex relationships that are different for different afferents. Thus, it is not possible to characterize the population response via a spatial response profile analysis as has been used for other stimuli (Goodwin et al. 1995; Dodson et al. 1998; Khalsa et al. 1998). In addition, the RFC anchored approach does not take into account the differences in mechanical properties of the finger at different locations, which are considerable at the forces and torques used in common manipulations. Therefore, further analysis using the RFC anchored approach was not pursued.

Effect of torque on discharge rate of FA-I afferents

FA-I afferent responses to normal force or torque occurred only during the dynamic phases of stimulation. Responses of a single FA-I afferent to torque, in both directions, are illustrated in Fig. 5A and B and summarized quantitatively during the three phases of stimulation in panel C. When torque was applied, responses of this representative afferent were scaled by the torque magnitude during both the loading and unloading phases, with a similar number of spikes evoked during both phases. This afferent responded to torque regardless of its direction (Fig. 5C). However, for FA-I afferents the total number of nerve impulses evoked by the stimuli was typically considerably lower than for SA-I afferents under the same conditions (cf. Fig. 5C with Fig. 3). Close inspection of the nerve impulse trains and instantaneous discharge rate histograms during the loading phase indicated that distinct differences in the spike train patterns could be discerned (Fig. 5A and B).

Figure 5. A typical single FA-I afferent showing scaled responses to torque magnitude.

Three torque magnitudes (2, 3.5 and 5.5 mNm) were applied on a background normal force of 2.5 N. Responses during the loading phase in the anticlockwise (A) and clockwise (B) directions are shown by mean (n= 6 trials) instantaneous discharge rate histograms with the single trial impulse ensembles below. C, mean spike count (n= 6) during different phases of stimulation in both directions. This afferent showed little difference between the loading and unloading phases. The location of the receptive field centre is shown on the fingertip outline.

During the loading phase, the majority (87%; 27/31) of FA-I afferents were scaled by torque regardless of direction (Fig. 6A). None of the FA-I afferents showed non-graded responses to torque magnitude during the loading phase. In fact all four FA-I afferents that were not scaled by torque were unresponsive to the 2 and 3.5 mN m torque magnitudes and only two of them responded, only occasionally, at the highest torque level (5.5 mN m). The receptive field centres of three of the four FA-I afferents that were not scaled by torque were in close proximity to the rotational centre of torque loading (Fig. 6B). The average torque sensitivity index (I_T) during the loading phase was 0.52 (s.d.= 0.34) for the clockwise direction and 0.46 (s.d.= 0.35) for the anticlockwise direction. For afferents with RFCs within the contact area, there was no correlation between I_T and the distance of the initial contact point from the RFC (P > 0.05; Spearman's rank correlation). Also, there was no difference in I_T between afferents with RFCs within and outside the contact area (P > 0.05; Mann–Whitney test).

Figure 6. Effect of torque on the population of FA-I afferents.

A, the proportion of FA-I afferents scaled by torque magnitude during the loading and unloading phases. Two patterns of hatched bars correspond to afferents scaled by torque in the clockwise or anticlockwise directions respectively. Black bars represent afferents that were scaled by torque in any direction, i.e. either clockwise, anticlockwise or both directions. B, torque effect during the loading phase shown in relation to the location of the afferents’ receptive field centres. Black arrows originating from the RFC indicate the torque direction in which excitatory scaling of afferent responses was significant as assessed by Spearman's rank correlation. The rotational centre of the applied torque (initial contact point) is indicated by the cross. RFCs of afferents not scaled by torque are represented by open circles. Torque was applied on a 2.5 N background normal force.

Fewer afferents were scaled by torque during the unloading phase than during the loading phase. In total 74% (23/31) of afferents were scaled by torque in either the clockwise, anticlockwise or both directions (Fig. 6A). Of the 23 torque-scaled afferents, nine were scaled in only one of the two directions; all nine of these afferents exhibited non-graded responses to torque in the opposite direction. In addition, there were two FA-I afferents that responded to torque only in a non-graded manner. This is in contrast to the loading phase where all torque-sensitive FA-I afferents were scaled in both directions and there were no afferents responding to torque in a non-graded manner.

The torque sensitivity index was compared during the loading and unloading phases for a matched sample of afferents scaled by torque. The index was higher during the loading phase (I_T= 0.43) than during the unloading phase (I_T= 0.19) (P < 0.05; Mann–Whitney test; n= 33; both directions pooled).

Effect of torque direction

For successful manipulation, torque direction must be signalled to the central nervous system by the tactile afferent populations, particularly during the loading phase. In this section we quantify directional effects, during the loading phase, in the populations of SA-I and FA-I afferents.

The greatest effect of torque direction was seen in the responses of SA-I afferents. A substantial fraction of torque-scaled SA-I afferents (28/55) were scaled for only one direction of torque. For five afferents, responses were excited in one direction and suppressed in the opposite direction. Comparison of afferent responses to torques with identical magnitudes but in opposite directions revealed that in 41% (27/55) of SA-I afferents the number of spikes evoked during the loading phase was different in the two directions at all torque levels tested (P < 0.017; Mann–Whitney test, Bonferroni adjusted significance level). In contrast, 15% (10/55) of torque-scaled SA-I afferents were indifferent to torque direction. For the remaining 18 torque-scaled SA-I afferents, the directional effect depended on the torque magnitude.

For all eight SA-I afferents in which only non-graded responses to torque could be demonstrated, torque direction showed an effect for at least one of the three torque magnitudes. In five of those afferents, the number of spikes during the loading phase was different in the two directions at all three torque levels tested.

All 27 torque-scaled FA-I afferents were scaled by torque magnitude, during the loading phase, in both directions (Fig. 6). For eight (30%) of those afferents, responses were significantly different in the two directions at each of the three torque magnitudes tested (P < 0.05; Mann–Whitney test). In contrast, another eight afferents (30%) were indifferent to torque direction at each of the torque magnitudes tested.

Considerations of symmetry may suggest that RFCs of afferents indifferent to torque direction might be located on or close to the longitudinal midline of the finger. However, this was not the case for either the SA-I or FA-I afferents. The RFCs of SA-I afferents were located 0.9–4.6 mm (median 3.4 mm) from the midline. The radial distance of the RFCs from the rotational centre of torque (initial contact point) was in the range 1.1–5.3 mm (median 4.8 mm). RFCs of FA-I afferents were located 0.7–4.0 mm (median 3.2 mm) from the midline and 0.7–5.9 mm (median 4.2 mm) away from the rotational centre.

Effect of background normal force on responses to torque

In this section we examine whether the effects of torque, described in the preceding sections for a background normal force of 2.5 N, differed when the normal force was 1.8 or 2.2 N.

First, we determined whether the number of torque-scaled afferents was different at different normal force levels. Only a few additional SA-I afferents were scaled by torque magnitude when background normal force was increased; an increase in force from 1.8 to 2.2 N and further to 2.5 N resulted in two and four more scaled afferents, respectively. Similarly, the level of normal force had minimal effect on the number of torque-scaled FA-I afferents. There was no difference between normal forces of 2.2 and 2.5 N, and there was only one more afferent scaled by torque at the lowest (1.8 N) normal force.

Afferents that were scaled by torque, and were tested at all three normal force levels, were selected for further analysis as detailed below. In the clockwise direction, 39 SA-I afferents and 24 FA-I afferents were analysed for normal force effects and in the anticlockwise direction 40 SA-I and 24 FA-I afferents were analysed.

SA-I afferents

The same trends were observed for torques in the two directions and therefore we report here on data pooled for both directions. The average torque sensitivity index (I_T) increased from 0.15 (s.d.= 0.20) to 0.17 (s.d.= 0.25) when normal force increased from 1.8 to 2.2 N, but remained at 0.17 (s.d.= 0.27) with a further increase in background normal force to 2.5 N. However, individual afferents within the population behaved differently. Table 1 shows the percentage of afferents falling into the five possible groups –I_T decreasing or increasing with an increase in normal force, having a maximum or minimum value at the intermediate normal force (2.2 N), and being unaffected by normal force.

Table 1.

Frequency of occurrence of the five possible patterns of normal force effects

To assess whether there was any relationship between the different patterns shown in Table 1 and the location of an afferent's RFC, a one-way analyses of variance by ranks (Kruskal–Wallis) was used. There was no statistically significant relationship between an afferent's pattern of normal force sensitivity and the distance between its RFC and the initial contact point.

FA-I afferents

The behaviour of the FA-I afferents was similar to that of the SA-I afferents. I_T increased from 0.46 (s.d.= 0.34) to 0.50 (s.d.= 0.33) when normal force increased from 1.8 to 2.2 N, and I_T was 0.49 (s.d.= 0.34) at a normal force of 2.5 N. Single afferents displayed one of the five distinct patterns of normal force effects (Table 1). The relative occurrence of the five patterns was different for FA-I and SA-I afferents. There was no relationship between the pattern of an FA-I afferent's normal force effect and the distance between its RFC and the initial contact point (Kruskal–Wallis ANOVA).

Effect of torque on first spike latency

Inspection of single afferent spike patterns (Fig. 5) indicates that applied torque affected the time of occurrence of the first spike, or the first spike latency, as well as the discharge rate. For our protocol, with a constant ramp time of 0.5 s (Fig. 1), there is a fixed relationship between torque magnitude and torque rate. It is the torque rate that is potentially encoded by the first spike latency because the first spike occurs before the peak torque is reached. Only FA-I afferents were considered in this analysis because more than 90% of the SA-I afferents exhibited an on-going discharge during the normal force plateau prior to the application of torque and thus response latency could not be assessed reliably.

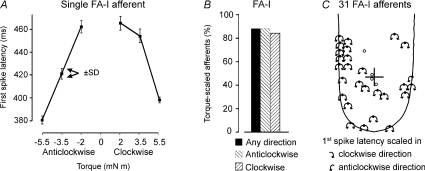
First spike latencies for the single FA-I afferent illustrated in Fig. 5 are summarised quantitatively in Fig. 7A. The mean values, and relatively small standard deviations, indicate that an increase in torque rate affected the first spike latency in a graded and reproducible manner. Most FA-I afferents with mean discharge rates that were scaled by torque showed a similar scaling when response was measured by the first spike latency. Eighty four percent (26/31) of the 31 FA-I afferents were scaled by an increase in torque rate in the clockwise direction and 87% (27/31) in the anticlockwise direction. Thus, 26 of the afferents were scaled by an increase in torque rate in both directions (Fig. 7B).

Figure 7. Effect of torque on the latency of the first spike in the response.

Note that for our protocol, torque rate is proportional to torque magnitude because the ramp duration was always 0.5 s. A, each data point represents the mean latency (±s.d., n= 6) for a single FA-I afferent (the same afferent as in Fig. 5. B, the proportion of FA-I afferents with first spike latencies scaled by torque. Hatched bars correspond to afferents scaled by torque in the clockwise or anticlockwise directions and the black bar represents afferents that were scaled by torque in any direction (i.e. clockwise, anticlockwise or both directions). C, arrows originating from the RFC indicate the direction in which the first spike latencies were scaled by torque as assessed by Spearman's rank correlation. The rotational centre of the applied torque (first contact point) is indicated by a cross. RFCs of afferents not scaled by torque are represented by open circles.

Three of the four FA-I afferents for which the first spike latencies were not influenced by torque rate had RFCs in contact with the stimulus (Fig. 7C). The same four afferents were not scaled by torque when response was measured by spike count (cf. Fig. 6B).

An index analogous to I_T was calculated using the first spike latency in place of the mean response. The median size of this torque sensitivity index was 28.7 ms (range: 1–82 ms). The index was not correlated with the distance between the rotational centre of torque (initial contact point) and the RFC.

Population encoding of multiple stimulus parameters

In the sections above we have analysed how single SA-I and FA-I afferents respond to torque magnitude and direction and what effect background normal force has on torque sensitivity. In the following section we examine the ability of the SA-I and FA-I populations to extract, concurrently, information about all three stimulus parameters. The population analysis is performed in time windows, progressively expanding by 10 ms commencing at the start of the applied torque.

A non-parametric Parzen window classifier, with a radial basis function, was trained to decode the population responses (see Methods). Stimuli not used in the training set were then used to test the performance of the population.

SA-I afferents

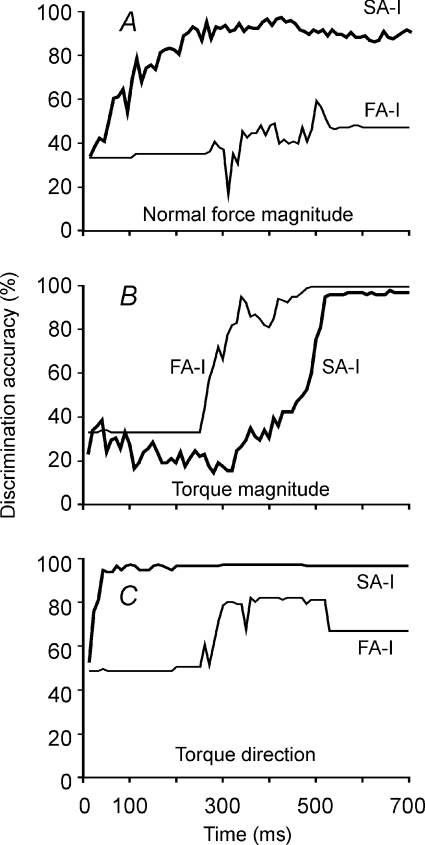
The accuracy with which the SA-I population extracted the three stimulus parameters is shown in Fig. 8 as a function of the time elapsed since the commencement of torque. The SA-I population could readily discriminate between all three concurrently changing parameters applied to the fingerpad. The accuracy of discriminating background normal force increased steadily from chance to reach 90% after about 250 ms (Fig. 8A). Torque magnitude was discriminated accurately, but the process was relatively slow (Fig. 8B). Accuracy above 90% was achieved only at the end of the torque loading phase (500 ms) and continued to improve during the plateau phase. In contrast, torque direction was discriminated early in the torque loading phase, rapidly reaching 100% accuracy (Fig. 8C).

Figure 8. Capacity of the SA-I population (thick lines) and the FA-I population (thin lines) to determine the values of the three stimulus parameters.

A, accuracy of classifying the three normal force magnitudes (1.8, 2.2, 2.5 N) as a function of time after the commencement of torque. B, accuracy of determining the three torque magnitudes (0, 2.0, 3.5 mNm). C, discrimination of two torque directions (clockwise, anticlockwise). There were 58 afferents in the SA-I population and 23 afferents in the FA-I population. Discrimination accuracy was estimated from 108 test stimuli.

FA-I afferents

The population of FA-I afferents discriminated torque magnitude accurately and more rapidly than the SA-I population, reaching 100% accuracy by the end of the torque loading phase (Fig. 8B). The FA-I afferents could discriminate between torque magnitudes with an accuracy above 80% as early as 300 ms after the commencement of torque whereas SA-I afferents performed at chance level until about the 400 ms mark. As expected from the single afferent analysis, performance of the FA-I afferent population in discriminating torque direction was inferior to that of the SA-I population (Fig. 8C). FA-I afferents provided little information about torque direction until near the end of the loading phase when some discrimination above chance occurred.

We have analysed the ability of the populations to determine values of the three stimulus parameters during the torque loading phase. During this phase, the FA-I population did not provide any meaningful assessment of the background normal force. However, FA-I afferents could provide some information about normal force magnitude during the normal force loading phase, which in our experimental protocol preceded the torque loading phase (not analysed).

Discussion

The importance of signals from mechanoreceptors in the hand for successful manipulation of objects has been demonstrated in many studies. These signals are used routinely to update stored representations, which underlie feedforward or predictive strategies resulting in rapid and accurate hand movements (Johansson & Cole, 1994; Witney et al. 2004; Johansson & Flanagan, 2009). On rare occasions, when movements are heading to instability, feedback signals may be used to form corrective movements (Johansson & Westling, 1987).

In most studies of manipulation, grasp and lift manoeuvres have been employed with an emphasis on grip forces, at right angles to the grasped surfaces, and load forces, tangential to the surfaces. However, the majority of everyday manipulations include an additional crucial parameter, the varying torques imposed on the digits. Even simple grasp and lift tasks invariably involve torsional loads because the grip axis rarely passes through the object's centre of mass. Sensory information signalling torque parameters is essential in most dextrous tasks from two points of view. Firstly, torsional loads would lead to slip in the absence of a corresponding increase in grip force. Secondly, successful use of stored representations in a predictive manner requires inclusion of torque in those representations. It has been demonstrated in behavioural studies that coordination of grip force and torque is governed by the same principles of predictive control, based on memory from past experiences, that govern coordination of grip force and load force (Goodwin et al. 1998; Johansson et al. 1999).

To our knowledge, there have been no prior studies of cutaneous mechanoreceptive afferent responses to torsional loads. In our experiments, we characterised the responses of single afferents under conditions equivalent to those occurring during natural human manipulations. We then used the single unit data to model the capacity of SA-I and FA-I afferent populations to discriminate, on a real-time scale, the multiple stimulus parameters using a Parzen window classifier and learning algorithm.

Single afferents respond to torque

Most of the SA-I and FA-I afferents, from all over the distal segment of the digit, responded to torque. This extends previous observations that tactile afferents from all over the fingertip potentially contribute to encoding of mechanical events when objects are manipulated under natural conditions (Bisley et al. 2000; Birznieks et al. 2001, 2009; Jenmalm et al. 2003).

There are two dimensions to torque, its magnitude and its direction, both of which are integral to hand function. Torque magnitude scaled responses of all FA-I afferents in both directions, and scaled responses of about half the SA-I afferents in both directions and half the SA-I afferents in one direction only. Torque direction affected responses mostly in the SA-I afferents and to a lesser degree in the FA-I afferents.

Some SA-I afferents responded to torque, but their responses were not scaled by torque magnitude. It is possible that these afferents would have been scaled by magnitudes outside the range used by us. Different optimal torque ranges among afferents would have the advantage of increasing the overall dynamic range of the whole population.

During natural manipulations torsional loads occur, of necessity, on a background of accompanying grip force. In our experiments, changing the equivalent background normal force could either increase or decrease an individual afferent's sensitivity to torque. These balanced changes in sensitivity could play a role in ensuring that rich information about torque is available at any level of normal force. We did not explore torque effects at contact forces below 1 N, where torque sensitivity may be altered because of the substantial changes in contact area (Westling & Johansson, 1987; Vega-Bermudez & Johnson, 1999) and coefficient of friction (Andrèet al. 2009) at low forces.

Phases of torque development

Our protocol allowed us to characterise afferent responses during three distinct phases of applied torque: the loading phase, the unloading phase and the static phase. Each of these phases plays a different role in manipulation.

To prevent rotational slips and ensure grasp stability, it is more critical to account for increases in torque during the loading phase than to account for torque changes during the unloading phase. However, highly skilled manipulations depend critically on sensory information about both torque increases and decreases. For example, an appropriate reaction to unloading is essential for terminating movements at the intended endpoint when a skilled wood carver has cut through the wood. SA-I and FA-I afferent responses were affected during both the loading and unloading phases, but more so during the loading phase.

When torque is constant (the plateau phase in our study), only SA-I afferents continue to signal the presence of torque. What role might this static signal play in manipulation? In principal, torque information from SA-I and FA-I afferents during only the dynamic loading and unloading phases could be sufficient for the motor control system to operate from internal models driven by sensory signals from a sequence of discrete events (Johansson & Cole, 1992; Flanagan et al. 2006). However, the static responses of SA-I afferents could play an important role in error correction and detection of cumulative torque changes that are too slow to activate afferents during the dynamic phases.

Spatial pattern of afferent responses

Across the population of afferents innervating the distal segment of the finger there was no obvious overall spatial pattern of response to torque. Nevertheless, some geometric trends were apparent.

SA-I afferents tended to be more sensitive to torque if their receptive field centres were located just outside the area in contact with the stimulus. One possible explanation is that friction causes the stimulus surface and the skin in contact with it to twist together as torque is applied, resulting in maximal stress and strain just outside the contact area. Modelling of the whole fingertip mechanics is necessary to test this hypothesis.

Spatial trends for the FA-I afferents differed from those of the SA-I afferents. There are at least two possible reasons for this. One explanation is that stress and strain close to the rotational centre change too slowly to excite the dynamically sensitive FA-I afferents. A second possibility is that some FA-I afferents responded to local micro-slips in addition to responding to torque (cf. Johansson & Westling, 1984). Due to the finger's curved shape, the normal force would result in a distribution of pressure with a maximum at the centre of contact and decreasing with increasing distance from the centre (Monzée et al. 2003). Conversely, the torque could result in a distribution of tangential force with a minimum at the centre of rotation and increasing with increasing distance from the centre. Thus, the ratio of local tangential to local normal force decreases towards the edges of the contact area where micro-slips could occur. It has been shown that FA-I afferents are sensitive to such localised slips (Johansson & Westling, 1984). Three FA-I afferents with receptive fields close to the centre of rotation were insensitive to torque and this may have been due to a combination of the absence of micro-slips and an insufficient dynamic component in stress and strain at the Meissner endings. SA-I afferents are also known to respond to micro-slips, but their responses in the current experiments are expected to be more strongly driven by the local stress and strain (Phillips & Johnson, 1981; Srinivasan & LaMotte, 1987; Vega-Bermudez & Johnson, 1999). These hypotheses are supported by the results of Levesque & Hayward (2003) who used high spatial and temporal resolution imaging to demonstrate the non-uniform nature of strain in the contact area.

The underlying principles of FA-I and SA-I afferent responses to torque that we have demonstrated for a flat surface are likely, in general, to apply to curved surfaces as well. We do not know of any experimental results that allow us to speculate meaningfully on the detailed effects of curvature on torque sensitivity; further neurophysiological and fingertip mechanics data are required for this.

First spike latencies

During manipulation, unpredictable variations in load conditions must be compensated for rapidly in order to maintain grasp stability. The most rapid source of tactile information from the digits is that potentially encoded in the relative latencies of the first spike in the afferents’ responses (Gautrais & Thorpe, 1998; Van Rullen et al. 1998; Van Rullen & Thorpe, 2001; Petersen et al. 2002; Johansson & Birznieks, 2004). It has been shown that the relative latencies form a viable code for the shape of a contacted object and the direction of the contact force (Johansson & Birznieks, 2004). Several coding mechanisms based on first spike latencies have been proposed (e.g. Ahissar et al. 2000; Buonomano, 2000; Carr et al. 2001; Thorpe et al. 2001; Wesson et al. 2008). In the current study, we demonstrated that an increase in torque rate affected the first spike latency in a graded and reproducible manner. Thus, the first spike latencies could form the basis for rapidly available information about torque rates.

How is torque encoded by the afferent populations?

During a natural manipulation, the central nervous system must extract, concurrently and in real-time, independent information about the three stimulus parameters we focussed on; torque magnitude, torque direction and background normal force. Moreover, the speed of information acquisition is an important consideration. We addressed these issues by modelling the SA-I and FA-I population responses using a Parzen window classifier and corresponding learning algorithms.

Both the SA-I and the FA-I populations could extract the torque magnitude, approaching 100% accuracy. However, the FA-I afferents signalled torque magnitude earlier than did the SA-I afferents by some 200 ms. Torque direction was extracted by the SA-I population more rapidly and more accurately than by the FA-I population. Due to the ongoing response to background normal force, the SA-I population also relayed accurate information about the magnitude of normal force during the torque loading phase. Information about the background normal force would also be provided by both the SA-I and FA-I populations during the normal force loading phase in our protocol (not analysed).

In our experimental design the Parzen window classifier used data from a small number of discrete combinations of stimulus parameters but the same principles apply to concurrent discrimination of continuously varying stimuli. This analytical approach, not pursued previously in the tactile system, points the way to investigate how the brain deals with the complex interactions between the numerous different parameters of fingertip stimulation. Discrimination analysis in real-time proved to be an effective tool for revealing key aspects of encoding of tactile information in the context of the speed required for effective manipulation. Knowledge about such real-time processes may also contribute to the development of tactile sensory systems for more effective prostheses and for robotic manipulators.

Author contributions

I.B., H.E.W., L.M.S. and A.W.G. conceived, designed and carried out the experiments; I.B. performed the majority of the data analysis; I.B., S.J.R and N.H.L. performed the Parzen classifier analysis; I.B. drafted the paper. All authors revised and approved the final version of the article. The experiments were performed at the Department of Anatomy and Cell Biology, Melbourne University, Australia.