Direct Associations or Internal Transformations? Exploring the Mechanisms Underlying Sequential Learning Behavior

Abstract

We evaluate two broad classes of cognitive mechanisms that might support the learning of sequential patterns. According to the first, learning is based on the gradual accumulation of direct associations between events based on simple conditioning principles. The other view describes learning as the process of inducing the transformational structure that defines the material. Each of these learning mechanisms predict differences in the rate of acquisition for differently organized sequences. Across a set of empirical studies, we compare the predictions of each class of model with the behavior of human subjects. We find that learning mechanisms based on transformations of an internal state, such as recurrent network architectures (e.g., Elman, 1990), have difficulty accounting for the pattern of human results relative to a simpler (but more limited) learning mechanism based on learning direct associations. Our results suggest new constraints on the cognitive mechanisms supporting sequential learning behavior.

The ability to learn about the stream of events we experience allows us to perceive melody and rhythm in music, to coordinate the movement of our bodies, to comprehend and produce utterances, and forms the basis of our ability to predict and anticipate. Despite the ubiquity of sequential learning in our mental lives, an understanding of the mechanisms which underly this ability has proven elusive. Over the last hundred years, the field has offered at least two major perspectives concerning the mechanisms supporting this ability. The first (which we will call the “Associationist” or “Behaviorist” view) describes learning as the process of incrementally acquiring associative relationships between events (stimuli or responses) that are repeatedly paired. A defining feature of this paradigm is the claim that behavior can be characterized without reference to internal mental processes or representations (Skinner, 1957). For example, consider a student practicing typing at a keyboard by repeatedly entering the phrase “we went camping by the water, and we got wet.” According to associative chain theory (an influential associationist account of sequential processing), each action, such as pressing the letter c, is represented as a primitive node. Sequences of actions or stimuli are captured through unidirectional links that chain these nodes together (Ebbinghaus, 1964; Wickelgren, 1965). Through the process of learning, associations are strengthened between elements which often follow one another, so that, in this example, the link between the letters w and e is made stronger than the link between w and a because w-e is a more common subsequence. Through this process of incrementally adjusting weights between units that follow one another, the most activated unit at any point in time becomes the unit which should follow next in the sequence. Critically, the associationist perspective directly ties learning to the statistical properties of the environment by emphasizing the relationship between stimuli and response (Estes, 1954; Myers, 1976).

A second view, offered by work following from the “cognitive revolution,” highlights the role that the transformations of intermediate representations play in cognitive processing. Broadly speaking, transformational systems refer to general computational systems who’s operation involves the iterative modification of internal representations. By this account, processes which apply structured transformations to internal mental states interact with feedback from the environment in order to control sequential behavior. For example, a cornerstone of contemporary linguistics is the idea that language depends on a set of structured internal representations (i.e., a universal grammar) which undergo a series of symbolic transformations (i.e., transformational grammar) before being realized as observable behavior (Chomsky, 1959; Lashley, 1951). Like the associative chain models just described, transformational system link together representations or behavior through time through input and output relationships and provide a solution to the problem of serial ordering. However, a critical difference is that while the associative chain account simply links together behavioral primitives, transformations output new, internal representations which can later serve as input to other transformations.

Transformation are often more flexible than simple associations. For example, systems that depend symbolic re-write rules can apply the same production when certain conditions are met, irrespective of surrounding context (i.e., a rewrite rule such as xABy → xBAy, which simply flips the order of elements A and B, applies equally well to strings like FXABTYU and DTABRRR due to the presence of the common AB pattern). This flexibility allows generalization between structurally similar inputs and outputs. In addition, while the selection of which transformation to apply at any given point may be probabilistic, the rules used in transformations tend to regularize their output since only a single mapping can be applied at any time. Critically, transformational system depend on an appropriately structure intermediate “state” or representation which is modified through additional processing (in contrast to the associationist account which learns direct relations between observed behavioral elements).

The importance of transformations as a general cognitive mechanism extends beyond strictly linguistic domains such as transformational grammars for which they are most easily identified. For example, theories of perceptual and conceptual similarity have been proposed which assume that the similarity of two entities is inversely proportional to the number of operations required to transform one entity so as to be identical to the other (Imai, 1977; Hahn, Chater, & Richardson, 2003). In addition, systems based on production rules (which also work via transformational processing of an intermediate mental state), have figured prominantly in many general theories of cognitive function (Anderson, 1993; Anderson & Libiere, 1998; Laird, Newell, & Rosenbloom, 1987; Lebiere & Wallach, 2000). In this paper, we argue that transformational systems represent a broad class of learning and representational mechanisms which are not limited to systems based on symbolic computations. Indeed, we will later argue that certain recurrent neural networks (Elman, 1990) are better thought of as general-purpose computational systems for learning transformation of hidden states. As a result, we use the term transformations throughout this paper to refer to a broad class of computational systems including productions, transformations, rewrite rules, or recurrent computational systems. Each of these systems has slightly different properties. For example, purely symbolic systems are typically lossless in their operation, while in recurrent computational systems, representations are more graded. Nevertheless, these systems share deep similarities, particularly with respect to the way that representation and processing unfold during learning and performance.

The goal of the present article is to evaluate these two proposals (i.e., simple associative learning vs. transformational processing) as candidate mechanisms for supporting human sequence learning. The two perspectives just outlined predict important differences in the number of training exposures needed to learn various types of sequentially structured information. By limiting learning to the experienced correlations between stimuli and responses, the associationist account predicts that the speed and fluency of learning is a direct function of the complexity of the statistical relationships that support prediction (such as conditional transition probabilities). In contrast, the transformational account predicts that learning will be sensitive to the number and type of transformations needed to represent the underlying structure of the material. Note that both of these approaches can learn to represent both probabilistic and deterministic sequences and, as a result, it maybe difficult to distinguish these accounts on the basis of learnability alone. However, as we will show, the time course of acquisition provides a powerful window into the nature of such mechanisms that can differentiate between competing theories.

To foreshadow, our results show that, at least on shorter time scales, human sequence learning appears more consistent with a process based on simple, direct associations. This conclusion is at odds with recent theoretical accounts which have argued for domain-general sequential learning processes based on transformations of an internal state (such as the Simple Recurrent Network, Elman, 1999). While it is often tempting to attribute sophisticated computational properties to human learners, our results are consistent with the idea that human learning is structured to enable rapid adaptation to changing contingencies in the environment, and that such adaptation may involve tradeoffs concerning representational flexibility and power. We begin by introducing two representative models that draw from these two paradigms. Despite the fact that both are based on incremental error-driven learning, each model makes different predictions about human learning performance in sequence learning tasks. Finally, using a popular sequential learning task (the serial reaction task or SRT), we explore the factors influencing the speed of sequence learning in human subjects and compare these findings to the predictions of each model.

Associations versus Transformations: Two Representative Models

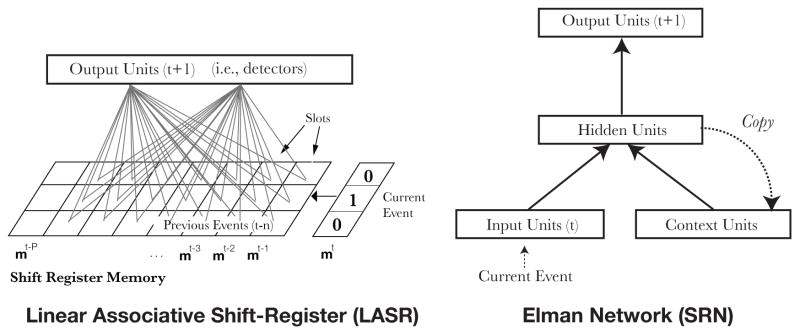
We begin our analysis by considering two models which are representative of the broad theoretical classes just described. The first, called the Linear Associative Shift-Register (LASR) is a simple associative learning system inspired by classic models of error-driven associative learning from the associationist tradition (Rescorla & Wagner, 1972; Wagner & Rescorla, 1972). The second is the simple recurrent network (SRN) first proposed by Elman (1990) and extended to statistical learning tasks by Cleeremans and McClelland (1991). Although related, these modeling accounts greatly differ in the types of internal representational and learning processes they assume (see Figure 1), which in turn lead them to predict both qualitative and quantitative differences in the rate of learning for various sequentially structured materials. In the following sections, we review the key principles and architecture of each model along with their key differences.

Figure 1.

The schematic architecture of the LASR (left) and SRN (right) networks. In LASR, memory takes the form of a shift-register. New events enter the register on the right and all previous register contents are shifted left by one position. A single layer of detector units learns to predict the next sequence element given the current contents of the register. Each detector is connected to all outcomes at all memory slots in the register. The model is composed of N detectors corresponding to the N event outcomes to be predicted (the weights for only two detectors is shown). In contrast, in the SRN, new inputs are presented on a bank of input units and combine with input from the context units to activate the hidden layer (here, solid arrows reflect fully connected layers, dashed arrows are one-to-one layers). On each trial, the last activation values of the hidden units are copied back to the context units giving the model a recurrent memory for recent processing. In both models, learning is accomplished via incremental error-driven adaptation of learning weights.

The Linear Associative Shift-Register (LASR) Model

LASR is a model of sequential processing based on direct stimulus-stimulus or stimulus-response mappings. The basic architecture of the model is shown in Figure 1 (left). Like associative chain models, LASR describes sequence learning as the task of appreciating the associative relationship between past events and future ones. LASR assumes that subjects maintain a limited memory for the sequential order of past events and that they use a simple error-driven associative learning rule (Rescorla & Wagner, 1972; Widrow & Hoff, 1960) to incrementally acquire information about sequential structure. The operation of the model is much like a variant of Rescorla-Wagner that learns to predict successive cues through time (see Appendix A for the mathematical details of the model).

The model is organized around two simple principles. First, LASR assumes a simple shift-register memory for past events (see Elman and Zipser, 1988, Hanson and Kegl, 1987, or Cleeremans’, 1993, Buffer network for similar approaches). Individual elements of the register are referred to as slots. New events encountered in time are inserted at one end of the register and all past events are accordingly shifted one time slot¹. Thus, the most recent event is always located in the right-most slot of the register (see Figure 1). The activation strength of each register position is attenuated according to how far back in time the event occurred. As a result, an event which happened at time t − 1 has more influence on future predictions than events which happened at t − 5 and learning is reduced for slots which are positioned further in the past (see Equation 4 in the Appendix).

Second, the simple shift-register memory mechanism is directly associated with output units called detectors (i.e., output units) without mediation by any internal representations or processing (see Figure 1). A detector is a simple, single-layer network or perceptron (Rosenblatt, 1958) which learns to predict the occurrence of a single future event based on past events. Because each detector predicts only a single event, a separate detector is needed for each possible event. Each detector has a weight from each event outcome at each time slot in the memory register. On each trial, activation from each memory-register slot is passed over a connection weight and summed to compute the activation of the detector’s prediction unit. The task of a detector is to adjust the weights from individual memory slots so that it can successfully predict the future occurrence of its assigned response. Weight updates are accomplished through a variant of the classic Rescorla-Wagner error-driven learning rule (Rescorla & Wagner, 1972; Widrow & Hoff, 1960). Each detector learns to strengthen the connection weights for memory slots which prove predictive of the detector’s response while weakening those which are not predictive or are counter-predictive. A positive weight between a particular time slot and a detector’s response unit indicates a positive cue about the occurrence of the detector’s response, whereas a negative weight acts as an inhibitory cue.

Note that in LASR, the critical determinants of performance are simply the relationship between stimulus and response. As a result, LASR is extremely limited in the kind of generalizations it can make. For example, the model cannot learn general mappings such as the aⁿ → bⁿ language, where any number (n) of type a events are input, and the model predicts the same number of b events. Even with regard to simple associations, LASR is limited by the fact that it lacks internal hidden units (Minsky & Papert, 1969, 1998). As a result, the model is unable to combine information from two or more prior elements of context at once (which is necessary in order to represent higher-order conditional probabilities). On the other hand, this simple, direct connectivity enables the model to learn very quickly. Since there are no internal representations to adjust and learn about, the model can quickly adapt to many simple sequence structures.

The Simple Recurrent Network (SRN)

We compare the predictions of LASR to a mechanism based on learning transformations of internal states. In particular, we consider Elman’s (1990) simple recurrent network (SRN). The SRN is a network architecture that learns via back-propagation to predict successive sequence elements on the basis of the last known element and a representation of the current context (see Figure 1). The general operation of the model is as follows: input to the SRN is a representation of the current sequence element. Activation from these input units passes over connection weights and is combined with input from the context layer in order to activate the hidden layer. The hidden layer then passes this activation across a second layer of connection weights which, in turn, activate each output unit. Error in prediction between the model’s output element (i.e., prediction of the next sequence) and the actual successor is used to adjust weights in the model. Critically, on each time step, the model passes a copy of the current activation values of the hidden layer back to the context units.

While the operation of the SRN is a simple variation on a standard multi-layer back-propagation network, recent theoretical analyses have suggested another way of looking at the processing of the SRN, namely as a dynamical system which continually transforms patterns of activation on the recurrent context and hidden layers (Beer, 2000; Rodriguez, Wiles, & Elman, 1999). In fact, the SRN is a prototypical example of a general class of mathematical systems called iterated function systems, which compositionally apply functional transformations to their outputs (Kolen, 1994). For example, on the first time step, the SRN maps the activation of the context unit state vector, c₁, and the input vector, i₁, to a new output, h₁, which is the activation pattern on the hidden layer, so that h₁ = f(c₁, i₁). On the next time-step, the situation is similar except now the model maps h₂ = f(h₁, i₂), which expands to h₂ = f(f(c₁, i₁), i₂). This process continues in a recurrent manner with outputs of one transformation continually feeding back in as an input to the next. As sequences of inputs are processed (i.e., i₁, i₂, …), each drives the network along one of several dynamic trajectories (Beer, 2000). What is unique to the SRN amongst this class of recurrent systems is the fact that the model learns (in an online fashion) how to appropriately structure its internal state space and the mappings between input and output in order to obtain better prediction of elements through time.

Due to the dynamic internal states in the model (represented by the patterns of activity on the hidden units), the SRN model is capable of building complex internal descriptions of the structure of its training material (Botvinick & Plaut, 2004; Cleeremans & McClelland, 1991; Elman, 1990, 1991). For example, dynamical attractors in the model can capture type/token distinctions (generally items of the same type fall around a single region in the hidden unit space), with subtle differences capturing context-sensitive token distinctions (Elman, 2004). Similarly, like the symbolic transformational systems described in the Introduction, the SRN is able to generalize over inputs with similar structure, such as the rule-based patterns studied by Marcus et al. (1999) (Calvo & Colunga, 2003; Christiansen, Conway, & Curtin, 2002). Indeed, part of the intense interest in the model stems from the fact that while it is implemented in a connectionist framework, the transformational processes in the model make it considerably more powerful than comparable models from this class (Dominey, Arbib, & Joseph, 1995; Keele & Jennings, 1992; Jordan, 1986). For example, early work proved that the SRN is able to universally approximate certain Finite State Automata (Cleeremans, Servan-Schreiber, & McClelland, 1989; Servan-Schreiber, Cleeremans, & McClelland, 1991). More recently, theorists have found that the representational power of the SRN might extend further to include simple context-free languages (such as the aⁿbⁿ language) because network states can evolve to represent dynamical counters (Rodriguez et al., 1999; Rodriguez, 2001).

How do these accounts differ?

Despite the fact that both models are developed in a connectionist framework with nodes, activations, and weights, LASR is more easily classified as a simple associationist model. LASR has no hidden units, and learning in the model is simply a function of the correlations between past events and future ones. As a result, LASR is considerably more limited in terms of representational power and flexibility relative to the SRN. In contrast, processing in the SRN is not limited to the relationship between inputs and outputs, but includes the evolution of latent activation patterns on the hidden and context layers. Over the course of learning, the recurrent patterns of activation in the hidden and context layer self-organize to capture the structure of the material on which it is trained. The role of inputs to the model can be seen as simply selecting which of the continually evolving transformations or functions to apply to the context units on the current time step (Landy, 2004). In addition, processing in the SRN is a continually generative process where hidden state activations from one transformation are fed back in as input to the next. As a result, the operation of the SRN is drawn closer to the transformational systems described in the introduction (Dennis & Mehay, 2008). Another difference is that LASR’s shift register adopts a very explicit representation of the sequence, while the representation in the SRN evolves through the dynamics of the recurrent processing.

Of course, our positioning of the SRN closer to symbolic production systems may appear odd at first given that at least some of the debate surrounding the SRN has attacked it on the grounds that it is a purely associative device (Marcus, 1999, 2001). However, as we will show in our simulations and analyses, the SRN is sensitive to sources of sequence structure that appear to be somewhat non-associative while our “properly” associationist model (LASR) appears to to be more directly tied to the statistical patterns of the training set. We believe this divergence warrants a more refined understanding of both the capabilities and limitations of the SRN. In addition, as we will see in the following sections, these additional processes lead the SRN to incorrectly predict the relative difficulty of learning different sequence structures by human subjects.

Statistical versus Transformational Complexity

Whether human learning is based on a mechanism utilizing direct associations (like LASR) or is based on learning transformations of internal states (like the SRN) has important implications for the types of sequence structures which should be learnable and their relative rates of acquisition. In the following section, we consider this issue in more detail by considering two different notions of sequence complexity.

Statistical Complexity

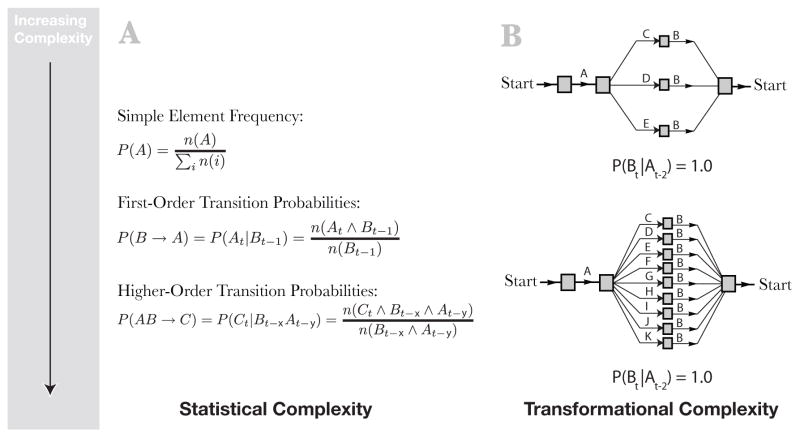
When learning a sequence, there are many types of information available to the learner which differ in intrinsic complexity (see Figure 2). For example, one particularly simple type of information is the overall base rate or frequency of particular elements, denoted P(A). Learning a more complex statistic, such as the first-order transition probability, P(A_t|B_{t − 1}) (defined as the probability of event A at time t given the specific event B at time t − 1), requires a memory of what occurred in the previous time step. Each successively higher-order transition statistic is more complex in the sense that it requires more resources (the number of distinct transition probabilities for any order n over k possible elements grows with kⁿ) and the amount and type of memory needed (see also a similar discussion of statistical complexity by Hunt and Aslin, 2001). Note that in the example shown in Figure 2A, a second-order relationship of the form P(C_t|B_{t − x}A_{t − y}) is shown. In general, any combination of two previous elements may constitute a second order relationship even when separated by a set of intervening elements or lag, for example A * B → C where * is a non-predictive wild card element².

Figure 2.

Dimensions of sequence complexity. Panel A: A hierarchy of statistical complexity. More complex statistical relationships require more memory and training in order to learn. Higher-order statistical relationship are distinguished by depending on more than on previous element of context. The order of a relationship is defined as the number of previous elements the prediction depends on. Thus, a pattern like ABC → D) is a third-order statistical relationship. Also, the elements of a n-th order conditional relationship may be separated by any number of intervening elements (or lag) as the definition only stipulates the number of previous elements required for current prediction. Panel B (top): A simple grammar with a small number of branches. Panel B (bottom): A more complex grammar with a large number of highly similar branches. Although the number of paths through each grammar increases, both are captured with a simple transition probability (shown beneath).

LASR is particularly sensitive to the statistical complexity of sequences. For example, LASR cannot learn sequences composed of higher-order conditional relationships because it lacks hidden units which would allow “configured” responding (i.e., building a unique association to a combination of two or more stimuli which is necessary to represent higher-order relationships). If human participants use a learning mechanism akin to LASR to learn about sequential information, more complex sequences which require abstracting higher-order conditional probabilities are predicted to be more difficult and learned at a slower rate³. On the other hand, models such as the SRN concurrently track a large number of statistics about the material it is trained on and no specific distinction is made concerning these types of knowledge.

Transformational Complexity

While the complexity of the statistical relationships between successive sequence elements may have a strong influence on the learnability of particular sequence structures by both human and artificial learners, other sources of structure may also play a role in determining learning performance. For example, Figure 2B (top) shows a simple artificial grammar. The sequence of labels output by crossing each path in the grammar defines probabilistic sequence. While it is possible to predict each element of the sequence by learning a set of transition probabilities, transformational systems such as the SRN take a different approach. For example, at the start of learning, the SRN bases its prediction of the next stimulus largely on the immediately preceding stimulus (i.e., C → B) because the connection weights between the context units and hidden layer are essentially random. Later, as the context units evolve to capture a coherent window of the processing history, the model is able to build more complex mappings such as AC → B separately from AD → B (Boyer, Destrebecqz, & Cleeremans, 2004; Cleeremans & McClelland, 1991).

Our claim is that models that use transformations to represent serial order are sensitive to the branching factor of the underlying Markov chain or finite-state grammar. For example, compare the grammar in the top panel of Figure 2B to the one on the bottom. The underlying structure of both of these grammars generates sequences of the form A-*-B where * is a wildcard element. As a result, both sequences are easily represented with the statistical relationship P(B_t|A_{t − 2}) = 1.0 (essentially the presence of cue A two trials back is a perfect predictor for B). However, systems based on transformations require a separate rule or production for each possible path through the grammar (i.e., AC → B, AD → B, AE → B, etc…). Thus, even though a relatively simple statistical description of the sequence exists, systems based on transformations often require a large amount of training and memory in order to capture the invariant relationship between the head and the tail of the sequence⁴. Indeed, some authors have noted limitations in SRN learning based on the number of possible continuation strings that follow from any particular point in the Markov process (Sang, 1995). In addition, the SRN has difficulty learning sequences in which there are long-distance sequential contingencies between events (such as T-E*-T or P-E*-P, where E* represents a number of irrelevant embedded elements). Note that work with human subjects has shown that they have little difficulty in learning such sequences in an SRT task (Cleeremans, 1993; Cleeremans & Destrebecqz, 1997).

Overview of Experiments

In summary, we have laid out two sources of sequence complexity that human or artificial learners may be sensitive to. In Experiments 1 and 2, we place these two notion of sequence complexity in contrast in order to identify the mechanisms that participants use to learn about sequentially presented information. In Experiment 1 we test human learning with a sequence with has low statistical complexity, but high transformational complexity (using the definition given above). In Experiment 2, we flip this by testing a sequence with low transformational complexity by higher statistical complex (see Figure 3). Our prediction is that if human learners utilize a sequential learning mechanism based on transformations on an internal state (such as the SRN), learning should be faster in Experiment 2 than Experiment 1. However, if learners rely on a simple associative learning mechanisms akin to LASR, the opposite patterns should obtain.

Figure 3.

The finite-state grammar underlying the sequences used in Experiment 1 (left) and 2 (right). The sequence used in Experiment 1 has a large branching factor and a large number of highly similar paths while the grammar underlying Experiment 2 is much simpler. In contrast, the sequence tested in Experiment 1 affords a simple, first-order statistical description, while the sequence tested in Experiment 2 relies entirely on higher-order conditional probabilities. See the introduction for each experiment for a detailed explanation.

In order to assess the rate of learning in both experiments, we utilized a popular sequence learning task known as the serial reaction time (SRT) task (Nissen & Bullemer, 1987; Willingham, Nissen, & Bullemer, 1989). One advantage of the SRT over other sequence learning tasks is that responses are recorded on each trial, allowing a fine-grained analysis of the time-course of learning. The basic procedure is as follows: on each trial, participants are presented with a set of response options spatially arranged on a computer monitor with a single option visually cued. Participants are simply asked to press a key on a keyboard corresponding to the cued response as fast as they can while remaining accurate. Learning is measured via changes in reaction time (RT) to predictable (i.e., pattern-following) stimuli versus unpredictable (i.e., random or non-pattern following) stimuli (Cleeremans & McClelland, 1991). The premise of this measure of learning is that differentially faster responses to predictable sequence elements over the course of training reflect learned anticipation of the next element.

Experiment 1: Low statistical complexity, High transformational complexity

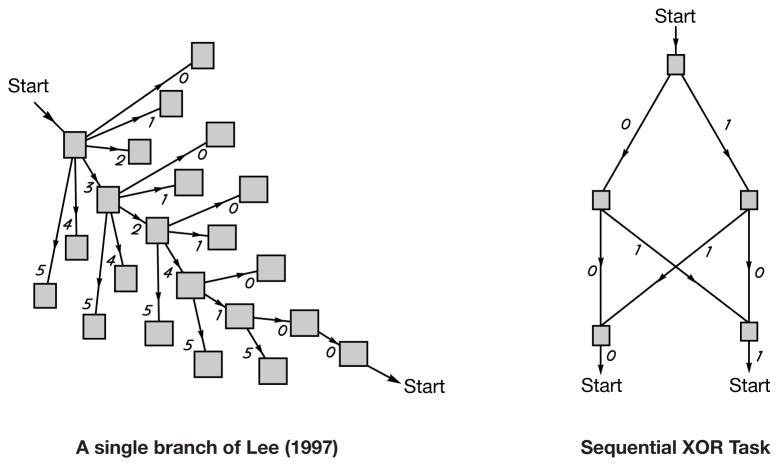
In Experiment 1, we test human learning with a sequence that is transformationally complex (i.e., has a high branching factor), but which has a relatively simple statistical description. The actual sequence used in Experiment 1 is generated probabilistically according to a simple rule: each one of six possible response options had to be visited once in a group of set of six trials, but in random order (with the additional constraint that the last element of one set could not be the first element of the next to prevent direct repetitions). Examples of legal six-element sequence sets are 0-2-1-4-3-5, 3-2-1-5-0-4, and 1-3-5-0-4-2 which are concatenated into a continuously presented series with no cues about when one group begins or ends (this type of structure was first described by Lee, 1997).

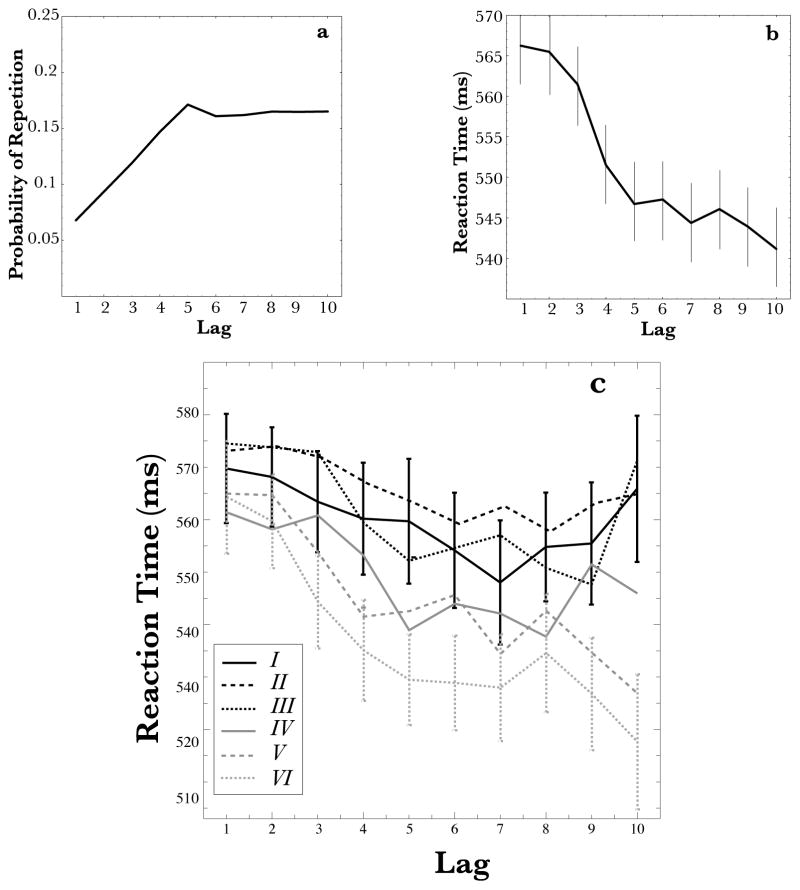
What sources of information might participants utilize to learn this sequence? Note that by definition, the same event cannot repeat on successive trials and thus repeated events are separated by a minimum of one trial (Boyer, et al., 2004). This might happen if, for example, the fifth element of one six-element sequence group repeated as the first element of the next sequence. The longest possible lag separating two repeating events is ten, which occurs when the first event of one six-element sequence group is repeated as the last event of the following six-element group. Figure 4A shows the probability of an event repeating as a function of the lag since its last occurrence in the sequence, created by averaging over 1000 sequences constructed randomly according to the procedure described above. The probability of encountering any particular event is an increasing function of how many trials since it was last encountered (i.e., lag).

Figure 4.

Panel A: The probability of an event repeating as a function of the number of trials since it was last experienced (lag). Responses become more likely as the number of trials since they were last executed increases. Panel B: RT as a function of the lag between two repeated stimuli in Exp. 1. RT is faster as lag increases, suggesting adaptation to the structure of the task. Panel C: The evolution of the lag effect over the course of the experiment. Each line represents the lag effect for one block of the experiment. In the first block, RT to lag-10 items is very close to the RT for lag-1 items. However, by block VI the speed advantage for lag-10 item has sharply increased. In panel B and C, error bars show standard errors of the mean. In panel C, for visual clarity, error bars are shown only for block 1 and 6, which reflect the beginning and endpoint of learning. However, the nature of variability was similar across all blocks.

From the perspective of statistical computations, using lag as a source of prediction depends only on first-order statistical information. For example, a participant might learn about the probability of element A given an A on trial t − 1, P(A_t|A_t−1), which is always zero (because events never repeat), or the probability of element A given a B on trial t − 2, P(A_t|B_{t − 2}). Both of these probabilities depend on a single element of context and are thus sources of first-order information. On the other hand, if the learner tried to track the second order conditional probability, P(A_t|A_t−1B_t−2), they would find it less useful since the probability of an A at time t only depends on the fact that A was recently experienced (at t − 1) and not on the occurrence of B at t − 2. Thus, successful prediction can be accomplished by simply computing transition probabilities of the type P(X_t|Y_{t − n}) (i.e., the probability of event X given event Y on trial t − n where n is any number of trials in the past). Finally, note that lag is just one way of examining changes in performance task as a function of experience, however previous studies used lag as a primary measure of learning which guides our analysis here (Boyer, et al, 2004).

Despite this simple statistical description, mechanisms based on learning transformations should have difficulty predicting successive sequence elements. Figure 3 (left) shows only one branch of the underlying finite-state grammar of the sequence. The large branching factor and the fact that the sequence has many similar, but non-indentical sequence paths means that a large number of transformational rules is necessary to represent the sequence. For example, while this transformation 01234→5 captures one path through the grammar, it is of little use for predicting the next sequence element following the pattern 23401 (which is also 5). In fact, there are 1956 total unique transformational rules which are needed to predict the next sequence element based on any set of prior elements (there are 6!=720 unique transformations alone that map the previous five sequence elements to enable prediction of the sixth). Sorting out which of these transformations apply at any given point in time requires considerable training, even with models such as the SRN which allow for “graded” generalization between similar paths.

Method

Participants

Forty-five Indiana University undergraduates participated for course credit and were additionally paid $8 for their participation. Subject were recruited on a voluntary basis through an introductory psychology class where the mean age was approximately 19 year olds, and the general population is approximately 68% female.

Apparatus

The experiment was run on standard desktop computers using an in-house data collection system written in Python. Stimuli and instructions were displayed on a 17-inch color LCD positioned about 47 cm way from the subjects. Response time accuracy was recorded via a USB keyboard with approximately 5–10 ms accuracy.

Design and Procedure

The materials used in Experiment 1 were constructed in accordance with Boyer, et al. (2004), Exp. 1 (and described briefly above). The experiment was organized into a series of blocks with each block consisting of 180 trials. For each subject, a full set of 720 possible permutations of six element sequence groups was created. In each block of the experiment, a randomly selected subset of 30 of these six-element groups was selected without replacement and concatenated into a continuous stream with the constraint that the last element of one six-element group was different from the first element of the following group in order to eliminate direct repetitions. Given the previous work suggesting that learning appeared early in the task (Boyer et al., 2004), we trained subjects in a short session consisting of only 6 blocks of training (in contrast to the 24 blocks used by Boyer et al.). As a result, there were a total of 1080 trials for the entire experiment and the task took around 40 minutes to complete. At the end of each block, subjects were shown a screen displaying their percent accuracy for the last block.

On each trial, subjects were presented with a display showing six colored circles arranged horizontally on the screen. The color of each circle was the same for each subject. From left to right, the colors were presented as blue, green, brown, red, yellow, and purple. Colored stickers which matched the color of the circles on the display were placed in a row on the keyboard which matched the arrangement on the display. At the beginning of each trial, a black circle appeared surrounding one of the colored circles. Subjects were instructed to quickly and accurately press the corresponding colored key. After subjects made their response, the display and keyboard became inactive for a response-stimuli interval (RSI) of 150 ms. During the RSI all further responses were ignored by the computer. If the subject responded incorrectly (i.e., their respond didn’t match the cued stimulus) an auditory beep sounded during the RSI, but otherwise the trial continued normally.

Participants were given instructions that they were in a task investigating the effect of practice on motor performance and that their goal was to go as fast as possible without making mistakes. In addition, they were shown a diagram illustrating how to arrange their fingers on the colored buttons (similar to normal typing position with one finger mapped to each key from left to right). Subject used one of three fingers (ring finger, middle finger, and pointer finger) on each hand to indicate their response. In order to control for the influence of within- and between-hand responses, the assignment of sequence elements to particular button positions was random for each subject with the constraint that each sequence element was assigned to each button an approximately equal number of times.

Prior to the start of the main experiment, subjects were given two sets of practice trials. In the first set, subjects were presented with ten psuedo-random trials (not conforming to the lag structure of the subsequent task) and were invited to make mistakes in order to experience the interface. This was followed by a second phase where subjects were asked to complete short blocks of ten pseudo-random trials (again lacking the structure of the training sequence) with no mistakes in order to emphasize that accuracy was important in the task. The experiment only began after subjects successfully completed two of these practice blocks in a row without error. Following these practice trials, subjects completed the six training blocks during which they were exposed to the six-choice SRT design described above.

Results

Learning performance was analyzed by finding the median RT for each subject for each block of learning as a function of the number of trials since a particular cue was last presented. Any trial in which subjects responded incorrectly was dropped from the analysis (mean accuracy was 96.9%). The basic results are shown in Figure 4. Panel B replicates the lag effect reported by Boyer et al. averaged over all subjects. Participants were faster to respond to an item the longer it had been since it was last visited, F(9,396) = 13.477, MSe = 3983, p < .0.001. A trend analysis on lag revealed a significant linear effect (t(44) = 4.99, p < .001) and a smaller but significant quadratic effect (t(44) = 3.241, p < .003). Like the Boyer, et al. and Lee (1997) study, our subjects showed evidence of adaptation to the structure of the sequence.

In order to assess if this effect was learned, we considered the evolution of the lag-effect over the course of the experiment. Figure 4C reveals that the difference in RT between recently repeated events and events separated by many intervening elements increases consistently over the course of the experiment. Early in learning (blocks 1 and 2), subjects show less than a 10ms facilitation for lag-9 or lag-10 items over lag-1 responses (close to the approximately 5ms resolution of our data entry device), while by the end of the experiment (blocks 5 and 6), this facilitation increases to about 45ms. These changes in RT cannot be explained by simple practice effects and instead depend on subjects being able to better predict elements of the sequence structure. These observations were confirmed via a two-way repeated measures ANOVA with lag (10 levels) and block (6 levels) which revealed a significant effect of lag (F(9,395) = 12.07, MSe = 186104, p < .001), block (F(5,219) = 11.84, MSe = 54901, p < .001), and a significant interaction (F(45,1979) = 1.52, MSe = 1737, p = .016). Critically, the significant interaction demonstrates that in the later blocks of the experiment, RT was faster for more predictable sequence elements and provides evidence for learned adaptation.

The results also replicated at the individual subject level. For each subject, a best fitting regression line (between level of lag and RT) was computed and the resulting β weights were analyzed. As expected, the distribution of best fitting β weights for each subject was significantly below zero (M=−2.87, t(44) = 4.989, p < .001). Similarly, a repeated measures ANOVA on regression weights fit to each subject for each block of the experiment also revealed a significant effect of block (F(5,220) = 3.4673, MSe = 75, p < .005) and a significant linear trend (t(44) = 3.19, p < .003) with the mean value of the β for each block decreasing monotonically over the course of the experiment.

Discussion

Subjects were able to quickly learn to anticipate sequences defined by a set of first-order relationships, despite the fact that the underlying transformational structure of the material was complex. Analysis of the early blocks of learning revealed a steady increase in the magnitude of the lag effect over the course of the experiment, suggesting that subjects were learning to anticipate cued responses which had not recently been presented. Overall, this result appears to support the associationist view (i.e., LASR) described above, a point we return to in the simulations.

Our results largely replicate previous reports of learning in a similar task. For example, Boyer et al. (2004) found evidence of rapid adaptation to the Lee (1997) sequence. However, in this study, it was suggested that performance in the task might be driven by a pre-existing bias towards inhibiting recent responses (Gilovich, Vallone, & Tversky, 1985; Jarvik, 1951; Tversky & Kahneman, 1971; Nicks, 1959). Because successful prediction of the next sequence element in this structure can be facilitated by simply inhibiting recent responses, the presence of this type of bias calls into question the necessity of a learning account. However, our analysis of the early block of learning appear to somewhat contradict this view. One way to reconcile our results is that we focused our analysis more directly on the early training blocks. Note however that the influence of pre-existing task biases is something we return to in the simulations.

Experiment 2: Higher statistical complexity, Low transformational complexity

In Experiment 1, we tested participant’s ability to learn a sequence which was transformationally complex but which had a simple statistical description that depended only on first-order statistical relationships. The speed with which subjects learned to predict this highly irregular sequence is interesting in light of the distinction between transformational and associative theories of sequential processing. In order to further evaluate our hypothesis, in Experiment 2 we examine the ability of human participants to learn about sequences defined by more complex, higher-order statistical relationships, but which can alternatively be represented by a small number of simple transformational rules.

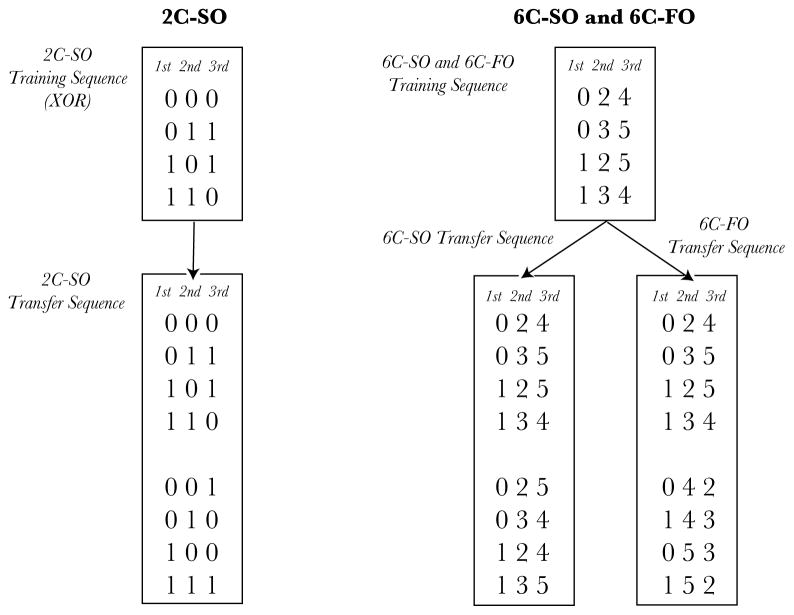
In particular, Experiment 2 tests learning in a task where the only statistical structure of predictive value are higher-order transitions (i.e., P(A_t|B_t−1C_t−2)). In the original paper on the SRN, Elman (1990) demonstrated how the network can learn to predict elements of a binary sequence defined by the following rule: every first and second element of the sequence was generated at random, while every third element was a logical XOR of the previous two. The abstract structure of this sequence is shown as a simple grammar in Figure 3 (right). The only predictable component of this sequence requires learners to integrate information from both time step t − 2 and t − 1 simultaneously to represent the following rule (or higher-order conditional probability): “if the last two events are the same, the next response will be 0, otherwise it will be 1.” Thus, unlike Experiment 1, no predictive information can be obtained using first-order transition probabilities alone. In terms of the hierarchy of statistical complexity described in the previous section, prediction or anticipation of the sequence elements in Experiment 2 depends on more complex statistical relationships than those used in Experiment 1. However, in a transformational sense, the sequence tested in Experiment 2 has a rather simple description made up of four simple transformational mappings (00→0, 11→0, 10→1,10→1).

Subjects were assigned to one of three conditions which each tested a slightly different aspect of learning. In the first condition, referred to as the 2-Choice Second-Order or 2C-SO condition, participants were given a binary (two choice) SRT task. This condition faithfully replicates the classic Elman (1990) simulation results with human participants (this is the first study to our knowledge to directly assess this). The second condition, the 6-Choice Second-Order or 6C-SO condition, extends the first condition by testing learning in a task with six response options (similar to the six-choice task used in Experiment 1). In addition, this condition helps to alleviate some of the issues with respond repetition that arise in binary SRT task (see Gureckis, 2005 for an extensive discussion). However, this sequence structure also introduces partial predictability in the form of first-order statistical relationships (similar to the graded prediction across lags available in Experiment 1). The third and final condition (6-Choice First-Order or 6C-FO condition) offers an additional source of control for the 6C-SO condition by testing learning of the first-order (linear) component of that sequence.

LASR’s prediction is that when both first-order and second-order sources of structure are available (such as in both the 6C-SO and 6C-FO conditions), participants will learn the first-order information and not the more complex, second-order information. In contrast, the SRN predicts that learning will be robust since it depends on a small number of simple transformations (matching the four separate paths through the grammar in Figure 3B).

Learning in all three conditions was assessed in two ways. First, because every third element of the sequence was fully predictable on the basis of the previous two (as in the XOR sequence), we were able to measure changes in RT between predictable and unpredictable sequence elements as we did with the lag structure in Experiment 1. In addition, in all three conditions we introduced transfer blocks near the end of the experiment which allowed us to measure RT changes to novel sequence patterns (Cohen, Ivry, & Keele, 1990; Nissen & Bullemer, 1987), a procedure akin to the logic of habituation. By carefully controlling the ways in which the transfer sequences differed from the training sequences, we were able to isolate what sources of structure subjects acquired during training (Reed & Johnson, 1994).

To foreshadow, in Experiment 2 participants were tested in a single, one-hour session. We were unable to find any evidence of higher order statistical learning. However, consistent with the predictions of LASR and the results of Experiment 1, participants in the 6C-FO condition were significantly slower in responding during the transfer blocks, which violated the first-order patterns of the training sequence.

Method

Participants

Seventy-eight University of Texas undergraduates participated for course credit and for a cash bonus (described above). Subjects were recruited on a voluntary basis through an introductory psychology class where the mean age was approximately 19 year olds, and the general population is approximately 68% female. In addition, eight members of the general University of Texas community participated in a followup study (reported in the discussion) which took place over multiple session and were paid a flat rate of $25 at the end of the final session.

Apparatus

The apparatus was the same as that used in Experiment 1.

Design and Procedure

Subjects were randomly assigned to one of three conditions: 2C-SO, 6C-SO, or 6C-FO. Twenty-six subjects participated in each condition. Subjects in the 6C-SO and 6C-FO conditions experienced a six-choice SRT task while in the 2C-SO condition the display from Experiment 1 was adapted to use two choice options instead of six. As in Experiment 1, colored stickers were placed in a row on the keyboard in a way compatible with the display. However, the mapping from the abstract structure shown in Figure 5 to response keys varied between participants. In addition, this mapping was subject to a set of constraints which avoided spatial assignments which might be obvious to the participant, such as all patterns in the experiment moving from left to right. Like Experiment 1, subjects were instructed to use both hands during the experiment and were told how to arrange their fingers on the keyboard.

Figure 5.

The abstract structure of the sequences used in Experiment 2. Each sequence was created by uniformly sampling triplets (one line at a time) from these tables and presenting each element to subjects one at a time (the columns of each table reflect possible outcomes on every 1st, 2nd, and 3rd trial).

On the basis of pilot data which failed to find a significant learning effect with this material, and following a number of other studies (Cleeremans & McClelland, 1991), we attempted to increase the motivation of our subjects by informing them they would earn a small amount of money for each fast response they made but that they would lose a larger amount of money for every incorrect response (so accuracy was overall better than excessive speed). Subjects earned 0.0004 cents for each RT under 400 ms (2C-SO) or 600 ms (6C-SO and 6C-FO), but lost 0.05 cents for each incorrect response. At the end of each block of the experiment, participants were shown how much money they earned so far, and their performance for the last block. Subject typically earned a $3–4 bonus in all conditions. In addition, subjects were given three practice blocks consisting of 30 trials each. Like Experiment 1, the session was divided into a set of blocks each consisting of 90 trials each. After completing 10 training blocks, participants were given two transfer blocks (180 trials total). After the two transfer blocks in each condition, the sequence returned to the original training sequence for an additional 3 blocks leading to a total of 15 blocks in the experiment (or 1350 trials). The structure of the transfer blocks depended on the condition to which subjects were assigned:

Materials

2C-SO Condition

The structure of the training materials used in the 2C-SO (two-choice, second-order) condition conformed to the sequential XOR structure. Learning was assessed during transfer blocks with sequences that violated this second-order relationship. The abstract structure of the transfer blocks are shown in Figure 5 under the column 2C-SO. Notice that the first four rows of this table are identical to the training sequence, while the final four rows have the identity of the critical, third position flipped. If subjects have learned the statistical structure of the 2C-SO training sequence, they should slow down and make more errors to these transfer sequences due to the presence of these novel patterns which violate the second-order structure of the training sequence. For example, in the training sequence P(0_t|0_{t − 1}0_{t − 2}) = 1.0, but in the transfer sequence this probability reduces to 0.5 (the transfer sequence is effectively a pseudo-random binary sequence).

6C-SO Condition

In the 6C-SO (six-choice, second-order) condition, a similar sequence was constructed where every third element was uniquely predictable based on a combination of the previous two (a second-order relationship). Like the 2C-SO sequence, any individual element was equally likely to be followed by two other elements (i.e., a 2 is equally likely to be followed by a 4 or a 5), and cannot be the basis of differential prediction. However, unlike the 2C-SO condition, the 6C-SO sequence utilized six response options (see the training sequence in Figure 5 under the column 6C-SO). The motivation for the 6C-SO condition is that it generalizes the results from the 2C-SO condition to a sequence structure utilizing the same six-choice SRT paradigm as was tested in Experiment 1. As in the 2C-SO condition, transfer sequences were constructed that violated the structure of the training-material by flipping the identity of the third, predictable element (see the transfer sequence table in Figure 5 under the column 6C-SO). Critically, the transfer sequences in both the 2C-SO and 6C-SO conditions preserved all sources of statistical structure.

6C-FO Condition

Note that the 6C-SO sequence has another dimension of structure, namely that responses 0 and 1 are equally likely to be followed by either a 2 or a 3, but are never immediately followed by a 4 or a 5. Thus, subjects can learn at least part of the 6C-SO sequence by learning which of the subset of response options are likely to follow any other subset, thereby improving the odds of successful guess from 1/6 to 2/6. This partial predictability is similar to the graded probability structure of Experiment 1 and is captured by simple first-order statistical relationships (i.e., P(5|2) or P(3|0)). Thus, in the 6C-FO (six-choice, first-order) condition, we test for learning of these simpler statistical relationships by examining subjects’ responses to transfer sequences which break this first-order relationship (see the transfer sequence in Figure 5 under the column 6C-FO). Note that like the other transfer sequences, the first four items of this table are the same patterns presented during training, but the four new items exchange two of the columns (i.e. positions 2 and 3). Thus, in the transfer blocks of the 6C-FO condition, subjects experience transitions between cued responses which were not present in the training set (i.e. 2 might be followed by 0 in transfer while it never appeared in that order during training). It is important to point out that the training sequences in the 6C-SO and 6C-FO were identical, with the only difference being the structure of the transfer blocks.

Results

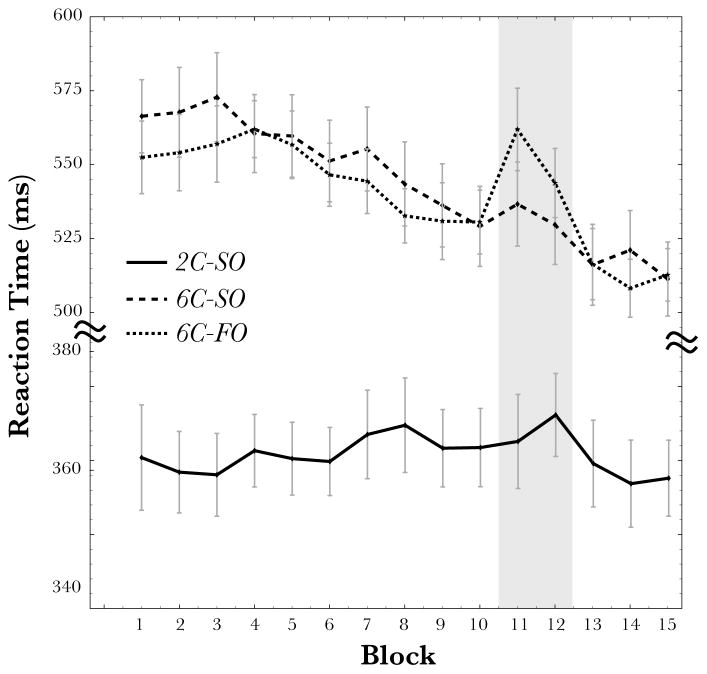
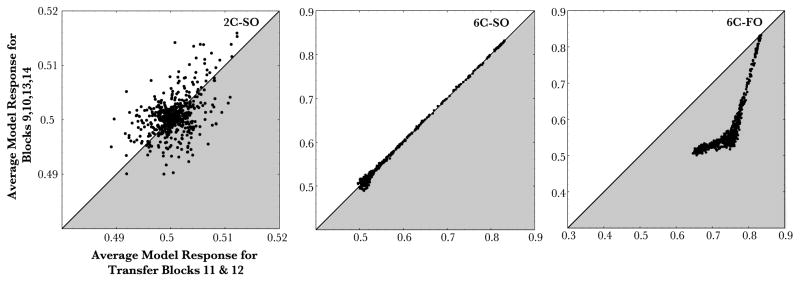
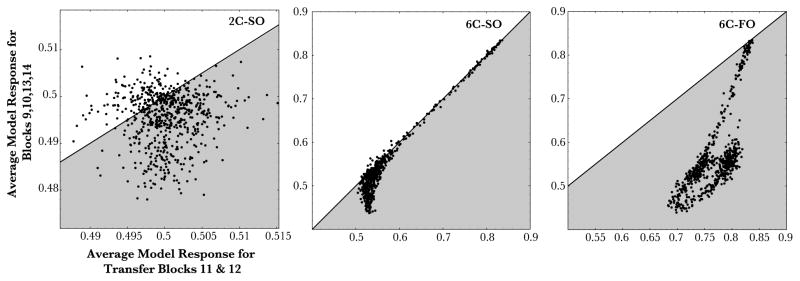
For each subject, the median RT was computed for every block of learning. Any trial in which subjects responded incorrectly was dropped from the analysis. Overall accuracy was 96.9% in condition 2C-SO, 97.8% in condition 6C-SO, and 96.4% in condition 6C-FO. Figure 6 shows the mean of median RT for each block of learning. Learning was assessed by examining RT during the transfer blocks (blocks 11 and 12, where the sequence structure changes) relative to the surrounding sequence blocks. In order to assess this effect, we computed a pre-transfer, transfer, and post-transfer score for each subject by averaging-over blocks 9 and 10 (pre-transfer), 11 and 12 (transfer), and 13 and 14 (post-transfer). Note that all analyses presented below are in terms of RT, although similar conclusions are found by analyzing accuracy scores ruling out strong speed-accuracy tradeoffs.

Figure 6.

Mean of median RTs for Experiment 2B as a function of training block. Error bars are standard errors of the mean. Transfer blocks are highlighted by the grey strip covering blocks 11 and 12.

In the 2C-SO condition, there were no significant differences between the pre-transfer and post-transfer RT compared with RT during the transfer phase, t(25) = .96, p > .3 or between the pre-transfer and transfer score, t(25) = .47, p > .6 (M= 356 ms, 354 ms, and 350 ms, respectively). Similarly, a linear trend test confirmed that RT monotonically decreased across the three phases of the experiment (t(25) = 2.40, p < 0.03), while a test for a quadratic relationship failed to reach significance (t(25) = 0.96, p > 0.3). Thus, we did not obtain evidence that subjects slow their responses during the transfer blocks relative to the surrounding blocks.

Likewise, in the 6C-SO condition, we found no significant difference between the pre-transfer and post-transfer RT compared with RT during the transfer phase, t(25) = 1.62, p > .1. RT values between the pre-transfer and transfer block scores also did not reach significance, t(25) = 1.26, p > .2 (M= 514 ms, 510 ms, and 499 ms, respectively). As in the 2C-SO condition, we found a significant linear trend across the three phases, t(25) = 3.60, p < 0.002, while the quadratic relationship failed to reach significance, t(25) = 1.62, p > 0.1. Thus, like the 2C-SO condition, we failed to find evidence that subjects slow their responses during the transfer blocks relative to the surrounding blocks.

However, in the 6C-FO we found a highly significant difference between the pre-transfer and post-transfer RT compared with RT during the transfer phase, t(25) = 7.16, p < .001, and between the pre-transfer and transfer score, t(25) = 4.28, p < .001 (M= 510 ms, 532 ms, and 491 ms, respectively). Both the linear and quadratic trends were significant, t(25) = 4.51, p < 0.001 and t(25) = 7.16, p < 0.001, respectively. Unlike condition 2C-SO or 6C-SO, subjects in this condition did slow down during the transfer blocks relative to the surrounding blocks (by about 22 ms on average). Another way to assess learning is to compare RT to predictable versus unpredictable sequence elements during the transfer blocks themselves. For example, roughly half the triplets each subject saw during the transfer set corresponded to those they saw during the training phase, while the others were new subsequences they had not experienced. In both the 2C-SO and 6C-SO condition we failed to detect a difference between predictable or unpredictable responses within the transfer blocks, t(25) < 1 and t(25) < 1, respectively. A similar analysis considering only every third trial (the one that was predictable on the basis of second-order information) found the same results with no evidence that subjects slowed their responses during the transfer block in either the 2C-SO or 6C-SO conditions.

Discussion

The results of Experiment 2 clearly demonstrate that subjects have difficulty learning the higher-order statistical patterns in the sequence. Unlike Experiment 1, subjects in this experiment were given additional incentive to perform well in the form of cash bonuses which were directly tied to their performance. Despite this extra motivation to perform at a high level, learning was less robust while subjects in Experiment 1 seem to learn a similar sequence within 50–100 trials⁵. This result is surprising given previously published results showing that subjects can learn higher-order sequence structures (Remillard & Clark, 2001; Fiser & Aslin, 2002). However, unlike at least some of these previous reports, the sequential XOR task we utilized carefully restricts the statistical information available to subjects. Particularly in the 2C-SO condition, the only information available to subjects is the second-order conditional relationship between every third element and the previous two. In addition, many previous studies have utilized extensive training regimes which took place over a number of days (Cleeremans & McClelland, 1991; Remillard & Clark, 2001). On the other hand, in the 6C-FO condition, we again observed robust first-order learning (like the results of Experiment 1).

Although a critical contrast between the training materials in Experiment 1 and 2 is the presence or absence of second-order statistical relationships, these sequence patterns differ in a number of other ways. However, along most of these measures it would appear that Experiment 2 should be the easier sequence to learn. For example, the relevant subsequences in Experiment 1 were six elements long (the overall sequence was constructed by concatenating random permutations of six elements), while in Experiment 2, stable subsequence patterns were only three elements long. In addition, on any given trial subjects had a 1/2 chance of randomly anticipating the next element in the 2C-FO condition while in Experiment 1 the odds of guessing were 1/6. Likewise, if subjects perfectly understood the rules used to create the sequence in Experiment 2, they could perfectly predict every third element. In contrast, perfect knowledge of the rules used to construct the sequence in Experiment 1 would only allow perfect prediction of every sixth element (i.e., given 12345, the subject would know with certainty the next element would be 6). Thus, by most intuitive accounts, the XOR sequence in Experiment 2 should be the easier of the two patterns to learn.

Despite the fact that few, if any, of our subjects demonstrated any evidence of learning the higher-order structure of the XOR task within the context of a single session, our conclusion is not that human subjects cannot learn such sequences. Instead, we believe that our results show that learning these relationships in isolation is considerably slower than learning for other types of information. While LASR is extreme in its simplicity as it utilizes direct associations that are limited to first-order patterns, the model could be augmented to include new conjunctive units (i.e., hidden units) which would allow it to capture higher-order patterns with extensive training (a point we return to in the discussion). As a test of these ideas, we ran eight additional subjects in the 2C-SO and 6C-SO conditions for two sessions per day for four days (a total of 9760 trials) in Experiment 2B. By session 5 (day 3), subjects showed unambiguous evidence of learning in terms of an increasingly large difference in RT between training versus transfer blocks in the later half of the experiment.

Model-Based Analyses

In the following section, we consider in more detail how our representative models (LASR and the SRN) account for human performance in each of our experiments. Each model was tested under conditions similar to those of human subjects, including the same sequence structure and number of training trials (the details of both models are provided in Appendices A and B).

Experiment 1 Simulation Results

Each simulation reported here consisted of running each model many times over the same sequences given to human participants, with a different random initial setting of the weights employed each time (in order to factor out the influence of any particular setting). Data were analyzed in the same way as the human data (i.e., the average model response was calculated as a function of the lag separating two repeated events). Extensive searches were conducted over a wide range of parameter values in order to find settings which minimized the RMSE between the model and human data (the specifics of how the models were applied to the task are presented in Appendix B).

LASR

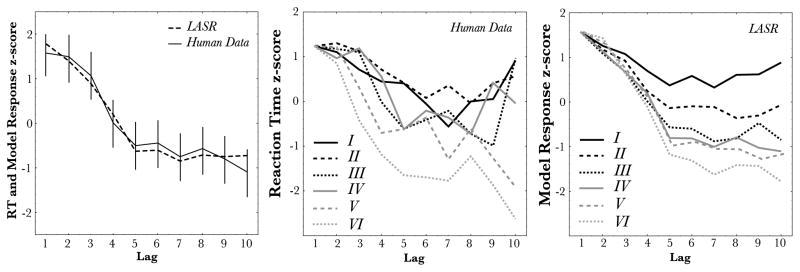
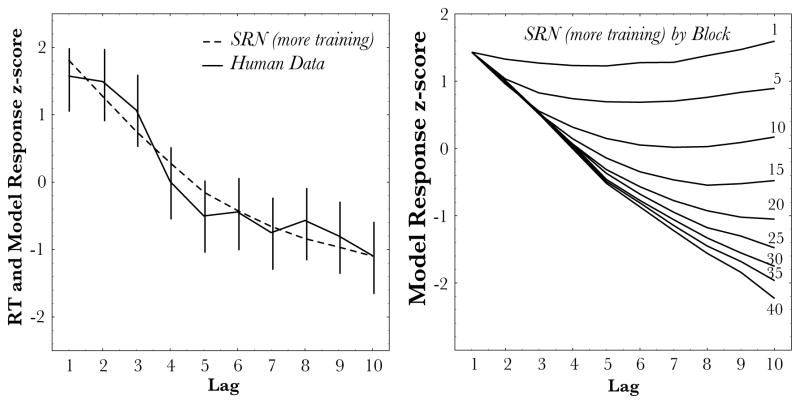
Figure 7 shows LASR’s response at each of the 10 levels of lag (left) along with the evolution of this lag effect over the learning blocks (right) compared to the human data (middle). Data in the middle and right panels of Figure 7 were first receded in terms of the amount of RT facilitation over lag-1 responding, thus RT to stimuli at lag-1 was always scored as 0 ms with increasingly negative values for longer lags. This allows us to measure the changes in learning to respond to stimuli with greater lag independent of unspecific practice effect over the course of learning blocks shown in Figure 4C. After adjusting these values relative to lag-1, all human and model responses were converted to average z-scores (around the individual simulation run or human subject’s mean response) for easier comparison.

Figure 7.

Left: The mean RT to stimuli separated by different lags in Experiment 1 compared to the predictions of LASR. Middle: Human data considered in each block of the experiment. RT values were subtracted from the lag-1 value for that block so that the differential improvements to stimuli at longer lags is more visible. Right: A similar plot for the predictions of LASR broken by block. In order to facilitate comparison between the model and human data, all data are plotted as z-scores.

Starting from a random initial weight setting, the model very quickly adapts to the lag structure of the stimuli. Like the human data, within the first block of training, LASR has already learned a strong lag effect. Furthermore, the strength of this learning effect continues to increase until the end of the experiment. Indeed, the model provides a very close quantitative fit of the data (the average correlation between the model and human data shown in the left panel of Figure 7 was M=0.981, SD = 0.005 and the mean RMSE was M=0.181, SD = 0.0026). The best fit parameters were found to be α = 0.1, η = 0.65, and momentum=0.9⁶.

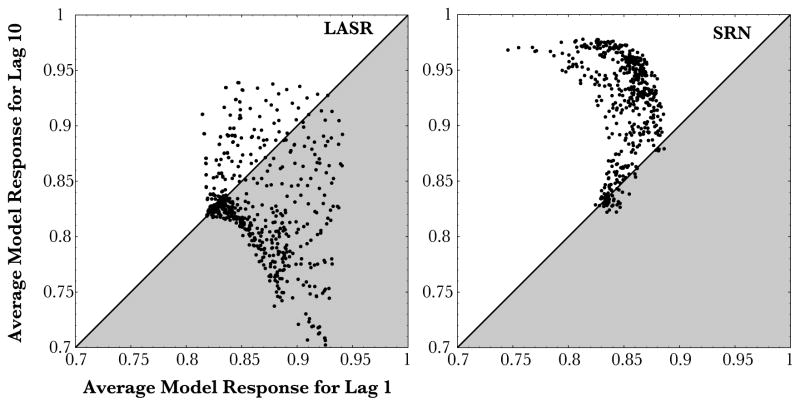
However, the overall pattern of results was not specific to this particular setting of the parameters. In the right panel of Figure 9, we show the model’s predicted relationship between lag-10 and lag-1 responses over a large number of parameter combinations (note that values of the model’s response which are closer to 1.0 indicate higher prediction error and thus slower responding). We considered the factorial combination of the following parameters: forgetting rate 0.001, 0.01, 0.1, 0.2, 0.5, 1.0, 1.5, 2.0, 5.0, or 10.0, learning-rate could be 0.001, 0.01, 0.05, 0.07, 0.09, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 1.5, or 2.0, and momentum values could be either 0.50, 0.7, 0.8, 0.85, or 0.9 for a total of 650 unique parameter combinations. Each point in the plot represents the performance of the LASR with a particular setting of the parameters (simulations were averaged over a smaller set of 90 independent runs of the model due to the size of the parameter space). Also plotted is the y < x region. If a point appears below the y = x line (the gray region of the graph), it means the model predicts faster responding to lag-10 events than to lag-1 (the correct pattern). The right panel of Figure 9 (left) shows that over the majority of parameter combinations, LASR predicts faster responding to lag-10 events. Indeed, of the 650 parameter combinations evaluated, 67% captured the correct qualitative pattern (those parameter sets that did not capture the correct trend were often associated with a forgetting rate parameter which was too sharp or a learning rate parameter which was too low to overcome the initial random settings of the weights).

Figure 9.

Explorations of the parameter space for LASR and the SRN in Exp. 1. Each model’s average response for lag-1 is plotted against the average response lag-10. The division between the grey and white regions represent the line y=x. Each point in the plot represents the performance of the respective model with a particular setting of the parameters. If the point appears below the y=x line in the grey area, it means the model predicts faster responding to lag-10 events than to lag-1 (the correct qualitative pattern). Note, however, that accounting for the full pattern of human results requires a monotonically decreasing function of predicted RT across all 10 event lags, while this figure only illustrates the two end points (lag-1 and lag-10). Thus, the few instances where the SRN appears to predict the correct pattern are not in general support for the model (see main text).

Looking more closely at how the model solves the problem reinforces our interpretation of the structure of the task. Figure 8 shows the setting of each of the weights in the model at the end of learning in a typical run. Each box in the figure represents the 6×6 array of weight from a particular memory slot in the register to each of the six output units (or detectors) in the model. The key pattern to notice is that the diagonal entries for each past time slot are strongly negative while all other weights are close to zero. The diagonal of each weight matrix represents the weight from each event to its own detector or output unit. Thus, the model attempts to inhibit any response that occurred in the last few trials by attempting to reduce the activation of that response. Despite the transformational complexity of the sequence, LASR (like human participants) appears to exploit simple first-order statistical patterns that enable successful prediction.

Figure 8.

The final LASR weights for Experiment 1. LASR learns negative receny by developing negative weights between events and the corresponding detector. Negative weights are darker red. Positive weights are darker blue. The weights leaving each memory slot (t − 1, t − 2, etc…) are shown as a separate matrix. Each matrix shows the weights from each stimulus element to each output unit. For example, the red matrix entry in the top left corner of t−1 slot is the weight from event 1 to the output for event 1. Likewise, the white cell to the immediate right of this cell represents the weight from event 1 to the output unit for event 2.

SRN

Consistent with our predictions concerning systems based on learning transformations, the SRN describes learning in a much different way. Despite extensive search, under no circumstances could we find parameters which allowed the SRN to learn the negative recency effect in the same number of trials as human subjects. A similar exploration of the parameter space as was conducted for LASR is shown in the left panel of Figure 9 (right). We considered the factorial combination of the following parameters: hidden units⁷ could be 5, 10, 30, 50, 80, 100, 120, or 150, learning rate could be 0.001, 0.01, 0.05, 0.07, 0.09, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0, 1.5, or 2.0, and momentum values could be either 0.50, 0.7, 0.8, 0.85, or 0.9 for a total of 520 unique parameter combinations. As shown in the figure, very few of these parameter combinations predict the correct ordering of lag-1 and lag-10 responses (i.e., very few points appear below the y=x line). In fact, of the 520 combinations evaluated, only 8% correctly ordered lag-1 relative to lag-10. However, manual examination of these rare cases revealed that in these situations the model failed to capture the more general pattern of successively faster responses across all 10 lags demonstrated by human subjects in Figure 4B. Given that the model failed to capture even the qualitative aspects of the human data across an entire range of reasonable parameters, we settled on the following “best-fit” parameters mostly in accordance with previous studies: momentum = 0.9, learning rate = 0.04, and number of hidden units = 80. The resulting quantitative fit of the model was very poor (the average correlation between the SRN and human data shown was M=−0.111, SD = 0.019 and the mean RMSE was M=1.414, SD = 0.012).

In order to evaluate whether the failure of the model to account for human learning was particular to some aspect of the SRN’s back-propagation training procedure, we explored the possibility of making a number of changes to the training procedure. In particular, we considered changes which might improve the speed of learning in the model, such as changing the steepness of the sigmoid squashing function (Izui & Pentland, 1990), using a variant of back-propogation called quick-prop (Falhman, 1988), changing the range of random values used to initialize the weights (from 0.001 to 2.0), and related variants of the SRN architecture such as the AARN (Maskara & Noetzel, 1992, 1993) in which the model predicts not only the next response but its current input and hidden unit activations. Under none of these circumstances were we able to find a pattern of learning which approximated human learning. In addition, we considered if this failure to learn was a function of the fact that the model has multiple layers of units to train by comparing the ability of other multi-layer sequence learning algorithms such as the Jordan network (Jordan, 1986; Jordan, Flash, & Arnon, 1994) and Cleereman’s buffer network (Cleeremans, 1993). Despite their hidden layer, these models all fit the data much better than did the SRN (the average correlation between the best fit version of the Buffer network and human data was 0.94, while it was 0.97 for the Jordan network), suggesting that the limitation is unique to the type of transformational processing in the SRN rather than some idiosyncratic aspect of training.

Evaluating the SRN

Following Boyer et al. (1998), when the SRN is given more extensive exposure to the material, such that training lasts for 30,240 trials (30 times the training that subjects in Experiment 1 experienced), the model is able to eventually adapt to the lag structure of the material (as shown in the bottom row of Figure 10). However, at the end of this extensive training, the model appears to have learned the structure of the material in a more perfect way than did human subjects in our experiment. For example, Figure 4A shows the probability of a sequence element repeating as a function of the number of trials since it was last experienced. Interestingly, this probability increases sharply only for the first five lag positions, after which it levels off. Human subjects RT and LASR’s fit (Figure 7, left) show a similar plateau (compare to Figure 10, right). It appears that the SRN regularizes the pattern, while human subjects are sensitive to the statistical properties of the training sequence.

Figure 10.

Comparison of the overall lag effect (left) and separately by blocks (right) when the SRN is given additional training in the task. In order facilitate comparison between the model and human data all data are plotted as z-scores.

Why is the SRN so slow to learn this negative recency pattern? In order to gain some insight into the operation of the model, we examined changes in the organization of the hidden unit space before learning and at various stage during training. Prior to any training, the hidden space in the model is largely organized around the last input to the model (i.e, the pattern of hidden unit activations in the model cluster strongly on the basis of the current input). As a result, the model is limited to simple transformations that map a single input to a single output (i.e., A→B). However, as the model receives more training, the organization of this hidden space changes. After extensive training, we find that the hidden unit space in the model has effectively been reorganized such that the current input is no longer the only factor influencing the model’s representation. Indeed, sequence paths which are similar, such as 1,2,3 and 2,1,3, end up in a similar region of the hidden unit space compared to highly dissimilar sequences like 5,4,6 or 6,3,5. This analysis explains the process by which the SRN learns the Lee material. At the start of learning, the model is heavily biased towards its current input despite the random initialization of the weights. However, after learning, sub-sequence paths which lead to similar future predictions are gradually mapped into similar regions of the hidden unit space. Uncovering this representation of the sequence takes many trials to properly elaborate.

As mentioned earlier, in order to address the disparity between the readiness with which subjects learn in the task compared to the difficulty facing the SRN, Boyer et al. (2004) suggested that subjects may have a pre-experiment learned bias towards negative recency. To evaluate this they pretrained the SRN with a sequence where a weak form of negative recency was present (by degrading the Experiment 1 sequence with random noise). Exposure to negative recency confounds two factors in the SRN: learning to properly elaborate the hidden unit representations versus learning the negative recency contingency between the hidden unit representations and the model outputs. In order to evaluate these separate components, we also pre-trained the SRN on a degraded form of the Experiment 1 sequence (by randomizing he input token on 10% of trials). However, prior to exposing the model to the actual Experiment 1 task, we re-randomized the network weights from the hidden units to the output units. This essentially resets the mapping from internal representations in the model to output responses, while leaving intact the recurrent connections and input weights which build the internal transformations in the model. This had little impact on the simulations results, and like Boyer, et al. (2004), we found the model showed effective learning in the first few blocks. In contrast, resetting the value of the weights in the lower level of the network (between the input and hidden units) severely interfered with the ability of the model to quickly re-learn.

In conclusion, the SRN has difficulty accounting for the speed with which human subjects adapt to the sequence defined by a negative recency relationship. This difficultly stems from a representational bias in the model toward building complex transformations of internal states and is not tied to a specific training procedure or the need to train multiple layers of network weights. The only way the model is able to account for the speed and efficiency of human learning is to assume additional training. However, the model appears to regularize its representation of the sequence in a way not observed by human participants.

Experiment 2 Simulation Results

Our goal in the following simulations was to evaluate the overall ability of each model to learn the sequential XOR tasks rather than to precisely fit the results of Experiment 2 which showed little evidence of learning in two out of the three conditions. Thus, we simulated both models over a large range of their parameters and considered what each set qualitatively predicted. Of particular interest was a comparison between this analysis and the parameter space analysis reported for Experiment 1. Overall, the simulations closely followed the modeling procedures used in Experiment 1. Each model was trained on sequences constructed in the exact same manner as those given to human subjects and for the same number of learning trials.

LASR

LASR predicts that subjects will only slow their responses during transfer blocks in the 6C-FO condition. This is because LASR, lacking hidden units, is unable to learn the higher-order statistical component of the sequence. Instead, it is limited to learning sequences with first-order relationships. The results of the parameter space analysis with LASR confirm these intuitions. The model was evaluated on the same ranges of parameters used in Experiment 1 for a total of 650 distinct combinations. To factor out the influence of particular random settings of the weights, for each parameter combination the model was run 200 times and the results were averaged. Figure 11 plots the average model responses during the transfer blocks (11 and 12) versus the surrounding training blocks (9, 10, 13, and 14) for each parameter combination. Points which fall below the y=x line (in the shaded region) represent cases where the model predicts slower responding during the transfer blocks. As is clearly visible, LASR predicts a strong difference between the transfer and surrounding block only in the 6C-FO condition. Interestingly, this is exactly the pattern which our subjects showed.

Figure 11.

Explorations of the parameter space of the LASR in the three conditions (2C-SO, 6C-SO, 6C-FO) of Experiment 2. The key behavioral pattern from Experiment 2 was that subjects only responded differently during transfer block in the 6C-FO condition. The model’s average response for the transfer blocks 11 and 12 are plotted against the average response for the surrounding learning block (9, 10, 13, and 14). Also plotted is the line y=x. Each point in the plot represents the performance of the LASR with a particular setting of the parameters. If the point appears below the y=x line, it means the model predicts slower responding during the transfer blocks (and thus evidence of learning). LASR predicts a systematic learning effect only in the 6C-FO condition (i.e. first-order, linear learning), like human subjects.

Of the 650 parameter combinations we evaluated in the 2C-SO condition, 49.8% demonstrated facilitation for XOR-consistent blocks, a pattern which is consistent with small random fluctuations in particular runs of the model. Indeed, the average difference between the model’s responses to transfer and surrounding blocks was marginal (M=−0.0006, SD=0.005). A similar conclusion characterizes the results of the 6C-SO condition (M=.0003, SD=.004). In contrast, in the 6C-FO condition, 100% of the parameter combinations evaluated showed a learning effect, the magnitude of which was significantly different from zero (M=.159, SD=.055, t(649)=74.3, p < .001). Thus, under no circumstances could we find parameters which predicted a change during transfer blocks except in the 6C-FO condition (similar to the pattern of human results). Of course, these findings are not surprising given the simple, associative learning mechanism in LASR. In the discussion, we consider how new knowledge structures and configural units may develop with extensive training in order to allow LASR to account for the results of Experiment 2 where subjects eventually learned the higher order relationships. However, in the context of a single training session, learning appears consistent with the simple, limited process advocated by LASR. As in human participants, it appears that statistical complexity, not transformational complexity, is a critical factor influencing learning performance.

SRN

Like our simulations with LASR, our emphasis was on exploring the performance of the SRN across a wide range of parameter values in order to assess the overall learnability of the sequence (see Boucher & Dienes, 2003 for a similar approach). In contrast to LASR, the SRN predicts that subjects will slow their responses during the transfer blocks in all three experimental conditions. This is confirmed in Figure 12 which shows the size of the predicted learning effect in terms of the mean prediction for transfer blocks 11 and 12 compared to the surrounding blocks: 9, 10, 13, and 14. Like Figure 9, points below the y=x line represent cases where the model predicts slower responding during the transfer blocks. We used the same 520 parameters as in Experiment 1. Due to the computational complexity of these parameter space analyses, the model was averaged over 30 runs. Overall, 74% of the parameter combinations fall below the y=x line in the 2C-SO condition, and the average magnitude of the difference between transfer and surrounding blocks was significantly different from zero (M=.004, SD=.007, t(519)=13.58, p < .001). In addition, 83% of the parameter combinations show learning in the 6C-SO condition (again, the magnitude of the effect was on average significantly different from zero, M=.01, SD=.02, t(649)=20.82, p < .001). Finally, like LASR, the SRN predicts that virtually all parameter combinations (99%) show learning in the 6C-FO condition (M=.2, SD=.07, t(649)=20.82, p < .001). In contrast to the SRN simulations of Experiment 1, it was much easier to find parameters which allowed the SRN to learn in all three conditions of Experiment 2. In Experiment 1, the entire sampled parameter space predicted no learning effect, while in Figure 12, a much larger proportion of parameters predict learning than the opposite pattern.

Figure 12.

Explorations of the parameter space of the SRN in the three conditions (2C-SO, 6C-SO, 6C-FO) of Experiment 2. The model’s average response for the transfer blocks (11 and 12) are plotted against the average response for the surrounding learning block (9, 10, 13, and 14). Also plotted is the line y=x. Each point in the plot represents the performance of the SRN with a particular setting of the parameters. If the point appears below the y=x line, it means the model predicts slower responding during the transfer blocks (and thus a learning effect). The SRN, unlike human subjects, shows a learning effect in all three conditions.

Finally, remember that one explanation for the results of Experiment 1 is that subjects came to the task with a pre-experimental bias towards negative recency. However, if this is the case, then we would expect that this same bias would come into play in Experiment 2. In order to evaluate the effect of pre-existing bias on learning, we pre-trained the SRN on the same material used in Experiment 1 for 24 blocks (180 trials each). After this pre-training we tested the learning ability of the SRN in the 6C-SO task. Interestingly, we found that rather than interfering with learning, the existence of a pre-existing, learned bias towards negative recency actually improves the magnitude of the learning effect (a paired t-test shows that the mean size of the facilitation for sequence blocks actually increased as a result of pre-training, t(649)=10.7, p < .001). Similarly, after training, for the same ranges of parameters, 97% of the parameters now predict the correct qualitative ordering.

General Discussion

Successful interaction with the world often requires the appreciation of subtle relationships between events arranged in time. What is the nature of the learning mechanisms that support these abilities? A common assumption in psychological research is that complex behavior implies the operation of correspondingly complex mental processes. However, this focus on only the highest forms of human competency may ignore many other, equally vital aspects of adaptive cognition. Our results show that learners are able to quickly acquire knowledge about complex sequential patterns in a way consistent with a simple learning mechanism based on direct associations. Rather than learn the complex, latent structures that define a sequential regularity, it appears that our learning processes may be biased to exploit simpler types of structure. As we will describe in the following sections, we believe this observation reflects a vital component of our cognitive toolbox, allowing us to quickly adapt to our environment in a variety of real-world situations. Limitations in the types of processing and structural regularities that are learned in the short-term may represent a solution to the computational tradeoff between between speed of learning and what is can be learned.

Implications for Models of Sequential Learning

Our findings raise a number of interesting issues concerning models of sequential learning. First, our results demonstrate potential limitations with popular accounts of sequential processing (i.e., the SRN). Rather than compare a single setting of “best-fit” parameters, we evaluated the prediction of the SRN across an entire parameter space. The failure of the SRN to capture the qualitative pattern of human results across our empirical studies was surprising given the broad success of the model at accounting for sequentially organized behavior. However, the time-course of acquisition provides an important theoretical constraint on learning which is often overlooked.

Also note that a common criticism of the simple associationist account is that it is unable to generalize beyond the training set to deal with unique constructions (something that even infants can accomplish, Marcus et al. 1999). However, in Experiment 1, the sequence structure was characterized by an abstract rule with a large number of valid constructions. Each subsequence encountered in the experiment was completely unique, yet predictable based on its underlying shared structure (or similarity) with previous subsequences. However, the novelty of each path through the sequence grammar is actually what leads the transformational processing in the SRN to have difficulty. In contrast, the direct associations in LASR were able to learn the abstract pattern in a rather concrete way by quickly adjusting its weights to inhibit repetition of recently cued responses. Only with extensive training does the SRN eventually learn the structure of the material, but it appears to regularize the pattern beyond the training set (by predicting faster response across all lags instead of matching the true statistical pattern of the sequence, see Figure 10 and associated discussion). Thus, the SRN appears to generalize in ways that people do not.

Implications for Language Acquisition

Given the extremely limited architecture of LASR, one might question the generality of our argument, particularly with respect to language. One possibility is that LASR is more applicable to perceptual-motor sequence learning as opposed to linguistic processing. However, there is growing evidence to suggest that relatively simple forms of statistical information may ago a long way towards disambiguating the sequential structure of language as well. For example, Karlsson (2007) found in a large corpus analysis, across multiple languages, that examples of double embedding (the type of patterns LASR is ill-equiped to handle) are extremely infrequent in spoken language. Thus, some of the arguments in favor of a complex processing scheme such as the SRN may rest on written and edited language rather than online cognitive performance. This observation lead Dennis and Mehay (2008) to propose a simple, single layer learning mechanisms akin to LASR that they show can capture the hierarchical phrase structure of sentences in a natural language corpus. One implication these studies is that linguistic processing may be readily accomplished by a system that attends to a much more limited set of statistical information. Understanding how far these simple forms of sequential adaptation can go in advancing our understanding of language and cognition is an important area of continued investigation.

Our view is that any complete account of sequential learning will likely have to recognize the multiple time scales on which learning takes place. The types of learning which characterize a lifetime of experience with grammar and syntax may not appropriately describe the learning used in acquiring a simple skill or adapting to the speech patterns of an unfamiliar accent. For example, the follow-up results of Experiment 2 reveals how different types of learning may unfold on shorter or longer time-scales. In the following sections, we consider one proposal for how more complex forms of processing may be brought online in an incremental fashion during learning.

Learning of Higher Order Conditional Relationships

In Experiment 2, we failed to find evidence of higher-order statistical learning in the context of a single one-hour training session. This result was surprising given that (outside of the dependence on higher order statistical relationships) there is nothing inherently more difficult about the sequential XOR pattern relative to the sequence used in Experiment 1 (and as discussed earlier, a number of intuitive reasons to expect that the XOR sequence should be easier to learn). One possibility is that different types of statistical information might be acquired by separate learning mechanisms which might operate on different time scales (Cohen, Ivry, & Keele, 1990; Gomez, 1997). Such a position would also be consistent with recent neuropsychological work which has found that different types of statistical information may be processed in different ways. For example, Curran (1997) found that medial-temporal lobe (MTL) amnesics are impaired at learning sequences composed of second-order transitions, but not first-order transitions. This finding was supported by fMRI work showing increased MTL involvement while learning sequences composed of higher order transitions (Schendan, Searl, Melrose, & Stern, 2003). Importantly, however, this study found increased MTL involvement for second-order sequences even when subjects showed little explicit knowledge of the sequence, suggesting that MTL involvement is a function of stimulus properties rather than conscious awareness (Chun & Phelps, 1999; Eichenbaum, 1999). Given that the MTL is thought to play a critical role in mediating stimulus associations to configurations or combinations of experienced stimuli (Love & Gureckis, 2007; McClelland, McNaughton, & O’Reilly, 1995; Sutherland & Rudy, 1989), one possibility is that the contribution of the MTL increases when the statistical structure of a sequence requires responses which depend on particular combinations of previous stimuli (such as second or higher order conditional probabilities which require learning the association between two or more distinct sequence elements and a subsequent response). Also, the increased role of the MTL in processing higher order statistical relationships would explain why such sequences are often harder to learn under dual-task conditions (Cohen, Ivry, & Keele, 1990).

In fact, one way of integrating the results just reviewed with our findings and simulations is to suggest that one of the key architectural principals of human learning is the process of incrementally adding complexity as needed (Carpenter & Grossberg, 1987; Love, Medin, & Gureckis, 2004; Quartz, 1993). On shorter time scales, the simple, more limited processing of a model like LASR may adequately capture performance. However, with more training (and depending on the nature of the material), new configural processing elements (i.e. hidden units) may be added to enrich the complexity of learning over longer time scales. From this perspective, our results may reflect an inherent computational trade-off between rate of acquisition and representational flexibility. LASR’s account suggests that one way to learn quickly is to focus on a simpler subset of statistical pattern (i.e., first order statistical patterns) to the exclusion of more complex forms of processing. Even partial or incomplete prediction is likely better than waiting for enough data to enrich a complex, transformational representation of the task or environment.

Finally, note that our failure to find evidence of learning in Exp. 2 is surprising in light of the extensive literature on “second-order conditional” learning in SRT task (Reed & Johnson, 1994; Remillard & Clark, 2001). However, as noted by Remillard & Clark (2001), previous investigations of SOC learning have sometimes failed to exclude other sources of first-order information that might aid learning. For instance, the 12-item SOC sequences tested by Reed & Johnson (1994, Experiment 2) can actually be learned by LASR because first-order lag information discriminates the training and test sequence. Remillard & Clark (2001) more directly controlled the influence that first-order information might have had on learning, but also introduced short pauses in the task at critical boundaries which might have helped participant segment the sequence into the higher order units. In addition, in this study, participants were often trained for multiple training sessions over a number of days. In contrast, in Experiment 2, we failed to find any evidence of learning in a single, 1-hour session (but did with extensive training). One hypothesis then is that when no first order information is available in a sequence (such as Exp. 2), it takes much longer to learn. Also note that one major difference between these sequences and the XOR sequences we tested are that our sequences critically depended on participants getting the “segmentation” of the sequence into triplets correct. For example, although 000 was a legal sequence triplet in the 2C-SO condition, it might also appear as the middle elements of the 110 and 000 (e.g., …110000…). However, when this subsequence crossed the two triplet subsequences, there was no actual predictability of the third element. Thus, in order to learn the 00→0 “rule” one needed to not only learn the configuration, but also “apply” it at the right time. This is less of a problem in previous studies of SOC learning because the non-predictive versions of the SOC relationship never appears.

Finally, note that across our studies we find a general bias toward learning simpler first-order patterns which can be learned with a simple linear network (LASR). Interestingly, in other domains such as category learning, the distinction between linear and nonlinear pattern learning has not been found to be a strong constraint on learnability (Medin & Schwanenflugel, 1981). One difference between these studies and ours may have to do with how easy or hard it is to chunk aspects of the stimulus in memory. In typical category learning context, all the features of a stimulus are presented simultaneously (unlike sequential tasks where events are arranged in time). In addition, in the non-linear XOR problem studies in Experiment 2, each higher-order chunk is highly similar to other task-relevant chunks which may impede the ability of participants to isolate the relative components of the sequence. In addition, performance in the SRT is unsupervised in the sense that sequential structure of the task was incidental to participant’s primary goal of correctly responding to each cue that in unsupervised concept learning, there appears to be a bias towards linearly separable patterns (Ashby, Queller, & Berretty, 1999; Love, 2002). We conclude with the suggestion that an important and often overlooked characteristic of human cognition is the ability to rapidly acquire complex sequential skills, and that this behavior may be supported by surprisingly simple and limited cognitive processes.

Appendix A: LASR Model Formalism

The following section describes the mathematical formalism of the LASR model.⁸

Input Representation

The input to the LASR model on each time step is a simple binary vector representing which of a set of events occurred at the current time step, t. Given N possible events, input to the model is a N-dimensional vector m^t where each entry $m_i^t$ corresponds to the presence ( $m_i^t=1$) or absence ( $m_i^t=0$) of event i on the current trial, t. For example, given three possible events (A, B, and C) an input vector [100] would encode that event A occurred on the present trial, while input vector [010] would encode that event B occurred, and [011] would encode that event B and C occured.

The model maintains a simple shift-register memory of past events which are indexed based on the current time t. Thus, m^t−1 refers to the input vector experienced on the previous time step, and m^t−2 refers to the input experienced two time steps in the past. The complete history of past events is a NxP matrix, M, where N is the number of possible events, and P is the number of events so far experienced and stored in memory.⁹

Response

Given N possible events or choice options, the model has N detectors. The activation d_k of the detector k at the current time t is computed as the weighted sum of all past events for all time steps multiplied by an exponential attenuation factor:

$$d_k=\sum _{i=1}^P\sum _{j=1}^N{w}_{(t-i)jk}·m_j^{t-i}·e^{-\alpha ·(i-1)}$$ (1)

where $m_j^{t-i}$ is the outcome of the jth option at time t − i, w_{(t − i)jk} is the weight from the jth outcome at time slot t − i to the kth detector, and e^{−α·(i−1)} is the exponential attenuation factor. The α is a free parameter (constrained to be positive) which controls the forgetting rate of the model. When α is large, the model has a steep forgetting curve and thus only events in the very recent past influence future prediction, while small settings of alpha cause a less steep forgetting function. The general form of Equation 1 shares much in common with well established single-layer feed-forward networks (McCulloch & Pitts, 1943; Minsky & Papert, 1969, 1998; Rosenblatt, 1958)

As is standard in most connectionist-type models, the final output of each detector, o_k, is a sigmoid transform of the activation, d_k, of each detector:

$$o_k=\frac{1}{1+e^{-d_k}}$$ (2)

This makes the formalism used in LASR identical to other comparable models such as the simple recurrent network (Elman, 1990) and standard back-propagation (Rumelhart, McClelland, & the PDF Research Group, 1986), highlight substantive differences in the learning processes between different models rather than differences in the output function.

Like other models of sequential learning, when comparing the model’s response to human data, the absolute activations of each detector are converted into response probabilities using the Luce choice rule (Luce, 1959):

$$p_k=\frac{o_k}{{\sum }_{j=1}^N{o}_j}$$ (3)

where p_k represents the probability of response k on the current time step. RT is assumed to be inversely related to p_k so that fast RTs correspond to high response probabilities (Cleeremans & McClelland, 1991).

Learning

Learning in the model is implemented using the well known delta-rule for training single layer networks (Rescorla & Wagner, 1972; Sutton & Barto, 1981; Wagner & Rescorla, 1972; Widrow & Hoff, 1960) with a small modification introduced by Rumelhart and McClelland (1986) which accounts for the sigmoid transform at the output of each detector (sometimes referred to as the generalized delta-rule for single layer networks). For each detector, the difference between the actual outcome of the current trial g_k and the detector output o_k is computed and used to adjust the weights:

$$\mathrm{\Delta }{w}_{\mathit{ijk}}(t)=\eta ·(g_k-o_k)·m_j^i·e^{-\alpha ·(i-1)}·d_k(1-d_k)+\lambda ·\mathrm{\Delta }{w}_{\mathit{ijk}}(t-1)$$ (4)

The Δw_ijk(t) value is added to the corresponding weight after each learning episode. The η is a learning rate parameter and e^{−α·(i−1)} is the exponential forgetting factor. The d_k (1 − d_k) is a factor representing the derivative of the sigmoid transfer function with respect to the weights and moves the weights in the direction of gradient descent on the error. In addition, the λ·Δw_ijk (t−1) is a momentum term which adds some fraction of the weight update from the previous trial, Δ w_ijk (t − 1) to the current one which is included here for compatibility with the SRN. The complete model has only three free parameters: α (forgeting rate), η (learning rate), and λ (momentum).

Appendix B: Simulation Details

Each model was initialized with six input units and six output units which corresponded to the six choice options in the task (in the Experiment 2 simulations, one network was tested with two inputs and two outputs corresponding to the 2C-SO condition). On each trial, the activation of one of the six input units was set to 1.0 (corresponding to the cued response shown to subjects) and the model’s task was to predict the next sequence element. The resulting pattern of activation across the six output units in response to this input pattern was converted into a choice probability. The error in the model’s prediction and the actual next element was used to adjust the learning weights on a trial-by-trial basis. Following Cleeremans and McClelland (1991) human RT in the experiment was assumed to relate directly to the value of 1 − p_k where p_k is the model’s response probability for the correct response, k, on that trial.

In the Experiment 1 simulations, each model was presented with 46 separate sequence streams (each consisting of 1080 trials) which matched exactly the sequences presented to our 46 subjects in Experiment 1. Each simulation consisted of running each model 200 times over each of these 46 sequences each time with a different, random initial setting of the weights (sampled from a uniform distribution between −1.0 and 1.0) resulting in a total of 200×46=9,200 independent runs of each model. The results were averaged over these independent runs of the model in order to factor out the influence of any particular setting of the initial weights. Extensive searches were conducted over a wide range of parameters values in order to find settings which minimized the RMSE and maximized the correlation between the model and human data.