Waved aCGH: to smooth or not to smooth

Abstract

Array-based comparative genomic hybridization (aCGH) is a powerful tool to detect genomic imbalances in the human genome. The analysis of aCGH data sets has revealed the existence of a widespread technical artifact termed as ‘waves’, characterized by an undulating data profile along the chromosome. Here, we describe the development of a novel noise-reduction algorithm, waves aCGH correction algorithm (WACA), based on GC content and fragment size correction. WACA efficiently removes the wave artifact, thereby greatly improving the accuracy of aCGH data analysis. We describe the application of WACA to both real and simulated aCGH data sets, and demonstrate that our algorithm, by systematically correcting for all known sources of bias, is a significant improvement on existing aCGH noise reduction algorithms. WACA and associated files are freely available as Supplementary Data.

INTRODUCTION

Array-based comparative genomic hybridization (aCGH) is a powerful molecular cytogenetic method for the detection of chromosomal imbalances (1) for which test and reference DNA are differentially labeled and co-hybridized on microarrays with DNA clones or oligonucleotides spanning the human genome (2,3). Array CGH has been instrumental in identifying regions of the genome encompassing copy number variations (CNVs) that contribute to the development of complex genetic diseases ranging from cancer to neurodegenerative disease (4,5). In the analysis of aCGH data sets, the choice of image processing and normalization methods, which are the first step in data analysis, can have a significant impact on aberration calling and data clustering. It is therefore essential to identify and remove all systematic sources of variation (e.g. unusual labeling efficiencies and scanning properties of the Cy3 and Cy5 dyes, print-tip or spatial effects) by appropriate normalization methods. One scatter-plot-based normalization technique that is particularly suitable for balancing the dye intensities uses ‘locally weighted scatter plot smoothing’ (lowess). Its original application was for smoothing scatter plots in a weighted, least-squares fashion (6). This technique is typically chosen to adjust microarray data in many microarray analysis software suites, such as the Feature Extraction software (Agilent).

The development of aCGH has revealed the presence of a significant technical artifact, termed ‘waves’, observed in many laboratories and first referred to by Cardoso et al. (7). These waves result from a spatial bias in aCGH profiles, generating an undulating (waved) profile instead of a flat one. It was previously thought to result from variable specificity in the DNA amplification process. However, this phenomenon was also described using the HapMap data (8), a result that argued against the first idea. What is clear is that waves can have an adverse effect on the accuracy of aberration calling and thus must be properly modeled and corrected for, in order to detect real copy number aberrations with high sensitivity and specificity. In a previous study, Nannya et al. (9) considered both the GC content of the hybridizing DNA fragments and their sizes in order to normalize aCGH data. Marioni’s study (8) found that the GC content of the BAC probes was strongly correlated with the waves. Thus, regions with a low GC content corresponded roughly to peaks of the waves, while regions with high GC probe content corresponded to troughs. However, they determined that fitting a lowess curve on the Log2Ratio versus chromosomal position plot was preferable to correcting for GC content. This was in contrast to Song’s study (10), which applied a correction based on the GC content of the probes. In contrast, a recent study presented an algorithm called NoWaves, not based on the GC content, but applying a correction based on a set of calibration profiles (11). Here we describe the development of a novel data correction algorithm, called waves aCGH correction algorithm (WACA) and principally based on GC content correction. We describe the application of WACA to both real and simulated aCGH data sets, and demonstrate that our algorithm, by systematically correcting for all known sources of bias, is a significant improvement on existing aCGH noise-reduction algorithms.

MATERIALS AND METHODS

Samples

To test for its efficacy and reliability on data analysis, we applied WACA on six sets of samples (Table 1). From our laboratory, we selected 20 samples from patients presenting with diffuse large B-cell lymphoma (DLBCL) and 11 samples from patients with chronic lymphocytic leukemia (CLL). Additionally, we selected 13 samples from patients suffering from developmental delay (CONSTIT) and used them as standard profiles for artificially creating aberrations, since they present few variations, none of them at precise locations as listed below. Raw data from these samples are available at the Gene Expression Omnibus database (GEO, http://www.ncbi.nlm.nih.gov/projects/geo/index.cgi) and their GEO accession numbers and platforms are listed in Table 1. Furthermore, 31 samples presenting with waves were selected from the GEO database as a second set for WACA development. We selected 10 human samples corresponding to T-cell acute lymphoblastic leukemia (TALL) patients extracted from the GPL2879 platform. Eleven glioblastoma (GBM) and 10 melanoma (MELANO) samples were also selected in the GEO database respectively from the GPL4091 and the GPL887 platform.

Table 1.

Selected samples for WACA design

Samples	GEO numbers	Number	Type of arrays	Origin
CLL (1–11)	GSM484836–46	11	Agilent 44k	private-GPL9797
DLBCL (1–20)	GSM484847–66	20	Agilent 4 × 44 K	private-GPL9798
CONSTIT	GSM484823–35	13	Agilent 4 × 44 k	private-GPL9796
GBM (1–11)	GSM231848–58	11	Agilent 244 K	GEO-GPL4091
MELANO (1–10)	GSM188319–28	10	Agilent 244 k	GEO-GPL887
TALL (1–10)	GSM183859–68	10	Agilent 44 K	GEO-GPL2879

All arrays, from our laboratory or extracted from the GEO database, were hybridized on 44 K (CLL, CONSTIT, DLBCL and TALL) or 244 K (GBM and MELANO) arrays, and scanned with the G2505B Micro-Array Scanner System (Agilent).

Derivative Log2Ratio Spread

The Derivative Log2Ratio Spread (DLRS), as described by Kincaid et al. (12), is implemented in the DNAanalytics software (Agilent) and is the noise quantification chosen by Agilent for their arrays. This metric calculates probe-to-probe Log2Ratio noise of an array and hence of the minimum Log2Ratio difference required to make reliable amplification or deletion calls. The principal assumption of this metric is that there are not >50% of probes delimiting breakpoints. It measures the difference between consecutive Log2Ratio. The DLRS, presented as a robust method of estimating noise from the sample array alone, can range under 0.2 for excellent array and higher than 0.3 for poor experiments. Following the indications given by the manufacturer, we computed the DLRS as:

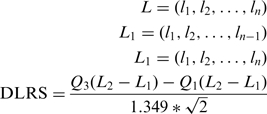Q₁ and Q₃ being respectively the first and third quartile, and L the Log2Ratios ordered by positions.

Standard deviation as a standard for quality evaluation

Without any real aberration, variation between consecutive probes is a consequence of technical noise defined as the standard deviation (SD), further referred to as inter-oligonucleotide variation and thereby reflecting the array quality. To estimate the quality of each array, we measured the SD of the Log2Ratio on the autosomes. The main pitfall of the SD is that it is biased by real aberration. However, SD is impacted by the waves, whereas DLRS is not. To assess the ability for our algorithm to correct for these wave effects and minimize the impact on real aberrations, we computed the SD correction efficiency (SDe). Given an uncorrected CGH profile and the normalized one, the SDe is calculated as follows:

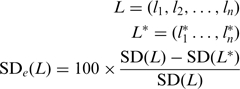with μ the mean value of L. L* is used for the corrected Log2Ratios ordered by positions.

WACA workflow

As a preliminary step to WACA, we computed all the listed biases for each probe. The GC content of the probes was included by parsing from the beginning to the end of each probe the hg18 NCBI Build 36 (wGCprobe). Following Agilent protocols, fragments are issued from DNA digestion by Alu I and Rsa I enzymes and therefore their sizes are in the majority comprised between 200 and 1500 bp. Sizes and GC contents of fragments are calculated by parsing the hg18 NCBI Build 36 for nearest enzymatic sites around each probe (wFragSize and wGCfrag). Consequently, fragments are theoretical and must correspond to a complete digestion. For the GC content of windows surrounding each probe, the procedure was the same as above with GC content of windows of 150 and 500 kb at each side of the probes (wGC150 and wGC500).

For each above-identified bias, one file with numeric values associated to each probe is created. Given these pre-computed data, WACA is based on a correction scheme as follows: after fitting a lowess curve to the Log2Ratio data without the X and Y chromosome versus the current analyzed bias, WACA subtracts to the Log2Ratio of each probe the computed variation between the lowess curve and the mean Log2Ratio. Under the assumption that aberrations (gains and loss) do not contain all the probes, the lowess computes the assessing error due to each bias, independently from gains and loss (we use the lowess implemented in the R packages with a classical smoothing parameter of 0.67). Those aberrations are therefore perfectly conserved because not linked to GC content nor fragment size but rather than with genomic position. WACA is the repeated corrections of the bias in this following order: wGC150, wGC500, wGCprobe, wGCfrag and wFragSize. Other window sizes and correction orders were tested and discussed further. All these biases were found to fit a lowess curve with probe Log2Ratio.

Implementation of WACA in RReportGenerator under R

For many conveniences, we used RReportGenerator that consists in providing a simple and user-friendly graphical user interface (GUI) that allows running routine and statistical analysis using R via predefined scenarios in a local and independent manner (13). The results (text, figures and tables) are automatically assembled into a pdf-formatted report. WACA was designed as a suite of scripts for RReportGenerator (i.e. preprocessing, correction and post-processing) to allow simple manipulation of files. Moreover, the specific GC design files corresponding to each of the bias that we detected and described are loaded as supplement files in RReportGenerator.

Statistical analysis

Hierarchical clustering (Hclust package) were computed based on the Pearson’s correlation. For clustering, the distance between two samples was 1 minus the absolute value of Pearson’s correlation of their Log2Ratio. Self-organizing maps (SOMs package) were obtained with the SOM R package querying for 2 × 2 clusters with default parameters (14). Normality test (Shapiro–Wilk) of each data set was assessed. T-tests were executed on the efficiencies of correction (Sde) and all statistical analyses were executed using R packages.

Artificial aberrations

We evaluated the capacities of WACA by simulating artificial profiles with aberrations at precise locations. The artificial profiles contain complete gain of chromosomal arm 1q (1968 probes on 103 Mb) and a partial one at 3p25.3 (only nine probes on 468 kb), total loss of chromosomal arm 2p (1061 probes on 91.3 Mb) associated with a limited one at 4q13.3 (103 probes on 5.9 Mb). We added 0.25 and −0.25, respectively for gain and loss, to the Log2Ratios of the corresponding probes of each profiles. We then applied our algorithm on the modified profiles and loaded in DNAanalytics (Agilent) raw profiles, in addition to modified profiles and WACA-corrected simulated profiles. We applied CBS as segmentation algorithm with a filter of three points and 0.2 at Log2Ratio to visually assess the effect of WACA.

RESULTS

Searching for optimal methods for waves correction

The artifactual wave effect is a general feature of aCGH data sets. It is observed worldwide and can occur in any sample, independent of the methods or the tissues used for DNA extraction. Indeed, we observed this effect on many samples varying from developmental delay to leukemia, with or without use of commercial DNA pool or autologous DNA as reference and independently of the commercial platform used (Agilent or Affymetrix). As detailed in Marioni’s study (8), the amplitude of the waves at any given chromosomal region can vary from sample to sample and, moreover, the polarity of the waves can even be reversed (Supplementary Figure S1). We hypothesized that multiple sources of bias were causing this phenomenon. Among the potential sources of bias, and assuming that all technical bias were accounted for, we focused on the GC content of the probe, of the fragments generated during DNA preparation, of the genomic windows neighboring each probe and the generated fragments sizes. In order to evaluate data corrections, two parameters could be tested: the DLRS and the SD. The first one is the Agilent’s standard for probes hybridization quality assumption and is not influenced by copy numbers, but since we hypothesized that waves were a more global phenomenon than previously described, the DLRS that computes the Log2Ratio differences between consecutive probes along the chromosomes, was not considered, although calculated, as the best metric to base on for corrections. Therefore, we preferred the SD, to evaluate the wave effect. In order to eliminate aberration effect on the SD, we rather compute the SDe as described earlier.

In an initial analysis, we aligned the wGCprobe and Log2Ratio profile across the genome of one of the TALL samples and found a correlation between both parameters (Pearson’s correlation test, r = 0.29), indicating that the wave artifact could be strongly associated with the GC content of the probes (Supplementary Figure S2A). This result was in agreement with previous studies (7). We also aligned the GC content of 150-kb windows flanking each probe with the Log2Ratio of the same sample (Supplementary Figure S2B) and obtained very similar results (Pearson’s correlation test, r = 0.30). We then tested the effect of different window sizes (ranging from 2 × 30 bp to 2 × 1 Mb) and DNA fragment sizes on aCGH data correction by computing the correction SDe of the Log2Ratio on five samples sets (62 arrays) with waves. We tested the effect of data correction based on the GC contents of the following parameters: the probe, the fragment, genomic windows spanning the probe and the fragment size. Window sizes were arbitrarily chosen at 2 × 30 bp, 2 × 200 bp, 2 × 1 kb, 2 × 10 kb, 2 × 100 kb, 2 × 150 kb, 2 × 250 kb, 2 × 500 kb and 2 × 1 Mb (Supplementary Table S1).

We employed both Student's; t-test and SDe to select the best parameters or combinations of parameters to apply for the most accurate correction. We established that correction using a 150-kb window, followed by correction using a window of 500 kb, the wGCprobe, the wGCfrag and the wFragSize was the most effective procedure (noted Wmulti10 in Supplementary Table S1). Our analysis shows that this choice of windows sizes is robust (mean SDe = 3.8873 %, P-value = 4.86 10⁻⁷). As illustrated by these results, amplitude effects of the waves are different from sample to sample, so that corrections do not act the same way for each of them.

Data analysis improvement with WACA

In order to assess WACA efficacy on data quality improvement, we considered quality parameters and SDe, and also measured the quality improvement on further classical analysis, such as hierarchical clustering, data segmentation and aberration calling.

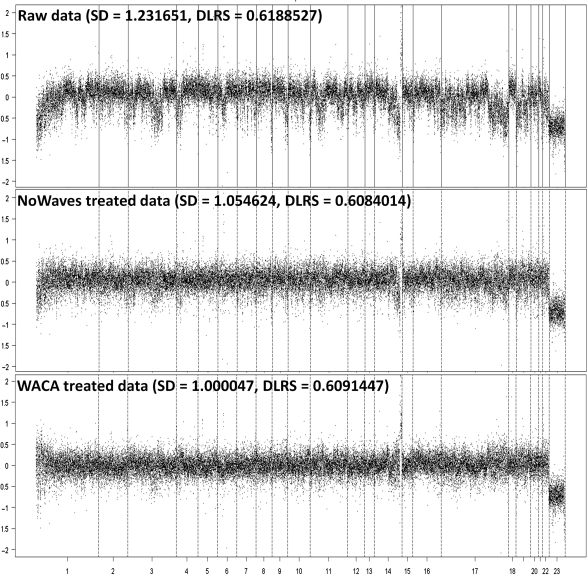
Each sample from the five sets used for correction testing was submitted to WACA using the optimal correction procedure described above. We plotted the Log2Ratio against the GC content for the 62 samples before and after WACA processing. The application of WACA significantly reduced the SD of the 62 samples (mean = 0.3408 ± 0.0805 for uncorrected data, 0.3267 ± 0.0757 after WACA; P-value = 4.86×10⁻⁷) in addition to their DLRS (mean = 0.1966 ± 0.0408 for uncorrected data, 0.1901 ± 0.0368 after WACA; P-value = 3.23×10⁻⁸).

In light of this and since both quality standards were improved by the application of WACA on aCGH data sets, we postulated that clustering of the five sets would be superior after WACA than without the treatment. We then constructed the Pearson’s correlation matrix for the 62 samples (we used the log2ratio of 21980 probes matching both 44 K and 244 K designs) and applied a hierarchical clustering to generate a dendrogram for the untreated and WACA treated samples (Supplementary Figure S3). WACA application to the raw data strongly rectified cluster formation with the five samples sets (Supplementary Figure S3). Before WACA correction, the TALL and CLL samples were not clearly separated and defined, whereas after correction, the samples clustered into five clearly distinct sets, with the exception of two CLL samples [number #1 and 5, the only samples showing a lack of large aberrations (data not shown)] and one DLBCL sample (number 10), for which the diagnosis of CLL was made before DLBCL onset. This indicated that WACA could significantly improve the analysis of aCGH data sets.

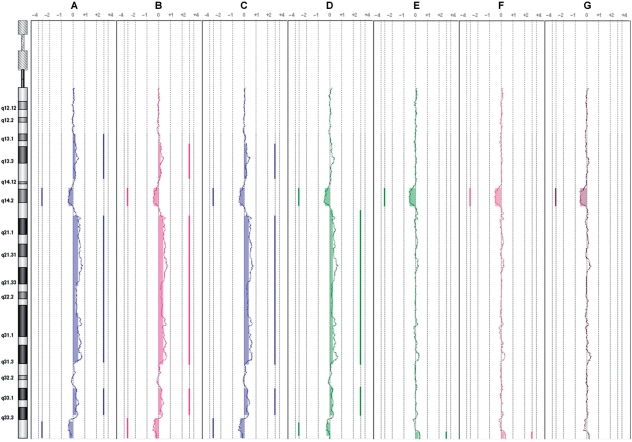
To further assess the WACA algorithm, and its interest on waves processing, we selected the noisiest CLL sample for data correction, CLL11 for which we had the karyotype [47, XX, +12, del (13)(q14.2)]. CLL11 was processed with WACA and reloaded in CGH-analytics for comparison to the uncorrected data. After circular binary segmentation (CBS) application (15), described as one of the best segmentation method (16), we confirmed that data correction with the optimal multiple parameter procedure was superior to single parameter correction alone (Figure 1). On chromosome 12 without WACA treatment, there were 11 segments. Applying WACA, only one amplified segment is detected. On chromosome 13 without WACA treatment, there were eight detected segments. With WACA, only three segments were detected, highlighting the loss at 13q14.2. It is clear that uncorrected Log2Ratios did not reflect the CLL11 sample karyotype, while the WACA-corrected sample revealed the duplication of the whole of chromosome 12 in association with a 13q14.2 deletion (5 Mb), in perfect concordance to the sample karyotype (Figure 2). This example shows that data correction by WACA considerably improved the Log2Ratio of the profile and thus the segmentation procedure. Moreover, SD and DLRS of the sample were both improved (DLRS = 0.260479 and SD = 0.4920178 before treatment; DLRS = 0.2539805 and SD = 0.3422664 after WACA treatment), allowing a more accurate characterization of the sample’s aberrations. This demonstrates undoubtedly that multiple corrections are necessary to overcome all biases since correction with part of the biases (Figure 1, lanes B–D for the GC of the probes, of the fragment and the fragment sizes, and also E and F for windows of 150 and 500 kb, in contrast to the complete correction we developed, in G) could let false aberrations (at 13q34 for lanes E and F, Figure 1). These results validate our hypothesis that bias is not only restricted to probes and neighboring fragments, but may also be acting in regions distant from the probe.

Figure 1.

Application of WACA to a noisy sample (1) WACA application on the CLL11 patient under different corrections (in order in the figure, A = raw data, B = wGCprobe, C = wGCfrag, D = wFragSize, E = wGC150k, F = wGC500k, G = wGC150k+wGC500k+wGCprobe+wGCfrag+wFragSize). Plots of the chromosome 13 are extracted from the DNAanalytics software, and moving averages of the CLL11 sample for each type of corrections are shown. Segments are represented by vertical lines on the right or the left of each profile, respectively, showing gains and losses underlined by filled boxes. As shown, only correction at line G shows a perfect correlation of the plot to the sample’s karyotype at chromosome 13.

Figure 2.

Application of WACA to a noisy sample (2) Chromosomes 12 and 13 screen captures (DNAanalytics) before and after treatment with WACA for the CLL11 sample selected as an example. Each dot represents the Log2Ratios and a moving average is also drawn. Segments are represented by vertical lines on the right or the left of each profile, respectively showing gains and losses underlined by filled boxes. The sample’s karyotype was [47, XX, +12, del (13)(q14.2)] as shown by the corrected profile.

Advanced analysis of WACA correction

In order to know whether the WACA corrections, and, hence the different corrected biases, could be associated with DNA extraction protocols, with choice of platform, sample, pathology and with DNA origin (tissue, cell and organ), a hierarchical cluster analysis was performed to group the 62 samples according to the degree of similarity present in the correction efficiencies of WACA treatment. In the resulting dendrogram (Supplementary Figure S4), the samples segregated in mainly six groups (the CLL11 sample being alone). This analysis perfectly shows that correction is independent from types of array or pathologies of samples.

At the beginning of this study, we hypothesized that there were three main biases which were independent: local GC, effect of GC in large windows and fragment sizes. Therefore, we performed a hierarchical clustering on SD efficiencies for each corrected bias. Hierarchical clustering of the windows and combinations of windows separated perfectly the type of correction that we used (Supplementary Figure S5). In this analysis, three main groups were formed: simple and small windows for correction (i.e. wGC30, wGCprobe, wGC200, wGCfrag and wGC30+wGC200), corrections with larger windows or combinations and at last one cluster grouping the corrections with the fragment size and associated combinations of windows.

Finally, we applied a current SOM approach to group samples under correction efficiency into four clusters (Supplementary Figure S6). Apart from the multiple corrections for which efficiencies remained the greatest (Supplementary Figure S6, features 10–12), samples were clustered into four sets revealing the main bias in each group. The first cluster shows a set of samples, which mainly have fragment size bias (feature1, cluster B and C), a second one for which the GC content of larger genomic regions is the main bias (cluster A, features 4–9) and samples for which correction does not change the Log2Ratio SDs considerably, which were initially of good quality (cluster D). This last analysis confirmed our above findings: first that array data correction is sample dependent, and second that corrections with GC content around each probe (in green), GC content of larger windows around these probes (in blue), fragment sizes (in gray) and combinations of these ones (in red), are typically independent (Supplementary Figure S6).

These results first show that there are almost two types of bias in addition of the fragment sizes: a local one based on probe composition, fragment size or their respective GC contents and another one more global based on the GC content of large windows; and, second, that array correction by WACA is sample dependent, but not associated with any other features, such as sample pathology, or array resolution.

Improvement of WACA with artificial aberrations

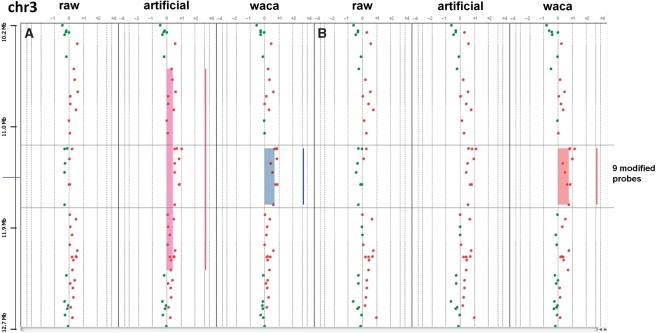
As a last test, we assessed the capacities of WACA by simulating artificial tumor profiles with no aberration at precise locations. All 13 samples showed to keep the artificial aberration after correction by WACA (data not shown). For chromosomes 1, 2 and 4 with large (up to one arm for chromosomes 1 and 2), application of WACA did not change the aberration calling. The aberrations at chromosomes 1, 2 and 4 were perfectly detected in both artificial and WACA-treated profiles and therefore are not represented. We then focused on the smallest artificial aberration at 3p25.3 (a gain of 468 kb with nine modified probes), correction by WACA provided impressing results. First, WACA application led to a more precise aberration calling after segmentation by CBS in DNAanalytics for one of the samples (sample A, Figure 3). Agilent’s software detected a gain of 1.7 Mb defined by 28 probes in the artificial sample at 3p25.3. This gain was refined to a region of 468 kb with nine probes for the WACA-corrected sample. Interestingly, those nine probes correspond to the probes for which we artificially simulated one aberration at 3p25.3. The second interesting point is the perfect recovery of this last artificial aberration for another sample (sample B, Figure 3): whereas the artificial profile does not show any aberration, the WACA corrected profile showed the aberration that we simulated.

Figure 3.

Chromosome views of artificial profiles. Two samples (A and B) are shown for the following conditions (raw data, modified data and WACA corrected modified data) for chromosome 3. CBS-detected segments are represented by vertical lines on the right of each profile, respectively, showing gains underlined by filled rectangles. The nine modified probes are underlined across the profiles. As shown, while WACA in sample A allows a better delimitation of the artificial aberration, our algorithm allows the recovery of the same aberration in sample B after CBS segmentation.

These last examples demonstrate perfectly that in addition to greatly improving data quality, our algorithm allows both a more precise aberration calling and the recovering of real aberrations in noisy samples, while false aberrations are skipped.

WACA comparison to GC-content-based and not-based algorithm

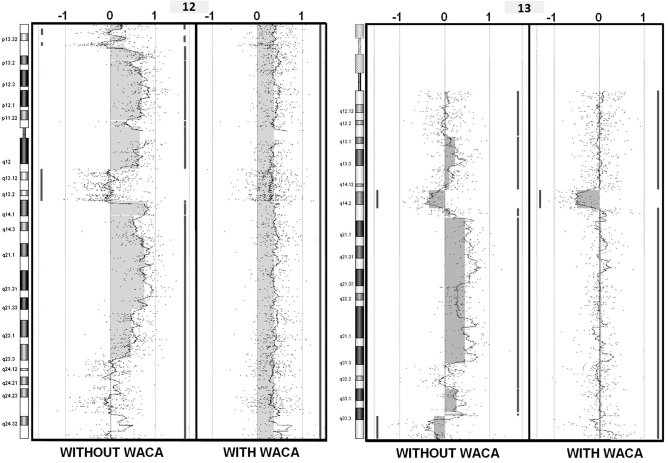
Finally, we compared our method to the algorithm presented by Nannya et al. (9), Song et al. (10) and Van de Wiel et al. (11) by using 20 Belgian tumor profiles extracted from this last study. We used these data and applied our algorithm (WACA) and theirs (in the order, CNAG, MA2C and NoWaves) and computed as described above the SDe and DLRS correction efficiencies (Table 2). Although we reached a better mean efficiency correction for WACA (17.09±6.04% for SDe, 5.41±4.47% for DLRS) compared to CNAG (1.24±0.76% for SDe, −1.46±1.51% for DLRS) and MA2C (0.47±0.34% for SDe, −0.39±0.98% for DLRS), corrections were not significantly different when comparing to NoWaves (14.42±7.92% for SDe, 1.13 ± 0.75% for DLRS). As illustrated in Figure 4, we plotted one Belgian sample data (n°7276), comparing the raw versus the NoWaves or the WACA-treated data. This figure shows that application of both algorithms greatly improved the quality of this noisy sample.

Table 2.

Algorithm comparison on data quality improvement efficiency (%)

	WACA	CNAG	MA2C	NoWaves
SDe
Mean	17.09	1.24	0.47	14.42
SD	6.04	0.76	0.34	7.92
T-test	1.07×10−10	6.05×10−7	6.83×10−6	1.27×10−7
DLRS
Mean	5.41	−1.46	−0.39	1.13
SD	4.47	1.51	0.98	0.75
T-test	3.19×10−5	3.84×10−4	9.23×10−2	1.94×10−6

Figure 4.

NoWaves and WACA comparison. Applying NoWaves methods, profiles of one of the Belgian samples (n°7276) showing raw data and data respectively treated by NoWaves and WACA.

We also compared our algorithm to CNVmix, described by Marioni et al. (8), by using the CLL11 sample for which the karyotype was known. For the smallest aberration (at chromosome 13q14.2), CNVmix let to identify a group of 34 probes spanning 4.428 Mb but divided in 21 segments (with lost, gain and normal status), whereas WACA allowed the detection of an entire lost segment (75 probes spanning 4.958 Mb), in perfect concordance to the sample karyotype. Assuming the fact that we were not able to compare both quality improvements (for WACA and CNVmix), since CNVmix does not provide the corrected Log2Ratios, this last test shows that our algorithm lets a more precise aberration calling.

DISCUSSION

We and others have noted the presence of the waves throughout the genome in a number of aCGH data sets but nevertheless, the mechanisms leading to these waves are still unclear. Many methods tried to correct the effects of these waves but did not reach our results (those algorithms are listed in Table 3). Marioni and colleagues (8) applied a lowess-threshold-based algorithm that does not take into account all biases associated with GC contents nor fragment sizes. Marioni’s paper furthermore shows a correlation between GC content of each probe and Log2Ratio, revealing that the GC content of huge windows (larger than oligonucleotides probes since they used BAC clones) can influence the wave effects. Another team proposed a correction for single nucleotide polymorphism (SNP) arrays based on the GC content of the probes (10) but still do not consider the whole effect of this GC content along the genome as we demonstrated. Komura’s method reaches a better correction in pointing some unreliable probes or clones, and in correcting the Log2Ratio by the probes adjacent GC contents (17), but still is limited to the local GC and the sizes of the fragments. The lowess algorithm proposed by Nannya et al. (9) takes into account only part of biological and experimental parameters (length and GC content of the PCR products). Some of the above parameters were included in our method of waves correction [as the GC content of the probes (10,17), the GC contents of fragments (9,17), and the sizes of fragments (17)]. These methods claimed their efficiency to extract all bias from microarray data sets and to produce more consistent data for analysis; however, we have shown that there was another bias related to the GC content of larger windows surrounding the probes. Our method that relies on the local GC content (of the probes and the fragment), associated with a larger GC content (defined by windows up to 2 × 500 kb) in addition to the sizes of the fragments, exhibits an advanced way to correct for aCGH data, independently from the platform, from the samples and the probe density of the arrays.

Table 3.

Algorithms comparison

Names	References	Technologies	Correction specification
–	Komura et al. (2006)	Affymetrix 10 K oligonucleotides microarrays	Probes and fragments GC contents and fragments sizes
CNVmix	Marioni et al. (2007)	26 K BAC clones arrays	Threshold based lowess
CNAG	Nannya et al. (2005)	Affymetrix 100 K oligonucleotides arrays	length and GC content of the PCR products using quadratic regressions
MA2C	Song et al. (2007)	NimbleGen 400 K tiling microarrays	GC-content of probes
NoWaves	Van de Wiel et al. (2009)	Agilent custom 44 K arrays	Regression on a reference array set
WACA	Leprêtre et al. (2010)	Agilent 44 and 244 K oligonucleotides arrays	GC contents of probes, fragments, windows of 150 and 500 kb, and fragment sizes

Van de Wiel et al. (11) present an interesting algorithm, independent of the GC contents. It is a regression method that removes the wave biases from tumor profiles, but it implies the creation of a calibration set. Making a calibration set for each design (for each number and choice of probes) is a complex task because data should contain no aberration. Amazingly, our method, which is based on known biases, is at least as good as their method. As they use calibration profiles, it should mean that we identified all common biases from their data. In this case, with all (or most of) biases identified, using WACA and skipping the difficult task of calibration emphasizes our method. By applying WACA, we significantly improved the quality of the majority of our data as illustrated by our analysis and examples. Furthermore, one of these examples illustrates clearly that multiple corrections are necessary to overcome all biases since correction with part of the biases could allow false aberrations. The application of WACA to the CLL11 sample strikingly demonstrates the utility of WACA for array data correction. This further illustrates that waves correction is likely to have a significant effect on advanced data analysis in aCGH experiments. The use of WACA to this sample clearly shows the precision of aCGH compared to classic cytogenetic methods, and the strong usefulness of our algorithm in array correction: while false aberrations are skipped, all real ones are conserved, and thus highlighted (as also illustrated on artificial aberrations). Hierarchical clustering analysis and application of WACA allowed us first to have a better classification of the five samples sets that we used, and second to show that waves are the contribution of at last three main causes, the GC content around each probes, the GC content of larger windows around theses probes, with a deep implication of the fragment sizes. We have described the development of WACA, a novel algorithm for noise (waves) reduction of aCGH data sets, based on GC content and fragment size corrections, and its implementation as a comprehensive, multiparameter correction procedure for aCGH data. One parameter that should be taken into account is the restriction enzymes used in the technical procedure. Enzymatic sites are computed from the University of California Santa Cruz (UCSC) database and should be adapted to each technical protocol used depending on the platform. We build the WACA scripts with the idea that each step is independent and thus wFragSize or wGCFrag files, associated with the enzymatic procedure, could be modified.

We propose WACA to be performed in CGH array data analysis, since we proved that this algorithm seriously increases data quality, and therefore allows more reliable analysis. As discussed in other studies, waves are detected in other platforms and therefore should be modeled as we have shown for Agilent. Thus, we emphasize to develop our algorithm to be performed on these platforms and for other applications with DNA hybridization such as ChIP-on-chip and DNA methylation studies.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

The INCa agency, Cancéropôle Nord-Ouest and French ministry for health and research. Funding for open access charge: Cancéropôle Nord-Ouest.

Conflict of interest statement. None declared.