Streamlined determination of processive run length and mechanochemical coupling of nucleic acid motor activities

Abstract

Quantitative determination of enzymatic rates, processivity and mechanochemical coupling is a key aspect in characterizing nucleotide triphosphate (NTP)-driven nucleic acid motor enzymes, for both basic research and technological applications. Here, we present a streamlined analytical method suitable for the determination of all key functional parameters based on measurement of NTP hydrolysis during interaction of motor enzymes with the nucleic acid track. The proposed method utilizes features of kinetic time courses of NTP hydrolysis that have not been addressed in previous analyses, and also accounts for the effect of protein traps used in kinetic experiments on processivity. This analysis is suitable for rapid and precise assessment of the effects of mutations, physical conditions, binding partners and other effectors on the functioning of translocases, helicases, polymerases and other NTP-consuming processive nucleic acid motors.

INTRODUCTION

Linear motor enzymes convert chemical energy derived from nucleotide triphosphate (NTP) hydrolysis into mechanical work, which results in the displacement of the motor along its polymer track. Cytoskeletal motors exert directed movement along actin filaments or microtubules, whereas a diverse set of motors (translocases, helicases, polymerases, chromosome remodeling enzymes, etc.) act on nucleic acid polymers (DNA, RNA or heteroduplexes). Motors generally show a directional bias and move toward one end of the structurally polar track (+ or − end of cytoskeletal filaments, and 3′- or 5′-end of nucleic acids).

Apart from directionality, the functionally most important macroscopic parameters of biological motors include the macroscopic rate of translocation [k_trans, defined as track length units (e.g. nucleotides, nt) traveled per unit time] and the mechanochemical coupling ratio (C, number of NTP molecules hydrolysed per enzyme per length unit traveled) (Table 1). Another key parameter is processivity, i.e. the ability of the motor to perform multiple mechanochemical cycles without dissociating from its track. Quantitatively, processivity (P) is expressed as the probability of taking the oncoming translocation cycle (as opposed to dissociation) (Table 1).

Table 1.

Parameters used in the analysis

Parameter	Unit	Description	Relation to other parameters
L	(nt)	Track length (nt = nucleotide unit)
b	(nt)	Binding site size
C	(nt−1)	Mechanochemical coupling ratio ([NTP hydrolyzed]/ [enzyme]/nt traveled)	C = ka/ktrans = c/m
ka	(s−1)	Steady-state NTP hydrolysis rate during translocation ([NTP hydrolyzed]/ [enzyme]/s)	ka = Cktrans = c(kt + kd); (kt + kd = net rate constant of kinetic step)
ktrans	(nt s−1)	Macroscopic rate of translocation	ktrans = ka/C = m(kt + kd)
c	–	Coupling stoichiometry ([NTP hydrolyzed]/ [enzyme]/kinetic step)	c = mka/ktrans = Cm
m	(nt)	Kinetic step size (nt traveled/kinetic step)	m = cktrans/ka = c/C
P	–	Kinetic processivity (probability of taking the next kinetic step)	P = kt/(kt + kd)
Pmacr	–	Macroscopic processivity, suitable for calculation of: Mean number of NTP molecules consumed in a single run (at infinite track length) = Pmacr/(1–Pmacr) Mean number of nucleotides travelled in a single run (at infinite track length) = Pmacr/(1–Pmacr)/C	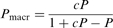[see also Equation (10)]

The above macroscopic parameters result from underlying multistep kinetic mechanisms of motors, for which a number of assay methods have been developed (1–11). Here, we present a streamlined analytical method utilizing the availability of fixed-length nucleic acid tracks and well-established sensors of NTP hydrolysis during motor activity. Using this analysis, all key macroscopic features of motor activity can be determined in a single set of experiments with high accuracy. The method is generally applicable for various NTP hydrolysis-linked mechanochemical activities of nucleic acid motors, including translocation, unwinding, branch migration and polymer synthesis.

MATERIALS AND METHODS

Kinetic simulations were performed using Gepasi 3.30 (www.gepasi.org). NLLS fitting was carried out using Origin (Microcal Corp.).

RESULTS AND DISCUSSION

Track length-dependence of NTP consumption in a processive run

During a processive run, processivity (P) can be defined as the probability of the motor taking the next step of translocation. Dissociation will thus occur at probability 1–P during any translocation step. The probability of the motor performing a run comprising exactly n steps (p(n)) on an infinite-length track will be

(1)

Consequently, the mean number of steps (<n>) performed in a single run on an infinite-length track at processivity P will be

(2)

On a track of finite length (permitting of N steps), however, the mean number of steps taken by the enzyme in a single run starting from one end of the track (<n_end(N)>) will be smaller than <n>, because the fraction of enzymes reaching the other end of the track (q_end(N) = P^N) cannot continue their way. Therefore, the expected number of their steps that would be taken further on from this end position if the track was infinite (which is also <n>) has to be discounted:

(3)

In the case of a random start position (leaving r steps ahead of the enzyme, distributed uniformly between 0 and N ), the fraction of enzymes reaching the end of the track will be

(4)

and, thus, the mean number of steps (<n_rand(N)>) taken in a single run will be

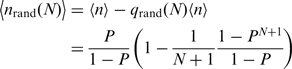(5)

In Equations (3–5), the unoccupied length of the track (N) is expressed in steps taken by the enzyme. Practically, it is more favourable to express the total length of the track (L) in nucleotide units, and also account for the stretch of the track occupied by the bound enzyme (b, also expressed in nt units; this is the minimum track length to which the enzyme can strongly bind but on which it cannot take any translocation steps, Table 1). A kinetic step of translocation is generally defined as a series of mechanochemical cycles between two successive rate-limiting events. N will thus equal (L–b)/m where m, the kinetic step size, is the average number of nucleotides advanced in a single kinetic step. Denoting the coupling stoichiometry (i.e. the average number of NTPs hydrolysed during a kinetic step) as c, the amplitude of NTP consumption (A, expressed as mol NTP per mol enzyme) during a single processive run can be expressed as

(6)

for runs starting from one end of the track [compare Equation (3)], and

(7)

for runs with a random start position [compare Equation (5)], respectively. Note that Equation (7) is equivalent to Equation (26) of a more general and mathematically more involved analysis by Fischer and Lohman (12).

If P is close to unity (P > 0.9, which is the practically relevant scenario in most studies), Equations (6) and (7) cannot be used in practice to resolve the values of c and m independently, because A will depend predominantly only on their ratio C = c/m, which is often referred to as the mechanochemical coupling ratio (average number of NTPs hydrolysed per nucleotide unit traveled) (Table 1). For practical reasons, in the following we will arbitrarily set c = 1 (and thus m = 1/C). This choice is also motivated by the fact that the majority of processive enzymes hydrolyze one NTP to take a step. Equations (6) and (7) will then become

(8)

for runs starting from one end of the track, and

(9)

for runs with a random start position, respectively. It is important to note that the processivity in the simplified formulas of Equations (8) and (9) (which we will call macroscopic processivity, denoted as P_macr) will be different from the true microscopic kinetic processivity P if the real value of c differs from unity. The two processivities are related to each other through the requirement that they both reproduce the same average run length (see also Table 1):

(10)

Equations (8) and (9) can readily be used for non-linear least-squares (NLLS) fitting of the track length-dependence of amplitudes of NTP consumption by motor enzymes in single-round translocation conditions (Figures 1 and 2). These experiments are typically performed in rapid-mixing (stopped-flow or quenched-flow) apparatuses, by mixing the contents of one syringe containing enzyme plus track, and the other syringe containing NTP (at saturating concentration) plus a protein trap (to prevent rebinding of the enzyme to another track molecule after completing a single round of translocation). The time course of the appearance of hydrolysis products is usually monitored by using either a well-characterized fluorescent sensor of inorganic phosphate [MDCC-PBP, (13)] or radioactively labeled (e.g. γ-³²P-) NTP. In these time courses, the initial rapid phase corresponding to NTP hydrolysis during translocation of the enzyme is followed by a slower phase of product appearance resulting from NTP hydrolysis by enzyme molecules bound to the protein trap. The amplitude of the translocation phase can be determined from the linear intercept of the two phases. In addition to the amplitude analysis, the slope of the translocation phase can be used to calculate the steady-state rate of NTP hydrolysis during translocation (k_a, Table 1) and, in turn, the macroscopic rate of translocation (k_trans = k_a/C, Table 1), which are usually independent of track length.

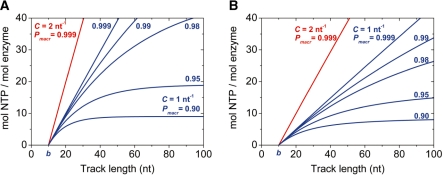
Figure 1.

Track length-dependence of the amplitude of NTP hydrolysis during single-round translocation starting from one end of the track (A) or a random site (B). Curves shown were simulated using Equations (8) (A) and (9) (B) for b = 10 nt, C = 1 nt⁻¹ (blue curves) or 2 nt^–1 (red curves), and the indicated P_macr values. The very low degree of parameter correlation is indicated by the fact that b defines the intercept of the horizontal axis [in (A) and (B)], C determines the initial slope [in (A) and, notably, C/2 in (B)], whereas the maximal amplitude at infinite track length is P_macr/(1–P_macr). Note that Equations (8) and (9) are interpreted for values of L ≥ b.

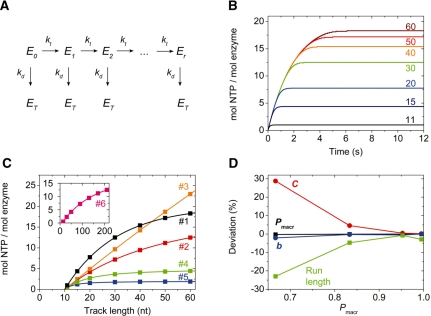
Figure 2.

Verification of the accuracy of NLLS analysis by global kinetic simulations. (A) Kinetic model of a motor enzyme (E) taking mechanical steps at a net rate constant k_t (at saturating NTP concentration), and dissociating from the track at a net rate constant k_d. E_i represents enzyme after taking the i-th step of translocation and E_T represents enzyme in the protein trap-bound state (after dissociating from the track). No NTP hydrolysis by E_T occurs in the model. (B) Simulated time courses of NTP hydrolysis based on the model in (A), using parameter set #1 in Table 2, concerning processive runs starting from one end of a series of tracks of different length (indicated in nt). (C) NLLS fits (solid lines) to the track length-dependence of the amplitude of NTP hydrolysis during single processive runs starting from one the end of the track [black symbols, from time courses in (B), parameter set #1 in Table 2] and from a random start position [parameter sets #2 (red), #3 (orange), #4 (green), #5 (blue) and #6 (pink) in Table 2]. Fits based on Equations (8) (black line) and (9) (all other lines) reproduced the input parameters of the simulations with high accuracy (Tables 2 and 3). (In each data set, 7 of 51 simulated data points are shown for clarity.) (D) Deviations of the fitted parameters from input values of simulations, as a function of P_macr (see also Tables 2 and 3).

Figure 1 shows examples of the track length dependence of NTP consumption during single-round translocation. Equation (8), describing runs starting at one end of the track, can be used for instance in double-stranded (ds) DNA unwinding experiments where the enzyme starts from a single-stranded (ss) DNA tail (Figure 1A). Many translocases exhibit random initial binding to the nucleic acid track (1–3,5,14–16). In these cases, the model described by Equation (9) is applicable (Figure 1B). The three floating parameters (P, C and b) contained in the models show very little correlation, which is highly advantageous for their precise determination using NLLS algorithms (see Figure 1 legend).

As detailed below, we verified the accuracy of the NLLS analysis by generating simulated time courses of NTP hydrolysis by an enzyme starting from one end of the track and from a random position, using a kinetic scheme of single-round translocation shown in Figure 2A. The amplitudes of NTP consumption in the simulated courses (Figure 2B) were fitted using Equations (8) and (9) (Figure 2C). The input parameters were reproduced by the NLLS fit with high accuracy (Figure 2D, Table 2).

Table 2.

Accuracy of NLLS fits of the track length dependence of NTP hydrolysis amplitudes

Parameter set	#1	#2	#3	#4	#5	#6
Start site	End of track	Random	Random	Random	Random	Random
Equation used in NLLS fit	Equation (8)	Equation (9)	Equation (9)	Equation (9)	Equation (9)	Equation (9)
kt (s−1)	10	10	100	10	10	10
kd (s−1)	0.5	0.5	0.5	2	5	0.5
b (nt)	10	10	10	10	10	10
b (nt, best-fit)	9.958	9.950	10.002	9.875	9.894	9.799
Deviation (%)	−0.42	−0.50	0. 020	−0.25	−1.1	−2.0
C (nt−1)	1	1	1	1	1	0.25
C (nt−1, best-fit)	1.00008	1.005	1.002	1.046	1.288	0.2512
Deviation (%)	0.0080	0.47	0.20	4.6	29	0.48
Pmacr	0.95238	0.95238	0.99502	0.83333	0.66667	0.95238
Pmacr (best-fit)	0.95244	0.95226	0.99488	0.83284	0.66508	0.95226
Deviation (%)	0.0063	−0.013	−0.014	−0.069	−0.24	−0.013
Mean run length on infinite-length track (nt, see Table 1)	20	20	200	5	2	80
Mean run length on infinite-length track (nt, from best-fit)	20.02	19.85	193.9	4.763	1.542	79.41
Deviation (%)	0.13	−0.74	−2.9	−4.7	−23	−0.74

Simulations of the time course of NTP hydrolysis in single-round translocation conditions (examples shown in Figure 2B) were based on the kinetic model shown in Figure 2A.

Input parameters used in simulations are shown in bold; parameters varied between simulations are italicized.

Equations were fitted to 51 simulated data points (representing amplitudes at different track lengths) in each case.

The precisions of the fitted parameters are indicated by displaying all of their significant digits obtained in the NLLS fits.

Effect of non-translocating ‘futile’ NTP hydrolysis cycles on the amplitude of NTP consumption

After completing translocation, some enzymes remain bound to the end of the track for significant time periods and may perform ‘futile’ rounds of NTP hydrolysis before track dissociation (2,3). This phenomenon may significantly affect the NTP consumption amplitudes defined in Equations (8) and (9). Taking c* as the mean number of extra NTP molecules hydrolyzed by an enzyme before track dissociation (c* = k_end/k_{off, end} where k_end is the net rate constant of NTP hydrolysis by the track-end-bound non-translocating enzyme and k_{off, end} is the net rate constant of enzyme dissociation from the track end), Equations (8) and (9) must be supplemented by c*·q_end(N) and c*·q_rand(N), respectively, leading to

(11)

for runs starting from one end of the track, and

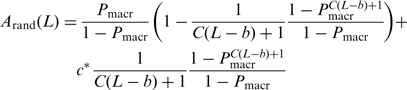(12)

for runs with a random start position. In contrast to Equations (8) and (9) in which all floating parameters (P_macr, C and b) are non-covariant and can thus be precisely determined, the introduction of c* results in significant parameter covariance in NLLS fits. This limits the utility of Equations (11) and (12) for fitting to experimental data. Therefore, we investigated the effect of NTP hydrolysis in the non-translocating state on the error introduced into the P_macr, C and b output values of Equation (9). We found that C and P_macr can be determined using Equation (9) with reasonable accuracy even at high c* values where NTP consumption in the non-translocating state is close to that during single-round translocation (Figure 3). The fitted parameter b is the only one that cannot be reliably determined in the presence of NTP hydrolysis in the non-translocating state. In summary, Equations (8) and (9) produce reliable values for C and P_macr even at significant extents of NTP hydrolysis by non-translocating enzymes (c*), whereas Equations (11) and (12) can be used for the determination of c* if an independent estimate of the binding site size (b) is available.

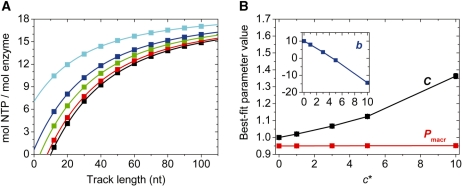
Figure 3.

Effect of extra NTP hydrolysis cycles by enzymes bound at the end of the track on the observed amplitude of NTP hydrolysis. In (A), squares indicate simulated amplitudes of NTP consumption by an enzyme performing a processive run based on the scheme shown in Figure 2A, with the modification that it consumes c* = 0, 1, 3, 5 or 10 NTP molecules (black, red, green, blue and cyan symbols, respectively) upon reaching the end of the track (E_r state in Figure 2A) before track dissociation [other parameters: b = 10 nt, c = 1 and m = 1 nt (defining C = 1 nt^–1), P = 0.95]. Solid lines show the results of fits to the data based on Equation (9), not accounting for NTP hydrolysis by non-translocating enzymes [equivalent to a fixed c* = 0 in Equation (12)]. The error introduced into the determined values of C, b and P by ignoring NTP hydrolysis in the non-translocating state [i.e. using Equation (9) for the data in (A)] is shown in (B). The value of P_macr was practically independent of c*: it increased from 0.95 to 0.95157 (equivalent to a mean number of 19.00 to 19.65 NTPs hydrolyzed in a single run) in the c* range investigated. The output value of C was moderately affected: it increased from 1.00 at c* = 0 to 1.36 at c* = 10. Parameter b is the only one whose output value is heavily affected by c*.

Effect of the protein trap on processivity

Heparin has been widely used as a protein trap to generate single-round conditions in which the motor cannot rebind to the track after dissociation (5,12,14–16). Heparin has the advantageous feature that, unlike the nucleic acid track, it does not activate the ATPase activity of nucleic acid motors. However, it has been shown to affect the processivity of enzymes; it generally increases k_d, but in principle it may also affect k_t (compare Figure 2A). In these conditions, the measured processivity [P = k_t/(k_t + k_d), Figure 2A] will depend on trap concentration ([T]) as

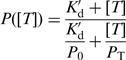(13)

where P₀ and P_T are processivity values at zero and saturating trap concentrations, respectively, and 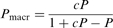is the apparent dissociation constant for trap binding to the motor (expressed in the same unit as [T]; 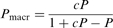= K_d(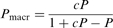/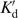) in which K_d is the net dissociation constant for trap binding to the motor during translocation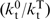, and and 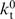are net rate constants of translocation in the trap-free and trap-bound states, respectively). Determination of P at a series of trap concentrations thus allows for the calculation of the value of processivity in the absence of trap (P₀). Equation (13) is valid for both kinetic (P) and macroscopic (P_macr) processivity values. Naturally, Equation (13) can generally be used also for protein traps other than heparin.

Validation of the models

The utility of the proposed equations was validated by performing numerical simulations based on a kinetic model shown in Figure 2A, considering runs starting either from one end of the track or from a random start point (Figure 2B and C, Table 2). Parameters k_t, k_d and C were varied to test the accuracy of the fits (Figure 2C and D, Table 2). The robustness of the fits is indicated by the fact that the fitted parameters P_macr and b could be determined with high accuracy at various k_d and k_t input values defining a broad processivity range (0.66667–0.99502) (Figure 2D, Table 2). At P_macr < 0.7, the determination of C is more difficult due to the very low value of <n>, though its accuracy is still reasonable (Figure 2D, Table 2). In contrast, in the range P_macr ≥ 0.83 (corresponding to <n> ≥ 5, which is the range relevant to the large majority of biological motors), the uncertainty in the fitted value of C is below 5% (Figure 2D, Table 2), which is comparable to the usual magnitude of experimental uncertainty. We also verified that P_macr and b can be accurately determined even if C markedly differs from unity (Figure 2C, inset, parameter set #6 in Table 2). Variation of the input parameter b simply causes a horizontal shift of the data points in Figure 2C and, thus, it does not influence the accuracy of the fitted parameters.

We have also assessed the effect of the number of data points (representing different track lengths) used in the NLLS fit. Table 3 shows that P_macr, b and C can be accurately determined even at a low number of data points (down to 6 points). This confirms the usefulness and applicability of the proposed equations even for experiments in which a limited number of oligonucleotides is used. However, considering the typical uncertainties present in actual experiments, the use of at least 10–12 different track lengths is advisable to ensure high accuracy. Data points at short track lengths improve the accuracy of the determination of b and C, while data points at long tracks more precisely define P_macr. Thus, we suggest a quasi-logarithmic sampling of track lengths around the expected run length of the given enzyme.

Table 3.

Dependence of the accuracy of NLLS fits on the number of data points used

Number of data points	Deviation (%)
	C	b	Pmacr	Mean run length on infinite-length track
51	0.47	−0.50	−0.013	−0.74
26	0.54	−0.43	−0.016	−0.87
14	0.51	−0.35	−0.017	−0.86
6	0.42	−0.14	−0.0042	−0.51

Deviations of fitted parameters from input values are shown, using parameter set #2 in Table 2 and different numbers of simulated data points (representing amplitudes at different track lengths).

Although the floating parameters P_macr, b and C can easily be initialized manually for the NLLS fits, accurate initial estimates are usually not required in order to find the global best-fit parameters instead of false local minima. For instance, the best-fit values for parameter set #5 in Table 2 were found in as little as 10 iteration cycles even at highly inaccurate parameter initialisation (P_macr = 0.99999, b = 1 nt and C = 100 nt^–1). As pointed out above, the robustness of the fit is due to the small number of non-covariant parameters in Equations (8) and (9).

Utility and limitations of the analysis

We demonstrate the utility of the analytical method proposed in this paper for the analysis of experimental data in the case of a human Bloom’s syndrome helicase construct (Gyimesi et al., accompanying manuscript under review). The major advantage of this method is that it effectively extracts information contained in NTPase time courses to determine all important macroscopic parameters of motor activity (rates of NTP hydrolysis and translocation, binding site size, mechanochemical coupling, mean number of nucleotides traveled and NTPs consumed in a processive run; Table 1), using relatively simple NLLS fits with a small number of non-covariant parameters [Equations (8) and (9)]. In experiments monitoring NTP consumption, no labeling of the enzyme or the track is necessary, which eliminates a potential source of artifacts. The proposed method provides accurate information on processive run length even in experiments performed in a track length range hardly exceeding the mean run length of the enzyme (Figures 2 and 3). Most evident examples for application include nucleic acid translocases, helicases and polymerases. The relative simplicity of the method makes it suitable for quantitative screening of the effects of various conditions (enzyme mutations, truncations, track composition/sequence, temperature, binding partners, inhibitors, etc.) on motor activity. [Translocation rate and processivity (but not mechanochemical coupling) can also be measured in single-molecule experiments, but in such assays the reliable determination of parameters is labor extensive even for a single set of conditions.]

Various methods of pre-steady-state kinetic analysis have been applied to nucleic acid motor activities, including ones based on time courses of NTP consumption (16). The analytical approach proposed here utilizes several features that have not been exploited or explicitly treated in previous analyses. First, we treat processivity (P_macr) as a global variable, as opposed to being calculated from net (non-elementary) rate constants of translocation (k_t) and track dissociation (k_d) (Figure 2; Table 1). The deviation from linearity of the track length-dependence of NTP consumption during single-round translocation has been observed in previous studies, but this phenomenon has not been addressed as a basis for determining processivity (2). Moreover, the proposed analysis of trap concentration dependence of processivity [Equation (13)] allows the direct determination of processivity in the absence of the trap. Further key features of the proposed analysis include the use of explicit summations (instead of approximations) for calculating the mean number of steps taken [Equations (2), (3) and (5)] and, in turn, NTP consumption [Equations (8), (9), (11) and (12)] and track length traveled (Table 1) in processive runs; and the applicability for runs starting from one end of the track and also for ones with random start positions [Equations (5–8)].

Equations (8) and (9) account for NTP consumption by motors prebound to the track and starting uniform progression along the track upon addition of NTP. However, in some cases, an initial slow kinetic step preceding the translocation phase has been identified (2,17). In other cases, a rapid initial product (P_i) release phase preceding steady-state translocation can occur, as we demonstrated in the case of the human Bloom’s syndrome helicase (Gyimesi et al., accompanying manuscript under review). Either of these scenarios can affect NTP hydrolysis time courses. However, the amplitude of NTP hydrolysis in the translocation phase will be affected only if NTP hydrolysis occurs in non-translocating enzymatic cycles. In such cases, Equations (8) and (9) should be supplemented by a constant term corresponding to the number of NTPs hydrolysed per enzyme in the non-translocating phase.

Another possible complication may arise from the recently described phenomenon that, during enzymatic unwinding of a dsDNA track, the last few base pairs may break spontaneously. This event may cause the motor to complete its processive run in ssDNA translocation mode in which its mechanochemical parameters may differ from those during dsDNA unwinding (7). In our analysis, NTP hydrolysis during translocation along the short remaining ssDNA stretch will influence the observed NTP hydrolysis amplitudes in a way similar to the ‘futile’ NTP hydrolysis cycles accounted for by the c* term in Equations (11) and (12) (see also Figure 3). As discussed above, such phenomena introduce uncertainty in the determination of b, whereas P_macr and C can still be accurately determined.

In principle, a translocation mechanism may be non-uniform, comprising repeated global ‘kinetic steps’ [occurring at a net rate constant (k_t + k_d), compare Figure 2A, Table 1] that involve multiple NTP-consuming (and coupled translocation) cycles with different kinetics, one of which is rate-limiting in the series (12). In this manner, the enzyme can consume a total number of c NTP molecules and travel m nucleotides (kinetic step size) per kinetic step, taken at probability P (kinetic processivity) (Table 1). The most important limitation of the method presented here is that, by determining the macroscopic rates of NTP consumption and translocation, it will not resolve uniform versus non-uniform ‘microscopic’ stepping mechanisms. This is a consequence of the fact that, as pointed out by Fischer and Lohman (12), the NTP consumption time courses alone do not contain all information necessary for the detailed resolution of non-uniform stepping schemes and the independent determination of the values of c and m. However, we emphasize that the macroscopic parameters determined in the proposed analysis using Equations (8), (9), (11) and (12) (as listed in Table 1 alongside with their relation to microscopic parameters) correctly define the key functional aspects of enzymatic activity even in the case of more complex underlying stepping mechanisms, with similar accuracy to those of previous analyses requiring more extensive experimentation (Figures 2C and D, and 3) (5,12,14–16). As noted above, the macroscopic processivity (P_macr) defined in the current analysis will be different from the ‘fundamental’ kinetic processivity (P) if c differs from unity (Table 1). Importantly, however, P_macr can be used for calculation of the essential functional parameters of NTP consumption and length traveled during a single run, regardless of the microscopic kinetic mechanism (i.e. the values of c and m) (Table 1).

As pointed out earlier, a serious disadvantage of more complicated NLLS analyses is the high degree of parameter correlation (12). The macroscopic parameters (e.g. C = c/m) are always better constrained than the microscopic ones (e.g. the individual values of c and m) even in those treatments. Similarly, global kinetic analyses of more complicated models are mostly unable to provide constrained estimates of all parameters (12). It also should be stressed that even the above ‘microscopic’ parameters reflect the net result of an intricate network of underlying elementary enzymatic steps (substrate binding, chemical hydrolysis step, product release and coupled conformational transitions). Information about these sub-processes and the directionality of translocation must be obtained from more detailed and labor-consuming sets of experiments monitoring the interaction of the enzyme with the NTP substrate and the nucleic acid track using various signals (5,12,14–16).

FUNDING

Funding for open access charge: Hungarian Scientific Research Fund (K60665 to I.D., 71915 to M.K.); Norway Grants (78783 to M.K.). M.K. is a Bolyai Fellow of the Hungarian Academy of Sciences.

Conflict of interest statement. None declared.