Selective Regions of the Visuomotor System Are Related to Gain-Induced Changes in Force Error

Abstract

When humans perform movements and receive on-line visual feedback about their performance, the spatial qualities of the visual information alter performance. The spatial qualities of visual information can be altered via the manipulation of visual gain and changes in visual gain lead to changes in force error. The current study used functional magnetic resonance imaging during a steady-state precision grip force task to examine how cortical and subcortical brain activity can change with visual gain induced changes in force error. Small increases in visual gain <1° were associated with a substantial reduction in force error and a small increase in the spatial amplitude of visual feedback. These behavioral effects corresponded with an increase in activation bilaterally in V3 and V5 and in left primary motor cortex and left ventral premotor cortex. Large increases in visual gain >1° were associated with a small change in force error and a large change in the spatial amplitude of visual feedback. These behavioral effects corresponded with increased activity bilaterally in dorsal and ventral premotor areas and right inferior parietal lobule. Finally, activity in the left and right lobule VI of the cerebellum and left and right putamen did not change with increases in visual gain. Together, these findings demonstrate that the visuomotor system does not respond uniformly to changes in the gain of visual feedback. Instead, specific regions of the visuomotor system selectively change in activity related to large changes in force error and large changes in the spatial amplitude of visual feedback.

INTRODUCTION

When humans perform movements and receive on-line visual feedback about their performance, the spatial qualities of visual information alter performance. For instance, a baseball player would find it easier to hit a ball with a larger circumference. Similarly, when a surgeon performs a procedure, magnifying the gain of visual feedback of the hand and the tissue being contacted improves the ability of the surgeon to make precise incisions (Rooks et al. 1993; Vasilakos et al. 1998). Laboratory studies have also shown that amplifying the gain of visual signals enhances performance on tasks such as drawing (Prager and Contreras-Vidal 2003), force control (Newell and McDonald 1994), and arm pointing (Seidler et al. 2001). When the visual gain is altered, the spatial amplitude of the visual feedback changes on the display and this influences performance error. The purpose of the current study was to examine how both cortical and subcortical brain activity change in relation to visual gain induced changes in force error.

One key feature of a change in visual gain is a change in the spatial amplitude of the visual stimulus. Spatial amplitude is an important component that affects our perception of object motion (Nakayama and Silverman 1984) and it is established that changing the spatial amplitude of a visual stimulus affects neurons in the nonhuman primate visual cortex (Mikami et al. 1986; Priebe et al. 2006; Rosenbluth and Allman 2002). Indeed, the processing of object motion has been localized to area MT in monkeys and the homologous hMT/V5 area in humans (Hesselmann et al. 2008; Liu and Newsome 2005; McKeefry et al. 2008; Moutoussis and Zeki 2008; Paradis et al. 2000; Sack et al. 2006). Single cell recordings from monkeys also suggest a role for MT in sensorimotor integration for feedback control (Dannenberg et al. 2009). In addition to MT, visually guided movements that are performed with low performance error are dependent on a distributed visuomotor system comprised of specific regions in parietal cortex, supplementary motor area, dorsal and ventral premotor cortex, putamen, and lobule VI of the cerebellum (Ebner and Fu 1997; Krakauer et al. 2004; Roitman et al. 2009; Vaillancourt et al. 2003, 2006b). Despite knowledge of the location of the regions of interest (ROIs) for the visuomotor system, it remains unclear whether all visuomotor ROIs respond uniformly to changes in visual gain and thus the spatial amplitude of the visual feedback.

The current study used functional magnetic resonance imaging (fMRI) in humans to determine how the gain of visual feedback influences blood oxygenation level dependent (BOLD) activation in visuomotor ROIs during a steady-state precision grip force task. Visual gain was parametrically manipulated across a wide range to compare changes in activation in the visuomotor system with changes in force error. Previous behavioral work using a similar precision grip paradigm manipulated visual gain. The authors found that small changes in visual gain lead to large changes in force performance up until gain levels <1° (Vaillancourt et al. 2006a). At visual gain levels >1°, force performance approached an asymptote. Thus the first goal of this study was to confirm that the asymptote in force performance occurs at 1° and then to determine how the fMRI signal in visuomotor ROIs changes with large changes in force error at visual gain levels <1°. At visual gain levels >1° we predicted that large changes in visual gain would be associated with very small improvements in force error, but with large changes in the spatial amplitude of visual feedback. The second goal was to determine how the fMRI signal in visuomotor ROIs changes with large changes in gain >1°, which increase the spatial amplitude of visual feedback. The findings demonstrate that the visuomotor system does not respond uniformly to changes in the gain of visual feedback and that specific regions of the visuomotor system selectively change in activity related to large changes in force error and to large changes in the spatial amplitude of visual feedback.

METHODS

Subjects

Fifteen healthy right-handed subjects with normal or corrected to normal vision participated in the study (8 females and 7 males, ages 19–31 yr: M = 22.3, SD = 3.72). Prior to the experiment, each subject provided informed consent to all procedures, which were approved by the local Institutional Review Board and were in accord with the Declaration of Helsinki.

Force data acquisition

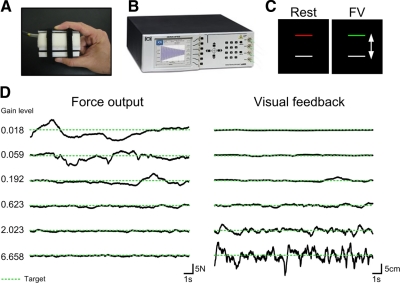
Figure 1A shows how subjects produced force against a custom fiber-optic force transducer (Aither Engineering). The force transducer was constructed from rigid, nonmetallic material to allow for its use inside the magnetic resonance environment. When prompted, subjects produced force against the transducer using their right thumb and right index finger and the force signal was transmitted via fiber-optic wire to the si425 Optical Sensing Interrogator (Micron Optics) outside the fMRI environment (see Fig. 1B). The fiber-optic si425 Optical Sensing Interrogator digitized the force data at 125 Hz and customized software written in LabVIEW (National Instruments, Austin, TX) collected the force data and converted the data to newtons (N). The force transducer was factory calibrated by Aither Engineering and had a resolution of 0.025 N. The output from the force transducer was presented to the subject using a visual display inside the MRI scanner. The feedback was projected via the parallax biofeedback system (Thulborn 1999), similar to previous experiments (Vaillancourt et al. 2003). A mirror located inside the MR environment displayed visual feedback onto a video screen located 35 cm from the subject's eyes. The force output was displayed on the screen at a resolution of 640 × 480 pixels and a refresh rate of 60 Hz. The force data were low-pass filtered using a Butterworth filter at 20 Hz (fourth-order dual-pass).

Fig. 1.

A: precision grip apparatus held between the thumb and index finger by the subject during the functional magnetic resonance imaging (fMRI) scan. B: si425 Optical Sensing Interrogator (Micron Optics). The force signal was transmitted via fiber-optic wire to the Interrogator outside the fMRI environment. C: visual display viewed by the subject during the Rest and Force with Vision (FV) condition. Participants were instructed to: 1) Rest: fixate on the red target bar, 2) FV: produce isometric force represented by the white bar to match the green target bar that was set at 15% of their maximum voluntary contraction (MVC) with on-line visual feedback. D: exemplar force output (left) and visual feedback (right) data from one subject during the FV condition at each level of visual gain. The dashed green line represents the target force level. Please note that the subject did not view these 2-dimensional time series, but rather a one-dimensional representation as shown in C.

MRI data acquisition

Magnetic resonance images were collected using a volume head coil inside a 3 Tesla MR Scanner (GE Healthcare 3T94 Excite 2.0). The subjects lay supine in the scanner while performing the task. The subject's head was stabilized using adjustable padding and then fitted with the projector-visor system for displaying visual feedback. The functional images were obtained using a T2*-sensitive, single shot, gradient-echo echo-planar pulse sequence (echo time [TE]: 25 ms; repeat time [TR]: 2,500 ms; flip angle [FA]: 90°; field of view [FOV]: 200 mm²; imaging matrix 64 × 64; 42 axial slices at 3 mm thickness; 0 mm gap between slices). The high-resolution anatomical scans were obtained using a T1-weighted SPGR (spoiled gradient echo) pulse sequence (TE: 3 ms; TR: 25 ms; FA: 40°; FOV: 240 mm²; imaging matrix 256 × 256; 120 axial slices at 1.5 mm thickness; 0 mm gap between slices).

Experimental design

Figure 1C shows the two stimulus conditions: Rest and Force with Vision (FV). The red/green target bar was set at 15% of each subject's maximum voluntary contraction (MVC). The white force bar was stationary during the rest condition (Rest) and fluctuated in real time according to the subject's force production in the FV condition. During the Rest condition subjects were instructed to fixate on the red target bar. During the FV condition subjects were instructed to produce sustained isometric force to a target level set at 15% of their MVC when the red bar turned green. During the FV condition subjects received on-line visual feedback. Rest and FV conditions each lasted 25 s and were alternated within scans. Each scan began and ended with a Rest block.

Subjects completed six functional scans and each scan followed the same R–FV–R sequence and lasted 225 s. The independent variable that was manipulated between scans was visual gain. The order of the scans/visual gain levels was randomized for each subject.

Visual gain was manipulated to ensure that we obtained gain values above and below 1° based on prior work (Vaillancourt et al. 2006a). Since the distance from the subject's eye to the projection screen surface remained constant, the height of the force fluctuations was manipulated to alter visual gain. The height of the force fluctuations viewed by the subject was manipulated using the following formula

$$\mathrm{\text{Cursor position}}=\left(Fp-Ft\right)\cdot G+Ft$$ (1)

in which Fp is the force produced by the subject, Ft is the target force, and G is the gain level used to manipulate the spatial amplitude of visual feedback. Based on prior work (Vaillancourt et al. 2006a), we calculated the visual angle by assuming a set force output SD of 0.3 N. This estimate was derived from previous studies (Laidlaw et al. 2000; Slifkin and Newell 1999). The value of the SD was multiplied by 6 to approximate the full range (±3SDs) of estimated variance for the height of the force fluctuations. The visual angle for each gain level was then calculated using the following formula

$$\alpha =2\times {\tan }^{-1}\left(\frac{H_1}{D}\right)$$ (2)

in which α is the visual angle, D is the distance to the display, and H₁ is the height of the total range of motion in the top half of the visual field. The six visual gain levels corresponded to visual angles of: 0.018, 0.059, 0.192, 0.623, 2.023, and 6.658°, confirming that the visual angle ranged from <1° to >1°.

Manipulating visual gain led to changes in the spatial amplitude of the visual feedback, which resulted in a change in force output. Figure 1D shows example data of force output and visual feedback during an 18.5 s portion of one block of the FV condition for one subject during each of the six visual gain manipulations. Gain related changes in force output are shown in Fig. 1D (left), where force output is quantified in newtons. Gain related changes in visual feedback are shown in Fig. 1D (right), where the visual feedback is quantified in units of spatial amplitude (cm). As expected, Fig. 1D shows that low gain levels resulted in an increase in the fluctuation of force output around the target force level (represented as the green dashed line) and a decrease in the spatial amplitude of visual feedback around the target force level. Comparatively higher gains lead to a reduction in the fluctuation of force output around the target force level and an increase in the spatial amplitude of visual feedback around the target force level.

Procedure

Prior to entering the magnet, each subject completed a 1 h training session to minimize learning effects when inside the scanner. Once in the fMRI environment, the individual's MVC was calculated. The subjects were asked to sustain a contraction of maximum force for three consecutive 5 s trials. Each trial was separated by a 60 s period of rest. The MVC was calculated as the average force during the sustained maximum force contraction. Subjects then completed six functional scans followed by the anatomical scan. The experimental session lasted about 1 h.

Force data analysis

Force data were analyzed using custom algorithms in LabVIEW. The force-time series data were digitally filtered by using a fourth-order Butterworth filter with a 20 Hz low-pass cutoff. Four dependent measures were calculated: 1) duration of force, 2) mean force, 3) force error measured in newtons (root mean squared error in newtons [RMSE_N]), and 4) visual feedback measured in centimeters on the visual display (RMSE_cm). Duration of force represented the entire length of each sustained contraction. The onset of each contraction was identified as the time point where force rose above twofold the baseline value. The offset of each contraction was identified as the next time point where force fell below twofold the baseline value. Baseline values were calculated as the mean force amplitude during the 300 ms prior to each 25 s block. Force error, visual feedback, and mean force were calculated from an 18.5 s portion of each contraction, beginning 4 s after force onset. Force error reflected how accurate force production was relative to the target force level and was calculated in newtons (RMSE_N) using the following equation

$$\mathrm{RMS}{E}_N={\left[{\displaystyle \sum {\left(s-f_i\right)}^2/n-1}\right]}^{1/2}$$ (3)

in which s is the target force, f_i is the ith force sample, and n is the number of samples. To calculate the spatial amplitude of visual feedback (RMSE_cm) we took the force that each subject produced during each visual gain manipulation and converted the deviation in the force trace into centimeters. Thus the force trace was converted to units that reflected the spatial amplitude of the visual feedback as viewed by each subject. We then used the same Eq. 3 to calculate RMSE_cm as was used to calculate RMSE_N, although the units were in centimeters.

Previous work predicted a breakpoint between visual gain and force error at 1° (Vaillancourt et al. 2006a). To confirm the breakpoint in RMSE_N across the visual gain level, each individual's RMSE_N data were subjected to a breakpoint analysis. A breakpoint analysis identifies the point of intersection of two linear functions of different slopes. The quasi-newton nonlinear estimation procedure, calculated in Statistica v. 6.1, was used to identify the breakpoint in each individual's data. This procedure calculates the second derivative of each value in the loss function associated with the best fitting exponential regression (Fletcher 1969), providing an index of how quickly the slope of the function changes at each successive value. The breakpoint in each function was identified as the predicted visual gain, where the second derivative value of the loss function first fell to <0.0001 (the convergence criterion). The breakpoint values were used to guide the fMRI analyses.

The four dependent variables (duration of force, mean force, RMSE_N, RMSE_cm) were calculated for each subject and for each scan. Each stimulus condition was repeated four times within each scan. Potential adaptation effects within each scan were examined with separate one-way repeated measures ANOVAs. However, because no significant effect of Block was found for all four dependent variables (all values of P > 0.05) an average of the four values at each gain level served as the summary statistic for each dependent variable. The effect of visual gain on the duration of force and mean force was analyzed in separate one-way repeated measures ANOVAs (SPSS, v.16; SPSS, Chicago, IL). For each analysis, violation of the sphericity assumption led to the application of the Greenhouse–Geisser degrees of freedom correction. The effect of visual gain on RMSE_N was analyzed using the following nonlinear three-parameter exponential decay regression equation

$$f=y_0+a\exp \left(-bx\right)$$ (4)

The effect of visual gain on RMSE_cm was analyzed using the following linear regression equation

$$f=y_0+ax$$ (5)

fMRI data analysis

AFNI (Automated Functional NeuroImaging program), the public domain software (http://afni.nimh.nih.gov/afni/), was used to process and analyze the fMRI data sets. First, we corrected for head motion using standard procedures. Combined motion in the x, y, and z planes was <1 mm for all subjects. All subjects were included in all analyses.

Voxelwise analysis

To determine whether the precision grip task led to activation of the visuomotor system independent of the visual gain level a voxelwise analysis was first performed on the data. Motion-corrected individual data sets were normalized by dividing the instantaneous signal in each voxel at each point in the time series by the mean signal in that voxel across each scan. A Gaussian filter was then applied to the data sets (full-width half-maximum at 3 mm). Next, the time-series data were regressed to a simulated hemodynamic response function for the task sequence. The dependent variable at this level of analysis was the estimated β-coefficient of the regressed time series and its associated t-statistic for the FV–R comparison. Before group analyses, each subject's anatomical data set was transformed to Montreal Neurological Institute (MNI) space, using the MNI implementation in AFNI. Then, each subject's individual functional data sets were transformed to MNI space using the normalized anatomical data set as a template. All six data sets for each ANOVA were corrected for multiple comparisons using a Monte Carlo simulation model (AlphaSim). The data sets were thresholded to remove all voxels with t < 3.32 with an activation cluster minimum of 205 μL (P < 0.05, corrected). Activation across all six gain levels was then averaged to provide an index of visuomotor activity that was independent of visual gain level.

ROI mask

An ROI mask, which includes the component parts of the visuomotor system, was created based on previous functional data related to visuomotor processing (Vaillancourt et al. 2003, 2006b) and motion processing (Culham et al. 1998; McKeefry et al. 2008; Nestor et al. 2008; Paradis et al. 2000; Waberski et al. 2008). Visuomotor areas were anatomically labeled using the Basal Ganglia Human Area Template (Prodoehl et al. 2008), the Human Motor Area Template (Mayka et al. 2006), and the Schmahmann MRI atlas of the human cerebellum (Schmahmann et al. 2000). The x, y, and z coordinates for the center of mass of each ROI in MNI space are presented in Table 1.

Table 1.

MNI coordinates for visuomotor areas that are responsive to small changes in visual gain <1° large changes in visual gain >1°, and small and large changes in visual gain, visual gain, and areas that are nonresponsive to visual gain

	MNI Coordinates			Nonlinear Regression			Post Hoc Tests
Visuomotor Area	RL	AP	IS	P	R Sq	b	1 vs. 4	4 vs. 6
Responsive to small changes in gain <1°
L V3	−36.1	−84.2	−4.8	0.05	0.87	5.01	P < 0.01**	P = 0.86
R V3	30.7	−84.0	4.4	0.04	0.88	3.59	P < 0.05*	P = 0.73
L V5	−43.8	−68.0	−5.7	0.02	0.92	2.11	P < 0.01**	P = 0.17
R V3	41.0	−66.1	−5.6	0.01	0.96	3.85	P < 0.01**	P = 0.70
L M1	−24.7	−28.4	53.9	0.01	0.95	1.88	P < 0.05*	P = 0.17
Responsive to large changes in gain >1°
R IPL	32.8	−50.1	41.8	<0.01	0.99	0.70	P = 0.35	P < 0.05*
L PMd	−33.7	−7.7	51.9	0.02	0.92	0.19	P = 0.13	P < 0.05*
R PMd	38.8	−7.3	51.1	0.05	0.86	0.35	P = 0.11	P < 0.05*
R PMv	48.2	4.0	31.0	0.05	0.87	0.00	P = 0.50	P < 0.01**
Responsive to small and large changes in gain
L PMv	−53.0	2.4	36.2	0.01	0.94	1.96	P < 0.01**	P < 0.05*
Responsive to changes in gain
SMA	−1.6	−13.8	57.3	0.03	0.91	1.49	P = 0.09	P = 0.13
L IPL	−36.8	−57.9	47.0	0.01	0.95	1.01	P = 0.09	P = 0.12
Nonresponsive to gain
R put	23.5	0.1	8.6	0.33	0.52	9.94
L put	−25.4	−2.8	3.2	0.27	0.59	8.12
R LobVI	27.0	−63.7	−29.2	0.46	0.40	2.61
L LobVI	−30.2	−67.3	−28.6	0.40	0.46	2.26

Mean BOLD activity in each visuomotor region (FV–R) was regressed against visual gain. Corresponding P values, r² values, and beta coefficients (b: gain constant) are shown. The last two columns show the P values from the post hoc t-tests between gain 1 and gain 4 and between gain 4 and gain 5. put, putamen.

^**P < 0.01;

^*P < 0.05.

Statistical analysis of ROIs

An ROI analysis of the mean BOLD percentage signal change was used to characterize the response function between visual gain and percentage signal change. First, each individual data set was motion corrected and then filtered using a Gaussian filter (full-width half-maximum at 3 mm). Next, mean BOLD percentage signal change was acquired by calculating the mean signal within each voxel for the FV and Rest blocks across each individual functional time series. The mean BOLD percentage signal change within each voxel was calculated using the following equation

$${\mu }_{\mathrm{PSC}}=\left[\left({\mu }_{\mathrm{T}}-{\mu }_{\mathrm{R}}\right)/{\mu }_{\mathrm{R}}\right]\times 100$$ (6)

where μ_T is the mean signal during the FV blocks and μ_R is the mean signal during the Rest blocks. Therefore the output data represented the percentage signal change in each voxel for each individual subject data set. Next, each subject's anatomical and functional data sets were transformed to MNI space. The mean percentage signal change within each ROI was completed for each subject at each gain level. To determine which visuomotor ROIs have an fMRI signal that changes with gain, the percentage signal change values were analyzed using nonlinear regression with visual gain as the independent variable. The form of the relation between visual gain and percentage signal change was characterized by the following three parameter exponential rise to maximum regression equation

$$f=y_0+a\left[1-\exp \left(-bx\right)\right]$$ (7)

In visuomotor ROIs in which this regression model was significant, we used the breakpoint analysis from the behavioral data to guide post hoc tests. The post hoc t-test allowed us to determine whether the fMRI signal changed similarly when small changes in visual gain led to large changes in force error, compared with when large changes in visual gain were associated with small changes in force error but large changes in the spatial amplitude of the visual feedback. We compared gain 1 with gain 4 because the breakpoint in the force error across visual gain was identified at 1° (mean = 1.002, SD = 0.469). Thus changes in visual gain <1° led to large changes in RMSE_N and very small changes in RMSE_cm. We also compared gain 4 to gain 6 because the behavioral data showed that changes in visual gain >1° led to very small changes in RMSE_N and large changes in RMSE_cm. All tests were evaluated as significant if the P value was <0.05.

RESULTS

Analyses that determine the effect of visual gain on force production and visual feedback will be presented first. Behavioral analyses will be followed by fMRI analyses. First, a voxelwise analysis will be used to show that when guided by visual feedback, producing force leads to increased BOLD signal activity in the visuomotor system. Second, ROI analyses will be presented to determine how the BOLD signal in the visuomotor system changes as a function of visual gain.

Force output results

Force duration.

Analyses comparing the mean duration of sustained force contractions revealed nonsignificant effects of visual gain [F(5,70) = 1.64, P > 0.05, η² = 0.11]. The findings verify that the duration of force output was not different across visual gain (range: 26.3–27.4 s).

Mean force.

The one-way repeated measures ANOVA for mean force revealed a significant main effect of visual gain [F(1.34,18.77) = 9.71, P < 0.05, η² = 0.41]. Subjects underestimated the target force at low visual gains, with increases in visual gain leading to an improved approximation of the target force level. Mean force increased progressively across visual gain levels by a total of 1.5 N (range: 9.31–10.86 N).

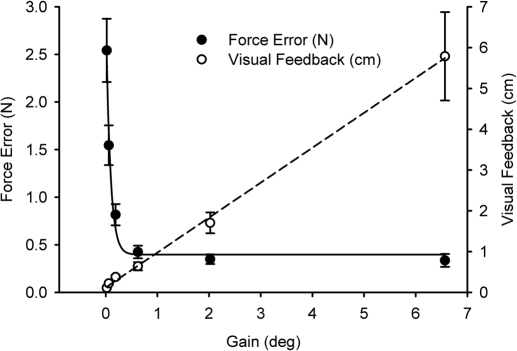
Force error (RMSE_N).

Figure 2 shows the mean RMSE_N (filled dots, left y-axis) across the six levels of visual gain. The solid black line shows the form of the relation between force error and visual gain. The relation was characterized well by a three parameter exponential decay function (r² = 0.98, P < 0.01). Post hoc analyses revealed a breakpoint at 1° (mean = 1.002, SD = 0.469), confirming that large changes in force error occurred with changes in visual gain <1° but not >1°. As shown in Fig. 2 the reduction in force error between gain levels of 0.018 and 0.623° (i.e., <1°) was 2.12 N, which was much larger than the reduction in force error between gain levels of 0.623 and 6.658°, which was 0.089 N.

Fig. 2.

Each data point represent the across participant mean at each level of visual gain. Force error (RMSE_N) is represented by filled circles. The spatial amplitude of visual feedback (RMSE_cm) is represented by open circles. Mean force error decreased with an increase in visual gain and post hoc analyses identified the breakpoint at 1°. Mean spatial amplitude of visual feedback increased with an increase in visual gain. Error bars represent ±1SE.

Visual feedback (RMSE_cm).

Figure 2 shows the mean RMSE_cm (open dots, right y-axis) across the six levels of visual gain. The dashed black line shows the form of the relation between RMSE_cm and visual gain. Linear regression between visual gain and visual feedback yielded a significant positive relation (r² = 0.99, P < 0.01). As shown in Fig. 2 the increase in the spatial amplitude of visual feedback between gain levels of 0.018 and 0.623° was 0.53 cm, which was much smaller than the large changes in visual feedback between gain levels of 0.623 and 6.658°, which was 5.15 cm.

Our behavioral findings demonstrate that changes in visual gain <1° led to a large change in force error and a small change in the spatial amplitude of visual feedback. In contrast, an increase in visual gain >1° led to a small change in force error but a large change in the spatial amplitude of visual feedback.

fMRI results

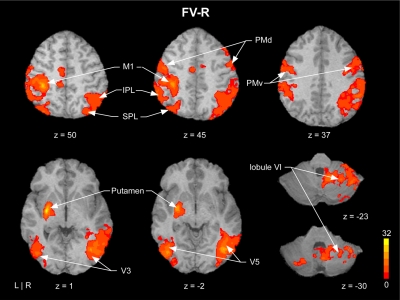
Figure 3 shows mean BOLD signal activity averaged across all six gain levels compared with rest. Figure 3 is clear in showing an increased BOLD signal in the key areas of the visuomotor system including motor cortex, premotor cortex, visual cortex, basal ganglia, and cerebellum. This figure confirms our expectation and corroborates previous evidence that has shown that when guided by visual feedback, producing force leads to increased BOLD signal activity in the visuomotor system.

Fig. 3.

Example axial slices showing mean blood oxygenation level dependent (BOLD) activation detected by voxelwise analyses overlaid on a single subject's transformed brain. The color bar ranges from t = 0 to t = 32, with a group activation threshold of P < 0.05, corrected. The corrected t-statistics associated with each voxel are displayed. This figure shows that performing the precision grip force task led to activity in the visuomotor system.

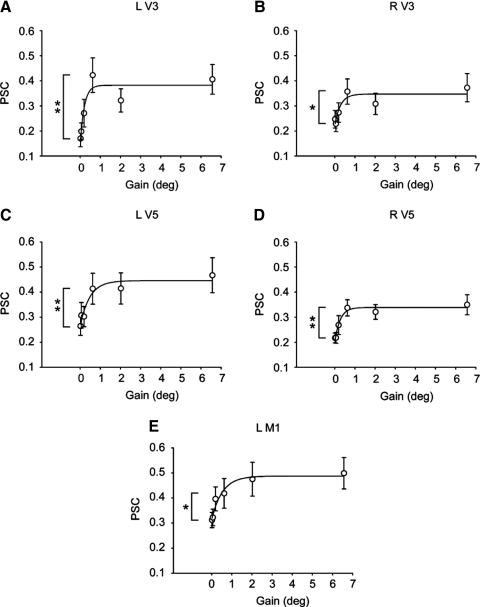
Figure 4 shows percentage signal change (PSC) values in the BOLD signal across gain levels in left V3 (A), right V3 (B), left V5 (C), right V5 (D), and in left primary motor cortex (M1, E). A three parameter exponential rise to maximum fit was calculated for each ROI and the line of best fit is shown in each figure. The P value, r² value, and gain constant (beta coefficient) for each ROI is shown in Table 1. For left V3, the regression model was significant (r² = 0.87) and the gain constant suggested a nonlinear shape (gain constant = 5.01), which can be seen in Fig. 4A. The post hoc t-test revealed that the BOLD signal in left V3 increased significantly from gain 1 to gain 4 but did not change from gain 4 to gain 6 (see Fig. 4A and Table 1). As shown in Fig. 4, B–E, a significant and similar pattern in the BOLD signal was evidenced in right V3, left V5, right V5, and in left M1 (also see Table 1). Importantly, in each of these brain areas a significant increase in PSC occurred between gain 1 and gain 4 (see Table 1), but not between gain 4 and gain 6. This finding was further validated by the gain constant values that indicate nonlinearity in the shape of the function. Together these findings suggest that an increase in PSC bilaterally in V3 and V5 and in left M1 is reflective of a large change in force error.

Fig. 4.

A–E: region of interest (ROI) analyses from visuomotor areas that change with a large change in force error. Regression results and post hoc t-test for all visuomotor areas are shown in Table 1. Individual graphs show brain areas that had increased BOLD activation between gain level 1 and gain level 4. Each data point represents the across participant mean at each level of visual gain. Error bars represent ±1SE. L, left, R, right. **P < 0.01; *P < 0.05.

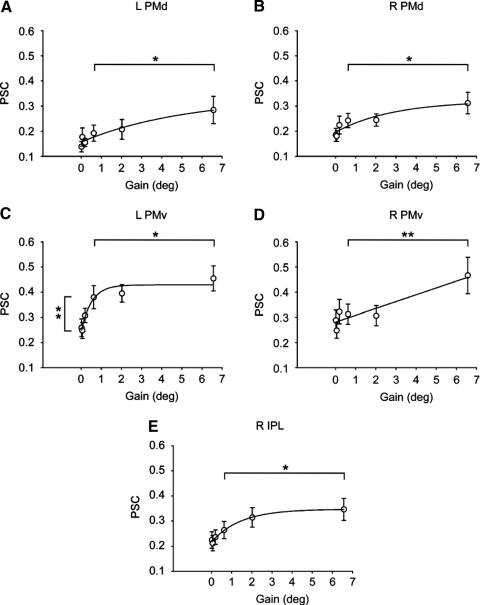
Figure 5 shows percentage signal change (PSC) values in the BOLD signal across gain levels in left dorsal premotor cortex (PMd, A), right PMd (B), left ventral premotor cortex (PMv, C), right PMv (D), and right inferior parietal lobule (IPL, E). The pattern in BOLD signal across gain levels in Fig. 5, A, B, D, and E is distinct from the pattern displayed in Fig. 4, A–E because small increases in BOLD are evidenced between gain 1 and gain 4, whereas large changes in BOLD are evidenced between gain 4 and gain 6. The regression model was significant in all four of these regions (see Table 1). Moreover, the small gain constants (b from Eq. 4: see Table 1) in left and right PMd, right PMv, and right IPL suggest a more linear relation between percentage signal change and gain, compared with the areas shown in Fig. 4, A–E that have higher gain constants. The regression model was also significant for left PMv and the nonlinear shape evident in Fig. 5C was confirmed by a higher gain constant (1.96). The post hoc t-test revealed significant differences between gain 4 and gain 6 in all five brain regions, but only between gain 1 and gain 4 in left PMv. These findings suggest that bilateral activity in dorsal and ventral premotor cortex and right IPL is reflective of large changes in the spatial amplitude of visual feedback associated with the maintenance of low force error. Significant differences in left PMv between gain 1 and gain 4 and between gain 4 and gain 6 suggest that this region is sensitive to very small and very large changes in the spatial amplitude of visual feedback.

Fig. 5.

A–E: ROI analyses from visuomotor areas that change with a large change in the spatial amplitude of visual feedback. Regression results and post hoc t-test for all visuomotor areas are shown in Table 1. Individual graphs show brain areas that had increased BOLD activation between gain level 4 and gain level 6. Each data point represents the across participant mean at each level of visual gain. Error bars represent ±1SE. L, left; R, right. **P < 0.01; *P < 0.05.

Effects of visual gain on BOLD signal change were found in left IPL and supplementary motor area (SMA) (see Table 1). However, post hoc t-tests between gain 1 and gain 4 and between gain 4 and gain 6 were not significant. In addition, left putamen, right putamen, left lobule VI of the cerebellum, and right lobule VI of the cerebellum were not sensitive to changes in visual gain and thus activity in these areas does not appear to be reflective of changes in force error or the spatial amplitude of visual feedback. Thus although these areas were active during the visuomotor task (see Fig. 3) they did not change systematically with changes in visual gain.

DISCUSSION

The current findings demonstrate that changes in gain <1° were associated with a substantial reduction in force error. These behavioral effects corresponded with an increase in the BOLD signal bilaterally in V3 and V5 and in left M1 and left PMv. Further, large increases in visual gain past 1° were associated with a small change in force error and a substantial increase in the spatial amplitude of visual feedback displayed to the subject. These behavioral effects corresponded with an increase in the BOLD signal bilaterally in dorsal and ventral premotor areas and right IPL. Finally, activity in subcortical areas of the visuomotor system, including left and right lobule VI of the cerebellum and left and right putamen, did not change with increases in visual gain.

Our behavioral findings replicate previous evidence that large changes in force error occurred with an increase in visual gain <1° and small changes in force error occurred with changes in visual gain >1° (Hong et al. 2008; Vaillancourt et al. 2006a). We next sought confirmation that the visuomotor task used was successful in activating the visuomotor system. As shown in Fig. 3, substantial activity was found in primary motor cortex, premotor cortex, parietal cortex, extrastriate visual cortex, basal ganglia, and cerebellum. Identification of this broadly distributed visuomotor system corroborates previous electrophysiology and imaging evidence (Ebner and Fu 1997; Krakauer et al. 2004; Roitman et al. 2009; Vaillancourt et al. 2003, 2006b). We next discuss the subregions of this visuomotor system that responded to a large change in force error and a small change in the spatial amplitude of visual feedback.

Force error

A reduction in force error was associated with increased activity in left M1. This finding is consistent with previous evidence that found that left M1 activity increased with increased precision of motor function (Carey et al. 2006) and corrective force adjustments to unpredictable stimuli (Jenmalm et al. 2006). For instance, Carey and colleagues (2006) required subjects to execute a sinusoidal force pattern using finger flexion and extension with visual feedback (track) and without visual feedback (move). The track condition required more precise force production that was associated with an increase in activity in left and right M1. The authors concluded that M1 plays a role in the spatial and temporal processing that underlies precise movement execution. This finding corroborates previous electrophysiology work in nonhuman primates, which localized spatial processing capabilities to M1 (Crowe et al. 2004). We extend each of these findings by demonstrating that increases in M1 activity are associated with a small increase in the spatial amplitude of visual feedback (i.e., the spatial properties of visual feedback) and a large reduction in error (i.e., more precise performance). It is important to note that visual gain also increased the mean force amplitude from 9.31 to 10.77 N (change of 2% MVC). Although most studies suggest that a greater increase in mean force is needed to induce a change in the BOLD response, there is general agreement that the relation between force amplitude and the BOLD signal in M1 is positive (Dai et al. 2001; Dettmers et al. 1996; Keisker et al. 2009; Kuhtz-Buschbeck et al. 2008; Spraker et al. 2007). Thus the slight increase in mean force amplitude resulted in subjects producing force that was closer to the target level that led to a reduction in force error. As such, we conclude that visual gain led to reduced force error and increased M1 activity, which was likely related to improved precision and a small increase in mean force amplitude.

In addition to increased activity in left M1, large changes in force error and small changes in the spatial amplitude of visual feedback were associated with increased BOLD activity in visuomotor areas of V3 and V5. This finding complements evidence from previous imaging studies that have demonstrated that viewing motion stimuli leads to increases in neural activity in regions of the visual cortex including areas V3 and V5 (Paradis et al. 2000). Related work by Martinez-Trujillo et al. (2007) demonstrated that activity in V5 provides the strongest response to judgments made about the direction of moving stimuli. Further validation of the role that V5 plays in motion perception comes from transcranial magnetic stimulation (TMS) evidence, which shows that motion perception is impaired when pulses are applied to V5 30–40 ms before and 130–150 ms after the onset of the motion stimuli (Sack et al. 2006). We extend these findings by demonstrating that increased activity in the visuomotor areas of V3 and V5 are associated with a substantial reduction in force error and a small increase in the spatial amplitude of visual feedback. The large increase in the spatial amplitude of visual feedback that occurred above a visual gain of 1° was not reflected in increased BOLD activity in visuomotor regions of V3 or V5 (Fig. 4). However, the ROI mask included only visuomotor regions. Thus it is possible that areas within visual cortex but outside the ROI mask may have continued to increase in BOLD signal with an increase in the spatial amplitude of visual feedback.

It is appealing to speculate that activity in visuomotor regions of the visual cortex is related to activity in visuomotor regions of M1. Evidence from a nonhuman primate study demonstrated that although neural activity in MT and M1 is coactivated and temporally overlapping during a visuomotor tracking task, it is not synchronized (Kruse et al. 2002). This suggests that intermediary regions including the parietal cortex, premotor cortex, and cerebellum serve as the interface between visual cortex and primary motor cortex (Caminiti et al. 1996; Glickstein 2000; Kelly and Strick 2003; Suzuki et al. 1990; Wise et al. 1997). Indeed, we also found BOLD activation (relative to Rest in Fig. 3) within premotor cortex, parietal cortex, basal ganglia, and cerebellum, but activation in these areas did not change with spatially driven changes in force performance. Together, these findings demonstrate that the BOLD response within regions of the extrastriate visual cortex and primary motor cortex are sensitive to changes in visual gain <1° and that these changes are sufficient to allow the visuomotor regions of V3, V5, and M1 to contribute to a reduction in force error.

Spatial amplitude of visual feedback

Increases in visual gain >1° resulted in a large change in the spatial amplitude of visual feedback and a small change in force error (Fig. 2). We found activity in left and right PMd and PMv and right IPL associated with this large increase in the spatial amplitude of visual feedback and maintenance of low force error. The involvement of these premotor and parietal regions is consistent with previous evidence that has shown that visual motion stimuli affect neural signals in the motor cortex via projections from the parietal cortex to the premotor cortex (Caminiti et al. 1996; Wise et al. 1997). More specifically, evidence from nonhuman primate studies has shown increased activity of left and right PMd neurons after the presentation of spatial cues that instruct direction specific responses (di Pellegrino and Wise 1993; Weinrich and Wise 1982; Wise 1985). This finding is consistent with TMS studies in humans that have shown that left PMd scales forces based on arbitrary visual cues (Chouinard et al. 2005) and that disrupting function in the left PMd leads to deficits in on-line visuomotor error corrections (Lee and van Donkelaar 2006). In addition, increased bilateral activity in PMd has been associated with the processing of visuospatial information related to motor processes (Hoshi and Tanji 2006; van Eimeren et al. 2006).

An increase in activity in the right IPL is consistent not only with previous data that have ascribed visuomotor coordinate transformations to IPL (Grefkes et al. 2004), but also with previous TMS data that have shown that disrupting function in posterior parietal cortex leads to deficits in on-line visuomotor error correction (Della-Maggiore et al. 2004; Desmurget et al. 1999; Van Donkelaar et al. 2000). However, previous findings have typically presented visual feedback and motor error on a 1:1 ratio and, as such, the component processes that contribute to visuomotor error corrections have not been isolated. The current findings address this issue and extend our current knowledge of the spatial amplitude of visual feedback by localizing this process to the ventral and dorsal premotor cortex and right IPL.

Areas not sensitive to visual gain

Activity in the cerebellum and putamen did not vary with visual gain either below or above 1°. A previous study that manipulated the gain of a joystick movement during an adaptation and learning protocol did show a gain-related increase in regional cerebral blood flow in the cerebellum and putamen (Krakauer et al. 2004). The authors found that gain increased activity only during rapid phase learning, but not during more complete gain learning. In the present study levels of visual gain were manipulated between blocks and adaptation was not studied. Thus our finding that cerebellar and putamen activity did not change across levels of visual gain is consistent with the findings of Krakauer and colleagues. A second study that manipulated movement gain demonstrated that movement extent and movement speed are positively associated with activity in the cerebellum and putamen (Turner et al. 2003). In the study by Turner and colleagues, changing gain caused subjects to move a joystick from 6 up to 24 cm. As such, the gain of feedback resulted in large changes in the movement extent and speed and neither movement speed nor movement extent was manipulated in the current study. Instead, the current study manipulated visual gain across a broad range, which allowed force error to decrease. The cerebellum and putamen were consistently active during the current task (Fig. 3), which demonstrates that our findings are consistent with previous studies that have associated cerebellar and putamen activity with accurate visuomotor processing (Ebner and Fu 1997; Roitman et al. 2009; Vaillancourt et al. 2003).

The effect of spatial gain of visual feedback does not appear to have the same effect on the cerebellum as increasing the temporal frequency of visual feedback. For instance, Vaillancourt and colleagues (2006b) previously reported that increasing the temporal frequency of visual feedback leads to an increase in cerebellar activity in lobule VI. Increasing the temporal feedback frequency may have allowed subjects to perform a greater number of visuomotor corrections, whereas it is possible that low and high visual gain results in the same number of corrections with different levels of accuracy. Future studies that vary the frequency and gain of feedback not only within the same study but also within a trial are necessary to disentangle feedback frequency effects and adaptation effects in the visuomotor system. In addition, the current study collected data at one force level and previous behavioral findings have shown that the sensitivity of visual information has a greater impact on force performance at lower force levels (Sosnoff and Newell 2006). As such, it is not clear whether the relation between brain activity and visual gain shown here will hold at different force levels.

In conclusion, we found that small increases in visual gain <1° were associated with a substantial reduction in force error that corresponded with an increase in activation bilaterally in V3 and V5 and in left M1 and left PMv. Large increases in visual gain >1° were associated with a small change in force error and a large change in the spatial amplitude of visual feedback, which corresponded with increased activity bilaterally in dorsal and ventral premotor areas and right IPL. Together, these findings demonstrate that specific regions of the visuomotor system selectively change in activity related to large changes in force error and large changes in the spatial amplitude of visual feedback.

GRANTS

This research was supported in part by National Institutes of Health Grants R01-NS-58487, R01-NS-52318, R01-NS-40902, R01-NS-28127, and F32-MH-83424.