Differences in Movement Mechanics, Electromyographic, and Motor Cortex Activity Between Accurate and Nonaccurate Stepping

Abstract

What are the differences in mechanics, muscle, and motor cortex activity between accurate and nonaccurate movements? We addressed this question in relation to walking. We assessed full-body mechanics (229 variables), activity of 8 limb muscles, and activity of 63 neurons from the motor cortex forelimb representation during well-trained locomotion with different demands on the accuracy of paw placement in cats: during locomotion on a continuous surface and along horizontal ladders with crosspieces of different widths. We found that with increasing accuracy demands, cats assumed a more bent-forward posture (by lowering the center of mass, rotating the neck and head down, and by increasing flexion of the distal joints) and stepped on the support surface with less spatial variability. On the ladder, the wrist flexion moment was lower throughout stance, whereas ankle and knee extension moments were higher and hip moment was lower during early stance compared with unconstrained locomotion. The horizontal velocity time histories of paws were symmetric and smooth and did not differ among the tasks. Most of the other mechanical variables also did not depend on accuracy demands. Selected distal muscles slightly enhanced their activity with increasing accuracy demands. However, in a majority of motor cortex cells, discharge rate means, peaks, and depths of stride-related frequency modulation changed dramatically during accurate stepping as compared with simple walking. In addition, in 30% of neurons periods of stride-related elevation in firing became shorter and in 20–25% of neurons activity or depth of frequency modulation increased, albeit not linearly, with increasing accuracy demands. Considering the relatively small changes in locomotor mechanics and substantial changes in motor cortex activity with increasing accuracy demands, we conclude that during practiced accurate stepping the activity of motor cortex reflects other processes, likely those that involve integration of visual information with ongoing locomotion.

INTRODUCTION

Most movements, ranging from walking on uneven terrain and reaching for objects to sophisticated movements in dancing and sports, have to be accurate. How is the accuracy in movements achieved?

Considerable research has been conducted on accurate arm reaching. It was found that accurate reaching is planned before movement initiation (Gordon et al. 1994; Soechting and Flanders 1989) and that movements can also be corrected on-line (Dounskaia et al. 2005; Goodale et al. 1986; Messier and Kalaska 1999; Novak et al. 2002; Prablanc and Martin 1992). Increasingly accurate movements take longer to complete (Fitts 1954; Woodworth 1899) and, during accurate reaching, antagonist arm muscles are more coactive (Gribble et al. 2003; Laursen et al. 1998; Osu et al. 2002, 2004). Lesions to a variety of brain centers severely affect the accuracy (e.g., Bastian et al. 2000; Beer et al. 2000; Martin and Ghez 1993; Mihaltchev et al. 2005) and the activity of the premotor cortex correlates with the accuracy demand (Gomez et al. 2000).

In earlier publications, we suggested that, during locomotion, the control of stepping accuracy is a special function of the motor cortex (Beloozerova and Sirota 1988, 1993a,b). This suggestion was based on results of previous lesion and inactivation studies demonstrating that the normal activity of the motor cortex is vital for accurate stepping (Beloozerova and Sirota 1993a; Burlachkova and Ioffe 1979; Trendelenburg 1911), and on results of our recording experiments that showed a significant dependence of motor cortical activity on the necessity to place feet on restricted support surfaces during stepping over series of obstacles or walking along a horizontal ladder (Beloozerova and Sirota 1988, 1993a,b). Although in those recording experiments only a limited relationship was found between the motor cortical activity and the effort exerted during locomotion, the possibility remained that during ladder locomotion some portion of the cortical activity reflected not the necessity to step on specific places (the ladder's crosspieces), but a difference in walking mechanics between the ladder locomotion and walking on a flat surface. Therefore the first aim of the present study was to compare in detail the mechanics of the highly trained ladder and flat surface locomotion and to determine exactly how similar or dissimilar these two motor behaviors are. If significant movement differences were found, then the difference in the motor cortical activity could reflect those mechanical differences. If ladder and flat surface locomotion were found to be mechanically identical, however, then the difference in the motor cortex activity between them could be related to the differences in other neural processes, such as integration of visual information with ongoing locomotion necessary for stepping on the ladder and not needed for walking on flat surface. We found that most of the over 200 mechanical variables were similar between the highly trained ladder and flat surface locomotion.

If there is a difference in motor cortex activity between mechanically similar movements with and without accuracy demands, how can this activity be explained? We have previously suggested that during ladder locomotion the activity of the motor cortex is related to the size of targets for feet landing, i.e., to the accuracy of stepping (Beloozerova and Sirota 1988, 1993a,b). The second aim of this study was to further explore the relationship between motor cortex activity and accuracy of stepping by testing the hypothesis that activity of the motor cortex is related to the level of accuracy in a quantitative manner. To reveal a possible quantitative relationship between motor cortex activity and accuracy of stepping, we constructed ladders with different widths of crosspieces: from very wide (continuous surface with small “cracks”) to very narrow (support little more than a foot). The activity of the motor cortex was now compared not only between walking on the flat surface and along a ladder, but also between walking along ladders with different requirements for stepping accuracy. We found that in 30% of neurons periods of stride-related elevation in firing became shorter as demands for accuracy increased. In 20–25% of neurons activity or depth of frequency modulation increased, albeit not linearly, with increasing accuracy demands. The mean normalized activity of the recorded neurons was enhanced during accurate stepping at the stance–swing and swing–stance transitions.

Brief accounts of parts of this study were published in abstract form (Farrell et al. 2008; Prilutsky et al. 2001; Sirota et al. 2005).

METHODS

Data were obtained from 11 chronically implanted freely walking cats (Table 1). Some of the methods have been described previously (Beloozerova and Sirota 1993a; Prilutsky et al. 2005; Sirota et al. 2005) and will be only briefly reported here. All experiments were conducted in accordance with National Institutes of Health guidelines and with the approval of the Institute Animal Care and Use Committees of both Barrow Neurological Institute and Georgia Institute of Technology.

Table 1.

Cats participating in experiments and their mass and hindlimb length

Cat	Gender	Mass, kg	Hindlimb Length, m	Full-Body Mechanics	Paw Placement	EMGs	Motor Cortex
7	Female	2.7					x
8	Male	4.5				x
11	Female	3.7				x
BA	Female	2.8	0.256	x	x
BL	Female	3.0	0.259	x
BU	Female	3.1	0.256	x
CL	Female	3.5					x
KO	Male	3.8	0.284	x	x		x
N1	Male	4.3			x	x
N3	Male	3.8			x	x
NC	Female	2.9	0.242	x	x

Hindlimb length was defined as the sum of tarsals, shank, and thigh lengths.

Locomotion tasks

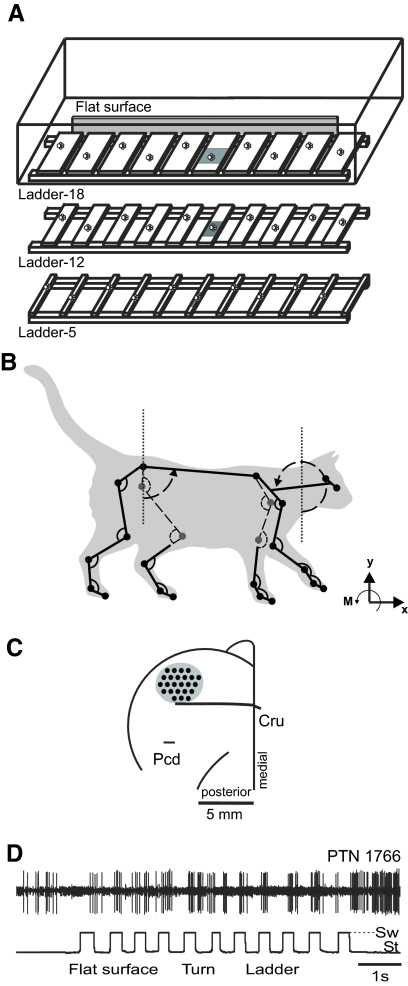
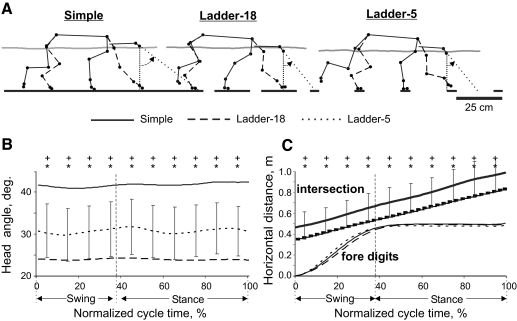
Positive reinforcement (food) was used to adapt cats to the experimental situation and to engage them in locomotion behavior (Pryor 1975; Skinner 1938). A box (2.5 m long; 0.5 m wide) made of Plexiglas served as the experimental chamber (Fig. 1A). Cats walked inside the chamber in circles at a self-selected pace. The following locomotion tasks with different accuracy demands on paw placement were studied: simple walking on a flat surface (simple locomotion) and walking on crosspieces of a horizontal ladder with crosspiece width of 18, 12, or 5 cm (complex locomotion ladder-18, ladder-12, or ladder-5; Fig. 1A). For cortical recordings (see following text), crosspieces with additional width were used: 9, 6, and 4 cm. In all ladders, the centers of the crosspieces were spaced at half of the mean stride length (22–25 cm) of participating cats observed during simple locomotion in the chamber at a self-selected speed. The top of the crosspieces was 6 cm above the floor of the chamber. In the middle of the walkway, a force plate (Bertec, Columbus, OH) was embedded in the floor or placed under a ladder crosspiece. The floor and the force plate were covered (separately) with a dark thin rubberized material as were the crosspieces of the ladders. Cats walked on the horizontal ladders 1 to 2 h per day 5–6 days a week for at least a month before recordings were made; thus the precise stepping behaviors described here were highly practiced.

Fig. 1.

Experimental setup. A: locomotion tasks: simple walking on a flat surface (simple locomotion) and walking along a horizontal ladder with crosspieces 18-, 12-, or 5-cm wide (complex locomotion). Paw prints on the crosspieces of the ladders schematically show placements of cat forelimb paws. The shaded area denotes a force platform. B: the cat model. Orientation of each segment was determined as the angle between the negative direction of the vertical axis and the longitudinal segment axis directed from the distal end of the segment to the proximal one, as indicated for the head/neck segment. C: a scheme of the recording area within the forelimb representation of the left motor cortex. The microelectrode entry points into the cortex (cortical plate openings through which penetrations have been made) were combined from all cats and shown by black circles (Cru, cruciate sulcus; Pcd, postcruciate dimple). D: a sample record of discharge of a pyramidal tract projecting neuron (PTN) during simple and complex locomotion. The bottom trace shows the swing (Sw, deflection up) and stance (St, deflection down) phases of the step cycle of the right forelimb recorded by an electromechanical sensor.

Cats used for mechanical data collection were accustomed to wearing light reflecting markers attached to their shaved body by adhesive tape. Cats used for muscle and motor cortex activity recordings were accustomed to wearing a cotton jacket, an electromechanical sensor on the paw for recording of swing and stance phases of stride, and a light backpack with electromyographic (EMG) preamplifiers. The cat from which mechanical and cortical recordings were collected simultaneously had all microamplifiers and connectors mounted on the skull.

Motion capture and inverse dynamics analysis

Mechanics of simple locomotion (flat, continuous surface) and of complex ladder-18 and ladder-5 locomotion were analyzed and compared. The full-body, 21-segment sagittal plane model of the cat (Fig. 1B) described previously (Prilutsky et al. 2005) was used. Briefly, the model included four limbs with either four (hindlimbs) or five (forelimbs) segments, the pelvis, the trunk, and the neck/head segment. The segments were assumed to be rigid and connected by frictionless hinge joints. The estimated centers of the joints were marked by 24 light-reflective markers, either 6 or 9 mm in diameter, attached to the shaved skin using double-sided adhesive tape. Two additional markers were attached to each lateral aspect of the head at the cross-points between the long axis of the head and the two perpendicular lines from the axis to the lateral corner of the eye and to the anterior edge of the ear. The midpoint between the two markers corresponds to the center of mass of the head (Hoy and Zernicke 1985).

Marker positions on the walking cat were digitally recorded using high-speed motion capture systems (Peak Performance, Englewood, CO or Vicon, Oxford, UK) at rates of 60 or 120 frames/s. The coordinates of the knee and elbow markers were recalculated using the markers of the adjacent joints and the measured lengths of the two segments forming the knee and elbow; this was done to minimize the effect of skin motion with respect to the joints (Goslow et al. 1973). Recorded marker coordinates were low-pass filtered (zero-phase lag Butterworth filter, cutoff frequencies 4–10 Hz as determined by spectral analysis of each marker coordinates; Prilutsky et al. 2005). The following 217 kinematic variables of locomotion as functions of step cycle time were computed: linear and angular displacements; velocities and accelerations of each body segment; angular displacements and velocities at each joint; and displacement, velocity, and acceleration of the cat center of mass (Table 2; for details, see Prilutsky et al. 2005). The definitions of fore- and hindlimb joint angles and the segment orientation (as shown for the neck/head and trunk segments) are demonstrated in Fig. 1B.

Table 2.

Mechanical variables analyzed and corresponding F-values

	Hind Digits		Tarsals		Shank		Thigh		Fore Digits		Carpals		Forearm		Arm		Scapula
Variable	R	L	R	L	R	L	R	L	R	L	R	L	R	L	R	L	R	L	Trunk	H/N	GCM
X-D	1.2	1.3	1.4	1.5	1.6	1.9	1.7	2.0	1.6	0.5	1.1	0.6	1.0	0.9	1.1	1.3	1.3	1.6	1.5	1.2	1.6
Y-D	0.2	0.4	1.5	0.2	2.8	2.0	5.0*	4.6*	0.1	0.9	0.2	0.5	2.0	8.2*	1.4	12.0*	12.0*	12.0*	6.9*	9.8*	9.7*
X-V	2.5	1.8	2.6	2.0	2.7	2.1	2.9	2.4	2.8	3.4	2.6	3.3	2.6	3.3	2.6	3.3	2.7	3.3	2.7	2.8	2.7
Y-V	3.5	0.4	2.7	1.3	0.5	1.3	1.4	1.2	0.8	2.4	1.0	5.6*	0.5	0.1	1.2	0.1	2.6	0.1	0.3	1.3	0.3
X-A	1.9	0.3	1.4	0.8	0.7	0.4	0.0	2.5	0.9	0.7	1.0	0.8	0.6	0.4	0.6	1.1	2.6	1.5	3.3	3.0	3.3
Y-A	0.2	0.2	0.2	0.5	0.7	0.5	1.1	0.6	3.3	1.3	2.2	1.6	2.6	1.6	3.2	1.4	3.2	1.2	4.3	2.7	—
S Ang	2.3	4.5*	0.1	1.7	7.0*	14.0*	1.7	1.2	2.5	3.8	0.5	0.9	0.2	9.4*	1.9	1.5	0.3	1.6	3.8	12.0*	—
S Ang V	5.0*	0.0	3.6	0.7	3.2	1.0	0.8	0.7	1.2	2.0	0.9	1.0	0.2	0.2	3.3	0.5	1.0	1.3	0.9	1.2	—
S Ang A	0.1	0.2	3.7	1.2	2.4	1.2	3.9	0.3	0.7	1.0	0.4	0.2	1.9	1.7	0.8	3.7	1.4	1.3	2.3	1.5	—

	MTP		Ankle		Knee		Hip		MCP		Wrist		Elbow		Shoulder
Variable	R	L	R	L	R	L	R	L	R	L	R	L	R	L	R	L
J Ang	14.0*	9.4*	6.6*	6.7*	2.2	3.6	0.5	1.2	8.0*	14.0*	7.6*	5.9*	0.3	2.0	0.5	0.5
J Ang V	2.4	0.6	3.2	0.6	1.3	0.6	0.3	1.0	1.2	2.4	2.0	1.0	2.1	0.1	1.5	1.7

										Hindlimb		Forelimb
Variable	MTP	Ankle	Knee	Hip	MCP	Wrist	Elbow	Shoulder		Fx	Fy	Fx	Fy
J Mom	8.3*	13.0*	19.0*	30.0*	2.6	10.0*	9.0*	5.7*	G Force	10.0*	14.0*	6.6*	5.8*

Mechanical variables: horizontal (X) and vertical (Y) displacements (D), velocities (V), and accelerations (A); segment angular orientation (S Ang), velocity (S Ang V), and acceleration (S Ang A); joint angle (J Ang), velocity (J Ang V), and moments (J Mom); and ground reaction force (G Force). H/N, head/neck. Asterisks (*) indicate significant F-values (P < 0.05) for accuracy effects computed using a two-way 3 × 10 [accuracy demand (simple, ladder-18, ladder-5) × cycle time (1, 2, …, 10)] repeated-measures ANOVA followed by a post hoc t-test. Otherwise, nonsignificant F-values are shown (P ≥ 0.05). Asterisks (*) in the last 3 rows indicate significant t-test values.

Accuracy of measuring distances on a rigid test object within the experimental chamber was better than 2.3 mm. The lengths of pelvis and tarsals calculated using three-dimensional coordinates of markers on the proximal and distal ends of the segments changed during a simple locomotion cycle on average by less than 7 and 8%, respectively. These changes were caused by skin movement and inconsistencies in marker placement between different experiments and cats. The coefficients of variation of joint/segment angles obtained on individual cats in repeated trials were typically smaller than 12%.

In addition, inverse dynamics analysis allowed us to compute moments of force at each fore- and hindlimb joint (eight variables) of the two cats that were tested with a force plate (recorded anterior–posterior and vertical forces for fore- and hindlimbs, four variables). The force plate embedded into the floor of the walkway or positioned under a crosspiece of a ladder recorded the ground reaction forces and the coordinates of the point of application of the force vector under the cat's paw. The joint angular velocities and moments were considered positive when the distal segment forming the joint rotated counterclockwise (Fig. 1B). For example, positive moments at the ankle, knee, and hip corresponded to joint flexion, extension, and flexion, respectively.

The mass and inertia properties of the body segments (segment mass, moment of inertia, center of segment mass location) necessary for computing the joint moments and displacements of the general center of mass (GCM) were calculated using regression equations (Hoy and Zernicke 1985) as functions of the cat mass and segment lengths.

To account for size differences between cats while combining data from different animals, variables such as segment linear displacements, velocities and accelerations, joint moments, and ground reaction forces, were normalized to obtain dimensionless numbers (e.g., Hof 1996). Linear displacements were normalized to leg length, which was defined as the sum of individual segment lengths (except the digits) in the right hindlimb (Table 1). Linear velocities were converted to the dimensionless Froude numbers, $\text{Fr}=v/\sqrt{gL}$Fr = v/gL, where v is the linear velocity of a segment at a given time instant, g is the gravitational acceleration, and L is leg length. Ground reaction forces were normalized to body weight and joint moments were normalized to body weight multiplied by the corresponding leg length. Accelerations were normalized to g, gravitational acceleration. The stride duration was divided into 10 or 100 equal bins. The 10-bin stride division was used for statistical analysis (see following text). The 100-bin division was used to average mechanical variables for each percentage of stride across different trials of each cat and across different cats. The onset of the right forelimb swing was taken as the beginning of the locomotion cycle. Time histories of all recorded kinematic and kinetic variables were averaged first within each bin and then across different trials for each cat and walking condition. A two-way 3 × 10 (respectively, accuracy demand levels: flat surface, 18-cm ladder, 5-cm ladder and time: bins 1, 2, …, 10) repeated-measures ANOVA was performed on each variable to test the effects of the accuracy demands. When the effect of accuracy demand was significant (P < 0.05), the means for each time bin and locomotion task were tested for statistical difference using the t-test for dependent variables. Statistical analysis was first conducted within each animal to determine whether behavior of analyzed variables was consistent among cats.

Surgical procedures

Electrodes for muscle activity recording and the devices for motor cortex activity sampling were surgically implanted under isoflurane anesthesia using aseptic procedures.

For muscle activity recordings, a pair of leads constructed from Teflon-insulated multistrand stainless steel wire (AS632, Cooner Wire, Chatsworth, CA) was implanted into the selected forelimb muscles: m. triceps lateralis, m. brachialis, m. extensor digitorum communis, m. extensor carpi ulnaris; and selected hindlimb muscles: m. vastus lateralis, m. biceps femoris medial, the lateral head of m. gastrocnemius, m. tibialis anterior. The electrode placements were verified by stimulation through the implanted wires before closure of the incision. The wires were led subcutaneously and connected to sockets on the head base. Screws were placed in the skull and served as a common ground.

For neuronal activity recordings, a headpiece was surgically implanted as follows. The skin and fascia were retracted from most of the dorsal surface of the skull. At 10 points around the circumference of the head, stainless steel screws were inserted into the skull and connected together with a wire. The screw heads and the wire were then inserted into a plastic cast to form a circular base. Later, awake cats were rigidly held by this base during a search for neurons before neuronal activity was tested during locomotion. The base was also used for fixation of connectors, a miniature microdrive, and a protective and electrically shielding cap. Parts of os frontale and os ethmoidale above the left motor cortex were removed. The dura above the rostral and a portion of the lateral sigmoid gyri and also above the rostral part of the posterior sigmoid gyri, over an area of about 0.6 cm², was removed. The region of the motor cortex was visually identified by surface features and photographed. The aperture was then covered by a plastic plate 1 mm thick, in which over 100 holes 0.36 mm in diameter had been drilled and filled with sterile wax. The plate was fixed to the surrounding bone by orthodontic resin (Densply Caulk). For identification of pyramidal tract neurons (PTNs) two stimulating electrodes were implanted in the pyramidal tract at the level of medullary pyramid, 1 mm apart.

Processing of EMGs

Muscle activity was analyzed during the three complex locomotion tasks: ladder-18, ladder-12, and ladder-5. Onsets of swing and stance phases of the stride were monitored by measuring the electrical resistance between the right forelimb paw and the ground (Beloozerova and Sirota 1993a,b, 2003). Muscle activity was preamplified using miniature preamplifiers on the cat's back. The activity was additionally amplified and filtered (30–1,500 Hz band-pass) using CyberAmp 380 amplifier (Axon Instruments), sampled at 3 kHz, and stored on a computer hard drive. For the analysis, raw EMGs were full-wave rectified and averaged using a central moving average with a time window of 20 ms. EMG analysis was conducted only for strides made in the middle of the walkway and whose durations did not differ by more than 50 ms. For each complex locomotion task, muscle activity was averaged over 10–40 strides recorded during the same approximately 30-min walking session and compared between the tasks. Each cat was repeatedly tested on multiple days, with the sequence of locomotion tasks randomized across sessions. Due to greater variability of stride lengths during simple locomotion and associated difficulties in collecting a sufficient number of strides with closely matched lengths, muscle activity during simple locomotion was not added to complex locomotion comparisons.

Recording and processing of cortical single-cell activity

Neuronal activity was analyzed during four locomotion tasks: simple walking on a flat surface and complex locomotion along ladders with crosspiece widths of 18, 12, or 5 cm. One of the cats was also tested on three other ladders with crosspiece widths of 9, 6, or 4 cm.

Neuronal activity was recorded extracellularly using conventional tungsten varnish-insulated electrodes. The electrode was advanced into cortical tissue through holes in the plastic plate implanted above the motor cortex (Prilutsky et al. 2005). A miniature manual single-axis micromanipulator, rigidly fixed to the skull, was used to lower the electrode. The cortical area, from which the neurons were sampled (microelectrode entry points), is shown schematically in Fig. 1C. After amplification and filtering (0.3–10 kHz band-pass; Power1401/Spike2 system; Cambridge Electronic Design, Cambridge, UK), recorded activity was displayed on the screen and archived on the computer hard drive.

All neurons encountered were tested for antidromic activation from the pyramidal tract using 0.2-ms rectangular pulses of graded intensity in the range of 0.1–0.5 mA. The principal criterion for the identification of antidromic activation was the test for collision of spikes (Bishop et al. 1962; Fuller and Schlag 1976). In addition, to aid in the identification of single neurons, waveform analysis was used to discriminate and identify the spikes of the neuron using the Power1401/Spike2 system waveform-matching algorithm. For the purpose of conduction velocity calculation, the conduction distance between the stimulation site in the pyramidal tract and the recording site in the precruciate cortex was estimated at 51.5 mm. This value includes the curvature of the internal capsule and accounts for the spread of current and the refractory period at the site of stimulation.

As with EMGs, onsets of swing and stance phases of the stride were monitored by measuring the electrical resistance between the right forelimb paw and the ground (Sw/St trace in Fig. 1D) (Beloozerova and Sirota 1993a,b, 2003). The Rayleigh test for directionality was used to determine whether the activity of a neuron was modulated in relation to the cycle (Batshelet 1981; Fisher 1993). If the activity of a neuron was judged to be stride-related, the duration of each walking cycle was divided into 10 equal bins, and a phase histogram of spike activity of the neuron in the walking cycle was generated and averaged over all successive cycles. The discharge frequency in a bin was derived according to the method of Udo et al. (1982), which weights the data according to the average of the instantaneous frequency of the intervals that fall within the bin as well as those that overlap with its beginning and end. The phase histograms were smoothed by recalculating the value of each bin as follows: F_n = 0.25F_n−1 + 0.5F_n + 0.25F_n+1, where F_n is the original value of the bin. The first bin was considered to follow the last one and vice versa. Using the histogram, the depth of modulation (dM) was calculated as a measure of periodic changes in a neuron's activity. It was defined as dM = [(N_max − N_min)/N] × 100%, where N_max and N_min are the number of spikes in the maximal and the minimal histogram bin and N is the total number of spikes in the histogram. In addition, the portion of the cycle in which the activity level exceeded 25% of the difference between the maximal and minimal frequencies in the histogram was defined as a “period of elevated firing” (PEF) (as illustrated later in Fig. 8, B, D, F, and H). The preferred phase of the discharge of each neuron in the step cycle was assessed using circular statistics (Batshelet 1981; Fisher 1993; see also Beloozerova et al. 2003). The occurrence of each spike was presented as a vector of a unit length. The angle (phase) of this vector was calculated by multiplying the relative position of the spike in the cycle (in portions of the cycle) by 2π. The preferred phase was then calculated as the phase of the mean vector divided by 2π. Preferred phases of all individual neurons were plotted against the phase of the step cycle to show their phase distribution.

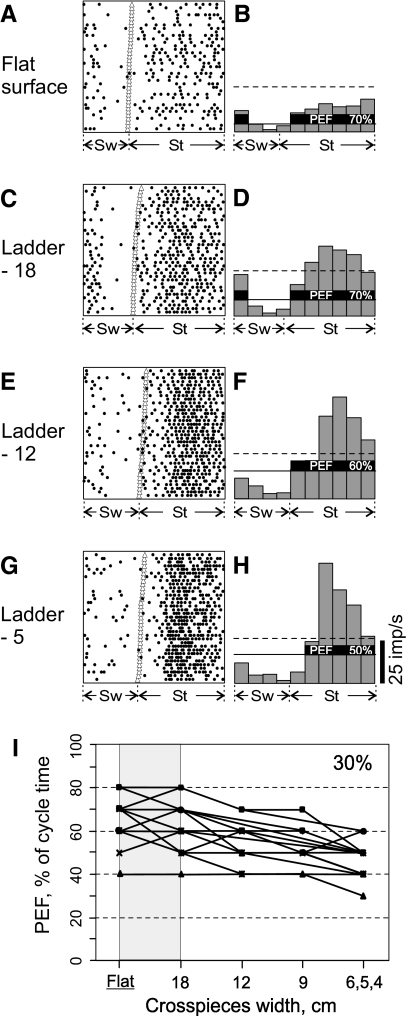
Fig. 8.

Period of elevated activity (period of elevated firing [PEF]), shortens as demand on accuracy of stepping increases. A and B: activity of a pyramidal tract projecting neuron during simple locomotion is presented as a raster of 35 step cycles (A) and as a histogram (B). In the raster, the duration of step cycles is normalized to 100% and the raster is rank-ordered according to the duration of the swing phase. The beginning of the stance phase in each stride is indicated by an open triangle. In the histogram, the horizontal dashed line shows the level of activity at rest. The horizontal continuous line shows the level above which the activity was considered “elevated” (see methods); and the duration of PEF is expressed as a portion of the step cycle that it encompasses, 70%. C and D: activity of the same neuron during ladder-18 locomotion. PEF has the same duration as that during simple locomotion. E and F: activity of the same neuron during ladder-12 locomotion. The portion of step cycle that includes PEF decreased to 60%. G and H: activity of the same neuron during ladder-5 locomotion. The portion of step cycle that PEF encompassed decreased further to 50%. I: durations of PEFs across locomotion tasks with different accuracy demands of all 19 neurons in which they progressively decreased as the width of ladder's crosspieces decreased.

The activity of each neuron was recorded during 15–40 (on average 20 ± 5) runs of each simple locomotion and of at least two complex locomotion tasks. From each run, 2 or 3 strides made in the middle of the walkway whose durations did not differ by more than 80 and 100 ms in swing and stance durations, respectively, and did not differ by more than 150 ms in duration of the entire stride were taken for the analysis. The activity of each neuron was sampled over 20–130 (on average 60 ± 20) strides of each locomotion task.

The activity of a neuron during a stride was computed by dividing the number of spikes by duration of the stride and averaged across all strides of the task. For each neuron, a t-test for dependent variables was performed for pairs of tasks adjacent in their accuracy demand: flat surface versus ladder-18, ladder-18 versus ladder-12, and so forth. The peak activity and the dM of each neuron in a locomotion task were obtained from the smoothed phase activity histogram of the neuron during the task. For each neuron during each locomotion task their values were compared similarly to the values of the average activity. The PEF of each neuron during a locomotion task was also obtained from the smoothed phase activity histogram. For each neuron, duration of PEF, expressed as a portion of step cycle that it encompassed during a task, was compared across the tasks. A difference by 1/10 of the step cycle was considered significant. Unless indicated otherwise, the SD is given for all mean values.

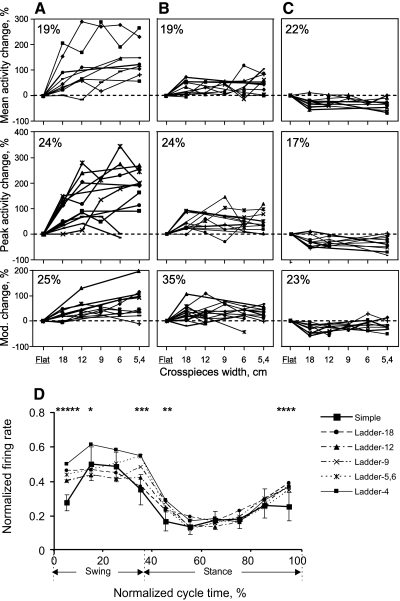
To determine the group activity of all recorded neurons in 10 cycle bins, the mean activity in each bin of each cell during different tasks was normalized to the maximum firing rate found across all tasks for a given cell. A two-way 6 × 10 (respectively, accuracy demand levels: flat surface, 18-cm ladder, 12-cm ladder; 9-cm ladder; 5- to 6-cm ladder; 4-cm ladder and time: bins 1, 2, …, 10) repeated-measures ANOVA was performed on the normalized firing rate to test the effects of the accuracy demands. When the effect was significant (P < 0.05), the means for each time bin and locomotion task were tested for statistical difference using the t-test for dependent variables.

Receptive field classification

The somatic receptive field of the neurons was examined while animals were resting with their head restrained. Stimulation was produced by palpation of muscle bellies, tendons, and by passive joint movements. Receptive field size was determined by listening to the audio monitor and measuring the entire area from which action potentials could be elicited.

Terminal experiment and histological procedures

At the termination of the experiments, the cats were deeply anesthetized with pentobarbital sodium and several reference electrolytic lesions were made in the recording area in the left motor cortex. Positions of the EMG electrodes in muscles were verified. Lengths of segments, as defined in Hoy and Zernicke (1985), were measured using an anthropometer. The cats were perfused with isotonic saline followed by a 10% formalin solution. Frozen sections (50-μm thickness) were cut in the regions of the motor cortex and medullary pyramid. The tissue was stained for Nissl substance with cresyl violet. The positions of tracks in the cortex were estimated in relation to the reference lesions. The locations of stimulating electrodes in the medullary pyramid were verified.

RESULTS

Mechanics of highly practiced accurate target stepping

STEP CYCLE CHARACTERISTICS ARE SIMILAR BETWEEN SIMPLE LOCOMOTION AND PRECISE STEPPING.

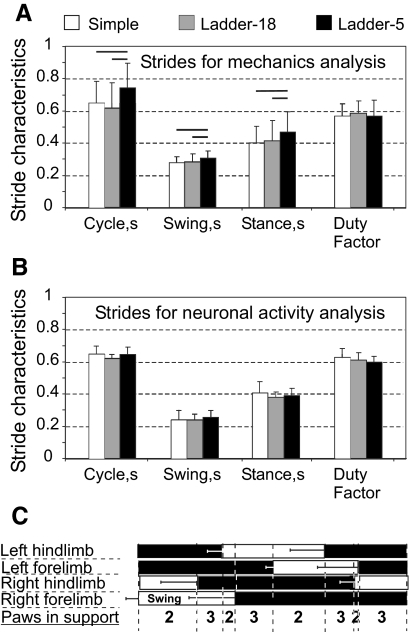
During simple locomotion at a self-selected speed, the stride length was in the range of 44–50 cm. The average stride length of individual cats was similar across all locomotion tasks, both complex and simple. This was explained by the fact that the crosspieces on the ladders were placed in accordance with the comfortable stride length of each cat (see methods). Cats, from which mechanical data were collected, walked slower on the most accuracy-demanding ladder-5, compared with simple locomotion or ladder-18: walking speeds were 0.68 ± 0.22 m/s (0.43 ± 0.14 Froude number [Fr]), 0.83 ± 0.25 m/s (Fr = 0.52 ± 0.16), and 0.92 ± 0.30 m/s (Fr = 0.58 ± 0.20), respectively (P < 0.05, t-test). Correspondingly, the swing and stance times were also longer on ladder-5 (P < 0.05, t-test), whereas there was no difference in the duty factor (the ratio of stance time to cycle time) (Fig. 2A). Cats, from which neuronal data were collected, walked with similar speeds during simple locomotion, ladder-18, and ladder-5 tasks (0.78 ± 0.7, 0.83 ± 0.18, and 0.80 ± 0.16 m/s, respectively; P > 0.05, t-test). The mean duration of the step cycle, the swing and stance phases, and the duty factors in these cats were similar across tasks (Fig. 2B).

Fig. 2.

Characteristics of the step cycle during different locomotion tasks. A: averaged durations of the cycle, the swing and stance phases, and the duty factor (the ratio of stance duration to cycle duration) for the 5 cats, data from which were included in full-body mechanical analysis. B: same as A for the 3 cats, data from which were included in motor cortex activity analysis. The horizontal lines above bars indicate statistically significant (P < 0.05) differences between tasks (t-test). C: a stride diagram derived from simple locomotion of 5 cats used for mechanical analysis. Empty bars indicate the swing phase and black bars the stance phase of each limb. Horizontal error bars show SD. Four periods of 2-limb support and 4 periods of 3-limb support in one stride of the right forelimb are marked, with the walk stride formula 2–3–2–3–2–3–2–3.

The gait, which all cats used during both simple and complex locomotion, was a walk with the support formula 2–3–2–3–2–3–2–3 (the succession of combinations of supporting limbs in a right forelimb [RF] step cycle; Hildebrand 1965; Fig. 2C). There was no difference in the phase of individual limb movement between different locomotion tasks (determined as the normalized time at which the peak horizontal velocity of each paw occurred in the cycle; not shown). In all cats except one during all locomotion tasks the hindlimb paw placement was slightly in front of the ipsilateral forelimb paw placement.

CATS STEP ON SMALLER TARGETS WITH LESS VARIABILITY.

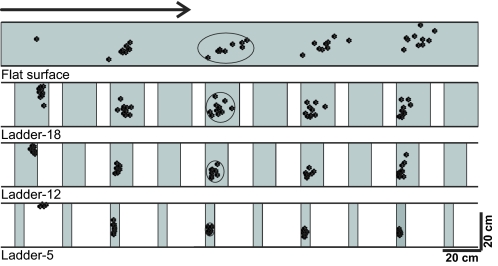
During simple locomotion, no restrictions were imposed on paw placements, whereas in complex locomotion tasks placements were progressively more restricted as the crosspiece width decreased. The variability of paw placement was affected significantly by the available support surface: as the area of the support surface decreased, variation in paw placements became smaller (Fig. 3). Paw placement variability was not related to the initial paw position on the walkway because this was not significantly different between accurate stepping conditions (P > 0.5, F-test). The major reduction in variability (SD) occurred on transition from simple locomotion (where, in the direction of progression, it was 70 mm) to locomotion on the ladder with the widest crosspieces, ladder-18 (where it was 25 mm; P < 0.05, F-test). Transition from ladder-18 to ladder-12, and further to ladder-5, was associated with additional reductions in the paw placement variability to 11 mm and then to 5 mm (P < 0.05, F-test). No difference in paw placement variability between fore- and hindlimbs was found (three cats tested: N1, N3, and NC; P > 0.05, F-test).

Fig. 3.

A typical distribution of right forelimb paw prints recorded from one animal (N3) during 10 walking trials performed in each condition: on a flat surface (simple locomotion) and along ladders with crosspieces 18, 12, and 5 cm wide (complex locomotion). View from above. The direction of the cat's progression is shown by the arrow on the top. For simple locomotion, paw prints are adjusted to start in the same position. For ladder tasks, note similarly small variability of paw prints at the start of walkway (±2 cm in the direction of progression). The first paw placement during ladder-5 locomotion was between the crosspieces. Ellipses enclose approximate areas in which 95% of paw prints were found.

The area of contact surface of the fore- or hindlimb paws with the ground in cats is about 7 cm² (an area of a circle with a diameter of ∼3 cm). During all complex locomotion tasks, cats placed their paws such that the entire paw was always in contact with the surface, even on ladder-5. On ladders with wider crosspieces, cats showed no preference in stepping on the closer or farther parts of the crosspieces and 95% of steps (2SDs from the mean paw position on a crosspiece) fell in the middle of the crosspiece inside an ellipse of an approximate area of 200, 100, and 40 cm² for ladder-18, ladder-12, and ladder-5, respectively (circled areas in Fig. 3).

CATS ASSUME A MORE BENT-FORWARD POSTURE WHEN ACCURACY DEMANDS ON STEPPING INCREASE.

In total, 30 strides of simple locomotion (9 from cat BU, 8 from BL, 5 from each KO and BA, and 3 from NC), 22 strides of complex locomotion on ladder-18 (5 from each of BU, KO, and NC; 4 from BA; and 3 from BL), and 25 strides of ladder-5 locomotion (9 from BU, 5 from BL, 4 from each of KO and BA, and 3 from NC) were included in detailed mechanical analysis. In all, 229 kinematic and kinetic variables as functions of cycle time were obtained and analyzed (Table 2).

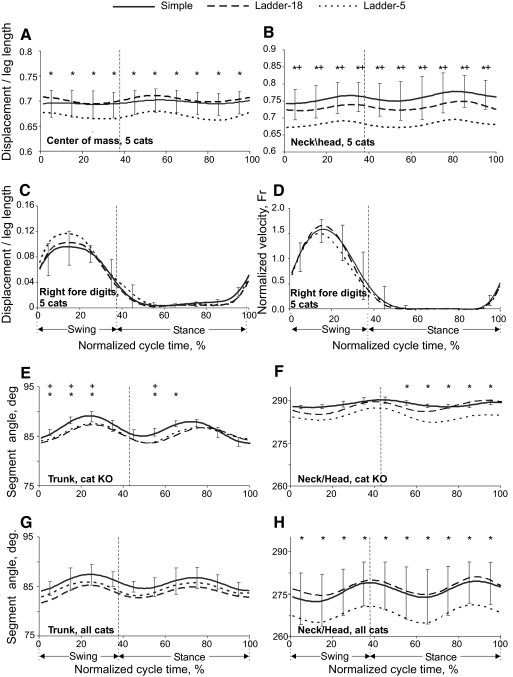
During a stride, the vertical position of the general center of mass (GCM, Fig. 4A) and the centers of mass of the neck/head (Fig. 4B) and trunk segments (not shown) were lower by about 1 to 2 cm during ladder-5 compared with ladder-18 or simple locomotion (F_(2,18) = 9.908, P < 0.05; F_(2,18) = 12.384, P < 0.05; and F_(2,18) = 6.910, P < 0.05, respectively). In contrast to GCM, neck/head, and trunk, the horizontal and vertical displacements of limb segments did not differ significantly between locomotion tasks during most of a step cycle (e.g., Fig. 4C; Table 2). The time histories of paw horizontal velocity were symmetric and smooth in all limbs (Fig. 4D; data shown only for the right hindlimb). No statistical differences were found in the paw velocities among the tasks (P > 0.05). The only difference in segment orientations was found in the neck/head (Fig. 4, F and H; Table 2). The neck/head angle, as defined in Fig. 1B, was <270° (the horizontal orientation) during the ladder-5 task, whereas during simple and ladder-18 locomotion it was greater (F_(2,18) = 12.125, P < 0.05). The mean trunk orientation was not significantly different among the tasks (P > 0.05; Fig. 4G). However, in several individual cats (BL, BU, KO), the trunk had a greater clockwise rotation from the horizontal (90°) in accuracy-demanding tasks compared with simple locomotion (e.g., Fig. 4E).

Fig. 4.

Displacements and orientation of body segments during simple and complex locomotion. A and B: vertical displacements of the general center of mass (GCM) (A) and the neck/head segment (B, as defined in Fig. 1B). C and D: vertical displacement (C) and horizontal velocity (D) of forelimb digits. E and F: averaged orientation angles of trunk (E) and neck/head (F) segments during simple and complex locomotion of cat KO. G and H: the same as E and F when averaged across 5 cats. Vertical dashed lines separate the swing and stance phases. SDs were similar across all tasks and for clarity are shown only for simple locomotion. Asterisk (*) indicates significant (P < 0.05, post hoc t-test) difference between simple and ladder-5 locomotion; + symbol indicates significant (P < 0.05, post hoc t-test) difference between simple locomotion and ladder-18 task.

Reduction in neck/head angle and lower vertical position of the body during complex locomotion brought the head closer to the ground by about 2 to 4 cm during both ladder-18 and ladder-5 tasks compared with simple locomotion. In addition, the head angle, as defined in Fig. 5A, was closer to the vertical (0°) during all ladder tasks compared with simple locomotion (F_(2,18) = 9.578, P < 0.05; Fig. 5, A and B). Consequently, during ladder locomotion the long axis of the head, if continued forward, intersected the ground much closer to the leading forepaw at ground contact (P < 0.05, t-test; Fig. 5, A and C).

Fig. 5.

Orientation of the head during locomotion tasks with different accuracy demands. A: representative stick figures of one cat (BL) near left forelimb paw contact during simple and complex locomotion. The right side of the body is indicated by the continuous line and the left side, by the dashed line. The trajectory of the GCM is shown by a gray line. Dotted lines show the angle between the long head axis and the vertical. B: averaged head angles during simple and complex locomotion. SDs during simple locomotion exceeded head angle ranges depicted in the plot and therefore are shown for ladder-5 task only. C: intersection: averaged horizontal position of the intersection point between the ground and the head axis during different tasks. SDs were similar across all tasks and for clarity are shown only for simple locomotion. C: fore digits: horizontal displacement of the leading forelimb digits. Other designations as in Fig. 4.

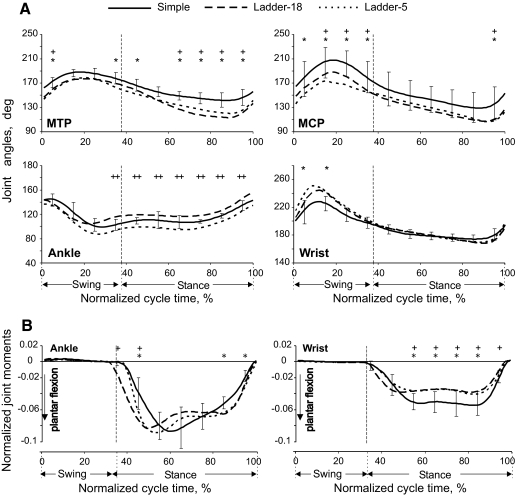
Angles at the distal joints [metatarsophalangeal (MTP) and metacarpophalangeal (MCP)] during ladder locomotion differed from those during simple locomotion (MTP: F_(2,18) = 3.243, P < 0.05; MCP: F_(2,18) = 3.940, P < 0.05; Fig. 6A). The MTP and MCP joints had greater dorsiflexion throughout the step cycle during complex locomotion, especially toward the end of stance. The wrist was more plantarflexed during swing (F_(2,18) = 2.091, P < 0.05; Fig. 6A), whereas the ankle showed differences between ladder-18 and ladder-5 tasks only during stance (F_(2,18) = 4.862, P < 0.05; Fig. 6A). There was no significant difference in the values of the proximal joint angles (hip, knee, shoulder, and elbow) during different locomotion tasks (Table 2).

Fig. 6.

Distal joint angles and moments of the hindlimb (left panels) and forelimb (right panels) during simple and complex locomotion. Designations as in Fig. 4.

Selected joint moments were accuracy demand dependent. During early stance, the ankle plantar flexion (Fig. 6B) and knee extension (not shown) moments were higher in the ladder-5 task than those during simple locomotion (P < 0.05, t-test). In midstance, the knee exerted smaller extension moments during the ladder-18 task, whereas the hip (not shown) exerted greater flexion moments during the ladder-5 task compared with those during the other tasks (P < 0.05, t-test). The wrist plantar flexion moment during most of the stance was lower in ladder-18 and ladder-5 tasks compared with that during simple locomotion (P < 0.05, t-test; Fig. 6B).

Activity of selected distal muscles is enhanced during accurate stepping

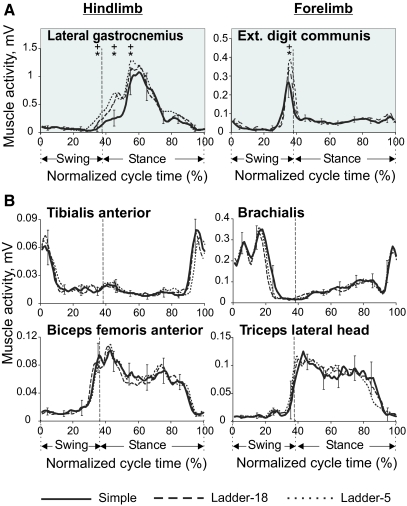
In four cats, the activity of eight fore- and hindlimb muscles was recorded (see Table 3 for muscle names). Two muscles: lateral gastrocnemius (ankle extensor and knee flexor) and extensor digitorum communis (wrist and MCP extensor), demonstrated accuracy demand dependent activity (Fig. 7A). The activity of the lateral gastrocnemius was progressively higher (P < 0.05, t-test) in more demanding tasks right before beginning of stance and also during early stance. The average peak difference was 16 ± 13%. In addition, the activity occasionally started slightly earlier in cycles with higher accuracy demand and was then higher at that time of cycle by 96 ± 61%. Similarly, the extensor digitorum communis, which was mainly active in late swing and early stance, demonstrated higher activity during more demanding tasks (P < 0.05, t-test, Fig. 7A). The average peak difference was 38 ± 8%. We found no significant difference in the magnitude or pattern of the EMG activity between the three complex locomotion tasks in other muscles tested (see e.g., Fig. 7B).

Table 3.

Muscles included in the analysis

Muscle	Side	Cat
Lateral gastrocnemius	Right	8, N1, N3
	Left	8, N3
Tibialis anterior	Right	N3
	Left	8
Vastus lateralis	Right	N1, N3
	Left	8, N1, N3
Biceps femoris anterior	Right	N1
	Left	8, N1
Brachialis	Right	—
	Left	8, N1, N3
Triceps, lateral head	Right	N1, 11
	Left	8, N1, N3, 11
Extensor digitorum communis	Right	11
	Left	11
Extensor carpi ulnaris	Right	11
	Left	11

Fig. 7.

Activity of selected limb muscles during 3 complex locomotion tasks. A: typical examples of the averaged activity patterns of muscles whose activity was related to accuracy demands. Each panel shows a representative activity of an individual muscle, which was averaged over 10–25 strides of each locomotion task, all recorded during one session (see methods for stride selection). SDs were similar across all tasks and for clarity are shown for ladder-18 task only. B: typical examples of the averaged activity patterns of flexor and extensor fore- and hindlimb muscles whose activity was not related to accuracy demands.

Motor cortex neuronal activity is accuracy demand dependent

Data on neuronal activity were collected from a total of 24 tracks through the forelimb representation in the left motor cortex in the rostral and lateral sigmoid gyri: 9 tracks from cat 7, 5 from cat KO, and 10 from cat CL, Figure 1C schematically shows microelectrode entry points into the area of recording; points are combined from all cats. All recording sites were within cortical area 4γ. The activity of 63 neurons was recorded, 30 of which were identified as pyramidal tract projecting neurons (PTNs). Roughly 80% of PTNs had conduction velocities in the range of 40–70 m/s (latent periods of 0.7–1.2 ms). At rest, all neurons except for one were active and their average discharge rate was 12.7 ± 8.1 impulses/s (range: 0.7–32 impulses/s). The activity of each neuron was recorded during 20–130 (on average 60 ± 20) step cycles of each simple locomotion and at least two complex locomotion tasks.

WIDTH OF PEF IS PROPORTIONAL TO WIDTH OF LADDER CROSSPIECES.

During simple locomotion, the activity of 94% of all neurons was modulated with the stepping rhythm, that is, it was higher in one phase of the step cycle and lower in another phase (e.g., Fig. 1D). The period of elevated activity (PEF) was defined as the portion of the step cycle in which the activity level of a neuron exceeded 25% of the difference between its maximal and minimal frequencies in the histogram (see methods). During simple locomotion, the average duration of PEFs was 60 ± 12% of the step cycle. In 71% of neurons (45/63) the duration of PEF changed on transition from simple to the ladder-18 locomotion, increasing in 35% or decreasing in 36% of them. PEF changed by 1/10 of the step cycle duration in 40% of neurons, by 1/5 of the cycle duration in 20% of them, and by 3/10 to 2/5 in the remaining 11% of neurons. There was no relationship between magnitude and direction of PEF change.

In addition, in 30% of neurons (19/63) PEFs systematically changed with accuracy demands of ladder locomotion. PEFs became progressively shorter as the ladder's crosspieces became narrower. An example is shown in Fig. 8. During simple locomotion (Fig. 8, A and B) the activity of this neuron was elevated during most of stance and also in beginning of swing and its PEF encompassed 70% of step cycle. On transition to ladder-18 locomotion, PEF stayed unchanged in spite of an increase in the overall activity of the neuron (Fig. 8, C and D). On transition to ladder-12 locomotion, however, the activity of the neuron concentrated in stance phase only and PEF became 10% shorter, now encompassing 60% of the cycle (Fig. 8, E and F). On transition to the most accuracy demanding ladder-5 task the activity of the neuron further consolidated in the middle of stance and PEF became still shorter by another 10%, now encompassing 50% of the cycle (Fig. 8, G and H).

Durations of PEFs across locomotion tasks with different accuracy demands for all 19 neurons in which PEF progressively decreased as widths of the ladder crosspieces diminished are shown in Fig. 8I. On transition from simple locomotion to the ladder-18 task duration of PEFs in this neuronal group could either decrease or increase (shaded in Fig. 8I). As the width of ladder crosspieces diminished in ladder locomotion tasks, however, PEFs of these neurons became progressively smaller, shrinking by as much as 30% during the most demanding task. The average duration of PEFs in this group during ladder-5 locomotion was 47 ± 8%, significantly shorter than the average PEF duration during the ladder-18 task (63 ± 11%, P < 0.05, t-test).

The reduction of PEF during more accuracy demanding locomotion tasks was not related to changes in neuronal average activity, peak activity, or depth of modulation. Among 19 neurons, whose PEF progressively shortened with the increase in the accuracy demands, there were 9 neurons whose activity and/or depth of modulation increased, 3 neurons whose activity and/or depth of modulation decreased, and 7 neurons in which these parameters were unchanged.

Although duration of PEF changed in many of neurons as the accuracy demands during locomotion changed, the preferred phase was unaffected in 78% (49/63) of them.

MEAN, PEAK ACTIVITY, AND DEPTH OF MODULATION OF SOME NEURONS INCREASE WITH THE LEVEL OF ACCURACY.

The mean activity of 60% (38/63) of the neurons changed on transition from simple to complex locomotion, increasing in 38% and decreasing in 22% (P < 0.05, t-test; Fig. 9, top row). In half of the neurons with increased activity, the increase occurred in two stages: first on transition from locomotion with a lower level of accuracy to that with a higher level and then again on transition to the next level of accuracy (Fig. 9A). In almost all of these neurons the first increase occurred on transition from simple to the least accuracy demanding task of ladder-18. The range of the increase was 25–200%. In almost all of these cells, the second increase (an additional 35–86%, P < 0.05, t-test) was on transition to the next demanding task of ladder-12. In only three neurons was there a third rise in activity during a still more demanding task.

Fig. 9.

Activity and depth of frequency modulation as functions of accuracy demands on stepping. A–C: top panels show the mean activity of individual neurons during different ladder tasks expressed as percentages of their activity during simple locomotion. Middle panels show that for the peak activity and bottom panels show changes in the depth of modulation. A: neurons whose activity or depth of modulation increased twice: first, typically during transition from simple to ladder-18 locomotion and then again during transition from ladder-18 to ladder-12. B: neurons whose activity or depth of modulation increased only once, typically during transition from simple to ladder-18 locomotion. C: neurons whose activity or depth of modulation decreased one time, typically during transition from simple to ladder-18 locomotion. D: normalized activity (±SD) of all recorded neurons as a function of normalized cycle time. Asterisk (*) indicates statistical difference between a precise stepping condition and simple walking (P < 0.05, post hoc t-test). For example, 5 symbols over the first time bin show that the activity in all 5 accurate stepping tasks was different from simple walking.

In the other half of neurons with enhanced activity in more accuracy demanding tasks, activity increased on transition from a less demanding task to the next one and did not change further with increasing accuracy demands (P > 0.05, t-test, Fig. 9B). Most often the activity increase occurred during transition from simple locomotion to the least demanding task of ladder-18. The range of the increase was 15–70%. Finally, in the neurons with a decrease in activity during complex locomotion, the decrease always occurred once during transition from simple to ladder-18 locomotion (Fig. 9C). The range of the decrease was 20–60% (P < 0.05, t-test).

The peak activity of 65% (35/63) of neurons changed on transition from simple to complex locomotion, increasing in 48% and decreasing in 17% (P < 0.05, t-test; Fig. 9, middle row). In individual neurons, the patterns of these changes were qualitatively similar to the changes in the average activity, but were somewhat larger (compare with Fig. 9, top row).

The depth of modulation of 83% (52/63) of neurons changed on transition from simple to complex locomotion, with an increase in 60% or decrease in 23% (P < 0.05, t-test; Fig. 9, bottom row). In 25% of neurons with the increased modulation depth, the rise in modulation occurred in two stages (Fig. 9A). Similar to activity changes, in most of these neurons the first increase was on transition from simple to the least accuracy demanding task of ladder-18. The range of the increase was 17–47%. In almost all of these cells, the second increase (additional 15–80%) was on transition to the next demanding task of ladder-12. In only two neurons was there a third increase at a still more demanding task. In 35% of neurons with the increased modulation depth in accuracy demanding tasks, the rise in modulation occurred once (Fig. 9B). In most of these neurons the modulation depth increased during transition from simple locomotion to the least demanding task of ladder-18. The range of this increase was 16–104%. Finally, in the neurons with a reduction in the modulation depth during complex locomotion, the decrease typically occurred once at the transition from simple to ladder-18 locomotion (Fig. 9C). The range of the decrease was 15–60%.

The mean normalized population activity of all recorded neurons was elevated during swing and late stance (Fig. 9D). The magnitude of this elevation was significantly greater during the majority of accurate stepping tasks, compared with simple walking (P < 0.5, t-test).

NEURONS WITH DIFFERENT RECEPTIVE FIELDS RESPOND DIFFERENTLY TO ACCURACY DEMANDS.

Receptive fields were tested in 32 neurons: 12 responded to movements in the right shoulder joint, 11 to flexion of the wrist or pressure on the paw plantar surface, and 7 to squeezing the forearm or movement in the elbow joint. The receptive field of one neuron extended over most of the forelimb and one neuron was not responsive.

Neurons with receptive fields on the shoulder tended to have two-stage increases in the average and peak activity or in modulation as demands on the accuracy of stepping increased (Fig. 9A; 8 of 12 neurons). In contrast, neurons with receptive fields on the wrist tended to have one-stage increases in the activity and/or modulation (Fig. 9B; 7/11 neurons) or decreases in the activity (Fig. 9C; 4/11 neurons). Neurons with receptive fields on the elbow had mixed responses. Neurons with various receptive fields responded by a change in duration of PEF to increasing accuracy demand during locomotion.

DISCUSSION

A detailed full-body mechanical analysis of accurate target stepping in the cat is done for the first time in this study; however, the walking mechanics of the cat on a continuous surface can be compared with those reported in previous publications. In general, the segment and joint kinematics, as well as ground reaction forces and joint moments reported in this study (Figs. 2, 4, and 6), are consistent with the literature (Fowler et al. 1993; Gregor et al. 2006; Maas et al. 2007; Manter et al. 1938; McFadyen et al. 1999; Prilutsky et al. 2005). The EMG activity patterns during simple walking in all eight recorded muscles (Fig. 7) were also consistent with previous reports (Krouchev et al. 2006; Pierotti et al. 1989; Rossignol 1996; Smith et al. 1998). Similarly, in accordance with previous findings (Armstrong and Drew 1984; Beloozerova and Sirota 1988, 1993a,b; Drew 1993), the activity of many motor cortex neurons was step-modulated, with higher modulation during complex visually controlled locomotion (Figs. 8 and 9).

Accurate target stepping requires control of stride length and changes in posture to improve stability and view of targets

The major mechanical changes seen with increasing accuracy demand were 1) reduction of spatial variability of paw placement (Fig. 3); 2) lowering the general center of mass (Fig. 4A); 3) reorientation of the neck and head toward the ground (Figs. 4, F and H and 5); and 4) modification of distal joint angles and joint moments (Fig. 6).

Locomotion tasks used in this study were designed so that, for every cat, the average length of strides was similar across the tasks. The variability of paw placements on the support surface, however, was quite different between the tasks, despite similar variability of initial paw position on the walkway (Fig. 3). Reduction of paw placement variability on the ladders could be achieved only by increasingly more precise control of length of each stride, the process based on visual information about the distance to and size of the next target.

It has been shown that locomotion on complex terrains requires vision (Beloozerova and Sirota 2003; Fowler and Sherk 2003; Gibson 1958; Hollands and Marple-Horvat 1996; Patla and Vickers 2003; Reynolds and Day 2005; Wilkinson and Sherk 2005). The position and orientation of the neck and head determine position of eyes in relation to support surface and stepping targets and thus the field and clarity of the view. We found that during complex locomotion, the neck and head of the cat changed their height and orientation to bring the eyes closer to the ground (Figs. 4 and 5). If the long axis of the head could be considered an approximation of the cat gaze direction (Fowler and Sherk 2003), then the stepping target's retinal image should be larger during more accuracy demanding tasks. A better view of the targets is likely to make control of paw placements easier and more effective. This benefit apparently exceeds the negative effects of the head and neck deviation from their neutral position on the accuracy of pointing movements (these negative effects are presumably caused by altered perception of the target and body segments in space; Berger et al. 1998; Fookson et al. 1994; Knox and Hodges 2005).

Lowering the GCM, thought to improve postural stability during complex locomotion, is achieved by forward rotation of the neck with head and extraflexion of the distal joints during stance (MTP, MCP, ankle). Given similar knee, hip, shoulder, and elbow angles during simple and complex locomotion, an additional contribution to lowering the GCM in accurate stepping could come from the pelvis–trunk and the scapular–trunk articulations (see Fig. 1B). However, angles of these “joints” were not determined in this study because of their anatomical complexity. Since there was no physical danger of falling off the ladders, which were elevated by only 6 cm above the floor, improving postural stability during accuracy demanding tasks appears to be a component of the mechanism for accurate target stepping.

The symmetry and smoothness of paw velocity profiles during complex locomotion, observed not only in the averaged profile (Fig. 4D) but in a majority of individual strides (not shown), suggest that, during the precise stepping tasks investigated in this study, the paw trajectories and placement positions were preplanned and no on-line corrections during swing were used. This conclusion is supported by the fact that paw horizontal velocity profiles of both the forelimbs and hindlimbs had similar features typical for preplanned movements: bell-like shape, symmetry, no statistical effects of accuracy demands. Also, if one assumes that target stepping by the hindlimbs is reaching to remembered targets, then it is likely preplanned and not corrected on-line (Adamovich et al. 1998, 1999). This conclusion is also in agreement with recently reported data in primates, which suggest that swing phase dynamics is set by a central neural mechanism at the onset of swing (Xiang et al. 2007).

Accurate target stepping is associated with an increased activity of selected distal muscles

With increasing accuracy demands and corresponding precision of stepping during complex locomotion, the activities of the lateral gastrocnemius (ankle extensor and knee flexor) and extensor digitorum communis (wrist and MCP dorsiflexor) were progressively higher (Fig. 7). These activations, however, only partly resulted in changes of the angles or moments of the corresponding joints (e.g., ankle extension moment in early stance was greater during complex locomotion, in agreement with enhanced activity of the lateral gastrocnemius; Fig. 6B). How the distal muscle activation affects variability of paw placements on smaller targets (Fig. 3) remains unclear.

It is believed that one of the strategies by which the motor system achieves accuracy in multijoint arm movements is co-contraction of antagonist muscles (e.g., Gribble et al. 2003). Indeed, several research groups observed co-contraction of antagonist muscles during accurate movements (Gribble et al. 2003; Laursen et al. 1998; Osu et al. 2002 2004). In our experiments, however, all studied muscles, except lateral gastrocnemius and extensor digitorum communis, strictly maintained their activity timing and magnitude with increased demands on accuracy of stepping. Thus we conclude that co-contraction of antagonist muscles was not the major feature of accurate well-trained target stepping. In other target pointing tasks it was shown that co-contraction of antagonist muscles decreases with practice (Gribble et al. 2003; Thoroughman and Shadmehr 1999) and therefore it should not be a major contributor to accurate execution of well-practiced movements.

Previous studies reported that the head and neck position can modulate limb-muscle activity in postural and locomotion tasks in the cat (Gottschall and Nichols 2007; Roberts 1967), presumably due to postural reflexes originating from vestibular and neck muscle receptors. Nose-down rotation of the head and neck in the decerebrate cat walking on a flat surface was reported to transiently increase EMG activity of the knee and hip extensors, but not the lateral gastrocnemius (Gottschall and Nichols 2007). The consistent increase in the EMG magnitude of both the lateral gastrocnemius and the extensor digitorum communis with increasing accuracy demands found in this study (Fig. 7) thus does not seem to be a consequence of head and neck downward rotations (Figs. 4H and 5), but is likely related to a difference in the muscle control mechanisms during simple and complex locomotion. Some other researchers have also reported higher EMG activities during more accurate movements (Kakuda et al. 1996; Laursen et al. 1998) and thus this could be one of the mechanisms by which accuracy is achieved.

Role of the motor cortex in control of accurate target stepping

In earlier publications, we suggested that the control of movement accuracy during locomotion is a special function of the motor cortex (Beloozerova and Sirota 1988, 1993a,b). The present study investigated details of the relationship between the motor cortex activity and the accuracy demands on stepping. We found that the period of elevated firing (PEF), which characterizes how well timed and trial-to-trial consistent a neuron's activity is in relation to the step cycle, became progressively shorter in 30% of neurons as demands on accuracy of stepping increased and cats stepped on ladder crosspieces with less variability (Fig. 8). That is, a decrease in variability of stepping was parallel to a decrease in time variability of discharges in these motor cortex neurons. In addition, the activity and depth of the locomotion-related modulation increased with the accuracy demands in 20–25% of neurons, albeit nonlinearly (Fig. 9A). These findings suggest that, during accurate stepping, a subpopulation of motor cortical neurons is involved in control of movement accuracy in a “dose-dependent” manner and the increasingly precise firing of these neurons during more accurate stepping is one of mechanisms by which accurate stepping is achieved. We hypothesize that the increasingly precise timing and the more vigorous activity of motor cortical neurons might contribute to control of stride length and thus reduction in variability of paw placement during accurate stepping. In the future, a stride-by-stride analysis should be used to reveal details of this relationship. Based on results of movement perturbations and motor cortex inactivation experiments, a role of the motor cortex in control of the physical position of paw landing was also previously suggested by Amos and Armstrong (1990) and Friel and colleagues (2007). Consistent with our hypothesis is also the fact that the normalized mean activity of all recorded neurons during accurate stepping was elevated in late stance and early swing of accurate stepping (Fig. 9D), suggesting that cortical regulation of paw placement might be conducted in advance, i.e., before paw-off or/and in early swing.

The differences in the activity of neurons in the forelimb representation of the motor cortex during simple and accuracy-requiring locomotion are likely to reflect the differences in wrist and MCP mechanics and in activation of wrist muscles (Figs. 6 and 7) during these tasks. Otherwise, this study showed that the two locomotion behaviors, simple locomotion and skilled precise stepping, had over 200 similar mechanical variables and that the activity of many motor cortex neurons was very different during these tasks. The peaks and the depths of modulation of neurons with proximal receptive fields were often significantly different (more often higher) during precise stepping, compared with simple locomotion, and tended at least partially respond to the increasing demand for accuracy despite little difference in shoulder or elbow angles and moments (Table 2). On the other hand, neurons with distal receptive fields had little sensitivity to the level of accuracy, despite progressive changes in wrist and MCP joint angles and moments (Fig. 6), and the activity of the distal extensor digitorum communis (Fig. 7). This group of findings suggests that during highly trained accurate target stepping the motor cortex does not control all aspects of multijoint body movement such as on-line trajectory planning and correction for each limb, coordinating muscle activity, and so forth. Rather, it provides high level commands to lower brain and spinal centers by setting certain task-dependent parameters that modulate generation of steps. The motor cortex may integrate visual information about the crosspiece position into the locomotion pattern about which it has detailed information (or receive the signal already integrated) and then change the timing and/or amplitude of its activity to effectively deliver the phase-dependent commands to the spinal executive mechanisms when necessary (e.g., Drew et al. 2008a,b; Grillner and Zangger 1979). The spinal centers execute their normal locomotion functions (alternative flexion–extension and agonist–antagonist muscle activation; limb trajectory formation; etc.) but stay within the parameters set by the motor cortex.

It has been previously shown that during some motor tasks the activity of selected subpopulations of the motor cortex does not correlate with the activity of muscles or movement mechanics and appears to have other control targets (e.g., Beloozerova and Sirota 1993b; Beloozerova et al. 2005, 2006; Kurtzer et al. 2005). This has been also demonstrated for several other motor centers including premotor and parietal cortex (e.g., Kakei et al. 2001; Ochiai et al. 2005; Scott et al. 1997) and basal ganglia (e.g., Gdowski et al. 2007; Mink and Thach 1991).

Conclusion

Many of the motor behaviors in people and animals including locomotion have to be accurate. In this study, we investigated the differences in mechanics, electromyographic, and motor cortex activity between highly practiced accurate target stepping and simple walking in the cat using the state-of-the-art full-body mechanical analysis of locomotion and muscle and single-unit motor cortical activity recordings. We found that accurate target stepping is characterized by: 1) reduced variability of paw placement; 2) postural changes that improve postural stability and view of targets; 3) preplanning of swing trajectory and paw placement; 4) an increased activity of selected distal muscles; and 5) changes in neuronal activity in the forelimb representation of the motor cortex, predominantly the increase in precision of discharge timing.

GRANTS

This work was supported by National Institutes of Health Grants R01 NS-39340 and NS-058659 to I. N. Beloozerova, HD-032571 and NS-048844 to B. I. Prilutsky, and by Center for Human Movement Studies, Georgia Tech to B. I. Prilutsky.