Influence of Bilateral Vestibular Loss on Spinal Stabilization in Humans

Abstract

The control of upper body (UB) orientation relative to the pelvis in the frontal plane was characterized in bilateral vestibular loss subjects (BVLs) and compared with healthy control subjects (Cs). UB responses to external perturbations were evoked using continuous pelvis tilts (eyes open and eyes closed) at various amplitudes. Lateral sway of the lower body was prevented on all tests. UB sway was summarized using root-mean-square measures and dynamic behavior was characterized using frequency response functions (FRFs) from 0.023 to 10.3 Hz. Both subject groups had similar FRF variations as a function of stimulus frequency and were relatively unaffected by visual availability, indicating that visual orientation cues contributed very little to UB control. BVLs had larger UB sway at frequencies below ∼1 Hz compared with Cs. A feedback model of UB orientation control was used to identify sensory contributions to spinal stability and differences between subject groups. The model-based interpretation of experimental results indicated that a phasic proprioceptive signal encoding the angular velocity of UB relative to lower body motion was a major contributor to overall system damping. Parametric system identification showed that BVLs used proprioceptive information that oriented the UB toward the pelvis to a greater extent compared with Cs. Both subject groups used sensory information that oriented the UB vertical in space to a greater extent as pelvis tilt amplitudes increased. In BVLs, proprioceptive information signaling the UB orientation relative to the fixed lower body provided the vertical reference, whereas in Cs, vestibular information also contributed to the vertical reference.

INTRODUCTION

Control of upper body (UB) segment orientation is essential to everyday behaviors such as stabilizing the trunk during sitting (Reeves et al. 2007) and bipedal stance. Poor bipedal stance control is often accompanied by poor UB control (Carpenter et al. 2001; Creath et al. 2008) and improper stabilization of the UB may be associated with chronic back pain (Radebold et al. 2001; Reeves et al. 2007). Stabilization of the UB with respect to the pelvis in the frontal plane is synonymous with spinal stabilization because rotational motion of the UB is often considered to occur about the L4/L5 spinal joint (Brown and McGill 2009; Cholewicki et al. 2000; McGill et al. 1994; Zhao et al. 2008). There is evidence that sensory integration of proprioceptive, visual, and vestibular information contribute to spinal stability (Day et al. 1997; Goodworth and Peterka 2009; Radebold et al. 2001; Reeves et al. 2006). It is also recognized that reflexive and biomechanical mechanisms (i.e., intrinsic mechanical stiffness and damping inherent in joints, spinal ligaments, and muscles/tendons in the trunk-pelvis musculoskeletal system that can be altered by cocontraction and intraabdominal pressure) contribute to spinal stability (Brown and McGill 2009; Cholewicki et al. 1999; Cresswell et al. 1994; Goodworth and Peterka 2009; Moorhouse and Granata 2007; Solomonow et al. 1998).

However, to our knowledge, only one recent study has attempted to understand the combined influences of these interacting mechanisms (Goodworth and Peterka 2009). In this previous study, frontal plane UB sway was evoked using continuous tilts of the pelvis and tilts of a visual surround which subjects faced, while lower body sway was prevented. Experimental results were accounted for with a model that included time-delayed medium- and long-latency sensory integration mechanisms, a short-latency reflexive mechanism, and intrinsic biomechanical properties of the UB.

One important prediction made by the model was that vestibular information made a major contribution to overall system damping mainly via a mechanism we referred to as a medium-latency phasic sensory integration mechanism. Furthermore, the model predicted that removal of vestibular information would result in instability without major compensatory changes in other mechanisms contributing to spinal stability. Specifically, we postulated that some combination of increased intrinsic stiffness and an enhanced contribution of a short-latency phasic reflex mechanism would be necessary to compensate for loss of the vestibular contribution to UB control. Because both of these mechanisms tend to orient the UB toward the pelvis, an enhancement of intrinsic stiffness and reflex contributions would make the UB more responsive to pelvis tilt stimuli over a wide bandwidth of input stimulus frequencies and therefore the dynamic characteristics of UB control would differ considerably from subjects with normal vestibular function.

Therefore the first goal of the present study was to test our predictions regarding the vestibular contributions to spinal stability by investigating the dynamic characteristics of UB control in bilateral vestibular loss subjects (BVLs). We tested BVLs in an experimental setup identical to the previous study (Goodworth and Peterka 2009). If the mechanisms we previously attributed to a vestibular source were truly of vestibular origin, then we expected BVLs to exhibit altered UB control dynamics due to compensation provided by increased intrinsic stiffness and short-latency reflex gains (Fig. 11 in Goodworth and Peterka 2009). Alternatively, if the mechanisms previously attributed to a vestibular source had a different origin, then UB sway behavior would differ from our predictions, necessitating a revised interpretation of the vestibular contribution to UB control.

The second goal of the current study was to characterize the nature of compensatory mechanisms adopted by BVLs using parametric system identification techniques. Parametric system identification involves the determination of model parameters based on experimental data where model parameters represent specific neural or biomechanical systems. By comparing parameter values between BVLs and healthy control subjects (Cs), we can quantify differences in the underlying mechanisms of spinal stability between subject groups. By analogy to results in whole body sway, we predicted that BVLs would have a heightened reliance on proprioceptive information in eyes closed (EC) conditions and would make greater use of visual information in eyes open (EO) conditions (Horak 2009; Nashner et al. 1982; Peterka 2002). More specifically, we expected that in EC conditions, the parameters that characterize the contributions of sensory orientation information in the sensory integration mechanism (i.e., sensory weights) would show that BVLs rely exclusively on proprioceptive signals that encode UB sway with respect to the pelvis and that this proprioceptive weighting factor would not change with changing pelvis tilt amplitude. Parametric system identification results could also identify other possible compensation mechanisms such as heightened intrinsic stiffness and/or reflexive gains.

METHODS

Subjects

Three BVLs [mean height: 175 ± 14 (SD) cm, mean mass 77 ± 10 kg, additional details in Table 1] participated in this experiment. Experimental data from eight Cs (3 male, 5 female, mean age: 31 ± 5 yr, mean height: 169 ± 6 cm, mean mass: 70.6 ± 11 kg) with no history of balance disorders were collected for our previous study (Goodworth and Peterka 2009). A subset of these previous results was used to compare with results obtained from BVLs in the current study. All subjects gave their informed consent prior to being tested using a protocol approved by the Institutional Review Board at Oregon Health & Science University.

Table 1.

Bilateral vestibular loss (BVL) subject information

Subject	BVL1	BVL2	BVL3
Gender	M	F	M
Age	36	44	53
Duration of loss, yr	4	13	5
Cause of loss	Unknown	Unknown	Unknown
HVOR gain
0.05 Hz	0.01	0.00	0.01
0.2 Hz	0.02	0.00	0.04
0.8 Hz	0.10	0.06	0.12
Eyes closed surface sway-referencing	Fell	Fell	Not Tested

Normal horizontal vestibular ocular reflex (HVOR) range is 0.39–1.02 for 0.05 Hz, 0.40–1.02 for 0.2 Hz, and 0.59–1.07 for 0.8 Hz (Peterka et al. 1990). Surface sway-referencing is a balance test whereby the surface rotates in direct proportion to the body sway angle. This test greatly reduces the contribution of proprioceptive information to balance control.

Stimulus and data collection

Stimuli and data collection were previously described in detail (Goodworth and Peterka 2009) and are briefly described in the following text. Frontal plane perturbations of the UB were evoked using continuous pelvis tilts elicited by rotating the surface that subjects stood on. Lateral displacement of the pelvis and lower body was prevented using a rigid frame with two roller carriages that pressed against the greater trochanters (Fig. 1A). The roller carriages permitted vertical motion of the hips but prevented lateral movement. The visual surround was stationary on all tests and was lined with a complex checkerboard pattern of white, black, and three gray levels.

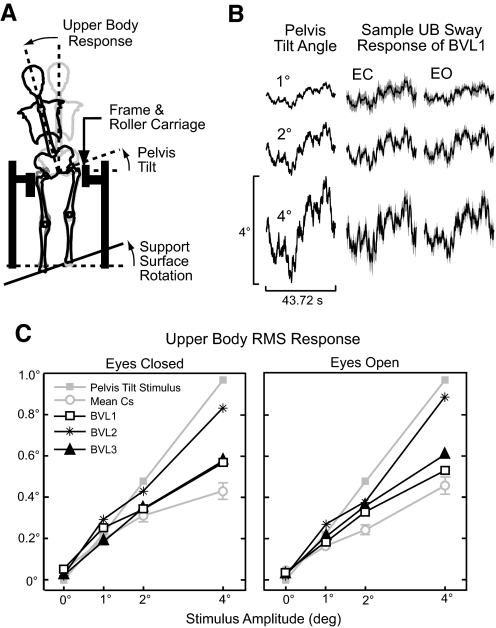
Fig. 1.

Upper body (UB) sway responses to pelvis tilt stimuli. A: surface rotations produced pelvis tilts that evoked UB sway while the lower body was prevented from moving laterally. B: Mean (±95% confidence intervals) UB sway from 1 bilateral vestibular loss (BVL) subject. C: root-mean-square (RMS) UB sway as a function of stimulus amplitude for individual BVLs and the mean (±1 SE) of control subjects (Cs).

The surface rotation angle was controlled by a servo motor, and the surface axis of rotation was halfway between the subjects' heels and was at ankle height. The distance between the middle of each subject's heels (mean of 17.9 ± 1.3 cm for BVLs and 17.1 ± 1.3 cm for Cs) was set to be equal to the distance between his/her hip joint centers as estimated using a regression equation relating hip-joint distance to inter-ASIS distance (Seidel et al. 1995), so that the lower body formed an approximate parallelogram. The lower body parallelogram mechanics enabled pelvis rotations to equal the surface rotations assuming no knee-joint motion.

In all experiments, stimulus delivery and data sampling occurred at 200 Hz. Pelvis stimuli were presented continuously according to a pseudorandom stimulus that had a power spectrum of stimulus velocity with approximately equal amplitude spectral components ranging from 0.023 to ∼16.7 Hz. The angular position waveform of pelvis stimuli was scaled to a specific peak-to-peak value for each stimulus condition and was used to drive the surface rotation. The stimulus waveform consisted of eight repeating cycles on the lowest stimulus amplitude test and seven repeating cycles on the remaining tests. Each stimulus cycle lasted 42.72 s.

Sampled data included the actual surface angular position, UB displacements in the frontal plane, and vertical leg displacements at knee level. The UB and vertical knee displacement data were collected with rods that were fixed to the upper back between the C6 and T3 vertebrae and the back of the knee, respectively. Rotational motion of each rod was recorded by a potentiometer. The vertical leg displacements were analyzed to ensure that subjects maintained straight knees on all tests and that the surface rotational motions were accurately transmitted to produce vertical leg displacements. We assumed that leg displacement motion was accurately transmitted to produce pelvis rotations. The upper trunk displacements were used to calculate the angular UB tilt with respect to earth-vertical. The angular UB tilt was considered to be the response variable that was compared with the pelvis tilt stimulus.

Protocol

BVLs performed a total of eight tests in a single test session lasting ∼2 h. The test session included two quiet stance tests with either EO or EC where no stimulus was given and six pelvis tilt tests with 1, 2, or 4° peak-to-peak amplitudes with either EO or EC. These eight tests were randomized to offset potential biases due to fatigue and learning. Each test lasted ∼5.5 min, and subjects were given the opportunity to rest after every test. Prior to beginning the test session, subjects “warmed-up” with an EC 2° stimulus amplitude test to become acquainted with the stimulus conditions.

Subjects were informed that there was no danger of falling and were instructed to maintain straight knees throughout the test and allow their UB to respond naturally. Subjects wore headphones and listened to their choice of novels or short stories to mask environmental equipment sounds and to maintain alertness.

Frequency domain analysis

Frequency domain analyses were previously described in detail (Goodworth and Peterka 2009) and are briefly described in the following text. Frequency-response functions (FRFs) were determined for each subject and test condition and were defined as the ratio of the discrete Fourier transform of the UB sway response to the discrete Fourier transform of the pelvis tilt stimulus (Pintelon and Schoukens 2001). FRFs were calculated for each stimulus cycle (except the 1st cycle to avoid transient behavior) and were then smoothed by first averaging FRFs over the stimulus cycles and then averaging FRFs across adjacent frequency points. An increasing number of adjacent points were averaged with increasing frequency (no averaging at the lowest 2 frequencies and 30 points averaged at the highest frequency) to reduce the variance of estimates at higher frequencies while maintaining adequate frequency resolution (Otnes and Enochson 1972). The final FRF estimates were approximately equally spaced on a logarithmic frequency scale ranging from 0.023 to 10.3 Hz (the upper frequency range was limited by the signal-to-noise ratio of the experimental data).

Each FRF was expressed as a set of gain and phase values that varied with frequency. Each gain value indicated the ratio of the UB response amplitude to the stimulus amplitude at its particular frequency and each phase value indicated the relative timing of the response compared with the stimulus expressed in degrees. A gain of 1 and phase of 0 at a particular frequency indicated perfect alignment of the UB to the pelvis tilt stimuli with no lead or lag in timing. Mean gain and phase curves were computed by first averaging the real components and imaginary components of FRFs across subjects and then calculating gains and phases. Mean FRFs for Cs include 95% confidence intervals that were determined using the percentile bootstrap method with 1,000 bootstrap samples at each stimulus frequency (Zoubir and Boashash 1998).

Coherence functions measured the extent to which the UB sway response was linearly related to the pelvis tilt stimulus. Coherence function values varied from 0 to 1 with values of 1 indicating a perfect linear relationship between stimulus and response with no noise in the system or measurements (Bendat and Piersol 2000). We estimated coherence functions via power spectra and cross-power spectral calculations as previously described (Peterka 2002).

Modeling and parameter estimation

To quantify differences in the underlying UB control system between BVLs and Cs, parametric system identification techniques were carried out based on an existing model of frontal plane spinal stability (Goodworth and Peterka 2009). Model parameters representing biomechanical properties of the trunk-pelvis system and neural control mechanisms were estimated from experimental results using a constrained nonlinear optimization routine “fmincon” (Matlab Optimization Toolbox, The MathWorks, Natick, MA) to minimize the total mean-square-error (MSE) of the normalized difference between model FRFs and experimental FRFs (Peterka 2002). Because only three BVLs were tested, the highest frequency FRF data contained too much noise, consistent with lower coherences, to confidently include in the model fits. Therefore FRF data >5.75 Hz were not included in model fits to both Cs and BVLs. Consistent with parameter estimation procedures previously described (Goodworth and Peterka 2009), we found that it was necessary to allow the neural controller parameters, medium-latency inter-segmental gain, and long-latency weights to vary across test conditions. Intrinsic stiffness, short-latency phasic gain, and all time delays were not allowed to vary across test conditions. The rationale behind fixing these model parameters across test conditions was based on impulse response function analyses (see Goodworth and Peterka 2009 for detailed description). The time course of impulse response functions at latencies prior to a fixed time delay did not show changes across test conditions, consistent with a fixed contribution of intrinsic stiffness and short-latency reflexes. Mean model parameters for Cs include 95% confidence intervals determined from model fits to 1,000 FRF bootstrap samples (Zoubir and Boashash 1998).

ANOVA statistics

Repeated-measures ANOVAs were used to determine if stimulus amplitude, visual availability (EO compared with EC), and subject group (BVLs compared with Cs) had statistically significant effects. Stimulus amplitude was a continuous variable in the statistical model and null hypothesis rejection was set to P < 0.05 for all tests. Data from Cs were obtained from our previous study (Goodworth and Peterka 2009).

RESULTS

UB sway evoked by pelvis tilt stimuli

Pelvis tilt stimuli and the UB responses for one exemplary BVL subject are shown in Fig. 1B. The UB sway response waveforms generally followed the pelvis tilt stimulus (similar to Cs) (Goodworth and Peterka 2009), meaning that subjects tended to align their UB to their pelvis, and root-mean-square (RMS) sway significantly increased with increasing tilt amplitude. There was minimal qualitative difference between EO and EC sway responses consistent with the finding that visual availability did not have a significant effect on RMS sway in either subject group (Fig. 1C). RMS sway was significantly different between subject groups with BVLs having larger RMS sway compared with Cs. There was also a significant interaction effect between subject group and stimulus amplitude related to the fact that increasing stimulus amplitude resulted in larger increases in RMS sway in BVLs compared with Cs.

Dynamic UB sway behavior

FRF GAINS.

The variation across frequency of FRF gains was similar across stimulus amplitudes and EO/EC conditions for both BVLs and Cs (Fig. 2, top row). Gains in the 0.02 to 0.6 Hz range increased with increasing frequency to reach a peak value around 0.6 to 0.9 Hz. Gains decreased rapidly above 1 Hz, showed a minor peak around 2–2.5 Hz, deceased rapidly again for frequencies >3 Hz, and then showed another minor peak at about 8 Hz.

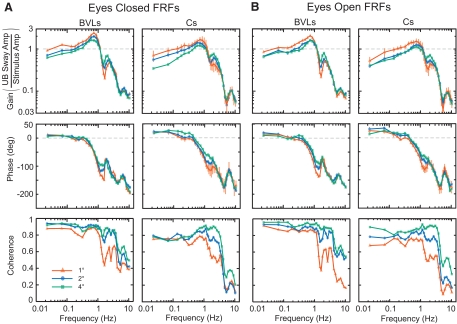
Fig. 2.

Mean experimental frequency-response functions (FRFs) and coherence functions in BVLs and Cs for eyes closed (A) and eyes open (B) conditions. Error bars on FRFs in Cs for the 1° stimulus amplitude represent 95% confidence intervals on mean gain and phase.

Both Cs and BVLs exhibited amplitude-dependent changes in FRF gains. At low- and mid-frequencies (less than ∼1.1–1.3 Hz), gains generally decreased with increasing pelvis tilt amplitude. However, between ∼1.3 and 2.5 Hz, gains generally increased with increasing pelvis tilt amplitude. At the highest frequencies (>∼3 Hz), there was little change in gain with changing pelvis tilt amplitudes.

Visual availability had a limited effect on FRF gains. In both Cs and BVLs, vision influenced gains at low frequencies where EO gains were slightly lower than EC during the 1° and 2° stimulus amplitudes below ∼0.3–1 Hz and were slightly larger than EC during the 4° stimulus amplitude below ∼0.1 Hz.

Gains in BVLs and Cs differed in several ways. First, gains in BVLs averaged across low stimulus frequencies (<1 Hz) were 1.27–1.37 times larger than gains in Cs. Second, the apparent resonant peak around 0.8 Hz was more pronounced in BVLs compared with Cs and this peak was more pronounced in EC compared with EO conditions for BVLs. Third, gains in BVLs were lower than gains in Cs at ∼1.6 Hz (1.3–2.2 times lower). Finally, at the highest frequencies (>4 Hz), gains in BVLs were larger than gains in Cs.

FRF PHASES.

Across all test conditions and in both BVLs and Cs, FRF phase curves generally showed decreasing values (more phase lag) with increasing frequency (Fig. 2, middle row). At frequencies below ∼0.2–0.4 Hz, pelvis tilt stimuli resulted in UB phase leads, while at mid- and high-frequencies (>0.4 Hz) all stimuli resulted in UB phase lags.

In both BVLs and Cs, there were small but systematic amplitude-dependent changes in phase curves between 0.2 and 2 Hz with increasing stimulus amplitudes resulting in more phase lead and/or less phase lag values. Visual availability had only a limited effect on phase curves.

Phase curves in BVLs showed less phase lead compared with Cs at frequencies <0.14 Hz. Also phase values showed more severe decline in BVLs compared with Cs between 0.6 and 1.2 Hz, resulting in more phase lag at 1.2 Hz (∼80–150° lag in BVLs and ∼60–120° lag Cs). At frequencies above ∼3 Hz, phases in BVLs exhibited smaller peaks and valleys compared with Cs.

COHERENCE FUNCTIONS.

Across all test conditions, coherences were between 0.6 and 0.9 at frequencies <1 Hz and coherences decreased at frequencies >3 Hz (Fig. 2, bottom row). Increases in stimulus amplitude were associated with higher coherences. BVLs had higher coherences than Cs at frequencies <1 and >4 Hz.

Model of spinal stability

MODEL DESCRIPTION.

A mathematical model (Fig. 3) was used to understand and quantify neural and mechanical mechanisms contributing to UB control. To explain our experimental results, we began with an existing model (Goodworth and Peterka 2009) and modified some previous model assumptions about what sensory information was available for UB control and how it was used. Each block represents a sensory, neural, neuromuscular, or mechanical system. The UB is assumed to sway as a single-link inverted pendulum about a joint that corresponds to L4/L5. The system output is upper body-in-space (UBS) tilt angle with respect to earth vertical. The UB block includes the UB moment of inertia (J) about the L4/L5 joint, the UB mass (m), and the UB center-of-mass height (h) above the L4/L5 joint. The values of J, m, and h were estimated for each subject using anthropometric methods (Erdmann 1997; Winter 2005). The mean values of these parameters in Cs were 3.2 kg·m², 40.2 kg, and 0.22 m, respectively. Two of the three BVLs happened to be taller and heavier than most Cs. Therefore mean values of J, m, and h in BVLs were larger than Cs and were equal to 5.8 kg·m², 44.0 kg, and 0.30 m, respectively.

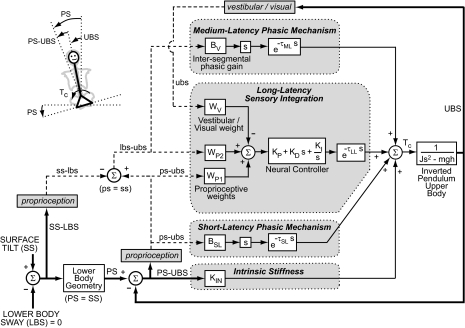
Fig. 3.

Model of UB control includes feedback from 4 mechanisms. The model input is surface tilt-in-space (SS) and output is upper body-in-space (UBS) tilt angle. Actual kinematic variables are represented as thick solid lines and capital letters while internal estimates of kinematic variables are represented as dashed lines and lower case letters.

The input to the UB block in Fig. 3 is a corrective torque (T_c) generated from four mechanisms that are distinguished from one another based on the time delay of torque generation. Input to these four mechanisms are based on either actual body kinematics (capital letters and thick solid lines) or internal representations of kinematics (lower case letters and dashed lines) derived from proprioception, vestibular, or visual sensory systems. Other types of feedback could have contributed to UB torque generation, such as UB torque feedback (Peterka 2003), or cutaneous information from pressure distributions on the feet (Maurer et al. 2006) or at the hips, but experimental data were sufficiently accounted for assuming feedback consisted only of segment kinematics.

The intrinsic stiffness mechanism tends to orient the UB perpendicular to the pelvis by generating instantaneous torque in proportion to the difference between the pelvis-in-space (PS) tilt angle and UBS. PS is a function of lower body sway (LBS), surface tilt (SS), and lower body geometry. However, because the lower body approximated a parallelogram, the model assumes PS = SS. The proportionality constant K_IN represents the intrinsic stiffness of tendons, joints, spinal ligaments, and muscles in the trunk-pelvis musculoskeletal system and includes the effects of muscle cocontraction and intraabdominal pressure. The short-latency phasic mechanism generates a torque proportional to sensory signals encoding the tilt velocity of UBS relative to PS (ps-ubs) with a short-latency time delay (τ_SL) and proportionality constant B_SL. This mechanism originates from proprioceptive cues and represents the contribution of phasic stretch reflex pathways. The model does not make fine distinctions between the other physiological and biomechanical contributions to intrinsic stiffness and short-latency phasic mechanisms, which include intrinsic damping in the trunk, tonic reflex mechanisms, and the effective time delay introduced by modeling nonrigid distributed spinal motion as a single link.

The medium-latency phasic mechanism generates a corrective torque proportional to sensory signals encoding the tilt velocity of the LBS relative to UBS (lbs-ubs). The proportionality constant is the intersegmental phasic gain (B_V). Sensory input to this mechanism is based on proprioceptive cues signaling the lower body proprioceptive sense of LBS relative to SS (ss-lbs) and the UB proprioceptive sense of PS-UBS (ps-ubs). The difference between ps-ubs and ss-lbs results in an intersegmental proprioceptive signal lbs-ubs. Because LBS was constrained to zero, the lower body effectively becomes a vertical reference frame that the UB orients to through the intersegmental proprioceptive signal lbs–ubs. This interpretation of the input to the medium-latency mechanism differs from our previous interpretation (Goodworth and Peterka 2009) where the input was previously assumed to be a ubs signal of primarily vestibular origin.

The long-latency sensory integration mechanism generates angular position-related, angular velocity-related, and time integrated angular position-related torques via a “neural controller” in relation to a summation of sensory orientation signals with a long-latency time delay (τ_LL). The sensory weights W_P1, W_P2, and W_V represent the relative contributions of sensory systems that orient the UB toward the pelvis, the lower body, and vertical, respectively. W_P1 and W_P2 are proprioceptive weights, and W_V is a vestibular weight in the EC condition and a combination of vestibular and visual weights in the EO condition. Sensory weights were constrained to sum to unity (W_P1 + W_P2 + W_V = 1). Our previous model included similar weight factors representing vestibular and visual contributions but included only one proprioceptive weight the input of which was ps-ubs.

MODEL PARAMETERS.

Model fits to individual BVLs data showed that overall stiffness (K_P + K_IN) in the system had a strong positive correlation coefficient (R = 0.93) with UB mass times UB center-of-mass height (mh). Similarly, parameters related to overall damping (K_D + B_SL + B_V) showed a strong positive correlation coefficient (R = 0.93) with mh. Because the BVLs sample size was only three, stiffness and damping correlations were not statistically significant although correlation values were similar to those in Cs. There was no apparent correlation between K_I and mh in BVLs. It was previously shown in Cs that overall stiffness, overall damping, and K_I had a strong positive correlation with mh, where R values equaled 0.98, 0.93, and 0.92, respectively, and were statistically significant (Goodworth and Peterka 2009). Because of these correlations, neural controller parameters as well as other parameters (K_IN, B_SL, and B_V) expected to vary with subject size were normalized by mh in Fig. 4.

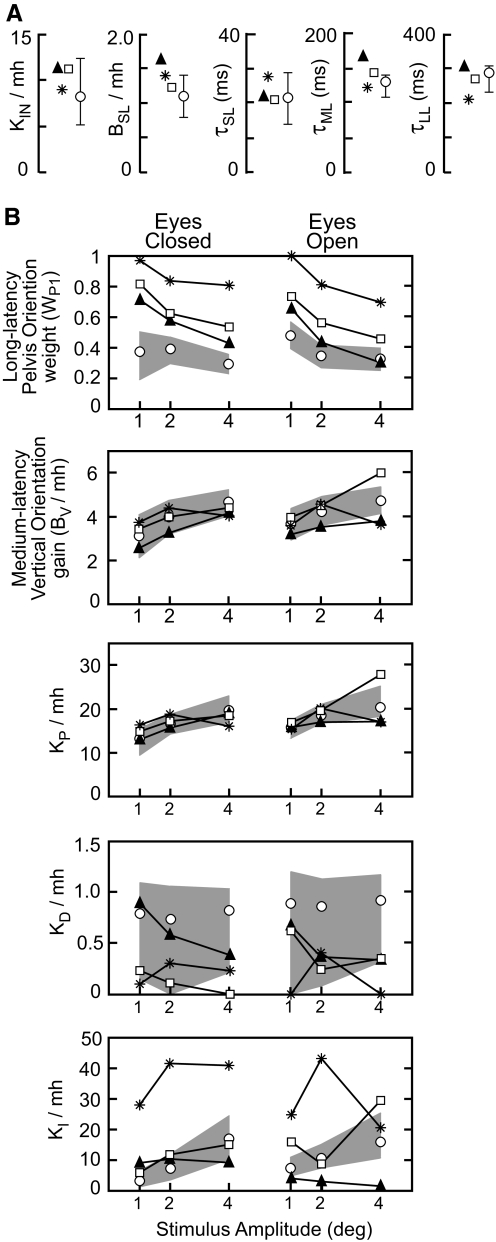
Fig. 4.

Model parameters for the 3 individual bilateral vestibular loss subjects (▴, *, or □) and mean of control subjects (○) with 95% confidence intervals (error bars or ▩). A: parameters that had fixed values across all test conditions. B: parameters that varied across test conditions. Units on K_P are N·m/rad, units on K_I are N·m/(rad·s), and units on K_D, B_V, and B_SL are N·m·s/rad. Sensory weight W_P1 is unitless. All parameters except W_P1 and time delays were normalized by UB mass, m, times UB center-of-mass height, h. The mean m·h was 9.0 kg·m in Cs and 13.2 kg·m in BVLs. Weight parameters W_P2 and W_V are not shown because they can be derived from W_P1. For BVLs in eyes closed conditions, W_V = 0 and W_P2 = 1 − W_P1. In eyes open conditions for BVLs and in all test conditions for Cs, W_P2 + W_V = 1 − W_P1.

Figure 4A shows the parameters that could be held at fixed values across test conditions. Individual model parameters in BVLs related to intrinsic stiffness, short-latency reflex gain, and all time delays were generally within the 95% confidence interval on the mean parameter values in Cs. In all BVLs, normalized K_IN and B_SL were larger than mean normalized K_IN and B_SL in Cs. The two BVLs with τ_ML exceeding the 95% confidence interval on the mean τ_ML in Cs also had larger mh (15.7 and 16.4 kg·m) compared with the mean Cs (9.1 kg·m), and there was a positive correlation coefficient (R = 0.90, although not statistically significant with 3 subjects) between τ_ML and mh in BVLs that was not present in Cs.

Figure 4B shows the parameters that were necessary to vary across test condition to account for the FRF data. In all EC conditions and most EO conditions, BVLs had larger W_P1 values compared with the upper 95% confidence interval on the mean W_P1 in Cs. This result implies that BVLs oriented their UB more toward the pelvis tilt (and less toward vertical) than Cs, consistent with the generally larger experimental FRF gains in BVLs compared with Cs. In both Cs and BVLs, W_P1 decreased with increasing stimulus amplitude and differences were small between EO and EC conditions. In EC BVLs, W_V = 0 and W_P2 = 1 − W_P1. Therefore the decrease in W_P1 implies that W_P2 increased with increasing pelvis tilt amplitude, indicating that BVLs shifted toward increased reliance on the intersegmental proprioceptive signal that provided a vertical reference. In EO BVLs, W_V represents the visual contribution and is functionally identical to W_P2, therefore W_P2 + W_V = 1 − W_P1. A comparison of W_P2 on EC tests to W_V + W_P2 on EO tests shows that these weights are similar (mean EC W_P2 = 0.30 across all BVLs and stimulus amplitudes; mean EO W_V + W_P2 = 0.37), suggesting that visual orientation cues made only a small contribution to UB control.

In Cs, W_V includes a representation of the vestibular contribution to UB control. The fact that W_P2 + W_V was larger in Cs than BVLs (mean W_P2 + W_V = 0.60 in EC and 0.57 in EO in Cs) and similar in EC and EO conditions suggests that visual cues do not contribute significantly to UB control in Cs but that vestibular cues do contribute to UB control through the long-latency sensory integration mechanism.

Despite the small number of BVLs, repeated-measures ANOVA showed that W_P1 was significantly larger in BVLs compared with Cs. There was also a significant interaction between subject group and visual availability. This interaction effect related to the fact that EO compared with EC W_P1 values were reduced more in BVLs compared with Cs, although visual availability did not have a significant effect on W_P1 in either BVLs or Cs. There was a significant reduction in W_P1 with increasing stimulus amplitude in both BVLs and Cs, and there was a significant interaction effect between subject group and stimulus amplitude. This interaction effect related to the fact that increasing stimulus amplitude resulted in a greater reduction in W_P1 values in BVLs compared with Cs.

The normalized B_V increased with stimulus amplitude in both Cs and BVLs and was slightly larger in EO compared with EC conditions (8.5% in BVLs and 10% in Cs). In EC conditions, B_V values in all BVLs were within the 95% confidence intervals on the mean B_V in Cs. In EO conditions, there was more variability across BVLs, but B_V values averaged across BVLs were within the 95% confidence intervals on the mean B_V values in Cs. The slightly higher B_V value in EO versus EC conditions indicates that there is a visual contribution to the medium-latency mechanism. For simplicity, this visual input is not represented in the Fig. 3 model but was represented in Fig. 5 of Goodworth and Peterka (2009).

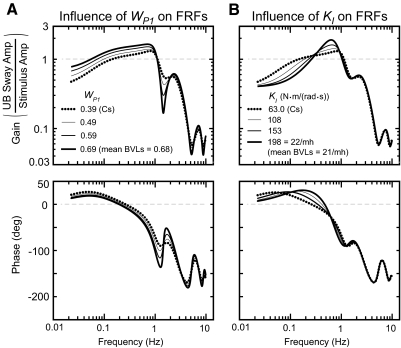
Fig. 5.

Influence of W_P1 and K_I on FRFs shows that most of the FRF features that differ between Cs and BVLs can be accounted for with larger W_P1 values in BVLs across all test conditions (A) and larger K_I values in BVLs across EC conditions (B). The thick dotted line is the FRF predicted for the EC 2° stimulus amplitude condition using the mean Cs model parameters: K_IN = 73.5 N·m/rad, B_SL = 9.87 N·m·s/rad, τ_SL = 21.7 ms, τ_ML = 131 ms, τ_LL = 288 ms, W_P1 = 0.390, B_V = 35.7 N·m·s/rad, K_P = 149 N·m/rad, K_D = 6.60 N·m·s/rad, and K_I = 63.7 N·m/(rad·s).

In both Cs and BVLs, normalized K_P increased with increasing stimulus amplitude and increased slightly with visual availability. K_P averaged across BVLs was within the 95% confidence intervals on the mean K_P in Cs. In both Cs and BVLs, normalized K_D showed no consistent variation across stimulus amplitude or between EO/EC conditions and contributed little to overall damping of the UB control system. Specifically, 13% of the total damping (total damping = K_D + B_SL + B_V) was attributable to K_D for Cs and 6% of the total damping was attributable to K_D for BVLs averaged over all test conditions. Normalized K_I exhibited large variability across BVLs, but the mean K_I in BVLs increased with stimulus amplitude and was ∼3.0 times larger than the mean K_I in Cs in EC conditions and ∼1.6 times larger in EO. For Cs, K_I was similarly highly variable across individual fits (Goodworth and Peterka 2009) and the mean K_I values increased with stimulus amplitude.

Parameter estimation results showed that the most consistent difference between BVLs and Cs was that BVLs had a larger pelvis orienting weight, W_P1. Therefore we explored the influence of W_P1 on FRFs to determine the extent to which differences in W_P1 values alone could explain the observed differences in the FRFs between subject groups. First, we generated the FRF predicted by the mean parameters in Cs shown in Fig. 4 for the EC 2° stimulus amplitude condition (Fig. 5A, …). Then W_P1 was progressively increased while all other model parameters remained fixed (Fig. 5A, —). The results showed that increases in W_P1 alone accounted for several of the differences in experimental FRFs between Cs and BVLs (compare Fig. 5A to Fig. 2). Specifically, increasing W_P1 resulted in FRF gain increases below ∼1.1 Hz, gain decreases at ∼1.6 Hz, slightly less phase lead below ∼0.14 Hz, and more severe declines in phase values between ∼0.6 and 1.2 Hz.

Increases in W_P1 could not fully account for the apparent resonant peak near 0.8 Hz in BVLs. This experimental feature was especially evident in EC conditions. Because parameter estimation results showed that the averaged normalized K_I in BVLs was ∼3.0 times larger than in Cs in EC conditions, the influence of K_I alone on FRFs was investigated. Results showed that a peak in the FRF gain curve developed as K_I was increased consistent with the results in BVLs (compare gains in Fig. 5B to Fig. 2).

Therefore the differences in experimental FRFs between BVLs and Cs were accounted for mainly by BVLs having a larger pelvis orienting sensory weight across all test conditions and a larger K_I in EC conditions. The remaining small differences in experimental FRFs between subject groups were accounted for through the small differences in other model parameters between BVLs and Cs.

DISCUSSION

The goals of this study were to test our previous model-based hypothesis regarding the vestibular contribution to frontal plane spinal stability and to identify compensatory mechanisms used by BVLs. UB responses were evoked using continuous pelvis tilts while lateral sway of the lower body was prevented in both BVLs and Cs. BVLs had larger RMS UB sway compared with Cs and FRFs differed in gain and phase values across various frequency ranges. However, the overall frequency-, amplitude-, and visual-dependent changes in UB responses were similar between subject groups and required us to consider that, in addition to vestibular cues, proprioceptive cues signaling UB motion relative to the lower body could provide a reference to vertical.

Proprioceptive input to medium-latency phasic mechanism

Results from the current study falsified our previous prediction (Goodworth and Peterka 2009) that the major source of system damping provided by the medium-latency phasic mechanism had a vestibular origin. Specifically, because the medium-latency intersegmental gain (B_V) was very similar in EC conditions between Cs and BVLs, the sensory input to this mechanism could not have a vestibular origin in BVLs. While it is possible that a vestibular contribution to this mechanism exists in Cs, a simpler interpretation would be that the sensory input to the medium-latency phasic mechanism was not of vestibular origin in both Cs and BVLs. Alternatively, a parsimonious explanation is that the sensory input to this mechanism is based on an intersegmental proprioceptive signal of UB relative to lower body (lbs-ubs) and therefore that a proprioceptive signal encoding intersegmental velocity is a major contributor to UB system damping under our experimental conditions. This result is consistent with evidence that intersegmental signals also contribute to whole body stance control (Kiemel et al. 2008). Therefore EC BVLs had no major loss of damping and did not need to compensate with the previously postulated increases in stretch reflex activation and intrinsic stiffness.

Compensation in BVLs

RELIANCE UPON PROPRIOCEPTION.

Previous studies investigating whole body sagittal plane sway in BVLs demonstrated that they compensate for absent vestibular function using heightened reliance on proprioceptive information signaling body sway relative to support surface in EC conditions (Maurer et al. 2006; Peterka 2002). From a modeling perspective, EC BVLs exhibited a proprioceptive weight of 1, indicating that they relied entirely on proprioception that oriented the body toward the tilted surface, and this proprioceptive weight did not vary across surface tilt amplitudes in EC conditions (Fig. 10 in Peterka 2002). In contrast, subjects with normal vestibular function shifted toward increased reliance on vestibular and decreased reliance on proprioception with increasing surface tilt amplitude for both sagittal and frontal plane sway (Cenciarini and Peterka 2006; Peterka 2002).

By analogy to whole body stance control, we previously postulated that EC BVLs would have an UB-on-pelvis proprioceptive weight of 1, causing the UB to orient toward the tilted pelvis, and this proprioceptive weight would not vary across pelvis tilt amplitudes (Goodworth and Peterka 2009). However, the identification of an intersegmental proprioceptive input to the medium-latency mechanism suggested that this signal could also be an input to the long-latency sensory integration mechanism. The relative contributions of these two proprioceptive inputs were represented in the Fig. 3 model as sensory weights W_P1 for pelvis orienting proprioception and W_P2 for intersegmental proprioception. In EC conditions, W_P1 + W_P2 = 1 because only proprioception information contributed to UB corrections in BVLs. Averaged across BVLs, W_P1 was 0.83 in the 1° pelvis tilt amplitude and monotonically decreased to 0.59 in the 4° pelvis tilt amplitude. W_P1 values larger than 0.5 indicate that BVLs had a greater reliance on pelvis orienting proprioceptive cues compared with reliance on inter-segmental proprioceptive cues. BVLs also had a greater reliance on pelvis orienting proprioceptive cues compared to Cs.

The systematic variation in W_P1 and W_P2 with pelvis tilt amplitude in EC conditions is similar to the sensory reweighting phenomenon whereby Cs shift away from reliance on one sensory system and toward reliance on a different sensory system (Maurer 2006; Oie et al. 2002; Peterka 2002). However, our model-based interpretation indicated that the variation in W_P1 and W_P2 values in BVLs in EC conditions was attributable to an intra-proprioceptive system reweighting. Specifically, BVLs shifted away from reliance on proprioceptive information that oriented the UB toward the pelvis and shifted toward reliance on proprioceptive information that oriented the UB toward the LB (and consequently more vertical in space) with increases in pelvis tilt amplitude.

RELIANCE UPON VISION.

It has also been shown that BVLs can compensate with a heightened reliance on visual information in freestanding conditions. During a visual sway-referenced test condition (i.e., visual surround rotation angle is equal to body sway rotation angle about the ankle joint at any point in time), Nashner et al. (1982) observed that subjects with vestibular deficits swayed more than Cs. Increased sway in this test condition indicated that subjects with vestibular deficits had a heightened reliance on visual information even when visual inputs were destabilizing and oriented their body away from upright. This compensation was also identified using external rotations of a visual surround and surface (Peterka 2002). Specifically, during surface rotations, EC BVLs had larger FRF gains compared with Cs, FRF gains were greatly reduced in EO compared with EC conditions in BVLs, and this reduction in EO FRF gains compared with EC was more prominent in BVLs compared with Cs.

In the current study, if BVLs had a heightened reliance on visual information, then we expected to find reductions in FRF gains and lower values of the model parameter W_P1 in EO compared with EC conditions. Experimental results showed only minor reductions in FRF gains with EO for the 1° and 2° stimulus amplitudes and no reduction for the 4° stimulus amplitude. Furthermore, these minor reductions were similar for both BVLs and Cs. W_P1 was slightly lower in EO compared with EC in BVLs (0.63 in EO compared with 0.70 in EC), whereas in Cs, there was no decrease in W_P1 with visual availability. Therefore there was some evidence that BVLs used a heightened reliance on visual information as a compensatory mechanism, but the overall visual contribution to UB control was small.

OTHER COMPENSATORY MECHANISMS.

Another compensation mechanism that BVLs could have used was to heighten intrinsic stiffness and/or reflex gains. Increased background trunk muscle activity could increase intrinsic stiffness (Hogan 1990) and reflex gains (Moorhouse and Granata 2007), and it has been observed that BVLs exhibit larger background muscle activity in the trunk following a transient surface rotation (Carpenter et al. 2001). In the present study, however, we found only minimal evidence that intrinsic stiffness of the trunk was greater in BVLs compared with Cs. Specifically, although the intrinsic stiffness gains (K_IN) in all BVLs were greater than the mean K_IN value in Cs, none were greater than the upper 95% confidence interval (Fig. 4A). Similarly, all three BVLs had a larger short-latency phasic gain (B_SL) than the mean B_SL in Cs, but the gain in only one BVL subject exceeded the upper 95% confidence limit on the mean B_SL in Cs.

BVLs exhibited an apparent resonance around 0.8 Hz where FRF gains were greater than gains in Cs. This resonance effect was especially prominent in EC conditions. It was found that increases in the neural controller integration factor K_I in BVLs compared with Cs accounted for this resonance feature (Fig. 5B). Functionally, an increase in FRF gain could be considered to be anti-compensatory in that higher gains indicate that the UB shows greater sensitivity to pelvis tilts. However, larger K_I values are also associated with lower gains at frequencies < ∼0.2 Hz and thus provide a beneficial compensatory effect at lower frequencies.

Vestibular contribution to spinal stability

If our conclusion is correct that a proprioceptive signal encoding intersegmental motion contributes to UB control through the long-latency sensory integration mechanism, then it theoretically would be possible for this sensory source to completely compensate for a vestibular loss. That is, with the lower body constrained, body orientation information derived from a vestibular signal encoding UB tilt with respect to earth vertical is equivalent to orientation information derived from a proprioceptive signal encoding UB motion relative to the lower body. Thus if both vestibular and intersegmental proprioceptive cues normally contribute to UB control (both W_V and W_P2 >0 in Cs), then responses to pelvis tilt stimuli in BVLs would be indistinguishable from those of Cs if the value of W_P2 in BVLs could be enhanced to the extent that W_P2 equaled the value W_V + W_P2 in Cs in a given test condition.

However, loss of vestibular function does in fact alter responses to pelvis tilt stimuli through changes primarily in the long-latency sensory integration mechanism. These changes provide evidence for a vestibular contribution to spinal stability in Cs and are in agreement with previous studies that inferred a vestibular contribution by evoking UB sway in seated subjects using galvanic vestibular stimulation (Day et al. 1997) and by observing that EC subjects can maintain stability while sitting on an unstable seat (Radebold et al. 2001; Reeves et al. 2006).

The fact that BVLs were unable to completely compensate for their vestibular loss by fully substituting the intersegmental proprioceptive signal for the vestibular signal could be indicative of the properties of neural mechanisms that control the fusion of sensory cues. Previous investigations demonstrated that a weighted combination of sensory cues can form an optimal, minimum variance perceptual estimate if the weights are determined by the signal-to-noise properties of the sensory sources such that the least noisy sensory source is weighted most heavily (Ernst and Banks 2002; van Beers et al. 1999). In the EC condition in our experiment, there were three sensory cues contributing to the long-latency sensory integration mechanism with their contributions represented by the weights W_V, W_P1, and W_P2. In EC Cs, W_P1 had a value of ∼0.40 while the value W_V + W_P2 (which equals 1 – W_P1) was therefore ∼0.60. The larger weighting on the combined sensory signals that encode UB tilt with respect to vertical (W_V + W_P2) compared with the sensory signal that encodes UB tilt with respect to the pelvis (W_P1) suggests that these combined sensory signals had lower variance than the sensory signal for UB-on-pelvis tilt. Without vestibular function, the variance improvement afforded by combining vestibular and intersegmental proprioceptive signals would be lost, W_P1 would be expected to increase, and the optimal sensory weights would be determined by the variances of the remaining two proprioceptive signals. The overall higher W_P1 values in BVLs of ∼0.7 across all test conditions suggests that the intersegmental proprioceptive signal had higher variance than the proprioceptive signal encoding UB-on-pelvis tilt.

Generality of the model

The model of UB control was identified while lower body sway was prevented. Because context dependency has been demonstrated in postural control (Cordo and Nashner 1982), it is likely that the UB system identified in the current study would change in some way to accommodate conditions where lower body sway is not prevented. Nevertheless, it is likely that many of the mechanisms identified in the current study would still contribute to frontal plane spinal stabilization. For example, the intrinsic stiffness mechanism represented the biomechanical properties of the trunk and pelvis system and would therefore be expected to contribute to spinal stability independent of constraints placed on the lower body. It is also likely that many of the sensory signals identified in the current study contribute to postural stability in more general conditions. Clearly the visual and vestibular signals could be beneficial in many contexts because these signals are used by subjects to estimate body orientation relative to earth vertical and to the visual field, respectively. It is also likely that the intersegmental proprioceptive signal, used to orient the UB toward the lower body, is used in postural control in general conditions. For example, in freestanding conditions, a mechanism that facilitates UB alignment with the lower body could contribute to the well known “ankle strategy” (Horak and Nashner 1986). A recent study by Kiemel et al. (2008) incorporated this intersegmental signal in a two-segment model of the control of freestanding sagittal plane sway.

CONCLUSION

Results suggest that in both Cs and BVLs the major contributions to UB system damping came through medium-latency intersegmental proprioceptive cues and major contributions to UB system stiffness came through intrinsic mechanical properties and long-latency sensory integration of intersegmental proprioceptive cues and pelvis orienting proprioceptive cues. Thus loss of vestibular function did not severely impair spinal stability. However, BVLs oriented their UB more toward their pelvis than Cs because vestibular inputs do in fact contribute to spinal stability in Cs. Finally, enhanced utilization of visual orientation cues played only a minor role in the compensation for vestibular loss.

GRANTS

This work was supported by National Institute on Aging Grant AG-17960.