Self-Motion and the Shaping of Sensory Signals

Abstract

Sensory systems must form stable representations of the external environment in the presence of self-induced variations in sensory signals. It is also possible that the variations themselves may provide useful information about self-motion relative to the external environment. Rats have been shown to be capable of fine texture discrimination and object localization based on palpation by facial vibrissae, or whiskers, alone. During behavior, the facial vibrissae brush against objects and undergo deflection patterns that are influenced both by the surface features of the objects and by the animal's own motion. The extent to which behavioral variability shapes the sensory inputs to this pathway is unknown. Using high-resolution, high-speed videography of unconstrained rats running on a linear track, we measured several behavioral variables including running speed, distance to the track wall, and head angle, as well as the proximal vibrissa deflections while the distal portions of the vibrissae were in contact with periodic gratings. The measured deflections, which serve as the sensory input to this pathway, were strongly modulated both by the properties of the gratings and the trial-to-trial variations in head-motion and locomotion. Using presumed internal knowledge of locomotion and head-rotation, gratings were classified using short-duration trials (<150 ms) from high-frequency vibrissa motion, and the continuous trajectory of the animal's own motion through the track was decoded from the low frequency content. Together, these results suggest that rats have simultaneous access to low- and high-frequency information about their environment, which has been shown to be parsed into different processing streams that are likely important for accurate object localization and texture coding.

INTRODUCTION

Sensory systems transduce physical signals into electrical signals that ultimately result in our perception of the external world. It has long been known that this is not a passive process and that we instead gather information about our environment through self-motion, by actively moving our sensors with respect to the outside world (Kleinfeld et al. 2006; Szwed et al. 2003), but the precise manner in which this happens is only beginning to be understood. Examples range from the large shifts in our visual field that occur during saccadic eye movement and head movement, to the manner in which we gather tactile information as we reach out to touch a wall with our hands or move our fingertips over a texture. Indeed, on one hand, a central challenge for the sensorimotor system is to form stable internal neural representations of the invariant properties of the external world in the presence of self-induced signal variations. On the other hand, it is also possible that present in these signals is useful information about our relationship to the outside world.

Rats and other rodents rely extensively on their tactile sense to navigate and perceive the external world. They do so primarily by actively using arrays of facial whiskers, or vibrissae, that serve as an exquisitely sensitive tactile sensory modality. In separate experimental paradigms, it has been shown that this sensory modality is endowed with the capability for fine texture discrimination (Brecht et al. 1997; Carvell and Simons 1990; Guic-Robles et al. 1989), while also providing signals useful for object localization (Hutson and Masterson 1986; Knutsen et al. 2006; Mehta et al. 2007; Shuler et al. 2002) and aperture discrimination (Krupa et al. 2001). It has been proposed that, beyond the sensory periphery, the lemniscal and paralemniscal pathways separately process high- and low-frequency vibrissa motion in parallel for texture coding and object localization, respectively (Ahissar et al. 2000). However, it is not presently known whether these seemingly disparate types of tasks are mutually exclusive behaviorally, nor is it known to what extent these frequency bands interact as the self-motion of the animal shapes the sensory input.

In this study, awake, freely behaving rats were trained to run along a linear track with periodic gratings lining the walls designed to engage their vibrissae. Using high-resolution, high-speed videography, we continuously measured the position of the animal relative to the walls, the angle of the head/face relative to the direction of locomotion, and the relative motion of the vibrissae close to the face that is the proximal mechanical signal transduced by mechanoreceptors in the vibrissa follicle. In the majority of cases, the animals did not produce self-generated movement of their vibrissae through whisking, and thus the self-motion we describe here is that of translational locomotion and head-rotation. From a decoding perspective, the observed low-frequency motions of the vibrissae significantly reduced the uncertainty in the instantaneous distance from the head to the wall, and the high-frequency content simultaneously provided grating discrimination performance significantly above chance despite short-duration signals typically <150 ms. Taken together, the results here suggest a conceptual model in which internal representations of head angle and locomotion, when combined with sensory input, provide access to the moment-to-moment proximity to objects in the external world while also providing an invariant sensory representation of the surface properties of the objects in the face of highly variable inputs to the pathway.

METHODS

Behavior

Five adult female rats (Long-Evans; 250 g; Charles River Laboratories, Wilmington, MA) were trained to run back and forth on a linear track (Fig. 1A).

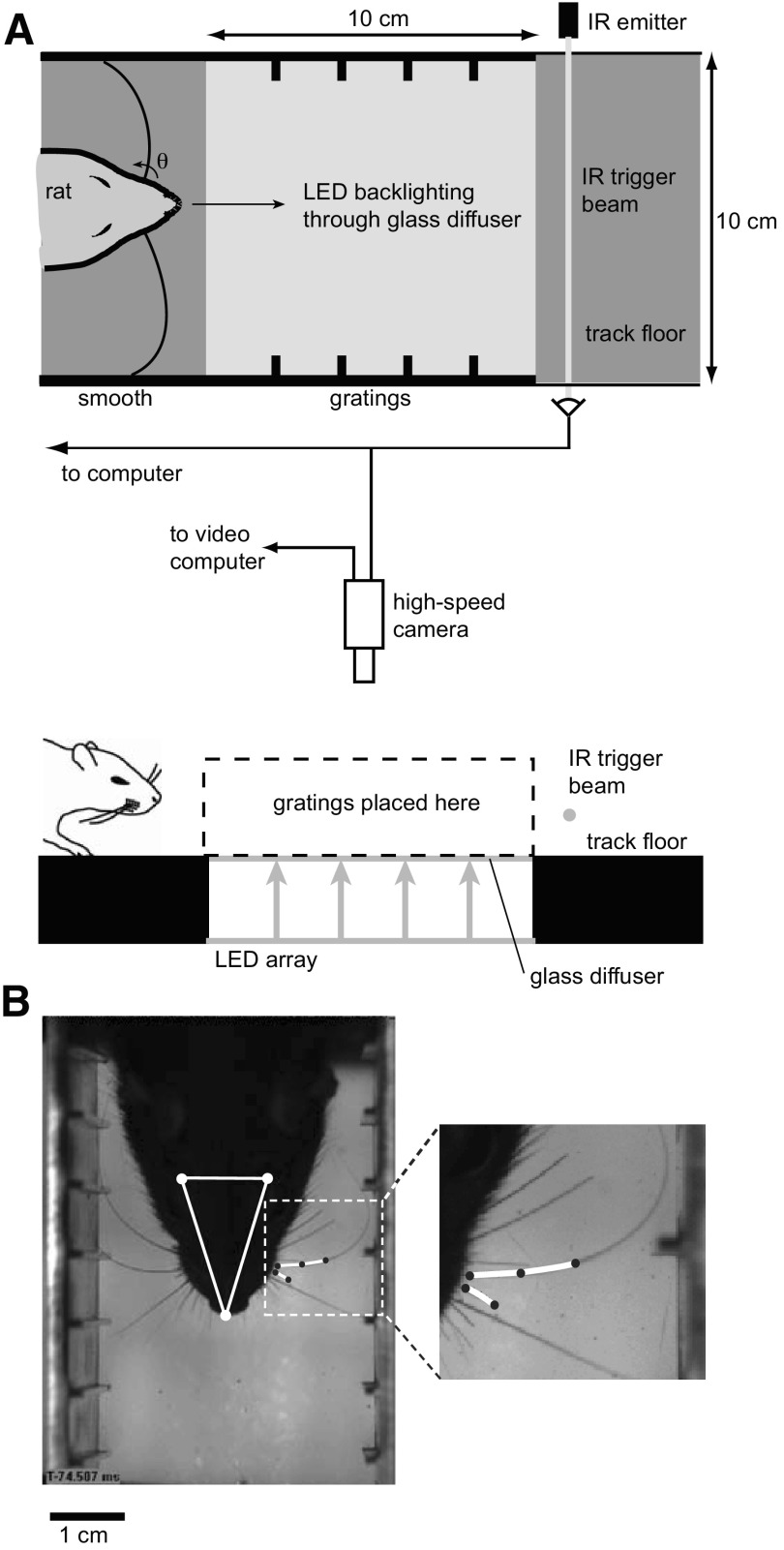
Fig. 1.

Experimental setup. A: schematic showing top view (top) and side view (bottom) of track. Rat runs from left to right through the grating-lined area of the track while the camera acquires video and then breaks an infrared trigger beam that signals the camera to send frames to computer. Rat and vibrissae are backlit with red LED array that shines through the glass diffuser floor of the grating-lined area of the track. B: single frame showing head and whisker tracking from high-speed video in which the head (triangle defined by white dots), reference vibrissa (short spline, left side of face), and a full vibrissa (longer spline, left side of face) are being tracked. See the corresponding movie file in the Supporting Information (WhiskerTrackingMovie.mov) for the full sequence. Inset: magnification of the spline tracking of a vibrissa in contact with the grating and a short reference vibrissa, highlighted with the white curves.

They were food deprived to 90% of nominal body weight and rewarded with fruit-flavored cereal on entering either end of the track, where there was room to turn around before traversing the track in the opposite direction. We trimmed rows A, B, and E of the vibrissa array to facilitate imaging. Animal maintenance and experimental procedures were conducted in accordance with guidelines established by the National Institutes of Health and the Animal Care and Use Committee at Harvard University.

Stimuli

Tactile stimuli were placed on either side of the track along a 100-mm length approximately equidistant from each end (Fig. 1A). The stimuli consisted of four different vertically oriented spatial gratings, constructed of aluminum plates 508 mm long, 76 mm wide, and 6.4 mm thick. Each of the four gratings consisted of 2.54-mm-tall and 1-mm-wide periodically spaced protrusions machined into one half of one face of the plate. The other half of the plate was left smooth, so that there was a boundary between the smooth and grating parts of the plate at the midpoint of the plate. The gratings were labeled 1 through 4, consisting of periodic spacings of 4.19, 7.37, 9.80, and 12.70 mm, respectively. These spacings are of the same order of magnitude as the “coarse textured” surfaces used in early studies of vibrissa-based sensory discrimination (Carvell and Simons 1990). Because of ambiguity in what actually defines a “texture,” we refer to the surfaces here as gratings. On a given day, each animal was exposed to each grating for one 10-trial set.

High-speed videography

Video was acquired using a high-speed CMOS camera (Phantom v5, Vision Research, Wayne, NJ). The camera was mounted directly above the region of interest defined by the tactile stimuli. Video was acquired at 2,000 frames/s and with a spatial resolution of between 700 × 400 and 950 × 512 pixels/frame. Each pixel had a luminance resolution of 8 bits. Exposure time per frame was limited to 0.2 ms. The lens (Sigma, Tokyo, Japan) had a focal length of 135 mm and was placed at a distance of 1 m from the track. This configuration allowed the entire 10 × 10-cm region of interest to be in focus and resulted in a spatial resolution of between 5 and 8.35 pixels/mm. Backlighting the field enhanced the quality of the video. We used a custom-made 10 × 10 array of lighting elements, each of which was a 2 × 4 subarray of red light–emitting diodes (Lumex, Platine, IL). A glass diffuser (ThorLabs, Newton, NJ) was placed 3 cm above the array and also formed the floor of the track in the region of interest (Fig. 1A). We obtained video data in individual trials consisting of several hundred frames. We triggered the camera using an infrared beam that passed perpendicularly across the track just outside the region of interest. Note that there was no attempt to maintain the lighting for videography outside of the range of wavelengths visible to the animal, and thus the animal presumably had access to visual cues during this task.

Tracking of head and vibrissae movements was implemented by modifying a software package provided by Knutsen et al. (2005). The software uses code written in MatLab (v6.5, MathWorks, Natick, MA) and the C programming language. To track vibrissae motion, it was necessary to track the position of the head. Head movements were tracked by following reflections of a halogen spotlight from the two aluminum ball bearings rigidly attached to the head, giving a measure of head angle in a two-dimensional plane. Once the head position and orientation were calculated in the laboratory frame of reference, two regions of interest defined close to either side of the head are translated and rotated into the head frame of reference. Shown in Fig. 1B is a typical frame from a movie in which the head, reference vibrissa, and an untrimmed vibrissa in contact with the grating are being tracked. Vibrissae are tracked in this frame of reference using a three-point spline-fitting algorithm (see Knutsen et al. 2005 for details). The inset shows a magnification of the spline-tracking of the vibrissae for this particular frame (short reference vibrissa, longer vibrissa in contact with grating, both highlighted in white). See the corresponding movie file in the Supporting Information (WhiskerTrackingMovie.mov) for the video of this trial.¹

For a fixed mystacial pad and hair follicles, such as that in an anesthetized preparation, the angle (and its time derivatives) of the vibrissae close to its base is a good measure of the input signal to the vibrissa system. However, because movement of the mystacial pad and rotation of the hair follicles cause rotation of the vibrissae, the angle of the base of the vibrissa alone is not sufficient to characterize the input signal for an awake behaving animal. To decouple mystacial pad and vibrissa follicle movement from externally induced movement of the vibrissae, we measured the angle both of the target vibrissae that were in contact with the grating and of a trimmed “reference” vibrissa in the same row that was not in contact with any surface (Fig. 2B). Previous studies have shown (Carvell and Simons 1990), and we observed, that vibrissae in the same row tend to move in phase with each other >95% of the time. Therefore in most cases, the reference vibrissa accounts for movement of the mystacial pad or follicle. We subtracted the angle of the reference vibrissa from the measured vibrissae angles. The angular deflection of a vibrissa close to its base was estimated by calculating the angle of a straight line segment between the extreme points of a short (3 mm long) spline fitted to a segment of the vibrissa close to its base (within 2 mm of the mystacial pad). Note that in the absence of whisking, or any other movement of the reference vibrissa relative to the head, the reference frame described here would be consistent with a head-centered coordinate system. However, because the reference vibrissa did move relative to the head on some of the trials, we do not adopt this terminology here.

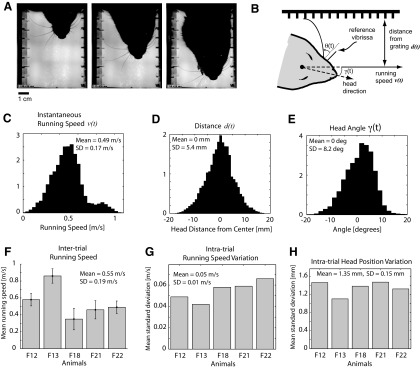
Fig. 2.

Behavioral variability. A: 3 frames of the high-speed video, separated by 25 ms each. See the accompanying movie file in the Supporting Information (RatMovie.mov) for the complete sequence. B: geometry of measured parameters. Base angle of vibrissa θ(t) is measured with respect to reference vibrissa that is not in contact with the grating. Velocity of head v(t) and distance of head from grating d(t) are measured using head-tracking reflections. C: histogram of instantaneous velocities, across all trials and all animals (×10⁴). D: histogram of instantaneous distance from head to wall, across all trials and all animals (×10⁴). E: histogram of instantaneous head angle (in degrees), across all trials and all animals (×10⁴). F: mean running speed for each animal. Error bars denote SE. F12–F22 are animal identifiers. G: mean (SD) across trials for each animal. H: mean (SD) in head position within a trial, for each animal.

We should also note that recent studies have implicated higher-order measures (i.e., curvature) as potentially important aspects of the mechanical signals transduced by the pathway (Birdwell et al. 2007). Although we were able to measure curvature from the high-speed video in controlled situations in which an isolated vibrissa was rigidly clamped and deflected, repeating previous studies, the relatively unconstrained nature of our behavioral paradigm resulted in exceedingly noisy measurements of curvature under these conditions due to the motion of the boundary, and thus these measures were excluded from this analysis. However, Birdwell et al. (2007) showed that for small angular deflections in nonwhisking conditions that the moment at the base of the vibrissa is linearly related to the angular position, and the static relationship we find between distance and differential angle during behavior is at least qualitatively similar to the reported relationship between the rate of change of angular momentum and distance. As we show for continuous contact of the vibrissae with a surface under these behavioral conditions, the angular deflection captures a significant element of the motion of the animal relative to the wall, providing perhaps a lower bound of the available information, which may only be enhanced with the consideration of higher-order representations.

Data analysis

Data obtained during the experimental trials consisted of mechanical signals of vibrissae motion. For each vibrissa, the angle signal measured from each trial was low-pass filtered with a cut-off frequency of 300 Hz to remove image jitter and other high-frequency noise, accounting for <1% of the signal power. Vibrissa motion was tracked in the presence of a smooth surface (or in the absence of gratings), and the spectral content was averaged to obtain the corresponding power distribution as a function of temporal frequency (n = 107 trials). SE was also calculated for each, and 95% CIs were formed for the estimates of the mean spectral content as the mean ± 2 SE, as shown in Fig. 3C. Overlap of the confidence bands thus represents statistically similar curves, whereas lack of overlap represents statistically different curves. The average spectral content in the presence of a grating surface (n = 1,248 trials) was not significantly different from that of the smooth surface below 40 Hz but was significantly larger above this frequency (black vs. gray in Fig. 3C—note the log scale). Based on these observations, we applied a high-pass filter with a cut-off frequency of 40 Hz to extract the high-frequency grating component and a low-pass filter with a cut-off of 40 Hz to extract the low-frequency distance component. All filtering was implemented digitally using a third-order Butterworth filter.

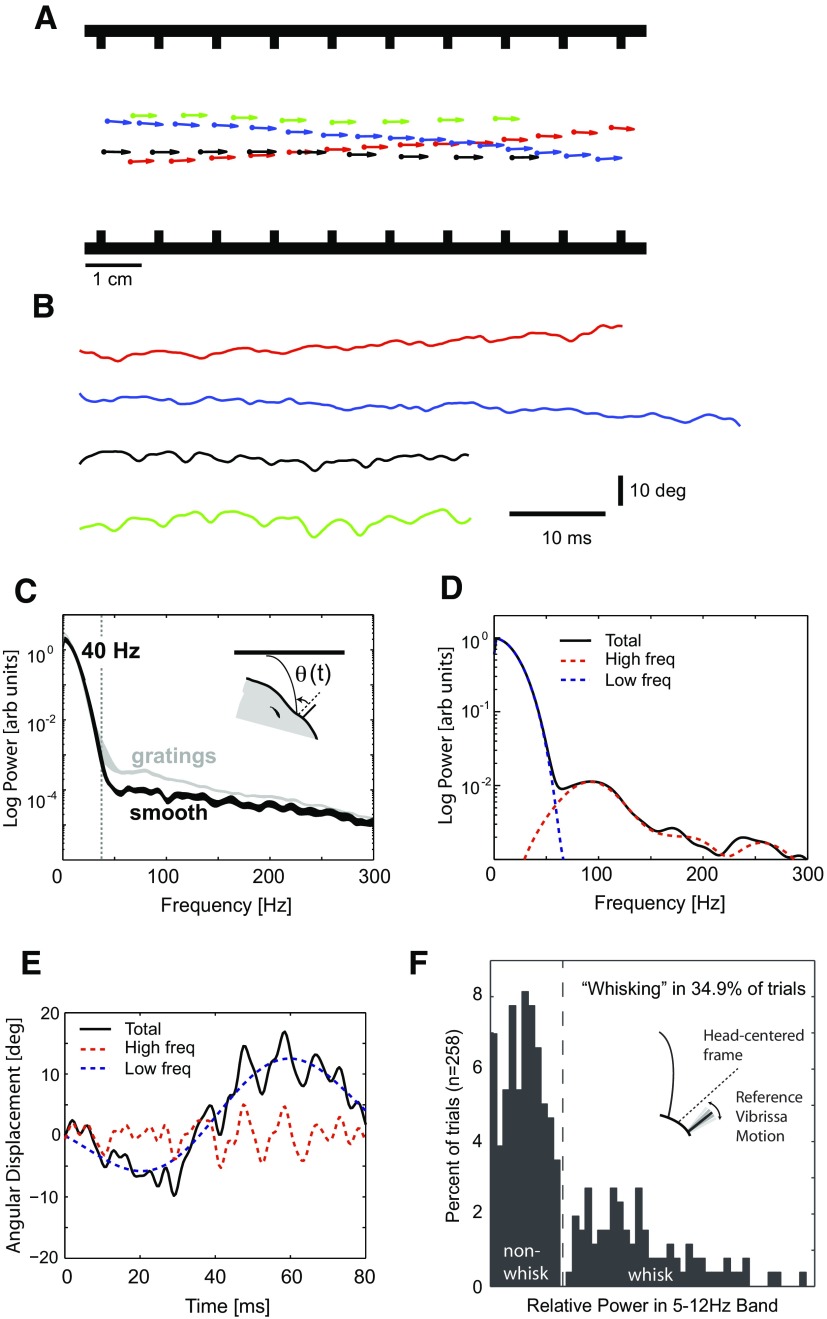
Fig. 3.

Vibrissa deflection contains both surface- and distance-related information separable by frequency. A: head position (circles) and angle (arrows) plotted in spatial coordinates at 10 ms intervals for 4 different trials with the same grating present (grating 3, 9.80 mm). Note the significant variation in head position relative to the sides of the track within single trials, as well as variation in velocity (proportional to distance between circles) between trials. Average head speeds during these 4 trials were 0.66, 0.58, 0.91, and 0.92 m/s, respectively. B: traces of measured angular deflection of vibrissa C2 on the left side of the face, from the same trials depicted in A. Note significant variability within and between trials because of animal's motion. C: average spectral content when the vibrissae were in contact with a smooth surface (n = 107 trials, black) compared with the average spectrum for the grating trials (n = 1,248 trials, gray). Bands represent 95% CIs for the mean spectral content, formed from ±2 SE. Smooth and grating spectra are not different at low frequency, but power in the grating spectrum increases significantly above the smooth at ∼40 Hz (vertical line). Note that the increase in variance in the gratings spectrum at approximately 40 Hz is primarily due to 3 trials with large power at this frequency (out of the 1248 total trials). D: components of the angular deflection signal from a single trial for vibrissa C3 in the presence of grating 3, shown in the frequency domain (power spectral density in arbitrary units). The signal (total, in black) can be separated into a low-frequency (0–40 Hz) component that depends on the motion of the animal's head (dashed blue), and a high-frequency (40–300 Hz) component that contains information about the grating (dashed red). E: analogous signals in the time domain. F: total power in the “whisking” frequency band of 5–12 Hz for the reference vibrissae, showing a clear delineation between whisking and nonwhisking trials.

Distance decoding

Previous studies have proposed simple approximations for the relationship between the bending of the vibrissae and the distance between the animal and the surface with which it is in contact (Birdwell et al. 2007; Szwed et al. 2003, 2006). We used the low-frequency component of the vibrissa mechanical signal to decode moment-by-moment changes in the distance of the animal's head from the grating plates. Note that the vibrissa angle is measured relative to a reference vibrissa on the face. The low-frequency component of the vibrissa can change because of head rotation or because of a translation of the animal's body toward the wall, or some combination, making the relationship between the low frequency component of the vibrissa angle and the distance to the wall ambiguous. If the distance between the pivot point of the animal's head and the vibrissa base is small relative to the length of the vibrissa, to a first approximation the low frequency component of the vibrissa angle is equivalent to the head rotation (i.e., from Fig. 2B, as γ gets small, so does θ, and vice versa). The residual component of low-frequency vibrissa angle is thus attributed to translation of the animal's body toward the wall (i.e., changes in d).

Based on the observed relationship between the low-frequency component of the vibrissa deflection and the distance of the mystacial pad to the surface, we constructed a model of distance decoding as d_pred(t) = d₀ + g⁻¹[θ_low(t) − γ(t)], where d_pred(t) is the predicted distance of the animal from the surface of the grating at time t, d₀ is the distance at time t₀ < t (the start of a trial), g is a static monotonic function relating the distance to the angle, θ_low(t) is the low-frequency component of the vibrissa angle signal, and γ(t) is the head direction. We parameterized the function g using a decaying exponential of the form g(d/L) = A × exp(−λ × d/L). When this function was fit to finite-element data using nonlinear least squares estimation, the parameters were estimated as A = 75° and λ = 4.8. Note that θ_low(t) and γ(t) are measured relative to their values at time t₀. We assessed the performance of the decoding algorithm by computing the root mean squared (RMS) error between the decoded distance and the actual distance for each trial and compared this performance to the null hypothesis that the animal did not move perpendicular to the running direction of the track from the initial distance d₀.

Finite element modeling

We observed a monotonic relationship between the normalized distance to the wall and the differential angle, as shown in Fig. 4A. To further investigate the relationship between distance, surface features, and vibrissa deflection, we developed a computational model using commercially available finite element software (ABAQUS, Providence, RI) (Vaziri et al. 2007). We modeled the vibrissae as linear elastic beams, with a Young's modulus of 7.8 GPa, a density of 1.2 mg/mm³, a Poisson ratio of 0.3, a length of 38 mm, and a radius at the base of 0.078 mm. The material constants were chosen based on the reported values for a typical C2 rat vibrissa (Hartmann et al. 2003; Neimark et al. 2003).

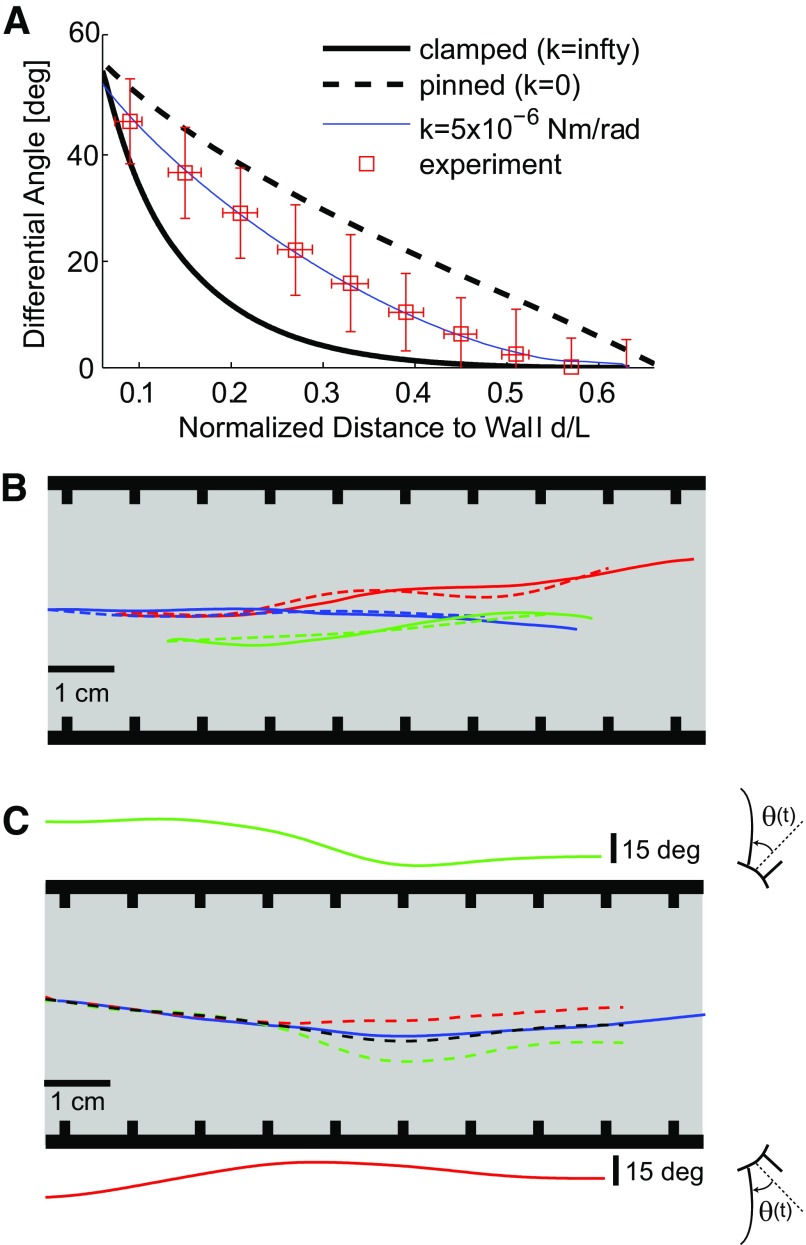
Fig. 4.

Distance of head from wall can be continuously decoded using vibrissae angles. A: relationship between the difference in static angular deflection and head angle (denoted here as Differential Angle), and the normalized distance to wall. Experimental observations shown with red open symbols, along with corresponding SD. Black curves show the relationship as predicted by finite-element model, using 3 different boundary conditions at the base. The experimental data lie between the extreme clamped and pinned cases and were best fit by a boundary condition that includes a torsional spring with spring constant k = 5 × 10⁻⁶ Nm/rad. B: example of measured head distance (solid) and decoded head distance (using low-frequency component of vibrissa signal, dashed) plotted in spatial coordinates for 3 representative trials. The grating-lined walls are depicted schematically on either side of the trajectories. C: bilateral integration improves distance decoding. Solid green (top, left side of face) and red (bottom, right side of face) traces show low-frequency component of angle signal from a single vibrissa on each side of the face. Note the mirror-image sign convention for the left and right sides of the face, where in either case a caudal deflection corresponds to a positive angle θ(t). The corresponding decoded distance signals (dashed) are plotted as a trajectory in spatial coordinates on the track. The actual trajectory is plotted in solid blue. Averaging the 2 angle signals and decoding results in the dashed black trajectory, a significant improvement over the decoding using individual vibrissae.

The finite element model is a mechanical model of the vibrissae based on a discretization of the tapered geometry that uses a three-dimensional grid of point masses connected with linear spring and frictional elements. The grid of elements that form the vibrissa model is coupled to the face, where the attachment of the vibrissa (beam) to the face was modeled via a pivot with a linear torsional spring that resists rotation, whose properties we varied. In the limit as the spring constant goes to 0, there is no resistance to rotation about the pivot, resulting in the situation we refer to as “pinned.” In the limit as the spring constant goes to infinity, the beam becomes rigidly clamped to the face, permitting no rotation about the pivot point and relegating any deflection of the beam to deformation/bending of the beam itself, resulting in the situation we refer to as “clamped.” The gratings were modeled as rigid surfaces with the same geometry as the actual gratings. Using the model, we computed the relationship between the head-to-surface distance and vibrissa angular deflection, as well as the relationship between the variations in angular deflection due to the surfaces and the distance.

As can be seen in Fig. 4A, the experimental data suggest a boundary condition intermediate between clamped (infinite stiffness) and pinned (zero stiffness), and the torsional spring constant that best matches the data were k = 5 × 10⁻⁶ Nm/rad, although there is a significant spread in the experimental data. This spread is caused by varying conditions on each trial, perhaps caused by different initial vibrissa angles changing conditions at the vibrissa base (Hartmann et al. 2003). Furthermore, because the amount of bending induced in the vibrissae by a deflection force is extremely sensitive to radius (it varies as radius to the 4th power), we explored the role of vibrissa geometry. Actual vibrissae have an approximately linearly tapered cross-section, with a tip radius of 0.0047 mm (Hartmann et al. 2003; Neimark et al. 2003). We performed simulations for both tapered cross-section and uniform cross-section vibrissae. Note that, although the different vibrissae do differ in their cross-sectional area and mechanical properties, the most significant parameter was by far the length. Numerical simulations based on normalized vibrissa length were therefore good approximations for the mechanical behavior of the different vibrissae.

Through both the experimental measurements and the finite element model, we envision a static, monotonic function g(·) that relates the distance from the wall to the difference between the angular deflection and the head angle: θ_low(t) − γ(t) = g[d(t)/L], parameterized as described above as a decaying exponential g(d/L) = A × exp(−λ × d/L), where A = 75° and λ = 4.8, as shown by the thin solid line in Fig. 4A. Note that, although the different facial vibrissae do have different mechanical properties (Neimark et al. 2003) and thus g(·) will vary across vibrissae to some degree, the length of each vibrissa was the primary determinant of the relationship. By normalizing by the length L, the relationships between distance and deflection for the different vibrissae collapse to a single function.

Grating classification

We characterized the high-frequency component of the vibrissae angle signals using their power spectra, shown to be an informative representation of vibrissae kinetics in previous studies (Arabzadeh et al. 2005; Hipp et al. 2006). The power spectrum S(f) of a signal was calculated by dividing the signal into three overlapping sections, each of which was two thirds the length of the signal, applying a Hanning window to each section, calculating the power spectral density (PSD) of each section, and averaging the PSDs together, improving the statistical properties (reduce the variance) of the spectral estimator (Ljung 1992). To generate significance bands on a process of similar temporal length with no spectral structure, each observed angular deflection signal θ(t) was shuffled temporally 200 times (destroying all correlation structure), and the average spectrum was computed across the shuffled set. To transform the spectra to spatial frequency, the temporal frequency f was simply mapped to the corresponding spatial frequency by normalizing by the mean running speed, f^s = f/v_mean.

The frequency of the peak of the spectrum, denoted ξ, was used as a simple classifier for the texture identity. We approximated the probability distribution of the classifier pertaining to each grating class as Gaussian. Given a set of classifiers ξ_n^T corresponding to grating T and trial n, we computed the class-specific means μ_T and variances σ_T². For appropriate cross-validation purposes, we divided the data into two randomly selected, disjoint subsets and used one of these (training dataset) to estimate the mean and variance of the class probability distribution. The other subset (testing dataset) was used to test the classification by assigning the classifiers for each trial to one of the grating classes using the maximum likelihood estimator, T(ξ) = arg max_T p(ξ|T, v_mean).

Performance measures

To characterize the performance of our classification algorithm, for the testing dataset, we computed the probability that on a given trial using grating T, the trial was classified as grating T_pred, or w_ij = p(T_pred = j|T = i). The overall performance P of the algorithm using various classifiers and under different conditions was characterized as the fraction of correct classifications: P = Σ_iw_ii/Σ_iΣ_jw_ij. We estimated error bounds for P by dividing the testing dataset into 30 randomly chosen subsets of one half the trials and computing the mean and SD of the performances calculated using those subsets.

Theoretical limits on classification

Although it is clear that the level of performance of the grating classifier described in Fig. 5 is significantly above chance (25%), it is less immediately clear what the upper limits on the classification are based on physical constraints. There are two significant factors limiting the classification: the extremely short-duration of the observed vibrissa angle signal, and any variations in running speed of the animal over the course of a trial beyond the level of fidelity of any internal representation of running speed. We expect a peak in the temporal spectrum of the vibrissa angle signal at a frequency of f_T = v_mean × f_T^s, where f_T^s is the spatial frequency of the grating and v_mean is the mean running speed of the animal. However, the fact that the angle signal from each trial is extremely short in duration places a fundamental limit on our ability to discriminate peaks from two different gratings using spectral estimation techniques. Consider a discretely sampled signal that is the sum of two perfect sinusoids whose frequencies differ by Δf and that has a finite length Δt. The peaks in the estimate of the spectrum of this signal overlap when Δf ≤ 1/Δt (Burrus et al. 1994).

Fig. 5.

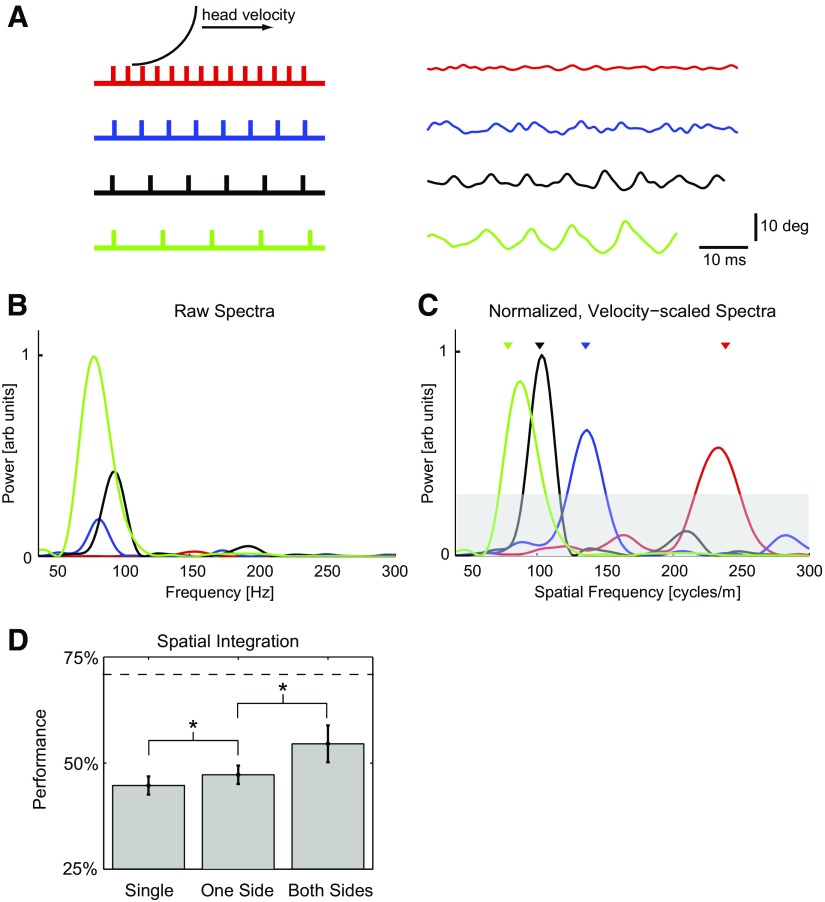
Spectral content of high-frequency component of vibrissae signals can be used to classify gratings. A: left: schematic showing vibrissa interacting with gratings 1–4 (gratings scaled correctly with respect to each other). Right: example high-frequency components of angular displacement signal from all 4 gratings for vibrissa C2. Average head speeds during these trials were 0.66, 0.62, 0.92, and 0.92 m/s, respectively. B: power spectra of signals in A, showing variation of total power and spectral peak with grating (arbitrary units, scaled to max of 1). Note that peaks are not easily discriminable. C: normalized, velocity-scaled power spectra of signals in A, showing clear separation of spectral peaks in the spatial frequency domain (arbitrary units, scaled to max of 1). Triangles show location of spatial frequency of the gratings. Gray band represents upper bound of 95% CI on signals of similar length with no significant spectral structure. Peaks emerging from this band are thus judged statistically significant. D: performance of classification algorithm using peak of spectrum is significantly above chance. In addition, spatial integration [across different vibrissae on one side of the face (One Side) and across both sides of the face (Both Sides) during a single trial] significantly improves performance. *, statistically significant difference at the level of P < 0.05.

This is the uncertainty principle as applied to discretely sampled signals, and it implies that, even in the absence of noise, two perfect sinusoids cannot be discriminated using the spectrum of the signal when the signal length is shorter than the value given above. The signal length for our data were typically <150 ms, imposing a frequency discrimination lower limit of 10 Hz (or 18 cycles/m in spatial frequency, based on the mean observed running speed).

Another effect leads to a broadening of the peak associated with the grating and the creation of sidebands around the central peak and results in an impaired ability to discriminate different peaks in the presence of noise. The rat's head speed, v_mean, is not exactly constant during a trial, leading to a modulation (assumed to be unknown at this level of resolution) of the instantaneous frequency of the grating-modulated part of the spectrum. In an idealized sense, we can treat the expected grating-induced central frequency as a “carrier” frequency and the variations around this frequency caused by variations in head speed as FM. It can be shown (e.g., Cook and Liff 1968) that the peak caused by the carrier of an FM signal is broadened and develops sidebands with a total bandwidth of Δf = 2(f_Δ + f_m), where f_Δ is the maximum deviation of the instantaneous frequency from the carrier frequency, and f_m is the maximum modulating frequency. For grating 3 and a 1 m/s mean running speed and the magnitude of variation we observed, the carrier frequency is 100 Hz, with an approximate deviation of f_Δ = 7 Hz. Because the vast majority of the low-frequency power in the angle signal is concentrated below 20 Hz, we can set f_m = 20 Hz. Thus a grating-associated peak will be broadened to a width of ∼60 Hz (or 109 cycles/m in spatial frequency, based on mean observed running speed), which is in the middle of the range of separations between grating-related peaks. This effect dominates the finite signal length effect. Numerical simulations suggest that the upper limit on classification performance under our experimental conditions is 70%, as shown by the upper dashed horizontal line in Fig. 5D.

RESULTS

Behavioral variability and the shaping of sensory input

The animals in our experiments were rewarded for running along a simple linear track lined with gratings on either side that were positioned to engage the facial vibrissa array (Fig. 1A and methods). The animals were not rewarded for any decisions related to the perceptual experience. High-speed video was acquired from a camera positioned above the track, with diffuse illumination from underneath. The diffuse illumination from below allows for good visualization of the individual vibrissae within a row. Figure 2A shows three frames of a particular trial, separated by 25 ms each. Vibrissae on both sides of the face were in contact with the respective gratings on the side, as the animal veers toward the left side of the track (relative to the direction of running). See the corresponding movie file in the Supporting Information (RatMovie.mov) for the complete video of this trial. Although the gross behavior of the animals became somewhat stereotyped with overtraining, the details of the motion nevertheless varied significantly as they traversed the track. Running speed, v(t), was defined as the speed of the head motion in the direction parallel to the track, as shown in Fig. 2B. The instantaneous running speed varied significantly across all observations, as did the position of the animal's head relative to the side of the track and the head angle relative to the running direction, γ(t). Figure 2C shows the histogram of the running speed at every instant of every trial, across all animals [0.49 ± 0.17 (SD) m/s]. Note that the vertical axis is ×10⁴ observations. Figure 2F shows the mean running speed for each of the five animals (0.55 ± 0.19 m/s, across animals; 35% variation across animals; F## indicates rat identification number). There was an average of ∼17% variation in mean running speed across trials for each animal relative to their own mean. As a measure of how much the speed varied within a trial, Fig. 2G shows the mean intratrial variation in instantaneous running speed for each animal (0.05 ± 0.01 m/s; 9% variation relative to the mean running speed of 0.55 m/s). There was no apparent relationship between the properties of the grating and the running speed of the animal in this paradigm in which the animal was not trained to discriminate between the different gratings.

In addition to tracking the running speed, the position of the animal's head relative to the side of the track was measured, as well as the head angle relative to the running direction. Figure 2D shows a summary of the distance from the center of the head to the center of the track at every instant of every trial, across all animals (0 ± 5.4 mm). Note that the track was 10 cm across, spanning −50 to +50 mm on these axes. Figure 2H shows the mean of the distance of the head from the wall within a trial, for each of the five animals (1.35 ± 0.15 mm across animals). Figure 2E shows a histogram of the observed head angle, γ(t), over all trials across all animals (0 ± 8.2°).

Example trials of head motion obtained in the presence of one specific grating are plotted in Fig. 3A. The head position (circles) and direction (arrows) are plotted in spatial coordinates at 10 ms intervals. Two trials for each of two distinctly different running speeds are shown (blue and red, slow; black and green, fast). As shown in Fig. 1B, the vibrissa motion was tracked as the animal traversed the region of interest (see methods). The details of vibrissa motion depended strongly on the properties of the surface, the distance of the head to the surface, and on the self-motion of the animal. We measured the angle, θ(t), of the individual vibrissae relative to a reference (an adjacent trimmed vibrissa that did not contact the surface). Figure 3B shows the angle signal θ(t) for vibrissa C2 on the left side of the face for each of the trials shown in Fig. 3A.

For all analyses, vibrissae were in continuous contact with the surface. Both distance and grating-related components were qualitatively present in the angle signals. The low-frequency (nonstationary) overall drift in the signals corresponded to motion of the animal's head relative to the grating. In the first trial (red), for example, as the animal's head moved toward the grating on the left wall, the vibrissa angle signal drifted upward (more positive) as the vibrissa on the left side of the face was deflected caudally (see Fig. 2B for sign conventions). Conversely, in the second trial (blue), the signal drifted downward (more negative), as the animal moved away from the grating on the left wall and the vibrissa was deflected less in the caudal direction. The last two trials depicted in Fig. 3B (black and green) had less overall drift, reflecting less change in the distance between the wall and head as shown by the plot in Fig. 3A. Superimposed on the low-frequency drift were higher-frequency variations that corresponded to interactions between the animal's vibrissae and surface properties of the walls. Contact with the periodic gratings induced high-frequency periodic variations in the signals. It is important to emphasize that the same grating was present in each of these trials and that it is the variability in the motion of the animal that produces the variations in the vibrissa angle.

The black curve of Fig. 3C shows the mean spectrum across trials in which the vibrissae contacted only a smooth surface (n = 107 trials; band represents the 95% CI on the mean spectral content, based on 2 SE). The average spectral content for trials in the presence of the different gratings is shown in gray for comparison (n = 1,248 trials, band again represents 95% CI). Below 40 Hz, the two confidence bands are significantly overlapped, and thus the two curves are not statistically different. Above 40 Hz, however, the two bands separate, with a significantly larger amount of power in the signal for the gratings compared with the smooth surface. Note that this is averaged across different gratings and different running speeds, resulting in a spreading of the higher-frequency spectral content, but nevertheless shows the disparity of spectral content on this logarithmic scale. Features of the signal occurring in the spectral band 0–40 Hz were thus attributed to input related to the head motion of the animal perpendicular to the surface. Low- and high-pass filters were designed to separate the angle signal into components below and above 40 Hz (see methods), representative of the head motion in the direction perpendicular to the wall and the grating-related motion, respectively. This separation in spectral content is clearly seen in the example shown in Fig. 3D, where the spectrum of the total signal (solid black), high-frequency component (dashed red), and low-frequency component (dashed blue) are shown for a single trial. Figure 3E shows the corresponding signals in the time domain for this particular trial.

There are several observations we made regarding the vibrissae as the animal traversed the grating-lined region. When the animal approached the grating-lined region where contact was initiated, the vibrissae were equally protracted and retracted, suggesting no particular preferred “set-point” for vibrissa position for the task described here. Furthermore, from the angle of the reference vibrissa, it was clear that, during these particular tasks, the rats did not “whisk” on a majority of trials. Specifically, to assess the extent of whisking during this behavioral paradigm, we analyzed the motion of the reference vibrissae. Because the reference vibrissae have been trimmed and are not in contact with the grating or any part of the track, any remaining motion is caused by head movement or whisking. By referencing this signal to the independently measured head angle, any residual motion is caused by whisking or other animal-generated movements of the vibrissae. We estimated the power spectra of all reference vibrissae over all trials and evaluated the total power in the presumed whisking frequency band of 5–12 Hz. The resulting histogram across all trials and all animals showed a bimodal distribution, suggesting a natural threshold above which the animal was judged to whisk, which was the minority of cases (<35% of the trials; Fig. 3F). Note that, because the angular deflection of a whisker in contact with a surface was measured relative to the reference vibrissa, any whisking related components were removed, assuming that all vibrissae whisk in phase.

Distance decoding

Large low-frequency deflections of the vibrissae can be produced by either movement toward the wall in the direction perpendicular to running or through head rotations, in which the perpendicular distance undergoes little if any change, or both, making the direct relationship between vibrissa angle and distance ambiguous. The relationship we consider therefore is based on the difference between the low-frequency component of the vibrissa angle and the head angle, θ_low(t) − γ(t), referred to as the differential angle. Head angle γ(t) serves as a rotation between the head-centered coordinate system and the world coordinates, providing a direct link between the two coordinate systems and context for the afferent input θ_low(t). Using data from all animals over all trials, we computed the mean angle corresponding to bins of specific mean distances (Fig. 4A, red squares). Note that the distance d has been normalized by the total vibrissa length L, resulting in a general relationship across all vibrissae.

A numerical finite element model (FEM) of the vibrissa mechanics was used to approximate the relationship between the normalized distance and the differential angle and to infer the boundary conditions at the face (curves in Fig. 4A, see methods). By matching the experimental observations with the FEM predictions, the boundary condition was inferred to be an intermediate condition between clamped and pinned, with a torsional spring constant of ∼5 × 10⁻⁶ Nm/rad (thin solid curve going through data points in Fig. 4A). This monotonic relationship was fit with a parametric exponential function that, with knowledge of θ_low(t), γ(t), and L, we used to decode/reconstruct the distance at each point in time. As an example of the interaction between head angle and the perceived distance, consider a differential angular rotation of the vibrissa of 20°. Perturbations around this differential angle consistent with those from the observed range of variation in head angle (Fig. 2E) would result in 17% variation in the decoded or inferred distance to the surface.

Figure 4B shows three example trials, one in each color, where the actual head trajectory (solid) is well tracked by the decoding (dashed). Taking into account all of the trials, the mean RMS error using single vibrissae to decode the distance was 2 mm (n = 1,248 trials). For comparison, the distance between grating plates on either side of the track was 70 mm, and the length of a typical C2 vibrissa was 38 mm. However, from a statistical perspective, decoding using single vibrissae was not always significantly better than the null hypothesis (i.e., simply assuming that the rat's head did not move at all in a direction perpendicular to the running direction during a trial). In 42% of the trials, the decoded trajectory was significantly better than the null hypothesis (t-test, P < 0.05). We integrated the low-frequency signals from all vibrissae during a single trial and decoded. An example of this integration is shown in Fig. 4C, in which there was one vibrissa on each side of the face. The low-frequency components of the signals from each vibrissa are plotted above and below the schematic of the track for reference, and the corresponding decoded trajectories (without integration) are plotted with dashed lines and matching colors on the track. Note the mirror image sign convention for the two sides of the face, where in each case a caudal deflection of the vibrissa corresponds to a positive angle θ(t). The solid line is the actual (measured) trajectory. The decoded trajectory obtained from integrating the two vibrissa signals is plotted using the dashed black line, showing significant improvement. Across all trials, the multi-whisker distance decoding produced results significantly better than the null hypothesis in 54% of the trials (RMS errors significantly smaller, t-test, P < 0.05). The performance in all cases, however, was strongly dependent on the overall magnitude of the motion toward or away from the walls on each trial. For the trials in which the animal moved >10% of the whisker's length relative to the wall, the decoded trajectory was significantly better than the null hypothesis for 70% of the trials (t-test, P < 0.05). Improved performance of decoding for larger head movements is a natural consequence of the increased magnitude of the modulation of the head movement relative to the magnitude of intrinsic variability in the measured signals (noise caused by measurement error, variability in the mechanical interface, etc.).

Grating classification

Although there was significant variability and noise in the high-frequency signals, the high-frequency component of this short-duration (typically <150 ms) signal contained features related to the gratings, seen both in the time series (Fig. 5A, right) and spectra (Fig. 5B). Note that the spectra have all been scaled so that the maximum peak (in green) has a value of 1 (arbitrary units). These high-frequency grating-related oscillations were strongly affected by the self-motion of the animal, which tended to shift and reshape spectral features. Although this particular example exhibits an interesting trend in which higher spatial frequencies are accompanied by slower running speeds, this was not the trend in general (i.e., the running speed was uncorrelated with the spatial frequency of the grating), which is not surprising, given that there is no explicit texture discrimination task involved. This particular example is an extreme case chosen to show the potential confound between spatial frequency properties of the gratings and the resulting temporal frequency of vibrissa motion, caused by the variations in behavior from trial-to-trial.

Using grating 2 as an example (135 cycles/m, blue trace), the range of observed variations in running speed (Fig. 2C) would result in the peak temporal frequency of the actual vibrissa deflection ranging from 49 to 100 Hz. This variation results in significant overlap of the spectral content for the different gratings, making the identity of the grating on a particular trial ambiguous. Dividing the temporal frequency by the running speed transformed the spectra to a function of spatial frequency, resulting in much better separation of the different gratings (Fig. 5C). Note that the gray band denotes the 95% CI for a signal of similar length, with no significant spectral structure, obtained from the average of the spectra of temporally shuffled signals over all trials (see methods). Peaks emerging from this band can thus be considered statistically significant. Note also that the spectra are again scaled so that the maximum peak (in black) has a value of 1.

We implemented a simple classifier based on the spatial frequency associated with the peak of the spectral power (see methods). To classify the gratings, we performed maximum likelihood classification using data from 323 running trials, each of which had between one and six vibrissae in contact with the gratings, yielding 1,248 sweeps of vibrissae across the gratings. Typically, a vibrissa was in contact with a grating for between 80 and 150 ms. Classification was performed on a single-trial basis using these very short signals. The maximum performance P was 47%, significantly above a chance level of performance of 25% (see performance level for single vibrissa in Fig. 5D).

Because the angle signals were extremely short and variable, performance is expected to improve by extending the classification to integrate over multiple vibrissae during a single run. Previous studies indeed suggested that increasing numbers of vibrissae enhance performance during texture and distance discrimination tasks (Carvell and Simons 1990; Krupa et al. 2001) and synthetic classification procedures (Hipp et al. 2006). We averaged together the spatial frequency spectra obtained from the angle signals of multiple vibrissae and evaluated changes in performance (Fig. 5D). We did so in two stages: first, we tested the performance when integrating spectra of vibrissa motion from one side of the face only on a given trial (Fig. 5D, One Side), and second, we tested the performance when integrating spectra of vibrissa motion from both sides of the face on a given trial (Fig. 5D, Both Sides). Spatial integration improved performance significantly, nearly reaching the theoretical upper bound on performance given the short duration of the observation and the behavioral variability (dashed horizontal line, see methods). Integration across one side of the face did improve performance, but the improvement when integrating across both sides of the face was more dramatic. Integrating over time (across multiple trials) did not improve performance.

Distance–surface interaction

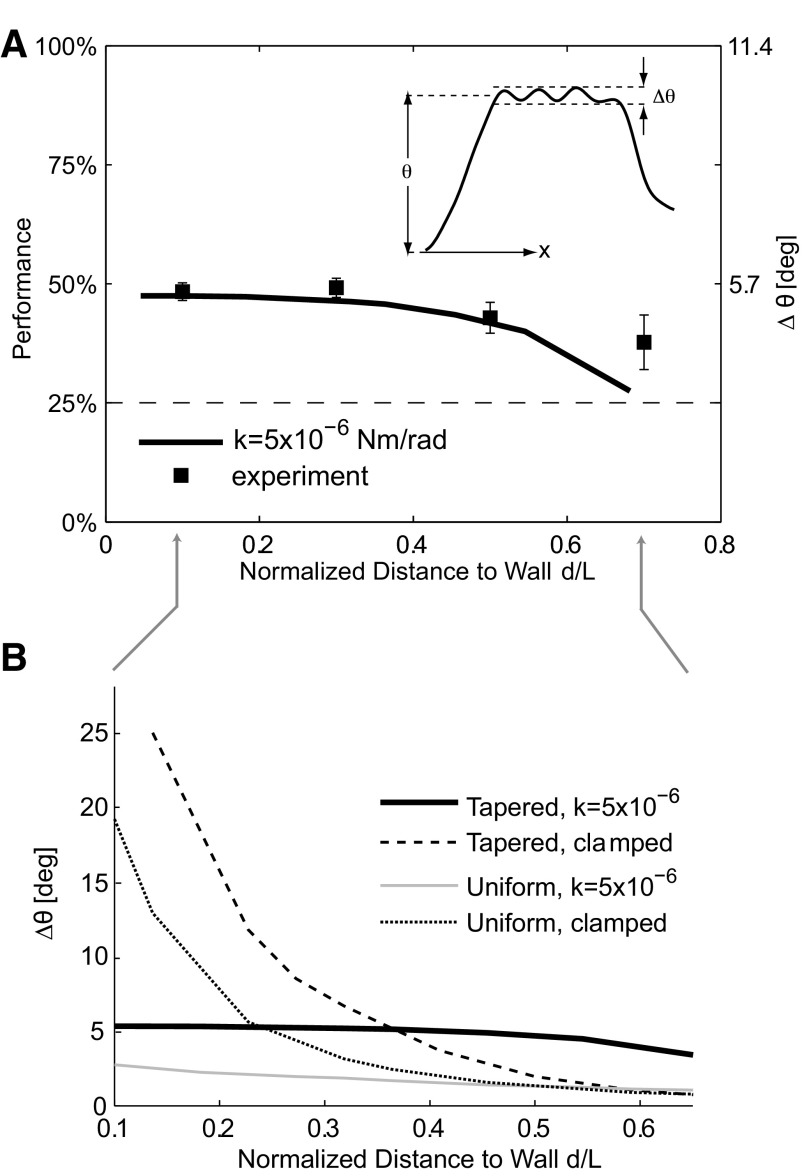
Although the distance and surface-related components of the vibrissa motion are generally separable by their relative frequency bands, it remains a possibility that the distance to the surface could strongly shape the signals related to the properties of the surface, in which case the behavior of the animal might improve or confound the sensory information related to the invariant properties of the surfaces. We therefore studied the possibility that the performance of the grating classification algorithm depended on the distance of the base of a vibrissa from the surface and thus on animal self-motion. To quantify this dependence, we computed mean classification performance as a function of the mean base-to-grating vibrissa distance, as summarized in Fig. 6A, across all trials (n = 1,248). The grating discrimination performance was maximal, and relatively constant, when the base of the vibrissa was <50% of its total (free) length away from the surface. The majority of trials (>80%) occurred within this distance range. This result suggests that, for the range of behavior exhibited, the grating classification performance is insensitive to distance and thus to the animal's self-motion.

Fig. 6.

Grating discriminability is insensitive to self-motion. A: square symbols, left axis: performance of the classification algorithm as a function of the normalized distance (distance divided by vibrissa length) of the vibrissa base away from the wall. Error bars are SE. The dashed horizontal line represents chance performance (25%). Solid line, right axis: numerically computed (using the finite-element model) amplitude of grating-related variations in the vibrissa angle Δθ (see inset) for grating 2, using the boundary parameters previously inferred (Fig. 4A). In both the experimental data and the model, grating-related information content is relatively invariant for a normalized distance of <0.5, although there is a decrease in grating-related information with distance for a normalized distance >0.5. B: variations in grating-related angle Δθ (for grating 2) as a function of distance as computed by the finite-element model using various boundary conditions and vibrissa geometries (i.e., tapered or uniform cross-section along the vibrissa length). Note that the clamped cases result in a large variation in Δθ, whereas the intermediate case results in a relatively constant Δθ. Furthermore, the tapered geometries result in larger overall responses than the uniform cross-section geometries. The tapered intermediate case, which is the one that most closely matches experimental data, has the largest invariant response over the entire distance range.

Although the classification performance was insensitive to animal motion for the majority of behaviorally relevant distances, when the base of a vibrissa was >50% of its length away from the surface, the performance decreased sharply. Given that the classification algorithm was based on the relative distribution of power in different frequency bands, this decrease in performance was obviously linked to changes in spectral content. To systematically explore this effect, we used the finite element model to compute the amplitude of the grating-related modulation in angle (denoted as Δθ; see Fig. 6A, inset) as a function of the distance. The amplitude of modulation relative to underlying nongrating related noise is a primary determinant of discriminability, consistent with a signal-to-noise ratio argument. There was qualitative agreement between the experimental performance data and the results of the model, both in the range of invariance and in the range where performance decreases with distance. It is thus clear that a major determinant of performance is the magnitude of grating-related modulation of the angle signal.

To further explore the details of this behavior, especially the somewhat surprising invariance to distance for shorter distances, we used the finite element model to compute the magnitude of the modulated part of the signal Δθ for several different boundary conditions and vibrissa geometries (Fig. 6B). The results for tapered and uniform cross-section geometries are plotted. The clamped boundary condition results are plotted using dashed lines, and the intermediate boundary condition uses solid lines. There are two effects that determine the shapes of these plots. First, the tapering leads to a larger overall grating-induced modulation in the vibrissa angle. Second, clamping the base results in a less uniform response, as a function of distance. The case that best matches experimental data is the tapered, intermediate boundary condition. Compared with other possible boundary conditions and geometries, the actual situation results in a grating-related signal that is both relatively constant (because of the boundary condition) and relatively large (because of the tapering) over the entire range of typical distances.

DISCUSSION

Proximity and object localization

Since the earliest exploration of the vibrissa system, it has been proposed that rats and other rodents use their vibrissae for navigation through contact with wall surfaces (Vincent 1912; for a review, see Diamond et al. 2008). More recent work showed that rats could use their vibrissae to assess the presence or absence of a target platform in a gap jumping experiment, for which the ability to detect contact of the vibrissae with the platform is implicit (Hutson and Masterson 1986). This proposition was more explicitly asserted by Brecht et al. (1997), where an extensive behavioral study led to a proposed scenario in which macro-vibrissae (as described here) are used for object localization and micro-vibrissae for texture representation. More recent studies have more directly measured the animal's ability to perceive the size of an “aperture” with its vibrissae (Krupa et al. 2001; Shuler et al. 2002) or the ability to perceive contact in the azimuthal plane during a whisk cycle with the animal's position relatively stationary (Hentschke et al. 2006; Knutsen et al. 2005; Mehta et al. 2007). In these studies, the interaction between the vibrissae and the object consisted of punctate contacts initiated over one or two whisk cycles (Mehta et al. 2007) or a single contact initiated through body movement (Krupa et al. 2001; Shuler et al. 2002), rather than continuous contact initiated through body/head movement as we describe here. Although it has been shown that whisking is necessary for horizontal object localization in some situations (Knutsen et al. 2006), studies of aperture discrimination during locomotion (Krupa et al. 2001, 2004; Shuler et al. 2002) and wall-following in maze navigation (Milani et al. 1989) report that whisking is not necessary in these cases, consistent with our observation that rats whisked on a minority of trials in a behavioral task that might best be described as wall-following. Although it is clear that rats and other rodents can and do whisk as an active sensing modality, other important aspects of self-motion such as head and body movement, are likely equally important, but have not been characterized in detail. One interesting parallel between the object localization studies and the perspective presented here is the ambiguity of object position on vibrissa contact in the absence of knowledge of vibrissa location or phase of whisk cycle (Mehta et al. 2007; Szwed et al. 2003), analogous to the ambiguity of distance in the absence of knowledge of head angle. Recent findings have suggested the possible necessity of the encoding of the moment induced by vibrissa bending (and thus vibrissa curvature) for the purpose of distance decoding, which was not addressed in this study. In any case, having access to sensory signals that provide distanced-related information is important for the localization of objects relative to the head, which in turn is important for the animal to plan movement (Kleinfeld et al. 2006).

Discrimination

Since the first studies explicitly showing the ability of the rat to discriminate between different textures based on vibrissa exploration alone (Carvell and Simons 1990; Guic-Robles et al. 1989), numerous efforts have been launched to explore this issue in more detail (Arabzadeh et al. 2003; Hipp et al. 2006; Ritt et al. 2008; von Heimendahl et al. 2007; Wolfe et al. 2008). Most relevant to this study, Hipp et al. (2006) explored the spectral content of angular deflections of fairly stereotyped movement of artificial vibrissae across textured surfaces and electrically induced whisking of intact vibrissae against textured surfaces in the anesthetized rat. From a discrimination algorithm based on spectral content of vibrissa motion, similar to that used here, it was determined that multiple features of spectral content were predictors of texture identity, notably those measures related to total power and the concentration of power at a peak frequency. However, this finding was based on sandpaper textures, providing a significantly more complex surface morphology than that described here, for which the primary driving frequency of the whisker motion was caused by the periodicity of the grating spacing. We did find, however, that there was a negative correlation between the peak frequency and the total power, suggesting that consideration of other measures could augment the classification.

Implicit in the framework developed here is the assumption that the frequency of vibration of the vibrissae is directly induced by surface texture and that this would depend primarily on the spacing of the surface features and the motion of the animal with respect to the surface. This perspective was recently described in the context of whisking against a grating with periodic spacing (Mehta and Kleinfeld 2004), where the relative motion would be induced through whisking rather than locomotion or head movement. A separation between the face and the surface of 25 mm is assumed, as is a whisking frequency of 9 Hz, a 10–15° amplitude sinusoidal whisking (0.17–0.26 radians), and a spacing of the features between 15 μm and 1 mm. Given the parameters used in this argument, we estimate the speed of the contact point traversing the surface to be ∼0.3–0.4 m/s, of the same order of magnitude as we describe here in the running paradigm (in the absence of whisking). A large difference, however, lies in the spacing of the surface features, for which Mehta and Kleinfeld consider to be on the order of 15 μm to 1 mm, compared with our minimum spacing of 4.2 mm. These high spatial frequencies result in temporal frequencies ranging from 300 Hz to 20 KHz, which far exceeds what we observe in the face of the grating sizes used here (never exceeding 300 Hz). Although this likely rules out this rather simplistic paradigm for the discrimination of fine textures, because of the exceedingly high frequencies (too high even for primary sensory neurons), this does not rule out the possibility of such a simple code for coarse discrimination, as we conceptually outline here.

We should note that the perspective that the vibrissa motion primarily reflects the properties of the surface and the motion of the animal (be it whisking or running) does not preclude a role for the intrinsic mechanical properties of the vibrissae, as has been recently proposed (Hartmann et al. 2003; Neimark et al. 2003). The experimental design of fairly coarse gratings typically placed the modulation of the base of the vibrissae in the 100–200 Hz frequency range. Despite the fact that the spatial frequencies of these gratings are far below those for the finer textures that are typically the focus of investigation, the resultant temporal frequencies are consistent with the resonant frequencies of the vibrissae described previously in vivo (Neimark et al. 2003; Wolfe et al. 2008). Although this was not explicitly part of the analysis here, we did qualitatively observe variations in power in the vibrissa motion for different combinations of running speeds and grating frequencies (Fig. 5, A and B), likely because of the intrinsic mechanics of the vibrissa and follicle complex. As Fig. 6B shows, the degree of modulation, and therefore presumably the power in the peak of the spectrum, is relatively invariant to the distance from the face to the wall, suggesting that the changes in power with different frequencies would also be an invariant property of the pathway, providing support for the possibility of a resonance-based coding scheme.

One particularly interesting observation is the relatively invariant modulation of the vibrissa base as a function of mean distance to the grating (Fig. 6). This property would be to great advantage if the rat did not have precise control over how far away its face was from the surface. Moreover, within the optimal range, the spectral “signature” of the surface would be relatively invariant to distance, allowing a further decoupling between animal-induced and surface-related variations in the vibrissa signal. It is reasonable to ask if the boundary conditions at the base of the vibrissa, which may vary in an awake animal, result in an optimal surface morphology detection probe. At least among the various boundary conditions and vibrissa geometries tested using our finite element model, the actual vibrissa geometry (linearly tapered) and boundary condition (torsional spring with intermediate spring constant) seem to fit one definition of optimal detection that is often met in biological sensing systems: it provides a relatively constant and large sensitivity to the stimuli of interest over the entire range of animal behavior that affects the signal. That is, surface morphology–induced modulations in angle (Δθ) are relatively constant and large compared with the other geometries and boundary conditions, over most of the possible range of distances at which the probe can engage the surface. It is quite likely, however, that the behavior of the animal still strongly influences the nature of the sensory input and is thus an important element of the acquisition of information about the outside world, as the recent findings related to compensatory movement in active sensation would suggest (Towal and Hartmann 2006). It is important to note that the boundary conditions we inferred here were primarily in the absence of whisking, which would likely dynamically alter the boundary conditions through changes in muscle tone at the follicle. Also note that, because of the nature of the behavioral task used here, we cannot label the exploration as “active,” and thus envision the sensory signals as being acquired passively even though it is through the animal's own motion that this occurs. Nevertheless, while active sensation in the context of the vibrissa system has usually been associated with whisking, body and head movement are also important elements of active sensation. Indeed it may simply be the case that relative motion is necessary, however achieved.

Neural encoding

Studies of first-order neurons in the trigeminal ganglion of the anesthetized rat have indicated the presence of “touch cells” that respond only on contact with objects (Szwed et al. 2003), subsequently reflected in the ventrolateral region of the ventro posterior medial nucleus (VPM) of the thalamus in the recently described extralemniscal pathway (Yu et al. 2006). The spike rate of such neurons in the trigeminal ganglion was subsequently shown to accurately encode the radial distance of object contact along the length of the vibrissa (Szwed et al. 2006), providing some neurophysiogical basis for the distance signals characterized here. It is possible that the relevant subclass of early sensory neurons for this behavioral paradigm is what Szwed et al. (2003) referred to as “pressure cells” that fire continuously during contact and are primarily the classical slowly adapting (SA) response type. However, the relationships between these cell classifications and psychophysical channels linked to SA and RA responses are presently unclear (Stüttgen et al. 2006).

Although primary afferents reliably encode low-frequency signals, including those in the 0–40 Hz range of the distance-related frequency band (Deschénes et al. 2003; Gibson and Welker 1983; Jones et al. 2004; Lichtenstein et al. 1990; Shoykhet et al. 2000; Szwed et al. 2006), there is ample evidence that low-level feedback loops exist between primary sensory afferents and motor efferents (Berg et al. 2005; Nguyen and Kleinfeld 2005) that might allow information in the sensory signal to be used by motor circuits below the level of cortex. These low-level loops would be useful to the animal in situations such as wall-following, where the animal would need to maintain some distance from the wall or avoid hitting it, enabling the dissociation of these signals from elements of the neural code related to object recognition presumably carried out by higher centers.

Finally, the cortical representation of texture-related information in this pathway has only recently begun to be studied intensely (Arabzadeh et al. 2003, 2004, 2005, 2006). An accumulating body of evidence suggests that the spike rate of neurons in primary somatosensory cortex increases with approximately logarithmic scaling with the frequency of vibrissa stimulus (Kleinfeld et al. 2006), at least up to the 300–400 Hz range, where “frequency” refers to the repetition rate of the vibrissa stimulus. Studies of cortical activity in response to electrically induced whisking across textured surfaces in anesthetized rats have shown temporally precise, stimulus locked spiking activity, described as a “kinetic” signature of neural activity defined by the temporal pattern of vibrissa deflections (Arabzadeh et al. 2005, 2006). However, observation of such structure requires relative homogeneity of the input to the pathway across repeated trials, the relevance of which may be justified by considering the kinetic signature a surrogate for local population activity across a single trial, but this issue certainly requires further study. A more recent study of cortical activity during a texture discrimination task showed significant trial-to-trial variability in the spike patterns (von Heimendahl et al. 2007), consistent with a significant degree of behavioral variability shaping the input to the pathway differently on each trial that we describe in detail here.

As our results show, the self-motion of the animal makes the interpretation of the incoming sensory signal ambiguous. Knowledge of the gross characteristics of the locomotion and the angle of the head relative to direction of locomotion (and therefore the body) is necessary to disambiguate these influences. There is ample evidence that head direction and locomotive speed are represented through neural activity in various brain regions (McCrea et al. 1999; Sharp et al. 2001, 2006). Therefore we conceptually treat the head speed and angle as “internal” variables known to the observer, and the invariant properties of the surface and the relative distance of the animal to the texture as “external” variables that may be accessible from representations of the motion of the vibrissae and gross knowledge of self-motion. We can postulate that internal estimates of these external variables ultimately guide the generation of motor commands, which in turn influence the incoming sensory signals, but further studies are necessary to fully explore this proposition.

GRANTS

This work was supported by a National Institute of Neurological Disorders and Stroke Grant R01 NS-48285.