Mechanism for the Universal Pattern of Activity in Developing Neuronal Networks

Abstract

Spontaneous episodic activity is a fundamental mode of operation of developing networks. Surprisingly, the duration of an episode of activity correlates with the length of the silent interval that precedes it, but not with the interval that follows. Here we use a modeling approach to explain this characteristic, but thus far unexplained, feature of developing networks. Because the correlation pattern is observed in networks with different structures and components, a satisfactory model needs to generate the right pattern of activity regardless of the details of network architecture or individual cell properties. We thus developed simple models incorporating excitatory coupling between heterogeneous neurons and activity-dependent synaptic depression. These models robustly generated episodic activity with the correct correlation pattern. The correlation pattern resulted from episodes being triggered at random levels of recovery from depression while they terminated around the same level of depression. To explain this fundamental difference between episode onset and termination, we used a mean field model, where only average activity and average level of recovery from synaptic depression are considered. In this model, episode onset is highly sensitive to inputs. Thus noise resulting from random coincidences in the spike times of individual neurons led to the high variability at episode onset and to the observed correlation pattern. This work further shows that networks with widely different architectures, different cell types, and different functions all operate according to the same general mechanism early in their development.

INTRODUCTION

Spontaneous activity is a fundamental property of developing networks (Ben Ari 2001; Feller 1999; O'Donovan 1999), characterized by episodes of intense activity separated by periods of quiescence. This episodic activity occurs at an early developmental stage when the networks are primarily excitatory and plays essential roles in the development of neuronal circuits (Hanson et al. 2008; Huberman et al. 2008; Katz and Shatz 1996; Spitzer 2006). Episodic activity is also observed in other hyperexcitable circuits such as disinhibited networks (Menendez de la Prida et al. 2006; Tscherter et al. 2001). One striking feature of this activity is the correlation between episode duration and the length of the preceding—but not following—interepisode interval (Fig. 1). The spontaneous activity of many networks exhibits this correlation pattern, including the developing spinal cord (Tabak et al. 2001), developing retina (Grzywacz and Sernagor 2000), developing cortical networks (Opitz et al. 2002), hyperexcitable hippocampal slices (Staley et al. 1998), disinhibited spinal cord (Rozzo et al. 2002), and spinal cord cultures (Streit 1993; Streit et al. 2001). The general occurrence of this correlation pattern suggests that a common mechanism of operation exists in networks that are structurally very different (O'Donovan 1999). Here, we identify such a general mechanism and explain how the correlation pattern is created.

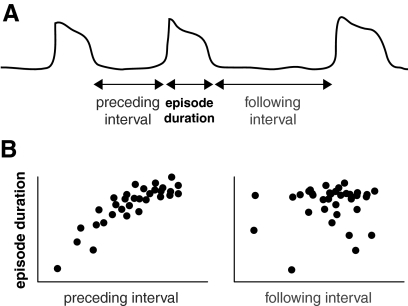
Fig. 1.

Correlation pattern typically observed in developing and hyperexcitable networks. A: cartoon representation of spontaneous activity, showing episodic increases of the average firing rate in the network. B: scatter plots of episode duration and interepisode interval, showing a positive correlation between episode duration and preceding (not following) interepisode interval. Time scale ranges from 100 ms to 1 min for the episodes of activity.

Computational studies have shown that primarily excitatory networks with slow, activity-dependent, network depression can generate episodic activity (Butts et al. 1999; Kosmidis et al. 2004; Tabak et al. 2000; van Vreeswijk and Hansel 2001; Vladimirski et al. 2008). The slow depression process (Darbon et al. 2002; Fedirchuk et al. 1999) could target either synaptic connections (synaptic depression) or the ability of the neurons to sustain spiking (cellular adaptation). Recurrent excitatory connectivity recruits neurons and sustains high network activity, whereas the slow depression eventually shuts down activity. The next episode may occur once the network has sufficiently recovered from depression. This general mechanism can account for activity in a wide range of networks. Can it produce the observed correlation pattern between the duration of episodes and interepisode intervals?

To answer this question, we use a network model of heterogeneous spiking neurons that is capable of generating spontaneous episodic activity. Given its ubiquity, the correlation pattern should be generated regardless of the details of neuronal properties or network architecture. We therefore begin with integrate-and-fire neurons and all-to-all excitatory connectivity. Such a model network with depressing synaptic connections produces the observed correlation pattern. We then show that the correlation pattern is robust to changes in network connectivity and cellular properties.

To explain why the observed correlation pattern is such a robust feature of excitatory networks with slow synaptic depression, we use a mean field model with added noise. The added noise represents the random fluctuations of network activity that may trigger episodes. In this model, episode onset is very sensitive to noise, whereas episode termination is not. This asymmetry in turn explains the correlation pattern. Thus a mechanism based solely on recurrent excitatory connectivity with slow activity-dependent synaptic depression can produce the correlation pattern that is the trademark of developing networks.

METHODS

Network models

We used a network of heterogeneous integrate-and-fire neurons with all-to-all excitatory connections as described by Vladimirski et al. (2008). This choice is motivated by the fact that neither a particular structure nor specific neuronal properties are necessary to generate the spontaneous activity. Heterogeneity of neuronal excitability prevents spike-to-spike synchrony and allows robust episodic behavior (Vladimirski et al. 2008). The voltage variation of neuron i is given by

$$\tau \frac{d{V}_{\mathrm{i}}}{dt}=-V_{\mathrm{i}}+I_{\mathrm{i}}-g_{\mathrm{syn}}\left(V_{\mathrm{i}}-V_{\mathrm{syn}}\right)$$ (1)

with V_i varying between 0 (resting potential) and 1 (spike threshold). The membrane time constant, τ, is set to 1 so time units are relative to the membrane time constant. Each neuron has a constant input, I_i, which sets its own excitability and is the source of heterogeneity. The distribution of I_i was chosen to be uniform over the interval [0.15 1.15] (unless mentioned otherwise), so a fraction of the neurons have inputs I_i > 1 and they spike spontaneously. This allows the stochastic triggering of episodes. The other input to each neuron is the synaptic term −g_syn(V_i − V_syn) with

$$g_{\mathrm{\text{syn}}}=\frac{{\overline{g}}_{\mathrm{syn}}}{N}{\displaystyle \sum _{j=1}^N{a}_j}={\overline{g}}_{\mathrm{syn}}\langle a\rangle$$ (2)

where N is the number of neurons in the network, ḡ_syn is the maximal synaptic activation, and a_j is the synaptic drive from neuron j to all other neurons. The term $\langle a\rangle =\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{a}_{\mathrm{j}}}$ represents the average activity in the network and is used as the output of the simulations. The synaptic drive from neuron j varies according to

$$\frac{d{a}_{\mathrm{j}}}{dt}={\Pi }_{\mathrm{a}}\left(t\right){\alpha }_a\left(1-a_{\mathrm{j}}\right)-{\beta }_{\mathrm{a}}{\mathrm{a}}_{\mathrm{j}}.$$ (3)

When neuron j fires (i.e., V_j reaches 1), its voltage is reset to 0 and kept at 0 for a refractory period T_ref. At the same time, this neuron's Π_a(t) is set to 1 for a brief period of time T_a; at any other time, Π_a(t) = 0, so the synaptic activation coming from neuron j decays with first-order kinetics with rate constant β_a. Note that all the synapses originating from a given presynaptic neuron are identical; this limits the number of synaptic activation variables to N. Finally, we subtract the contribution of each neuron from its own voltage equation (no self-synapses).

Equations 1–3 thus define the basic network model without any type of depression. To this basic model, we can add synaptic depression or cellular adaptation. Synaptic depression is modeled by a variable, s_j, for the synapses originating from neuron j. It varies according to

$$\frac{d{s}_{\mathrm{j}}}{dt}={\alpha }_{\mathrm{s}}\left(1-s_{\mathrm{j}}\right)-{\Pi }_{\mathrm{s}}\left(t\right){\beta }_{\mathrm{s}}{s}_{\mathrm{j},}$$ (4)

where Π_s(t) = 0 at all times except for a period of time, T_dep, immediately following a presynaptic spike, during which it is set to 1. Thus spiking causes s_j to decrease. This depression factor decreases synaptic efficacy such that the effective synaptic input becomes

$$g_{\mathrm{syn}}=\frac{{\overline{g}}_{\mathrm{syn}}}{N}{\displaystyle \sum _{j=1}^N{a}_{\mathrm{j}}{s}_{\mathrm{j}}}$$ 2′

The network model with synaptic depression is thus defined by Eqs. 1, 2′, 3, and 4. For the model with cellular adaptation, we add a slow outward current to the voltage equation

$$\tau \frac{d{V}_{\mathrm{i}}}{dt}=-V_{\mathrm{i}}+I_{\mathrm{i}}-g_{\mathrm{syn}}\left(V_{\mathrm{i}}-V_{\mathrm{syn}}\right)-{\overline{g}}_{\theta }{\theta }_{\mathrm{i}}\left(V_{\mathrm{i}}-V_{\theta }\right)$$ (1′)

with V_θ < 0 and the activation of the outward current, θ_i, varying according to

$$\frac{d{\theta }_{\mathrm{i}}}{dt}={\Pi }_{\theta }\left(t\right){\alpha }_{\theta }\left(1-{\theta }_{\mathrm{i}}\right)-{\beta }_{\theta }{\theta }_{\mathrm{i}}$$ (5)

with neuron i's Π_θ(t) switched from 0 to 1 during a period of time, T_θ, immediately after a spike. The network model with cellular adaptation is defined by Eqs. 1′, 2, 3, and 5. Parameters for the network models are given in Table 1. Simulations were run with XPPAUT (Ermentrout 2002). The fourth-order Runge-Kutta method was used, with a time step of 0.001. Results are presented for n = 100 neurons; simulations with 30–300 neurons gave similar correlation patterns. The time courses for the model with synaptic depression were also similar to simulations run with 1,000 neurons (Vladimirski et al. 2008).

Table 1.

Parameters of the network models using integrate-and-fire neurons (normalized units)

Parameter	Description	Value (Model With Synaptic Depression)	Value (Model With Cellular Adaptation)
Ii	Input to neuron i	0.15–1.15	0.5–1.5
Tref	Refractory period	0.25	0.25
ḡsyn	Max. synaptic conductance	2.8	1.4
Vsyn	Synaptic reversal potential	5	5
αa	Synaptic activation rate	10	10
βa	Synaptic decay rate	1	1
Ta	Synaptic activation duration	0.05	0.05
αs	Synaptic recovery rate	0.004	—
βs	Synaptic depression rate	0.4	—
Tdep	Synaptic depression duration	0.05	—
ḡθ	Max. adaptation conductance	—	0.5–1.5
Vθ	Reversal potential	—	−1
αθ	Adaptation activation rate	—	0.2
βθ	Adaptation deactivation rate	—	0.004
Tθ	Adapt. activation duration	—	0.05

Times are relative to the membrane time constant, conductances are relative to the leak conductance and potentials relative to threshold voltage.

Mean field model

Conceptually, a mean field neuronal model represents the activity of a neuronal population averaged over the population and over a short period of time (Gutkin et al. 2003; Wilson and Cowan 1972). It is a useful approximation when, as in the current system, there is no structure in the connectivity pattern. Also, in the current system, the entire neuronal population is activated almost synchronously on the episodic time scale (but not on the spike time scale), so the average is a good indicator of network behavior. It leads to a differential equation describing the variation of the averaged neuronal activity

$${\tau }_{\mathrm{a}}\frac{da}{dt}=-a+a_{\infty }\left(wa-{\theta }_0\right)$$ (6)

In this equation, a represents the averaged neuronal activity. This is analogous to the average synaptic activation $\langle a\rangle =\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{a}_{\mathrm{j}}}$ used above (Eq. 2), also called synaptic drive (Pinto et al. 1996). This equation implies that activity tends to reach a value given by the network steady-state input/output function, a_∞, with time constant τ_a. This time constant represents the network recruitment time constant and is set to 1, so all time units are relative to it. The parameter w is a measure of the connectivity in the network and is analogous to ḡ_syn in the network model. The parameter θ₀ sets the average cell excitability in the network, analogous to – I in the network model (where I is the average of the individual neuronal inputs I_i). The term wa − θ₀ represents the input to the network; thus the connectivity parameter w sets the amount of positive feedback within the network (Tabak et al. 2000, 2006).

Equation 6 can have bistable solutions, where the activity a can be either high (∼1) or low (∼0) depending on initial conditions. To generate episodic behavior, we add a slow synaptic depression process that can switch the network between the high and low states. This model is defined by

$$\frac{da}{dt}=-a+a_{\infty }\left(\mathrm{wsa}-{\theta }_0\right)$$ (6′)

$${\tau }_s\frac{ds}{dt}=-s+s_{\infty }\left(a\right)$$ (7)

where s is the synaptic depression variable and s_∞ is a decreasing function of a, such that s decreases during high activity episodes and recovers during interepisode intervals. The steady-state network output function is $a_{\infty }\left(i\right)=1/\left(1+e^{-\mathrm{i}/{\mathrm{k}}_{\mathrm{a}}}\right)$ and the steady-state synaptic availability is $s_{\infty }\left(a\right)=1/\left(1+e^{\left(\mathrm{a}-{\theta }_{\mathrm{s}}\right)/{\mathrm{k}}_{\mathrm{s}}}\right)$ (see Table 2 for parameter descriptions).

Table 2.

Parameters of the mean field model

Parameter	Description	Value
w	Connectivity	0.8
θ0	Input for half activation	0.17
ka	Spread of a∞	0.05
θs	Activity for half depression	0.2
ks	Spread of s∞	0.05

Steady-state network output function is a_∞(i) = 1/(1 + e^−i/k_a) and steady-state synaptic availability is s_∞(a) = 1/(1 + e^{(a−θ_s)/k_s}).

This model can generate episodic behavior (Tabak et al. 2006), but it is deterministic and therefore produces constant durations for the episodes and interepisode intervals. To study the variability of these durations, we introduce stochastic noise. This noise represents the combination of factors that leads to variability in the durations of episodes and interepisode intervals. Episodes are triggered when a sufficient number of cells fire in a short interval of time, leading to a synaptic event that can bring the rest of the network above threshold (Menendez de la Prida and Sanchez-Andres 1999; Wenner and O'Donovan 2001). Therefore noise represents random correlated activity in the network; in our network models, noisy fluctuations in average activity result from heterogeneity and finite size effects and not from additional noise to the input of each individual neuron (added noise to individual neurons would mostly result in a different shape for the network output function a_∞; Giugliano et al. 2004; Nesse et al. 2008). We model random correlated activity by adding Gaussian white noise to the activity equation, which becomes

$$da=\left[(-a+a_{\infty }\left(wsa-{\theta }_0\right)\right]dt+n\eta \sqrt{dt}$$ (8)

where n is the noise amplitude and η is a random number drawn at each time step from a normal distribution.

Parameter values for the mean field model with noise are given in Table 2. The simulations were run with XPPAUT using the forward Euler method with a time step of 0.05. All XPPAUT files used in this work are available for download from www.math.fsu.edu/∼bertram/software/neuron.

RESULTS

Excitatory network models with synaptic depression generate the observed correlation pattern

Can a simple neural network model reproduce the episodic activity and associated correlation pattern observed in many developing neuronal networks? To answer this question, we use a network with no special architecture (all-to-all coupling) and composed of excitable cells with no endogenous bursting properties (modeled as integrate-and-fire neurons; see methods). All synapses are excitatory and slowly depress because of presynaptic activity. This creates a circuit with minimal complexity with the capacity to generate spontaneous episodic activity (Vladimirski et al. 2008). All cells are identical, except for their input current I_i, which is randomly chosen such that a small fraction of the neurons are spontaneously spiking. At the beginning of an episode, activity quickly spreads from the most to the least excitable cells. Typically, all cells spike asynchronously during an episode (Vladimirski et al. 2008).

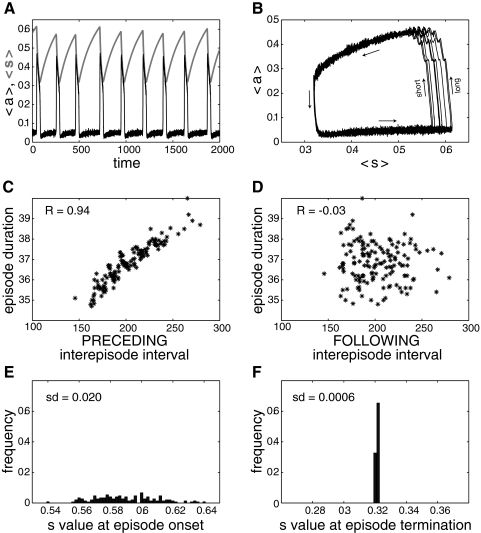
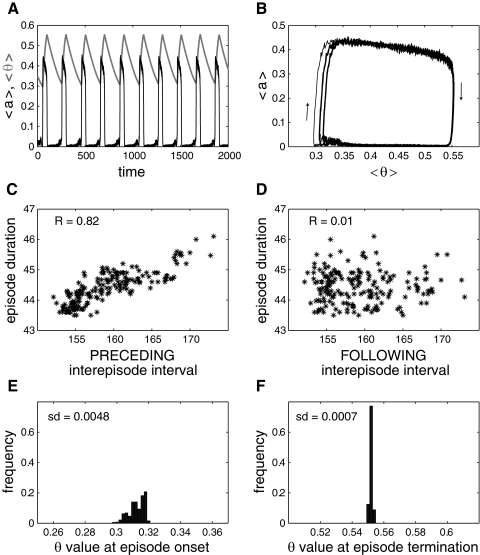
Figure 2A shows the time courses for the model average activity $\langle a\rangle =\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{a}_{\mathrm{j}}}$ (where a_j is the synaptic drive from neuron j, i.e., the firing pattern of that neuron filtered by the synaptic machinery; see methods) and average depression variable $\langle s\rangle =\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{s}_{\mathrm{j}}}$ (where s_j is the level of recovery from depression of all synapses from neuron j; s_j = 0 when the synapses are fully depressed and s_j = 1 when the synapses are fully recovered). The activity is episodic, with 〈s〉 decreasing during an episode, eventually terminating the episode when synaptic efficacy becomes too low to sustain activity. Then 〈s〉 recovers during the interepisode interval, until a new episode is initiated. Note that the maximal value reached by 〈s〉, i.e., its value at episode onset, varies from episode to episode. This is also visible in Fig. 2B where the 〈a〉 versus 〈s〉 trajectory is plotted. There is more variability of 〈s〉 at episode onset than at episode termination. This difference in variability results in a significant positive correlation between episode duration and the preceding (Fig. 2C) but not the following interepisode interval (Fig. 2D). This is because a longer preceding interval (“long” on Fig. 2B) means a higher 〈s〉 at episode onset and therefore a longer episode duration before 〈s〉 decreases enough to stop the episode. On the other hand, because episodes terminate close to the same 〈s〉 value, regardless of episode duration, there is no significant correlation between episode duration and the following interval.

Fig. 2.

Episodic activity and correlation pattern of the excitatory network of integrate-and-fire (I&F) neurons with synaptic depression and all-to-all coupling. A: time courses of activity, 〈a〉 (thin, black curve), and average recovery from depression, 〈s〉 (thick, light green curve). Note how the value of 〈s〉 at episode onset varies from episode to episode, while the value of 〈s〉 at episode termination remains almost constant. B: “phase plane” representation, where 〈a〉 is plotted as a function of 〈s〉 for each time point shown in A. This defines a trajectory with the bottom part of the trajectory corresponding to the interepisode intervals, the upper part corresponding to the episodes and the right and left parts corresponding to the transitions between episodes and silent intervals (arrows indicate direction of movement). This representation clearly shows the greater variability of episode onset than episode termination. Short, episode starting after a short interval; long, episode starting after a long interval. C: the correlation between episode duration and preceding interepisode interval is high. D: absence of correlation between episode duration and following interepisode interval. E: wide distribution of 〈s〉 values at episode onset. F: narrow distribution of 〈s〉 values at episode termination. sd, SD of the corresponding distribution.

The correlation pattern results from the large variability of 〈s〉 at episode onset compared with the low variability at episode termination. To illustrate this difference, we plot the distribution of the average recovery variable 〈s〉 at episode onset and episode termination. The width of the onset distribution (Fig. 2E) is much greater than that of the termination distribution (Fig. 2F). Note that this stochasticity of the episode onset is an intrinsic property of the network, because there is no added source of noise in the model (Thivierge and Cisek 2008). A fraction of the neurons spike slowly during the recovery period, so an episode can be triggered at any time if enough neurons fire together to trigger a wave of recruitment of other neurons. This seems to be a stochastic event, and the probability that such an event occurs increases with recovery time.

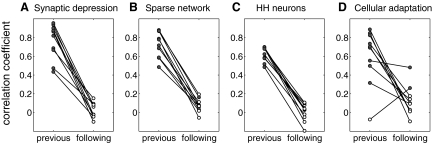
Thus the simple excitatory network model generates spontaneous episodic activity with the correlation pattern observed experimentally. This correlation pattern is the result of the greater variability of episode onset compared with episode termination. To test whether the correlation pattern is robust, we ran 10 simulations with different, randomly chosen distributions of input current I_i. The correlation coefficients between episode duration and interepisode intervals are plotted on Fig. 3A. In all cases, episode onset was more variable than episode termination, resulting in a significant correlation between episode duration and preceding interval, but not with following interval.

Fig. 3.

Robustness of the correlation pattern to model implementation. Each plot indicates the correlation coefficient between episode duration and preceding or following interepisode interval obtained from 10 simulations. Filled circles indicate significant correlation (P < 0.01). A: results from a network of I&F neurons with synaptic depression and all-to-all coupling. Input currents were uniformly distributed on the interval [0.15, 1.15] (the minimal input current that results in spiking, or rheobase, is 1). Each simulation corresponds to a different, randomly chosen, distribution of bias currents. B: results from a network of I&F neurons with synaptic depression as in A, but with sparse (10%) connectivity. Here, all simulations used the same, uniformly spaced distribution of bias current on [0.15, 1.15], but differed in the connectivity matrix. For each simulation, each neuron was assigned to project to 10 randomly chosen postsynaptic neurons. C: results from a network of Hodgkin-Huxley neurons with synaptic depression and all-to-all coupling. Bias currents were uniformly distributed on the interval [−10, 5] (rheobase ∼3 μA/cm²). Each simulation corresponds to a different, randomly chosen, distribution of bias currents. D: results from a network of I&F neurons with cellular adaptation and all-to-all coupling. Both bias currents and strength of the adaptation process g_θ were uniformly distributed on the interval [0.5, 1.5]. Each simulation corresponds to 2 different, randomly chosen, distributions for bias currents and g_θ.

Robustness of the correlation pattern to changes in cellular and network properties

Is the correlation pattern still observed if some features of the model are modified? Our hypothesis is that as long as the two key features of the model—recurrent excitatory connectivity and slow activity-dependent depression of network excitability—are present, the correlation pattern will be observed. To test this, we alter some features of the network—one at a time—and check if the same correlation pattern is present. Note that we limit the scope of this study to all-to-all and random connectivity patterns.

First, we change the connectivity of the network. We do not consider networks with ordered topologies because there is no common structure in the many developing and other hyperexcitable networks that exhibit the correlation pattern (O'Donovan 1999). Instead, we replace the all-to-all coupling connectivity of our network model by random connectivity whereby each neuron projects to 10% of the population. This randomly connected sparse network exhibits episodic activity with a high degree of variability at episode onset, resulting in the same robust correlation pattern as the fully connected networks (Fig. 3B). The same robust correlation pattern is also obtained with connection probability decreased to 5%.

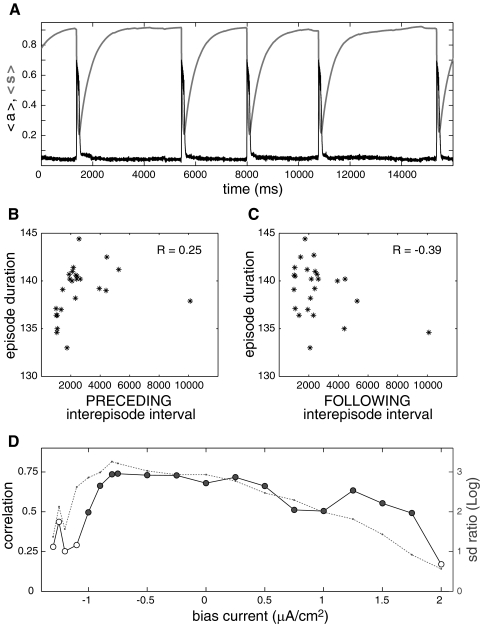
Next, we replace the integrate-and-fire neurons (with all-to-all coupling) with Hodgkin-Huxley–type neurons (see appendix for the formulation of this model). That is, we change the neuronal model from an integrator to a resonator (Izhikevich 2001). This network requires a high degree of heterogeneity in the distribution of input current to generate episodic activity, and the activity is less regular (both onset and termination are more variable than with I&F neurons). The baseline level can also vary during the interepisode interval (Fig. 4, A and B) in some simulations, which was never observed with the network of I&F neurons with all-to-all coupling. Nevertheless, as shown in Figs. 3C and 4, C and D, this model network still produces activity with the variability of 〈s〉 much higher at episode onset (Fig. 4E) than episode termination (Fig. 4F), leading to a robust correlation between episode duration and the preceding, but not the following, interepisode interval.

Fig. 4.

Episodic activity and correlation pattern of the excitatory network of Hodgkin-Huxley (HH) neurons with synaptic depression and all-to-all coupling. A: time courses of activity, 〈a〉 (thin, black curve), and average recovery from depression, 〈s〉 (thick, light green curve). B: “phase plane” trajectory. C: the correlation between episode duration and preceding interepisode interval is high. D: absence of correlation between episode duration and following interepisode interval. E: wide distribution of 〈s〉 values at episode onset. F: narrow distribution of 〈s〉 values at episode termination.

Finally, we change the slow negative feedback process that terminates the episodes. For this last model, synapses do not depress, but each individual neuron has a slow outward current with activation θ_j (see methods). This model generates episodic activity similar to the model using synaptic depression (Fig. 5A), but with the average cellular depression $\langle \theta \rangle =\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{\theta }_{\mathrm{j}}}$ increasing during an episode and recovering (decreasing) during the interepisode interval. This network model tends to produce very regular activity because the adaptation process slows down the faster firing cells (the cells with higher input current) more than the slower cells. This tends to homogenize the network. To limit this effect, we chose the conductance parameter for the adaptation process randomly, over a wide interval, for each cell. Simulation results for the model with cellular adaptation are shown in Figs. 3D and 5. Although the same pattern of correlation is generally observed, the variability at onset relative to termination is less (Fig. 5, E and F) than for the other model networks. In a minority of cases, this resulted in the absence of a significant correlation between episode duration and preceding interval or the presence of a significant correlation between episode duration and following interval (Fig. 3D). Thus the correlation pattern seems less robust in the model with cellular adaptation.

Fig. 5.

Episodic activity and correlation pattern of the excitatory network of I&F neurons with cellular adaptation and all-to-all coupling. A: time courses of activity, 〈a〉 (thin, black curve), and average adaptation 〈θ〉 (thick, light green curve). Note that the activity appears more regular than for the previous examples (Figs. 2 and 4). B: “phase plane” trajectory. C: the correlation between episode duration and preceding interepisode interval is high. D: absence of correlation between episode duration and following interepisode interval. E: distribution of 〈θ〉 values at episode onset. F: narrow distribution of 〈θ〉 values at episode termination.

Emergence and disappearance of the correlation pattern as cellular excitability is increased

The results shown in Figs. 2–4 show that simple excitatory network models with slow synaptic depression can generate episodic activity with the observed correlation between episode duration and interepisode interval. We note that episodic activity is observed for a wide range of parameter values (Vladimirski et al. 2008) and that we did not need to tune parameter values to obtain the correlation pattern shown in the preceding sections, suggesting that it is also a robust feature of the episodic activity generated by these networks. In this section, we focus on the all-to-all coupled network of Hodgkin-Huxley–type neurons with synaptic depression (Figs. 3C and 4) and test the robustness of the correlation pattern on parameter values. A complete parameter study is outside the scope of this paper; here, we describe the effects of cell excitability on the correlation pattern, because this is motivated by experimental findings (Menendez de la Prida et al. 2006).

We noticed that simulations resulting in low correlations between episode duration and preceding interepisode interval are often the ones for which cell excitability (i.e., input current) in the network is the lowest. This is in agreement with experimental findings from disinhibited hippocampus slices (Menendez de la Prida et al. 2006), which showed no correlation between episode duration and interepisode interval, unless cellular excitability was increased using a high extracellular concentration of potassium ions. Figure 6A shows the time course of network activity and slow recovery from depression for a network with all cells receiving an additional hyperpolarizing current of −1.2 μA/cm². In this case, there are practically no episodes starting before the recovery from synaptic depression reaches its asymptotic level. Thus all episodes start around the same value of 〈s〉, so they all have a similar duration regardless of the preceding interepisode interval. Therefore there is no correlation between episode duration and preceding interepisode interval (Fig. 6B) or episode duration and the following interepisode interval (Fig. 6C).

Fig. 6.

Dependence of the correlation pattern on cell excitability. A: time course of activity (〈a〉, black) and recovery from depression (〈s〉, thick light green) for a network of 100 HH neurons with all-to-all coupling and synaptic depression. Input currents to the neurons are uniformly distributed on the interval [−10, 5], and an additional bias current of −1.2 μA/cm² is applied to all cells of the network. Note that episodes occur after random amounts of time once 〈s〉 has reached its maximal value. B: absence of correlation between episode duration and preceding interepisode interval. C: absence of correlation between episode duration and following interepisode interval. D: correlation coefficient between episode duration and preceding interepisode interval (circles, black line) and variability of 〈s〉 at episode onset relative to variability at episode termination (dotted green line), plotted as a function of the bias current. The relative variability is measured as the log of the ratio of the SD of 〈s〉 at onset and at termination. For the most negative bias currents (≤ −1 μA/cm²), the correlation is not significant because the variability of 〈s〉 at episode onset is low. As the variability at onset increases, the correlation between episode duration and interepisode interval becomes significant and remains high until higher values of bias current lead to lower relative variability of 〈s〉 at episode onset.

As the additional bias current is made less hyperpolarizing, episodes can more often start before maximal recovery is reached, increasing the variability of 〈s〉 at episode onset (Fig. 6D, green dotted curve representing the ratio between the SD of 〈s〉 at onset and the SD of 〈s〉 at termination). As 〈s〉 at onset becomes more variable relative to 〈s〉 at termination, the episodes that start at higher 〈s〉 have a longer duration. That is, a correlation between episode duration and interepisode interval appears (Fig. 6D, •). As the bias current is increased to depolarizing values, episode onset is facilitated and becomes less variable relative to episode termination. The correlation between episode duration and preceding interval therefore becomes lower. Further increasing the bias current led to activity with less clearly defined episodes, so the detection of episode onset and termination became ambiguous and the correlation pattern could not be determined. Although not shown here, we obtained similar results with I&F neurons, that is, low correlation (or no correlation) for very low cellular excitability, strong correlation at intermediate excitability and again lower correlation for high cell excitability.

Thus the mechanism of synaptic depression reproduces the experimental finding that a correlation pattern emerges when the cellular activity level of a hyperexcitable network is increased. Also, the correlation pattern is robust to changes in cell excitability, because a significant correlation is observed for most of the range of bias current that supports episodic activity. We obtained similar results when we varied synaptic efficacy instead of cellular excitability (data not shown). This robustness to parameter values, together with the robustness to model choices (Fig. 3), imply that the correlation pattern is a general feature of excitatory networks with activity-dependent depression.

Mean field model with noise reproduces the correlation pattern

Figures 2, 4, and 5 suggest that the mean activity and mean depression variables may provide sufficient information to understand the correlation patterns generated by the network models. Thus we now use a mean field model that describes the global activity of the whole population in the network in terms of the mean firing rate (averaged over the population and over the synaptic time scale) a and a mean depression variable s (see methods). Although such models may not capture all the effects of cellular heterogeneity in a network (Vladimirski et al. 2008), they qualitatively describe many features of episodic activity (Latham et al. 2000; Tabak et al. 2000) and can be easily analyzed.

We modified a mean field model of an excitatory network with synaptic depression (Tabak et al. 2006) by adding noise to the mean activity to generate variability in episode duration and interepisode interval (methods). This noise is meant to reflect coincident firing of a subset of neurons in the finite network population. If several cells spike within a short period of time, they create a small bump in the mean activity level in the network. The noise we add to the global activity therefore represents the fluctuations caused by correlated activity of subsets of the network (Doiron et al. 2006; Holcman and Tsodyks 2006).

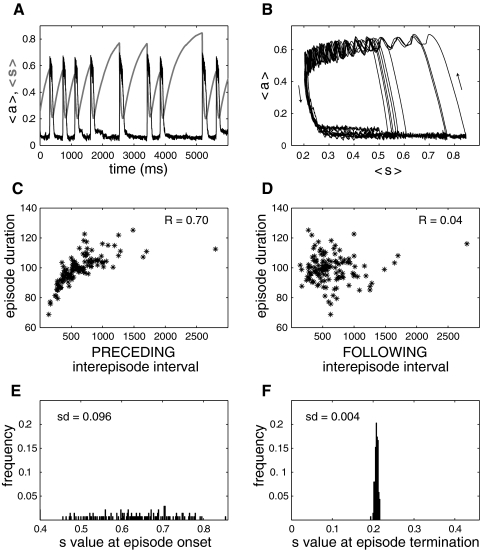
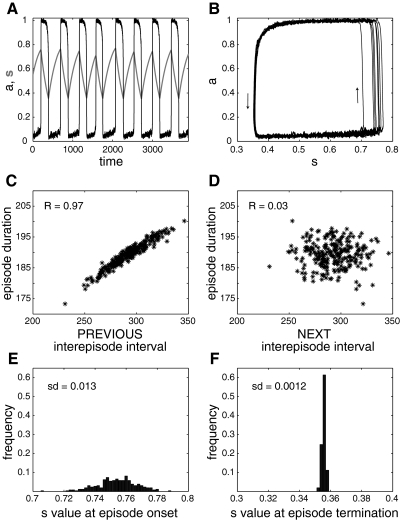
First, we show that the mean field model with noise generates episodic activity with correlation patterns similar to those of the network models used above. Figure 7 shows the activity and correlation patterns produced by the mean field model. The activity is episodic (Fig. 7A), with slow oscillations of the synaptic recovery variable s. Furthermore, the variability of s at episode onset is much greater than its variability at episode termination (Fig. 7, A, B, E, and F), leading to a correlation between episode duration and preceding—not following—interepisode interval (Fig. 7, C and D). These results are qualitatively similar to the ones obtained for the network model with spiking neurons (Fig. 2). Therefore the mean field model captures not only the mechanism for generating spontaneous episodic activity but also for producing the observed correlation pattern.

Fig. 7.

Episodic activity and correlation pattern of the excitatory mean field model with synaptic depression. A: time courses of activity, a (thin, black curve), and average recovery from depression, s (thick, light green curve). The value of s at episode onset varies from episode to episode, whereas the value of s at episode termination remains almost constant, as for the network of spiking neurons (Fig. 2). Noise amplitude was 0.01. B: phase plane representation, where a is plotted as a function of s for each time point shown in A. C: the correlation between episode duration and preceding interepisode interval is high. D: absence of correlation between episode duration and following interepisode interval. E: wide distribution of s values at episode onset. F: narrow distribution of s values at episode termination. These distributions compare with the ones shown in Figs. 2 and 4.

Qualitative explanation for the correlation pattern

We now take advantage of the simplicity of the mean field model to perform a geometric analysis of the effects of the noise that lead to the correlation pattern shown in Fig. 7, C and D. More sophisticated tools have been used previously (Lim and Rinzel 2010; Pedersen and Sorensen 2006). Our analysis uses the fact that one model variable (a) is fast, whereas the other (s) is slow.

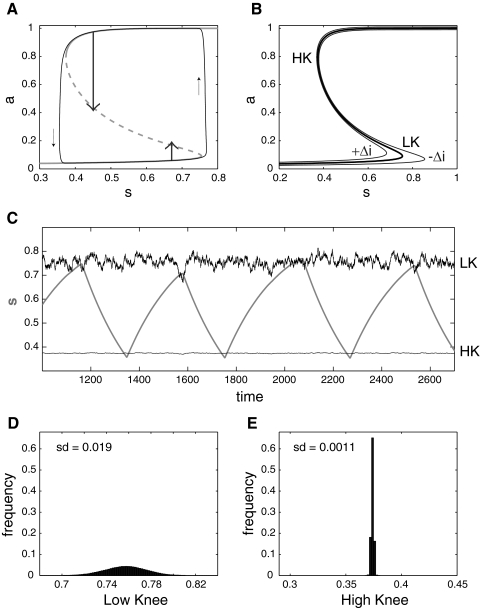
The mechanism underlying episodic activity in the deterministic version of our mean field model can be visualized using a phase portrait (Fig. 8A). We start by treating s as a constant. The S-shaped curve represents the possible steady states of the activity for each value of s; this is the a-nullcline and is defined by a = a_∞(wsa − θ₀), where a_∞ is the steady-state output function of the network (see methods). For a range of values of s, there are three steady states, one on the low branch with a ≈ 0 (the network is silent), one on the high branch with a ≈ 1 (network active), and one on the middle branch (dashed). Unlike the high and low steady states, the steady state on the middle branch is unstable and serves as a threshold for the network activity: at a given s, if a is above the threshold value, the activity will quickly equilibrate to the high state; if a is below threshold, it will fall to the low state. The S-shaped steady-state curve allows hysteresis to occur when s is allowed to vary. Thus when s slowly varies (according to Eq. 7), the activity becomes episodic, switching between the high and low branch of the a-nullcline. For example, when activity is high, synapses depress so s decreases. The state of the network, represented by a point in the (a, s) plane, tracks the high branch moving to the left, until it reaches the point where the high and middle branch meet [high knee (HK)]. Beyond this point, there is only one steady state, on the lower branch. Thus activity falls down and the system then tracks the low branch moving to the right, as s recovers. This is the silent phase. Beyond the point where the low and middle branches meet [low knee (LK)], the system jumps back to the high branch, starting the next episode, and the cycle repeats.

Fig. 8.

Phase plane argument for higher variability at episode onset. A: the trajectory of the deterministic model tracks low and high branches of the a-nullcline (the S-shaped curve). Episode onset and termination occur at the knees of the S-curve: LK, low knee, the transition point from silent to active phase; HK, high knee, the transition point from active to silent phase. Note that the trajectory slightly overshoots the knees. When the system is close to the low knee during the silent phase, a small perturbation (short upward arrow) brings it above threshold (dashed portion of the S-curve). When the system is close to the high knee during the episode, a stronger perturbation (long downward arrow) is needed to bring it below threshold. B: effect of an input on the a-nullcline. Thick curve, control position as in A; thin curves, effect of small input ± Δi with Δi = 0.01. The low knee is more affected than the high knee. The ratio of their horizontal displacements is given by Δs_lk/Δs_hk = (s_lk/s_hk)(a_hk/a_lk) = 17.4 for the parameters given in Table 2. C: portion of the time course of s from Fig. 7A (thick green curve), together with the time courses of the knees positions s_lk (LK) and s_hk (HK). The knees positions are filtered according to τ_kdLK/dt = s_lk − LK (and similarly for the high knee). Episode onset occurs when s passes above s_lk, whereas episode termination occurs when s falls below s_hk. D: distribution of all s_lks obtained during the entire simulation. E: distribution of all s_hks obtained during the entire simulation. The ratio of their SD was 17.4. Compare these distributions with the distributions shown in Fig. 7, E and F.

How does this picture change when noise is added to the system? We first consider perturbations to the deterministic system and ask whether a sudden input that provokes a jump in activity level can make the system switch between the active/silent phases. In Fig. 8A, we consider two cases, where the system is in either the active or the silent phase and approaching the transition point (HK or LK). For the perturbation to induce a transition, it must bring the system across the middle branch. If the system is in the silent phase, a small jump in the activity will successfully bring it above threshold (upward arrow) and thus switch it to the active state. On the other hand, if the system is in the active phase, a comparatively large decrease in activity will be necessary to bring it below threshold (downward arrow), because the a-nullcline (the S-curve) has a rounder shape at the high knee. Thus it is more difficult to perturb the system from the active to silent phase than from the silent to the active phase. This implies that noise of a given amplitude will be able to initiate an episode of activity for a relatively wide range of s values compared with the range of s values where episodes terminate.

However, this is not the only factor explaining the higher variability of s values at episode onset compared with episode termination. The noise term is in the differential equation describing activity. To understand its contribution in the framework of deterministic dynamical systems, we consider noise as an extra input to the network, an input that varies quickly with time but whose effects are integrated over time. If that extra input was constant, Δi, it would affect the shape of the a-nullcline, now defined by a = a_∞(wsa − θ₀) + Δi. This affects the low knee of the S-curve more than the high knee, as shown on Fig. 8B. That is, an input to the network has a greater effect on the transition point at episode onset than at episode termination. If Δi is small, the change in the horizontal position of the knee, Δs_k, is given approximately by Δs_k/Δi = −s_k/a_k, where s_k is the value of s at the knee, and a_k is the activity level at the knee (as shown in appendix). Thus the ratio of the changes in the low and high knee postitions caused by a small perturbing input is Δs_lk/Δs_hk = (s_lk/s_hk)(a_hk/a_lk). For the case shown in Fig. 8B, this ratio is 17.4, so the effect of an input on the low knee is ∼17 times greater than the effect on the high knee.

If the input is not constant but noisy, the a-nullcline is constantly deformed. As shown in Fig. 8B, this will have a much greater effect at episode onset than episode termination. As an illustration, in Fig. 8C, we plot the time course of the positions of the knees s_lk and s_hk on the s-axis during the simulation shown in Fig. 7A (a portion of the time course of s from Fig. 7A is also shown as a thick green curve). Because the knees' positions can vary with a large amplitude, for illustration purposes, we filtered them according to ${\tau }_{\mathrm{k}}\frac{dLK}{dt}=s_{\mathrm{lk}}-LK$, where LK is the filtered low knee position (and with a similar equation for the high knee HK), with a time constant τ_k = 10. It is clear that the low knee varies more widely than the high knee, with a ratio of SD sd(LK)/sd(HK) = 17.4, as predicted from our analysis with a small constant input (Fig. 8B). Consequently, during the silent phase, if the low knee's position s_lk falls below the current value of s and does not immediately come back up, an episode can be triggered even if s is far from having fully recovered. Similarly, if the knee's position moves up, the occurrence of an episode can be delayed. These early or delayed transitions occur to a much lesser extent for episode termination. Thus the difference in the spread of the distribution of the low and high knee locations (Fig. 8, D and E) can explain the difference in the spread of the values of s at episode onset and termination (Fig. 7, E and F).

Finally, we note that the higher sensitivity of the lower knee to perturbations (Fig. 8B) does not occur for a model where the slow negative feedback process is cellular adaptation instead of synaptic depression (Tabak et al. 2006). In the case of cellular adaptation, both knees are equally affected by noise, so the correlation pattern mainly depends on the shape of the a-nullcline, which in turn depends on the shape of the network steady state input/output function a_∞. For a network of I&F neurons, a_∞ has a sharp increase at low activity and a smooth saturation at high activity, which results in a nullcline with a flatter shape at the bottom (sharp low knee, round high knee, as in Fig. 8A). This leads to a significant correlation between episode duration and preceding, but not following, interval (data not shown, but observed for the network case, Fig. 5, C and D). However, for a symmetrical a_∞ such as the one used here, the shape of the a-nullcline is symmetrical too, unlike the nullcline obtained with synaptic depression (Fig. 8A). In that case, noise can induce transitions between active to silent phase and silent to active phase with equal probability. This results in a weak but significant correlation between episode duration and both the preceding and following intervals (Lim and Rinzel 2010; Tabak et al. 2007). Thus when the slow negative feedback process is cellular adaptation, the correlation pattern may depend on network parameters. In contrast, for synaptic depression, even if we choose a_∞ such that the S-shaped nullcline is symmetrical, a strong correlation between episode duration and preceding (not following) interval is still observed because of the high sensitivity of the low knee to perturbations.

DISCUSSION

The correlation between episode duration and previous—not following—interepisode interval may represent a signature of developing networks (O'Donovan 1999), but its cause has not been studied until now. Here, we show that two characteristic features of developing networks are sufficient to produce activity with this correlation pattern: recurrent excitatory connectivity and activity-dependent synaptic depression. We show that this pattern can emerge naturally in diverse developing networks because the correlation pattern is robust to changes in connectivity or cell properties. The correlation pattern is a direct consequence of the high sensitivity to noise of episode onset compared with episode termination.

What causes higher variability at episode onset?

In developing spinal and hippocampal networks, episodes (spinal cord) or network bursts (hippocampus) of activity are stochastic events, triggered by random fluctuations in basal activity (Menendez de la Prida and Sanchez-Andres 1999; Wenner and O'Donovan 2001). In the heterogeneous networks of excitatory neurons with synaptic depression used here, episode onset only occurs once a small subpopulation of neurons with intermediate excitability becomes active (Tsodyks et al. 2000; Vladimirski et al. 2008; Wiedemann and Luthi 2003). The recruitment of this subpopulation seems to be a stochastic event, requiring the synchronous firing of some of the spontaneously spiking cells. Thus the variability observed at episode onset results from heterogeneity (Thivierge and Cisek 2008) of cell excitability. In comparison, episode termination is highly predictable, the variability of the average depression variable being about one order of magnitude less at episode termination than episode onset.

To explain this asymmetry between episode onset and episode termination, we used a mean field model with noise. The stochastic recruitment of a subpopulation of neurons caused by variations in the degree of synchrony between spontaneously firing cells cannot be incorporated directly in a simple mean field model. Instead, we modeled the varying degree of correlated activity by adding noise to the mean activity a (Holcman and Tsodyks 2006; Venzl 1976). The mean field model with noise exhibits a similar correlation pattern and asymmetry between episode onset and termination as the network models. Therefore details of individual neuron interactions are not necessary to produce the correlation pattern, which simply results from population dynamics and activity fluctuations.

Here, we considered noise as either a perturbing stimulus or a rapidly varying input to gain intuition into the production of the correlation pattern using phase plane analysis. This geometric analysis suggests that the greater variability of the level of recovery from depression at episode onset is caused by two reasons: 1) a smaller stimulus is required to reset the system from the silent to active than from active to silent phase (Fig. 8A); and 2) the sensitivity of the transition point to perturbations is one order of magnitude greater at episode onset than termination (Fig. 8B). Note that 1) is dependent on the shape of the network steady state input/output relationship, which itself is determined by the individual cell properties, degree of heterogeneity, and synaptic properties. On the other hand, 2) requires that the slow process that terminates the episode be a divisive factor, like synaptic depression.

If the slow negative feedback process is instead subtractive, like cellular adaptation, the correlation pattern can only be present because of 1). Thus for a network with cellular adaptation, the presence of the correlation pattern is not a robust feature and depends on cell and synaptic properties. If the network input/output function is a symmetrical sigmoid such as the one used in our mean field model, the correlation pattern is not present (Lim and Rinzel 2010; Tabak et al. 2007). The network simulations with cellular adaptation exhibit the correlation pattern (Fig. 5) because the input/output function of the network is asymmetrical, being much sharper at low activity than high activity levels. Thus if the episodic activity generated by an excitatory network does not exhibit the correlation pattern, our results suggest that the slow feedback process responsible for episode termination might be of the subtractive type, i.e., not synaptic depression.

Although these results were obtained using the framework of deterministic dynamics to provide an intuitive geometric explanation for the correlation pattern, we note that a stochastic analysis, in the context of single cell oscillations, provides similar results (Lim and Rinzel 2010). This analysis shows that the spread of the distribution of the slow variable at the transitions between silent and active phases (such as Fig. 7, E and F) depends on two factors. These two factors are equivalent to points 1) and 2) above (shown in appendix).

Does the mechanism described here occur in biological networks?

Could a different mechanism than the one presented here produce the correlation pattern? We are aware of one alternative mechanism that might generate a similar correlation pattern. Suppose that there is a slow, unobserved rhythm that underlies the appearance of episodes of activity. Episodes can occur at any phase of this rhythm, but their likelihood and duration are greater before or at the peak of the slow underlying rhythm. An episode preceded by a short silent phase would more likely occur before the peak of the slow oscillation and would be shorter than an episode occurring after a long silent phase (more likely to occur around the peak), hence a correlation between episode duration and preceding silent phase. On the other hand, episode duration would not affect the following silent phase, so little correlation would be observed between them. Thus this mechanism might reproduce the observed correlation pattern, if certain conditions are met. However, the presence of the underlying oscillation was not detected in data from the chick embryonic spinal cord. This mechanism also requires more assumptions than the mechanism presented here.

The mechanism presented in this paper is simple and produces a correlation pattern that is robust, mostly independent of anatomical or biophysical details or parameter values. We used all-to-all coupling and random coupling (as well as more ordered architecture, data not shown), integrate-and-fire, and Hodgkin-Huxley neurons and found that for all of these networks the correlation pattern was produced in a similar way. Parameter tuning was not required, and we found that a wide range of parameter values supporting episodic activity produced the correlation pattern. In short, the correlation pattern emerges naturally from excitatory model networks with slow activity-dependent synaptic depression. This mechanism is therefore likely to occur in biological networks regardless of the actual biophysical processes found in these networks. Synaptic depression may be caused by transmitter depletion (Jones et al. 2007; Staley et al. 1998), chloride extrusion (Chub and O'Donovan 2001; Marchetti et al. 2005), or activation of GABA_B receptors (Menendez de la Prida et al. 2006), but these different biophysical processes all underlie the same basic mechanism and therefore should all contribute to produce the same correlation pattern.

Furthermore, our model makes predictions, some of which have been verified experimentally. The high sensitivity to bias input at episode onset exhibited by the mean field model translates into a high sensitivity of the interepisode interval (but not episode duration) to cell excitability (Tabak et al. 2006). This is also observed in the network models (data not shown). Thus if developing and other hyperexcitable networks generate the correlation pattern according to the mechanism described here, they should respond to acute changes in experimental manipulations affecting cell excitability with a large change in interepisode interval but a smaller change in episode duration. This has been shown in bursting hippocampal networks (Staley et al. 1998). Our model also predicts (Fig. 6) that the correlation pattern may be low or absent when cell excitability is so low that most episodes do not start before full recovery. This is observed experimentally in hyperexcitable hippocampus networks that do not exhibit the correlation pattern unless cell excitability is raised by increasing the extracellular potassium concentration (Menendez de la Prida et al. 2006). More generally, the correlation pattern is observed for most of the range of parameter values that support episodic activity, except toward the edges of that range (i.e., at high or low network excitability). This predicts that the correlation pattern may be weak or absent early in development when the activity just emerges or later in development as spontaneous activity disappears.

As developing networks mature, a refinement of the synaptic topology takes place, creating specific network structures. This change in structure might affect the correlation pattern. Replacing long-range, random connections with short-range connections can switch the activity pattern of a network from synchronized episodes to propagating waves (Netoff et al. 2004). Although spontaneous waves in two-dimensional networks may exhibit the correlation pattern typical of developing networks (Grzywacz and Sernagor 2000), the effect of network structure on the correlation pattern may weaken some of our predictions and should be studied.

Significance of the findings

Neuronal networks are complex and plastic, and they display a variety of structures and functions. Can we find unifying concepts of neuronal network activity? This study strengthens the view that developing networks may have a common mode of operation. Not only does the combination of fast excitation and slow activity-dependent depression generate spontaneous episodic activity in model networks, but it also naturally produces the correlation pattern observed in many developing networks, regardless of model details. This suggests that networks with different architectures, different components, and different functions all share a common mechanism of operation early in development. This could form the basis of a general framework for the study of neuronal network operations.

As networks mature, GABAergic and glycinergic transmission switch from functionally excitatory to inhibitory, silencing episodic activity. This switch, together with the refinement of synaptic connectivity, leads to different structures and functions in the various networks. Nevertheless, mechanisms for rhythm generation in many mature networks rely on recurrent excitation with slow synaptic depression or cellular adaptation. This is the case of the slow wave cortical oscillations during sleep (Compte et al. 2003; Sanchez-Vives and McCormick 2000), the inspiratory rhythm (Rubin et al. 2009), and the pulsatile secretion of oxytocin during lactation (Rossoni et al. 2008). The same mechanism also readily emerges when the balance between excitation and inhibition is broken (Darbon et al. 2002; Golomb et al. 2006; Staley et al. 1998). Interestingly, nonrhythmic cortical circuits may also rely on a recurrent excitatory core (Yuste et al. 2005). We speculate that much progress in our understanding of neuronal networks may be obtained by asking how network structure and inhibitory connectivity alters the basic rhythm generation mechanism found in immature networks.

GRANTS

This work was supported by National Institute on Drug Abuse Grant DA-19356.

APPENDIX

Network model with Hodgkin-Huxley–type neurons

Here, we use a reduced Hodgkin-Huxley model for each neuron with two variables: voltage (V) and activation of delayed rectifier potassium current (n) (Rinzel 1985). Each neuron is described by the following two equations $C\frac{d{V}_{\mathrm{i}}}{dt}=-g_{\mathrm{\text{leak}}}\left(V_{\mathrm{i}}-V_{\mathrm{\text{leak}}}\right)-{\overline{g}}_{\mathrm{Na}}{m}_{\infty }^3\left(V_{\mathrm{i}}\right)\left(0.8-n_{\mathrm{i}}\right)\left(V_{\mathrm{i}}-V_{\mathrm{\text{leak}}}\right)-{\overline{g}}_{\mathrm{K}}{n}_{\mathrm{i}}^4\left(V_{\mathrm{i}}-V_{\mathrm{\text{leak}}}\right)+I_i-g_{\mathrm{\text{syn}}}\left(V_i-V_{\mathrm{\text{syn}}}\right)$ $\frac{d{n}_{\mathrm{i}}}{dt}={\alpha }_{\mathrm{n}}\left(V_{\mathrm{i}}\right)\left(1-n_{\mathrm{i}}\right)-{\beta }_{\mathrm{n}}\left(V_{\mathrm{i}}\right)n_{\mathrm{i}}$ where the synaptic conductance is given by

$$g_{\mathrm{\text{syn}}}=\frac{{\overline{g}}_{\mathrm{\text{syn}}}}{N}{\displaystyle {\sum }_{j=1}^N{a}_{\mathrm{j}}{s}_{\mathrm{j}}}$$

as for the integrate-and-fire network model, with a_j (synaptic drive from neuron j) and s_j (depression variable for neuron j) calculated as described in methods (Eq. 3 and 4) with the Π(t) functions now replaced by Π(V) = 1/(1 + e^{(Vthresh − V)/kv}). Voltage unit is millivolts, time unit is milliseconds, and the capacitance, conductances, and currents are normalized with respect to surface (with C = 1 μF/cm²). Integration time step was 0.01 ms. A computer code, along with all parameter values, is available for download from www.math.fsu.edu/∼bertram/software/neuron.

Sensitivity of the knees' position to perturbation

We add a perturbing input i to the network activity equation as follows

$$\frac{da}{dt}=-a+a_{\infty }\left(wsa-{\theta }_0\right)+i$$ (A1)

and ask how this input affects the horizontal location of the knees (i.e., the value of s at episode onset and termination), as shown on Fig. 8B. The a-nullcline is the curve s(a) for which a is at steady state (da/dt = 0). Thus it is defined by

$$a-i=a_{\infty }\left(wsa-{\theta }_0\right)$$ (A2)

To find how this curve is affected by i, we differentiate Eq. A2 with respect to i. This results in

$$\frac{\partial a}{\partial i}-1=\left(ws\frac{\partial a}{\partial i}+wa\frac{\partial s}{\partial i}\right)a_{\infty }^{\text{'}}\left(wsa-{\theta }_0\right)$$ (A3)

The knees are the special solutions of Eq. A2 for which the two sides of the equation are not only equal but have the same slope, that is, same derivative with respect to a. Thus at the knees, differentiating Eq. A2 gives

$$1=ws{a}_{\infty }^{\text{'}}\left(wsa-{\theta }_0\right)$$ (A4)

Substituting in Eq. A3, we obtain

$$\frac{\partial s}{\partial i}=-\frac{s}{a}\left(\mathrm{\text{at the knees}}\right)$$ (A5)

We see that a knee's position can be highly sensitive to i if activity at the knee is very low; this is the case for the low knee. Activity is high at the high knee, so the high knee is not very sensitive to i (cf. Fig. 8B). This is true regardless of the shape of the network output function a_∞. Here we only assume that a_∞ is differentiable.

Distribution of the slow variable at the transitions

Lim and Rinzel reformulated the equation describing the dynamics of the fast variable (a in our case) using a potential function U(a,s) = ∫[a − a_∞(wsa − θ₀)]da. For any fixed s, this function has a double-well shape. The stable steady states of the activity now correspond to the minima of the potential and the unstable (middle) steady state corresponds to the maximum separating the two wells. Noise-induced transitions between the low and high states of activity pictured on Fig. 8A are now transitions between the two potential wells. The distribution of the slow variable at the transitions can be obtained using the probability of transitions above the energy barrier ΔU(s) (Kramers rate). If the noise amplitude is small such that all transitions occur around s = s^* and the time scale of s is close to the time scale of the transitions, the SD of s at the transitions can be approximately expressed as

$$sd=K{n}^2/\left|\frac{d\Delta U\left(s*\right)}{ds}\right|$$ (A6)

where K is a constant and n is the noise amplitude. The denominator represents the sensitivity of the depth of the potential well to the slow process, which is

$$\frac{d\Delta U\left(s*\right)}{ds}={\displaystyle \int \left[wa{a}_{\infty }^{\text{'}}\left(wsa-{\theta }_0\right)\right]}da$$ (A7)

where the bounds of integration are the values of a at the bottom of the well and at the top of the energy barrier. Because the transitions occur near the knees of the a-nullcline, we can use Eq. A4 and substitute it in Eq. A7 to get $\frac{d\Delta U\left(s*\right)}{ds}\approx {\displaystyle \int \left(a/s\right)da}$. Making the approximation that a and s are close to their values at the knees before the transition, we finally find that the SD of s at the transitions is proportional to $\frac{1}{\Delta a}\frac{s_k}{a_k}$.

The first term is the inverse of the size of the jump required to cross the middle steady state shown in Fig. 8A, and the second term is the absolute sensitivity of the knee position to a perturbation (cf. Eq. A5) represented graphically in Fig. 8B. Both terms are larger at low activity level, so the transition from silent to active phase is more sensitive to noise than the transition from active to silent phase.

The second term is the largest and therefore the asymmetric sensitivity of the knees to perturbations is the main factor in the asymmetric sensitivity of the transitions to noise. We emphasize that the term s/a appears because the slow negative feedback process is of the divisive type. If the model uses cellular adaptation (subtractive feedback) instead of synaptic depression as the slow process, the term s/a is replaced by the parameter w (the connectivity), so there is no asymmetry between high and low activity. In that case, the only factor that can cause asymmetry in the sensitivity to noise is 1/Δa.