Abstract
A new, region-based mathematical model of the urine concentrating mechanism of the rat renal inner medulla (IM) was used to investigate the significance of transport and structural properties revealed in recent studies that employed immunohistochemical methods combined with three-dimensional computerized reconstruction. The model simulates preferential interactions among tubules and vessels by representing two concentric regions. The inner region, which represents a collecting duct (CD) cluster, contains CDs, some ascending thin limbs (ATLs), and some ascending vasa recta; the outer region, which represents the intercluster region, contains descending thin limbs, descending vasa recta, remaining ATLs, and additional ascending vasa recta. In the upper portion of the IM, the model predicts that interstitial Na+ and urea concentrations (and osmolality) in the CD clusters differ significantly from those in the intercluster regions: model calculations predict that those CD clusters have higher urea concentrations than the intercluster regions, a finding that is consistent with a concentrating mechanism that depends principally on the mixing of NaCl from ATLs and urea from CDs. In the lower IM, the model predicts that limited or nearly zero water permeability in descending thin limb segments will increase concentrating effectiveness by increasing the rate of solute-free water absorption. The model predicts that high urea permeabilities in the upper portions of ATLs and increased contact areas of longest loop bends with CDs both modestly increase concentrating capability. A surprising finding is that the concentrating capability of this region-based model falls short of the capability of a model IM that has radially homogeneous interstitial fluid at each level but is otherwise analogous to the region-based model.
Keywords: countercurrent system, NaCl transport, urea transport, mathematical model
despite decades of sustained experimental and theoretical investigation (21, 29, 49, 54), the nature of the urine concentrating mechanism in the inner medulla (IM) of the mammalian kidney remains controversial. Recent experiments that combined the techniques of immunohistochemical localization and computerized three-dimensional reconstruction have revealed structural and transport properties in the rat kidney that likely impact the IM urine concentrating mechanism. These studies in the rat kidney have shown that 1) IM descending thin limbs (DTLs) have at least two or three functionally distinct segments; 2) most ascending thin limbs (ATLs) and about half of the ascending vasa recta (AVR) are arranged among clusters of collecting ducts (CDs), which form the organizing motif in the upper 3–3.5 mm of the IM, whereas other ATLs and AVR, along with aquaporin 1 (AQP1)-positive portions of DTLs and UT-B-positive descending vasa recta (DVR), are external to the CD clusters; 3) ATLs, AVR, CDs, and interstitial cells delimit interstitial microdomains within the CD clusters; and 4) many of the longest loops of Henle form bends that include subsegments that run transversely along CDs that lie within the terminal 500 μm of the papillary tip.
Previously, in a simple mathematical model of the IM, we incorporated the functional inhomogeneity of the DTLs into a “solute-separation, solute-mixing” mechanism, which may be regarded as a refinement of the “passive” mechanism proposed by Kokko and Rector (24) and by Stephenson (61). The fundamental principle of the passive mechanism is that sustained diffusive absorption of NaCl from the loops of Henle can be promoted by a favorable concentration gradient that is sustained by diffusive absorption of urea from CDs; the absorption of NaCl from loops, with little or no accompanying water absorption from loops, concentrates other medullary structures, and dilute ATL tubular fluid provides for a solute and water mass balance configuration that promotes the generation of an axial medullary gradient. Despite its similarity to the passive mechanism, the solute-separation, solute-mixing mechanism is distinctive in that 1) the lower 60% of sufficiently long DTLs need not osmotically equilibrate with the adjacent interstitium; 2) most NaCl absorption from loops of Henle occurs near loop bends; and 3) a high urea concentration in IMCD tubular fluid is maintained by active NaCl absorption, especially in the upper IMCD. The predictions of the mathematical model of the solute-separation, solute-mixing mechanism (30) are consistent with studies in rats by Pennell and coworkers (51) and with studies in transgenic mice (1, 2, 39, 59, 67, 77).
In a recent review (49), we suggested that the functional implications of the three-dimensional architecture of the IM may be understood in terms of three distinct countercurrent systems. Two are in the upper 3–3.5 mm of the IM: an intercluster system that is between clusters, and an intracluster system that is within clusters. A third countercurrent system is in the lower 1.5–2 mm (49) of the IM, where a clear distinction between the intra- and intercluster systems can no longer be identified. The three-dimensional architecture of the IM cannot be adequately represented in our previous simple mathematical model (30), which assumed that the composition of the interstitial fluid is homogeneous at each IM axial level.
To assess implications of the functional anatomy of the renal medulla, we have developed, in the present study, a new, region-based mathematical model of the urine concentrating mechanism of the rat IM. We have used that model to evaluate hypotheses, previously set forth by us (49), that are suggested by the functional anatomy. Among these hypotheses are 1) the absence of AQP1 in some segments of DTLs promotes concentrating function by eliminating the need to concentrate all fluid at each medullary level; 2) the organizing motif of tubules and vessels within and around CD clusters in the upper IM results in differing interstitial fluid composition within, and external to, the CD clusters; these differing concentrations are made possible by the nodal microdomains within the CD clusters; 3) in the innermost IM, loop bends that run transversely along CDs in the innermost IM enhance preferential solute mixing of NaCl and urea; and 4) specialized properties and functions of the three distinct countercurrent systems support the concentrating function of the IM.
The findings of this modeling study give general support to most aspects of these hypotheses.
MATHEMATICAL MODEL
Our mathematical model of the IM has a region-based formulation that is similar to that used previously in a model of the outer medulla (OM) (26, 27). Tubules and vasa recta are represented by rigid tubes that extend from the OM-IM boundary (x = 0) to the papillary tip (x = L). The model represents loops of Henle that turn at all levels of the IM, a composite DVR, two composite AVR, and a composite CD. The model is formulated for three solutes: NaCl, urea, and a nonreabsorbable solute; NaCl is represented by Na+. The nonreabsorbable solute, denoted “NR,” is assumed to be present only in significant amounts in the tubular fluid of the CD and is represented only in the CD tubular fluid. The model predicts fluid flow, solute concentrations, transepithelial water and solute fluxes, and fluid osmolality, as a function of medullary depth, in the tubules, vasa recta, and interstitium of the IM.
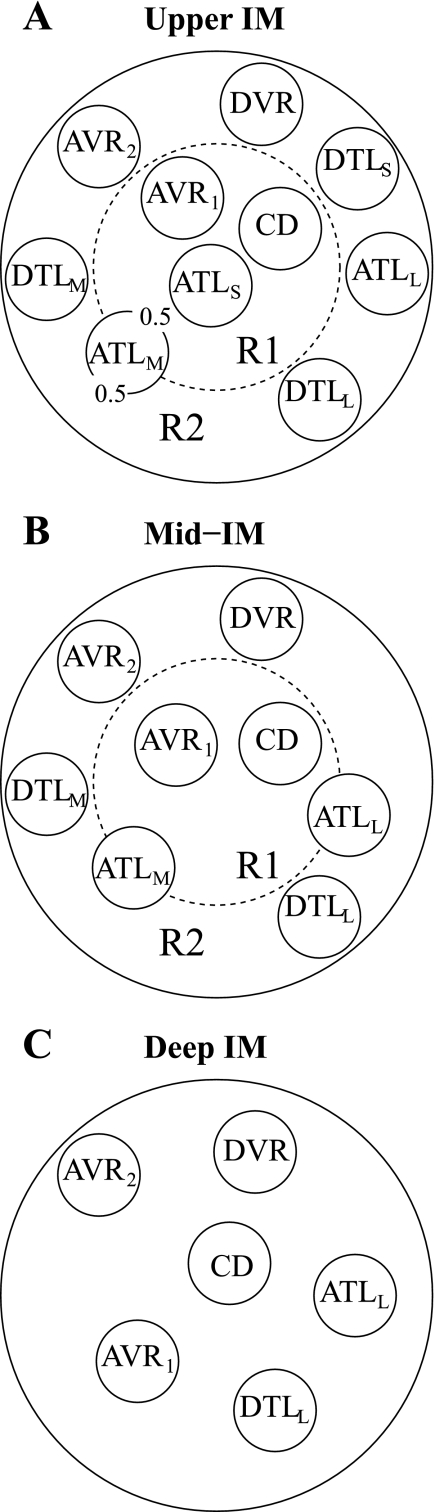
Radial organization with respect to a CD cluster, as revealed in anatomic studies of the rat IM (45, 46, 47, 48), is represented by means of two concentric regions: an intracluster region, denoted by “R1,” which represents a CD cluster; and an outer, intercluster region, denoted by “R2.” Model positions of tubules and vasa recta are shown in Fig. 1. The portion of each concentric region that is exterior to both tubules and vasa recta represents interstitial cells, interstitial spaces, and merged capillaries. At each medullary level, a concentric region is assumed to be a well-mixed compartment with which tubules and vasa recta interact. To represent the relative positions or distributions of the tubules and vasa recta and to simulate the potential preferential interactions among them, each tubule or vas rectum is assigned to a particular concentric region, or, in the case of the ATL, fractions of an ATL are distributed between two concentric regions. The tubules and vasa recta within a region interact with each other via that region's interstitial fluid, which has solute concentrations that differ from those in the other region.
Fig. 1.
Schematic diagram of a cross section through the upper inner medulla (IM; A), mid-IM (B), and deep IM (C), showing concentric regions and relative positions of tubules and vessels. Decimal numbers in A indicate relative interaction weightings with regions. R1, R2, concentric regions; DTLS, ATLS, descending/ascending limb of long loop of Henle that turns within the first millimeter of the IM; DTLM, ATLM, descending/ascending limb of long loop of Henle that turns within the mid-IM; DTLL, ATLL, descending/ascending limb of long loop of Henle that reaches into the deep IM; CD, collecting duct; DVR, descending vas rectum; AVR1 and AVR2 , two populations of ascending vasa recta.
Recent anatomic studies have shown that, in the upper 3–3.5 mm of the rat IM, clusters of IMCD provide the organizing motif around which loops of Henle and vessels are arranged (46, 48). Most ATLs and about half of the AVR are within these CD clusters, whereas other ATLs and AVR, along with AQP1-positive DTLs and DVR, are external to the CD clusters. Schematic diagrams of cross sections through the model IM are shown in Fig. 1, A–C. Two distinct populations of AVR were used to avoid having AVR straddle regional boundaries in the upper and mid-IM. Otherwise, unrealistic mixing between regions would be introduced, owing to the high solute permeabilities assumed for AVR.
In the model, we assume that 7,300 CDs and 12,667 loops of Henle extend into the IM; these loops correspond to one-third of a total of 38,000 loops of Henle per rat kidney (20); the remaining two-thirds of these loops turn within the OM (13). Thus the ratio of CDs to long loops, which we denote by nCD, is given by 7,300/12,667. We assume a ratio of DVR to long loops of nDVR = 2/3; a ratio of AVR1 (AVR that lie within the CD cluster) to long loops of nAVR1 = 2/3; and a ratio of AVR2 (AVR that lie outside the CD cluster) to long loops of nAVR2 = 7/3.
In the rat IM, the number of loops of Henle decreases as a function of increasing medullary depth (13). As in previous studies (30, 31), this loop configuration is represented by continuously distributed loops that have bends at all IM levels; see appendix a. Recent measurements in rats suggest a biexponential-like loop population (50); therefore, the fraction wl of loops remaining at IM depth x was approximated by
| (1) |
where a1 = 4.42, a2 = 8.016, a3 = 21.08, a4 = 304.8, and a5 = 0.7782.
The population of CDs also decreases as a function of increasing IM depth, as the CDs undergo successive coalescences. As in Ref. 30, we represent the effect of such coalescences on CD tubular area (13) by multiplying the CD radius by the fraction wCD of CDs remaining at a given medullary level x; that fraction was approximated by
| (2) |
As previously noted, the model represents the vasa recta by three tubes, one for DVR and two for AVR. Each tube represents a population of vasa recta that reach to differing levels of the IM. To represent the break-up of DVR into capillaries, a fraction of the DVR flow is directed into the interstitium at each medullary level; that fraction is computed from the population distribution of the DVR. Each of the DVR and AVR population distributions is given by
| (3) |
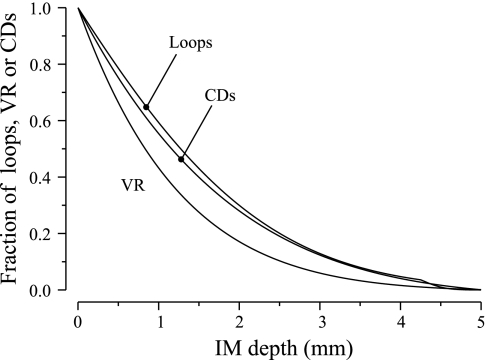
Anatomic studies indicate that in the final 1.5–2.0 mm of the IM, all or most vasa recta and capillaries are fenestrated, and that there are no urea transporter UTB-positive vessels (37, 47). That configuration is represented in Eq. 3 by allowing most of the DVR to break up into capillaries, and most of the AVR to originate before the final 2.0 mm. The loop of Henle, CD, and VR population fractions, as approximated by Eqs. 1–3, are shown in Fig. 2. In each of the two regions, net fluid accumulation from tubular reabsorption is taken up by that region's composite AVR.
Fig. 2.
Fractions of long loops of Henle, vasa recta (VR), or CDs remaining as a function of IM depth.
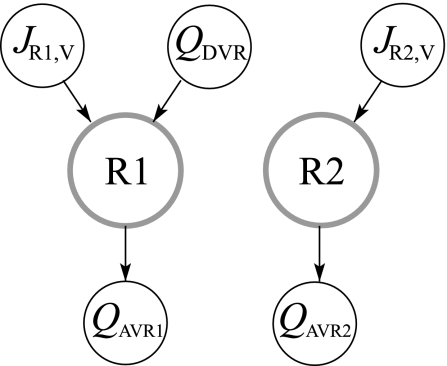
The region-based model framework was developed for the rat OM, first in a prototype model that used two concentric regions (26), and then in a more realistic four-region model (27). Most of the model equations in the present study are the same as the equations for the two-region OM model (26); the equations that differ most significantly from that study are summarized in appendix a. Some of the model equations embody the principle of mass conservation of solute and water; others represent transmural transport of solutes and water by means of single-barrier equations that provide a summary representation of double-barrier transepithelial or transendothelial transport. Transmural solute diffusion is characterized by solute permeabilities; active transport is represented by a saturable expression that has the form of Michaelis-Menten kinetics. Transport equations for water represent osmotically driven fluxes, except for AVR, where water flux is assumed to be pressure-driven advection through fenestrations. However, pressure is not explicitly represented; instead, water flux is computed by enforcing mass balance. A schematic representation of water conservation in the concentric regions is given in Fig. 3 (see appendix a).
Fig. 3.
Steady-state blood flow patterns at a given medullary level. QDVR, DVR blood source; JR1,V and JR2,V, net transtubular water fluxes from tubules and vasa recta into R1 and R2, respectively; QAVR1, QAVR2, net fluid accumulation drained by AVR1 and AVR2 from R1 and R2, respectively. Arrows indicate flow direction.
The axial length L of the model IM was taken to be 5 mm (20). Tubular diameters were assumed to vary as a function of medullary depth. Luminal diameters for loops of Henle were based on measurements by Koepsell et al. (23): DTL diameter decreases linearly, from 15 μm at the OM-IM boundary (i.e., at x = 0) to 11 μm at the beginning of the prebend segment, where it abruptly increases to 13 μm and remains at that value to the loop bend; along the ATL, diameter increases linearly from 13 μm at the loop bend to 20 μm at the OM-IM boundary. The CD diameter, based on measurements by Knepper et al. (20), increases from 20 at the OM-IM boundary to 25 μm at the papillary tip. The diameters of the DVR were taken to be 11 μm; the diameters of the AVR were assumed to decrease from 28 μm at the OM-IM boundary to 10 μm at the papillary tip (16, 41).
Base-case parameters for transtubular transport are given in Table 1. (In a series of parameter studies, we varied some of these parameters to assess implications of the functional anatomy of the IM; see results.) The model DTL of a loop of Henle that reaches beyond the first millimeter of the model IM was divided structurally and functionally into three segments. The first segment, which we call “LDL2” and which spans the initial 40% of the DTL, was assumed to be highly water permeable but NaCl impermeable. The second IM segment, which we call “LDL3,” corresponds to the AQP1-null segment of the DTL. The LDL3 segment was assumed to be impermeable to NaCl (15, 38) and to water (5). The third segment corresponds to the prebend segment, which was assigned the transport properties of the contiguous ATL segment. In a loop that turns within the first 4.5 mm of the model IM, the prebend segment has a length of 166.7 μm (45). The prebends of some of the longer loops of Henle change drastically in the terminal 500 μm of the IM. About half of the loops that reach into that level have very broad transverse prebend segments which tend to lie alongside, and to be curved laterally around, the terminal portions of CDs (48). The axially running portions of the prebend segments have lengths of ∼100 μm; each laterally running prebend segment is also ∼100 μm, so that the tubule portion that wraps laterally around a CD is ∼100 μm. The effect of laterally running prebends on DTL and ATL tubular areas is represented by increasing the radii of both the DTL and ATL near the loop bend. We let rDTL(x) and rATL(x) denote the inner radius of a DTL and ATL, respectively; the radius of the prebend or postbend segment, before it is increased to account for the effect of the laterally-running prebends, is denoted by rPB,0; the length of the axially running portion of the prebend segment is denoted by LPB, which equals 100 μm (48). Then, for a loop of length Lloop, where 4.5 mm ≤ Lloop ≤ 5 mm,
| (4) |
By augmenting the tubular radius near the loop bend, the total tubular area along the prebend and postbend segments in a loop that reaches beyond 4.5 mm is 2 × [2πrPB,0(LPB/2 + 2LPB/4 + 4LPB/4)] = 8πrPB,0LPB, which is equal to the total tubular area along the axially running and laterally running portions of the prebend and postbend, given by 2 × [2πrPB,0(LPB + LPB)].
Table 1.
Base-case transtubular transport parameters
| Pf, μm/s | PNa,10−5 cm/s | Purea, 10−5 cm/s | Vmax,Na, nmol·cm−2·s−1 | |
|---|---|---|---|---|
| LDL2S | 0 (45) | 0 (45) | 1 | 0 |
| LDL2 | 2,200 (14) | 0 (45) | 13 (40,68) | 0 |
| LDL3 | 0 | 0 (45) | 1 | 0 |
| ATLS* | 0 (14) | 80 (14) | 1 | 0 |
| ATLM* | 0 (14) | 80 (14) | 1 | 0 |
| ATLL* | 0 (14) | 80 (14) | 1 or 20† | 0 |
| CD | 460→750§ (55) | 1 (57) | 1 to 90§ (18, 56) | 10.5→5→3§ (72) |
| DVR | 1,257 (42) | 76 (44) | 360 (44) | 0 |
| AVR | 750 | 690 | 0 |
Parameters are given by, based on, estimated from, or suggested by references given in parentheses. P, premeability; Pf, osmotic water permeability coefficient, ATL, ascending thin limb; LDL, segment of a descending thin limb; CD, collecting duct; DVR and AVR, descending and ascending vasa recta, respectively.
A prebend segment is assumed to have the same transport parameters as its contiguous ATL.
The higher urea permeability (20 ×10−5 cm/s) applies only to the upper 40% of the ATLL; the urea permeability of the lower portion of the ATLL is 1×10−5 cm/s. ‡Parameter increases exponentially as medullary depth x increases from 1.0 to 5.0 mm.
Arrows indicate that parameter varies linearly between the given values as medullary depth x increases; see details in text.
The DTL of a loop of Henle that turns within the first millimeter of the model IM was assumed to be water impermeable; it is divided functionally and structurally into two segments. The first segment, which is denoted by “LDL2S” (“S” for “short”) and assumed to be impermeable to NaCl, extends to the second segment, the prebend segment, which was assumed to have a length of 166.7 μm and to be functionally like its contiguous ATL, which is denoted by “ATLS.”
The ATL of a loop that turns within the second and third millimeters of the model IM is denoted “ATLM;” the ATL of a loop that reaches into the final 2 mm of the model is denoted “ATLL.” All model ATLs were assumed to be water impermeable but highly NaCl permeable (14). The ATLL was assumed to occupy a position external to the CD cluster in the upper IM. Because microperfusion studies have shown a substantial scatter in urea permeabilities in ATLs (14) (in the hamster, values from ∼3 to 40 × 10−5 cm/s; in the rat, ∼12 to 40 × 10−5 cm/s), it seems likely that urea permeability in ATLs is spatially heterogeneous. Therefore, the upper 40% of the ATLL was assumed to be highly permeable to urea (20 × 10−5 cm/s), whereas the remainder of the ATLL was assumed to have a lower urea permeability (1 × 10−5 cm/s).
The CD urea permeability was assumed to be 1 (in units of 10−5 cm/s) for the first 20% of the model IM (i.e., for x ∈ [0, 0.2]); for the remainder of the IM (x ∈ [0.2, L]), CD urea permeability was assumed to increase exponentially, according to the formula
| (5) |
where P0 and P1 are the initial and terminal CD urea permeabilities, 1 and 90, respectively, and where xCD = 0.2 and α = 9. This profile was constructed to be consistent with experiments in antidiuretic rats showing high urea permeabilities in the terminal CD (18, 56) and to ensure sufficient urea delivery to the deep IM to support the hypothesized mode of concentration.
The CD water permeability was assumed to be 460 (in units of μm/s) for the initial 3/10 of the model IM and to increase linearly to 750 for the remainder of the IM (55).
The CD Na+ maximum transport rate Vmax,Na (in units of mol·cm−2·s−1) was assumed to be 10.5 for the initial 3/10 of the model IM, to decrease linearly to 5 for the next 2/10 of the IM, and to decrease linearly to 3 along the remainder of the IM (as in Fig. 3C in Ref. 30). Substantial evidence, summarized by Weinstein (72), indicates that the IMCD is capable of brisk active NaCl absorption. The profile for Vmax,Na was chosen to ensure that substantial urea was absorbed from the CD (by means of maintaining a sufficient transepithelial urea gradient) and that the solute load reaching the terminal CD was consistent with experimental evidence for moderately antidiuretic rats (see below). The Michaelis constant for CD Na+ active transport was set to 40 mM (11). All tubules and vessels were assumed to have no active urea transport: although active urea transport has been found in the CD (19), the rate of such transport appears to be small relative to passive fluxes.
DVR were assumed to be highly permeable to water, Na+, and urea (42, 44). Effective AVR Na+ and urea permeabilities, defined by PAVR,k ≡ ρAVRDk/lAVR, were computed 1) by setting the fenestration fraction ρAVR to 0.01, 2) by setting Na+ and urea diffusivities, DNa+ and Durea, to 1.5 × 10−5 cm2/s and 1.38 × 10−5 cm2/s, respectively, their self-diffusion coefficients in dilute aqueous solution (36, 71); and 3) by setting the AVR wall thicknesses lAVR to 0.2 μm. The fenestration fraction and the wall thicknesses were based on generic properties of vascular endothelium (60) and on the need for a sufficiently large permeability to limit washout of the medullary gradient (27).
In the initial IM (0 ≤ x ≤ 0.2L), where the CD clusters are well defined, interregion solute permeabilities, which characterize diffusive solute fluxes between the two regions, were set to zero. In the mid-IM (0.2L ≤ x ≤ 0.7L), where structural organization gradually diminishes (48), the interregion solute permeabilities were assumed to increase exponentially. In the remainder of the IM (0.7L ≤ x ≤ L), where CD clusters can no longer be clearly distinguished, interregion permeabilities were set to 100 × 10−5 cm/s.
The osmotic coefficients ϕk were set to be 1.84 for NaCl and NR and 0.97 for urea (71). The reflection coefficients σi,k for all solutes were set to 1 for all tubules and for DVR (52). The partial molar volume of water V̄w was set to 0.018136 cm3/mM for 37°C (Ref. 71, p. B-152 and F-5.).
Water flows and solute concentrations were specified at the OM-IM boundary (i.e., x = 0) for the DTL, DVR, and CD (see Table 2). The water flow in DTL at x = 0 was assumed to increase linearly as a function of loop length, based on evidence that juxtamedullary glomeruli have higher SNGFRs than the glomeruli that give rise to short-looped nephrons (6).
Table 2.
Boundary conditions at OM-IM boundary
RESULTS
The base case.
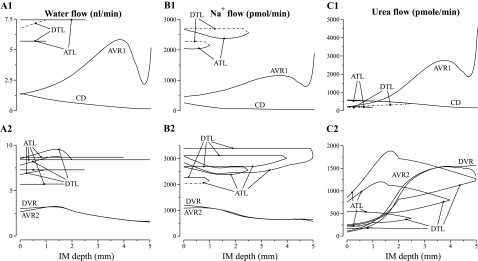
The model equations were solved to obtain steady-state solutions for the base-case configuration, parameter set, and boundary conditions. Key results are displayed graphically in Figs. 4, 5, and 6. Figure 4 shows axial osmolality, Na+ concentration, and urea concentration profiles in the concentric regions and in each class of tubule and vessel. Figure 5 shows corresponding water, Na+, and urea luminal flow profiles; this figure portrays flow magnitudes, so both descending and ascending flows are considered to be positive. Flows in ATL and AVR are directed toward the OM; flows in DTL, DVR, and CD are directed toward the papillary tip. Figure 6 shows axial osmolality profiles along loops of Henle of differing lengths.
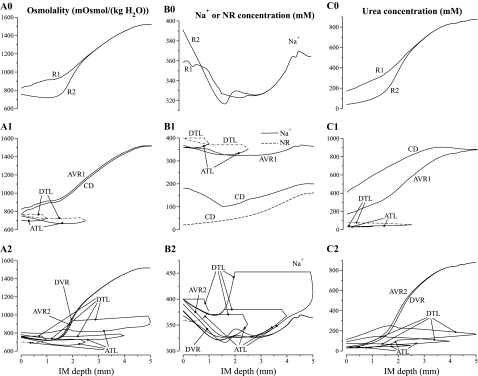
Fig. 4.
Osmolalities and concentration profiles of concentric regions, tubules, and vasa recta. The ordinate is identified at the top of each column: column A, osmolality; column B, Na+ or NR concentration; column C, urea concentration. Row numbers 1 and 2 indicate the region R1 and R2, respectively, to which a tubule or vas rectum is principally assigned. The topmost row, indicated by 0, contains profiles for the interstitia of the regions. Dotted-dashed lines show the 2 DTLs that reside in R2 but are included in A1–C1 for comparison with their associated ATLs, and the ATLs that resides in R1 but is included in A2–C2 for comparison with its associated DTL. Note variation, among panels, in ordinate scalings.
Fig. 5.
Water and solute flows in regions, tubules, and vasa recta, given per long loop of Henle. Notation is analogous to that used in Fig. 4; however, the ordinates, given above each column, are column A, water flow; column B, Na+ flow; and column C, urea flow. Flows in ATL and AVR are directed toward the OM; flows in DTL, DVR, and CD are directed toward the papillary tip. No axial flow is assumed in the regions.
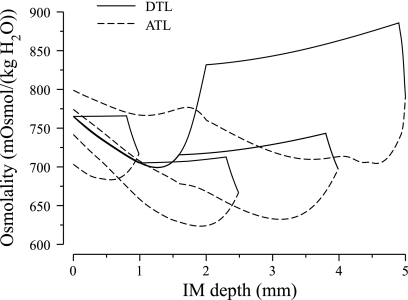
Fig. 6.
Osmolality profiles for loops of Henle reaching to IM depths of 1.0, 2.5, 4.0, and 5.0 mm.
In Figs. 4 and 5, the designations A, B, and C are used in a roughly analogous way: A designates either osmolality or water, B designates Na+ or NR, and C designates urea. In Fig. 4, the row number designation “0” corresponds to the portion of the region lying outside of tubules and vasa recta, but including capillaries and interstitium; in Figs. 4 and 5, the row numbers 1 and 2 indicate the principal region (R1 or R2, respectively) in which a structure is situated. (Exceptions are 2 DTLs that reside in R2 but are included in panels A1–C1 for comparison with their associated ATLs, and the ATLS that resides in R1 but is included in panels A2–C2 for comparison with its associated DTL. These profiles are shown using dotted-dashed lines.) As was described in mathematical model, the DTL and ATL are represented by a continuous distribution, with the loops turning at all IM levels. However, Figs. 4 and 5 contain only the profiles that correspond to representative loops of Henle, specifically, those that turn at x = 1, 2.5, 4, and 5 mm.
The model predicts a urine osmolality of 1,516 mosmol/kgH2O and a urine flow rate of 0.0600 nl·min−1·nephron−1, or 2.28 μl·min−1·kidney−1, assuming 38,000 nephrons/kidney. Assuming an average SNGFR of 33 nl/min (6), the base-case urine flow corresponds to a U/P inulin ratio of 550. Model urine Na+, urea, and NR concentrations are 200, 880, and 160 mM, respectively (see Table 3, column labeled “Base Case”). These concentrations are consistent with experimental measurements in rats by Pennell et al. (51) and by Hai and Thomas (12).
Table 3.
Comparison of base-case predictions with parameter studies
| Base Case | Case 1 | Case 2 | Case 3 | |
|---|---|---|---|---|
| Urine | ||||
| Osmolality, mosmol/kgH2O | 1,516 | 1,513 | 1,489 | 1,656 |
| Na+ concentration, mM | 200 | 199 | 193 | 248 |
| Urea concentration,. mM | 880 | 881 | 871 | 915 |
| NR concentration, mM | 160 | 159 | 157 | 170 |
| Flow, nl·min−1·nephron−1 | 0.0600 | 0.0603 | 0.0615 | 0.0566 |
| U/P inulin | 550 | 547 | 537 | 583 |
| Loop bend | ||||
| Osmolality, mosmol/kgH2O | 923 | 925 | 898 | 1,078 |
| Na+ concentration, mM | 414 | 417 | 406 | 462 |
| Urea concentration, mM | 166 | 163 | 156 | 234 |
| Flow. nl·min−1·nephron−1 | 7.51 | 7.52 | 7.66 | 6.84 |
| TF/P inulin | 5.19 | 5.19 | 5.87 | 6.58 |
| Interstitium at papillary tip | ||||
| Osmolality, mosmol/kgH2O | 1,520 | 1,516 | 1,492 | 1,659 |
| Na+ concentration, mM | 365 | 361 | 355 | 422 |
| Urea concentration, mM | 875 | 877 | 866 | 911 |
NR, nonreabsorbable solute.
Figure 4, column A, shows an increasing osmolality gradient along the model's corticomedullary axis in both regions, and in tubules and vasa recta in the final 3 mm of the IM (except in the prebend segments and near the papillary tip). Along the CD, the tubular fluid osmolality increases from 765.1 to 1,516 mosmolol/kgH2O, i.e., by a factor of 1.98. A similar increase in fluid osmolality was obtained along the longest DVR, from 765.1 to 1,520 mosmol/kgH2O.
Osmolality profiles for loops of Henle of lengths 1.0, 2.5, 4.0, and 5.0 mm are shown in Fig. 6. Because the loops of Henle that turn within the first millimeter of the IM are assumed to be entirely water impermeable, the osmolality in the LDL2S segments of those loops show only a small increase, which is due to a small amount of diffusive urea entry. Along the LDL2 segment, which spans the first 40% of the longer loops and which is highly water permeable, fluid osmolality first drops, owing to water entry, and then increases, owing to water absorption, driven by the higher interstitial fluid osmolality in R2. Along the LDL3 segment, which is assumed to be water impermeable, DTL fluid osmolality shows a small increase, owing to diffusive urea entry.
Beginning at the transition to the prebend segment, osmolality decreases abruptly in all loops; and a rapid rate of decrease continues around the loop bend. Along the contiguous ATL, osmolality continues to decrease along the tubular flow direction, for a portion of that ATL that is about 1/5 to 1/4 of its length. In sufficiently long loops, ATL tubular fluid osmolality eventually exceeds that of its corresponding DTL at that same level, which will tend to dissipate the IM osmolality gradient. Nonetheless, because of the overlapping of shorter loops that have an ATL osmolality that is lower than corresponding DTL osmolality, the osmolality of ATL fluid, taken as a whole at each medullary level, is dilute relative to fluid in descending flows. Thus the ATLs, taken as a whole, carry dilute fluid out of the IM, and the mass-balance requirement for the production of a concentrated urine is satisfied. (Vasa recta and CD flows do not have much affect on the mass-balance calculation because they are nearly in osmotic equilibration with the local interstitium.)
The interstitial fluid in R1 is more concentrated near the OM-IM boundary (823 mosmol/kgH2O at the boundary) relative to CD tubular fluid (765.1 mosmol/kgH2O) because of Na+ reabsorption from the prebends of the Henle's loops and from the CD. Water reabsorption from the CD follows, but because the initial IMCD is assumed to be only moderately water permeable, CD fluid osmolality lags that of the surrounding interstitium. In contrast, fluid in R2 is slightly dilute near the OM-IM boundary (759 mosmol/kgH2O) relative to DTL and DVR fluid (765.1 mosmol/kgH2O) because net Na+ secretion into ATLs (ATLL and half of the ATLM) is sufficiently large near that boundary to have a net diluting effect on the local interstitial fluid. Indeed, R2 fluid osmolality decreases along the first millimeter of the IM. That net decrease in fluid osmolality is a result of the competing effects of decreasing Na+ concentration in R2, owing mostly to Na+ secretion into ATLs, and increasing urea concentration, owing to urea reabsorption from ATLL's. In contrast, R1 fluid osmolality rises along the first millimeter of the IM. The largest difference between the fluid osmolalities in the two regions occurs ∼1.0 mm from the OM-IM boundary, where R1 fluid osmolality is ∼197 mosmol/kgH2O higher than R2; most of that difference is attributable to the difference in urea concentration, which is ∼193 mM higher in R1 than in R2. The higher urea concentration within the CD cluster serves to hinder urea absorption from the initial CD and thereby maintain a sufficiently high urea flow to the terminal CD, where urea absorption has a larger impact on the overall concentrating effect.
Because of sufficiently high DVR water and solute permeabilities, and because of sufficiently high AVR fenestration fraction, vasa recta osmolality tends to track the osmolality and solute concentrations of the local interstitium. This tracking allows DVR and AVR2 to serve the traditionally ascribed roles as countercurrent exchangers: at each level of the IM, DVR flow tends to have an osmolality or a solute concentration that is slightly below that of the surrounding region (except near the OM-IM boundary, where the R2 fluid osmolality decreases); AVR2 flow tends to have an osmolality or solute concentration that is slightly above that of the surrounding region. Thus, taken as a whole, the transport properties and the countercurrent anatomic arrangement of the vasa recta allow them to return the solute and water that is absorbed from the tubules back to the general circulation while at the same time minimizing the washout effect of vascular flow on local medullary osmolality and concentrations, and, more generally, on the axial IM osmolality and concentration gradients.
The sharp decrease in tubular fluid osmolality around the loop bend is caused by the vigorous absorption of Na+, which is a consequence of the abrupt increase in Na+ permeability and a transepithelial gradient that favors Na+ absorption. That gradient arises because urea absorbed from the CD results in a high interstitial urea concentration relative to the interstitial Na+ concentration. Indeed, the resulting interstitial Na+ concentration is below that of the loop Na+ concentration, and thus a substantial transepithelial outwardly directed Na+ concentration gradient is maintained around the loop bend and along the initial part of the ATL. This effect is particularly marked for loops that reach sufficiently deep into the IM because of the particularly high prebend Na+ permeability that was used to simulate the laterally running prebends, and because of the high CD urea permeability and thus large CD urea absorption rate along the terminal CD.
Fluid flow rates, given in units of nanoliters per minute per long loop of Henle, are shown in Fig. 5A for the CD, vasa recta, and selected loops of Henle. Along the IM, 89.3% of the tubular fluid in the CD is reabsorbed. In the initial IM, most of that water reabsorption is driven by the active transport of Na+ from the CD (water accompanies the Na+ to preserve nearly equal osmolalities on each side of the CD epithelium); in the deep IM, water reabsorption from the CD is driven mostly by the diffusive efflux of urea. Also, because the model assumes that only a small fraction of the vessels reach into the deep IM, water flow along each individual AVR that reaches into the deep IM is substantial. Despite the high fluid flow rates in the AVR, vascular fluid solute concentrations closely track local interstitial solute concentrations.
Solute flow rates per long loop of Henle are shown in Fig. 5, B and C, for the CD, vasa recta, and selected loops of Henle. The CD loses 71.5% of its Na+ in the first 1.5 mm of the IM, because, by our modeling assumption, Na+ is vigorously and actively absorbed (at a rate of Vmax,Na of 10.5 nmol·cm−2·s−1). This active absorption promotes water absorption from the early CD, because the model's low CD urea permeability (1 × 10−5 cm/s) restricts the participation of urea flux in transepithelial osmotic equilibration. Moreover, the active Na+ absorption and the accompanying water reabsorption raise the relative concentration of urea in CD tubular fluid (see Fig. 4C1), which ultimately promotes vigorous urea absorption from the terminal CD, where urea permeability greatly increases. In the innermost millimeter of the IM, active Na+ transport from the CD is only sufficient to nearly balance diffusive Na+ backleak.
NaCl permeability of DTLs.
We have assumed a zero permeability of DTLs to NaCl based on the absence of labeling for ClC-K1 (45), a low value of 3.5 × 10−5 cm/s measured in hamster DTL (15), and evidence of nearly zero transmural flux in the hamster (38). To determine whether a value of zero is essential to model results, however, we conducted a simulation in which the permeability was set to 3.5 × 10−5 cm/s but all other parameters were maintained at base-case values. We found a urine osmolality of 1,475 mosmol/kgH2O, Na+ and urea concentrations of 160 and 868 mM, respectively, and a urine flow per nephron of 0.0612 nl/min. These values do not differ substantially from the values reported in Table 3 for the base case.
Laterally running prebends.
Recent anatomic studies have revealed that loops of Henle that reach into the final 500 μm of the IM have laterally running prebends that abut the terminal CD (48). In the model, the laterally running prebends are represented by increasing the radii of both the DTL and ATL near the loop bend (see Eq. 4). Previous modeling studies have predicted that the concentrating effect of the Na+ reabsorbed from the loops is larger when that reabsorption is localized near the loop bend (30, 33). To investigate the effect of the laterally running prebends on the concentrating capability of the model, we conducted a simulation in which laterally running prebends were not represented, i.e., the DTL and ATL radii were not increased near the loop bend, and all prebends were set to 167 μm (longer than the 100-μm axial length of the laterally running prebends). Results of that simulation are shown in Table 3 under the column “Case 1.” The model predicted that the elimination of laterally running prebends resulted in only a modest decrease in urine osmolality, from the base-case value of 1,516 to 1,513 (mosmol/kgH2O), which corresponds to a 0.40% decrease in the osmolality increase along the IM.1 These results appear to suggest that the laterally running prebends have a small impact on the concentrating capability of the model IM. Nonetheless, we note that in the final 500 μm of the model IM, where the laterally running prebends are populated, the interstitial solute concentrations are assumed to be radially homogeneous. Thus the preferential interactions that likely occur between the laterally running prebends and the terminal CDs that they wrap around are not represented in the present model formulation. Such preferential interactions may more effectively promote the absorption of Na+ from the prebends and of urea and water from the CD, thereby more substantially raising the osmolality of the CD tubular fluid.
Initial ATLL urea permeability.
Recall that the urea permeability of ATLs associated with loops that reach into the final 1.5 mm of the IM was set to 20 × 10−5 cm/s in the upper 40% of its length, a value that is 20 times larger than the urea permeability of the remaining portion of that and other ATLs. A high urea permeability in the upper ATL segment promotes urea cycling: the urea that enters the ATLs in the urea-rich deep IM diffuses out of the ATLs into the intercluster region near the OM-IM boundary, raising the urea concentration and osmolality there. This urea permeability in the upper ATL is consistent with experimental measurements in the rat and hamster (14); however, as previously noted, the scatter in the experiments was substantial. To assess the effect of having a highly urea-permeable segment along the upper 40% of the long ATLs, we conducted a simulation in which the urea permeability of that ATL segment was reduced to 10−5 cm/s. Model predictions are shown in Table 3 under the column “Case 2.” Without the highly urea-permeable ATL segment, urea cycling was reduced; thus, the urea concentration outside the CD cluster (where the ATLL segments reside) was reduced, by 13.2 mM at 1.0 mm below the OM-IM boundary. The lower interstitial urea concentration resulted in lower urea concentrations in the DTL and DVR fluid, which in turn lowered the amount of urea delivered into the deep IM. As a result, the concentrating capability of the model IM was reduced, with the osmolality increase along the IM reduced by 3.64% (from the base-case value of 1,516 to 1,489 mosmol/kgH2O).
Radial organization of tubules and vessels.
To assess the impact of regionalization on model results, we conducted an experiment in which the radial organization of tubules and vessels was eliminated; that was achieved by assigning all tubules and vessels to R1, and by setting the solute permeabilities of concentric region boundary to 100 × 10−5 cm/s throughout the IM. Results of that simulation are shown in Table 3 under the column “Case 3.” The model predicted that when regionalization was eliminated, the concentrating capability of the model significantly increased. A more concentrated urine was produced with an osmolality of 1,656, compared with the base-case value of 1,516 (mosmol/kgH2O), which corresponds to a 9.23% increase.
This result suggests that the concentrating capability of the IM would be significantly improved if the tubules and vessels were randomly distributed and surrounded by a common interstitial fluid at each medullary level, rather than being organized around CD clusters in the initial IM. That is, concentrating capability would be improved, if at each medullary level, all tubules and vessels interacted through a well-stirred bath. (This configuration is similar to the single-region model formulation used in central core models, see e.g., Refs. 30 and 61.) In the discussion we spectulate on the origin and role of renal function in the context of the concentrating mechanism.
DVR flow rates at the OM-IM boundary.
The model does not include explicit representation of the OM; rather, the actions of the OM are represented implicitly by means of boundary conditions imposed at the OM-IM border. Specifically, we assume that the flow rates and solute concentrations of the DTL, DVR, and CD are known a priori. Because it has been proposed that blood flow along DVR may be regulated by their intrinsic contractile capability (43), we investigated how variation in DVR flow rate affects the model's concentrating capability. The base-case OM-IM boundary flow rate of 4.5 nl·min−1·DVR−1 was varied by ±10 and ±20%; DVR boundary solute concentrations were kept at the base-case values. Decreasing the DVR boundary flow rate by 10 and 20% resulted in 0.33 and 0.59% increases, respectively, in CD fluid osmolality at the OM-IM boundary, whereas increasing the flow rate by 10 and 20% resulted in decreases of 0.33 and 0.73%, respectively. Thus these findings yield the intuitive result that decreasing DVR flow decreases the load on the concentrating mechanism, but the effect is not substantial. The insensitivity of model results to DVR flow rates may be attributable to the separation of the CD and DVR in the initial IM. At the mid-IM (x = 0.5L), where there is sufficient mixing between the two regions that interstitial fluid solute concentrations in the two regions are nearly indistinguishable, 90% of the DVR have terminated. Thus, only the 10% of the DVR that reach into the second half of the IM have significant interactions with the CD. As a result, varying DVR inflow rates has only minimal impacts on the model's urine osmolality.
LDL3 water permeability.
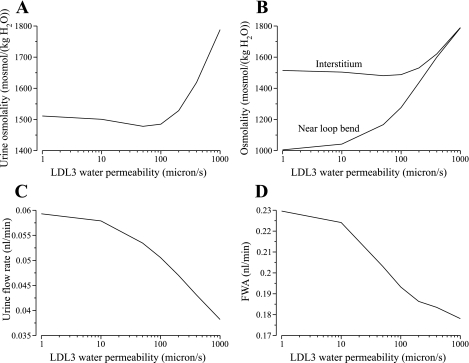
In most previous model studies, the rat DTL has been assumed to be highly water permeable up to the loop bend, or until the beginning of the prebend segment (34, 62, 69; an exception is Ref. 64). That assumption was based on studies that appear to suggest that all DTL segments in the IM are highly water permeable (14, 15). However, recent experiments in isolated perfused tubules have not indicated any significant water permeability in the LDL3 segment (5). Thus we investigated the impact of LDL3 osmotic water permeability by varying model values from 0 to 1,000 μm/s; results are shown in Fig. 7.
Fig. 7.
Parameter studies for water permeability of LDL3. Effects are evaluated in terms of urine osmolality (A), DTL tubular fluid osmolality at the beginning of the prebend of the longest DTL and the local interstitial fluid osmolality (B), urine flow rate (C), and free water absorption rate (FWA; D).
Initially, as LDL3 water permeability (in μm/s) increased from 0 to 50, urine osmolality (in mosmol/kgH2O) decreased slightly from the base-case value of 1,516 to 1,478, by 2.50%; as LDL3 water permeability further increased from 50 to 1,000, urine osmolality increased from 1,478 to 1,788, by 21.0%; see Fig. 7A. The increased urine osmolality arises from increased water absorption from LDL3. As shown in Fig. 7B, DTL tubular fluid osmolality at the beginning of the prebend of the longest loop increased from 988 in the base case to 1,788 for PLDL3,f = 1,000 μm/s, and the difference between the osmolality of the fluid entering the prebend and the local interstitium decreased from 531 to 1.91, as DTL tubular fluid nearly equilibrated with the surrounding interstitial fluid. Because the LDL3 tubular fluid osmolality is hyposmotic relative to the surrounding region, more water was absorbed from the LDL3 as it became increasingly more water permeable. The absorption of water increased DTL tubular fluid Na+ concentration and promoted increased rates of loop-bend Na+ absorption. However, increased LDL3 water permeability also resulted in reduced urine flow rates (see Fig. 7C): water absorbed from the LDL3 reduced interstitial urea concentration and increased urea absorption from the CD, and this urea absorption was accompanied by water absorption from the CD. As LDL3 water permeability increased from 0 to 1,000, urine flow rate (in nl·min−1·nephron−1) decreased from 0.0600 to 0.0382, which corresponds to a 36.3% decrease.
We also computed free-water absorption rate (FWA) for the differing LDL3 water permeabilities.2 FWA is the volume, per unit time, of blood plasma that could be considered to be completely cleared of solutes by the production of urine that is more concentrated than blood plasma (16, 74):
| (6) |
where Furine,V is the urine flow rate and U/P is the urine-to-plasma osmolality ratio; we assumed that rat blood plasma osmolality is 308 mosmol/kgH2O (12). As shown in Fig. 7D, as LDL3 water permeability increased from 0 to 1,000, FWA (in nl/min) decreased monotonically from 0.232 to 0.178, which corresponds to a 23.3% decrease. These results suggest that, although a sufficiently high LDL3 water permeability can generate a urine with an osmolality much higher than base case, a water-impermeable LDL3 segment yields the highest FWA because it produces a urine at a much higher flow rate.
DISCUSSION
Model formulation and implications.
We have developed the first mathematical model that seeks to understand the implications, for the urine concentrating mechanism, of the anatomic and functional heterogeneity that have been revealed, both axially and transversely, in anatomic studies by Pannabecker and coworkers (29, 49); these studies have been recently reviewed. The mathematical model represents radial organization of renal tubules and vessels, with respect to CD clusters, by means of a region-based formulation: the model represents two concentric regions, which are centered on a CD cluster, and radial structure is incorporated by assigning appropriate tubules and vasa recta to each concentric region.
Along the corticomedullary axis of the IM, the model predicts an osmolality increase of about a factor of 2 in CDs, an increase consistent with experiments in rats having moderately elevated urine osmolalities (12, 51). Moreover, the model indicates that the marked radial organization of the upper IM, which is centered on the CD clusters, has a significant impact on the interstitial concentrations that surround tubules and vessels. Most notably, the model predicts a sequestration of urea in the CD clusters (see Fig. 4C0). (“We will say that a solute is “sequestered” within a CD cluster when its average fractional contribution to fluid osmolality in the lumina and interstitium of a cluster at a particular level of the IM substantially exceeds its fractional contribution to average fluid osmolality in the lumina and interstitium in nearby intercluster tissue.”) This sequestration is consistent with our predictions in the recent reviews (29, 49) in which we distinguished three distinct countercurrent systems in the rat IM: two in the upper 3–3.5 mm of the IM, an intracluster system and an intercluster system, and a third countercurrent system in the final 1.5–2 mm of the IM. We hypothesized that the intracluster countercurrent system functions to raise the osmolality of CD tubular fluid by facilitating targeted delivery of NaCl via prebend segments and corresponding postbend segments of long loops and by sequestering the urea that is absorbed from CDs within the CD clusters (see Fig. 4C0). Furthermore, we hypothesized that urea sequestration would tend to limit the diffusion of urea from CDs so that sufficient urea for an effective solute-separation, solute-mixing mechanism can be delivered by the CD tubular fluid to the deeper IM.
In our model of an intercluster countercurrent system of the upper IM, DTLs of Henle and upper portions of sufficiently long ATLs are shielded from the higher interstitial urea concentrations inside the CD clusters; the lower urea concentration in the intercluster region, relative to the intracluster region (see Fig. 4C0), serves to promote absorption of NaCl and urea from the intercluster ATLs into the interstitium of the cluster periphery.
In the reviews, we hypothesized that the countercurrent system of the intercluster region would promote water absorption from the water-permeable portions of DTLs (the upper 40% of these limbs) and thus raise the tubular fluid NaCl concentration within DTLs before the DTLs enter the CD clusters (29, 49). Our model, however, predicts that water is secreted into the upper water-permeable portions of the DTLs, resulting in decreasing tubular fluid NaCl concentration along these DTLs (see Figs. 4, B1 and B2, and 5, A1 and A2). Moreover, although urea is absorbed from the ATLs in the intercluster region, ATL tubular fluid osmolality (in sufficiently long loops) eventually exceeds values in the corresponding DTL at the same level (see Fig. 4, A2 and C2); this difference tends to dissipate the axial osmolality gradient. However, because of the overlapping of shorter loops that have an ATL osmolality that is lower than corresponding DTL osmolality, the osmolality of ATL fluid, taken as a whole at each medullary level, is dilute relative to DTL fluid; thus the ATLs as a whole carry dilute fluid out of the IM, which satisfies the mass-balance requirement for the production of concentrated urine.
The papillary countercurrent system is found in the lower 1.5–2 mm of the inner IM, where intra- and intercluster systems can no longer be distinguished. The model predicts that, as a result of the actions of the two countercurrent systems in the 3–3.5 mm of the initial IM, tubular fluid entering the inner IM via the DTLs and CDs is well suited for the delivery of NaCl and urea, respectively, that are essential to an effective solute-separation, solute-mixing mechanism: tubular fluid NaCl concentration in DTLs is higher than that in the local interstitium, and CD tubular fluid is not only well concentrated in the upper IM but also has its urea concentration raised, relative to NaCl concentration, so that urea diffusion is enhanced in the lower IM where CD urea permeability is reported to be highest (18, 53, 56).
The transport properties for loops of Henle in the present model correspond to the “pipe mode” hypothesis proposed in Ref. 30. In the pipe mode, the AQP1-null portions of the loops of Henle are assumed to have a nearly zero urea permeability (however, the present model assumes a urea permeability in the upper portion of sufficiently long ATLs that is 20 times higher than the lower portion of those ATLs or along the ATLs of shorter loops), and the DTL AQP1-null segments are assumed to have zero NaCl permeability. In a previous model study (30), we assumed a moderate water permeability of 400 μm/s for the DTL AQP1-null segments (as reported in Ref. 3), whereas the present model assumes zero water permeability, based on preliminary studies in isolated perfused tubules (5). The pipe mode concentrates by vigorous absorption of NaCl from loop bends that is unaccompanied by water absorption from loop bends and that is not matched by significant solute (e.g., urea) secretion.
Because the present model has a water-impermeable DTL terminal segment, tubular fluid osmolality at loop bends differs significantly from local interstitium: fluid osmolality at the bend of the longest loop is predicted to be 923 (in mosmol/kgH2O), whereas interstitial fluid at the papillary tip has an osmolality of 1,520. In the previous model (30), DTL tubular fluid more nearly equilibrates with surrounding interstitial fluid, and thus longest loop-bend and papillary tip fluid osmolalities were predicted to be 1,073 and 1,277, respectively, with a much smaller difference of 204. Moreover, micropuncture experiments in moderately concentrating rats (51) yielded loop-bend fluid osmolality of 1,264, which is substantially higher than our prediction, but consistent with the previous model study.
The large discrepancy between loop osmolality and local interstitial osmolality is contrary to experimental evidence for similar osmolalities among IM structures at the same medullary level (9, 10). On the one hand, the discrepancy may be an indicator that model assumptions are incorrect. For example, an alternative mode of concentration that we have proposed, the solute-secretion mode (30), would allow the near equilibration of urea concentrations across the loops of Henle and would thereby result in a closer approximation to osmotic equilibration across the loops. On the other hand, this discrepancy may arise from invalid conclusions about experimental findings. For example, the osmolalities in tubules and vessels that are near the surface of the IM, and thus accessible to micropuncture, may not be representative of those that are deeper within the IM; thus there may be distinct populations of loops, with some having much greater osmotic permeability than others.
The model concentrates moderately well and predicts a generally increasing, axial Na+ concentration in the interstitial fluid along the medullary axis. That gradient, as well as the simulated urine flow and concentrations, are highly sensitive to the transport properties of the IMCD (results not shown), and frequently it is difficult to predict a priori the effects of changes in CD transport parameters on model behavior. In particular, there is much uncertainty about the nature and spatial distribution of the active, outward-directed Na+ transport of the IMCD, which is crucial in the pipe mode concentrating mechanism and in the generation of an increasing interstitial fluid Na+ concentration.
Context of the model among previous models.
Our region-based model formulation owes much to the conceptual configurations that were proposed by Kriz and Lever (25). Our model formulation is similar to, but distinguishable from, the mathematical model developed by Knepper et al. (22), which includes two “parallel systems” in the renal medulla. In the configurations proposed by Kriz and Lever (25), and in the mathematical model developed by Knepper et al. (22), the ATLs and CDs were assumed to preferentially interact in one system, whereas DTLs and VR interacted in a second system; the systems were assumed to interact with each other through transversely running capillaries.
We regard our region-based model as a step toward a more faithful representation of those aspects of the complex three-dimensional IM structure that are likely to have a bearing on the urine concentrating mechanism. Previously, we used a region-based formulation to represent the concentrating mechanism of the OM (27, 28). We believe that the region-based formulation provides an appropriate representation for the OM, because large numbers of essentially identical OM structures are arranged in regular groups around the vascular bundles, and because the population numbers of tubules and of long vessels as a function of medullary depth do not vary much in the OM. However, the structural configuration of the IM differs in significant ways from that of the OM, and the differences make the region-based methodology more difficult to apply. In the IM, the tubules and vessels appear to be arranged around bundles of CDs, with each bundle starting with ∼11 CDs at the OM-IM boundary; and these CDs coalesce systematically as a function of IM depth. The loops of Henle decrease in number as a function of IM depth by forming loop bends at various depths. Consequently, the structural configuration of model regions changes substantially as a function of IM depth. Moreover, the region-based methodology does not represent the interstitial nodal compartments that are bounded by CDs, ATLs, and AVR and which appear to promote preferential interactions among these three structures (47), nor does it well represent the wrapping of laterally running prebends around the terminal CDs (48) and the likely direct interactions at the points of contact.
Even though the region-based methodology results in a model that is complex by the standards of many of its precursors [notably, the central core model formulation introduced by Stephenson (61) and frequently used by ourselves and other modelers (32)], the complex three-dimensional organization of the IM may be better represented by means of a “connection-based” methodology that aims to faithfully represent interactions between adjacent structures (i.e., tubule-tubule, tubule-vessel, and vessel-vessel interactions). The connection methodology was introduced by Wexler, Kalaba, and Marsh (75, 76) in the “WKM” model, published in 1991, and subsequently, this methodology was used in a series of studies (65, 66, 69, 70). In a connection-based model of the IM, one might model a portion, or sector, of a CD cluster, which by means of symmetry can be extended to represent an entire cluster. Each tubule, vessel, or nodal space structure in that cluster portion would be modeled as an individual and discrete entity, and its appropriate relationship with adjacent structures would be represented.
The configurations of the connections appearing in studies using the WKM model resemble, in important ways, the configuration we have adopted in this study, which is based on more complete information about IM structure. In the original WKM model (75), the IMCD was represented as having preferential interaction with ATLs while having much weaker interactions with DTLs and with DVR (as does our configuration in the outer portion of the IM). Criticisms of the original WKM model (13) led to a revised WKM model (70), which had three axial zones (as does ours) and which promoted progressively stronger interaction of the IMCD with other tubules and with vessels as an increasing function of IM depth (as does ours).
It is important, however, to distinguish between the “nodal spaces” reported by Pannabecker and Dantzler (47) from the nodes used by Wexler and coworkers to represent transversely running capillaries (65, 66, 69, 70, 75, 76). The nodal spaces reported by Pannabecker and Dantzler are interstitial microdomains through which CDs, ATLs, and AVR of the IM may interact preferentially; these microdomains may serve as solute-mixing chambers. Moreover, in the model structure used by Wexler and coworkers, and in the analysis of that structure by Stephenson and coworkers (17, 62, 63), the vasa recta of the upper IM were considered to have no direct interaction with ATLs and CDs, which appears to be contrary to the true anatomy in rats, where the AVR, ATLs, and CDs form the fundamental components of the CD clusters of the upper IM (in their parameter studies, however, Stephenson and coworkers considered varying degrees of AVR interaction with DTLs, ATLs, and CDs) (17, 62, 63). An accurate representation of the CD clusters should be a fundamental goal for the next generation of connection-based models.
The present model assumes that in the initial IM, where CD clusters are well defined in vivo, there are no interactions, neither diffusion nor advection, between the two regions. That assumption may represent a separation that is more complete than that in vivo. Nonetheless, we have adopted this configuration to better reveal the functional implications of the three-dimensional IM architecture. Indeed, we believe that for this model, which we consider to be a prototype, or a first-generation model, a marked separation in the initial IM is preferable, especially since isolated microdomains within the CD clusters are not explicitly represented here. In future second-generation models, we plan to include more nearly isolated microdomains and more accurate region-to-region interactions.
In this study, we found that when the regions of our model were merged into a single region (by increasing the solute permeabilities of the region boundary) the urine concentrating capability was increased by 9.23%. A possible interpretation of this finding is that it casts doubt on the importance of regionalization for concentrating efficacy. However, such doubt would be unfounded because the comparison is based on an idealized configuration in which all tubules and vessels interact through a well-stirred bath, a configuration that is likely physiologically unattainable. When the regions are merged, the region-based model resembles a central core model, in that, at each medullary level each tubule or structure is in contact with the same interstitial environment of solute concentrations. Not only is such a configuration contrary to fact, but, moreover, structural integrity, developmental processes, and the sustained identity of the tissues as a function of location are all, we believe, to some degree dependent on tightly packed tubules and vessels and the microenvironments that they maintain. A more proper comparison can only be made between a region-based model and a more truly representative model formulation, such as, e.g., a model that uses a connection-based methodology. Moreover, ultimately, the test for a model, whether it uses a region-based or a connection-based approach, is whether the model makes good predictions for flow rates and concentrations in all the tubules and vessels, and for interstitial solute concentrations.
Previously, we proposed an alternative IM concentrating mechanism, the “solute-secretion” mode, in which both the DTL AQP1-null segments and the ATLs of sufficiently long loops are assumed to be water impermeable but highly permeable to urea (30). Unlike the pipe mode, where the loops of Henle have a relatively low urea permeability, the loops of Henle in the solute secretion mode function as a highly effective countercurrent urea exchangers. In principle, the solute-secretion mode, like the pipe mode, can concentrate by means of vigorous absorption of NaCl from loop bends, which is unaccompanied by water absorption; indeed, we exemplified this mode in a mathematical model (30).
A limitation of the region-based model (a limitation that this model shares with its central-core based precursor) (30) is that the model concentrates at most up to ∼1,700 mosmol/kgH2O with a flow of ∼0.05 nl·min−1·nephron−1. Efforts to significantly increase model osmolality and flow, by means of an informal optimization of parameters, were unsuccessful. Therefore, if solute mixing is indeed the mechanism by which the IM concentrates urine, experimental studies that have reported much higher urine osmolalities or higher urine flows in rats and mice and other mammals (4, 7, 8, 58, 73) are difficult to explain within the context of the region-based model presented herein. In a companion manuscript (study 2), we consider the hypothesis that hyperfiltration and a hypertrophy of the inner stripe may play a role in the generation of these higher urine flows and osmolalities.
GRANTS
This research was supported by National Institutes of Health Grants DK-42091 (to H. E. Layton) and DK-16294 (to W. H. Dantzler); ES-06694 (for the Southwest Environmental Health Sciences Center at the University of Arizona); and by National Science Foundation Grant DMS-0701412 (to A. T. Layton).
DISCLOSURES
No conflicts of interest are declared by the authors.
ACKNOWLEDGMENTS
Portions of this work were presented at the 2009 Annual Meeting of the American Society of Nephrology and were published in abstract form (abstract no. SA-PO2086; J Am Soc Nephrol 19: 583A, 2008).
APPENDIX A: MODEL EQUATIONS
Model equations represent the conservation and transmural transport of solutes and water. Detailed justification for the model equations can be found elsewhere (26, 35, 78). The equations given below are a reduced set that includes only those that are needed to explain the most significant ways in which the present study differs from the two-region model for the rat OM (26).
Distributed Loop Formulation
The OM model in Ref. 26 includes two model loops of Henle: a short loop that reaches to the OM-IM boundary and the OM portion of a long loop that extends into the IM. In contrast, the current model, which is formulated for the IM, includes only long loops, which form loop bends at all levels of the IM; thus the population of loops decreases as a function of increasing medullary depth. That decreasing loop population can be represented using continuously distributed loops (30, 31). In a distributed-loop configuration, a loop of Henle reaches to each medullary level, and two space variables are used: x denotes the level of the IM, whereas y indexes a loop by the level at which it turns; both x and y range along the IM from 0 to L = 5 mm, with x ≤ y . Thus at time t, in a distributed DTL or ATL reaching to medullary level y, the water flow rate at level x is denoted by Fi,V = Fi,V (x,y,t), i = DTL or i = ATL. Analogous function notation and arguments are used for other loop variables. At each medullary level, the effective transmural fluxes from the loops are weighted according to the number of loops of a particular length remaining at that depth (see below).
Composite Vas Rectum Formulation
Unlike the loops of Henle, the transport properties and fluid composition of the vasa recta are assumed to be independent of their lengths. Thus, to reduce computational cost, the composite vas rectum model is used to represent the population decrease of the vasa recta as a function of medullary depth. The model DVR, AVR1, and AVR2 are each merged into a composite vas rectum, and an appropriate amount of flow (see below), given by the vas rectum population distribution (Eq. 3), is directed from the DVR to the interstitium as capillary flow, and an appropriate amount of flow, given by the vas rectum population distribution and by the net fluid accumulation at that medullary level, is added to the AVR flow. The tubular areas of the composite vasa recta are scaled in proportion to the vas rectum population.
Water conservation along the composite DVR and AVR is given by
| (A1) |
for i = DVR, AVR2, or AVR2, where FiV represents water flow rate, JiV represents transendothelial water fluxes, and Si represents capillary flow rate; both JiV and Si are assumed positive for water transport into the vessel. At medullary level x, DVR break up at a rate of −w′VR and empty into capillaries. Capillary flow out of the DVR at level x, denoted by SDVR(x), is defined as follows:
| (A2) |
The AVR flow source terms SAVR1(x) and SAVR2(x) are given by the net fluid accumulation at medullary level x in R1 and R2; see below. Solute conservation equations for the composite DVR and AVR are given by
| (A3) |
| (A4) |
for i = 1, 2.
Water and Solute Conservation in Concentric Regions
A schematic representation of water conservation at steady state is given in Fig. 3. Water conservation in the concentric regions is represented by
| (A5) |
| (A6) |
JR1,V and JR2,V denote the total water flux into R1 or R2 from tubules and DVRs, given per long loop of Henle. The second term in Eq. A5 is the vasa recta source term. The net fluid accumulations in the two regions, i.e., nAVR1SAVR1 and nAVR2SAVR2, are taken up, via fenestrations, by the respective AVR populations that reside in each region.
Solute conservation for the concentric regions is given by
| (A7) |
| (A8) |
The first term on the right-hand side of the equality represents transmural solute from tubules and vasa recta; the second term in Eq. A7 represents capillary solute sources (i.e., terminating DVR); and the third term represents the solute that is carried by flow at the local interstitial concentration into AVR.
Water and Solute Fluxes in Concentric Regions
The concentric regions exchange solutes with each other, and they exchange water and solutes with the tubules and vasa recta that are in contact with them. For the loops turning at y ≥ x, the composite water flux at level x directed into region R (R = R1 or R2) is given by
| (A9) |
where i = DTL or ATL. The total water flux into region R (R = R1 or R2) from CD, DVRs, and loops turning at y ≥ x is given by
| (A10) |
The relative position of a tubule or vas rectum i is specified by the parameters κi,R1 and κi,R2, which denote the fractions of the tubule or vas rectum i that are in contact with concentric regions R1 and R2, respectively; thus κi,R1 + κi,R2 = 1. The transmural fluxes from a tubule or vas rectum i into the concentric regions R1 and R2 are scaled by κi,R1 and κi,R2, respectively.
The total solute flux into region R (R = R1 or R2) is given by
| (A11) |
where δR = 1 for R = R1, and δR = −1 for R = R2. The first term on the right-hand side of Eq. A11 is the diffusive solute flux between R1 and R2, taken positive into R1 and characterized by the solute permeability PR1,R2,k(x) of the boundary between the two regions. The remaining terms are the solute fluxes from tubules and vasa recta into region R. The composite DTL and ATL solute fluxes (i = DTL or ATL) from the distributed loops into region R (R = R1 or R2) are given by
| (A12) |
Footnotes
The relative percent osmolality increase along the IM is given by (U − COM/COM) × 100%, where U is the model urine osmolality, and COM is the osmolality of tubular fluid entering the IMCD from the OMCD at the OM-IM boundary (i.e., at x = 0), which is 765.1 mosmol/kgH2O.
The free-water absorption rate has also been called the “solute-free water absorption rate” (16); it is identical to the negative of the solute-free water clearance. The solute-free water clearance (also called the “free water clearance”) is frequently denoted by CH2O (74). Thus FWA = −CH2O.
REFERENCES
- 1.Akizuki N, Uchida S, Sasaki S, Marumo F. Impaired solute accumulation in inner medulla of Clcnk1−/− mice kidney. Am J Physiol Renal Physiol 280: F79–F87, 2001 [DOI] [PubMed] [Google Scholar]
- 2.Bankir L, Chen K, Yang B. Lack of UT-B in vasa recta and red blood cells prevents urea-induced improvement of urine concentrating ability. Am J Physiol Renal Physiol 286: F144–F151, 2004 [DOI] [PubMed] [Google Scholar]
- 3.Chou CL, Knepper MA. In vitro perfusion of chinchilla thin limb segments: segmentation and osmotic water permeability. Am J Physiol Renal Fluid Electrolyte Physiol 263: F417–F426, 1992 [DOI] [PubMed] [Google Scholar]
- 4.Collins BG. Water metabolism and the distribution of two species of Australian murids, Rattus rattus and R attus villosissimus. Comp Biochem Physiol 61A: 647–651, 1978 [Google Scholar]
- 5.Dantzler WH, Evans KK, Pannabecker TL. Osmotic water permeabilities in specific segments of rat inner medullary thin limbs of Henle's loops. FASEB J 23: 970.3, 2009 [Google Scholar]
- 6.de Rouffignac C, Bouvalet JP. Étude chez le rat des variations du débit individuel de filtration glomérulaire des néphron superficiels et profonds en fonction de l'apport sodé. Pflügers Arch 317: 141–156, 1970 [DOI] [PubMed] [Google Scholar]
- 7.Fenton RA, Chou CL, Stewart GS, Smith CP, Knepper MA. Urinary concentrating defect in mice with selective deletion of phloretin-sensitive urea transporters in the renal collecting duct. PNAS 101: 7469–7474, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fenton RA, Chou CL, Sowersby H, Smith CP, Knepper MA. Gamble's “economy of water” revisited: studies in urea transporter knockout mice. Am J Physiol Renal Physiol 291: F148–F154, 2006 [DOI] [PubMed] [Google Scholar]
- 9.Gottschalk CW, Lassiter WE, Mylle M, Ullrich KJ, Schmidt-Nielsen B, O'Dell R, Pehling G. Micropuncture study of composition of loop of Henle fluid in desert rodents. Am J Physiol 204: 532–535, 1963 [DOI] [PubMed] [Google Scholar]
- 10.Gottschalk CW, Mylle M. Micropuncture study of the mammalian urinary concentrating mechanism: evidence for the countercurrent hypothesis. Am J Physiol 196: 927–936, 1959 [DOI] [PubMed] [Google Scholar]
- 11.Greger R, Velázquez H. The cortical thick ascending limb and early distal convoluted tubule in the concentrating mechanism. Kidney Int 31: 590–596, 1987 [DOI] [PubMed] [Google Scholar]
- 12.Hai MA, Thomas S. The time-course of changes in renal tissue composition during lysine vasopressin infusion in the rat. Pflügers Arch 310: 297–319, 1969 [DOI] [PubMed] [Google Scholar]
- 13.Han JS, Thompson KA, Chou CL, Knepper MA. Experimental tests of three-dimensional model of urinary concentrating mechanism. J Am Soc Nephrol 2: 1677–1688, 1992 [DOI] [PubMed] [Google Scholar]
- 14.Imai M. Function of the thin ascending limb of Henle of rats and hamsters perfused in vitro. Am J Physiol Renal Fluid Electrolyte Physiol 232: F201–F209, 1977 [DOI] [PubMed] [Google Scholar]
- 15.Imai M, Taniguchi J, Yoshitomi K. Transition of permeability properties along the descending limb of long-loop nephron. Am J Physiol Renal Fluid Electrolyte Physiol 254: F323–F328, 1988 [DOI] [PubMed] [Google Scholar]
- 16.Jamison RL, Kriz W. Urinary Concentrating Mechanism: Structure and Function New York: Oxford University Press, 1982 [Google Scholar]
- 17.Jen JF, Wang H, Tewarson RP, Stephenson JL. Comparison of central core and radially separated models of renal inner medulla. Am J Physiol Renal Fluid Electrolyte Physiol 268: F693–F697, 1995 [DOI] [PubMed] [Google Scholar]
- 18.Kato A, Naruse M, Knepper MA, Sands JM. Long-term regulation of inner medullary collecting duct urea transport in rat. J Am Soc Nephrol 9: 737–745, 1998 [DOI] [PubMed] [Google Scholar]
- 19.Kato A, Sands JM. Evidence for sodium-dependent active urea secretion in the deepest subsegment of the rat inner medullary collecting duct. J Clin Invest 101: 423–428, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Knepper MA, Danielson RA, Saidel GM, Post RS. Quantitative analysis of renal medullary anatomy in rats and rabbits. Kidney Int 12: 313–323, 1977 [DOI] [PubMed] [Google Scholar]
- 21.Knepper MA, Saidel GM, Hascall VC, Dwyer T. Concentration of solutes in the renal inner medulla: interstitial hyaluronan as a mechano-osmotic transducer. Am J Physiol Renal Physiol 284: F433–F446, 2003 [DOI] [PubMed] [Google Scholar]
- 22.Knepper MA, Saidel GM, Palatt PJ. Mathematical model of renal regulation of urea excretion. Med Biol Eng 14: 408–425, 1976 [DOI] [PubMed] [Google Scholar]
- 23.Koepsell H, Kriz W, Schnermann J. Pattern of luminal diameter changes along the descending and ascending thin limbs of the loop of Henle in the inner medullary zone of the rat kidney. Z Anat Entwiekl-Gesch 138: 321–328, 1972 [DOI] [PubMed] [Google Scholar]
- 24.Kokko JP, Rector FC. Countercurrent multiplication system without active transport in the inner medulla. Kidney Int 2: 214–223, 1972 [DOI] [PubMed] [Google Scholar]
- 25.Kriz W, Lever AF. Renal countercurrent mechanisms: structure and function. Am Heart J 78: 101–118, 1969 [DOI] [PubMed] [Google Scholar]
- 26.Layton AT, Layton HE. A region-based model framework for the rat urine concentrating mechanism. Bull Math Biol 65: 859–901, 2003 [DOI] [PubMed] [Google Scholar]
- 27.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol 289: F1346–F1366, 2005 [DOI] [PubMed] [Google Scholar]
- 28.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. II. Parameter sensitivity and tubular inhomogeneity. Am J Physiol Renal Physiol 289: F1367–F1381, 2005 [DOI] [PubMed] [Google Scholar]
- 29.Layton AT, Layton HE, Pannabecker TL, Dantzler WH. The mammalian urine concentrating mechanism: hypotheses and uncertainties. Physiology 24: 250–256, 2009 [DOI] [PubMed] [Google Scholar]
- 30.Layton AT, Pannabecker TL, Dantzler WH, Layton HE. Two modes for concentrating urine in the rat inner medulla. Am J Physiol Renal Physiol 287: F816–F839, 2004 [DOI] [PubMed] [Google Scholar]
- 31.Layton HE. Distribution of Henle's loops may enhance urine concentrating capability. Biophys J 49: 1033–1040, 1986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Layton HE. Mathematical models of the mammalian urine concentrating mechanism. In: Membrane Transport and Renal Physiology, The IMA Volumes in Mathematics and Its Applications, edited by Layton HE, Weinstein AM. New York: Springer, 2002, p. 233–272 [Google Scholar]
- 33.Layton HE, Davies JM. Distributed solute and water reabsorption in a central core model of the renal medulla. Math Biosci 116: 169–196, 1993 [DOI] [PubMed] [Google Scholar]
- 34.Layton HE, Knepper MA, Chou CL. Permeability criteria for effective function of passive countercurrent multiplier. Am J Physiol Renal Fluid Electrolyte Physiol 270: F9–F20, 1996 [DOI] [PubMed] [Google Scholar]
- 35.Layton HE, Pitman EB. A dynamic numerical method for models of renal tubules. Bull Math Biol 56: 547–565, 1994 [DOI] [PubMed] [Google Scholar]
- 36.Lide DR. (Editor). CRC Handbook of Chemistry and Physics (82nd ed.). Cleveland, OH: CRC, 2001 [Google Scholar]
- 37.MacPhee PJ. Fluid uptake by the renal medullary vasa recta: an estimate based on a quantitative analysis of the distribution of fenestrae in the vasa recta of young Sprague-Dawley rats. Exp Physiol 83: 23–34, 1998 [DOI] [PubMed] [Google Scholar]
- 38.Marsh DJ. Solute and water flows in thin limbs of Henle's loop in the hamster kidney. Am J Physiol 218: 824–831, 1970 [DOI] [PubMed] [Google Scholar]
- 39.Matsumura Y, Uchida S, Kondo Y, Miyazaki H, Ko SB, Hayama A, Morimoto T, Liu W, Arisawa M, Sasaki S, Marumo F. Overt nephrogenic diabetes insipidus in mice lacking the CLC-K1 chloride channel. Nat Genet 21: 95–98, 1999 [DOI] [PubMed] [Google Scholar]
- 40.Morgan T, Berliner RW. Permeability of the loop of Henle, vasa recta, and collecting duct to water, urea, and sodium. Am J Physiol 215: 108–115, 1968 [DOI] [PubMed] [Google Scholar]
- 41.Pallone TL. The extraglomerular microcirculation of the kidney. In: The Kidney: Physiology and Pathophysiology (3 ed.). Philadelphia, PA: Lippincott Williams & Wilkins, 2000, p. 791–821 [Google Scholar]
- 42.Pallone TL, Kishore BK, Nielsen S. Evidence that aquaporin I mediates NaCl induced water flux across rat descending vasa recta. Am J Physiol Renal Physiol 272: F587–F596, 1997 [DOI] [PubMed] [Google Scholar]
- 43.Pallone TL, Turner MR, Edwards A, Jamison RL. Countercurrent exchange in the renal medulla. Physiol Regul Integr Comp Physiol 284: R113–R1175, 2003 [DOI] [PubMed] [Google Scholar]
- 44.Pallone TL, Work J, Myers R, Jamison RL. Transport of sodium and urea in outer medullary vascular bundles. J Clin Invest 93: 212–222, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pannabecker TL, Abbott DE, Dantzler WH. Three-dimensional functional reconstruction of inner medullary thin limbs of Henle's loop. Am J Physiol Renal Physiol 286: F38–F45, 2004 [DOI] [PubMed] [Google Scholar]
- 46.Pannabecker TL, Dantzler WH. Three-dimensional lateral and vertical relationship of inner medullary loops of Henle and collecting duct. Am J Physiol Renal Physiol 287: F767–F774, 2004 [DOI] [PubMed] [Google Scholar]
- 47.Pannabecker TL, Dantzler WH. Three-dimensional architecture of inner medullary vasa recta. Am J Physiol Renal Physiol 290: F1355–F1366, 2006 [DOI] [PubMed] [Google Scholar]
- 48.Pannabecker TL, Dantzler WH. Three-dimensional architecture of collecting ducts, loops of Henle, and blood vessels in the renal papilla. Am J Physiol Renal Physiol 293: F696–F704, 2007 [DOI] [PubMed] [Google Scholar]
- 49.Pannabecker TL, Dantzler WH, Layton HE, Layton AT. Role of three-dimensional architecture in the urine concentrating mechanism of the rat renal inner medulla. Am J Physiol Renal Physiol 295: F1217–F1285, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pannabecker TL, Henderson CS, Dantzler WH. Quantitative analysis of functional reconstruction reveals lateral and axial zonation in the renal inner medulla. Am J Physiol Renal Physiol 294: F1306–F1314, 2008 [DOI] [PubMed] [Google Scholar]
- 51.Pennell JP, Lacy FB, Jamison RL. An in vivo study of the concentrating process in the descending limb of Henle's loop. Kidney Int 5: 337–347, 1974 [DOI] [PubMed] [Google Scholar]
- 52.Sands JM. Urine concentrating mechanism: measured permeability values in medullary nephron segments and urea transport processes. In: Membrane Transport and Renal Physiology, The IMA Volumes in Mathematics and Its Applications, edited by Layton HE, Weinstein AM. New York: Springer, 2002, p. 193–210 [Google Scholar]
- 53.Sands JM, Knepper MA. Urea permeability of mammalian inner medullary collecting duct system and papillary surface epithelium. J Clin Invest 79: 138–147, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sands JM, Layton HE. The urine concentrating mechanism and urea transporters. In: Seldin and Giebisch's The Kidney: Physiology and Pathophysiology (4th ed.), edited by Alpern RJ, Hebert SC. New York: Elsevier, 2007, p. 1143–1178 [Google Scholar]
- 55.Sands JM, Naruse M, Jacobs JD, Wilcox JM, Klein JD. Changes in aquaporin-2 protein contribute to the urine concentrating defect in rats fed a low-protein diet. J Clin Invest 97: 2807–2814, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Sands JM, Nonoguchi H, Knepper MA. Vasopressin effects on urea and H2O transport in inner medullary collecting duct subsegments. Am J Physiol Renal Fluid Electrolyte Physiol 253: F823–F832, 1987 [DOI] [PubMed] [Google Scholar]
- 57.Sands JM, Nonoguchi H, Knepper MA. Hormone effects on NaCl permeability of rat inner medullary collecting duct segments. Am J Physiol Renal Fluid Electrolyte Physiol 255: F421–F428, 1988 [DOI] [PubMed] [Google Scholar]
- 58.Sasidharan TO, Goyal SP, Chand P, Ghosh PK. The effects of water deprivation and salt load on water conservation efficiency in two Indian desert gerbils. J Comp Physiol B 160: 413–422, 1990 [DOI] [PubMed] [Google Scholar]
- 59.Schnermann J, Chou CL, MA T, Traynor T, Knepper MA, Verkman AS. Defective proximal tubular fluid reabsorption in transgenic aquaporin-1 null mice. Proc Natl Acad Sci USA 95: 9660–9664, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Simionescu N. Cellular aspects of transcapillary exchange. Physiol Rev 63: 1536–1579, 1983 [DOI] [PubMed] [Google Scholar]
- 61.Stephenson JL. Central core model of the renal counterflow system. Kidney Int 2: 85–94, 1972 [DOI] [PubMed] [Google Scholar]
- 62.Stephenson JL, Jen JF, Wang H, Tewarson RP. Convective uphill transport of NaCl from ascending thin limb of the loop of Henle. Am J Physiol Renal Fluid Electrolyte Physiol 268: F680–F692, 1995 [DOI] [PubMed] [Google Scholar]
- 63.Stephenson JL, Wang H, Tewarson RP. Effect of vasa recta flow on concentrating ability of models of the renal inner medulla. Am J Physiol Renal Fluid Electrolyte Physiol 268: F698–F709, 1995 [DOI] [PubMed] [Google Scholar]
- 64.Stephenson JL, Zhang Y, Tewarson R. Electrolyte, urea, and water transport in a two-nephron central core model of the renal medulla. Am J Physiol Renal Fluid Electrolyte Physiol 257: F399–F413, 1989 [DOI] [PubMed] [Google Scholar]
- 65.Thomas SR. Cycles and separations in a model of the renal medulla. Am J Physiol Renal Physiol 275: F671–F690, 1998 [DOI] [PubMed] [Google Scholar]
- 66.Thomas SR, Wexler AS. Inner medullary external osmotic driving force in a 3-D model of the renal concentrating mechanism. Am J Physiol Renal Fluid Electrolyte Physiol 269: F159–F171, 1995 [DOI] [PubMed] [Google Scholar]
- 67.Verkman AS. Lessons on renal physiology from transgenic mice lacking aquaporin water channels. J Am Soc Nephrol 10: 1126–1135, 1999 [DOI] [PubMed] [Google Scholar]
- 68.Wade JB, Lee AJ, Ecelbarger CA, Mitchell C, Bradford AD, Terris J, Kim GH, Knepper MA. UT-A2: a 55-kDa urea transporter in thin descending limb whose abundance is regulated by vasopressin. Am J Physiol Renal Physiol 278: F52–F62, 2000 [DOI] [PubMed] [Google Scholar]
- 69.Wang X, Thomas SR, Wexler AS. Outer medullary anatomy and the urine concentrating mechanism. Am J Physiol Renal Physiol 274: F413–F424, 1998 [DOI] [PubMed] [Google Scholar]
- 70.Wang X, Wexler AS. The effects of collecting duct active NaCl reabsorption and inner medulla anatomy on renal concentrating mechanism. Am J Physiol Renal Fluid Electrolyte Physiol 270: F900–F911, 1996 [DOI] [PubMed] [Google Scholar]
- 71.Weast RC. (Editor). CRC Handbook of Chemistry and Physics (55th ed.). Cleveland, OH: CRC, 1974 [Google Scholar]
- 72.Weinstein AM. A mathematical model of the inner medullary collecting duct of the rat: pathways for Na and K transport. Am J Physiol Renal Physiol 274: F841–F855, 1998 [DOI] [PubMed] [Google Scholar]
- 73.Weisser F, Lacy FB, Weber H, Jamison RL. Renal function in chinchilla. Am J Physiol 219: 1706–1713, 1970 [DOI] [PubMed] [Google Scholar]
- 74.Wesson LG, Anslow WP. Effect of osmotic and mercurial diuresis on simultaneous water diuresis. Am J Physiol 170: 255–269, 1952 [DOI] [PubMed] [Google Scholar]
- 75.Wexler AS, Kalaba RE, Marsh DJ. Three-dimensional anatomy and renal concentrating mechanism. I. Modeling results. Am J Physiol Renal Fluid Electrolyte Physiol 260: F368–F383, 1991 [DOI] [PubMed] [Google Scholar]
- 76.Wexler AS, Kalaba RE, Marsh DJ. Three-dimensional anatomy and renal concentrating mechanism. II. Sensitivity results. Am J Physiol Renal Fluid Electrolyte Physiol 260: F384–F394, 1991 [DOI] [PubMed] [Google Scholar]
- 77.Yang B, Bankir L, Gillespie A, Epstein CJ, Verkman AS. Urea-selective concentrating defect in transgenic mice lacking urea transporter UT-B. J Biol Chem 277: 10633–10637, 2002 [DOI] [PubMed] [Google Scholar]
- 78.Zhang W, Edwards A. Transport of plasma proteins across vasa recta in the renal medulla. Am J Physiol Renal Physiol 281: F278–F492, 2001 [DOI] [PubMed] [Google Scholar]