Hyperfiltration and inner stripe hypertrophy may explain findings by Gamble and coworkers

Abstract

Simulations conducted in a mathematical model were used to exemplify the hypothesis that elevated solute concentrations and tubular flows at the boundary of the renal outer and inner medullas of rats may contribute to increased urine osmolalities and urine flow rates. Such elevated quantities at that boundary may arise from hyperfiltration and from inner stripe hypertrophy, which are correlated with increased concentrating activity (Bankir L, Kriz W. Kidney Int. 47: 7–24, 1995). The simulations used the region-based model for the rat inner medulla that was presented in the companion study (Layton AT, Pannabecker TL, Dantzler WH, Layton HE. Am J Physiol Renal Physiol 298: F000–F000, 2010). The simulations were suggested by experiments which were conducted in rat by Gamble et al. (Gamble JL, McKhann CF, Butler AM, Tuthill E. Am J Physiol 109: 139–154, 1934) in which the ratio of NaCl to urea in the diet was systematically varied in eight successive 5-day intervals. The simulations predict that changes in boundary conditions at the boundary of the outer and inner medulla, accompanied by plausible modifications in transport properties of the collecting duct system, can significantly increase urine osmolality and flow rate. This hyperfiltration-hypertrophy hypothesis may explain the finding by Gamble et al. that the maximum urine osmolality attained from supplemental feeding of urea and NaCl in the eight intervals depends on NaCl being the initial predominant solute and on urea being the final predominant solute, because urea in sufficient quantity appears to stimulate concentrating activity. More generally, the hypothesis suggests that high osmolalities and urine flow rates may depend, in large part, on adaptive modifications of cortical hemodynamics and on outer medullary structure and not entirely on an extraordinary concentrating capability that is intrinsic to the inner medulla.

in a companion paper (26), henceforth called “study 1,” we formulated a region-based mathematical model of the urine concentrating mechanism (UCM) in the inner medulla (IM) of the rat kidney. In that model, the structural organization of the IM (32) is represented by means of two concentric regions: an inner region that represents a collecting duct (CD) cluster, and an outer region that represents the tubules and vessels that surround and separate CD clusters. The positions of descending thin limbs (DTL), ascending thin limbs, descending vasa recta (DVR), and ascending vasa recta are represented by assigning tubules and vasa recta (or portions thereof) to the appropriate concentric regions.

Although the region-based model of the IM can produce a significant concentrating effect, it does not explain the very high urine osmolalities that have sometimes been found in rats, and it does not explain how moderately concentrating rats can achieve moderately high urine flow rates (see discussion in study 1). Thus the comparison of the model with physiological experiments suggests that important features of the urine concentrating function may not be represented in the model. It may be that a connection-based model will be needed to faithfully represent the UCM of the IM (see discussion in study 1); it may be that the transport properties that we have assumed will require substantial modification as new experimental data emerge; it may be that a concentrating mechanism much different from the ones we have proposed (25, 32) will need to be modeled.

In the present study (called “study 2”), however, we consider a hypothesis for a fundamentally different mechanism that, in part, may explain high urine osmolalities and flows. As we pondered the limited concentrating capability and modest urine flow rates predicted by the region-based model, we were intrigued by experiments in rats which indicate that particular sustained conditions, viz., a high-protein diet, water restriction, or administration of antidiuretic hormone (ADH), can all stimulate hyperfiltration in glomeruli and hypertrophy of the inner stripe (IS) of the outer medulla (OM) as well as increased urine concentrating capability (3). Indeed, Bankir et al. (2) hypothesized that hyperfiltration and hypertrophy would alter the tubular fluid flows and solute concentrations that enter the IM in ways that would enhance urine concentrating capability; we will call this the “hyperfiltration-hypertrophy hypothesis.” We were further intrigued by the realization that findings by Gamble and coworkers (12) published in 1934 appear to be consistent with effects of hyperfiltration and hypertrophy that accompany concentrating activity (as explained, below, in results). The concentrating activity found by Gamble and coworkers appears to be activated or enhanced by the supplementary feeding of urea, and that activity diminishes as the amount of supplementary urea is reduced (12). Hendrikx and Epstein (16) also reported concentrating activity arising from feeding of urea.

By means of the region-based model for the IM that was formulated in study 1, we have here in study 2 exemplified in mathematical simulations, and in the context of the experiments by Gamble and coworkers, the hypothesis that the production of a plentiful and highly concentrated urine is attributable, in substantial measure, to hyperfiltration and to an augmented concentrating effect in the IS of the OM, rather than to an extraordinary concentrating capability in the IM.

METHODS AND CONTEXT

The present study is based on the mathematical model of the IM developed in study 1. To represent the effects of varying the amount of urea in a rat's diet, we modified, in plausible ways, the model's assumptions for flows and concentrations in vessels and tubules that enter the IM from the OM; in some cases, we also modified and the transepithelial transport parameters of the inner medullary CD (IMCD). The tubular fluid flows and solute concentrations that enter the IM will be called “boundary conditions.”

The model was used to simulate experiments conducted by Gamble and coworkers (12) in which it was found that less water was required for the excretion of urea and NaCl fed together than was required for the excretion of either urea or NaCl fed separately. These findings were interpreted as evidence for a special role for urea in the UCM, a role described as “an economy of water in renal function referable to urea” (12). In two of the experiments conducted by Gamble and coworkers (12), a supplementary diet containing urea and NaCl was added, in progressive increments or decrements, to a basal maintenance diet; the added urea and NaCl were administered so that the diet of each rat contained a fixed number of osmoles. In one experiment, urea was decreased in the supplementary diet while NaCl was increased; in another, urea was increased while NaCl was decreased. The supplementary diet was administered in eight intervals (called “periods” by Gamble and coworkers), each having a duration of 5 days. The rats' access to water was unrestricted. The composition and amount of urine collected in the last 3 days of each interval were recorded and reported in tabular and/or graphical form (the urine amount was reported in only one experiment; see Table 1 in Ref. 12).

Table 1.

Simulation 1: CD inflow concentrations and resulting urine flow and content

			Urine
	CD Inflow*		Flow rate†
Stage	Na+, mM	Urea, mM	nl/min	ml/day	Total osmolality, mosmol/kgH2O	Na+, mM	Urea, mM	NaCl+Urea, mosmol/kgH2O
1	0.0‡	750.8	0.0581	6.36	2,075	116.1	1,605	1,770
2	39.58	675.7	0.0492	5.38	2,094	129.6	1,543	1,736
3	79.16	600.7	0.0447	4.89	2,031	141.2	1,419	1,636
4	118.7	525.6	0.0451	4.94	1,881	156.0	1,239	1,489
5	158.3	450.5	0.0524	5.73	1,655	181.7	1,013	1,317
6	197.9	375.4	0.0681	7.45	1,404	215.0	772	1,144
7	237.5	300.3	0.0907	9.93	1,186	246.4	554.0	990.8
8	277.1	225.2	0.117	12.8	1,018	273.5	375.7	867.7
9	316.7	150.2	0.145	15.9	893.3	279.3	231.3	738.3
10	356.2	75.08	0.173	18.9	798.3	319.4	111.5	695.9
11	395.8	0.0	0.199	21.8	725.5	341.1	9.2	636.5

^*At each stage, nonreabsorbable (NR) solute is present in collecting duct (CD) inflow at a concentration of 20 mM.

^†Urine flow rate is given in nl·min⁻¹·nephron⁻¹ and in ml·day⁻¹·animal⁻¹.

^‡Although a 0 NaCl content is likely unphysiological, this inflow condition is provided for comparison with the other stages.

We simulated both the experiment in which urea in the supplementary diet was decreased (simulations 1 and 2 in results below) and the experiment in which urea was increased (simulation 3). For each simulation, the specific modifications to boundary conditions and transport properties are described in results. Unlike the experiments by Gamble and coworkers (12) which involved 8 periods, each of our simulations used 11 “stages,” which are differing steady states that correspond to differing boundary conditions; in simulation 2, CD transport properties were also varied. The 11 stages represent an initial state and 10 successive modified states. The initial state (stage 1) and the 10th modified state (stage 11) simulate the endpoints of the range of the experimental results, which correspond to the extrapolated endpoints in Figs. 3 and 4 in the paper by Gamble and coworkers.

Fig. 3.

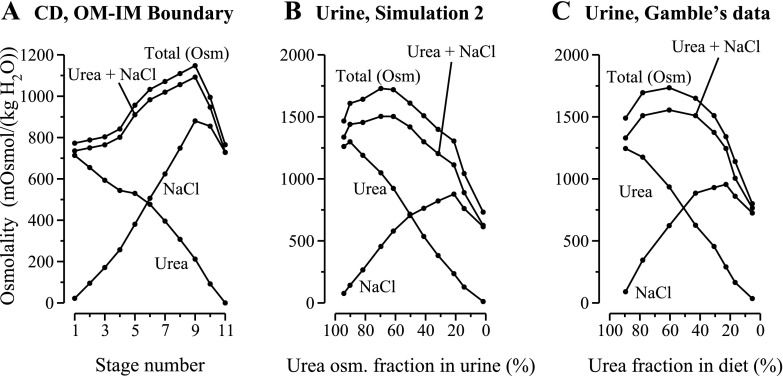
A: CD boundary conditions at the OM-IM boundary for simulation 2 as a function of stage number. B: results from simulation 2: urine composition computed by mathematical model for decreasing urea-to-salt ratio in supplementary diet; multiple parameters, in addition to CD boundary conditions, were modified as a function of stage number. C: experimental results redrawn from Fig. 3 in study by Gamble et al. (12) (same graph as in Fig. 1B). Terms are defined as in Fig. 1. In the simulation, urine flow at maximum osmolality (stage 4) was 0.11 nl·min⁻¹·nephron⁻¹; a corresponding experimental urine flow was not reported by Gamble et al.

Fig. 4.

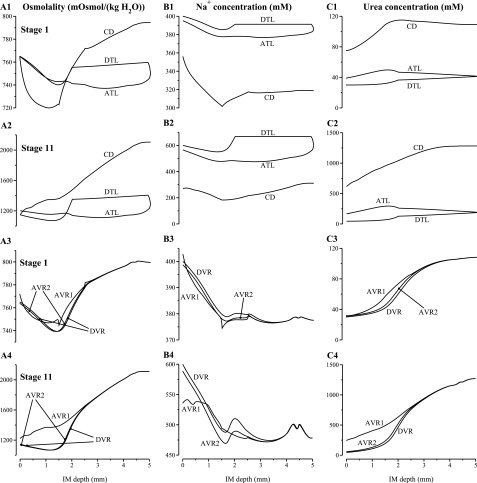
Tubular fluid osmolality, Na⁺ concentration, and urea concentration profiles for the longest loop of Henle, CD, and the longest vasa recta. A1 and A3: results for stage 1 in simulation 2; A2 and A4: results for stage 4 in simulation 2.

RESULTS

Simulation 1: decreasing urea-to-NaCl ratio in supplementary diet.

We first simulated the experiment conducted by Gamble et al. (12) in which the fraction of urea in the supplementary diet was progressively decreased while NaCl was increased [this experiment was recently reproduced in mice by Fenton et al. (11) with results that are in remarkable agreement with those obtained by Gamble et al. (12)]. Because our simulation was conducted by means of a mathematical model of the IM (and that model is neither a whole-animal, nor even a whole-kidney, representation of a rat's NaCl and urea regulation), we adopted a simple protocol in which we varied only IMCD tubular fluid Na⁺ and urea concentrations at the OM-IM boundary; the rate of water inflow into the IMCD, the boundary conditions for DTLs and DVR at the OM-IM boundary, and all transmural transport parameters were set to the base-case values given in Tables 1 and 2 of study I. In the IMCD tubular fluid at the OM-IM boundary (henceforth called “IMCD inflow”), the concentration of Cl⁻ was assumed to be equal to that of Na⁺; and the concentration of nonreabsorbable (NR) solute was maintained at a fixed level of 20 mM (with an osmotic coefficient of 1.84, because it was assumed to consist predominantly of KCl) (4, 35, 42).

Table 2.

Parameters varied in simulation 2

Parameter	Stage 1	Stage 2	Stage 3	Stage 4	Stage 5	Stage 6	Stage 7	Stage 8	Stage 9	Stage 10	Stage 11
CD inflow rate, percent change*	10%	10%	15%	25%	15%	5%	−5%	−15%	−25%	−20%	−10%
Boundary tubular fluid osmolality, percent change*	+1%	+3%	+5%	+10%	+25%	+35%	+40%	+45%	+50%	+30%	0%
Initial CD Pf, ×10−5 cm/s	460	460	460	460	460	460	300	400	400	200	200
CD PNa, ×10−5 cm/s	0.5	0.5	0.5	0.5	0.75	1.0	1.0	1.0	1.0	1.0	1.0
IM depth where CD Purea changes, (xCD), mm	2.25	2.25	2.00	1.75	1.75	1.75	1.50	1.50	1.50	1.75	2.25
CD Purea exponential growth rate	9.0	7.5	6.0	3.0	3.0	2.0	2.0	2.0	1.0	3.0	9.0
CD Na+ Vmax, percent change*	−30%	−40%	−40%	−30%	−10%	0%	+10%	+10%	+10%	+10%	0%

P_f, P_Na, P_urea, water permeability, sodium permeability, urea permeability, respectively; V_max, maximum transport rate; IM, inner medulla.

^*Relative to base-case value.

The IMCD inflow Na⁺ and urea concentrations were varied by increasing Na⁺ concentration stepwise by 10% for 10 steps while decreasing urea concentration stepwise for each of those steps. Each concentration decrease in urea was calculated so that urea's contribution to tubular fluid osmolality was reduced by the same amount as increased Na⁺ and Cl⁻ concentrations increased tubular fluid osmolality; thus, by this means, the CD inflow fluid osmolality was maintained at the base-case value of 765.1 mosmol/kgH₂O. The stages of the simulation extended from an initial stage 1 to a final stage 11; the 10 step increases in Na⁺ concentration were applied to obtain the results reported in stages 2–11.

Table 1 summarizes key simulation data and predictions: IMCD Na⁺ and urea inflow concentrations and the urine flow rates, solute concentrations, and osmolalities. In Fig. 1A, the portions of urine osmolality arising from NaCl and urea separately, the osmolality portion from NaCl and urea taken together, and the total osmolality arising from these solutes and from the NR solute are plotted. Note that these quantities are plotted as a function of the corresponding percentage of urine osmolality arising from urea, and not as a function of urea percentage in the supplementary diet as in Ref. 12: because the relationship between diet and IMCD inflow content is unknown, the content of the supplementary diet is not a suitable independent variable for the simulation results. The dots on the curves in Fig. 1A correspond to the 11 simulation stages, but some dots are nearly superimposed at urine urea osmolality percentages that are near 100%; therefore, 11 distinct dots cannot be distinguished in each curve of Fig. 1A.

Fig. 1.

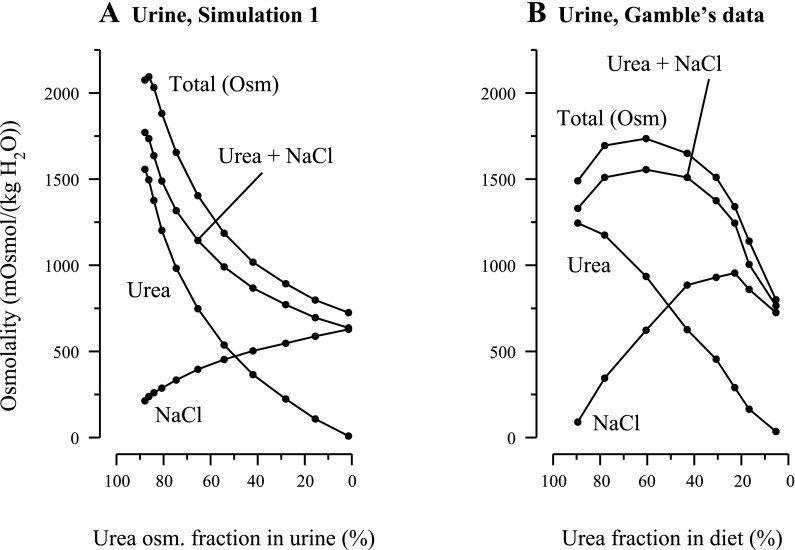
A: results for simulation 1: urine composition computed by mathematical model as a function of fractional contribution of urea to osmolality in urine. To represent a decreasing urea-to-salt ratio in a supplementary diet, the tubular fluid urea and NaCl concentrations at the outer medulla (OM)-inner medulla (IM) boundary were the only parameters that were modified [total osmolality collecting duct (CD) inflow boundary was fixed at a constant value; see details in main text]. B: experimental findings redrawn from Fig. 3 in study by Gamble et al. (12). Urea, portion of osmolality arising from urea; NaCl, portion of osmolality arising from NaCl; Urea+NaCl, portion of osmolality arising from urea and NaCl, taken together; Total (Osm), total osmolality arising from urea, NaCl, and nonreabsorbed solute. In the simulation, urine flow at maximum osmolality was 0.04492 nl·min⁻¹·nephron⁻¹ (stage 2). Urine flow for the corresponding experiment was not reported by Gamble et al. The results in A may be compared with the experimental findings in B and contrasted with the simulation results in Fig. 3B.

As simulated IMCD inflow Na⁺ concentration increased from 0 in stage 1 to 39.58 mM in stage 2, urine osmolality increased from 2,075 to 2,094 mosmol/kgH₂O. Urine osmolality increased because the increased availability of Na⁺ in the early IMCD allowed more Na⁺ to be actively pumped into the interstitium, and this absorbed Na⁺ was accompanied by substantial water absorption from the IMCD to maintain near osmotic equilibrium of IMCD tubular fluid and adjacent interstitial fluid. The resulting reduction in the flow rate of IMCD tubular fluid lowered the load on the IM concentrating mechanism and thereby promoted increased urine osmolality. After the maximum urine osmolality of 2,094 mosmol/kgH₂O was attained at stage 2, further increases in IMCD inflow Na⁺ concentration, accompanied by corresponding decreases in IMCD inflow urea concentration, resulted in successive urine osmolality decreases. These osmolality decreases resulted from decreased urea concentrations in IMCD tubular fluid, which resulted in a reduced urea absorption rate from the IMCD. In the mathematical model, which represents a solute-separation, solute-mixing UCM (see study 1 and Refs. 25 and 32), the reduced urea absorption rate resulted in decreased Na⁺ absorption from loops of Henle and thus reduced interstitial osmolality, reduced water absorption from the IMCD, and reduced IMCD tubular fluid osmolality.

Some aspects of the predictions of simulation 1 are qualitatively similar to the findings of Gamble and coworkers that were exhibited in Fig. 3 of Ref. 12; the urine osmolalities and solute concentrations from that figure were redrawn by us and are shown in Fig. 1B. In both the simulation and the experiment, the urine osmolality initially increased, reached a maximum value, and then decreased, although the initial increase in the model urine is much smaller than in the experiment. Also, urine urea concentration (and thus its contribution to osmolality) decreased monotonically in both, and excepting cases where the urea concentration in urine was nearly zero, urine Na⁺ concentration increased monotonically in both.

Despite the similarities between the model simulations and the findings by Gamble and coworkers (12), there are significant differences. First, in the in vivo experiments corresponding to simulation 1, Gamble and coworkers measured a maximum urine Na⁺ concentration of ∼500 mM when the urine NaCl-to-urea osmolality ratio was ∼4:1, and a maximum urine osmolality of ∼1,700 mosmol/kgH₂O when the urine NaCl-to-urea osmolality ratio was ∼2:3. Our model predicts that urine Na⁺ concentration reaches its maximum of 341 mM when IMCD inflow consists entirely of NaCl and when the model urine NaCl-to-urea osmolality ratio is ∼100:1; the model attains a maximum urine osmolality of 2,094 mosmol/kgH₂O at a urine NaCl-to-urea osmolality ratio of nearly 1:6. In stages 2 and 3, where the model urine osmolality was among the highest, urine flow rates were predicted to be 0.0492 and 0.0447 nl·min⁻¹·nephron⁻¹, which correspond to amounts of 5.38 and 4.89 ml/day, consistent with measurements reported by Atherton et al. (1). Although Gamble et al. did not report urine flow rates for this case in Ref. 12, Fenton et al. (11), who conducted experiments in mice, reported a urine flow of 5 ml·day⁻¹·mouse⁻¹ (Fig. 1A, second data point of “Wild-type” in Ref. 11) which corresponds to a urine flow of ∼0.14 nl·min⁻¹·nephron⁻¹ in rats (based on 12,000 nephrons/mouse kidney) (5). That flow rate is more than twice that predicted in stages 2 and 3 of simulation 1.

Simulation 2: decreasing urea-to-NaCl ratio in supplementary diet, revisited.

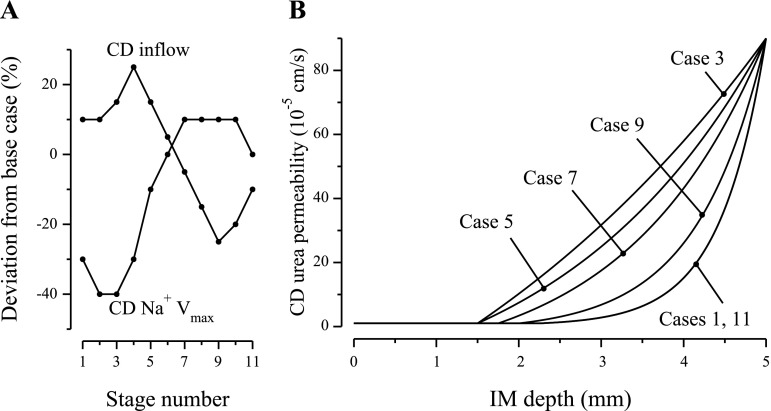
In an effort to reconcile the differences between the results of simulation 1 and the experimental findings of Gamble et al. (12), a second simulation was conducted. In addition to varying the urea-to-Na⁺ concentration ratio in IMCD inflow, we also varied IMCD inflow tubular fluid osmolality, IMCD tubular fluid inflow rate, IMCD water permeability, IMCD Na⁺ permeability, IMCD maximum active Na⁺ transport rate (V_max,Na⁺), and the axial IMCD urea permeability profile. Moreover, DTL and DVR inflows and osmolality were increased by the same percentages that IMCD inflow rate and osmolality were increased, although in the DTL and DVR inflows the proportions of Na⁺ to urea were not modified from the base case. Using an informal optimization procedure, we selected parameter sets that were within physiological ranges, that yielded model predictions consistent with measurements in experiments by Gamble et al., and that were consistent with a solute-separation, solute-mixing hypothesis of the rat UCM (25). Parameter values for the 11 stages of the simulation are shown in Table 2. The IMCD fluid inflow rate and the maximum Na⁺ transport rate from the IMCD are shown in Fig. 2A. The IMCD axial urea permeability profiles are shown in Fig. 2B.

Fig. 2.

Selected parameters used in simulation 2 plotted as a function of stage number. A: rate of fluid entry into the inner medullary collecting duct (IMCD) and rate of maximum Na⁺ transport (V_max) from IMCD. B: IMCD urea permeability as a function of IM depth.

Key simulation results are given in Table 3, which contains the assumed urea and Na⁺ concentrations of the IMCD inflow and the predicted urine flow rates, solute concentrations, and osmolalities. Figure 3A shows the IMCD inflow osmolality and the contributions of NaCl and urea to that osmolality. Figure 3B shows the urine osmolality portions arising from NaCl, urea, NaCl and urea taken together, and from all three model solutes (i.e., Na⁺, urea, and NR), plotted as functions of the urea osmolality percentage in urine.

Table 3.

Simulation 2: CD inflow conditions and resulting urine flow and content

				Urine
	CD Inflow*			Flow rate†
Stage	Na+, mM	Urea, mM	Osmolality, mosmol/kgH2O	nl/min	ml/day	Total osmolality, mosmol/kgH2O	Na+, mM	Urea, mM	NaCl+Urea, mosmol/kgH2O
1	11.99	735.6	772.8	0.151	16.5	1,467	41.40	1,300	1,337
2	51.78	675.1	788.1	0.119	13.0	1,609	76.96	1,339	1,440
3	93.10	611.8	803.4	0.114	12.5	1,641	144.4	1,226	1,455
4	139.8	560.8	841.6	0.108	11.8	1,729	247.3	1,081	1,504
5	206.8	546.2	956.4	0.118	12.9	1,719	314.8	951.8	1,502
6	275.2	491.6	1,032.9	0.130	14.2	1,611	382.4	737.1	1,419
7	339.1	407.8	1,071.1	0.112	12.3	1,508	414.7	552.2	1,299
8	406.9	316.8	1,109.4	0.112	12.3	1,399	447.1	393.6	1,204
9	478.5	218.5	1,147.7	0.103	11.3	1,305	476.6	242.9	1,113
10	464.6	9.468	994.6	0.119	13.0	1,043	413.8	132.0	889.4
11	395.8	0.0	765.1	0.148	16.2	732.2	333.6	11.3	624.8

^*At each stage, NR solute is present in CD inflow at a concentration of 20 mM multiplied by the percentage osmolality increase indicated in Table 2.

^†Urine flow rate is given in nl·min⁻¹·nephron⁻¹ and in ml·day⁻¹·animal⁻¹.

The first five stages in simulation 2, which are indicated by the first five dots, counting from the left-hand side, in Fig. 3, A and B, correspond to results by Gamble et al. (12) in which the rats were fed a supplementary diet that had decreasing urea content but that was still rich in urea relative to the basal maintenance diet. These experimental results were displayed graphically in about the left-hand-side half of the left-hand-side panel of Fig. 3, in Ref. 12, and they are redrawn by us in our Fig. 3C. The dots in Fig. 3C correspond to the eight periods in the experiment by Gamble et al. We hypothesize that during the first three experimental periods, OM hypertrophy gradually increased, and that as hypertrophy increased, so did single-nephron glomerular filtration rate (SNGFR) and OM concentrating capability. Thus, in the model, tubular fluid osmolality at the OM-IM boundary (in DTLs, DVR, and the IMCD) was increased, from the near base-case value, in stage 1 (+1%), to a maximum that was +25% higher than the base case, for stage 5. If SNGFR increases in vivo, a likely consequence of a higher OM concentrating capability is that more water is reabsorbed from OM DTLs, DVR, and CDs. These two competing factors (increased OM concentrating capability and hyperfiltration) suggested the model assumption that boundary inflow rate increased from 10% higher than base case in stage 1, to a maximum of +25% in stage 4, and then decreased to +15% in stage 5. Model urine osmolality reached a maximum of 1,729 mosmol/kgH₂O in stage 4, and a similarly high value of 1,719 mosmol/kgH₂O in stage 5. These urine osmolalities correspond to tubular fluid osmolality increases along the IMCD of ∼105 and 79.7% relative to the IMCD inflow osmolalities of 841.6 and 956.4 mosmol/kgH₂O, respectively. We assumed that IMCD transport properties varied in response to changes in NaCl and urea concentrations and to IMCD water load; see Table 2 for corresponding model parameters.

Figure 4 shows tubular fluid osmolality, Na⁺ concentration, and urea concentration profiles for the longest loop of Henle, CD, and the longest vasa recta for stage 1 (at the beginning of the experiment) and stage 4 (at which the highest urine osmolality was attained). In stage 1, CD inflow Na⁺ concentration was set to be low at 11.77 mM (see Table 1). As a result, CD tubular fluid Na⁺ concentration and active Na⁺ reabsorption from the CD were low, compared with other stages, throughout the IM (see Fig. 4B1). That resulted in a rapid fall in interstitial fluid Na⁺ concentration near the papillary tip (Fig. 4B3), despite the larger Na⁺ efflux from the loop prebends (compare Fig. 4, B1 and B2), because the number of remaining CDs exceeds that of remaining loops at the papillary tip (see Fig. 2 in Ref. 26). It is also noteworthy that in stage 1, the CD tubular fluid osmolality generally increased, except in the axial region ∼1–1.5 mm from the OM-IM boundary. That drop in CD fluid osmolality occurred as the two regions merged, which resulted in a significant decrease in the urea concentration and osmolality of the CD cluster interstitial fluid (see Fig. 4, A1 and C1), and, consequently, in water secretion into the CD. In stage 4, where the interstitial fluid urea concentration difference between the two regions is smaller, the CD cluster fluid osmolality did not exhibit a significant decrease when the two regions merged; thus, water was not secreted into the CD lumen and CD tubular fluid osmolality increased throughout the IM.

In the next four stages (stages 6–9), we assumed that OM hypertrophy continued to increase while urea in the supplementary diet progressively decreased. Thus IMCD inflow osmolality and the osmolality in DTLs and DVR at the OM-IM boundary were gradually increased to +50% above base case. However, as the urea content in the diet was decreased, we assumed that hyperfiltration also decreased. To simulate that effect, the IMCD inflow rate, and the inflow rates in DTLs and DVR, were gradually decreased to −25% below base case. Despite increased osmolality at the OM-IM boundary, urine osmolality decreased, from 1,611 in stage 6 to 1,305 mosmol/kgH₂O in stage 9. The erosion of the model's IM concentrating capability resulted from progressively reduced availability of urea, which is an essential component of the solute-separation, solute-mixing UCM. The rate of IMCD urea inflow decreased from 0.130 in stage 6 to 0.103 pmol·min⁻¹·nephron⁻¹ in stage 9, which correspond to 14.2 and 11.3 ml·day⁻¹·animal⁻¹, respectively, and the urea concentration in IMCD inflow decreased from 491.6 to 218.5 mM.

In stages 10 and 11, we assumed that, as a result of low urea content in the diet, both OM hypertrophy and SNGFR decreased. Thus boundary fluid osmolality in the IMCD, DTLs, and DVR was reduced to +30% above base case in stage 10 and to 0% in stage 11; corresponding boundary inflows were changed to 20 and 10% below base case, respectively (see Fig. 2A). In stage 11, the model predicted a urine osmolality of 732.2 mosmol/kgH₂O. The correspondence between simulation stages 6 through 11 and experimental periods 4 through 8 is illustrated in Figs. 3B and 3C.

A reasonable inference from simulation 2 is that the development of OM hypertrophy and hyperfiltration, as a response to urea-induced concentrating activity, and subsequent erosion of OM hypertrophy and hyperfiltration as urea in the diet was decreased, provides a plausible explanation for the observations of Gamble and coworkers (12).

Simulation 3: increasing urea-to-salt ratio in supplementary diet.

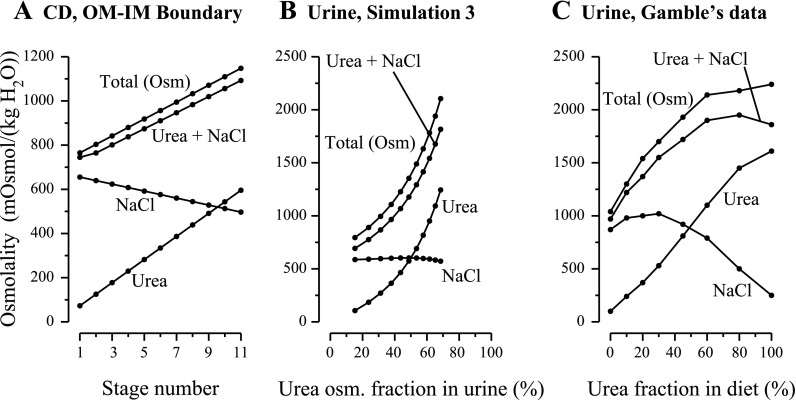
In a separate experiment by Gamble and coworkers (12), rats were fed a diet in which the amount of urea was progressively increased while NaCl was decreased. Unlike the cases of decreasing urea in the diet that were represented in simulations 1 and 2, urine osmolality was found by Gamble et al. to be monotonically increasing as the amount of urea in diet was increased. In Ref. 12, these results were summarized in Table 1 and in the right-hand panel of Fig. 4. Some of these results were redrawn by us and are shown in Fig. 5C.

Fig. 5.

A: CD boundary conditions at the OM-IM boundary for simulation 3 as a function of stage number. B: results from simulation 3: urine composition computed by mathematical model. C: experimental results redrawn from Fig. 4 in study by Gamble et al. (12). Terms are defined as in Fig. 1. In the simulation, urine flow at maximum osmolality was 0.12 nl·min⁻¹·nephron⁻¹; the experiment by Gamble et al., the corresponding urine flow was 0.13 nl·min⁻¹·nephron⁻¹.

In the simulation of this experiment, we used model changes (relative to the base case) that were similar to the simple changes used in simulation 1. At the beginning of the experiment, when for 5 days the rats were fed no urea, the IMCD inflow urea concentration was likely low. Thus we set the IMCD boundary conditions to be those in simulation 1, stage 10, which yielded urine composition that approximates values reported in Ref. 12 for the first stage in simulation 2. In the final stage (i.e., stage 11), which corresponds to the diet with the highest urea content, we hypothesize that maximal hypertrophy was achieved, and that increased IS thickness increased the concentrating capability of the OM and resulted in the delivery of tubular fluid to the IMCD that had a significantly elevated osmolality. Thus, in stage 11 of the simulation, we set the IMCD inflow concentrations of Na⁺, urea, and NR solute to be 50% higher than base-case values. For the intermediate stages (i.e., stages 2–10), IMCD inflow solute concentrations were obtained by linearly interpolating those concentrations between those prescribed for stages 1 and 11. Thus, for example, in stage 3, IMCD inflow urea concentration was given by (75.08 × 8 + 614.1 × 2)/10 = 156.1 mM. IMCD inflow osmolality and the contributions of NaCl and urea to that osmolality are shown in Fig. 5A as functions of stage number. The IMCD water inflow rate was set to base-case value in stage 1, and linearly increased to 30% above base-case value in stage 11. DTL and DVR water inflow rates were left unchanged. Solute concentrations for the DTLs and DVR at the OM-IM boundary were set to base-case values in stage 1, and linearly increased to 50% above base-case value in stage 11. The same increase (base-case value to 50% above) was applied to the IMCD maximum active Na⁺ transport rate (V_max,Na⁺).

Key simulation results are given in Table 4, which contains the assumed urea and Na⁺ concentrations of the IMCD inflow and the predicted urine flow rates, solute concentrations, and osmolalities. Figure 5B shows the urine osmolality portions arising from NaCl, urea, NaCl and urea taken together, and from all three model solutes (i.e., Na⁺, urea, and NR), plotted as functions of the urea osmolality percentage in urine. Figure 6 shows tubular fluid osmolality, Na⁺ concentration, and urea concentration profiles for the longest loop of Henle, the CD, and the longest vasa recta for stages 1 and 11 (the beginning and end stages). In stage 1, CD inflow Na⁺ concentration was set to a high value of 356.2 mM. The resulting CD Na⁺ active reabsorption was sufficiently high that CD tubular fluid osmolality decreased along the initial IM. The concentration of urea in IMCD inflow increased from 75.08 mM in stage 1 to 614.1 mM in stage 11 (i.e., by a factor of 8.18); model urine osmolality increased from 794.5 to 2,104 mosmol/kgH₂O (i.e., by a factor of 2.65). Because we have assumed that OM hypertrophy was progressively increasing from stage 1 to stage 11, and because we have assumed that the OM concentrating capability increased with that hypertrophy, tubular fluid osmolality at the OM-IM boundary was increased by 50% in the model from 765.1 in stage 1 to 1,148 mosmol/kgH₂O in stage 11. Thus IM concentrating capability, measured by the increase in IMCD tubular fluid osmolality along the IM, relative to IMCD fluid osmolality at the OM-IM boundary, is negligible in stage 1 and 83.3% in stage 11. That increase in IM concentrating capability arises from the increase in IMCD urea inflow, which increases the urea available to drive Na⁺ absorption from the loops of Henle that reach deep into the IM.

Table 4.

Simulation 3: CD inflow concentrations and resulting urine flow and content

			Urine
	CD Inflow*		Flow rate†
Stage	Na+, mM	Urea, mM	nl/min	ml/day	Total osmolality, mosmol/kgH2O	Na+, mM	Urea, mM	NaCl+Urea, mosmol/kgH2O
1	356.2	75.08	0.173	18.9	794.5	318.8	109.1	692.4
2	347.6	129.0	0.167	18.3	890.3	321.4	190.5	776.2
3	339.0	182.9	0.161	17.6	995.0	324.1	279.1	867.1
4	330.3	236.8	0.155	17.0	1,107	326.3	375.4	964.5
5	321.7	290.7	0.149	16.3	1,227	327.6	479.5	1,068
6	313.1	344.6	0.143	15.6	1,354	327.8	591.8	1,177
7	304.5	398.5	0.138	15.1	1,489	327.0	712.5	1,293
8	295.9	452.4	0.133	14.6	1,632	324.9	841.9	1,414
9	287.2	506.3	0.128	14.0	1,782	321.6	980.0	1,542
10	278.6	560.2	0.124	13.6	1,940	317.0	1,127	1,676
11	270.0	614.1	0.119	13.0	2,104	311.0	1,283	1,817

^*At stage 1, NR solute was present in CD inflow at a concentration of 20 mM and total CD inflow osmolality was 765.7 mosmol/kgH₂O. In each successive stage, NR solute concentration was increased by 1 mM. Thus at stage 11, NR solute concentration is 30 mM, and total osmolality was 1,148 mosmol/kgH₂O.

^†Urine flow rate is given in nl·min⁻¹·nephron⁻¹ and in ml·day⁻¹·animal⁻¹.

Fig. 6.

Tubular fluid osmolality, Na⁺ concentration, and urea concentration profiles for the longest loop of Henle, CD, and the longest vasa recta. A1 and A3: results for stage 1 in simulation 3; A2 and A4: results for stage 11 in simulation 3. Note variation, among panels, in ordinate scalings.

The simpler protocol used in simulation 3 (relative to simulation 2) does not result in the same degree of similarity between Fig. 5, B and C, as that between Fig. 3, B and C. Indeed, three of the data curves in Fig. 5B are concave up, whereas all of the data curves in Fig. 5C are concave down. Nonetheless, the trends and the magnitudes are similar in Fig. 5, B and C, and Fig. 5B could be made more similar to Fig. 5C by means similar to those used in simulation 2. Thus it seems reasonable to assume that the simple modifications to the base-case model that represent the progressive consequences of hypertrophy and hyperfiltration, arising as a result of urea-induced concentrating activity, are a plausible explanation for the findings of Gamble and coworkers (12).

DISCUSSION

Experiments by others in rats have shown that sustained interventions, e.g., elevated protein intake, water restriction, or administration of ADH, result in modifications of renal structure and function in both the cortex and the OM, and in significantly increased urine concentrating capability (2, 3). The modifications include hyperfiltration, in which SNGFR may be increased by ∼50% or more, and hypertrophy of the IS. The hypertrophy involves not only an increase in the axial length of the tubules and vessels of the IS (up to 30%), but also a significant thickening of thick ascending limb (TAL) cells, and increased Na⁺-K⁺-ATPase activity in TAL cells (by ∼50% or more).

The increased urine concentrating capability that accompanies these changes should be distinguished from that which arises from an acute intervention, e.g., an infusion of ADH (as in Ref. 15) or a 24-h interval of water deprivation. For example, in an experiment conducted by Bouby et al. (7), Sprague-Dawley rats were maintained on either a low-protein diet or a high-protein diet for 6 wk; water was consumed ad libitum. After the 6-wk interval, both groups of rats were excreting concentrated urine having a mean osmolality of ∼1,600 mosmol/kgH₂O. When both groups were deprived of water for 24 h, the mean urine osmolality of those rats on the low-protein diet increased to ∼1,900 mosmol/kgH₂O, whereas the mean urine osmolality of those rats on the high-protein diet increased to ∼2,900 mosmol/kgH₂O. Thus acute water deprivation resulted in a much higher urine osmolality in those rats fed a high-protein than in those fed a low-protein diet. Analysis of kidneys from the two groups revealed marked IS hypertrophy and evidence of hyperfiltration (significantly increased surface area of deep glomeruli) of those rats fed the high-protein diet, relative to the low-protein controls.¹ These results suggest that the animal's concentrating capability can be strongly influenced by its dietary history.

Likely consequences of hyperfiltration and hypertrophy include increased rates of the fluid flows in DTLs, DVR, and CDs, from the OM into the IM; altered solute concentrations in these flows; and significantly elevated osmolalities in these flows. Such changes in OM-IM boundary conditions have the potential to significantly affect the IM concentrating mechanism and the quantity and composition of urine. Indeed, Bankir et al. (2) pointed out that the greater length of thick and thin limbs of Henle in a hypertrophied IS, in conjunction with a thickened TAL epithelium having elevated metabolic activity, would likely improve the performance of the OM concentrating mechanism and result in a higher interstitial osmolality at the boundary between the OM and the IM. However, no mathematical modeling studies have examined the impact that such changes might have on the UCM of the IM. Although some consideration has been given to how assumptions about OM function impact IM function (41, 44), most modeling studies have made generally consistent and comparable assumptions about the content and rate of tubular and vascular flow from the OM into the IM, without a systematic consideration of the impact of variability of OM function on model results (17, 20, 25, 28, 37).

In the modeling study presented herein, we have sought to assess, by means of model simulations involving modifications of OM-IM boundary conditions, the potential impact of hyperfiltration and OM hypertrophy on IM concentrating capability and urine flow. It should be borne in mind that this model study is an exemplification of the hyperfiltration-hypertrophy hypothesis rather than a standard parameter study. Our simulations can be considered to be representations of one hypothesis that, perhaps among many other possible hypotheses, proposes a plausible mechanism which may explain, or explain in part, the extraordinary capability of the IM in some mammals to produce highly concentrated urine.

This model study is not a comprehensive instance of physiological prediction: the model does not encompass an explicit representation of OM function, nor of glomerular filtration, absorption from the proximal tubule, or modifications to tubular fluid in the distal convoluted tubule and cortical CD. Moreover, the model is in most respects a schematic representation of IM function, inasmuch as it does not contain explicit models of the cells that make up tubular and vascular walls, it does not represent detailed transmural transport in those walls, it does not represent the cells, spaces, and hyaluronan of the interstitium, and it does not represent the peristaltic contractions of the pelvic wall and the resulting periodic flows in the renal tubules of the IM. The model, which assumes a solute-separation, solute-mixing mechanism for concentrating urine, predicts, within the context of the model assumptions and limitations, that alterations in boundary conditions might result in larger urine flows and in higher urine osmolalities than would be the case with boundary conditions like those that have typically been used in modeling studies. It seems likely that any of the mathematical models that have shown a concentrating effect in the IM (e.g., Refs. 17, 20, 25, 28, 37) would also have their concentrating capabilities augmented by the OM-IM boundary conditions that appear to accompany hyperfiltration and IS hypertrophy, since the concentrating process would do its work, by about the same factor as before, on the more concentrated tubular fluid entering from the OM.

The OM-IM boundary conditions that have been used in mathematical models have been influenced by several considerations, including model calculations for the OM concentrating mechanism (23, 28, 38, 43, 44) and tissue slice studies (15, 22, 39). Some experimental studies have been interpreted to indicate that at each level of the IM, all of the structures and spaces are in near osmotic equilibrium (13, 14). However, model calculations can be no better than the assumptions on which they are based. Tissue-slice studies provide gross averages at low spatial resolution; the belief that osmotic differences among IM structures are small at each level is largely based on micropuncture studies of tubular fluid content near the papilla. Moreover, findings by Wade et al. (40) in the rat and by Zhai et al. (46) in the mouse suggest that in the IS, the descending limbs of short loops of Henle express essentially no aquaporin-1 channels. Thus tubular fluid in these limbs may be dilute relative to flows at the same medullary level in some other tubules and vessels. Similarly, the descending limbs of loops that turn in the upper IM also appear to express no aquaporin-1 (31), and thus these limbs may contain tubular fluid that differs from the osmolality of flows in other structures at the same medullary level. Recent studies in IM functional anatomy indicate that the IM has a complex three-dimensional structure in which tubules and vessels are organized within and around CD clusters. Moreover, several anatomically distinct zones can be distinguished along the corticomedullary axis of the IM, and four distinct subpopulations of loops of Henle have been identified (32). These sundry considerations suggest that the complex three-dimensional structures of the IM may harbor as yet undetected lateral inhomogeneity in tubular fluid solute concentrations and osmolality. Such lateral inhomogeneity could conceal elevated tubular osmolalities at the OM-IM boundary (6).

In the experiments by Gamble at al. (12) [notably, the experiment in which urea in the supplementary diet was progressively increased while NaCl was decreased (Table 1 and Fig. 4 in Ref. 12)], a correlation was found between increased urea in the diet and elevated urine osmolality. Also, as can be reasonably expected, the proportion of urea relative to NaCl in urine was larger in those rats fed a larger proportion of urea relative to NaCl. It seems reasonable to assume that increased urea consumption resulted in elevated concentrations of circulating ADH (as reported in experiments in humans by Zerbe and Robinson) (45) and in increased urine concentrating activity, although experiments that used very different protocols than those used by Zerbe and Robinson suggest that the capability of urea to elicit that response in rats may be limited (18, 29). Moreover, the causal link between urea consumption on the one hand, and, on the other hand, elevated ADH and urine concentrating activity, is not clear.

It has long been known, however, that urea in the diet can promote renal hypertrophy in rats, although the effect of urea is less than that obtained when supplementary protein is added to the diet (30). Thus it may well be that urea stimulates hyperfiltration and hypertrophy, and it seems reasonable to assume that these effects are mediated or accompanied by elevated circulating ADH. A consequence of elevated ADH will be increased water and urea permeabilities of the IMCD (21, 34), which promote the absorption of water and urea from the IMCD. Moreover, in the experiment where urea in the diet was increased (Fig. 4 in Ref. 12), it may be that elevated circulating ADH was a generally chronic condition over several weeks, inasmuch as the duration of the study was 40 days, and in the final 15 days, urea was >60% of the supplementary portion of the diet. Experiments have indicated that sustained elevated ADH would result in both hyperfiltration and hypertrophy of the IS and also in elevated NaCl transport by TALs (2, 3). Thus, as hypothesized in results, these modifications in cortical and OM function would have consequences for IM function that may explain patterns in the data gathered by Gamble et al. (12) and by Fenton et al. (11).

The model simulations described herein, the accumulating evidence that the IM is an intricate, highly complex entity (32), and the compelling inferences from the experimental studies that have demonstrated hyperfiltration and hypertrophy (2, 3), suggest that consideration should be given to the hypothesis that sustained challenges (e.g., water deprivation or modified diet) or stimuli (e.g., administration of ADH) lead to functional changes in the cortex and the OM that significantly affect IM function and may thereby contribute to the capability to reach urine osmolalities consistent with the highest osmolalities that have been measured. Indeed, if the OM has the capability to greatly augment the concentration of CD flow into the IM, perhaps by as much as 50–100% above values that have been inferred from tissue slice studies or mathematical models (∼600 to ∼900 mosmol/kgH₂O) (15, 23, 24), then the OM may be capable of raising the osmolality of CD tubular fluid at the OM-IM boundary to 1,200 mosmol/kgH₂O, or even to 1,800 mosmol/kgH₂O. Such osmolalities might then be increased along the IMCD by a factor of 2 or 3, to produce concentrations that are consistent with maximum urine concentrations reported in rat and mouse, ∼3,000 and ∼4,000 mosmol/kgH₂O, respectively (9, 10). It should, however, be acknowledged that the issue of oxygen distribution, in particular, the means by which sufficient oxygen is delivered to the TAL cells to support the metabolic demands of their increased Na⁺-K⁺-ATPase activity, remains to be resolved (8).

Manifold physiological experiments and mathematical models have been motivated by the enduring mystery of how some mammals can produce highly concentrated urine (see studies cited in Refs. 19, 27, 33, and 36). Investigators have generally assumed that the resolution of this mystery depends on a more complete understanding of IM function. However, in consideration of the modifications of OM function that can be caused by various stimuli, and the resulting impact on IM function, it seems prudent, before expending more effort in a search for mechanisms intrinsic to the IM that can produce extraordinary concentrating effects, to determine whether modifications in OM-IM boundary conditions contribute significantly to high urine osmolalities. A recapitulation of the Gamble experiments, accompanied by systematic measurements of glomerular filtration and medullary anatomy, might well be illuminating.

GRANTS

This research was supported by National Institutes of Health Grants DK-42091 (to H. E. Layton) and DK-16294 (to W. H. Dantzler); ES-06694 (for the Southwest Environmental Health Sciences Center at the University of Arizona); and by National Science Foundation Grant DMS-0701412 (to A. T. Layton).

DISCLOSURES

No conflicts of interest are declared by the authors.